A&A 377, 161-174 (2001)
DOI: 10.1051/0004-6361:20011083
A. T. Okazaki1,2 - I. Negueruela3
1 -
Faculty of Engineering, Hokkai-Gakuen University, Toyohira-ku,
Sapporo 062-8605, Japan
2 -
Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, UK
3 -
Observatoire de Strasbourg, 11 rue de l'Université, Strasbourg
67000, France
Received 1 June 2001 / Accepted 23 July 2001
Abstract
When applied to Be/X-ray binaries, the viscous decretion disc model,
which can successfully account for most properties of Be stars,
naturally predicts the truncation of the circumstellar disc. The
distance at which the circumstellar disc is truncated depends mainly
on the orbital parameters and the viscosity. In systems with low
eccentricity, the disc is expected to be truncated at the 3:1
resonance radius, for which the gap between the disc outer radius and
the critical lobe radius of the Be star is so wide that,
under normal conditions, the neutron star cannot accrete enough gas
at periastron passage to show periodic X-ray outbursts
(type I outbursts). These systems will display only occasional
giant X-ray outbursts (type II outbursts). On the other hand, in
systems with high orbital eccentricity, the disc truncation occurs at
a much higher resonance radius, which is very close to or slightly
beyond the critical lobe radius at periastron unless the viscosity is
very low. In these systems, disc truncation cannot be efficient,
allowing the neutron star to capture gas from the disc at every
periastron passage and display type I outbursts regularly. In contrast
to the rather robust results for systems with low eccentricity and
high eccentricity, the result for systems with moderate eccentricity
depends on rather subtle details. Systems in which the disc is
truncated in the vicinity of the critical lobe will regularly display
type I outbursts, whereas those with the disc significantly smaller
than the critical lobe will show only type II outbursts
under normal conditions and temporary type I outbursts when
the disc is strongly disturbed. In Be/X-ray binaries, material will be
accreted via the first Lagrangian point with low velocities relative
to the neutron star and carrying high angular momentum. This may
result in the temporary formation of accretion discs during type I
outbursts, something that seems to be confirmed by observations.
Key words: stars: circumstellar matter - emission-line, Be - binaries: close - neutron - X-ray: stars, bursts
Be/X-ray binaries are X-ray sources composed of a Be star and a neutron star. The high-energy radiation is believed to arise owing to accretion of material associated with the Be star by the compact object (see Negueruela 1998; see also Bildsten et al. 1997).
A "Be star'' is an early-type non-supergiant star, which at some time has shown emission in the Balmer series lines (Slettebak 1988, for a review). Both the emission lines and the characteristic strong infrared excess when compared to normal stars of the same spectral types are attributed to the presence of circumstellar material in a disc-like geometry. The causes that give rise to the disc are not well understood. Different mechanisms (fast rotation, non-radial pulsation, magnetic loops) have been proposed, but it is still unclear whether any of them can explain the observed phenomenology on its own. The discs are rotationally dominated and motion seems to be quasi-Keplerian (Hanuschik 1996). However, some kind of global outflow is needed to explain the X-ray emission from Be/X-ray binaries (Waters et al. 1988).
Some Be/X-ray binaries are persistent X-ray sources (see Reig & Roche
1999), displaying low luminosity (
![]() )
at a relatively constant level
(varying by up to a factor of
)
at a relatively constant level
(varying by up to a factor of ![]() 10). On the other hand, most
known Be/X-ray binaries (though this is probably a selection effect)
undergo periods in which the X-ray luminosity suddenly increases by a
factor
10). On the other hand, most
known Be/X-ray binaries (though this is probably a selection effect)
undergo periods in which the X-ray luminosity suddenly increases by a
factor
![]() 10 and are termed Be/X-ray transients.
10 and are termed Be/X-ray transients.
Be/X-ray transients fall within a relatively narrow area in the
![]() /
/
![]() diagram (see Corbet 1986;
Waters & van Kerkwijk 1989), indicating that some mechanism
must be responsible for the correlation. Those systems with
fast-spinning neutron stars do not show pulsed X-ray emission during
quiescence (though non-pulsed radiation could be caused by accretion
on to the magnetosphere) because of the centrifugal inhibition of
accretion (Stella et al. 1986). Systems with more slowly
rotating pulsars show X-ray emission at a level
diagram (see Corbet 1986;
Waters & van Kerkwijk 1989), indicating that some mechanism
must be responsible for the correlation. Those systems with
fast-spinning neutron stars do not show pulsed X-ray emission during
quiescence (though non-pulsed radiation could be caused by accretion
on to the magnetosphere) because of the centrifugal inhibition of
accretion (Stella et al. 1986). Systems with more slowly
rotating pulsars show X-ray emission at a level
![]() erg s-1 when in quiescence. Transients show two
different kinds of outbursts:
erg s-1 when in quiescence. Transients show two
different kinds of outbursts:
Attempts at modelling the X-ray luminosities of Be/X-ray transients
during outbursts have made use of a simple wind accretion model, in
which the neutron star accretes from a relatively fast radial
outflow. The disc of the central Be star is supposed to have a
power-law density distribution
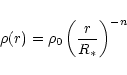 |
(1) |
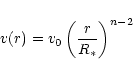 |
(2) |
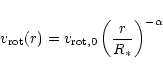 |
(3) |
Accretion is considered to follow the classical Bondi-Hoyle-Littleton
(BHL) approximation. The most important parameter, the relative
velocity between the outflow and the neutron star, can be written as
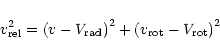 |
(4) |
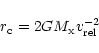 |
(5) |
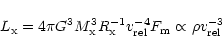 |
(6) |
The use of the BHL approximation implies a number of simplifying
assumptions which are not always easy to justify. For example, it
neglects any effect of the mass-losing star, which for periastron
distances of ![]()
![]() and mass ratios
and mass ratios
![]() seems to be
an excessive simplification. In addition, while the use of the
accretion radius formalism is adequate for an accreting object
immersed in a medium, its application to an outflow characterised by a
relatively small scale-height (H), such as a Be disc, is dubious.
seems to be
an excessive simplification. In addition, while the use of the
accretion radius formalism is adequate for an accreting object
immersed in a medium, its application to an outflow characterised by a
relatively small scale-height (H), such as a Be disc, is dubious.
Moreover, when the low outflow velocities required to explain type II
outbursts are considered, the formalism breaks down completely, since
the capture radius becomes far too large to have any physical
meaning. For example, for
![]() ,
,
![]() ,
which is one order of magnitude larger than the
binary separation. A crude way round this problem is to consider that
the radius of the effective Roche lobe of the neutron star
,
which is one order of magnitude larger than the
binary separation. A crude way round this problem is to consider that
the radius of the effective Roche lobe of the neutron star
![]() should be used instead of
should be used instead of
![]() whenever the
calculated value is larger than
whenever the
calculated value is larger than
![]() (e.g., Ikhnasov
2001). In spite of these shortcomings, the model has been
repeatedly used in an attempt to model lightcurves of Be/X-ray
binaries (Raguzova & Lipunov 1998; Reig et al. 1998)
with only moderate success.
(e.g., Ikhnasov
2001). In spite of these shortcomings, the model has been
repeatedly used in an attempt to model lightcurves of Be/X-ray
binaries (Raguzova & Lipunov 1998; Reig et al. 1998)
with only moderate success.
Beyond the purely formal aspects, one obvious difficulty for the model
is the fact that many Be/X-ray binaries (e.g., A0535+262)
show low-luminosity X-ray emission when they are not in outburst. It
is believed that all Be/X-ray binaries for which centrifugal
inhibition of accretion is not effective display this emission. Motch
et al. (1991) detected A0535+262 on several
occasions at luminosities of ![]()
![]() .
In order to explain this luminosity within the framework
described above and taking into account that optical and infrared
observations do not show any sign of the large variations that would
be associated with a change of several orders of magnitude in the
density of material, enormous relative velocities (of the order of
.
In order to explain this luminosity within the framework
described above and taking into account that optical and infrared
observations do not show any sign of the large variations that would
be associated with a change of several orders of magnitude in the
density of material, enormous relative velocities (of the order of
![]()
![]() )
are needed.
)
are needed.
One further complication comes from the fact that Be/X-ray binaries spend most of their time in the quiescent state described in the previous paragraph and only occasionally show series of outbursts. The model does not offer any explanation as to why there could be a change from quiescence to outburst, unless again very large and sudden changes in the density and velocity of the flow are assumed. Given the changes in relative velocities needed to account for the observed range of X-ray luminosities and the lack of any physical mechanism that could explain them, it is clear that direct accretion from a wind-like outflow is not the best approximation to the way in which matter is fed on to the neutron star.
But the major objection to the model is simply the fact that there
is no observational evidence whatsoever supporting the
existence of such fast outflows. All observations of Be stars imply
bulk outflow velocities smaller than a few
![]() (Hanuschik 2000).
The evidence for rotationally dominated quasi-Keplerian discs around Be
stars is overwhelming (see Hanuschik et al. 1996; Hummel &
Hanuschik 1997; Okazaki 1997), especially owing to the
success of the one-armed global oscillation model to explain V/R
variability in the emission lines of Be stars (Kato
1983; Okazaki 1991, 1996; Papaloizou et al. 1992; Hummel & Hanuschik 1997).
(Hanuschik 2000).
The evidence for rotationally dominated quasi-Keplerian discs around Be
stars is overwhelming (see Hanuschik et al. 1996; Hummel &
Hanuschik 1997; Okazaki 1997), especially owing to the
success of the one-armed global oscillation model to explain V/R
variability in the emission lines of Be stars (Kato
1983; Okazaki 1991, 1996; Papaloizou et al. 1992; Hummel & Hanuschik 1997).
Therefore it seems necessary to attempt an explanation of the outburst behaviour of Be/X-ray binaries that does not imply large outflow velocities.
Whatever the mechanism originating the Be phenomenon, the model which
at present appears more applicable to explaining the discs surrounding
Be stars is the viscous decretion disc model (Lee et al. 1991;
see Porter 1999; Okazaki 2001 for detailed
discussion). In this scenario, angular momentum is transferred from
the central star by some mechanism still to be determined
(perhaps associated with non-radial pulsations) to the inner edge of
the disc, increasing its angular velocity to Keplerian. Viscosity
then, operating in a way opposite to an accretion disc, conducts
material outwards. In this scenario, material in the disc moves in
quasi-Keplerian orbits and the radial velocity component is highly
subsonic until the material reaches a distance much larger than the
line-emitting regions (Okazaki 2001). The outflow is very
subsonic for the distances at which neutron stars orbit in close
Be/X-ray transients
![]() and
still subsonic for the orbital sizes of all Be/X-ray binaries for
which there is an orbital solution. The viscous decretion disc model
successfully accounts for most of the observational characteristics of
Be discs.
and
still subsonic for the orbital sizes of all Be/X-ray binaries for
which there is an orbital solution. The viscous decretion disc model
successfully accounts for most of the observational characteristics of
Be discs.
Negueruela & Okazaki (2001, henceforth Paper I) have modelled
the disc surrounding the Be primary in the Be/X-ray transient
4U0115+63 as a viscous decretion disc and found that the
tidal interaction of the neutron star naturally produces the
truncation of the circumstellar disc, as it does for accretion
discs in close binaries (Paczynski 1977).
The result of Negueruela & Okazaki (2001) is in agreement with
the results of Reig et al. (1997), who showed that there is a
correlation between the orbital size and the maximum equivalent width
of H![]() ever observed in a system. Even though it is clear that
the equivalent width of H
ever observed in a system. Even though it is clear that
the equivalent width of H![]() is not an effective measurement of
the size of the disc owing to several effects (see, for example,
Negueruela et al. 1998), the maximum equivalent width ever
observed becomes a significant indicator if the system has been
monitored during a period which is long in comparison with the typical
time-scale for changes in the disc (which, if viscosity is dominant,
should be only a few months). Therefore the result of Reig et al. (1997) clearly indicates that the neutron star has some
sort of effect on the size of the disc.
is not an effective measurement of
the size of the disc owing to several effects (see, for example,
Negueruela et al. 1998), the maximum equivalent width ever
observed becomes a significant indicator if the system has been
monitored during a period which is long in comparison with the typical
time-scale for changes in the disc (which, if viscosity is dominant,
should be only a few months). Therefore the result of Reig et al. (1997) clearly indicates that the neutron star has some
sort of effect on the size of the disc.
In this paper we apply the model presented in Paper I to several Be/X-ray transients for which orbital solutions exist and investigate how the truncation radius depends on different orbital parameters.
The model developed in Paper I describes a binary system in which a
primary Be star of mass M* and radius R* is orbited by a
neutron star of mass
![]() which moves in an
orbit of eccentricity e and period
which moves in an
orbit of eccentricity e and period
![]() .
The Be star is
assumed to be surrounded by a near-Keplerian disc which is primarily
governed by pressure and viscosity. For simplicity, the disc is
assumed to be isothermal and Shakura-Sunyaev's viscosity prescription
is adopted.
.
The Be star is
assumed to be surrounded by a near-Keplerian disc which is primarily
governed by pressure and viscosity. For simplicity, the disc is
assumed to be isothermal and Shakura-Sunyaev's viscosity prescription
is adopted.
In such a disc, angular momentum is added to the disc by the viscous torque, whereas it is removed from the disc by the resonant torque exerted by the neutron star companion, which becomes non-zero only at radii where the ratio between the angular frequency of disc rotation and the angular frequency of the mean binary motion is a rational number. As a result, the disc decretes outward owing to the transfer of angular momentum by viscosity until the resonant torque becomes larger than the viscous torque at a resonant radius.
Therefore, the criterion for the disc truncation at a given resonance
radius is written as
The viscous torque
![]() is written as
is written as
The resonant torque
![]() is calculated by using Goldreich &
Tremaine's (1979, 1980) torque formula, after
decomposing the binary potential
is calculated by using Goldreich &
Tremaine's (1979, 1980) torque formula, after
decomposing the binary potential ![]() into a double Fourier series
as
into a double Fourier series
as
For each potential component, there can be three kinds of resonances,
i.e., the outer and inner Lindblad resonances at radii
![]() ,
where
,
where
![]() ,
and
a corotation resonance (CR) at the radius
(m/l)2/3(1+q)-1/3 a,
where
,
and
a corotation resonance (CR) at the radius
(m/l)2/3(1+q)-1/3 a,
where
![]() .
Here,
.
Here, ![]() is the epicyclic frequency and
the upper and lower signs correspond to the outer Lindblad resonance
(OLR) and inner Lindblad resonance (ILR), respectively.
In circumstellar discs, however, the resonant torque from the inner
Lindblad resonance, which is given by
is the epicyclic frequency and
the upper and lower signs correspond to the outer Lindblad resonance
(OLR) and inner Lindblad resonance (ILR), respectively.
In circumstellar discs, however, the resonant torque from the inner
Lindblad resonance, which is given by
For a given set of stellar and orbital parameters and disc
temperature, criterion (7) at a given resonance is
met for ![]() smaller than a critical value
smaller than a critical value
![]() and
we assume that the disc is truncated at the resonance if
and
we assume that the disc is truncated at the resonance if
![]() .
.
In Paper I it was shown that for any subsonic outflow, the drift
time-scale
![]() was considerably
longer than a typical truncation time-scale
was considerably
longer than a typical truncation time-scale
![]() ,
where
,
where ![]() is the gap
size between the truncation radius and the radius where the gravity by
the neutron star begins to dominate, and
is the gap
size between the truncation radius and the radius where the gravity by
the neutron star begins to dominate, and ![]() and
and
![]() are the radial velocity and Mach number, respectively. As a
consequence, the tidal and resonant interaction with the neutron star
leads to disc truncation.
are the radial velocity and Mach number, respectively. As a
consequence, the tidal and resonant interaction with the neutron star
leads to disc truncation.
One important consequence of the above is that the discs surrounding the primaries in Be/X-ray binaries cannot reach a steady state. Most of the outflowing material loses angular momentum and falls back towards the central star. As a consequence of the interaction with the material which is coming outwards from the inner regions, it is likely that the disc becomes denser and the density distribution in the radial direction becomes flatter with increasing time. We note that we do not expect the truncation effect to be one hundred per cent efficient. This is not only owing to theoretical considerations (see below), but probably required by the existence of pulsed low-luminosity X-ray emission during quiescence.
In the formulation above only torques integrated over the whole orbit are considered. Given the large eccentricities observed in Be/X-ray binaries (mostly larger than 0.3 and sometimes approaching 0.9), the gravitational effect of the neutron star is very strongly dependent on the orbital phase. This means that in such systems the disc radius and the truncation radius are also phase-dependent. The disc will shrink at periastron, at which the truncation radius becomes smallest, while it will spread when the neutron star is far away and its gravitational effect is not felt so strongly. The spread of the disc will continue until the truncation radius becomes smaller than the disc radius at some phase before the next periastron passage. This variation in disc radius will be larger for a larger eccentricity. For a longer orbital period, the effect will be yet stronger. Given that, for some systems considered (see Sect. 5), the model truncation radius is close to the critical lobe radius at periastron, this will provide a mechanism by which disc material can reach the neutron star (see also Fig. 3 for scenarios for two families of type I outbursts).
Table 1 shows a list of known X-ray binaries which have exhibited outbursting behaviour or some sort of orbital modulation in their X-ray lightcurve. The top panel contains Be/X-ray binaries with an identified Be counterpart which have displayed type I X-ray outbursts, i.e., a series of outbursts separated by their orbital period (note that in many cases there is no orbital solution for the system and the recurrence period of the outbursts is taken to be the orbital period). The middle panel shows other systems without identified optical counterparts whose X-ray behaviour marks them out as Be/X-ray binaries. Finally the bottom panel contains a few other Be/X-ray binaries with identified counterparts whose X-ray behaviour deviates slightly from what is considered typical (and which will be discussed individually in Sect. 6).
In this section, we apply our model to systems for which exact orbital solutions have been deduced from the analysis of Doppler shifts in the arrival times of X-ray photons. They include five Be/X-ray binaries in the top panel (V0332+53, A0535+262, GROJ1008-57, 2S1417-624, and EXO2030+375) and a likely Be/X-ray binary in the middle panel (2S1845-024). These systems are discussed individually in the following subsections. The case of the Be/X-ray transient 4U0115+63 has been carefully discussed in Paper I and therefore it will not be included here.
| Name | Optical | Spectral |
|
|
e |
| Counterpart | Type | ||||
| 4U0115+634 | V635 Cas | B0.2V
|
3.6 | 24.3 | 0.34 |
| V0332+53 | BQ Cam | O8.5V
|
4.4 | 34.2 | 0.31 |
| A0535+262 | V725 Tau | B0III | 103 | 111 | 0.47 |
| RX J0812.4-3114 | LS 992 | B0.2III
|
31.9 | 81*
|
- |
| GS0834-430 | star
|
- | 12.3 | 105.8 |
0.1<e<0.17
|
| GROJ1008-57 | star | - | 93.5 | 247.5* | 0.66*
|
| 4U1145-619 | V801 Cen | B0.2III
|
292 | 187* | large |
| 4U1258-61 | V850 Cen | B0.7V
|
272 | 132.5* | large |
| 2S1417-624 | star | - | 17.6 | 42.1 | 0.45 |
| XTEJ1946+274 | star | - | 15.8 | 172
|
- |
| EXO2030+375 | star | - | 41.7 | 46.03 | 0.41
|
| XTEJ1543-568 | - | - | 27.1 | 76.6 | <0.03
|
| 2S1845-024 | - | - | 94.3 | 242.2 | 0.88
|
| GROJ2058+42 | - | - | 198 | 110*
|
- |
| A0535-668 | star | B0.5III
|
0.07 | 16.7* | large |
| A0726-26 | V441 Pup | O8.5V | 103.2 | 35* | - |
| A1118-616 | Wray 977 | O9.5V | 406.5 | - | - |
| Cep X-4 | star | B1V? | 66.3 | - | - |
| SAXJ2239.3+6116 | star | - | - | 262*
|
- |
As mentioned in the previous section, we adopt Shakura-Sunyaev's
viscosity prescription, in which the viscosity parameter ![]() is a
free parameter, and assume the Be disc to be isothermal.
In what follows, we adopt
is a
free parameter, and assume the Be disc to be isothermal.
In what follows, we adopt
![]() .
Note that our assumption of the disc temperature is consistent
with the results by Millar & Marlborough (1998, 1999),
who computed the distribution of the disc temperature within
100 R* around the B0 star
.
Note that our assumption of the disc temperature is consistent
with the results by Millar & Marlborough (1998, 1999),
who computed the distribution of the disc temperature within
100 R* around the B0 star ![]() Cas and the B8-9 star 1 Del
by balancing at each position the rates of energy gain and energy loss
and found that the disc is roughly isothermal at a temperature about
half the effective temperature of the star.
Cas and the B8-9 star 1 Del
by balancing at each position the rates of energy gain and energy loss
and found that the disc is roughly isothermal at a temperature about
half the effective temperature of the star.
When adopting a particular model for a system, the main source of uncertainty comes from the choice of mass for the primary, a parameter which can only be guessed from the spectral type. We find two main difficulties. In some cases, the spectral type of the primary is not well determined. Moreover, there is some evidence that fast rotators may be moderately over-luminous for their masses (see Gies et al. 1998). For this reason, in general we have taken masses slightly lower than those given in the calibration of Vacca et al. (1996). The spectral distribution of primaries of Be/X-ray binaries (Negueruela 1998) is strongly peaked at B0. Therefore for systems without exact determination of the spectral type, we have calculated models corresponding to B0V and B0III primaries. In any case, our results show that the exact mass of the primary is not one of the main factors in the X-ray behaviour of the sources.
This transient pulsar has an orbital period
![]() with a relatively
low eccentricity of e =0.31 (Stella et al. 1985).
The optical component of this system is an unevolved star in the
O8-9 range (Negueruela et al. 1999). For O8.5V stars
Vacca et al. (1996) give an spectroscopic mass
with a relatively
low eccentricity of e =0.31 (Stella et al. 1985).
The optical component of this system is an unevolved star in the
O8-9 range (Negueruela et al. 1999). For O8.5V stars
Vacca et al. (1996) give an spectroscopic mass
![]() and a theoretical mass
and a theoretical mass
![]() .
Here we
will assume as a conservative model the lower limit of
.
Here we
will assume as a conservative model the lower limit of
![]() and
and
![]() .
The mass function f(M)
=0.1 then implies
.
The mass function f(M)
=0.1 then implies
![]() ,
resulting in an orbital
separation
,
resulting in an orbital
separation
![]() (
(
![]() ).
).
This system has been rarely detected in X-rays. A type II outburst was observed in 1973 (see Negueruela et al. 1999 for references). Ten years later, it was observed during a series of three type I outbursts. Finally it was observed during another type II outburst in 1989. Between 1991 and 2000 it has not been detected by either the BATSE instrument on board the ComptonGRO satellite or the All Sky Monitor on board RossiXTE and it is believed to be in a dormant state (Negueruela et al. 1999).
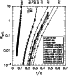 |
Figure 1:
Critical values of |
| Open with DEXTER | |
In Fig. 1, we plot
![]() at the n:1
resonance radii for those Be/X-ray binaries which will be discussed in
this section. The resonant torques at the n:1 radii are stronger
than those at radii with other period commensurabilities located
nearby. Note that we have adopted a particular disc temperature,
at the n:1
resonance radii for those Be/X-ray binaries which will be discussed in
this section. The resonant torques at the n:1 radii are stronger
than those at radii with other period commensurabilities located
nearby. Note that we have adopted a particular disc temperature,
![]() ,
for each stellar model. For
other disc temperatures,
,
for each stellar model. For
other disc temperatures,
![]() should be multiplied by a
factor of
should be multiplied by a
factor of
![]() ,
taking account of the fact that
the viscous torque is proportional to
,
taking account of the fact that
the viscous torque is proportional to ![]() .
.
Figure 1 shows that the Be disc in V0332+53 is
expected to be truncated at the 3:1 resonance radius (
![]() ,
where
,
where ![]() is the truncation radius) for
is the truncation radius) for
![]() and at the 4:1 resonance radius (
and at the 4:1 resonance radius (
![]() )
for
)
for
![]() .
.
It is interesting to see how close the truncation radius is to the
size of the critical lobe at periastron. Figure 2 shows
orbital models for the systems discussed in this section. The
potential ![]() describing the effects of the gravitational and
centrifugal forces on the motion of test particles orbiting the Be
star is given by
describing the effects of the gravitational and
centrifugal forces on the motion of test particles orbiting the Be
star is given by
From Figs. 1 and 2a, we note that
the truncation radii of the Be disc in V0332+53 for
![]() is smaller than the critical lobe size at periastron. In
other words, the Be disc never fills the critical lobe even at
periastron unless the viscosity is very high (
is smaller than the critical lobe size at periastron. In
other words, the Be disc never fills the critical lobe even at
periastron unless the viscosity is very high (
![]() ).
).
Table 2 gives the gap size
![]() ,
where
,
where
![]() is the mean radius of the critical lobe at
periastron, together with stellar parameters adopted and the resulting
truncation radii. Table 2 also gives lower limits for the
drift timescale,
is the mean radius of the critical lobe at
periastron, together with stellar parameters adopted and the resulting
truncation radii. Table 2 also gives lower limits for the
drift timescale,
![]() ,
which is given by
,
which is given by
![]() .
For a system with
.
For a system with
![]() ,
the gap is wide and the truncation is efficient, while the spread
of the disc can make the truncation inefficient for a system with
,
the gap is wide and the truncation is efficient, while the spread
of the disc can make the truncation inefficient for a system with
![]() .
.
Given that we expect the viscosity in the disc to be of the order of
![]() ,
the Be disc in V0332+53 is likely to be
truncated at the 3:1 resonance radius or the 4:1 resonance radius. If
the disc is truncated at the 3:1 radius, which is close to the mean
critical radius at periastron [
,
the Be disc in V0332+53 is likely to be
truncated at the 3:1 resonance radius or the 4:1 resonance radius. If
the disc is truncated at the 3:1 radius, which is close to the mean
critical radius at periastron [
![]() and
and
![]() ],
a small perturbation easily causes the
outermost part of the disc to fall into the gravitational well of the
neutron star. However, the X-ray history of this system described
above suggests that the system shows no type I X-ray outburst in its
normal state. Therefore, we expect that the disc in
V0332+53 has a viscosity parameter
(slightly) less than 0.1 and/or a temperature (slightly) lower than
],
a small perturbation easily causes the
outermost part of the disc to fall into the gravitational well of the
neutron star. However, the X-ray history of this system described
above suggests that the system shows no type I X-ray outburst in its
normal state. Therefore, we expect that the disc in
V0332+53 has a viscosity parameter
(slightly) less than 0.1 and/or a temperature (slightly) lower than
![]() .
Under those sconditions, it will be
truncated at the 4:1 resonance radius
[
.
Under those sconditions, it will be
truncated at the 4:1 resonance radius
[
![]() and
and
![]() ].
].
![\begin{figure}
\includegraphics[width=12cm,clip]{H2911F2.eps} \end{figure}](/articles/aa/full/2001/37/aah2911/Timg127.gif) |
Figure 2:
Description of the orbital model adopted for each system,
in the reference system centred on the Be star. The dash-dotted
line represents the orbit of the neutron star. The thick dashed
line represents the position of the first Lagrangian point (L1)
around the orbit. The solid thin lines are the critical
lobes of the two stars at apastron and periastron (the position
of the neutron star is marked with a cross). The labelled solid
lines represent the locations of the n:1 commensurabilities of
disc and binary orbital periods at which truncation occurs for
|
| Open with DEXTER | |
|
|
|
|
|||||||||||||||||
| Name |
|
|
|
|
|
|
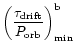 |
|
|
|
|
||||||||
| 4U0115+634 | B0V | 16.0 | 8.0 |
|
0.46 | 0.13 | 2.8 | 0.08 | 1.7 | -0.003 | - | ||||||||
| V0332+53 | O8.5V | 20.0 | 8.8 |
|
0.50 | 0.11 | 2.1 | 0.03 | 0.56 | 0.03 | 0.56 | ||||||||
| A0535+262 | B0III | 20.0 | 15.0 |
|
0.38 | 0.09 | 1.2 | 0.05 | 0.66 | -0.004 | - | ||||||||
| EXO2030+375 | O9III | 22.0 | 15.0 |
|
0.43 | 0.09 | 1.7 | 0.04 | 0.72 | -0.04 | - | ||||||||
| B0III | 20.0 | 14.0 |
|
0.42 | 0.09 | 1.7 | 0.04 | 0.69 | 0.04 | 0.69 | |||||||||
| B0V | 16.0 | 8.0 |
|
0.41 | 0.12 | 2.0 | 0.08 | 1.4 | 0.03 | 0.45 | |||||||||
| 2S1417-624 | O9V | 20.0 | 9.0 |
|
0.40 | 0.10 | 1.8 | 0.06 | 1.1 | 0.01 | 0.18 | ||||||||
| B1V | 12.0 | 7.0 |
|
0.37 | 0.11 | 1.9 | 0.08 | 1.4 | 0.04 | 0.75 | |||||||||
| GROJ1008-57 | B0III | 20.0 | 14.0 |
|
0.25 | 0.04 | 0.38 | 0.002 | 0.020 | -0.02 | - | ||||||||
| B0V | 16.0 | 8.0 |
|
0.24 | 0.04 | 0.41 | -0.004 | - | -0.03 | - | |||||||||
| 2S1845-024 | B0V | 16.0 | 8.0 |
|
0.084 | 0.014 | 0.13 | 0.001 | 0.013 | -0.010 | - | ||||||||
| B1V | 12.0 | 7.0 |
|
0.081 | 0.015 | 0.15 | 0.004 | 0.038 | -0.007 | - | |||||||||
This pulsar has an orbital period
![]() and an
eccentricity e =0.47 (Finger et al. 1996a). There is some
discussion about the exact spectral type of the optical counterpart.
Most authors support a giant in the range O9.5-B0, but Wang &
Gies (1998) cannot rule out a main-sequence classification
based on UV spectra. Wang & Gies (1998) constrain the mass of
the optical component to the range
and an
eccentricity e =0.47 (Finger et al. 1996a). There is some
discussion about the exact spectral type of the optical counterpart.
Most authors support a giant in the range O9.5-B0, but Wang &
Gies (1998) cannot rule out a main-sequence classification
based on UV spectra. Wang & Gies (1998) constrain the mass of
the optical component to the range
![]() .
If the object is a giant, the mass should be close to the
upper limit. Taking
.
If the object is a giant, the mass should be close to the
upper limit. Taking
![]() ,
the mass function indicates
,
the mass function indicates
![]() ,
resulting in an orbital separation
,
resulting in an orbital separation
![]() .
.
Four type II X-ray outbursts from A0535+262 have been observed (in 1975, 1980, 1989 and 1994). The system also displays series of type I outbursts interspersed with periods of quiescence. The length of the series or of the quiescent states is very variable. A series of three type I outbursts was observed by BATSE during 1993, followed by a type II outburst and later two weaker type I outbursts (1996a). After that, the source has been in quiescence and the optical counterpart has lost and reformed its circumstellar disc (Haigh et al. 1999).
Figure 1 shows that the Be disc in A0535+262
is expected to be truncated at the 4:1 resonance radius (
![]() )
for
)
for
![]() and at the 5:1 resonance
radius (
and at the 5:1 resonance
radius (
![]() )
for
)
for
![]() .
As
shown in Fig. 2b and Table 2, the 4:1
resonance radius is slightly larger than the mean radius of the
critical lobe at periastron, while the higher resonance radii are
significantly smaller than the critical lobe. The X-ray history of
A0535+262 suggests that the Be disc in this system has
.
As
shown in Fig. 2b and Table 2, the 4:1
resonance radius is slightly larger than the mean radius of the
critical lobe at periastron, while the higher resonance radii are
significantly smaller than the critical lobe. The X-ray history of
A0535+262 suggests that the Be disc in this system has
![]() and
and
![]() and is
truncated at the 4:1 resonance radius, which will allow enough mass
accretion on to the neutron star at every periastron passage to cause
a type I outburst regularly (see scenario A in
Fig. 3). If this is the case, a slight decrease in
viscosity (and/or disc temperature) will lower the disc radius
to the 5:1 resonance radius and therefore change the system to a
dormant state, as has been repeatedly observed.
and is
truncated at the 4:1 resonance radius, which will allow enough mass
accretion on to the neutron star at every periastron passage to cause
a type I outburst regularly (see scenario A in
Fig. 3). If this is the case, a slight decrease in
viscosity (and/or disc temperature) will lower the disc radius
to the 5:1 resonance radius and therefore change the system to a
dormant state, as has been repeatedly observed.
 |
Figure 3: Scenarios for two families of type I outbursts. A) Regular type I outbusts induced by viscous decretion in an axisymmetric disc. a) Near periastron, the gas continues to overflow through the L1 point, replenishing the accretion disc around the neutron star. (The accretion disc begins to form at panel d).) b) At the phase at which the critical lobe radius becomes larger than the disc radius, the overflow stops and the accretion disc begins to fade. c) While the neutron star orbits far from periastron, the disc material drifts outward by viscous decretion. d) At the phase at which the critical lobe radius becomes smaller than the disc radius, the gas in the outermost part of the disc begins to overflow. The accretion disc is formed around the neutron star. B) Temporary type I outbursts induced by a slowly precessing density wave. a) If the disc is elongated roughly toward the periastron by chance, the overflow occurs around periastron. b) At the phase at which the critical lobe radius becomes larger than the elongated disk size, the overflow stops and the accretion disc begins to fade. c) Same as panel c) in scenario A. d) If the axis of elongation is still roughly toward the periastron, at the phase at which the critical lobe radius becomes smaller than the elongated disk size, the gas in the outermost part of the disc begins to overflow. The accretion disc is formed around the neutron star. |
| Open with DEXTER | |
This transient X-ray pulsar was discovered during a type II outburst
in 1985. Since then, it has displayed tens of type I X-ray outbursts
in long series separated by periods of quiescence. The orbit is
characterised by
![]() and eccentricity
e=0.41 (Wilson et al. 2001). The optical component of this
system is heavily obscured and no determination of the spectral type
has been possible, but both the measured mass function and the
infrared spectrum imply a spectral type earlier than about B1 (Reig et al. 1998). Coe et al. (1988) showed that the colours
of the object are compatible with a B0 spectral type. The reddening
and eccentricity
e=0.41 (Wilson et al. 2001). The optical component of this
system is heavily obscured and no determination of the spectral type
has been possible, but both the measured mass function and the
infrared spectrum imply a spectral type earlier than about B1 (Reig et al. 1998). Coe et al. (1988) showed that the colours
of the object are compatible with a B0 spectral type. The reddening
![]() derived by Motch & Janet-Pacheco (1987) and
the distance of 5.3 kpc derived by Parmar et al. (1989) from
the change rates in spin period and X-ray luminosity can only be
compatible if the object is a giant. However, given that the
distance determination has a large uncertainty, the possibility
that the object is a main-sequence star cannot be ruled out.
derived by Motch & Janet-Pacheco (1987) and
the distance of 5.3 kpc derived by Parmar et al. (1989) from
the change rates in spin period and X-ray luminosity can only be
compatible if the object is a giant. However, given that the
distance determination has a large uncertainty, the possibility
that the object is a main-sequence star cannot be ruled out.
If the spectral type is B0III, a mass of around
![]() is expected. We have adopted a model with
is expected. We have adopted a model with
![]() and
and
![]() ,
in which case the mass function implies an
inclination angle
,
in which case the mass function implies an
inclination angle
![]() - this is consistent with the fact
that the shape of the H
- this is consistent with the fact
that the shape of the H![]() emission lines shown by Norton et al. (1994) is typical of a Be star with moderate
inclination. The orbital separation would then be
emission lines shown by Norton et al. (1994) is typical of a Be star with moderate
inclination. The orbital separation would then be
![]() .
In
order to investigate the dependence of our model on the mass of the
primary, we have also considered the case of
.
In
order to investigate the dependence of our model on the mass of the
primary, we have also considered the case of
![]() ,
,
![]() (a typical B0V star).
(a typical B0V star).
Figure 1 shows that the difference in
![]() between the B0III star model and the B0V star model is small.
In the B0III star model, the disc is truncated at the 4:1 resonance
radius (
between the B0III star model and the B0V star model is small.
In the B0III star model, the disc is truncated at the 4:1 resonance
radius (
![]() )
for
)
for
![]() and at the 5:1 resonance radius
(
and at the 5:1 resonance radius
(
![]() )
for
)
for
![]() ,
while in the B0V star model the disc is truncated at the 4:1 resonance
radius for
,
while in the B0V star model the disc is truncated at the 4:1 resonance
radius for
![]() and at the 5:1 resonance radius
for
and at the 5:1 resonance radius
for
![]() .
We have also tried a slightly earlier
spectral type, O9III, for the primary, expecting that a higher disc
temperature would result in a larger truncation radius. However, the
resulting radii are almost the same as those for a B0III primary,
unless
.
We have also tried a slightly earlier
spectral type, O9III, for the primary, expecting that a higher disc
temperature would result in a larger truncation radius. However, the
resulting radii are almost the same as those for a B0III primary,
unless ![]() is as high as 0.3 (see Table 2).
is as high as 0.3 (see Table 2).
As shown in Fig. 2c, the 4:1 resonance radius is close
to the mean radius of the critical lobe at periastron, while the
higher resonance radii are significantly smaller than the critical
lobe. Our result suggests that the observed X-ray behaviour of
EXO2030+375, which has regularly exhibited type I X-ray
outbursts, favours a B0III or a O9III primary star with a disc with
![]() and/or
and/or
![]() that is
truncated at the 4:1 resonance radius (see scenario A in
Fig. 3).
that is
truncated at the 4:1 resonance radius (see scenario A in
Fig. 3).
2S1417-624 was observed once in 1978 and was not detected again until 1994, when a type II outburst was observed by BATSE (Finger et al. 1996b). This was followed by five type I outbursts peaking near apastron.
The pulsar in this Be/X-ray transient has
![]() and an eccentricity e=0.45 (Finger et al. 1996b). The
optical component of the system was studied by Grindlay et al. (1984). Owing to the low signal-to-noise of their spectra,
they did not assign an spectral type, though several He II
lines seem to be present in the spectrum displayed, suggesting an
O-type star. Therefore we will consider again two models, one
corresponding to an O9V star (
and an eccentricity e=0.45 (Finger et al. 1996b). The
optical component of the system was studied by Grindlay et al. (1984). Owing to the low signal-to-noise of their spectra,
they did not assign an spectral type, though several He II
lines seem to be present in the spectrum displayed, suggesting an
O-type star. Therefore we will consider again two models, one
corresponding to an O9V star (
![]() ,
,
![]() )
and one roughly corresponding to a B1V star (
)
and one roughly corresponding to a B1V star (
![]() ,
,
![]() ).
).
As shown in Fig. 1, the O9V star model and the B1V
star model give rather different values of
![]() :
the
O9V star model results in a value for
:
the
O9V star model results in a value for
![]() similar
to that in the model for A0535+262, whereas
the B1V star model gives a significantly higher value of
similar
to that in the model for A0535+262, whereas
the B1V star model gives a significantly higher value of
![]() .
In the O9V star model, the disc is truncated at the 4:1
resonance radius (
.
In the O9V star model, the disc is truncated at the 4:1
resonance radius (
![]() )
for
)
for
![]() and at the 5:1 resonance radius
(
and at the 5:1 resonance radius
(
![]() )
for
)
for
![]() ,
while in the B1V star model the disc is truncated at the 4:1 resonance
radius for
,
while in the B1V star model the disc is truncated at the 4:1 resonance
radius for
![]() and at the 5:1 resonance radius
for
and at the 5:1 resonance radius
for
![]() .
Therefore, if the optical counterpart
of 2S1417-624 is a B1V star, the disc is likely to be
truncated at the 5:1 resonance radius or the 6:1 resonance radius,
which is significantly smaller than the critical lobe at periastron
(see also Table 2). In this case, the system is unlikely
to display type I X-ray outbursts in a normal state, which is
consistent with the X-ray history of this system. The O9V star model
is also consistent with the X-ray history if
.
Therefore, if the optical counterpart
of 2S1417-624 is a B1V star, the disc is likely to be
truncated at the 5:1 resonance radius or the 6:1 resonance radius,
which is significantly smaller than the critical lobe at periastron
(see also Table 2). In this case, the system is unlikely
to display type I X-ray outbursts in a normal state, which is
consistent with the X-ray history of this system. The O9V star model
is also consistent with the X-ray history if
![]() .
.
We interpret the sequence of type I outbursts which followed the 1994 type II outburst as a temporary phenomenon caused by a strong disturbance in the disc. After type II outbursts, the disc is expected to be strongly disturbed (see Negueruela et al. 2001, from now on Paper II, for a discussion of the possible causes of type II outbursts). Such a disc is likely to be strongly asymmetric and to be temporarily capable of fuelling the neutron star (see scenario B in Fig. 3).
BATSE discovered GROJ1008-57 during a type II outburst in
July 1993. Four weak X-ray outbursts separated by ![]() 248 days
followed. The source is believed to emit some X-ray flux during
quiescence, but no further outbursts have been observed. The optical
counterpart was identified by Coe et al. (1994), but no
information exists about its exact spectral type.
248 days
followed. The source is believed to emit some X-ray flux during
quiescence, but no further outbursts have been observed. The optical
counterpart was identified by Coe et al. (1994), but no
information exists about its exact spectral type.
The orbit of this pulsar is not exactly determined. However, from the
analysis of data from the BATSE experiment, a most probable orbit can
be determined if the separation between type I outbursts
(
![]() )
is taken to be the orbital
period (M. Scott, priv. comm.). In that case, the eccentricity is
e=0.66 and
)
is taken to be the orbital
period (M. Scott, priv. comm.). In that case, the eccentricity is
e=0.66 and
![]() .
Again the
colours of the primary are
compatible with a B0 star. Therefore we use models for a B0V
(
.
Again the
colours of the primary are
compatible with a B0 star. Therefore we use models for a B0V
(
![]() ,
,
![]() )
and a B0III (
)
and a B0III (
![]() ,
,
![]() )
primary.
)
primary.
Figure 1 shows that both stellar models give similar
values of
![]() .
In the B0III star model, the disc is
truncated at the 7:1 resonance radius (
.
In the B0III star model, the disc is
truncated at the 7:1 resonance radius (
![]() )
for
)
for
![]() and at the 8:1 resonance radius
(
and at the 8:1 resonance radius
(
![]() )
for for
)
for for
![]() .
In
the B0V star model,
.
In
the B0V star model,
![]() becomes higher by about 20%.
becomes higher by about 20%.
From Fig. 2e, we immediately observe that
the truncation radius is close to or slightly beyond the critical lobe
radius at periastron unless the viscosity is very low (
![]() ). It should be noted that this is a typical feature in systems
with high orbital eccentricity, because the resonance radii are
distributed more densely for higher resonances. In other words, disc
truncation is less efficient in systems with high orbital eccentricity
than in systems with low or mild eccentricity. Moreover,
GROJ1008-57 has a rather long orbital
period. Consequently, the Be disc in this system can spread out
significantly while the neutron star is far away from the Be star. These features should enable GROJ1008-57 to display
type I outbursts regularly.
). It should be noted that this is a typical feature in systems
with high orbital eccentricity, because the resonance radii are
distributed more densely for higher resonances. In other words, disc
truncation is less efficient in systems with high orbital eccentricity
than in systems with low or mild eccentricity. Moreover,
GROJ1008-57 has a rather long orbital
period. Consequently, the Be disc in this system can spread out
significantly while the neutron star is far away from the Be star. These features should enable GROJ1008-57 to display
type I outbursts regularly.
2S1845-024 has been detected by several satellites at luminosities compatible with type I outbursts (see Finger et al. 1999 for references). Between the launch of the ComptonGRO satellite and 1997, BATSE detected type I outbursts from 2S1845-024 at every periastron passage. This behaviour has continued at least until 2000 (Finger, priv. comm.).
This X-ray pulsar is in a very eccentric (e=0.88) and wide (
![]() )
orbit (Finger et al. 1999). The optical
counterpart has not been identified, but the mass function constrains
it to have
)
orbit (Finger et al. 1999). The optical
counterpart has not been identified, but the mass function constrains
it to have
![]() .
Given that it has an exact orbital
solution, we have modelled the system in spite of the lack of data on
the optical companion. We have considered two models: one in which the
primary is our typical B0V star (
.
Given that it has an exact orbital
solution, we have modelled the system in spite of the lack of data on
the optical companion. We have considered two models: one in which the
primary is our typical B0V star (
![]() ,
,
![]() )
- adopting the parameters of a B0III star did not alter
significantly the value of
)
- adopting the parameters of a B0III star did not alter
significantly the value of
![]() - and one with
- and one with
![]() ,
which is close to the value used by Finger et
al. (1999) for their evolutionary model
(
,
which is close to the value used by Finger et
al. (1999) for their evolutionary model
(
![]() ), and then
), and then
![]() for a typical
B1V star.
for a typical
B1V star.
As in GROJ1008-57, both stellar models make little
difference in the value of
![]() (Fig. 1), and the truncation radius is close to or
slightly beyond the critical lobe radius at periastron unless the
viscosity is very low (
(Fig. 1), and the truncation radius is close to or
slightly beyond the critical lobe radius at periastron unless the
viscosity is very low (
![]() )
(Fig. 2f
and Table 2). With the extremely high orbital
eccentricity, the disc truncation in this system is expected to be
even less efficient than in GROJ1008-57. In addition, the
system has a long orbital period. Therefore, it is no surprise that
2S1845-024 has regularly shown type I outbursts without
failure.
)
(Fig. 2f
and Table 2). With the extremely high orbital
eccentricity, the disc truncation in this system is expected to be
even less efficient than in GROJ1008-57. In addition, the
system has a long orbital period. Therefore, it is no surprise that
2S1845-024 has regularly shown type I outbursts without
failure.
In Paper I, we analysed the disc size of V635 Cas, the optical counterpart of 4U0115+63, and found that the truncated disc size is significantly smaller than the distance to the first Lagrangian (L1) point at periastron. Among our conclusions, we found that it is precisely this wide gap between the disc outer radius and the position of the L1 point that prevents the system from displaying type I outbursts, by drastically reducing the accretion rate on to the neutron star. In Paper II we pointed out that, for the very same reason, the density in the disc of V635 Cas is likely to grow with time, to a point where the disc becomes optically thick and unstable to the radiation-driven warping, which seems to be at the origin of type II X-ray outbursts.
As discussed in the end of Sect. 4, we cannot expect a perfect truncation. Since the disc density is expected to decrease rapidly beyond the truncation radius, the gap size determines how effective the disc truncation is. For systems with a wide gap, like 4U0115+63, the truncation is so effective that the system does not show type I outbursts under normal conditions. Whatever little amount of disc material manages to overcome the tidal truncation may be easily ejected from the vicinity of the neutron star by the propeller effect (Stella et al. 1986). On the other hand, for systems with a narrow gap, the truncation will not be efficient, allowing the neutron star to capture gas from the disc at every periastron passage and display type I outbursts.
Therefore, the main purpose of this paper is to find out the general trend in the dependence of the gap size on various parameters. A second purpose is to understand why we can see two different kinds of type I outburst series: regular series of outbursts of similar intensity in some systems and short series of outbursts of varying intensity (generally associated with type II outbursts) in other systems.
We have found that, in systems with high orbital eccentricity, say
![]() ,
such as GROJ1008-57 (e=0.66) and
2S1417-624 (e=0.88), the truncation radius of the Be
disc is very close to, in the sense that
,
such as GROJ1008-57 (e=0.66) and
2S1417-624 (e=0.88), the truncation radius of the Be
disc is very close to, in the sense that
![]() ,
or slightly beyond the critical lobe radius at
periastron unless the viscosity is very low (
,
or slightly beyond the critical lobe radius at
periastron unless the viscosity is very low (
![]() ). Under
such conditions, we expect disc truncation not to be efficient,
allowing the accretion by the neutron star of enough mass at every
periastron passage to cause a type I X-ray outburst regularly (see
scenario A in Fig. 3). Moreover, the long orbital
period of GROJ1008-57 (
). Under
such conditions, we expect disc truncation not to be efficient,
allowing the accretion by the neutron star of enough mass at every
periastron passage to cause a type I X-ray outburst regularly (see
scenario A in Fig. 3). Moreover, the long orbital
period of GROJ1008-57 (
![]() )
and
2S1845-024 (
)
and
2S1845-024 (
![]() )
will enable the
Be disc in these systems to spread out significantly while the neutron
star is far from periastron. This larger drift time will allow the
neutron star in such systems to accrete rather more matter at
periastron passage than in a system with shorter orbital period.
)
will enable the
Be disc in these systems to spread out significantly while the neutron
star is far from periastron. This larger drift time will allow the
neutron star in such systems to accrete rather more matter at
periastron passage than in a system with shorter orbital period.
Among systems which we expect to be relatively well described by these
conditions, we list 4U 1258-61 (GX 304-1) which
displayed regular type I outbursts every
![]() during most
of the 1970s (Corbet et al. 1986) and which has been dormant
ever since because of the disappearance of the Be disc. Similarly, the
behaviour of 4U1145-619, which displays short and not
very strong outbursts every
during most
of the 1970s (Corbet et al. 1986) and which has been dormant
ever since because of the disappearance of the Be disc. Similarly, the
behaviour of 4U1145-619, which displays short and not
very strong outbursts every ![]() 188 d, is indicative of a
large eccentric orbit. This is supported by the lower limit
188 d, is indicative of a
large eccentric orbit. This is supported by the lower limit
![]() found by Cook & Warwick (1987) from the analysis of changes in
the X-ray pulse timing. Occasionally, some of the periodic outbursts
from 4U1145-619 are rather stronger (challenging the
conventional definition of type II outbursts, since they cannot be
described as very bright). This may be related to a large global
perturbation in the Be disc, reflected in the profile of emission
lines (Stevens et al. 1997). RX J0812.4-3114 has
also shown a long series of type I outbursts without any intervening
type II outburst during a 4-year quasi-cycle of Be disc formation and
dissipation (Reig et al. 2001). Finally
SAXJ2239.3+6116, which has shown several type I outbursts
separated by
found by Cook & Warwick (1987) from the analysis of changes in
the X-ray pulse timing. Occasionally, some of the periodic outbursts
from 4U1145-619 are rather stronger (challenging the
conventional definition of type II outbursts, since they cannot be
described as very bright). This may be related to a large global
perturbation in the Be disc, reflected in the profile of emission
lines (Stevens et al. 1997). RX J0812.4-3114 has
also shown a long series of type I outbursts without any intervening
type II outburst during a 4-year quasi-cycle of Be disc formation and
dissipation (Reig et al. 2001). Finally
SAXJ2239.3+6116, which has shown several type I outbursts
separated by ![]() 262 d, could also belong to this
category.
262 d, could also belong to this
category.
One very peculiar system is A0535-668, which has a very
short orbital period (
![]() )
and is believed to
have a very high eccentricity (Charles et al. 1983). If the
eccentricity is really
)
and is believed to
have a very high eccentricity (Charles et al. 1983). If the
eccentricity is really
![]() ,
the neutron star passes close to the
surface of the Be star at periastron. Our model is simply not
applicable to such an extreme system.
,
the neutron star passes close to the
surface of the Be star at periastron. Our model is simply not
applicable to such an extreme system.
It must be noted that the observed behaviour of GROJ1008-57 is only partially compatible with the orbital model. The type I outbursts are short and not very strong, with similar luminosities, as expected for such a high-eccentricity system. However, the fact that only four have been observed and that they occurred after a type II outburst casts some doubts about the validity of the orbital solution used.
It is well known
that accretion discs in circular binaries with mass ratio
![]() are truncated at the 3:1 resonance radius by the
tidally driven eccentric instability (e.g., Osaki 1996). Since the
mass ratios of all Be/X-ray binaries fall within this range and the
mechanism of truncation is the same for decretion discs as for
accretion discs, we expect that
Be discs in systems with very low orbital eccentricity, say
are truncated at the 3:1 resonance radius by the
tidally driven eccentric instability (e.g., Osaki 1996). Since the
mass ratios of all Be/X-ray binaries fall within this range and the
mechanism of truncation is the same for decretion discs as for
accretion discs, we expect that
Be discs in systems with very low orbital eccentricity, say
![]() ,
are also truncated at the 3:1 resonance radius.
Consequently, the gap size in these systems should be much wider than in
systems with larger eccentricities. Wide gaps in
low-eccentricity systems will result in disc truncation being so effective
that no type I outbursts should occur unless the Be disc is very
strongly disturbed. Therefore it is likely that systems with very low
orbital eccentricity will show only type II outbursts (and perhaps
temporarily type I outbursts only when the disc is strongly disturbed).
,
are also truncated at the 3:1 resonance radius.
Consequently, the gap size in these systems should be much wider than in
systems with larger eccentricities. Wide gaps in
low-eccentricity systems will result in disc truncation being so effective
that no type I outbursts should occur unless the Be disc is very
strongly disturbed. Therefore it is likely that systems with very low
orbital eccentricity will show only type II outbursts (and perhaps
temporarily type I outbursts only when the disc is strongly disturbed).
From this point of view, GS0834-430 is an extraordinary system,
since it has rather low eccentricity (constrained to be
![]() ), but has shown a long series of
type I outbursts (Wilson et al. 1997). It must be noted that the
abrupt change in the separation between outbursts observed during this
series is highly
unusual. Moreover, the decrease in peak intensity of the outbursts
along the series suggests that the Be disc was strongly
perturbed at the time of the outbursts. We have to admit, however,
that with the information available, our model obviously fails to
explain this system.
), but has shown a long series of
type I outbursts (Wilson et al. 1997). It must be noted that the
abrupt change in the separation between outbursts observed during this
series is highly
unusual. Moreover, the decrease in peak intensity of the outbursts
along the series suggests that the Be disc was strongly
perturbed at the time of the outbursts. We have to admit, however,
that with the information available, our model obviously fails to
explain this system.
Apart from X Per, which shows no outbursts, systems with low eccentricity are XTEJ1543-568 (e< 0.03), which has been detected only recently and does not seem to show any clear modulation of its X-ray lightcurve at the orbital period (in't Zand et al. 2001), and 2S1553-542 (e< 0.09), which was only detected once in 1975 (Kelley et al. 1983). Our interpretation of their behaviour is that these objects, because of effective disc truncation, never display type I outbursts. Their discs therefore accumulate mass until very large perturbations develop. Only occasionally will one of these perturbations result in transfer of matter towards the neutron star, producing a bright type II outburst.
In this respect, it is necessary to insist that the physical mechanisms leading to type II outbursts are not well understood. Our model indicates that the truncated discs in Be/X-ray binaries cannot reach a steady state and will continuously grow denser. As a consequence, we expect the discs to become dynamically unstable. In the case of 4U0115+63, which has been carefully studied (and perhaps also in A0535+262), there is observational evidence that links big dynamical instabilities and type II outbursts (Paper II). From this observational fact, we conclude that the dynamical perturbation somehow results in the transfer of large amounts of material from the Be disc to the neutron star. No aspect of our model implies that such mass transfer must occur. It may well be that in systems with low eccentricity, dynamical instability generally leads to the collapse of the disc and its fallback on to the Be star without any substantial amount of material reaching the neutron star. If this is the case, low-eccentricity transients would be completely undetectable most of the time.
Until recently, it had been generally assumed that the orbits of Be/X-ray binaries were in general rather eccentric owing to the effect of supernova kicks. The recent determination of orbital parameters for several systems with low eccentricity (Delgado-Martí et al. 2001; in't Zand et al. 2001) may represent a challenge to this idea. If there is a selection effect against the detection of systems with low eccentricities, their population could be rather larger than previously suspected. If eccentric systems display X-ray outbursts rather more frequently than systems with low eccentricities, they would be more likely to be detected over a limited time-span (such as the time since the start of X-ray astronomy).
The orbit of the pulsar GROJ1948+32 is constrained to have
an eccentricity
![]() and an orbital period
and an orbital period
![]() (Chakrabarty et al. 1995). Its recent
identification with the Be/X-ray transient KS1947+300 means
that it has probably displayed at least three type II outbursts
between 1989 and 2001. An accurate determination of its orbit would
therefore be very important in understanding whether this selection
effect really exists. If its eccentricity turns out to be very low,
then we will have to conclude that low-eccentricity systems may
display type II outbursts as frequently as systems with moderate
eccentricities. If, in contrast, its eccentricity is close to
e=0.25, the available data would suggest that systems with low
eccentricities have less frequent type II outbursts.
(Chakrabarty et al. 1995). Its recent
identification with the Be/X-ray transient KS1947+300 means
that it has probably displayed at least three type II outbursts
between 1989 and 2001. An accurate determination of its orbit would
therefore be very important in understanding whether this selection
effect really exists. If its eccentricity turns out to be very low,
then we will have to conclude that low-eccentricity systems may
display type II outbursts as frequently as systems with moderate
eccentricities. If, in contrast, its eccentricity is close to
e=0.25, the available data would suggest that systems with low
eccentricities have less frequent type II outbursts.
A second system that could serve to understand the outbursting
behaviour of systems with low eccentricities is the LMC transient
EXO0531.1-6609. Based on a statistical parameter
study, Dennerl et al. (1996) conclude that this pulsar
(
![]() )
is likely to have an orbital period
)
is likely to have an orbital period
![]() and low eccentricity
and low eccentricity
![]() .
EXO0531.1-6609 has displayed at least
three relatively bright outbursts extending over more than one orbital
period (i.e., type II) in 1983, 1985 and 1993, but also seems to have
been occasionally detected by ROSAT at a low X-ray luminosity
close to periastron. Obviously confirmation of the orbital parameters
is necessary before any conclusions can be drawn.
.
EXO0531.1-6609 has displayed at least
three relatively bright outbursts extending over more than one orbital
period (i.e., type II) in 1983, 1985 and 1993, but also seems to have
been occasionally detected by ROSAT at a low X-ray luminosity
close to periastron. Obviously confirmation of the orbital parameters
is necessary before any conclusions can be drawn.
Four systems (V0332+53, A0535+262, EXO2030+375, 2S1417-624) among the six Be/X-ray binaries discussed in the previous section have moderate eccentricity. As we have already seen, the model results for these systems turn out to depend on rather subtle details, in contrast to the much more robust predictions for systems with high eccentricity and very low eccentricity. Since the spacing of the candidate truncation radii is rather larger in these systems than in high-eccentricity Be/X-ray binaries, a small difference in the system parameters (orbital, stellar or disc parameters) can produce significantly different X-ray behaviour, depending on whether the resulting truncation radius happens to be close to the critical lobe radius or not. Therefore we have not tried to present general predictions for these systems. Instead, in the previous section we have estimated the truncation radii and system parameters by comparing the model results with the observed X-ray behaviour. In this sense, the current status of our model can still be considered to be "at the qualitative level'' for mildly eccentric systems. We estimated that Be discs in V0332+53, A0535+262 in the X-ray active state, and EXO2030+375 are truncated at the 4:1 resonance radius, while those in A0535+262 in quiescence and 2S1417-624 are truncated at the 5:1 resonance radius. The smaller truncation radius for A0535+262 in quiescence might suggest a slightly lower disc temperature in this state than in the X-ray active state. To understand more about these systems, we need a more sophisticated model for the interaction between the Be disc and the neutron star.
It is worth noting, however, that all the intermediate
eccentricity Be/X-ray binaries known have displayed type II
outbursts. This is the case for the four systems listed here and also
for GROJ1750-27, a presumably very distant source (with
![]() and e=0.36) which has only been
detected once during a type II outburst (Scott et al. 1997). This fact suggests that disc truncation is
generally rather effective for orbital eccentricities
and e=0.36) which has only been
detected once during a type II outburst (Scott et al. 1997). This fact suggests that disc truncation is
generally rather effective for orbital eccentricities
![]() ,
even
though the discs in A0535+262 and EXO2030+375,
under certain conditions, seem to reach a state in which truncation is
not so effective and long series of type I outbursts occur (not
surprisingly, these two systems have the largest eccentricities and
longest periods among the five known).
,
even
though the discs in A0535+262 and EXO2030+375,
under certain conditions, seem to reach a state in which truncation is
not so effective and long series of type I outbursts occur (not
surprisingly, these two systems have the largest eccentricities and
longest periods among the five known).
Though systems with moderate eccentricities dominate the sample of Be/X-ray binaries for which orbital solutions exist at present, it is important to note that at least two important selection effects may have been at work in the definition of this sample:
Because of these two factors, judgement on what sort of X-ray behaviour is more "typical'' among Be/X-ray binaries has to be suspended until a rather larger sample is known.
Many of the systems under discussion have shown short series of irregular type I outbursts. This category includes 4U0115+63, V0332+53, 2S1417-624 and presumably GROJ2058+42, for which no orbital solution exists. These series have generally occurred in connection with type II outbursts (in most cases, after a type II outburst). The behaviour of A0535+262 has also been similar on some occasions. As mentioned in Sect. 5.4, we expect that the temporary type I outbursts occur in systems in which the Be disc has a radius significantly smaller than (but not too small compared to) the critical lobe radius under normal conditions. These systems will be mostly mildly eccentric systems. If the Be disc in such a system is strongly disturbed by, e.g., radiation-driven warping and/or a global density wave, it will become strongly asymmetric. Then, if the disc elongation is roughly in the periastron direction, the disc will be capable of fuelling the neutron star and cause a sequence of type I X-ray outbursts (see scenario B in Fig. 3). Since GROJ2058+42 has apparently displayed similar behaviour, we expect it to have moderate eccentricity.
A relationship between the X-ray behaviour and the orbital eccentricity stems naturally from the truncated disc model. In general, the presence of regular type I X-ray outbursts indicates that the truncated disc around the Be star has a radius close to or slightly larger than the critical lobe radius at periastron. Such a situation occurs in all systems with highly eccentric orbit, some mildly eccentric systems, and no systems with low eccentricity (GS0834-430 may be an exception). In a rough sense, the lower the orbital eccentricity, the wider the gap between the truncation radius and the critical lobe radius and therefore the more difficult the accretion on to the neutron star.
A source which hardly fits in this picture is
A0726-26. This persistent low-luminosity X-ray source
which has never shown outbursts displays, however, a 35-d modulation
in its X-ray emission (Corbet & Peele 1997). If this is the
orbital period, A0726-26 presents very few similarities
to other Be/X-ray binaries, falls very far away from the
![]() correlation and cannot be explained by our
model.
correlation and cannot be explained by our
model.
Among the Be/X-ray binaries with known counterparts, two systems have been very rarely detected as X-ray sources, and even then they have been relatively weak. A1118-616 has only been detected twice, in 1975 and in 1991. In both cases, the outburst was long, but not very bright. Cep X-4 has been detected four times between 1972 and 1997. All the outbursts have also been relatively weak. The two sources display permanent low-luminosity X-ray emission when not in outburst. In both cases, the counterparts present evidence for very large circumstellar discs. Therefore we expect these two systems to have wide and not very eccentric orbits.
We note that even at the qualitative level our model has some predictive power and can thus be tested. Finding out, for example, that RX J0812.4-3114 has an orbital eccentricity close to zero or that A1118-616 has a very eccentric orbit would certainly force us to reconsider most of the conclusions reached here.
We have applied the resonantly truncated disc model developed by
Negueruela & Okazaki (2001) to six systems which have
displayed type I X-ray outbursts.
We have found that the model
naturally explains the X-ray behaviour of these systems and
that all systems are consistent with having a similar viscosity parameter
![]() .
.
In our model, regular type I X-ray outbursts occur in all systems with high orbital eccentricity, some mildly eccentric systems, and no systems with low eccentricity. On the other hand, systems which have temporarily shown type I outbursts will be mostly mildly eccentric systems, in which the Be disc temporarily becomes strongly asymmetric.
In the scenario presented here for Be/X-ray transients, disc material can reach the neutron star only via the L1 point, and will therefore have a not very high velocity relative to the neutron star. Since such a flow (which may be said to represent the disc version of Roche-lobe overflow) carries high angular momentum, an accretion disc may temporarily be formed around the neutron star during each X-ray outburst. Such temporary accretion discs have probably been observed in 2S1845-024 (Finger et al. 1999), but extensive searches have failed to detect them around A0535+262 (Motch et al. 1991). The accretion flow in the vicinity of the neutron star (i.e., once it has left the effective Roche lobe of the Be star) should be modelled in detail in order to understand if such discs should always form and to predict the X-ray lightcurves derived from our scenario.
Acknowledgements
We thank J. M. Porter, M. H. Finger, and G. I. Ogilvie for many helpful discussions. We also thank the referee M. H. van Kerkwijk for his valuable comments. ATO thanks the Institute of Astronomy, Cambridge, UK, and the Observatoire de Strasbourg, France, for the warm hospitality.