This paper scrutinizes the validity of the thin-flux-tube approximation for magnetic flux tubes embedded in a surrounding magnetic plasma. It is shown that the thin-flux-tube approximation gives an accurate description of surface waves for
A&A 377, 330-342 (2001)
DOI: 10.1051/0004-6361:20011094
Y. D. Zhugzhda1,2 - M. Goossens1
1 - Center for Plasma Astrophysics, K.U. Leuven, 3001
Heverlee, Belgium
2 - IZMIRAN, Troitsk, Moscow Region, 142092,
Russia
Received 9 November 2000 / Accepted 31 July 2001
Abstract
This paper scrutinizes the validity of the thin-flux-tube
approximation for magnetic flux tubes embedded in a surrounding
magnetic plasma. It is shown that the thin-flux-tube
approximation gives an accurate description of surface waves for
![]() ,
body waves for
,
body waves for
![]() and surface leaky waves for
and surface leaky waves for
![]() .
The Leibovich-Roberts equation for nonlinear
surface waves in a flux tube embedded in a field free plasma is
generalized to a flux tube immersed in a magnetic plasma. The
generalized Leibovich-Roberts (GLR) equation describes the
propagation of nonlinear slow surface, body and surface leaky
waves in tubes. The shortcomings of the GLR equation are
discussed. The Korteweg-de Vries equation (KdV) is generalized
for surface waves. The advantage of the second order
thin-flux-tube approximation is shown. Two scenarios for the
heating of coronal loops are discussed. It is emphasized, that
the application of the thin-flux-tube approximation to thin tubes
of non-zero diameter has to take into account possible wave
emission by the tube and shock front formation for amplitudes in
excess of some critical value.
.
The Leibovich-Roberts equation for nonlinear
surface waves in a flux tube embedded in a field free plasma is
generalized to a flux tube immersed in a magnetic plasma. The
generalized Leibovich-Roberts (GLR) equation describes the
propagation of nonlinear slow surface, body and surface leaky
waves in tubes. The shortcomings of the GLR equation are
discussed. The Korteweg-de Vries equation (KdV) is generalized
for surface waves. The advantage of the second order
thin-flux-tube approximation is shown. Two scenarios for the
heating of coronal loops are discussed. It is emphasized, that
the application of the thin-flux-tube approximation to thin tubes
of non-zero diameter has to take into account possible wave
emission by the tube and shock front formation for amplitudes in
excess of some critical value.
Key words: agnetohydrodynamics (MHD) - waves - Sun: corona - oscillations
The study of the dynamics of magnetic solar and stellar
atmospheres is severely complicated by the joint presence of
stratification due to gravity and structuring due to the
inhomogeneous magnetic field. Part of this complication can be
circumvented by using the thin-flux-tube approximation introduced
by Roberts & Webb (1978). This approximation is often used for
studying MHD waves in magnetic flux tubes. A major advantage of
this approximation is that a 3D-problem is reduced to a set of 1D
equations. This makes a wide variety of problems of linear and
nonlinear waves in the solar atmosphere tractable for theoretical
analysis and numerical simulation. However, when approximations
are introduced, it is necessary to try and understand when and
where they give an accurate description of physical reality and
to see whether or not essential effects have been omitted.
Naively one might assume that
![]() (k is the
longitudinal wavenumber and
(k is the
longitudinal wavenumber and ![]() is the tube radius) is the only
condition to be satisfied for the thin-flux-tube approximation to
be valid. The aim of the current paper is to show that the
conditions for the thin-flux-tube approximation to be valid are
more subtle and are related to the effects of the surrounding
plasma on the tube dynamics.
is the tube radius) is the only
condition to be satisfied for the thin-flux-tube approximation to
be valid. The aim of the current paper is to show that the
conditions for the thin-flux-tube approximation to be valid are
more subtle and are related to the effects of the surrounding
plasma on the tube dynamics.
Roberts & Webb (1978) showed that the thin-flux-tube
approximation describes slow surface modes. Ferriz-Mas et al.
(1989) reconsidered the problem and confirmed that the thin-flux-tube
approximation describes slow surface modes. Both
investigations dealt with waves in an isolated flux tube embedded
in a magnetic field free plasma. However, the thin flux tube
approximation is also used for studying waves in magnetic flux
tubes in the solar chromosphere and corona, where the tubes are
surrounded by a magnetic plasma (Herboldt et al. 1985;
Ulmschneider et al. 1991). The free boundary condition, which
is used in the thin-flux-tube approximation, assumes just
constancy of the external pressure without specifying whether
this is gas pressure or magnetic pressure or both. As a matter
of fact the thin-flux-tube approximation is valid only for an
infinitely thin tube, when
![]() ,
while it is used
for thin tubes with
,
while it is used
for thin tubes with
![]() .
In that case, the effect of the
surroundings depends on the the parameters of the surrounding
plasma. In addition, so far the thin-flux-tube limit has only
shown to exist for a magnetic field-free external plasma. As a
consequence, the conditions for the thin-tube approximation to be
valid have not yet been explored for tubes embedded in a magnetic
plasma. We focus here on this problem for both linear and
nonlinear waves in a thin tube, which sometimes will be referred
to as tube waves.
.
In that case, the effect of the
surroundings depends on the the parameters of the surrounding
plasma. In addition, so far the thin-flux-tube limit has only
shown to exist for a magnetic field-free external plasma. As a
consequence, the conditions for the thin-tube approximation to be
valid have not yet been explored for tubes embedded in a magnetic
plasma. We focus here on this problem for both linear and
nonlinear waves in a thin tube, which sometimes will be referred
to as tube waves.
The paper is organized as follows. First, the dispersion equation for waves in flux tubes is rewritten to separate the dispersion equation for slow waves. The thin tube limit is explored for a thin tube surrounded by a magnetic plasma. The approximate dispersion relation for tube waves in thin tubes of non-zero diameter is obtained. The advantage of the second order thin-flux-tube approximation (Zhugzhda 1996) is discussed shortly. Weakly nonlinear waves in thin tubes are studied and the Leibovich-Roberts equation is generalized. The KdV equation for slow body waves in a thin tube (Zhugzhda & Nakariakov 1997a) is generalized to surface waves. Finally, two scenarios for the heating of coronal loops by slow waves are discussed using the current analysis of linear and nonlinear waves in thin tubes.
In the thin-flux-tube approximation (Roberts & Webb 1978)
the full set of non-linear MHD equations is reduced to the
following set of equations:
Before proceeding to hidden problems of the thin-flux-tube approximation we first explore in this section the crucial point whether the thin tube limit exists for an arbitrary external medium. Only then does it make sense to look at possible inaccuracies introduced by using the thin-flux-tube approximation to study waves in thin tubes of non-zero diameter.
To attack the problem we modify the dispersion equation for
axisymmetric waves in a flux tube immersed in a magnetic
plasma, which was derived by (Meerson et al. 1978; Wilson 1980;
Spruit 1982; Edwin & Roberts 1983). In what follows we refer to
the paper by Edwin & Roberts (1983), as it contains the most
complete exploration of the rather complex array of wave modes
governed by this equation. For body waves it reads
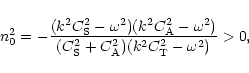
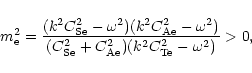
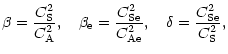 |
|||
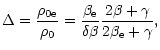 |
(7) |
In order to separate the equation for the slow body waves we
rewrite the dispersion Eq. (6) as
The separation of the slow from the fast waves is possible due to
choice of the sign in front of the square root in the expression
for the frequency
![]() .
When
.
When ![]() ,
,
![]() ,
,
![]() and x are fixed, Eq. (9) is an equation with
respect to j, and, in general, j
and x are fixed, Eq. (9) is an equation with
respect to j, and, in general, j
![]() .
The frequency of the slow body
waves as a function of the dimensionless wavenumber x for fixed
.
The frequency of the slow body
waves as a function of the dimensionless wavenumber x for fixed
![]() ,
,
![]() and
and ![]() is defined by (11) after
substitution of the root j of Eq. (9). The dispersion
equation for fast body waves can be obtained by a change of the
sign in front of the square root in (11).
is defined by (11) after
substitution of the root j of Eq. (9). The dispersion
equation for fast body waves can be obtained by a change of the
sign in front of the square root in (11).
For the surface waves the dispersion equation (Roberts & Edwin 1983) reads
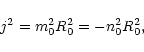 |
(13) |
![\begin{displaymath}m_{\rm s}=\sqrt{\frac{[\delta(1+\beta)-\Omega_{\rm s}^2][\del...
...+\beta)[\delta(1+\beta)-
(1+\beta_{\rm e})\Omega_{\rm s}^2]}},
\end{displaymath}](/articles/aa/full/2001/37/aah2536/img65.gif) |
(15) |
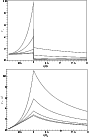 |
Figure 1:
The eigenfunctions of longitudinal velocity
|
| Open with DEXTER | |
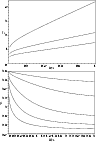 |
Figure 2:
The dependence of the first root |
| Open with DEXTER | |
In most cases the flux tubes in the photospheric and
subphotospheric layers are isolated from each other by magnetic
field free plasmas with
![]() and
and
![]() It
is our impression that Roberts & Webb (1978) had this situation
in mind, when they studied the thin tube limit. We consider this
situation first to explain our approach, which differs from that
of Roberts & Webb (1978). Figure 2 shows the results of
numerically solving the dispersion Eq. (14) for slow body
(9) and slow surface (14) modes for
It
is our impression that Roberts & Webb (1978) had this situation
in mind, when they studied the thin tube limit. We consider this
situation first to explain our approach, which differs from that
of Roberts & Webb (1978). Figure 2 shows the results of
numerically solving the dispersion Eq. (14) for slow body
(9) and slow surface (14) modes for ![]() ,
,
![]() and for different ratios of external
and internal sound velocities
and for different ratios of external
and internal sound velocities
![]() .
The first
root of the dispersion Eq. (14) for slow surface
modes tends to zero, when we decrease the diameter of the tube for
a fixed wavenumber (
.
The first
root of the dispersion Eq. (14) for slow surface
modes tends to zero, when we decrease the diameter of the tube for
a fixed wavenumber (
![]() ,
,
![]() )
and for all values
of the ratio of the external and internal sound speeds
)
and for all values
of the ratio of the external and internal sound speeds ![]() .
It is well-known (Edwin & Roberts 1983) that the
eigenfunctions of the wave quantities in a flux tube can be
expressed in terms of Bessel functions. Here the eigenfunctions
of
.
It is well-known (Edwin & Roberts 1983) that the
eigenfunctions of the wave quantities in a flux tube can be
expressed in terms of Bessel functions. Here the eigenfunctions
of
![]() and
and
![]() are proportional to
are proportional to
![]() and
and
![]() respectively. When
respectively. When
![]() the longitudinal velocity tends
to a non-zero constant across the tube, while the radial velocity
tends to zero. Results of exact calculations for the
eigenfunctions of the surface mode in a thin flux tube
(
the longitudinal velocity tends
to a non-zero constant across the tube, while the radial velocity
tends to zero. Results of exact calculations for the
eigenfunctions of the surface mode in a thin flux tube
(
![]() )
are shown in Fig. 1. The amplitude of
the longitudinal velocity is almost constant across the tube for
)
are shown in Fig. 1. The amplitude of
the longitudinal velocity is almost constant across the tube for
![]() ,
while it increases toward the boundary for
,
while it increases toward the boundary for
![]() .
The radial velocity is one order of magnitude
smaller. When we decrease the diameter of the tube the
longitudinal velocity tends more and more to a constant across
the tube. The eigenfunctions of the slow mode show that the
accuracy of the thin-flux-tube approximation for describing the
surface slow modes in thin flux tubes depends on the value of
.
The radial velocity is one order of magnitude
smaller. When we decrease the diameter of the tube the
longitudinal velocity tends more and more to a constant across
the tube. The eigenfunctions of the slow mode show that the
accuracy of the thin-flux-tube approximation for describing the
surface slow modes in thin flux tubes depends on the value of
![]() .
Hence, the thin tube limit exists, because there is
a root of the dispersion Eq. (14), which tends to
zero with
.
Hence, the thin tube limit exists, because there is
a root of the dispersion Eq. (14), which tends to
zero with
![]() (see, Fig. 2). In summary, the
present analysis shows, that the thin-flux-tube approximation
gives a correct description of the slow surface modes for a flux
tube embedded in a magnetic free plasma. We arrive at the same
conclusion as Roberts & Webb (1978). It is straightforward to
check, whether there is a similar root of the dispersion
Eq. (14) for surface waves when
(see, Fig. 2). In summary, the
present analysis shows, that the thin-flux-tube approximation
gives a correct description of the slow surface modes for a flux
tube embedded in a magnetic free plasma. We arrive at the same
conclusion as Roberts & Webb (1978). It is straightforward to
check, whether there is a similar root of the dispersion
Eq. (14) for surface waves when
![]() .
The dispersion Eq. (14) has a root, which tends to
zero for
.
The dispersion Eq. (14) has a root, which tends to
zero for
![]() ,
when the condition
,
when the condition
It is instructive to explore the dispersion Eq. (9) for
slow body waves, when the condition (18)
is valid. First of all Eq. (9) has an infinite number of
real roots, while Eq. (14) has only one real root.
Figure 2 shows numerical solutions to Eq. (9). The
first root of the dispersion Eq. (9) of the slow body modes
varies in the range
![]() and in the
limit
and in the
limit
![]() it tends to
it tends to
![]() for all values
of
for all values
of ![]() .
The behaviour of the first root for the general case
of
.
The behaviour of the first root for the general case
of
![]() is the same. The eigenfunction of the
longitudinal velocity of the body mode changes sign inside the
tube and does not become constant across the tube, as it should
do according to the thin flux tube approximation. In addition,
the eigenfunction of the radial velocity does not tend to zero,
and this also is in contradiction with the assumption of a free
boundary in the thin-flux-tube approximation. Thus, the
thin-flux-tube approximation can not describe slow body modes for
the case of (18).
is the same. The eigenfunction of the
longitudinal velocity of the body mode changes sign inside the
tube and does not become constant across the tube, as it should
do according to the thin flux tube approximation. In addition,
the eigenfunction of the radial velocity does not tend to zero,
and this also is in contradiction with the assumption of a free
boundary in the thin-flux-tube approximation. Thus, the
thin-flux-tube approximation can not describe slow body modes for
the case of (18).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{H2536F3.eps} \end{figure}](/articles/aa/full/2001/37/aah2536/Timg90.gif) |
Figure 3:
The dependence of the first root |
| Open with DEXTER | |
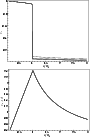 |
Figure 4:
The eigenfunctions of longitudinal velocity
|
| Open with DEXTER | |
Flux tubes in the chromosphere and corona cannot be embedded in a field free plasma, because the gas pressure is small in comparison to the magnetic pressure. Thus, the flux tubes in the chromosphere and corona differ from the surrounding plasma in density and/or temperature. Also, in the case of the solar corona and chromosphere the name flux tubes is rather misleading, as the magnetic field can be weaker inside the structure than outside since the gas pressure is lower outside due to the temperature or density difference. Although the gas pressure is negligible in comparison with the magnetic pressure in the corona, it is essential for the properties of waves in tubes. The equilibrium magnetic configuration in the corona can be considered as a force-free. The thin-flux tube approximation for swaying tubes is used to explore the dynamics of flux tubes in the chromosphere and corona (Herboldt et al. 1985; Ulmschneider et al. 1991). The longitudinal waves in a swaying tube obey the same equation as for straight tubes except for the effect of the nonlinear coupling with the kink mode (Nakariakov et al. 1996).
Let us explore the dispersion Eq. (9) for slow body waves,
when the condition
In the previous sections we showed that for "weak'' and "strong''
external fields defined by the conditions (17) and (20) the thin-flux-tube approximation describes slow
surface or slow body waves, respectively. But in the range
defined by the inequalities
![\begin{displaymath}n_{\rm s}=\sqrt{\frac{[\Omega_{\rm s}^2-\delta(1+\beta)][\del...
...(1+\beta)[\delta(1+\beta)-(1+\beta_{\rm e})\Omega_{\rm s}^2]}}
\end{displaymath}](/articles/aa/full/2001/37/aah2536/img112.gif) |
(27) |
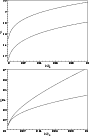 |
Figure 5:
The dependence of the real (top) and
imaginary (bottom) parts of the first root |
| Open with DEXTER | |
![\begin{displaymath}n_{\rm b}=\sqrt{\frac{[\Omega_{\rm b}^2-\delta(1+\beta)][\del...
...1+\beta)[\delta(1+\beta)-(1+\beta_{\rm e})\Omega_{\rm b}^2]}},
\end{displaymath}](/articles/aa/full/2001/37/aah2536/img115.gif) |
(29) |
Thus the thin-flux-tube limit exists for all ranges of magnetic fields and sound velocities outside and inside tube. It shows up as the limit of either the slow surface or leaky surface or body waves depending on the value of the external magnetic field. It is remarkable that all of these modes exist only when the effect of the external medium is taken into account. The tube waves in an infinitely thin tube exist because of the effect of the external plasma. A paradox of the thin-flux-tube approximation is that the set of Eqs. ((1)-(5)) of the thin-flux-tube approximation does not depend on parameters of the external plasma. It becomes possible due the absence of the wave dispersion as well as the wave attenuation due to wave emission in the thin tube limit. The ignorance of this hidden problem can lead to erroneous results when the thin-flux-tube approximation is applied to waves in thin tubes with a finite diameter. Slow waves could undergo essential attenuation in thin tubes immersed in a plasma with a "intermediate'' magnetic field. This effect is completely lost in the thin-flux-tube approximation.
Intuitively it might be anticipated that the neglect of wave dispersion in the thin-tube approximation is less severe than the neglect of attenuation, because dispersion is weak in thin tubes. However, this is not correct. The neglect of wave dispersion is essential for the nonlinear waves. The effects of dispersion on nonlinear waves in a thin tube are considered in Sect. 5.
Once the thin tube limit for an arbitrary external medium is known, it is simple to obtain the approximate dispersion relation for a thin tube with a non-zero diameter. The approximate dispersion relation defines the dispersion, which is not significant for linear waves in a sufficiently thin tube, but which is crucial for the properties of nonlinear waves. The attenuation of waves due to wave emission by the tube can also be estimated from the approximate dispersion equation and is essential for both linear and nonlinear waves.
For a "weak'' external magnetic field, when the condition (18) is valid, the dispersion Eq. (14) for
slow surface waves has a single root, which in the thin
tube limit tends to zero ![]() and equals, approximately, to
and equals, approximately, to
For weak dispersion the dimensionless frequency of the surface
waves (16) equals approximately
![\begin{displaymath}m=\sqrt{\frac{[\delta(1+\beta)-1][\delta(1+\beta)-
\beta_{\rm e}]}{\delta(1+\beta)[\delta(1+\beta)-(1+\beta_{\rm e})]}},
\end{displaymath}](/articles/aa/full/2001/37/aah2536/img132.gif) |
(33) |
For the discussion of nonlinear waves in later sections we
need to know the short wavelength limit
![]() of the
dimensionless frequency (phase velocity)
of the
dimensionless frequency (phase velocity) ![]() of the surface
waves. Using the appropriate asymptotic expressions of the
modified Bessel functions for large arguments we can rewrite the
dispersion Eq. (14) of the surface waves as
of the surface
waves. Using the appropriate asymptotic expressions of the
modified Bessel functions for large arguments we can rewrite the
dispersion Eq. (14) of the surface waves as
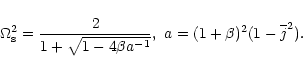 |
(36) |
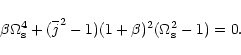 |
(37) |
The dispersion Eq. (9) for the slow body waves
has an infinite number of roots. Only for a "strong'' external
magnetic, when condition (23) is satisfied, does the first
root of (9) tend to zero in the thin tube limit. The root equals
approximately to
When we use the asymptotics of the modified Bessel function
![]() ,
we can further simplify the approximate dispersion
Eq. (34) for surface waves in a "weak''
magnetic field and for body waves in a "strong'' magnetic field to
,
we can further simplify the approximate dispersion
Eq. (34) for surface waves in a "weak''
magnetic field and for body waves in a "strong'' magnetic field to
The first root of the exact dispersion Eq. (9)
varies from
![]() to
to
![]() while the dimensionless
wavenumber increases from x=0 to
while the dimensionless
wavenumber increases from x=0 to ![]() ,
because the Bessel
function
,
because the Bessel
function
![]() changes its sign for j=2.405 and Eq. (9)
has not any real roots.
changes its sign for j=2.405 and Eq. (9)
has not any real roots.
The next roots, as it was mentioned in Sect. 2.3, are in the
ranges
j1,n-1<jn<j0,n+1. The roots of Eq. (9)
exist only for the ranges of j, where the Bessel functions
![]() and
and
![]() have the same signs. The approximate
dispersion relations for the next roots of the exact dispersion
Eq. (9) for body waves in the thin tube limit reads
have the same signs. The approximate
dispersion relations for the next roots of the exact dispersion
Eq. (9) for body waves in the thin tube limit reads
The short wavelength limit
![]() of the dimensionles
frequency (11) is the same for all slow body modes. It
does not depend on the parameters of external plasma
of the dimensionles
frequency (11) is the same for all slow body modes. It
does not depend on the parameters of external plasma
When the condition of an "intermediate'' external field (23) is satisfied, the approximate dispersion equation
can be obtained by a similar procedure to either the dispersion
Eq. (26) for the leaky surface waves or the
dispersion Eq. (28) for the leaky body waves (28). The
result is the same in both cases. The first root of the
dispersion Eq. (26) for leaky surface waves for
![]() equals approximately
equals approximately
![\begin{displaymath}n=\sqrt{\frac{[1-\delta(1+\beta)][\delta(1+\beta)-
\beta_{\rm e}]}{\delta(1+\beta)[\delta(1+\beta)-(1+\beta_{\rm e})]}}\cdot
\end{displaymath}](/articles/aa/full/2001/37/aah2536/img165.gif) |
(46) |
Particular attention has been given to the dispersion of waves because the difference of the sign of the dispersion of slow waves in thin tubes immersed in "weak'' and "strong'' external magnetic fields is crucial for the properties of nonlinear waves, which are considered below.
Zhugzhda (1996) derived a second order thin-flux-tube approximation, which takes into account wave dispersion, as distinct from the zero order approximation discussed above.
The basic set of equations of the second-order approximations
reads
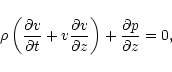 |
(47) |
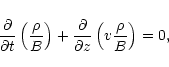 |
(48) |
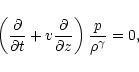 |
(49) |
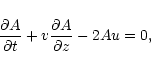 |
(50) |
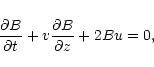 |
(51) |
![$\displaystyle p + \displaystyle\frac{B^2}{8 \pi} - \displaystyle\frac{A}{2 \pi}...
...playstyle\frac{
\partial B}{\partial z}\right)^2\right ) \bigg ] = p_{\rm ext},$](/articles/aa/full/2001/37/aah2536/img172.gif) |
(52) |
In this approximation the dispersion relation reads in our
dimensionless variables
Moreover, the dispersion Eq. (53) provides the
exact value of the short wavelength limit
![]() for the
dimensionless frequency
for the
dimensionless frequency
![]() (to compare with
(43)). Thus, the second order thin-flux-tube
approximation works also for a thick tube, when
(to compare with
(43)). Thus, the second order thin-flux-tube
approximation works also for a thick tube, when
![]() .
It seems likely, that the second order thin flux tube
approximation (Zhugzhda 1996) is a two mode approximation, which
describes the first slow and fast modes in the tube (Zhugzhda 2001).
.
It seems likely, that the second order thin flux tube
approximation (Zhugzhda 1996) is a two mode approximation, which
describes the first slow and fast modes in the tube (Zhugzhda 2001).
The second order thin tube approximation needs a detailed exploration similar to the current analysis of the zero order thin-flux-tube approximation. However, this is beyond the scope of our present paper. But it is evident, that there is a basic difference between the zero and the second order approximations. The last one is a powerful tool for exploring nonlinear waves by analytical and numerical methods, because it takes into account the wave dispersion.
Within the thin-flux-tube approximation the waves of finite amplitude cannot but form shocks. This is not the case for a thin tube of non-zero diameter due to the effect of the wave dispersion. When the wave amplitudes are sufficiently small for the nonlinear effects to be compensated by the dispersion, shock fronts do not appear and the waves are weakly nonlinear. The theory of weakly nonlinear waves in thin tubes embedded in an non-magnetic plasma was developed by Roberts (1985). The above analysis of the thin tube limit makes it possible to extend the theory of Roberts to an arbitrary external medium. We follow mainly the approach developed by Zhugzhda (2000).
Roberts (1985) derived the equation for weakly nonlinear surface
slow waves in a thin flux tube embedded in a magnetic field
free plasma. The equation is known as the Leibovich-Roberts (LR)
equation and reads
![\begin{displaymath}\frac{\partial v}{\partial t} + C_{\rm T} \frac{\partial
v}{\...
... ,t) {\rm
d}z^\prime}{[\lambda^2 +(z^\prime-z)^2]^{1/2}} = 0,
\end{displaymath}](/articles/aa/full/2001/37/aah2536/img180.gif)
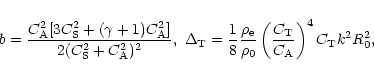
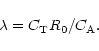
The LR equation can be derived by the method of Whitham (1974),
when the dispersion law is known. Whitham showed, that the 1-D
wave equation for a given dependence of the phase
velocity C(k) on the wave number reads
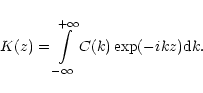
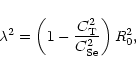 |
(62) |
In order to obtain the nonlinear equation for the leaky surface
waves we have to extend the method of Whitham (1974) to
![]() ,
which corresponds to the condition (24)
for the leaky surface waves to exist in a thin tube. We can
write the approximate dispersion Eq. (45) for this case
as
,
which corresponds to the condition (24)
for the leaky surface waves to exist in a thin tube. We can
write the approximate dispersion Eq. (45) for this case
as
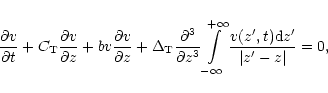 |
(65) |
On first sight the derivation of GLR equation gives a solid basis
for studying weakly nonlinear waves in a thin tube and the only
problem to be handled is this nonlinear equation. But there are
hidden problems in both the LR and the GLR equation. An
analytical solution of the Leibovich equation (Leibovich 1970) is
not yet known for waves on a cylindrical vortex core. Solitary
solutions have been found experimentally by Pritchard (1970) and
numerically by Leibovich & Randall (1972). As for the LR
equation, Bogdan & Lerche (1988) claimed that there are
soliton-like solutions of this equation. Numerical solutions of
the LR equation have been obtained by Weisshaar (1989). He
pointed out that the scale parameter ![]() ,
which appears in
the LR equation but not in the Leibovich equation, introduces
essential differences in the properties of the solutions. The
numerical analysis (Weisshaar 1989) showed, that the solitary
wave solutions of the LR equation are not self-similar and exist
only up to some critical amplitude. The critical amplitude shows
up because phase velocity as defined by (57) has a
maximum. If the amplitude exceeds a critical value, the
dispersion appears to be insufficient to smooth out the wave
front and a shock has to form. The same effect has to be present
for the GLR equation, because the approximate dispersion Eq. (57)
is valid for both a non-magnetic and a magnetic
plasma outside the tube. Thus, the GLR equation describes the
behaviour of weakly nonlinear waves, whose phase velocity has an
extremum in the linear limit. In the limit of large and small
wavenumbers the phase velocity of the linear waves is the same.
,
which appears in
the LR equation but not in the Leibovich equation, introduces
essential differences in the properties of the solutions. The
numerical analysis (Weisshaar 1989) showed, that the solitary
wave solutions of the LR equation are not self-similar and exist
only up to some critical amplitude. The critical amplitude shows
up because phase velocity as defined by (57) has a
maximum. If the amplitude exceeds a critical value, the
dispersion appears to be insufficient to smooth out the wave
front and a shock has to form. The same effect has to be present
for the GLR equation, because the approximate dispersion Eq. (57)
is valid for both a non-magnetic and a magnetic
plasma outside the tube. Thus, the GLR equation describes the
behaviour of weakly nonlinear waves, whose phase velocity has an
extremum in the linear limit. In the limit of large and small
wavenumbers the phase velocity of the linear waves is the same.
As a matter of fact the derivation of the GLR equation suffers
from an inconsistency as the equation takes large wavenumbers
into account, while its derivation is based on the approximate
dispersion relation for small wavenumbers, which has an
extremum. It is shown earlier in this paper, that the phase
speed of surface waves decreases and tends to a velocity below
the tube velocity ![]() ,
without having a minimum. While the
phase velocity of body waves for a "strong'' external field
increases and tends to the sound speed without attaining a
maximum. A similar problem exists for the leaky surface waves,
because the dispersion and absorption terms in the approximate
dispersion Eq. (63) become oscillatory for large
k. The numerical solutions of the exact dispersion Eq. (26)
reveal that the dispersion and absorption of
leaky surface waves depend monotonically on the wavenumber, which
is the only physically admissible behaviour. Therefore, the GLR
and LR equations are, strictly speaking, not suited for treating
weakly nonlinear body and surface waves with amplitudes, which
are affected by the existence of an extremum in the phase
velocity.
,
without having a minimum. While the
phase velocity of body waves for a "strong'' external field
increases and tends to the sound speed without attaining a
maximum. A similar problem exists for the leaky surface waves,
because the dispersion and absorption terms in the approximate
dispersion Eq. (63) become oscillatory for large
k. The numerical solutions of the exact dispersion Eq. (26)
reveal that the dispersion and absorption of
leaky surface waves depend monotonically on the wavenumber, which
is the only physically admissible behaviour. Therefore, the GLR
and LR equations are, strictly speaking, not suited for treating
weakly nonlinear body and surface waves with amplitudes, which
are affected by the existence of an extremum in the phase
velocity.
Zhugzhda & Nakariakov (1997a) derived the KdV equation for slow
body waves in the thin flux tube. They used the second order
thin-flux-tube approximation (Zhugzhda 1996). First, they
obtained the nonlinear wave equation by the expansion of the
equations up to the second order of the amplitude. Second, they
obtained the KdV equation from the nonlinear wave equation by
multi-scale analysis. It was revealed above, that the
second-order thin-flux-tube approximation describes slow body
waves in a thin tube immersed in a plasma with a "very strong''
magnetic field, that is in the limit
![]() .
Because
of the coefficient b in front of the nonlinear term is known,
the use of Whitham's equation makes it possible to obtain the KdV
equation for both slow surface waves in a thin tube with a "weak''
field and for slow body waves in a thin tube with a "strong''
field. In the co-moving coordinate system it reads
.
Because
of the coefficient b in front of the nonlinear term is known,
the use of Whitham's equation makes it possible to obtain the KdV
equation for both slow surface waves in a thin tube with a "weak''
field and for slow body waves in a thin tube with a "strong''
field. In the co-moving coordinate system it reads
The KdV Eq. (66) is useful for astrophysical
applications, because its solutions are simple and well explored.
On the other hand, the absence of exact analytical solutions of
the LR equation prevents us from making qualitative statements on
weakly nonlinear waves in astrophysical plasmas. The KdV
equation is valid for any amplitudes of the solitons, as
unbounded increasing of the dispersion is assumed. As it was
shown above the phase velocity of the slow surface and the body
waves tend to a finite limit for
![]() .
Thus, the KdV
equation suffices only for describing solitons, which have a
relatively small amplitude, and for which the high harmonics
.
Thus, the KdV
equation suffices only for describing solitons, which have a
relatively small amplitude, and for which the high harmonics
![]() are not essential.
are not essential.
The paper shows that the thin-flux-tube approximation is valid for any plasma environment of the tube. In fact, the thin flux tube approximation is used to treat the dynamics of thin flux tubes of a small diameter, but not infinitely thin tubes, which are just a very useful mathematical limit. Our analysis identifies which physical effects are dropped, when the thin flux tube approximation is applied to thin tubes with a non-zero diameter. In addition, it makes it possible to take into account the effects that were omitted originally, namely, the wave dispersion and emission. Dispersion, omitted originally in the thin tube approximation, is not very important for linear waves in thin flux tubes, because the discrepancy between the tube velocity and exact phase velocity in a thin tube is so small that the wave propagation along the tube is not changed radically. Attenuation of waves due to radiation of waves by the tube, which occurs when the condition (25) is satisfied, is a different story. In this case linear waves are not trapped in the tube.
The attenuation due to the wave radiation by the tube decreases
with decreasing diameter. This is crucial for a scenario of the
heating of the upper solar atmosphere by waves excited in tubes
by convective turbulence. There are two main scenarios in
connection with the effect of wave radiation. The first scenario
operates, when the loop in the corona is sufficiently thin and
the wave damping due to radiation is a negligibly small. In this
case the waves form shocks and dissipate. If the loop is
sufficiently thick most of the wave energy goes into radiation of
waves, and shocks do not appear in the tube. In this second
scenario the dissipation of the radiated waves has to be
considered. Thus, the classical scheme of heating of flux tubes
in the chromosphere or corona is valid only for rather thin flux
tubes. This effect can be considered as a possible explanation
of the fine structure of the upper solar atmosphere. In
addition, the condition for wave radiation (23) can be
rewritten as
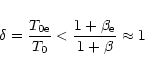 |
(67) |
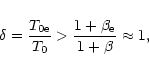 |
(68) |
Waves of finite amplitude in an infinitely thin tube governed by
the thin-flux-tube approximation form shocks after some time due
to the absence of dispersion. Waves in thin tubes of finite
diameter however are dispersive. Dispersion can balance the
nonlinear effects and smooth out the shock fronts so that weakly
nonlinear waves can exist in thin tubes with a non-zero diameter.
Moreover the key properties of the weakly nonlinear tube modes in
a thin flux tube depend on the value of the magnetic field in the
surrounding plasma. The tube mode appears as a running hump of
hot dense plasma, when there is not any magnetic field or when
the magnetic field is relatively weak outside the tube
![]() .
If the magnetic field is relatively strong
outside the tube
.
If the magnetic field is relatively strong
outside the tube
![]() ,
the tube mode appears as a
running narrowing of the tube, where the plasma is cooled down,
the density is decreased and the plasma is accelerated. This
happens because of the different signs of the dispersion law. A
detailed description of the effect was done by Zhugzhda &
Nakariakov (1997a,b). Besides, a breaking of a tube mode can be
different for these two limiting cases. Breaking of hot humps of
large amplitude has to be connected with formation of shocks on
the front side of the disturbances. In the case of a tube
narrowing, a breaking can result from the cooling and
acceleration of the plasma in the neck of the narrowing
(Zhugzhda & Nakariakov 1997b). This is a very different scenario
for astrophysical plasmas. In the case of the solar corona
humps can occur in the hot loops, while narrowings in the cold
loops. It has been found, that the second-order thin-flux-tube
approximation (Zhugzhda 1996) is ideally suited for a simulation
of slow waves in the case
,
the tube mode appears as a
running narrowing of the tube, where the plasma is cooled down,
the density is decreased and the plasma is accelerated. This
happens because of the different signs of the dispersion law. A
detailed description of the effect was done by Zhugzhda &
Nakariakov (1997a,b). Besides, a breaking of a tube mode can be
different for these two limiting cases. Breaking of hot humps of
large amplitude has to be connected with formation of shocks on
the front side of the disturbances. In the case of a tube
narrowing, a breaking can result from the cooling and
acceleration of the plasma in the neck of the narrowing
(Zhugzhda & Nakariakov 1997b). This is a very different scenario
for astrophysical plasmas. In the case of the solar corona
humps can occur in the hot loops, while narrowings in the cold
loops. It has been found, that the second-order thin-flux-tube
approximation (Zhugzhda 1996) is ideally suited for a simulation
of slow waves in the case
![]() ,
because it provides the
correct description of the dispersion and includes all nonlinear
effects. Thus, simulations have to show solitons for relatively
small amplitudes of the disturbances, and its breaking with shock
front formation with increasing of the soliton amplitudes.
,
because it provides the
correct description of the dispersion and includes all nonlinear
effects. Thus, simulations have to show solitons for relatively
small amplitudes of the disturbances, and its breaking with shock
front formation with increasing of the soliton amplitudes.
Acknowledgements
We are thankful to the referee Dr. M. G. Linton for the detailed critical comments, which helped to improve an earlier version of the paper. It is a pleasure for one of us (YZ) to acknowledge the financial support by the "Onderzoeksfonds K.U. Leuven'' (senior fellowship F/97/095).