Although the telescope beam for the Pluto observations encompasses both Pluto and Charon, we assume that only Pluto contributes to the CO emission.
There is no clear observational evidence for the presence of an atmosphere
around Charon. For a similar atmospheric composition and structure, atmospheric escape per surface
unit would be about five times larger at Charon than at Pluto
(Trafton et al. 1988; Yelle & Elliot 1997;
Trafton et al. 1997). For atmospheres buffered by volatile ices,
an integration of the escape fluxes over the Solar System
age suggests a typical loss of N2 ice surface layers of 3 km for
Pluto and 8 km for Charon. Therefore, in both cases, volatiles initially
exposed on the surface are likely to be exhausted, but both
bodies must have retained some of their original inventory.
Whether an atmosphere is present now depends on resupply
mechanisms. The presence of an atmosphere around Pluto and of
volatile ices on its surface suggest that geological processes must
operate on Pluto. Such processes, however, are less likely
on Charon because of its small size, and the absence of
volatile ice signatures from Charon's surface (see Cruikshank et al.
1997) suggests that Charon currently has no atmosphere. The
possibility that Charon may capture some of Pluto's escaping atmosphere leads
to a negligible, 10-7 ![]() bar, pressure at Charon. Yet, we note
that, from stellar occultation data, Elliot & Young (1991)
reported a hint of a charonian bound atmosphere with low scale height,
implying the presence of heavy species (Ar, etc.). The reality of the detection is
however not considered likely by Trafton et al. (1997). In any event,
there is currently no support for the presence of CO in an hypothetical
Charon atmosphere, justifying our assumption to attribute all of the
observed signal to Pluto.
bar, pressure at Charon. Yet, we note
that, from stellar occultation data, Elliot & Young (1991)
reported a hint of a charonian bound atmosphere with low scale height,
implying the presence of heavy species (Ar, etc.). The reality of the detection is
however not considered likely by Trafton et al. (1997). In any event,
there is currently no support for the presence of CO in an hypothetical
Charon atmosphere, justifying our assumption to attribute all of the
observed signal to Pluto.
Modelling of the CO emission from Pluto was performed using a standard
atmospheric radiative transfer code. Indeed, as shown by Strobel et al.
(1996), the CO emission occurs in local thermodynamical equilibrium
conditions down to pressure levels of about 10-5 ![]() bar. This is
11.7 scale heights above the 1.2
bar. This is
11.7 scale heights above the 1.2 ![]() bar, 1250 km radius reference level indicated
by the stellar occultation (Yelle & Elliot 1997).
For an upper atmospheric temperature in the range 80-106 K, this corresponds
to a 900-1400 km altitude above the 1250 km radius.
bar, 1250 km radius reference level indicated
by the stellar occultation (Yelle & Elliot 1997).
For an upper atmospheric temperature in the range 80-106 K, this corresponds
to a 900-1400 km altitude above the 1250 km radius.
Because there remains considerable uncertainty about Pluto's atmospheric thermal
structure, we used two different atmospheric models, both
of which assume hydrostatic equilibrium. The first one is based on the
thermal models of Strobel et al. (1996). These models account for
solar heating in the near-infrared bands of CH4, and cooling in the 7.6 ![]() m CH4 band and
in the CO rotational lines. Strobel et al. investigated the sensitivity of
their calculations to the surface pressure and CH4 abundance and
vertical distribution. We specifically adopted the model with a 3
m CH4 band and
in the CO rotational lines. Strobel et al. investigated the sensitivity of
their calculations to the surface pressure and CH4 abundance and
vertical distribution. We specifically adopted the model with a 3 ![]() bar
surface pressure, in which most of the CH4 is confined to the bottom two scale
heights (see their Fig. 11). This model reproduces the major features
indicated by the stellar occultation data, namely a 15 Kkm-1
temperature gradient at the surface and a
bar
surface pressure, in which most of the CH4 is confined to the bottom two scale
heights (see their Fig. 11). This model reproduces the major features
indicated by the stellar occultation data, namely a 15 Kkm-1
temperature gradient at the surface and a ![]() 100 K quasi-isothermal
temperature just above the
100 K quasi-isothermal
temperature just above the ![]() bar level. Yet, it implies
a value of
bar level. Yet, it implies
a value of ![]() 1200 km for Pluto's surface radius, distinctly different from the radius indicated
by the mutual event data (about 1158 km, Buie et al. 1992). For this
reason, Stansberry et al. (1994) suggested that Pluto may possess a
1200 km for Pluto's surface radius, distinctly different from the radius indicated
by the mutual event data (about 1158 km, Buie et al. 1992). For this
reason, Stansberry et al. (1994) suggested that Pluto may possess a ![]() 40 km
deep "hidden'' troposphere. They formulated a suite of models based on various
tropospheric lapse rates and a Bates profile for the thermosphere. We
adopted, as an alternative model, their profile with a tropospheric
40 km
deep "hidden'' troposphere. They formulated a suite of models based on various
tropospheric lapse rates and a Bates profile for the thermosphere. We
adopted, as an alternative model, their profile with a tropospheric
![]() K kms-1 lapse rate, and a surface pressure of
24
K kms-1 lapse rate, and a surface pressure of
24 ![]() bar. This profile becomes isothermal
at 106 K,
bar. This profile becomes isothermal
at 106 K, ![]() 45 km above Pluto's surface.
45 km above Pluto's surface.
In both cases, the models were extended up to the
![]() bar
level, which corresponds to 980 km and 1520 km altitudes, for the "Strobel''
and "Stansberry'' models, respectively. The two models are shown in
Fig. 2 with the distance from Pluto's center as the altitude
variable. We verified that the hydrodynamically escaping CO atmosphere
has a negligible contribution to the CO line emission. This was done using the
cometary model presented in Sect. 3.2 (see the related discussion). The
only difference in the modelling with respect to Centaurs and KBOs is that
collisional excitation is from CO-N2 impacts instead of CO-CO impacts.
With
bar
level, which corresponds to 980 km and 1520 km altitudes, for the "Strobel''
and "Stansberry'' models, respectively. The two models are shown in
Fig. 2 with the distance from Pluto's center as the altitude
variable. We verified that the hydrodynamically escaping CO atmosphere
has a negligible contribution to the CO line emission. This was done using the
cometary model presented in Sect. 3.2 (see the related discussion). The
only difference in the modelling with respect to Centaurs and KBOs is that
collisional excitation is from CO-N2 impacts instead of CO-CO impacts.
With
![]() kms-1, T=60 K at the exobase,
a N2 escape rate of
kms-1, T=60 K at the exobase,
a N2 escape rate of
![]() mols-1
(e.g. Krasnopolsky 1999) and
CO/N2 = 1%, the contribution of the escaping atmosphere to the
CO J(2-1) line intensity is 0.05 mK MHz.
mols-1
(e.g. Krasnopolsky 1999) and
CO/N2 = 1%, the contribution of the escaping atmosphere to the
CO J(2-1) line intensity is 0.05 mK MHz.
In all models, CO, which has the same mass as N2 and is photochemically stable, was assigned a vertically uniform distribution, and the CO mixing ratio was varied from 0.01% to 10%. Pluto's brightness surface temperature was taken to be 31.5 K, in agreement with bolometric measurements in the same wavelength range (Altenhoff et al. 1988; Lellouch et al. 2000).
Line opacities were calculated using Voigt profiles, using broadening
coefficients (CO by N2) from Colmont & Monnanteuil (1986) and
Semmoud-Monnanteuil & Colmont (1987). The transfer equation was
integrated over all emission angles. As Pluto's atmosphere has considerable
extent compared to the planet's radius, limb emission was taken into account. Because
the CO lines are heavily saturated already in vertical viewing, they remain
optically thick in horizontal viewing up to large altitudes. For example,
in the case of the Stansberry model and for CO/N2 = 0.1%, the ![]() level in horizontal viewing for the CO J(2-1) line is reached at p = 2 nanobar,
i.e. 450 km above Pluto's surface. This gives an additional 106 K emitting area essentially equal to Pluto's solid area. Therefore, the brightness temperature contrast in the
line core is boosted from a maximum of 75 K for the vertical viewing to an actual value
of
level in horizontal viewing for the CO J(2-1) line is reached at p = 2 nanobar,
i.e. 450 km above Pluto's surface. This gives an additional 106 K emitting area essentially equal to Pluto's solid area. Therefore, the brightness temperature contrast in the
line core is boosted from a maximum of 75 K for the vertical viewing to an actual value
of ![]() 190 K!
190 K!
| Mixing ratio | Line area [mK MHz] | |
| Strobel model | Stansberry model | |
| 10-4 | 4.13 | 4.73 |
| 10-3 | 7.59 | 9.02 |
| 10-2 | 13.2 | 17.0 |
| 10-1 | 18.2 | 27.1 |
Figure 1 shows the comparison between observations and models for
the CO J(2-1) line.
Calculated line areas are given in Table 4. The effect of
saturation is clearly
evident, with the line contrast growing by only a factor of 2-3
for a CO abundance increasing by three orders of magnitude. The tentatively measured area
of 18 mK MHz and the spectrum appearance is reproduced for
CO/N2 = 7%, in the
case of the Strobel model, and CO/N2 = 1.2% for the
Stansberry model, but,
as mentioned above, we regard these values as upper limits (note that, taking
instead the 3-![]() upper limit on the line area of 11.7 mK MHz, the
upper limits would be CO/N2 < 0.6% and 0.3%, for the Strobel
and Stansberry models, respectively). The higher
sensitivity for the Stansberry model is due to the higher upper atmosphere
temperature than in the Strobel model, which also causes it to be more extended. The possible presence of a troposphere and the exact value of the surface pressure are, in contrast,
inconsequential to first order. We note that, with these values,
the CO J(1-0) line shows a contrast of
upper limit on the line area of 11.7 mK MHz, the
upper limits would be CO/N2 < 0.6% and 0.3%, for the Strobel
and Stansberry models, respectively). The higher
sensitivity for the Stansberry model is due to the higher upper atmosphere
temperature than in the Strobel model, which also causes it to be more extended. The possible presence of a troposphere and the exact value of the surface pressure are, in contrast,
inconsequential to first order. We note that, with these values,
the CO J(1-0) line shows a contrast of ![]() 0.003 mK for both models and
an integrated area of 3.1 (respectively 2.0) mK MHz for the Strobel
(respectively Stansberry)
model. This is fully consistent with the upper limit for this line given in
Table 1. Essentially, the
115.271 GHz line does not appear to be constraining because the filling
factor of Pluto in the telescope main beam is four times smaller than at 230.538 GHz.
0.003 mK for both models and
an integrated area of 3.1 (respectively 2.0) mK MHz for the Strobel
(respectively Stansberry)
model. This is fully consistent with the upper limit for this line given in
Table 1. Essentially, the
115.271 GHz line does not appear to be constraining because the filling
factor of Pluto in the telescope main beam is four times smaller than at 230.538 GHz.
While our observations constrain the CO mixing ratio in Pluto's atmosphere rather
than the integrated abundances, the above upper limits correspond to
CO column densities of
![]() molcm-2 for the Strobel model
and
molcm-2 for the Strobel model
and
![]() molcm-2 for the Stansberry model. For a
"Stansberry-type'' model with a 58
molcm-2 for the Stansberry model. For a
"Stansberry-type'' model with a 58 ![]() bar surface pressure, the upper limit on the column
density would be
bar surface pressure, the upper limit on the column
density would be ![]()
![]() molcm-2, significantly more
constraining than the
molcm-2, significantly more
constraining than the
![]() molcm-2 values reported
by Young et al. (2001). We note also that the Young et al. observations do not
provide any useful constraint in the case of a "Strobel'' 3
molcm-2 values reported
by Young et al. (2001). We note also that the Young et al. observations do not
provide any useful constraint in the case of a "Strobel'' 3 ![]() bar atmosphere.
Yet, our improved upper limits of (1.2-7%) remain clearly insufficient for further
understanding of Pluto's thermal structure and surface-atmosphere interaction.
As mentioned in the introduction, the expected atmospheric CO mixing ratio for an ideal
solid solution of CO in N2 is at least an order of magnitude less
than our upper limits. As shown by Young et al. (2001), even if a
"detailed balance''
model is envisaged (Trafton et al. 1998), the CO atmospheric abundance cannot
exceed (0.1-0.5)%. The only situation that our upper limits can exclude
is the case of isolated CO patches at temperatures similar or higher than N2 ice,
which would dictate CO/N2 mixing ratios of 5-20% for
T = 35-50 K. This
situation is unlikely because CO and N2 ices are miscible in all
proportions and have only a weak difference in volatility, which must
strongly inhibit a CO segregation.
bar atmosphere.
Yet, our improved upper limits of (1.2-7%) remain clearly insufficient for further
understanding of Pluto's thermal structure and surface-atmosphere interaction.
As mentioned in the introduction, the expected atmospheric CO mixing ratio for an ideal
solid solution of CO in N2 is at least an order of magnitude less
than our upper limits. As shown by Young et al. (2001), even if a
"detailed balance''
model is envisaged (Trafton et al. 1998), the CO atmospheric abundance cannot
exceed (0.1-0.5)%. The only situation that our upper limits can exclude
is the case of isolated CO patches at temperatures similar or higher than N2 ice,
which would dictate CO/N2 mixing ratios of 5-20% for
T = 35-50 K. This
situation is unlikely because CO and N2 ices are miscible in all
proportions and have only a weak difference in volatility, which must
strongly inhibit a CO segregation.
| Designation | Name | Type | Ha | Db[km] |
| 1977 UB | 2060
|
Centaur | 6.5 | 168-180 |
| 1992 AD | 5145
|
Centaur | 7.0 | 189 |
| 1993 HA2 | 7066
|
Centaur | 9.6 | 80 |
| 1995 GO | 8405
|
Centaur | 9.0 | 106 |
| 1997 CU26 | 10199 Chariklo | Centaur | 6.4 | 275-302 |
| 1998 SG35 | Centaur | 11.3 | 37 | |
| 1994 TB | 15820 | KBO | 7.1 | 254 |
| 1996 TL66 | 15874 | SKBO | 5.4 | 555 |
| 1996 TO66 | 19308 | KBO | 4.5 | 840 |
| 1996 TP66 | 15875 | KBO | 6.8 | 290 |
| 1998 WH24 | 19521 | KBO | 4.9 | 700 |
|
a Absolute magnitude from Central Bureau for Astronomical Telegrams.
b References for diameters: Chiron (Bus et al. 1996; Groussin et al. 2000; Campins et al. 1994; Altenhoff & Stumpff 1995); Pholus (Davies et al. 1993); Chariklo (Jewitt & Kalas 1998; Altenhoff et al. 2001); for other objects, they were calculated from optical photometry alone, assuming a geometrical albedo of 0.04. |
CO observations of Centaurs and KBOs, and the single observation of HCN
in 10199 Chariklo (Table 3), were interpreted using models
developed for cometary atmospheres. These models assume freely escaping gas from the
surface at constant velocity, namely a Haser density distribution:
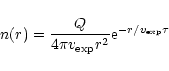 |
(1) |
Conservatively, we have assumed an expansion velocity
![]() kms-1
for all objects, regardless of their distance to the Sun.
CO outflow velocities
kms-1
for all objects, regardless of their distance to the Sun.
CO outflow velocities ![]() 0.4-0.5 kms-1 have been
measured in comets Hale-Bopp and
29P/Schwassmann-Wachmann 1 (P/SW1) at
0.4-0.5 kms-1 have been
measured in comets Hale-Bopp and
29P/Schwassmann-Wachmann 1 (P/SW1) at
![]() AU
(Crovisier et al. 1995;
Biver et al. 1999a). This value of 0.4 kms-1
is higher, by a factor of a few (2-4 for the observed objects, assuming an
albedo of 0.04), than the
initial sonic gas velocity expected near the surface for freely escaping
gas. This might account for the increase of the radial gas velocity during adiabatic
expansion, although, for tenuous atmospheres, the small extent of the
collision zone limits gas acceleration. For weakly
bound atmospheres with hydrodynamically escaping gas,
the sonic level is predicted to lie below the exobase (Chamberlain &
Hunten 1987). Therefore, terminal outflow velocities of a fraction of
kilometer per second might be also expected. This is also the case for
Pluto's atmosphere. Modelling shows
that its escaping atmosphere does not fit completely the hydrodynamic case.
At the exobase, 1500-4000 km altitude above the surface
according to Krasnopolsky (1999), the gas radial velocity is
subsonic and estimated to
AU
(Crovisier et al. 1995;
Biver et al. 1999a). This value of 0.4 kms-1
is higher, by a factor of a few (2-4 for the observed objects, assuming an
albedo of 0.04), than the
initial sonic gas velocity expected near the surface for freely escaping
gas. This might account for the increase of the radial gas velocity during adiabatic
expansion, although, for tenuous atmospheres, the small extent of the
collision zone limits gas acceleration. For weakly
bound atmospheres with hydrodynamically escaping gas,
the sonic level is predicted to lie below the exobase (Chamberlain &
Hunten 1987). Therefore, terminal outflow velocities of a fraction of
kilometer per second might be also expected. This is also the case for
Pluto's atmosphere. Modelling shows
that its escaping atmosphere does not fit completely the hydrodynamic case.
At the exobase, 1500-4000 km altitude above the surface
according to Krasnopolsky (1999), the gas radial velocity is
subsonic and estimated to ![]() 1-2 ms-1 only
(Krasnopolsky 1999; see also Trafton et al. 1997).
However, due to the geometric effect (Hodges 1990), the transverse
velocity due to random thermal motions at the exobase (where
1-2 ms-1 only
(Krasnopolsky 1999; see also Trafton et al. 1997).
However, due to the geometric effect (Hodges 1990), the transverse
velocity due to random thermal motions at the exobase (where ![]() K;
Krasnopolsky 1999) will be converted at larger distances, in the
collisionless atmosphere, to a radial velocity component. Taking
into account that 3-
K;
Krasnopolsky 1999) will be converted at larger distances, in the
collisionless atmosphere, to a radial velocity component. Taking
into account that 3-![]() upper limits on the line areas vary as
the square root of the velocity window where they are computed,
production rates upper limits
scale proportionally to
upper limits on the line areas vary as
the square root of the velocity window where they are computed,
production rates upper limits
scale proportionally to
![]() .
Possibly,
in most cases, the
.
Possibly,
in most cases, the
![]() upper limits given in Tables 3
and 6 may be somewhat too conservative.
upper limits given in Tables 3
and 6 may be somewhat too conservative.
The computation of production rates upper limits requires the modelling of the CO rotational
population distribution. We used a CO excitation model developed for
cometary atmospheres, which includes collisional excitation by CO-CO
impacts and radiative excitation by the Sun and 3 K cosmic background radiation (Biver et al. 1999b, and references therein). This model computes CO rotational
populations as function of distance to object's center. An important
parameter for CO excitation in distant objects is the gas kinetic temperature.
Indeed, although the radial extent of the collisional region at thermal
equilibrium is small compared to that of the region
sampled by the beam, fluorescence equilibrium does not apply for the
relevant rotational levels because of their long radiative lifetimes. In
Table 3, we present calculations performed with T=10 K
and T=50 K. Kinetic temperatures ![]() 10 K were measured
in comets P/SW1 and Hale-Bopp at
10 K were measured
in comets P/SW1 and Hale-Bopp at
![]() AU
(Crovisier et al. 1995;
Biver et al. 1999a), in good agreement with fast adiabatic cooling
(Crifo et al. 1999). We explore a temperature of 50 K, because
expansion cooling can be "frozen'' out
in tenuous atmospheres and we cannot exclude significant heating linked to
gravity (e.g. heating by dust in case of Chiron, Boice et al. 1993,
or from near-IR CH4 bands in the extreme case of Pluto's atmosphere).
AU
(Crovisier et al. 1995;
Biver et al. 1999a), in good agreement with fast adiabatic cooling
(Crifo et al. 1999). We explore a temperature of 50 K, because
expansion cooling can be "frozen'' out
in tenuous atmospheres and we cannot exclude significant heating linked to
gravity (e.g. heating by dust in case of Chiron, Boice et al. 1993,
or from near-IR CH4 bands in the extreme case of Pluto's atmosphere).
Table 3 presents 3-![]() upper limits obtained on the
CO and HCN production rates. Data acquired on the same line and with the same
telescope, but at different dates, have been averaged. The final
3-
upper limits obtained on the
CO and HCN production rates. Data acquired on the same line and with the same
telescope, but at different dates, have been averaged. The final
3-![]()
![]() upper limits, obtained by combining upper limits from
different lines and telescopes, are
given in Table 6. These upper limits are
typically
upper limits, obtained by combining upper limits from
different lines and telescopes, are
given in Table 6. These upper limits are
typically
![]() 1028 mols-1 for Centaurs, and between 1 and
1028 mols-1 for Centaurs, and between 1 and
![]() mols-1 for the best observed KBOs.
The upper limit obtained for the HCN production rate in 10199 Chariklo is
strongly model dependent and is equal to
mols-1 for the best observed KBOs.
The upper limit obtained for the HCN production rate in 10199 Chariklo is
strongly model dependent and is equal to
![]() mols-1 for T = 10 K, and
mols-1 for T = 10 K, and
![]() mols-1 for T = 50 K.
mols-1 for T = 50 K.
| Object |
|
minimum CO |
| [1028 mols-1] | depletionb | |
| 2060 Chiron | <0.31-0.45 | 38-55 |
| 5145 Pholus | <1.0-2.3 | 4-9 |
| 7066 Nessus | <4.6-5.6 | |
| 8405 Asbolus | <1.2-1.9 | 4-6 |
| 10199 Chariklo | <0.51-1.1 | 20-43 |
| 1998 SG35 | <0.77-1.8 | |
| 1994 TB | <5.1-8.3 | |
| 1996 TL66 | <1.3-4.4 | 3-10 |
| 1996 TO66 | <1.5-5.5 | 3-11 |
| 1996 TP66 | <1.0-4.5 | 1-6 |
| 1998 WH24 | <10-19 |
|
a 3- b Minimum CO depletion with respect to comet Hale-Bopp, assuming and using D = 40 km (Altenhoff et al. 1999) and for comet Hale-Bopp (Biver et al. 1999c). Only depletions greater than 1 are given. |
Because Chiron presents cometary-like activity, rotational lines of CO were
searched for in this Centaur on several occasions. Womack & Stern
(1999) announced the detection of the J(1-0) line in June 1995, using
the NRAO 12-m telescope. With a pure
thermal model at T = 10 K and
![]() kms-1, assuming that
CO emission fills the telescope beam, they inferred a CO production
rate of
kms-1, assuming that
CO emission fills the telescope beam, they inferred a CO production
rate of
![]() mols-1.
The production rate we derive from their observations using our model
with
mols-1.
The production rate we derive from their observations using our model
with
![]() kms-1 is
kms-1 is
![]() mols-1 and
mols-1 and
![]() mols-1, for T =
10 and 50 K, respectively. Boice et al. (1999) observed the
J(1-0) line in February 1998 with the Nobeyama 45-m telescope, from which
we derive
mols-1, for T =
10 and 50 K, respectively. Boice et al. (1999) observed the
J(1-0) line in February 1998 with the Nobeyama 45-m telescope, from which
we derive
![]() mols-1 for
T=10 K. Rauer et al. (1997) observed both the J(1-0) and J(2-1) lines
with the IRAM 30-m in June, September and November 1995 and used the same
model as ours for their interpretation. Their 3-
mols-1 for
T=10 K. Rauer et al. (1997) observed both the J(1-0) and J(2-1) lines
with the IRAM 30-m in June, September and November 1995 and used the same
model as ours for their interpretation. Their 3-![]() upper limit obtained in June 1995 is consistent with the Womack and
Stern's result, but the upper limit derived from the combined June 1995 to
November 1995 data (
upper limit obtained in June 1995 is consistent with the Womack and
Stern's result, but the upper limit derived from the combined June 1995 to
November 1995 data (
![]() mols-1 for T = 10 K)
is clearly below the Womack &
Stern's value. Our derived upper limit of
mols-1 for T = 10 K)
is clearly below the Womack &
Stern's value. Our derived upper limit of ![]()
![]() mols-1 for 1998-2000 (Table 6) is even more
stringent, a factor of
mols-1 for 1998-2000 (Table 6) is even more
stringent, a factor of ![]() 10
lower than the production rate derived from Womack and
Stern's marginal detection using same modelling. From optical photometry,
Chiron's activity shows short-term variability and
a long-term trend to be lower near perihelion (February 1996) than
near the aphelion (Bus et al. 2001; Lazzaro et al. 1997).
Photometric measurements obtained
in March, May 1995 (Bauer et al. 1997), January 1998, May 1999 and
June 2000 (Bauer, private communication) show that Chiron was fainter over
the years 1998-2000 by 0.3 magnitude (in absolute magnitude units)
when compared to 1995. This 0.3 magnitude variation would correspond to
a CO production rate variation of 40% only, using the
correlation between CO production rates and heliocentric magnitudes
established from comet Hale-Bopp data (Biver 2001).
Yet, the absolute V magnitudes deduced from the
1998 to 2000 observations, (
10
lower than the production rate derived from Womack and
Stern's marginal detection using same modelling. From optical photometry,
Chiron's activity shows short-term variability and
a long-term trend to be lower near perihelion (February 1996) than
near the aphelion (Bus et al. 2001; Lazzaro et al. 1997).
Photometric measurements obtained
in March, May 1995 (Bauer et al. 1997), January 1998, May 1999 and
June 2000 (Bauer, private communication) show that Chiron was fainter over
the years 1998-2000 by 0.3 magnitude (in absolute magnitude units)
when compared to 1995. This 0.3 magnitude variation would correspond to
a CO production rate variation of 40% only, using the
correlation between CO production rates and heliocentric magnitudes
established from comet Hale-Bopp data (Biver 2001).
Yet, the absolute V magnitudes deduced from the
1998 to 2000 observations, (
![]() ,
not corrected from phase
function; Bauer, private
communication) indicate that Chiron was in its most quiescent state
since its discovery. Therefore, we cannot
exclude that Chiron was in outburst in June 1995, but, without any additional
evidence for that, the low CO production rates derived for the
June-September 1995 (Rauer et al. 1997) and 1998-2000 periods
make the proposed detection of Womack and Stern at best tentative.
,
not corrected from phase
function; Bauer, private
communication) indicate that Chiron was in its most quiescent state
since its discovery. Therefore, we cannot
exclude that Chiron was in outburst in June 1995, but, without any additional
evidence for that, the low CO production rates derived for the
June-September 1995 (Rauer et al. 1997) and 1998-2000 periods
make the proposed detection of Womack and Stern at best tentative.
Thermal models of the interiors of Centaurs and KBOs have been developed to follow their evolution and differentiation and better understand their relationships with short-period comets (Capria et al. 2000; De Sanctis et al. 2000; De Sanctis et al. 2001). These models assume that these objects are porous bodies made of ices of different volatilities (amorphous H2O, CO and CO2 as main constituents) and dust. They treat the heat diffusion in the porous material, the sublimation of volatile ices, the amorphous/crystalline phase transition, the diffusion of the produced gases and their recondensation or their escape into space. The model developed by De Sanctis et al. (2001) for KBOs includes the combined effects of radiogenic and solar heating. They show that the upper layers of Kuiper Belt objects could be strongly volatile-depleted, with CO ice completely absent down to several kilometers below the surface. CO production rates are expected to be very low (less than 1023 mols-1 for an object of 200 km diameter; De Sanctis et al. 2000), making our upper limits meaningless in that context. However, the results of these simulations are strongly dependent upon size and model parameters, such as porosity and thermal conductivity, and more investigations of the thermal differentiation of KBOs are needed. Other simulations predict, for large objects, a runaway increase of their internal temperature due to radiogenic heating, which can squeeze out volatiles trapped in water amorphous ice and concentrate them near the surface where the temperature is lower (Haruyama et al. 1993; Prialnik & Podolak 1995). Impacts may play also an important role in redistributing materials towards the surface, or ablating CO depleted layers. Transient cometary activity around 1996 TO66 has been proposed to explain a strong change of its lightcurve between September 1997 and September 1998 (Hainaut et al. 2000).
From their study of the thermal evolution of 2060 Chiron, Capria et al.
(2000) concluded that Chiron's activity, if driven by CO, can be explained only if CO is
present near the surface as an ice, or as a gas trapped in the amorphous water ice. It is believed that Chiron originated from the
Kuiper Belt and moved to its present orbit by gravitational
perturbations. If the upper layers underwent CO-ice devolatization in the
Kuiper Belt, as it follows from the model of De Sanctis et al. (2001), then
Chiron's activity could be explained by the release of trapped CO during
the amorphous to crystalline transition. Although there are many
assumptions in their model, Capria et al. (2000)
show that CO production rates strong enough to explain the dust coma, and
comparable to or even larger than our upper limits, can
be obtained with this mechanism. The activity could also be explained by
the outgassing of CO2 ice (Capria et al. 2000), for which no
significant devolatilization is expected
in the Kuiper Belt due to its relatively low volatility
(De Sanctis et al. 2001). But, this would require Chiron to have
moved on its present orbit recently. The model developed for Pholus predicts
CO fluxes lower than for Chiron because of its more distant
orbit (De Sanctis et al. 2000), which might partly explain its
inactive appearance.
Finally, it is interesting to note that the comparison between the Hale-Bopp
CO outgassing rates measured at large distances from the Sun and the upper
limits obtained for Centaurs and KBOs
demonstrates that, indeed, these latter underwent significant CO-depletion
since their formation, when compared to Oort cloud comets. A CO
production rate varying approximately in
![]() and equal to
and equal to
![]() 1028 mols-1 at
1028 mols-1 at
![]() AU was
measured in comet Hale-Bopp post-perihelion
(Biver et al. 1999c). If we apply a scaling law in
AU was
measured in comet Hale-Bopp post-perihelion
(Biver et al. 1999c). If we apply a scaling law in
![]() ,
then the CO production rates we infer for the corresponding (D,
,
then the CO production rates we infer for the corresponding (D, ![]() )
of
our objects are, in most cases, significantly larger than the measured upper
limits (Table 6).
)
of
our objects are, in most cases, significantly larger than the measured upper
limits (Table 6).
Copyright ESO 2001