5 Comparison of terminal velocities

 

 

Table 2: Stellar and wind parameters of O6-B5 stars selected from LSL. $\dot{\mbox{\eufont M}}$ is computed mass-loss rate. Terminal velocities measured by LSL (Col. $v_{\infty }$ (LSL)) are compared with theoretical values obtained by LSL using a "cooking formula'' of KPPA (Col. $v_{\infty }$ (KPPA)) and with predicted ones computed with an assumption of a nonisothermal wind model (Col. $v_{\infty }$ (predicted)).

HD	Stellar parameters				Wind parameters				Terminal velocities
number	$\mbox{\eufont M}$	R*	$T_{\rm eff}$	z*	k	$\alpha$	$\delta$	$\dot{\mbox{\eufont M}}$	$v_{\infty }$ (LSL)	$v_{\infty }$ (KPPA)	$v_{\infty }$ (predicted)
	$[{\mbox{\eufont M}}_{\odot}]$	$[R_{\odot}]$	$[{\rm K}]$					$[{\mbox{\eufont M}}_{\odot}\,{\rm yr}^{-1}]$	$[{\rm km}\,{\rm s}^{-1}]$	$[{\rm km}\,{\rm s}^{-1}]$	$[{\rm km}\,{\rm s}^{-1}]$
30614	43.0	27.6	$30\,900$	1.0	0.158	0.609	0.120	${8.9\times 10^{-6}}$	$1500\,\pm\,200$	2241	1450
34656	30.0	9.9	$38\,100$	1.0	0.171	0.607	0.120	${1.0\times 10^{-6}}$	$2100\,\pm\,100$	3598	2590
36861	30.0	12.3	$36\,000$	1.0	0.167	0.607	0.120	${1.5\times 10^{-6}}$	$2200\,\pm\,300$	3084	2230
41117	25.0	43.4	$18\,500$	1.0	0.410	0.507	0.098	${2.8\times 10^{-6}}$	$500\,\pm\,50$	1058	740
43384	19.0	39.8	$16\,300$	1.0	0.311	0.510	0.112	${4.0\times 10^{-7}}$	$500\,\pm\,100$	1015	690
47240	17.0	23.4	$20\,800$	1.0	0.451	0.514	0.091	${9.7\times 10^{-7}}$	$1000\,\pm\,100$	1267	930
51309	11.0	16.3	$16\,700$	1.0	0.329	0.509	0.109	${1.7\times 10^{-8}}$	$700\,\pm\,100$	1309	910
52382	17.0	20.4	$20\,800$	1.0	0.451	0.514	0.091	${4.9\times 10^{-7}}$	$1200\,\pm\,100$	1381	1030
69464	49.0	20.1	$37\,200$	1.0	0.169	0.607	0.120	${9.9\times 10^{-6}}$	$2100\,\pm\,200$	2721	1840
74194	28.0	14.5	$33\,000$	1.0	0.161	0.608	0.120	${1.4\times 10^{-6}}$	$2000\,\pm\,300$	2829	1970
79186	18.0	62.4	$13\,600$	1.0	0.284	0.519	0.100	${6.6\times 10^{-7}}$	$450\,\pm\,50$	772	530
91572	38.0	9.6	$42\,200$	1.0	0.175	0.606	0.114	${1.6\times 10^{-6}}$	$2400\,\pm\,100$	3989	2940
91969	25.0	22.9	$26\,000$	1.0	0.284	0.568	0.108	${3.0\times 10^{-6}}$	$1500\,\pm\,100$	1816	1240
92964	29.0	68.4	$17\,400$	1.0	0.361	0.509	0.105	${1.1\times 10^{-5}}$	$550\,\pm\,50$	807	530
93130	43.0	13.8	$40\,200$	1.0	0.174	0.606	0.119	${4.5\times 10^{-6}}$	$2500 \,\pm\, 300$	3337	2370
96248	25.0	38.9	$20\,800$	1.0	0.451	0.514	0.091	${7.3\times 10^{-6}}$	$650\,\pm\,50$	1116	770
96917	46.0	25.2	$33\,000$	1.0	0.161	0.608	0.120	${9.5\times 10^{-6}}$	$1800\,\pm\,200$	2430	1600
101190	48.0	13.9	$42\,200$	1.0	0.175	0.606	0.114	${6.3\times 10^{-6}}$	$2800\,\pm\,200$	3452	2450
101436	42.0	12.4	$41\,200$	1.0	0.174	0.606	0.117	${3.5\times 10^{-6}}$	$2700\,\pm\,200$	3487	2570
106343	24.0	40.7	$19\,700$	1.0	0.464	0.506	0.091	${5.3\times 10^{-6}}$	$800\,\pm\,100$	1074	730
109867	26.0	38.9	$20\,800$	1.0	0.451	0.514	0.091	${6.7\times 10^{-6}}$	$1200\,\pm\,200$	1144	800
112244	46.0	25.2	$33\,000$	1.0	0.161	0.608	0.120	${9.5\times 10^{-6}}$	$1600\,\pm\,100$	2430	1580
116084	15.0	24.8	$17\,400$	1.0	0.361	0.509	0.105	${1.4\times 10^{-7}}$	$500\,\pm\,100$	1201	830
148379	24.0	40.7	$19\,700$	1.0	0.464	0.506	0.091	${5.3\times 10^{-6}}$	$500\,\pm\,100$	1074	730
151515	41.0	14.9	$38\,100$	1.0	0.171	0.607	0.120	${4.1\times 10^{-6}}$	$2400\,\pm\,100$	3196	2230
151804	70.0	34.0	$34\,000$	1.0	0.163	0.608	0.120	${3.6\times 10^{-5}}$	$1500\,\pm\,200$	2226	1370
152405	25.0	15.3	$30\,500$	1.0	0.157	0.609	0.120	${1.0\times 10^{-6}}$	$1800\,\pm\,200$	2616	1800
152424	52.0	33.4	$30\,500$	1.0	0.157	0.609	0.120	${1.5\times 10^{-5}}$	$1500\,\pm\,100$	2056	1350
154090	26.0	38.9	$20\,800$	1.0	0.451	0.514	0.091	${6.7\times 10^{-6}}$	$950\,\pm\,50$	1144	800
157246	17.0	23.4	$20\,800$	1.0	0.451	0.514	0.091	${9.7\times 10^{-7}}$	$900\,\pm\,200$	1267	930
162978	40.0	16.0	$37\,100$	1.0	0.169	0.607	0.120	${4.4\times 10^{-6}}$	$2200\,\pm\,200$	2939	2090
163758	50.0	20.1	$37\,200$	1.0	0.169	0.607	0.120	${9.5\times 10^{-6}}$	$2300\,\pm\,200$	2765	1890
166596	9.7	9.8	$18\,700$	1.0	0.419	0.507	0.097	${9.6\times 10^{-9}}$	$700\,\pm\,50$	1551	1170
175754	34.0	14.2	$36\,000$	1.0	0.167	0.607	0.120	${2.4\times 10^{-6}}$	$2000\,\pm\,100$	2998	2130
186980	35.0	13.9	$37\,100$	1.0	0.169	0.607	0.120	${2.8\times 10^{-6}}$	$2100\,\pm\,100$	3028	2180
188209	43.0	27.6	$30\,900$	1.0	0.158	0.609	0.120	${8.9\times 10^{-6}}$	$1600\,\pm\,100$	2241	1450
190603	24.0	40.7	$19\,700$	1.0	0.464	0.506	0.091	${5.3\times 10^{-6}}$	$500\,\pm\,50$	1074	730
190864	42.0	14.0	$39\,200$	1.0	0.173	0.606	0.120	${3.8\times 10^{-6}}$	$2300\,\pm\,200$	3338	2340
198478	17.0	36.3	$16\,300$	1.0	0.311	0.510	0.112	${3.0\times 10^{-7}}$	$550\,\pm\,100$	1009	690
204172	23.0	20.0	$26\,000$	1.0	0.284	0.568	0.108	${1.8\times 10^{-6}}$	$1600\,\pm\,200$	1911	1320
206165	19.0	35.8	$18\,500$	1.0	0.410	0.507	0.098	${1.6\times 10^{-6}}$	$600\,\pm\,50$	1011	720
210809	38.0	21.4	$32\,000$	1.0	0.160	0.608	0.120	${4.2\times 10^{-6}}$	$2000\,\pm\,200$	2588	1700
210839	51.0	19.6	$38\,200$	1.0	0.171	0.607	0.120	${1.1\times 10^{-5}}$	$2200\,\pm\,200$	2882	1930
213087	21.0	23.4	$23\,400$	1.0	0.368	0.541	0.100	${1.9\times 10^{-6}}$	$1400\,\pm\,200$	1533	1080
218915	43.0	27.6	$30\,900$	1.0	0.158	0.609	0.120	${8.9\times 10^{-6}}$	$1800\,\pm\,100$	2241	1450

Figure 12: Comparison of predicted and observational (taken from LSL) values of terminal velocities. Vertical lines denote uncertainty of observed values. Straight line is one-to-relation. For comparison, we plotted theoretical terminal velocities computed by LSL using "cooking formula'' (crosses).

In addition, we decided to compare our predicted terminal velocities with that measured by Lamers et al. (1995, hereafter LSL). They found a discrepancy between theoretical values obtained from a "cooking formula'' of Kudritzki et al. (1989, hereafter KPPA) and their experimental values. We computed wind models of O6-B5 stars for which LSL measured the terminal velocity. Parameters of each wind model are given in Table 2. Stellar parameters are taken from LSL, wind parameters are adopted from Abbott (1982). For many stars we found quite a good agreement between observed and predicted terminal velocities (see Fig. 12 for comparison of predicted and observed values). Although some values of predicted terminal velocities miss the measured value significantly (e.g. for the star HD166596), it is evident that the overall agreement between our predicted terminal velocities and the observed ones is much better than that of the "cooking formula'' of KPPA and the systematic difference, which was previously attributed to an overestimation of $\alpha$(by LSL), has been removed.

However, there are still differences between observed and predicted values of 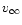$v_{\infty }$. There are three basic reasons for this discrepancy. First, rotation lowers the terminal velocity (cf. Friend & Abbott 1986). However, Petrenz & Puls (2000) using 2D models showed that the influence of the rotation on terminal velocity in many cases is only marginal. Second, our wind models (especially the radiative force) are constrained. Although we included physical processes that have not been included yet (frictional heating, Gayley-Owocki heating, multicomponent nature of the wind), there are still limits. Our treatment of ionization is only approximate, the equilibrium is not determined consistently with radiation field. In addition, our models are not fully consistent with respect to the radiative force, a proper NLTE treatment of the radiative transfer problem would be very useful. This two reasons causes that many of the terminal velocities are not within quoted uncertainties. However, we plan to improve our models in near future.

Another source of differences may come from uncertainties of stellar parameters derived from observations. Note that, e.g., stars HD106343, HD148379, and HD190603 have roughly the same parameters, however different observed terminal velocities.

The "cooking formula'' of KPPA should be consistent with detailed calculations of Pauldrach et al. (1986) with an accuracy about 5%. However, our predicted terminal velocities correspond to those computed by Pauldrach et al. (1986), too. Thus, there is not clear source of discrepancy between terminal velocities observed by LSL and predicted using formula of KPPA. We stress that the effect of frictional or Gayley-Owocki heating on the terminal velocity are negligible for the models described in this section.