The formation of low-mass X-ray binaries containing a rather massive (
A&A 376, 950-954 (2001)
DOI: 10.1051/0004-6361:20010949
G. Nelemans - E. P. J. van den Heuvel
Astronomical Institute "Anton Pannekoek'', Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
Received 17 April 2001 / Accepted 27 June 2001
Abstract
The formation of low-mass X-ray binaries containing a rather
massive (
![]() )
black hole is problematic because in most
recent stellar evolutionary calculations the immediate progenitors
of these black holes (Wolf-Rayet stars) lose so much mass via their
stellar wind that their final masses are well below the observed
black hole masses. We discuss the recently proposed solution that
these binaries are formed through case C mass transfer (i.e. mass
transfer after core helium burning is completed), avoiding a long
Wolf-Rayet phase and thus significant mass loss. We show that only
some of the currently available models for the evolution of massive
stars allow this formation channel. We also investigate the effect
of the downward revised Wolf-Rayet mass-loss rate as is suggested by
observations, and conclude that in that case Wolf-Rayet stars end
their lives with significantly higher masses than previously found
and may be able to form a black holes.
)
black hole is problematic because in most
recent stellar evolutionary calculations the immediate progenitors
of these black holes (Wolf-Rayet stars) lose so much mass via their
stellar wind that their final masses are well below the observed
black hole masses. We discuss the recently proposed solution that
these binaries are formed through case C mass transfer (i.e. mass
transfer after core helium burning is completed), avoiding a long
Wolf-Rayet phase and thus significant mass loss. We show that only
some of the currently available models for the evolution of massive
stars allow this formation channel. We also investigate the effect
of the downward revised Wolf-Rayet mass-loss rate as is suggested by
observations, and conclude that in that case Wolf-Rayet stars end
their lives with significantly higher masses than previously found
and may be able to form a black holes.
Key words: stars: statistics - binaries: close - binaries: evolution
In low-mass X-ray binaries a neutron star or a black hole accretes
from a low-mass (
![]() )
companion. A scenario to form such
stars begins with a relatively wide binary of a massive star and a
low-mass companion. When the massive star becomes a giant, mass
transfer is unstable and a common-envelope forms in which the
companion spirals down towards the core of the giant, leaving a close
binary consisting of the helium core of the giant and the low-mass
companion (van den Heuvel 1983). The helium star explodes in a supernova and
depending on the (core) mass of the helium star, a neutron star or
black hole is formed. With the discovery of A0620-00
(Eyles et al. 1975; Elvis et al. 1975) and the determination of the mass function of 3.18 (McClintock & Remillard 1986), the existence of the class of black hole low-mass
X-ray binaries was established. Currently we know 6 to 8 such systems
depending on the membership criteria (Charles 1998; Bailyn et al. 1998). An
evolutionary scenario for these objects is given in de Kool et al. (1987).
)
companion. A scenario to form such
stars begins with a relatively wide binary of a massive star and a
low-mass companion. When the massive star becomes a giant, mass
transfer is unstable and a common-envelope forms in which the
companion spirals down towards the core of the giant, leaving a close
binary consisting of the helium core of the giant and the low-mass
companion (van den Heuvel 1983). The helium star explodes in a supernova and
depending on the (core) mass of the helium star, a neutron star or
black hole is formed. With the discovery of A0620-00
(Eyles et al. 1975; Elvis et al. 1975) and the determination of the mass function of 3.18 (McClintock & Remillard 1986), the existence of the class of black hole low-mass
X-ray binaries was established. Currently we know 6 to 8 such systems
depending on the membership criteria (Charles 1998; Bailyn et al. 1998). An
evolutionary scenario for these objects is given in de Kool et al. (1987).
To make a black hole, the initial mass of the primary must exceed a
critical value, which currently is believed to be around 20 ![]() (Fryer 1999). However, large mass-loss rates for massive stars and
Wolf-Rayet stars have been inferred from observations
(e.g. de Jager et al. 1988) and are found from the comparison of Wolf-Rayet
models with these observations (Langer 1989a). Applying these rates to
evolutionary calculations resulted in the conclusion that even massive
single stars might end their evolution as relatively low-mass objects
when they explode (Schaller et al. 1992; Meynet et al. 1994; Woosley et al. 1995) and are thus unable to
produce the observed black holes (see also Kalogera 1999). For
massive stars in close binaries, which lose their hydrogen envelopes
due to mass transfer early in their evolution the situation is even
worse; the most recent calculations predict masses of helium stars as
they explode as low as 3
(Fryer 1999). However, large mass-loss rates for massive stars and
Wolf-Rayet stars have been inferred from observations
(e.g. de Jager et al. 1988) and are found from the comparison of Wolf-Rayet
models with these observations (Langer 1989a). Applying these rates to
evolutionary calculations resulted in the conclusion that even massive
single stars might end their evolution as relatively low-mass objects
when they explode (Schaller et al. 1992; Meynet et al. 1994; Woosley et al. 1995) and are thus unable to
produce the observed black holes (see also Kalogera 1999). For
massive stars in close binaries, which lose their hydrogen envelopes
due to mass transfer early in their evolution the situation is even
worse; the most recent calculations predict masses of helium stars as
they explode as low as 3 ![]() ,
almost independent of their initial
mass (Wellstein & Langer 1999).
,
almost independent of their initial
mass (Wellstein & Langer 1999).
In this article we first discuss the formation of black hole low-mass X-ray binaries through case C evolution as suggested by Brown et al. (1999) and Wellstein & Langer (1999): mass transfer starting after core-helium burning has been completed (Kippenhahn & Weigert 1967). In this case a long-duration Wolf-Rayet phase in which the star loses a lot of mass is avoided (Sect. 2). Then we discuss the most recently observed mass-loss rates for Wolf-Rayet stars and the implication of lower mass-loss rates on the final helium-star masses of exploding stars in binaries (Sect. 3). At the end we discuss uncertainties and possible alternatives for the formation of black hole low-mass X-ray binaries (Sect. 4) and end with our conclusions (Sect. 5).
It has been suggested that case C mass transfer could be invoked to avoid a long-duration Wolf-Rayet phase in the evolution of the massive star, in order that this star does not lose too much mass and still is able to form a massive black hole (Brown et al. 1999; Wellstein & Langer 1999).
The occurrence of case C mass transfer depends on the radius evolution of massive stars. For supergiants the radius of the star is not very well defined, since the outer layers of the giant envelope are extremely dilute. However, the best we can do is use the calculated values of the radii of giants. We also neglect the interaction between the wind of the massive star and the companion which may influence the separation of the two stars.
We calculate the initial separation with which a binary should start
in order to undergo case C mass transfer as follows (see
also Portegies Zwart et al. 1997). The separation at the moment the Roche-lobe overflow
(RLOF) starts is given by
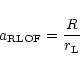 |
(1) |
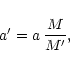 |
(2) |
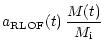 |
|
=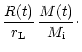 |
(3) |
![\begin{figure}
\par\resizebox{\columnwidth}{!}{\includegraphics[angle=-90]{H2816f1.ps}}\end{figure}](/articles/aa/full/2001/36/aah2816/Timg12.gif) |
Figure 1:
Initial separations |
| Open with DEXTER | |
We conclude that since case C evolution depends strongly on the radius evolution of massive stars which is very uncertain, it seems possible but is not certain whether black hole low-mass X-ray binaries can be formed in this way.
A different way to avoid too much mass loss may be the fact that
observed mass loss rates (which are the basis for the mass-loss rates
used in the evolutionary calculations) are revised downward
(Hamann & Koesterke 1998; Nugis & Lamers 2000), which may make it possible to prevent helium stars
in binaries to lose so much mass they no longer can become black
holes. In a recent paper with drastically lower mass-loss rates,
derived from one particularly well-studied object and extrapolated,
final masses over 20 ![]() for the most massive helium stars are found
(Cherepashchuk 2001). As shown by Kalogera (1999) the helium stars that were
the progenitors of the black holes in binaries cannot have lost more
than half of their initial mass. This includes both mass loss in the
stellar wind and in the supernova explosion.
for the most massive helium stars are found
(Cherepashchuk 2001). As shown by Kalogera (1999) the helium stars that were
the progenitors of the black holes in binaries cannot have lost more
than half of their initial mass. This includes both mass loss in the
stellar wind and in the supernova explosion.
![\begin{figure}
\par\resizebox{\columnwidth}{!}{\includegraphics[angle=-90]{H2816f2.ps}}
\end{figure}](/articles/aa/full/2001/36/aah2816/Timg13.gif) |
Figure 2: Mass-loss rates for Wolf-Rayet stars as observed (triangles for WN and circles for WC/WO stars, from Nugis & Lamers 2000, where we excluded the hydrogen rich Wolf-Rayet stars) and various relations used for evolutionary calculations. The solid lines are the relations assumed by Woosley et al. (1995) for WC (upper) and WN (lower) stars. The dashed lines are the ones used by Wellstein & Langer (1999), where we converted the mass loss-luminosity relations to mass loss-mass relations using the mass - luminosity relation of Langer (1989b). The upper dashed line is for their standard case, the lower for their reduced mass loss case. The dash-dotted line is a rectangular least square fit to all points (see also the text and Eq. (4)). |
| Open with DEXTER | |
A recent compilation of observed mass-loss rates for Wolf-Rayet stars is made by Nugis & Lamers (2000). In Fig. 2 we show these inferred mass-loss rates for WN and WC/WO stars (excluding the hydrogen rich Wolf-Rayet stars). We overplotted mass-loss rates for WN and WC stars as used by Woosley et al. (1995) as the solid lines. The mass-loss rates used recently by Wellstein & Langer (1999) are shown as the dashed lines, where we used the luminosity-mass relation as given by Langer (1989b) to convert the mass loss-luminosity relation used by these authors, to a mass loss-mass relation. The top dashed line is their standard case, the bottom a reduced mass-loss rate, which they used to account for the lower observed mass-loss rates.
The most recently determined mass-loss rates thus suggest that the
rates used by Wellstein & Langer (1999) are still too high. We will investigate the
effect of using a lower mass-loss rate law, which is shown in the
figure as the dash-dotted line and is given by
For a mass-loss rate of the form
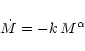 |
(5) |
| |
Figure 3: Final helium star masses as function of the initial helium star mass with the mass-loss rates according to Woosley et al. (1995, solid line, some of their results are potted as solid triangles) and Wellstein & Langer (1999, dashed line) assuming a helium star lifetime as given by Woosley et al. (1995). A selection of their results is plotted as the open triangles. The numbers at the top give an estimate of the ZAMS mass of the progenitor of the helium star. |
| Open with DEXTER | |
As a check of our calculations we show in Fig. 3 the final masses that we obtain using the top two lines (dashed and solid) from Fig. 2 and the helium star lifetimes as given by Woosley et al. (1995) and compare these with the results obtained with the same mass-loss rates by Woosley et al. (1995) and Wellstein & Langer (1999). For the dashed line the final mass is obtained by numerical integration of the mass evolution. The final masses do not completely agree with the masses obtained by Wellstein & Langer (1999), probably because these high mass-loss rates lead to even longer lifetimes.
| |
Figure 4: Final helium star masses as function of initial helium star mass with the mass-loss rates given by Eq. (4) using a helium-star lifetime as given by Woosley et al. (1995, solid line), as given by Pols et al. (1991, dash-dotted line) and a helium-star lifetime halfway in-between these two (dashed line). ZAMS masses for the helium star progenitors are indicated at the top. |
| Open with DEXTER | |
We now calculated the final masses for the revised mass-loss rate
given by Eq. (4), which yields
![\begin{displaymath}M_{\rm f} = \left[M_{\rm i}^{-1.87} + 2.6 \, \times 10^{-8} \,
\tau \right]^{-1/1.87}.
\end{displaymath}](/articles/aa/full/2001/36/aah2816/img22.gif) |
(7) |
The horizontal line is at 7 ![]() ,
the typical observed mass of the
black holes in the low-mass X-ray binaries. The limiting ZAMS mass
for which the final helium star mass exceeds 7
,
the typical observed mass of the
black holes in the low-mass X-ray binaries. The limiting ZAMS mass
for which the final helium star mass exceeds 7 ![]() with the masses
loss rate used here is
with the masses
loss rate used here is ![]() 30-37
30-37 ![]() .
.
We thus conclude that with revised mass-loss rates helium stars end their lives with significantly higher masses than previously found and may be able to form black holes even after case B mass transfer.
The analysis in Sect. 2 neglects the influence of the wind
of the massive star on the companion star. The companion moves through
the wind and already feels friction, which counteracts the widening of
the orbit due to the stellar wind. However, even for a wind mass-loss
rate of
![]() yr-1, the density in the wind at the
companion is almost four orders of magnitude lower than the density at
the edge of the giant for a giant with radius of 1000
yr-1, the density in the wind at the
companion is almost four orders of magnitude lower than the density at
the edge of the giant for a giant with radius of 1000 ![]() and a
binary separation of 1600
and a
binary separation of 1600 ![]() .
.
The whole argument presented in Sect. 3 is based on the observed mass-loss rates. However, it should be noted that all mass-loss rates proposed for Wolf-Rayet stars and used in evolutionary calculations are based on the observed rates. The valid question still remains what the uncertainty is in the observed mass-loss rates and in the inferred stellar masses and how this could influence our main conclusion.
The mass-loss rates as determined by Nugis & Lamers (2000) are the most accurate, but still suffer from the general problem that not all quantities (mass, mass-loss rate and luminosity) can be determined independently. They therefore use the mass-luminosity relation of Schaerer & Maeder (1992) to obtain the final mass estimates from the luminosity. Using a different mass-luminosity relation may change the resulting mass/mass-loss rate combinations.
Taking the masses and mass-loss rates as plotted in Fig. 2, one would not say that there is a unique mass-loss rate-mass relation, as is expected on theoretical grounds (Langer 1989b). The scatter is larger than the quoted uncertainty in the observations. This either points to underestimates of the errors in the observations, to variability or to additional physical processes, which were not taken into account in the calculations by Langer (1989b) and can change the mass-loss rate for a given Wolf-Rayet star mass. One could think of rotation, magnetic fields or maybe the evolutionary history.
In the last respect it might be that stars in binaries that lose their hydrogen envelopes by mass transfer evolve differently from stars that lose their envelopes due to their own stellar winds (which possibly is enhanced by a companion). The question which stars actually form black holes and which neutron stars is considerably more complex than the question of the final mass of helium stars (e.g. Fryer 1999). In particular the evolution of the core is important. As long as the collapse of the core is not understood this question will remain unanswered.
Finally, it should be noted that to form a black hole low-mass X-ray binary the companion must survive the common-envelope phase. The outcome of the common envelope depends on the binding energy and density structure of the giants envelope, which are quite different for giants that undergo case B and case C mass transfer. It could for instance be that that all binaries that undergo case B mass transfer to a low-mass companion will completely merge. That would mean that we need the small allowed initial separation range for case C.
We calculated the possible initial separations for which case C mass
transfer is likely to occur for binaries containing a massive
star and a low-mass star, using different stellar evolution models.
We find that case C mass transfer becomes impossible for
primaries more massive than around 19 ![]() for the models of
Heger et al. (2000) and Hurley et al. (2000) and more massive than around 25
for the models of
Heger et al. (2000) and Hurley et al. (2000) and more massive than around 25 ![]() for the models by Schaller et al. (1992). For such binaries either
case B mass transfer occurs, or no mass transfer at all. Unless
the current models for massive stars underestimate the radius
expansion after the end of core helium burning the chances for forming
black holes in binaries through case C mass transfer are therefore
limited.
for the models by Schaller et al. (1992). For such binaries either
case B mass transfer occurs, or no mass transfer at all. Unless
the current models for massive stars underestimate the radius
expansion after the end of core helium burning the chances for forming
black holes in binaries through case C mass transfer are therefore
limited.
We also investigated the influence of the assumed mass-loss rate on
the final mass of helium stars in binaries and conclude that with a
downward revised mass-loss rate as suggested by the observations
(e.g. Nugis & Lamers 2000) helium stars end their lives with significantly
higher masses than previously found and may be able to form black
holes even after case B mass transfer for primaries more massive than
![]() 30-40
30-40 ![]() .
.
Acknowledgements
We thank J. Dewi and N. Langer for helpful discussion and trial calculations of helium star evolution and A. Heger for providing details of his evolutionary calculations. This work was supported by NWO Spinoza grant 08-0 to E. P. J. van den Heuvel.