A&A 376, 955-965 (2001)
DOI: 10.1051/0004-6361:20010982
Atomic diffusion in metal-poor stars
II. Predictions for the Spite plateau
M. Salaris1,2 - A. Weiss2,3,4
1 - Astrophysics Research Institute, Liverpool John Moores
University, Twelve Quays House, Egerton Wharf, Birkenhead CH41 1LD, UK
2 -
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1, 85748 Garching,
Germany
3 - Institute for Advanced Study, Olden Lane, Princeton, USA
4 - Princeton University Observatory, Peyton Hall,
Princeton, USA
Received 9 April 2001 / Accepted 5 July 2001
Abstract
We have computed a grid of up-to-date stellar evolutionary
models including atomic diffusion, in order to study the
evolution with time of the surface Li
abundance in low-mass metal-poor stars. We discuss in detail the
dependence of the surface Li evolution on the initial metallicity and stellar
mass, and compare the abundances obtained from our models with the
available Li measurements in Pop II stars. While it is widely accepted that
the existence of the Spite Li-plateau for these stars is a strong evidence
that diffusion is inhibited, we show that, when
taking into account observational errors, uncertainties in the Li
abundance determinations, in the
 scale, and in particular the size of the observed samples of stars,
the Spite plateau and the Li abundances in subgiant branch stars
can be reproduced also by models including fully efficient diffusion,
provided that the most metal-poor field halo objects are
between 13.5 and 14 Gyr old. We provide the value of the minimum
number of plateau stars to observe, for discriminating
between efficient or inhibited diffusion.
From our models with diffusion we derive that
the average Li abundance along the Spite plateau is
about a factor of 2 lower than the primordial one.
As a consequence, the derived primordial Li abundance
would be consistent
with a high helium and low deuterium Big Bang Nucleosynthesis;
this implies a high cosmological baryon density as inferred
from the analyses of the cosmic microwave background.
scale, and in particular the size of the observed samples of stars,
the Spite plateau and the Li abundances in subgiant branch stars
can be reproduced also by models including fully efficient diffusion,
provided that the most metal-poor field halo objects are
between 13.5 and 14 Gyr old. We provide the value of the minimum
number of plateau stars to observe, for discriminating
between efficient or inhibited diffusion.
From our models with diffusion we derive that
the average Li abundance along the Spite plateau is
about a factor of 2 lower than the primordial one.
As a consequence, the derived primordial Li abundance
would be consistent
with a high helium and low deuterium Big Bang Nucleosynthesis;
this implies a high cosmological baryon density as inferred
from the analyses of the cosmic microwave background.
Key words: stars: Population II - evolution - abundances -
physical data and processes: diffusion
Microscopic diffusion is a fundamental physical mechanism, which in
principle has to be considered when computing stellar models.
In particular, since the
highly accurate seismic determination of the solar sound speed profile
has become available, diffusion is an integral part of the standard solar
model. Taking diffusion into account, not only the sound speed, but
also the depth of the solar convective zone and the present surface
helium abundance are in very good agreement with observations (see,
for example Richard et al. 1996; Bahcall et al. 1997). Only in
the region immediately below the convective envelope the theoretical
models deviate from the seismic Sun significantly, indicating that
diffusion might not operate exactly in the way calculated or pointing
to some neglected additional physical process partially counter-working
diffusion (Brun et al. 1999).
With the Sun as our best laboratory for stellar physics strengthening
the case for the presence of atomic diffusion, it immediately becomes
mandatory to consider it also for other stars. Since diffusion is an
intrinsically slow process operating over cosmic times, long-lived
low-mass stars, in particular those of Population II, are evidently the
best suited candidates.
Atomic diffusion affects the
evolution of stars in two ways.
In the deep interior, the sinking of helium towards the core leads to an
effectively faster nuclear aging of the star, thus reducing its
Main Sequence (MS) lifetime. For age determinations of globular clusters
making use of the absolute brightness of the colour-magnitude diagram (CMD)
turn-off (TO), when the cluster distance is known, diffusion eventually leads to
lower ages; the effect accounts for a reduction of the order of 1 Gyr for
old globular clusters (Chaboyer et al. 1992; Castellani et al. 1997). The modified
chemical structure also affects
later evolutionary stages, such that age determination methods using
differential quantities, for example the brightness difference between
TO and horizontal branch, are less affected (about 0.5 Gyr;
Cassisi et al. 1998; Castellani & Degl'Innocenti 1999).
In the envelope of the star, diffusion leads to a depletion of the
heavy elements and helium. This has the direct consequence
that the present abundance of metals is lower than the initial one. In
Salaris et al. (2000) we discussed in detail the consequences for the
MS fitting method, the resulting distances, and subdwarfs
ages. Furthermore, due to the decreased metals, the colours of the
star change. The stellar radius and thus the effective temperature,
however, also depend on the molecular weight in the star's core, which
is increased in the presence of sedimentation.
Taking diffusion into account, a much better agreement
between models and observed colours or effective temperature results,
as has been noted by Lebreton et al. (1999; see also Morel & Baglin 1999 and Salaris et al. 2000).
Similarly, an improved isochrone fitting for globular clusters, and consistency
between the age from the cluster CMD and that from its integrated spectrum
might be obtained (Vazdekis et al. 2001 for 47 Tuc).
A general prediction of models including atomic diffusion
is that very metal-poor low-mass stars, with their
high effective temperatures and thus very shallow convective envelopes,
are readily depleted of metals over the MS lifetime (see
the seminal paper by Deliyannis et al. 1990); this
prediction can be contrasted with observations. In the present paper,
we will therefore confront theoretical models with the observational
result that the 7Li abundance in such stars of
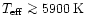 forms a well-defined plateau below
forms a well-defined plateau below
![$\mathrm
{[Fe/H]} \approx -1.5$](/articles/aa/full/2001/36/aah2788/img13.gif) (Spite & Spite 1982). In the past, this so-called Li- or
Spite-plateau has been used repeatedly as an, if not the
argument against the full efficiency of
diffusion (Deliyannis & Demarque 1991; Vauclair & Charbonnel 1998;
Ryan et al. 1996), because the degree of depletion by diffusion increases with
effective temperature. Stated differently,
the necessity for an additional effect counteracting diffusion was
claimed (Chaboyer et al. 1995a; Vauclair 1999). Candidate
processes are rotationally induced mixing
(Chaboyer et al. 1995a, 1995b) or a
rather strong mass loss by a stellar wind (Vauclair & Charbonnel 1995).
(Spite & Spite 1982). In the past, this so-called Li- or
Spite-plateau has been used repeatedly as an, if not the
argument against the full efficiency of
diffusion (Deliyannis & Demarque 1991; Vauclair & Charbonnel 1998;
Ryan et al. 1996), because the degree of depletion by diffusion increases with
effective temperature. Stated differently,
the necessity for an additional effect counteracting diffusion was
claimed (Chaboyer et al. 1995a; Vauclair 1999). Candidate
processes are rotationally induced mixing
(Chaboyer et al. 1995a, 1995b) or a
rather strong mass loss by a stellar wind (Vauclair & Charbonnel 1995).
Although, therefore, the Li-plateau seems to make a strong case
against diffusion, there are a number of issues that warrant a new
look at this problem. First of all, the input physics for the stellar
models has changed a lot in the last few years, and the improved
equations of state, opacities and nuclear reaction rates all affect
the stellar models (see Cassisi et al. 1998 for an overview). Secondly, and as
a consequence, the deduced ages for the oldest
clusters and stars has been reduced from 16-18 Gyr to 12-14 Gyr
(Salaris et al. 1997). Thirdly, the observed field stars have a distribution of metallicities
and possibly of ages, while often the comparison is performed by
considering models of different masses all with the same age and metallicity
(as, e.g., in Deliyannis et al. 1990 or Vauclair & Charbonnel 1998).
Finally, it is important to consider, when comparing theory with
observations, not only the observational errors, but also the actual
size of the sample of stars with Li abundance determinations.
The inclusion of diffusion does not only lead to a depletion of the
surface lithium content, but to a second effect which could be
measurable; the diffused Li is stored immediately below the thin
convective envelope (see Vauclair & Charbonnel 1998 for illustrative interior
profiles) but remains at temperatures too low for lithium-destruction
by proton capture. After the TO, the deepening convective
envelope at first mixes this surplus to the surface, such that for some time
subgiants should have Li-abundances somewhat above the Spite-plateau
level which, in the case of effective diffusion, does not represent
the primordial abundance.
To recall, in case of no diffusion there is no difference between the
initial Li-abundance and that on the main sequence and subgiant branch.
With further expansion the convective
envelope deepens until regions where the initial lithium was destroyed
are diluting the envelope lithium content and a decrease in the
surface abundance will ensue.
In this paper we will therefore investigate theoretical predictions
for the Li-abundance![[*]](/icons/foot_motif.gif) of low-mass metal-poor stars, making use of the
latest stellar models, which will be presented in Sect. 2. The
calculations were used to prepare data about the lithium abundance as
a function of metallicity, effective temperature and age.
The comparison with the observed Li abundances of plateau
and subgiant branch stars will be described in Sect. 3, while
in Sect. 4 we will discuss the
consequences of our results and, in particular, to which extent the
Spite plateau can be used to make statements about the efficiency
of diffusion operating in old metal-poor stars.
of low-mass metal-poor stars, making use of the
latest stellar models, which will be presented in Sect. 2. The
calculations were used to prepare data about the lithium abundance as
a function of metallicity, effective temperature and age.
The comparison with the observed Li abundances of plateau
and subgiant branch stars will be described in Sect. 3, while
in Sect. 4 we will discuss the
consequences of our results and, in particular, to which extent the
Spite plateau can be used to make statements about the efficiency
of diffusion operating in old metal-poor stars.
We started out with stellar evolution calculations using the same
input physics as in Salaris & Weiss (1998) and Salaris et al. (2000). We computed
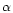 -enhanced models (average enhancement by 0.4 dex, as in
Salaris & Weiss 1998) for initial
iron contents
-enhanced models (average enhancement by 0.4 dex, as in
Salaris & Weiss 1998) for initial
iron contents
![${\rm [Fe/H]_o} = -3.2,\, -2.6,\, -2.3,\, -1.8$](/articles/aa/full/2001/36/aah2788/img19.gif) (corresponding to
(corresponding to
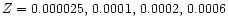 )
and masses between 0.6 and 1.0
)
and masses between 0.6 and 1.0 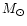 ,
from the pre-MS phase until the beginning of
the Red Giant Branch (RGB).
The initial He content has been fixed at Y=0.23+3Z, and we used
an initial lithium abundance
,
from the pre-MS phase until the beginning of
the Red Giant Branch (RGB).
The initial He content has been fixed at Y=0.23+3Z, and we used
an initial lithium abundance
![$\rm [Li]_{\rm o}=2.50$](/articles/aa/full/2001/36/aah2788/img22.gif) .
Diffusion was included by solving the Burgers equations following
Thoul et al. (1994), and considered for H, He, Li, C, N, O, and Fe.
The other elements have been assumed to diffuse like Fe.
The rates for the Li destruction reactions are from the NACRE compilation
(Angulo et al. 1999).
.
Diffusion was included by solving the Burgers equations following
Thoul et al. (1994), and considered for H, He, Li, C, N, O, and Fe.
The other elements have been assumed to diffuse like Fe.
The rates for the Li destruction reactions are from the NACRE compilation
(Angulo et al. 1999).
Pre-MS evolution was followed
to assess the possible Li-depletion in this phase, although it is
expected to lead to substantial lithium destruction only for stellar
masses below
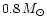 (D'Antona & Mazzitelli 1984; Deliyannis et al. 1990).
For these pre-MS calculations, the Garching stellar evolution code was used
(see, e.g., Weiss & Schlattl 2000 and references therein), in
contrast to the variant of the FRANEC program for all other
calculations. Both codes use in most aspects essentially the same and
in some (opacities, diffusion coefficients) identical physics and
produce very similar results, as shown, for example, in
Weiss & Schlattl (2000).
The derived Li abundances at the Zero Age Main Sequence where then provided
to the code we have employed in all our previous evolutionary computations.
Selected results about the surface Li-depletion exclusively due to nuclear
burning are summarized in Table 1.
(D'Antona & Mazzitelli 1984; Deliyannis et al. 1990).
For these pre-MS calculations, the Garching stellar evolution code was used
(see, e.g., Weiss & Schlattl 2000 and references therein), in
contrast to the variant of the FRANEC program for all other
calculations. Both codes use in most aspects essentially the same and
in some (opacities, diffusion coefficients) identical physics and
produce very similar results, as shown, for example, in
Weiss & Schlattl (2000).
The derived Li abundances at the Zero Age Main Sequence where then provided
to the code we have employed in all our previous evolutionary computations.
Selected results about the surface Li-depletion exclusively due to nuclear
burning are summarized in Table 1.
These numbers can be compared with, for example, the results of
Deliyannis et al. (1990). We get a definitely higher depletion
at the lower masses than in these older
calculations (with older opacities and equation of state). For
example (see their Fig. 14), our
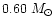 model shows strong
depletion already on the pre-MS for all metallicities,
and continuing depletion on the
MS, while the depletion in the Z=0.0001 models by Deliyannis et al. (1990) levels off at
-0.4 dex already at the beginning of the MS phase.
This behaviour is
similar to that found by Ventura et al. (1998), when comparing with their
older models (D'Antona & Mazzitelli 1984): the more up-to-date physics leads to a
higher depletion.
model shows strong
depletion already on the pre-MS for all metallicities,
and continuing depletion on the
MS, while the depletion in the Z=0.0001 models by Deliyannis et al. (1990) levels off at
-0.4 dex already at the beginning of the MS phase.
This behaviour is
similar to that found by Ventura et al. (1998), when comparing with their
older models (D'Antona & Mazzitelli 1984): the more up-to-date physics leads to a
higher depletion.
When comparing our diffusion calculations with the results
from the scaled-solar models by
Vauclair & Charbonnel (1998), for ages of 12 and 14 Gyr,
we find good agreement, with large differences only
for the
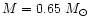 models, which are
mainly due to differences in the pre-MS phase, since for these
masses and ages the depletion due to diffusion from the convective
envelope is only a small contribution.
models, which are
mainly due to differences in the pre-MS phase, since for these
masses and ages the depletion due to diffusion from the convective
envelope is only a small contribution.
From the computed grid of stellar models we then produced
Li-isochrones (i.e. Li-abundances along isochrones as in
Deliyannis et al. 1990) for different ages and different initial [Fe/H] values.
It is important to remark here that along an isochrone the surface
[Fe/H] is
not constant, again due to the effect of diffusion
(Morel & Baglin 1999; Salaris et al. 2000). At a given age of some
Gyr, the surface [Fe/H] is lower than the initial value; it also shows a
decrease towards the TO and than increases along the
Sub Giant Branch (SGB) until it reaches the initial value along the
RGB (see Fig. 2).
Therefore our isochrones, for ages larger than 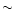 5 Gyr, cover
a range of surface [Fe/H] between
5 Gyr, cover
a range of surface [Fe/H] between
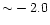 and
and
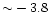 .
.
Figure 1 displays in panels a) and b)
Li-isochrones as a function of
 and mass for ages of 12, 13, 14 Gyr and
initial metallicity
and mass for ages of 12, 13, 14 Gyr and
initial metallicity
![$\rm [Fe/H]_{o}=-2.6$](/articles/aa/full/2001/36/aah2788/img5.gif) ,
from the unevolved lower main
sequence up to the TO.
The shape of the isochrones looks very similar for the various ages
apart from the different value of
,
from the unevolved lower main
sequence up to the TO.
The shape of the isochrones looks very similar for the various ages
apart from the different value of
 at both the TO and at the cool end.
Li depletion at the coolest end of the isochrones is
dominated by the pre-MS depletion (masses populating these region
range from 0.60 up to
at both the TO and at the cool end.
Li depletion at the coolest end of the isochrones is
dominated by the pre-MS depletion (masses populating these region
range from 0.60 up to
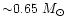 ), while for
), while for
 larger than
larger than
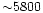 K Li diffusion is mainly responsible for the
surface Li depletion, since pre-MS depletion is negligible.
The isochrones for t=12 Gyr show more depletion at the TO since, in
spite of the shorter time available for diffusion to deplete the surface Li,
TO stars are hotter and have shallower convective regions and therefore the surface Li
depletion is more efficient.
The Li-isochrones show also an extended region, with
K Li diffusion is mainly responsible for the
surface Li depletion, since pre-MS depletion is negligible.
The isochrones for t=12 Gyr show more depletion at the TO since, in
spite of the shorter time available for diffusion to deplete the surface Li,
TO stars are hotter and have shallower convective regions and therefore the surface Li
depletion is more efficient.
The Li-isochrones show also an extended region, with
 ranging between
ranging between
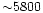 and 6300 K (the extension depends on the
age), in which the depletion does not change by more than 0.2 dex.
At these ages the depletion at the level of this plateau is of the
order of 0.3 dex.
and 6300 K (the extension depends on the
age), in which the depletion does not change by more than 0.2 dex.
At these ages the depletion at the level of this plateau is of the
order of 0.3 dex.
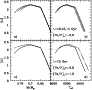 |
Figure 1:
Panels a) and b): Run of [Li] as a function of the stellar mass
and
 for isochrones with initial metallicity
for isochrones with initial metallicity
![$\rm [Fe/H]_{o}=-2.6$](/articles/aa/full/2001/36/aah2788/img5.gif) and ages of 12 (solid line), 13 (dotted line) and 14 Gyr (dashed line).
Panels c) and d): As in panels a) and b), but for
isochrones with t=12 Gyr and and ages of 12 (solid line), 13 (dotted line) and 14 Gyr (dashed line).
Panels c) and d): As in panels a) and b), but for
isochrones with t=12 Gyr and
![$\rm [Fe/H]_{o}=-2.6$](/articles/aa/full/2001/36/aah2788/img5.gif) (solid line) and
-1.8 (dashed line).
(solid line) and
-1.8 (dashed line). |
| Open with DEXTER |
In panels c) and d) of Fig. 1
we compare the [Li] values along two
isochrones with the same age of 12 Gyr but two different initial metallicities.
The shape of the isochrones again is very similar, with the more metal-rich
models being less depleted at the TO (larger convective envelopes)
and in general more Li-rich for a given value of
 .
.
Finally, in Fig. 2 we display the run of [Li] as a
function of
 for 12 and 14 Gyr isochrones with
for 12 and 14 Gyr isochrones with
![$\rm [Fe/H]_{o}=-2.6$](/articles/aa/full/2001/36/aah2788/img5.gif) ,
from the MS to the base of the
RGB. It is very interesting to notice that after the TO [Li]
continues to decrease for the next 50 K, with a further depletion by
about 0.1 dex. The maximum depletion is a function of age,
strongly decreasing for increasing age. It also depends on
metallicity, in the sense that at a given age the maximum depletion
decreases with increasing metallicities. This behaviour is easy to
understand if one recalls that the extension of the convective
envelope in TO stars increases for increasing age at a given
metallicity, or for increasing metallicity at a given age,
reducing thus the effect of diffusion on the surface abundances.
,
from the MS to the base of the
RGB. It is very interesting to notice that after the TO [Li]
continues to decrease for the next 50 K, with a further depletion by
about 0.1 dex. The maximum depletion is a function of age,
strongly decreasing for increasing age. It also depends on
metallicity, in the sense that at a given age the maximum depletion
decreases with increasing metallicities. This behaviour is easy to
understand if one recalls that the extension of the convective
envelope in TO stars increases for increasing age at a given
metallicity, or for increasing metallicity at a given age,
reducing thus the effect of diffusion on the surface abundances.
Later on, with decreasing temperature, the [Li] abundance starts to
rise again due to the deepening of the convective region which
returns to the surface the Li diffused outside the envelope
along the MS. [Li] reaches a peak
when
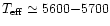 K, with an abundance within 0.1 dex
from the initial one; then the Li surface abundance starts to drop,
since the convective envelope reaches regions where Li had been
burned due to the higher temperatures of the stellar matter.
We note that the location and level of the Li abundance peak is
fairly independent of age and metallicity (see Fig. 7) and, in
addition, is within 0.1 dex of the primordial value, independent of
the effectiveness of diffusion.
If this peak is found by analyzing the [Li] distribution in a
large sample of stars spanning the entire SGB temperature range,
it would provide an estimate of the
primordial Li abundance to this accuracy.
K, with an abundance within 0.1 dex
from the initial one; then the Li surface abundance starts to drop,
since the convective envelope reaches regions where Li had been
burned due to the higher temperatures of the stellar matter.
We note that the location and level of the Li abundance peak is
fairly independent of age and metallicity (see Fig. 7) and, in
addition, is within 0.1 dex of the primordial value, independent of
the effectiveness of diffusion.
If this peak is found by analyzing the [Li] distribution in a
large sample of stars spanning the entire SGB temperature range,
it would provide an estimate of the
primordial Li abundance to this accuracy.
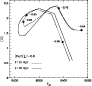 |
Figure 2:
[Li] as a function of
 for isochrones
of 12 and 14 Gyr, with
for isochrones
of 12 and 14 Gyr, with
![$\rm [Fe/H]_{o}=-$](/articles/aa/full/2001/36/aah2788/img6.gif) 2.6, from the MS to
the lower RGB. Selected values of [Fe/H] along the
14 Gyr isochrone are also shown. 2.6, from the MS to
the lower RGB. Selected values of [Fe/H] along the
14 Gyr isochrone are also shown. |
| Open with DEXTER |
In this section we will compare the behaviour of the
[Li] abundances obtained from our MS and SGB models
with the observations of metal-poor field and globular cluster stars.
We concentrate our attention on stars
with [Fe/H] 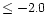 ,
which constitute the largest fraction
of the currently available samples of PopII Li-plateau stars;
in the last part of this section we will
discuss briefly also the case of stars with [Fe/H] up to
,
which constitute the largest fraction
of the currently available samples of PopII Li-plateau stars;
in the last part of this section we will
discuss briefly also the case of stars with [Fe/H] up to
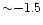 ,
which
is approximately the upper metallicity boundary of the Spite plateau.
,
which
is approximately the upper metallicity boundary of the Spite plateau.
Observations of Li abundances in metal-poor MS field stars
provide a qualitative picture that is basically consistent among the
different authors, but which can differ a lot in the details
(see, e.g., Thorburn 1994; Ryan et al. 1996; Spite et al. 1996; Bonifacio & Molaro 1997;
Ryan et al. 1999; Ryan et al. 2001 and references therein).
The main result (as an example we show in Fig. 3
the Thorburn 1994 data for the metallicity range spanned by our models)
is that metal-poor MS stars with
 larger than approximately 5800 K show a remarkably
constant [Li] value (Li-plateau), while there is a larger
depletion at lower temperatures, increasing for decreasing temperature.
Moreover, in the plateau region, a handful of stars show a much lower
[Li] than the plateau counterpart (e.g. Thorburn 1994).
larger than approximately 5800 K show a remarkably
constant [Li] value (Li-plateau), while there is a larger
depletion at lower temperatures, increasing for decreasing temperature.
Moreover, in the plateau region, a handful of stars show a much lower
[Li] than the plateau counterpart (e.g. Thorburn 1994).
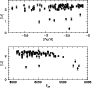 |
Figure 3:
Run of [Li] as a function of [Fe/H] (upper panel) and
 (lower panel) from the Thorburn (1994) data for MS
stars with
(lower panel) from the Thorburn (1994) data for MS
stars with
![$\rm [Fe/H]\leq -2.0$](/articles/aa/full/2001/36/aah2788/img7.gif) .
Upper limit detections are also shown.
For the sake of clarity we did not plot the error bars on the .
Upper limit detections are also shown.
For the sake of clarity we did not plot the error bars on the
 values (of the order of, typically, 80-100 K, see Thorburn 1994 for more
details).
values (of the order of, typically, 80-100 K, see Thorburn 1994 for more
details). |
| Open with DEXTER |
The details of this picture, however, differ from author to author.
The exact
 location and extent of the plateau varies
slightly; some trend of [Li] with
location and extent of the plateau varies
slightly; some trend of [Li] with
 along the plateau was
detected by Thorburn (1994) and Ryan et al. (1996),
but it is absent in the analyses by Bonifacio & Molaro (1997) and Ryan et al. (1999).
A trend of [Li] with respect to [Fe/H] for plateau stars is claimed by
Thorburn (1994), Ryan et al. (1996), Ryan et al. (1999) and Ryan et al. (2001),
while it is missing in Bonifacio & Molaro (1997).
Also the absolute average value of [Li] for plateau stars shows
differences between different authors.
along the plateau was
detected by Thorburn (1994) and Ryan et al. (1996),
but it is absent in the analyses by Bonifacio & Molaro (1997) and Ryan et al. (1999).
A trend of [Li] with respect to [Fe/H] for plateau stars is claimed by
Thorburn (1994), Ryan et al. (1996), Ryan et al. (1999) and Ryan et al. (2001),
while it is missing in Bonifacio & Molaro (1997).
Also the absolute average value of [Li] for plateau stars shows
differences between different authors.
In addition to the purely observational errors and
differences in the adopted metallicity
scale, there are other sources of uncertainty
that should be mentioned. The first one is the set of model atmospheres
used in the spectral analyses.
As dicussed by Ryan et al. (1996), the differences between Li abundances
derived from different sets of model atmospheres show
trends with respect to both
 and [Fe/H].
Very recently Asplund et al. (1999) discussed the differences in the [Li]
values derived using either 1D, plane
parallel, hydrostatic model atmospheres, like the MARCS (Gustafsson et al. 1975
with subsequent updates) and ATLAS9 (Kurucz 1993) ones used in all recent
papers on [Li] abundances,
or their 3D hydrodynamical model atmospheres. A remarkable
result is that not only the absolute values of [Li] are changed when
passing from 1D to 3D models, but that also the spread in
[Li] values is changed. They discuss the case of HD 140283 and HD 84937
whose [Li] derived from MARCS models is, respectively, 2.12 and 2.28.
Using their 3D hydrodynamical models, Asplund et al. (1999) obtain 1.78
and 2.08; the difference between the two values is almost doubled
with respect to the case of 1D hydrostatic models.
Keeping in mind their cautionary remarks about the
assumption of LTE in their models, it is nevertheless important to
notice that the derived [Li] spread may underestimate
the real variation.
and [Fe/H].
Very recently Asplund et al. (1999) discussed the differences in the [Li]
values derived using either 1D, plane
parallel, hydrostatic model atmospheres, like the MARCS (Gustafsson et al. 1975
with subsequent updates) and ATLAS9 (Kurucz 1993) ones used in all recent
papers on [Li] abundances,
or their 3D hydrodynamical model atmospheres. A remarkable
result is that not only the absolute values of [Li] are changed when
passing from 1D to 3D models, but that also the spread in
[Li] values is changed. They discuss the case of HD 140283 and HD 84937
whose [Li] derived from MARCS models is, respectively, 2.12 and 2.28.
Using their 3D hydrodynamical models, Asplund et al. (1999) obtain 1.78
and 2.08; the difference between the two values is almost doubled
with respect to the case of 1D hydrostatic models.
Keeping in mind their cautionary remarks about the
assumption of LTE in their models, it is nevertheless important to
notice that the derived [Li] spread may underestimate
the real variation.
Another important source of uncertainty
is the
 scale itself. Different authors use
temperature scales which often differ not just by a constant
offset, but also show differential trends with respect to the metallicity.
To investigate better this point we have considered 8 plateau stars in common among the
investigations by Thorburn (1994), Ryan et al. (1999) and Ryan et al. (1999).
scale itself. Different authors use
temperature scales which often differ not just by a constant
offset, but also show differential trends with respect to the metallicity.
To investigate better this point we have considered 8 plateau stars in common among the
investigations by Thorburn (1994), Ryan et al. (1999) and Ryan et al. (1999).
It turned out that
the spread of the
 values is not constant and
in some cases quite remarkable. The differences of the Ryan et al. (1999)
values is not constant and
in some cases quite remarkable. The differences of the Ryan et al. (1999)
 values to the Bonifacio & Molaro (1997) ones range from about
-150 K up to almost 300 K.
Somewhat smaller values (ranging between about -20 K
and 150 K) are obtained when considering the difference to the
values to the Bonifacio & Molaro (1997) ones range from about
-150 K up to almost 300 K.
Somewhat smaller values (ranging between about -20 K
and 150 K) are obtained when considering the difference to the
 by Thorburn (1994). If
one takes into account that a
by Thorburn (1994). If
one takes into account that a
 variation by 100 K
changes the derived [Li] value by about 0.07 dex (Ryan et al. 1999),
it may well be that the current uncertainty about Li
trends along the plateau is due mainly to uncertainties of the
temperature scale.
Also the [Fe/H] values adopted in different
investigations show a spread which reaches values larger than
variation by 100 K
changes the derived [Li] value by about 0.07 dex (Ryan et al. 1999),
it may well be that the current uncertainty about Li
trends along the plateau is due mainly to uncertainties of the
temperature scale.
Also the [Fe/H] values adopted in different
investigations show a spread which reaches values larger than 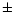 0.5 dex.
0.5 dex.
In order to analyze the predictions of theoretical diffusive models
regarding the trends of [Li] with respect to
 and [Fe/H] in metal-poor stars, we resorted to Monte-Carlo (MC)
simulations using our own isochrones.
In this way we will be able to take into account the fact that the
subdwarfs with [Li] measurements have a metallicity distribution and
possibly an age distribution. As
we have shown before, the initial metallicity and age alter the
location and shape of
Li-isochrones, and it is important to take these two factors into
account. Moreover, with MC simulations we will be also able to account for
the actual number of MS stars with [Li] measurements. This point - as
we will see later on - is of fundamental importance when trying to
constrain the efficiency of diffusion from Li-plateau stars.
It is important to remark at this stage that, since the observations provide
contradictory results about the properties of the Spite plateau,
we can just discuss whether our models with diffusion are able to
reproduce the plateau, and if its derived properties are within the
range allowed by existing data.
and [Fe/H] in metal-poor stars, we resorted to Monte-Carlo (MC)
simulations using our own isochrones.
In this way we will be able to take into account the fact that the
subdwarfs with [Li] measurements have a metallicity distribution and
possibly an age distribution. As
we have shown before, the initial metallicity and age alter the
location and shape of
Li-isochrones, and it is important to take these two factors into
account. Moreover, with MC simulations we will be also able to account for
the actual number of MS stars with [Li] measurements. This point - as
we will see later on - is of fundamental importance when trying to
constrain the efficiency of diffusion from Li-plateau stars.
It is important to remark at this stage that, since the observations provide
contradictory results about the properties of the Spite plateau,
we can just discuss whether our models with diffusion are able to
reproduce the plateau, and if its derived properties are within the
range allowed by existing data.
In our simulations we assumed that present [Li] observations of
field MS subdwarfs cover also TO stars.
We prescribed an age-initial metallicity relationship
and, by interpolating among our isochrones,
we have drawn a large sample of 10000 MS stars, according to a Salpeter
Initial Mass Function, with an initial [Fe/H] distribution adjusted
(by trial and error) in such a way that the 10000 stars show
a metallicity distribution in agreement with the typical metallicity
distribution of halo stars as determined by
Ryan & Norris (1991).
For each star we determined the value of its mass, bolometric
luminosity, surface [Fe/H] and [Li], and
 .
We then added to the values of [Fe/H], [Li], and
.
We then added to the values of [Fe/H], [Li], and
 1
1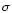 random observational errors by, respectively,
0.20 dex, 0.07 dex and 65 K. These observational errors
are approximately an average of the values quoted by Thorburn (1994),
Ryan et al. (1996), Spite et al. (1996), Bonifacio & Molaro (1997).
random observational errors by, respectively,
0.20 dex, 0.07 dex and 65 K. These observational errors
are approximately an average of the values quoted by Thorburn (1994),
Ryan et al. (1996), Spite et al. (1996), Bonifacio & Molaro (1997).
From this sample of 10000 stars representing the halo population we
have randomly drawn 30 smaller samples of
120 stars each, which represent the MC realizations of the observational
data; about 65 objects populate the plateau region (which we define as being
the region with
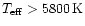 ).
This number of plateau stars correponds approximately to the largest sample with [Li]
abundances and
).
This number of plateau stars correponds approximately to the largest sample with [Li]
abundances and
![$\rm [Fe/H]\leq -2.0$](/articles/aa/full/2001/36/aah2788/img7.gif) available to this day (see, e.g.,
Thorburn 1994; Ryan et al. 1996).
For each of these
samples we studied the distribution of stars in the [Li]-
available to this day (see, e.g.,
Thorburn 1994; Ryan et al. 1996).
For each of these
samples we studied the distribution of stars in the [Li]-
 and [Li]-[Fe/H] planes.
and [Li]-[Fe/H] planes.
 |
Figure 4:
Run of [Li] as a function of [Fe/H] (upper panel) and
 (lower panel) for stars in one of our MC simulations,
considering an age randomly distributed between 13.5 and 14 Gyr.
Filled circles represent plateau stars (see text for details).
(lower panel) for stars in one of our MC simulations,
considering an age randomly distributed between 13.5 and 14 Gyr.
Filled circles represent plateau stars (see text for details). |
| Open with DEXTER |
We have been able to obtain a plateau-like feature
for
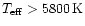 only when the age of the sample is equal or higher than about 13.5 Gyr. Lower
ages show a pronounced drop of [Li] at the TO which is not observed.
Above this age, in the limit of the actual
available observational samples and typical errors, the theoretical plateau region
looks quite similar to the observational counterpart.
In Fig. 4 we display the outcome of one simulation, where the age of the
stars is randomly distributed between 13.5 and 14 Gyr.
The result is quite typical of the ensemble of the 30 samples we have
drawn with this age distribution.
The plateau for
only when the age of the sample is equal or higher than about 13.5 Gyr. Lower
ages show a pronounced drop of [Li] at the TO which is not observed.
Above this age, in the limit of the actual
available observational samples and typical errors, the theoretical plateau region
looks quite similar to the observational counterpart.
In Fig. 4 we display the outcome of one simulation, where the age of the
stars is randomly distributed between 13.5 and 14 Gyr.
The result is quite typical of the ensemble of the 30 samples we have
drawn with this age distribution.
The plateau for
 higher than about
5800 K (filled circles) is clearly visible together with a drop at lower
higher than about
5800 K (filled circles) is clearly visible together with a drop at lower
 (open circles) due to the effect of pre-MS depletion.
The solid line in the plane [Li]-
(open circles) due to the effect of pre-MS depletion.
The solid line in the plane [Li]-
 shows the average
[Li] value for these plateau objects
(
shows the average
[Li] value for these plateau objects
(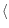 [Li]
[Li]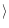 ), while the dashed lines indicate
), while the dashed lines indicate
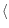 [Li]
[Li]
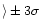 ,
where
,
where 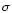 is the typical
observational error on [Li] adopted in our simulations (0.07 dex).
Only 4 plateau stars appear to be outside the zone
limited by the dashed lines (with lower [Li] values).
If we take out these 4 stars and recompute
is the typical
observational error on [Li] adopted in our simulations (0.07 dex).
Only 4 plateau stars appear to be outside the zone
limited by the dashed lines (with lower [Li] values).
If we take out these 4 stars and recompute 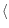 [Li]
[Li]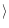 ,
its
value is not affected appreciably and all the remaining stars
still lie within
,
its
value is not affected appreciably and all the remaining stars
still lie within 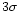 of
of 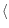 [Li]
[Li]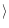 .
For the stars within
.
For the stars within 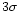 of
of 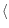 [Li]
[Li]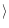 there is no significant correlation between
[Li] and
there is no significant correlation between
[Li] and
 .
Plateau stars outside this region
we will call "outliers''. In all our simulations the
outliers lie always below
.
Plateau stars outside this region
we will call "outliers''. In all our simulations the
outliers lie always below 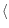 [Li]
[Li]
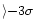 ,
and they
look like the theoretical counterpart of the observed Li-depleted
stars in the plateau region (see Fig. 3;
Thorburn 1994; Ryan et al. 2001). It is important to notice that in the
observational analyses of the plateau, the (few) stars showing a substantial depletion
with respect to the average plateau value, are not considered in the
derivation of the plateau properties. As we did the same with our
outliers, our selection closely mimicks the observational analyses.
,
and they
look like the theoretical counterpart of the observed Li-depleted
stars in the plateau region (see Fig. 3;
Thorburn 1994; Ryan et al. 2001). It is important to notice that in the
observational analyses of the plateau, the (few) stars showing a substantial depletion
with respect to the average plateau value, are not considered in the
derivation of the plateau properties. As we did the same with our
outliers, our selection closely mimicks the observational analyses.
By averaging over the 30 realizations with this same age distribution, we
derived for the plateau stars a [Li] depletion by 0.27 dex and a
derivative
![${\rm\Delta[Li]}/{\rm\Delta[Fe/H]}=0.06$](/articles/aa/full/2001/36/aah2788/img52.gif) .
The average
number of outliers (Li-depleted stars) is 6.
This latter number compares well with the actually observed number
of Li-depleted stars in this same [Fe/H] and
.
The average
number of outliers (Li-depleted stars) is 6.
This latter number compares well with the actually observed number
of Li-depleted stars in this same [Fe/H] and
 range
(see Thorburn 1994). Also the average plateau value
range
(see Thorburn 1994). Also the average plateau value
![$\rm [Li]=2.23$](/articles/aa/full/2001/36/aah2788/img53.gif) ,
obtained from an initial lithium abundance
,
obtained from an initial lithium abundance
![$\rm [Li]_{\rm o}=2.50$](/articles/aa/full/2001/36/aah2788/img22.gif) ,
agrees well with the values provided in the literature, which
span a relatively large range
from
,
agrees well with the values provided in the literature, which
span a relatively large range
from
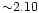 (Ryan et al. 1999) up to
(Ryan et al. 1999) up to
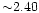 (Gratton et al. 2000).
The slope
(Gratton et al. 2000).
The slope
![${\rm\Delta[Li]}/{\rm\Delta[Fe/H]}$](/articles/aa/full/2001/36/aah2788/img56.gif) is halfway between the value
is halfway between the value
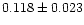 claimed by Ryan et al. (1999), and the results by
Bonifacio & Molaro (1997), who did not find any dependence on [Fe/H]
for the plateau [Li] values.
claimed by Ryan et al. (1999), and the results by
Bonifacio & Molaro (1997), who did not find any dependence on [Fe/H]
for the plateau [Li] values.
The lower
 limit off the plateau has been, somewhat
arbitrarily, set to 5800 K, which is a typical value as deduced from
the observations. Had we increased it up to 5900 K (again, compatible
with observations), the situation would have changed only slightly,
with just a small decrease of the average [Li] depletion along the
plateau, and a somewhat narrower distribution of the plateau stars
around
limit off the plateau has been, somewhat
arbitrarily, set to 5800 K, which is a typical value as deduced from
the observations. Had we increased it up to 5900 K (again, compatible
with observations), the situation would have changed only slightly,
with just a small decrease of the average [Li] depletion along the
plateau, and a somewhat narrower distribution of the plateau stars
around 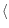 [Li]
[Li] .
.
We made simulations also assuming a constant age of, respectively,
13.5 and 14.0 Gyr, and ages between 14 and 15 Gyr;
the results are substantially the same, in the sense that a
plateau-like feature is always found, without a significant depletion
at its hotter end. We did
not explore ages larger than about 15 Gyr because of the constraints
put on the ages of field halo stars by the current estimates of
globular clusters ages (see next section), and also by the fact that
the horizontal extension of the plateau region is very much reduced
and, even taking into account current uncertainties in the
 ,
it is too much reduced in comparison with
observational data.
,
it is too much reduced in comparison with
observational data.
We now investigate whether our assumed metallicity distribution for
halo stars leads to properties of the simulated sample in agreement
with observed ones.
To this end we compare in Fig. 5
the distribution of plateau stars
(
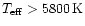 )
as a function of the actual
metallicity [Fe/H] and
)
as a function of the actual
metallicity [Fe/H] and
 in case of one of our MC samples,
and the data by Thorburn (1994) with
in case of one of our MC samples,
and the data by Thorburn (1994) with
![$\rm [Fe/H]< -2.0$](/articles/aa/full/2001/36/aah2788/img58.gif) (the bin size is equal to 70 K in
(the bin size is equal to 70 K in
 and 0.20 dex in [Fe/H]). The number of plateau
stars in both cases is the same.
and 0.20 dex in [Fe/H]). The number of plateau
stars in both cases is the same.
If one takes into account the spread of the empirical
determinations of
 and [Fe/H] previously discussed
the differences between the distributions of stars
in the observed and synthetic samples are probably not very
significant.
However, as a test, we computed a series of MC simulations
in the same way as before (ages again distributed
uniformly between 13.5 and 14.0 Gyr), but considering
an actual metallicity distribution biased towards lower metallicities with
respect to the Ryan & Norris (1991) one.
This corresponds, basically, to have synthetic samples of plateau
stars with a higher fraction of very metal-poor stars, in the
assumptions that the observations were biased towards the most metal
poor objects.
and [Fe/H] previously discussed
the differences between the distributions of stars
in the observed and synthetic samples are probably not very
significant.
However, as a test, we computed a series of MC simulations
in the same way as before (ages again distributed
uniformly between 13.5 and 14.0 Gyr), but considering
an actual metallicity distribution biased towards lower metallicities with
respect to the Ryan & Norris (1991) one.
This corresponds, basically, to have synthetic samples of plateau
stars with a higher fraction of very metal-poor stars, in the
assumptions that the observations were biased towards the most metal
poor objects.
The distribution of plateau stars as a function of [Fe/H] and
 for one of these latest simulations is shown in
Fig. 6; the agreement between the two distributions is improved.
The analysis of the [Li] abundances in these latest samples
does not reveal any appreciable change with
respect to the case of a standard halo metallicity distribution. This
strengthens our conclusions, in the sense that they are not critically
dependent on the actual [Fe/H] distribution adopted in the simulations.
for one of these latest simulations is shown in
Fig. 6; the agreement between the two distributions is improved.
The analysis of the [Li] abundances in these latest samples
does not reveal any appreciable change with
respect to the case of a standard halo metallicity distribution. This
strengthens our conclusions, in the sense that they are not critically
dependent on the actual [Fe/H] distribution adopted in the simulations.
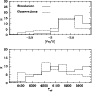 |
Figure 5:
Comparison of the number of plateau stars as a function
of their [Fe/H] (upper panel)
and
 (lower panel), between one of our MC samples and
the observational data by Thorburn (1994) (see text for details).
(lower panel), between one of our MC samples and
the observational data by Thorburn (1994) (see text for details). |
| Open with DEXTER |
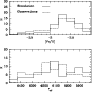 |
Figure 6:
As in the previous figure, but for a synthetic sample
drawn from a metallicity distribution biased towards the most metal
poor objects. |
| Open with DEXTER |
Before concluding this section, we would like to discuss briefly the
spread of the plateau (
![$\sigma_{\rm [Li]}^{\rm p}$](/articles/aa/full/2001/36/aah2788/img61.gif) )
obtained in our simulations.
If we consider all stars in the plateau region
bar the outliers, we obtain a dispersion
)
obtained in our simulations.
If we consider all stars in the plateau region
bar the outliers, we obtain a dispersion
![$\sigma_{\rm [Li]}^{\rm p}=0.09$](/articles/aa/full/2001/36/aah2788/img62.gif) .
This number compares very well with the values of
.
This number compares very well with the values of
![$\sigma_{\rm [Li]}^{\rm p}$](/articles/aa/full/2001/36/aah2788/img61.gif) derived by, e.g., Spite et al. (1996) and Bonifacio & Molaro (1997), for observational
errors in [Li] similar to the ones used in our simulations.
On the other hand,
derived by, e.g., Spite et al. (1996) and Bonifacio & Molaro (1997), for observational
errors in [Li] similar to the ones used in our simulations.
On the other hand,
![$\sigma_{\rm [Li]}^{\rm p}=0.09$](/articles/aa/full/2001/36/aah2788/img62.gif) is definitely larger than
the value given by Ryan et al. (1999). They have reobserved a sample of known
plateau stars (thus avoiding contamination from Li-depleted objects),
claiming average 1
is definitely larger than
the value given by Ryan et al. (1999). They have reobserved a sample of known
plateau stars (thus avoiding contamination from Li-depleted objects),
claiming average 1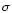 errors by
errors by 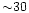 K in the stellar
temperatures, and by 0.033 dex in the derived [Li] values.
They selected 22 stars around the TO of the field
population, with
K in the stellar
temperatures, and by 0.033 dex in the derived [Li] values.
They selected 22 stars around the TO of the field
population, with
 between
between
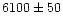 K and
K and
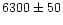 K, [Fe/H] between
-2.5 and -3.5, and found that the 1
K, [Fe/H] between
-2.5 and -3.5, and found that the 1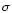 dispersion of [Li] around an
average value of 2.11 is equal to 0.053 dex (they went on discarding 3 stars
more discrepant from the average to obtain an even smaller dispersion).
dispersion of [Li] around an
average value of 2.11 is equal to 0.053 dex (they went on discarding 3 stars
more discrepant from the average to obtain an even smaller dispersion).
We performed a series of MC simulations by drawing samples of 25 stars
among the samples of plateau stars obtained from the previous simulations.
We selected the stars in the same [Fe/H] range as Ryan et al. (1999); under
the hypothesis that their hottest stars were stars at the TO, and for avoiding
problems related to zero-point uncertainties in the temperature scale,
we restricted our sample to stars
with
 ranging between the hottest value reached in our
simulations and a value 200 K lower. The extremes of this
ranging between the hottest value reached in our
simulations and a value 200 K lower. The extremes of this
 range
are similar to the values adopted by Ryan et al. (1999).
By averaging over 30 of these realizations we obtained an average
range
are similar to the values adopted by Ryan et al. (1999).
By averaging over 30 of these realizations we obtained an average
![$\rm [Li]=2.17$](/articles/aa/full/2001/36/aah2788/img66.gif) ,
with a 1
,
with a 1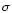 dispersion of 0.075 dex. This average [Li] value is
lower than the value derived previously; this is easily explained by
the derivative
dispersion of 0.075 dex. This average [Li] value is
lower than the value derived previously; this is easily explained by
the derivative
![$\Delta [\rm Li]/\Delta [\rm Fe/H]=0.06$](/articles/aa/full/2001/36/aah2788/img67.gif) obtained before, and the
fact that in these latter simulations we are considering only
obtained before, and the
fact that in these latter simulations we are considering only
![$\rm [Fe/H]\le -2.5$](/articles/aa/full/2001/36/aah2788/img68.gif) .
What is probably relevant is that the spread we find is larger
than the value obtained by Ryan et al. (1999), but we would like to recall
the results by Asplund et al. (1999) which clearly raise the possibility that
current determinations of the plateau dispersion
(and this would hold also for the larger samples discussed earlier)
are underestimated appreciably.
.
What is probably relevant is that the spread we find is larger
than the value obtained by Ryan et al. (1999), but we would like to recall
the results by Asplund et al. (1999) which clearly raise the possibility that
current determinations of the plateau dispersion
(and this would hold also for the larger samples discussed earlier)
are underestimated appreciably.
If one accepts, as a working hypothesis, an age between 13.5 and 14 Gyr
for the most metal-poor field stars, it is
necessary to see if this value satisfies constraints coming from Li
abundances in the SGB phase.
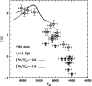 |
Figure 7:
Comparison in the [Li]-
 plane, between
the field subgiant data by Pilachowski et al. (1993) for
plane, between
the field subgiant data by Pilachowski et al. (1993) for
![$\rm [Fe/H]\leq -2.0$](/articles/aa/full/2001/36/aah2788/img7.gif) ,
and our isochrones with t=14 Gyr for two different initial
metallicities. Squares correspond to upper limits. ,
and our isochrones with t=14 Gyr for two different initial
metallicities. Squares correspond to upper limits. |
| Open with DEXTER |
We compare our models with observational data
by Pilachowski et al. (1993) for metallicities
lower than
![${\rm [Fe/H]}=-2 $](/articles/aa/full/2001/36/aah2788/img3.gif) .
In Fig. 7 we show the comparison of the data with the SGB part of our
isochrones, for an initial
.
In Fig. 7 we show the comparison of the data with the SGB part of our
isochrones, for an initial
![${\rm [Fe/H]_o}$](/articles/aa/full/2001/36/aah2788/img70.gif) equal to -3.2 (solid line) and
-1.8 (dashed line), and t=14 Gyr.
Because of the extremely low number of data points on the SGB and
the size of their error bars, we simply compared the position of the
observational data with SGB isochrones bracketing the metallicity
range spanned by the observations.
Keeping in mind possible systematic errors in the
equal to -3.2 (solid line) and
-1.8 (dashed line), and t=14 Gyr.
Because of the extremely low number of data points on the SGB and
the size of their error bars, we simply compared the position of the
observational data with SGB isochrones bracketing the metallicity
range spanned by the observations.
Keeping in mind possible systematic errors in the
 scale (which translates also into systematic errors in [Li]), with
respect to the data for the MS, it is
interesting to notice that the models with diffusion together with our assumed
initial
scale (which translates also into systematic errors in [Li]), with
respect to the data for the MS, it is
interesting to notice that the models with diffusion together with our assumed
initial
![${\rm [Li]_o}=2.50$](/articles/aa/full/2001/36/aah2788/img71.gif) ,
are not in contradiction with
observations. However, the size of the observed sample and
of the error bars does not permit to definitely assess the presence
(or absence) of the peak in
the [Li] abundance predicted by models with diffusion.
,
are not in contradiction with
observations. However, the size of the observed sample and
of the error bars does not permit to definitely assess the presence
(or absence) of the peak in
the [Li] abundance predicted by models with diffusion.
The steep decrease of [Li] for decreasing
 (equivalently: for increasing luminosity) along
the RGB is neither reproduced by models with diffusion, nor by
standard models (see the discussion in Pilachowski et al. 1993). At
temperatures lower than the endpoint of the isochrones shown in
Fig. 7, [Li] would stay constant, since the convective
envelope has reached its maximum extension and starts now to recede
slowly due to the outward movement of the H-burning shell.
The further depletion can be explained only by invoking extra deep
mixing (see, e.g., Kraft 1994; Denissenkov & Weiss 1996; Weiss et al. 2000).
(equivalently: for increasing luminosity) along
the RGB is neither reproduced by models with diffusion, nor by
standard models (see the discussion in Pilachowski et al. 1993). At
temperatures lower than the endpoint of the isochrones shown in
Fig. 7, [Li] would stay constant, since the convective
envelope has reached its maximum extension and starts now to recede
slowly due to the outward movement of the H-burning shell.
The further depletion can be explained only by invoking extra deep
mixing (see, e.g., Kraft 1994; Denissenkov & Weiss 1996; Weiss et al. 2000).
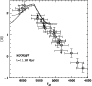 |
Figure 8:
Run of [Li] as a function of
 for SGB and
base of the RGB stars in the globular clusters NGC 6397.
Symbols are as in Fig. 7.
for SGB and
base of the RGB stars in the globular clusters NGC 6397.
Symbols are as in Fig. 7. |
| Open with DEXTER |
Figure 8 shows a comparison with Li abundances in
the globular cluster NGC6397 SGB stars.
In a globular cluster, all stars have the same initial
chemical composition and the same age; we adopted
an initial
![${\rm [Fe/H]_o}$](/articles/aa/full/2001/36/aah2788/img70.gif) equal to -1.8, following the results by Carretta & Gratton (1997)
for RGB stars belonging to this cluster. This choice is justified by the fact that
at the photosphere of RGB stars the metallicity is restored to the initial
value due to the deepening of the convective envelope, which engulfs
almost all the metals diffused towards the core during the MS phase
(Fig. 2).
Ages of 11 and 12 Gyr have been employed, according to the results by Salaris & Weiss (1998).
It is worth noticing that in this case the constraint on the stellar
ages comes from a method completely unrelated to the Li abundance determinations.
This age is lower than the age of the halo
field stars previously derived from the Li-plateau, but in any case
an increase of NGC 6397 age by 1-2 Gyr
would not alter substantially the result of this comparison.
equal to -1.8, following the results by Carretta & Gratton (1997)
for RGB stars belonging to this cluster. This choice is justified by the fact that
at the photosphere of RGB stars the metallicity is restored to the initial
value due to the deepening of the convective envelope, which engulfs
almost all the metals diffused towards the core during the MS phase
(Fig. 2).
Ages of 11 and 12 Gyr have been employed, according to the results by Salaris & Weiss (1998).
It is worth noticing that in this case the constraint on the stellar
ages comes from a method completely unrelated to the Li abundance determinations.
This age is lower than the age of the halo
field stars previously derived from the Li-plateau, but in any case
an increase of NGC 6397 age by 1-2 Gyr
would not alter substantially the result of this comparison.
The observational data are from Pasquini & Molaro (1996)
for SGB stars and Castilho et al. (2000) for RGB stars.
The
 values by Pasquini & Molaro (1996) have been reduced by 60 K to
take into account the fact that their assumed
reddening was 0.01 mag larger than the one used by Castilho et al. (2000);
the corresponding [Li] values consequently have been reduced
according to the derivative
values by Pasquini & Molaro (1996) have been reduced by 60 K to
take into account the fact that their assumed
reddening was 0.01 mag larger than the one used by Castilho et al. (2000);
the corresponding [Li] values consequently have been reduced
according to the derivative 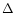 [Li]/
[Li]/
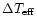 provided
in the mentioned papers.
provided
in the mentioned papers.
Due to the small sample of SGB stars observed,
their comparison with models including
diffusion does not permit - like in the case of field SGB stars -
to draw definitive conclusions about the
efficiency of this process in globular clusters stars.
An analogous conclusion is reached comparing our models
with the small sample of 6 SGB stars in the cluster M 92
observed by Boesgaard et al. (1998).
Notice, again, the problem along the RGB - very similar
to the case of field stars - where models
(standard and diffusive ones) cannot reproduce the trend of [Li] with
repect to
 .
.
Up to now we concentrated on the low-metallicity end of the
Spite-plateau, which, however extends also to higher [Fe/H].
We now consider stars with
![$-2.0 <{\rm [Fe/H]}< -1.5$](/articles/aa/full/2001/36/aah2788/img75.gif) ,
in order to see if a plateau can be found also when including
this metallicity range. We computed a series of models and Li-isochrones
with initial iron content
,
in order to see if a plateau can be found also when including
this metallicity range. We computed a series of models and Li-isochrones
with initial iron content
![${\rm [Fe/H]_o}=-1.3$](/articles/aa/full/2001/36/aah2788/img76.gif) (Z=0.002) and then
performed MC simulations selecting this time a sample
of
(Z=0.002) and then
performed MC simulations selecting this time a sample
of 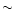 35 plateau stars with
35 plateau stars with
![$-2.0 <{\rm [Fe/H]}< -1.5$](/articles/aa/full/2001/36/aah2788/img75.gif) (which is
approximately the size of the observed sample in this metallicity range).
In Fig. 9 we plot (filled circles) the result of one
simulation (only plateau stars),
together with the result for the stars with
(which is
approximately the size of the observed sample in this metallicity range).
In Fig. 9 we plot (filled circles) the result of one
simulation (only plateau stars),
together with the result for the stars with
![$\rm [Fe/H]\le -2.0$](/articles/aa/full/2001/36/aah2788/img8.gif) (open circles) from Fig. 4.
The solid and dashed lines have the same meaning as in Fig. 4.
For the more metal-rich stars we have assumed an age randomly distributed
between 12.5 and 13 Gyr, to simulate a decrease of the average age of
Pop II field stars for increasing metallicity, above
(open circles) from Fig. 4.
The solid and dashed lines have the same meaning as in Fig. 4.
For the more metal-rich stars we have assumed an age randomly distributed
between 12.5 and 13 Gyr, to simulate a decrease of the average age of
Pop II field stars for increasing metallicity, above
![$\rm [Fe/H]=-2.0$](/articles/aa/full/2001/36/aah2788/img77.gif) .
The average value of [Li] is still 2.23, as in the case of the sample
including only stars with [Fe/H]
.
The average value of [Li] is still 2.23, as in the case of the sample
including only stars with [Fe/H] 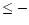 2.0.
The selected age does not play a decisive role. Variations of the
order of
2.0.
The selected age does not play a decisive role. Variations of the
order of 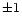 Gyr do not affect appreciably the overall picture.
Gyr do not affect appreciably the overall picture.
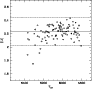 |
Figure 9:
Run of [Li] as a function of
 for stars in one of our MC simulations (see
text for details); open circles are stars
with
for stars in one of our MC simulations (see
text for details); open circles are stars
with
![$\rm [Fe/H]\le -2.0$](/articles/aa/full/2001/36/aah2788/img8.gif) ,
while filled circles are stars
with ,
while filled circles are stars
with
![$\rm -2.0 <[Fe/H]< -1.5$](/articles/aa/full/2001/36/aah2788/img9.gif) . . |
| Open with DEXTER |
We have also compared the Li abundances from our models with
the observations by Pilachowski et al. (1993) for more metal-rich SGB and RGB
stars of
![$\rm -2.0 <[Fe/H]< -1.5$](/articles/aa/full/2001/36/aah2788/img9.gif) .
There appears no inconsistency between theory and
observations besides the fact that also in this metallicity range
there is the well-known
problem of an additional depletion observed in RGB stars.
The Li-peak predicted around 5600 K might be visible, but given the
scarce data and rather large errors cannot be claimed to exist, just
as in the case of the very metal-poor field stars.
.
There appears no inconsistency between theory and
observations besides the fact that also in this metallicity range
there is the well-known
problem of an additional depletion observed in RGB stars.
The Li-peak predicted around 5600 K might be visible, but given the
scarce data and rather large errors cannot be claimed to exist, just
as in the case of the very metal-poor field stars.
In the previous section we have compared our stellar models including
uninhibited atomic diffusion with observations of [Li] in metal-poor
(
![$\rm [Fe/H]\le -2.0$](/articles/aa/full/2001/36/aah2788/img8.gif) )
halo field and globular clusters stars.
We have shown that there is no apparent contradiction with
observations, at least with the present
observational data, as long as the age of field subdwarfs is of the
order of 13.5 Gyr or more when
)
halo field and globular clusters stars.
We have shown that there is no apparent contradiction with
observations, at least with the present
observational data, as long as the age of field subdwarfs is of the
order of 13.5 Gyr or more when
![$\rm [Fe/H]\le -2.0$](/articles/aa/full/2001/36/aah2788/img8.gif) .
This is, of course, not a proof that
diffusion is fully efficient in halo stars (since in general also standard
isochrones can explain the observations; e.g., Vauclair & Charbonnel 1995);
however, our analysis shows that
it is not justified to discard models with fully efficient diffusion
on the base of current measurements of [Li] in metal-poor stars.
.
This is, of course, not a proof that
diffusion is fully efficient in halo stars (since in general also standard
isochrones can explain the observations; e.g., Vauclair & Charbonnel 1995);
however, our analysis shows that
it is not justified to discard models with fully efficient diffusion
on the base of current measurements of [Li] in metal-poor stars.
In particular, the Li-plateau region is satisfactorily reproduced by
our MC simulations, for the ages discussed before. This is at
odds with conclusions from previous analyses which were based mainly
on the comparison of an isochrone of a given age and a single value of [Fe/H]
with the moderately small observational samples of stars
with different metallicities and possibly different ages.
In our MC simulations we could take into account the actual number of
stars with [Li] measurements, their observed metallicity
distribution and the typical observational errors.
The fact that we do not find in the simulations
a clear depletion of [Li] at the hotter end of the plateau is only
partly due to the ages we selected for the stars with
![$\rm [Fe/H]< -2.0$](/articles/aa/full/2001/36/aah2788/img58.gif) .
In fact, lower ages
(see Fig. 1) produce a more visible depletion at the TO,
but still, even for ages of about 14 Gyr and taking into account the
observational errors, when
.
In fact, lower ages
(see Fig. 1) produce a more visible depletion at the TO,
but still, even for ages of about 14 Gyr and taking into account the
observational errors, when
![$\rm [Fe/H]\le -2.6$](/articles/aa/full/2001/36/aah2788/img11.gif) ,
a drop at the highest end of the plateau has to be visible,
provided that a sufficiently high number of stars is observed.
From our simulations we derive that [Li] measurements of
a sample of about 200 plateau stars (about 40-50 of them at the hottest
end of the plateau)
with
,
a drop at the highest end of the plateau has to be visible,
provided that a sufficiently high number of stars is observed.
From our simulations we derive that [Li] measurements of
a sample of about 200 plateau stars (about 40-50 of them at the hottest
end of the plateau)
with
![$\rm [Fe/H]\le -2.6$](/articles/aa/full/2001/36/aah2788/img11.gif) are needed
in order to clearly detect this drop, keeping unchanged
the observational errors (see Fig. 10).
are needed
in order to clearly detect this drop, keeping unchanged
the observational errors (see Fig. 10).
For the more metal-rich objects of Sect. 3.4 with [Fe/H] above
-2.0 an increase of the observed sample size would not change
the plateau morphology, since at these metallicities
there is no abrupt drop of [Li] at the TO region, but an almost
constant value of [Li] all along the plateau region.
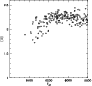 |
Figure 10:
Results of a MC simulation with 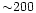 plateau stars
and
plateau stars
and
![$\rm [Fe/H]\le -2.6$](/articles/aa/full/2001/36/aah2788/img11.gif) (see text for details). The drop in [Li] at
the TO due to diffusion is now clearly apparent.
(see text for details). The drop in [Li] at
the TO due to diffusion is now clearly apparent. |
| Open with DEXTER |
It has been mentioned several times in the literature that
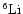 ,
which is destroyed by proton-captures at
even lower temperatures than
,
which is destroyed by proton-captures at
even lower temperatures than
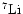 (
(
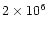 K), would be an additional and
strong indicator of
K), would be an additional and
strong indicator of
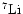 destruction (see, for example,
Vangioni-Flam et al. 1999).
What observations provide is the sum
destruction (see, for example,
Vangioni-Flam et al. 1999).
What observations provide is the sum
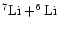 .
Disentangling the abundance of one isotope from the other one is a
very difficult task;
it is based on fitting the observed profile of the Li I blend
with theoretical profiles calculated from model stellar atmospheres
characterized by different
.
Disentangling the abundance of one isotope from the other one is a
very difficult task;
it is based on fitting the observed profile of the Li I blend
with theoretical profiles calculated from model stellar atmospheres
characterized by different
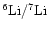 ratios
(see, e.g., Hobbs et al. 1999).
Until now all (very few) measured Li-isotope ratios (e.g. Nissen et al. 1999; Hobbs et al. 1999; Nissen et al. 2000) are either upper limits
only or are so high (
ratios
(see, e.g., Hobbs et al. 1999).
Until now all (very few) measured Li-isotope ratios (e.g. Nissen et al. 1999; Hobbs et al. 1999; Nissen et al. 2000) are either upper limits
only or are so high (
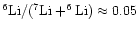 )
that
they exceed limits from Big Bang Nucleosynthesis by orders of
magnitude, such that galactic chemical evolution (Vangioni-Flam et al. 1999) has
to be taken into account to explain them. From this point on, of course,
all conclusions about stellar depletion of lithium isotopes are
subject to the acceptance of these chemical evolution models.
The quoted papers arrive at conclusions both excluding
(Vangioni-Flam et al. 1999) and requiring stellar depletion (Hobbs et al. 1999).
We therefore conclude that presently
)
that
they exceed limits from Big Bang Nucleosynthesis by orders of
magnitude, such that galactic chemical evolution (Vangioni-Flam et al. 1999) has
to be taken into account to explain them. From this point on, of course,
all conclusions about stellar depletion of lithium isotopes are
subject to the acceptance of these chemical evolution models.
The quoted papers arrive at conclusions both excluding
(Vangioni-Flam et al. 1999) and requiring stellar depletion (Hobbs et al. 1999).
We therefore conclude that presently
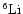 does not provide
additional conclusive information about diffusive processes in
low-mass stars. We note that along the MS diffusion alone
would only mildly change the isotope ratio, anyway, with an increase
of the initial
does not provide
additional conclusive information about diffusive processes in
low-mass stars. We note that along the MS diffusion alone
would only mildly change the isotope ratio, anyway, with an increase
of the initial
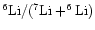 value
by at most 40%.
value
by at most 40%.
In principle, useful constraints on diffusion in low-mass stars could
come from spectroscopy along globular cluster CMDs, as the one shown
in Fig. 8 for NGC 6397. Recently, Gratton et al. (2001) have
presented VLT/UVES results about element abundances in stars at
the TO and at the RGB base in the same cluster and in NGC 6752.
In NGC 6397 rather constant abundance values are found,
and in particular [Fe/H] appears to be exactly the same in both groups
of stars, a fact which would strongly disfavour diffusion. Also Li,
which is not discussed in this paper,
shows very small star-to-star variations (Gratton, private
communication).
Although comparable work (Carretta & Gratton 1997; Castilho et al. 2000)
returned somewhat different results concerning the Fe-abundance,
Gratton et al. (2001) certainly have
presented a strong case against the efficiency of diffusion in
NGC 6397.
On the contrary in NGC 6752, even if
[Fe/H] appears to be the same
in TO and SGB stars,
large star-to-star scatter in element abundances is present
within stars of the same evolutionary stage,
indicating additional stellar processes at work. This applies also to
lithium (Gratton, private communication). It therefore appears that
cluster-to-cluster differences may be present and much more work along
the line of Gratton et al. (2001) - in particular for the lowest
metallicity clusters, where the effect of diffusion, if
present, should be larger -
is needed to clarify this. It might also
turn out that there are systematic differences between the efficiency
of diffusion in clusters
and field stars, just as in the case of RGB abundance anomalies
(Gratton et al. 2000).
Assuming that diffusion indeed has taken place in field
Spite-plateau stars,
our results have significant bearings for the question
concerning the cosmological baryon density.
We reproduce the observed
Spite-plateau [Li]-abundance when assuming a primordial value of
![${\rm [Li]} = 2.5$](/articles/aa/full/2001/36/aah2788/img87.gif) .
According to standard Big Bang Nucleosynthesis
(see, for example, the recent calculations by Vangioni-Flam et al. 2000), this
corresponds to a baryon-to-photon ratio
.
According to standard Big Bang Nucleosynthesis
(see, for example, the recent calculations by Vangioni-Flam et al. 2000), this
corresponds to a baryon-to-photon ratio 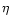 of
of
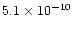 (see Fig. 4 of the quoted paper), which is in almost perfect agreement
with the low deuterium value (
(see Fig. 4 of the quoted paper), which is in almost perfect agreement
with the low deuterium value (
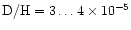 )
by Tytler et al. (2000) and the high 4He abundance of 0.244 by
Izotov & Thuan (1998). Since
)
by Tytler et al. (2000) and the high 4He abundance of 0.244 by
Izotov & Thuan (1998). Since 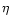 is related to the baryonic density via
is related to the baryonic density via
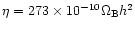 (with h being the
Hubble constant in units of
(with h being the
Hubble constant in units of
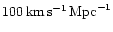 ), this results in
), this results in
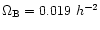 .
Taking h=0.71 (Mould et al. 2000) yields
.
Taking h=0.71 (Mould et al. 2000) yields
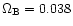 .
This result is within
.
This result is within 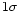 of the value
inferred from the BOOMERANG experiment (Netterfield et al. 2001), which is
of the value
inferred from the BOOMERANG experiment (Netterfield et al. 2001), which is
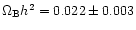 .
.
Our derived cosmological baryon density is obtained under the assumption
of no significant galactic production of
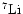 .
.
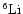 measurements can in principle
be used also to put useful constraints on the amount of
measurements can in principle
be used also to put useful constraints on the amount of
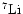 produced by galactic chemical evolution, but the available
measurements (see also
the previous discussion) do not provide yet a consistent picture
of the abundance ratio of these two isotopes.
As an example, the value
produced by galactic chemical evolution, but the available
measurements (see also
the previous discussion) do not provide yet a consistent picture
of the abundance ratio of these two isotopes.
As an example, the value
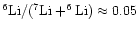 for the metal poor
TO star HD 84937 (
for the metal poor
TO star HD 84937 (
![$\rm [Fe/H]\approx -2.3$](/articles/aa/full/2001/36/aah2788/img97.gif) )
points to a
non-negligible contribution
of
)
points to a
non-negligible contribution
of
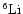 - and therefore also
- and therefore also
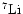 - from
cosmic ray production. However, measurements of the same quantity for
HD 218502, a star with similar metallicity and
evolutionary status, provide an upper limit of only 0.02
and a best fit value equal to zero (see Hobbs et al. 1999), consistent with
no contribution from galactic chemical evolution.
If in the future
- from
cosmic ray production. However, measurements of the same quantity for
HD 218502, a star with similar metallicity and
evolutionary status, provide an upper limit of only 0.02
and a best fit value equal to zero (see Hobbs et al. 1999), consistent with
no contribution from galactic chemical evolution.
If in the future
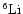 measurements will consistently indicate
a significant influence of galactic production of
measurements will consistently indicate
a significant influence of galactic production of
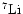 (of order 0.1 dex or more), one will have to reconsider our
conclusions about the cosmological baryon density.
(of order 0.1 dex or more), one will have to reconsider our
conclusions about the cosmological baryon density.
One could in principle worry about the fact that our adopted initial [Li]
abundance implies a primordial
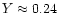 ,
while in our
models we used Y=0.23. However, as we have verified with appropriate
computations, the effect of using Y=0.24 as the initial He abundance
for our models is just an age shift. More in detail,
the [Li] abundance as a function of
,
while in our
models we used Y=0.23. However, as we have verified with appropriate
computations, the effect of using Y=0.24 as the initial He abundance
for our models is just an age shift. More in detail,
the [Li] abundance as a function of
 along an isochrone of fixed initial
along an isochrone of fixed initial
![${\rm [Fe/H]_o}$](/articles/aa/full/2001/36/aah2788/img70.gif) and age
computed with an initial Y=0.23 would be equal to the abundances of an isochrone
with the same initial
and age
computed with an initial Y=0.23 would be equal to the abundances of an isochrone
with the same initial
![${\rm [Fe/H]_o}$](/articles/aa/full/2001/36/aah2788/img70.gif) but an age lower by 1 Gyr, if an
initial Y=0.24 is used. The same holds for the [Fe/H] values along an isochrone.
Our conclusions about the Li-plateau are therefore not affected at all,
apart from the fact that in
this case the minimum age required to reproduce the observed
plateau would be 12.5 Gyr.
but an age lower by 1 Gyr, if an
initial Y=0.24 is used. The same holds for the [Fe/H] values along an isochrone.
Our conclusions about the Li-plateau are therefore not affected at all,
apart from the fact that in
this case the minimum age required to reproduce the observed
plateau would be 12.5 Gyr.
We finally mention that our treatment of
diffusion does not take into account the effect of radiative
levitation. The diffusive velocities by
Thoul et al. (1994), which we are using, might be overestimated
by 25% on average, at least in the case of the Sun,
according to Turcotte et al. (1998). It is plausible,
but not certain, that a similar overestimate might happen for
metal-poor stars. We neither included mass loss in the calculations,
which is also known to reduce the effect of diffusion.
For mass loss rates compatible with current observations
the surface abundances depletion is not affected appreciably, but
strong stellar wind on the MS may inhibit diffusion completely
(Vauclair & Charbonnel 1995).
Due to the neglect of both radiative levitation
and mass loss, our models probably overestimate the depletion to some
degree, even if we cannot quantify this up to now.
We can conclude that the Spite plateau, given present
day observational sample sizes, can be reproduced by models including
atomic diffusion and is therefore (alone) no strong argument against
the presence of sedimentation in low-mass metal-poor field
stars.
Acknowledgements
A.W. is grateful for the hospitality at the Institute for Advanced Study
and Princeton Observatory and for a Fulbright fellowship which allowed
visiting both places. Helpful discussions with J. Truran, L. M. Hobbs,
R. Cayrel, C. Deliyannis, K. Jedamzik, and F. D'Antona are acknowledged.
We thank an anonymous referee for his/her comments, which helped to
improve the quality of the paper.
-
Angulo, C., Arnould, M., Rayet, M., et al. 1999,
Nucl. Phys. A, 656, 3
In the text
NASA ADS
-
Bahcall, J. N., Pinsonneault, M. H., Basu, S., & Christensen-Dalsgaard, J.
1997, Phys. Rev. Lett., 78, 171
In the text
NASA ADS
-
Bonifacio, P., & Molaro, P. 1997, MNRAS, 285, 847
In the text
NASA ADS
-
Brun, A. S., Turck-Chiéze, S., & Zahn, J. P. 1999, ApJ, 525, 1032
In the text
NASA ADS
-
Carretta, E., & Gratton, R. G. 1997, A&AS, 121, 95
In the text
NASA ADS
-
Cassisi, S., Castellani, V., Degl'Innocenti, S., & Weiss, A. 1998, A&AS, 129,
267
In the text
NASA ADS
-
Castellani, V., Ciacio, F., Degl'Innocenti, S., & Fiorentini, G. 1997, A&A,
322, 801
In the text
NASA ADS
-
Castellani, V., & Degl'Innocenti, S. 1999, A&A, 344, 97
In the text
NASA ADS
-
Castilho, B. V., Pasquini, L., Allen, D. M., Barbuy, B., & Molaro, P. 2000,
A&A, 361, 92
In the text
NASA ADS
-
Chaboyer, B., Deliyannis, C. P., Demarque, P., Pinsonneault, M. H., &
Sarajedini, A. 1992, ApJ, 388, 372
In the text
NASA ADS
-
Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995, ApJ, 441, 865
In the text
NASA ADS
-
D'Antona, F., & Mazzitelli, I. 1984, A&A, 138, 431
In the text
NASA ADS
-
Deliyannis, C. P., & Demarque, P. 1991, ApJ, 379, 216
In the text
NASA ADS
-
Deliyannis, C. P., Demarque, P., & Kawaler, S. D. 1990, ApJS, 73, 21
In the text
NASA ADS
-
Denissenkov, P. A. & Weiss, A. 1996, A&A, 308, 773
In the text
NASA ADS
-
Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169
In the text
NASA ADS
-
Gustafsson, B., Bell, R. A., Eriksson, K., & Nordlund, A. 1975, A&A,
42, 407
In the text
NASA ADS
-
Hobbs, L. M., Thorburn, J. A., & Rebull, L. M. 1999, ApJ, 523, 797
In the text
NASA ADS
-
Kraft, R. P. 1994, PASP, 106, 553
In the text
NASA ADS
-
Kurucz, R. L. 1993, ATLAS9 Stellar Atmosphere Programs, CD-ROM 13
In the text
-
Morel, P., & Baglin, A. 1999, A&A, 345, 156
In the text
NASA ADS
-
Mould, J. R., Huchra, J. P., Freedman, W. L., et al. 2000, ApJ, 529, 786
In the text
NASA ADS
-
Netterfield, C. B., Ade, R. A. R., Bock, J. J., et al. 2001, preprint [astro-ph/0104460]
In the text
-
Nissen, P., Lambert, D., Primas, F., & Smith, V. 1999, A&A, 348, 211
In the text
NASA ADS
-
Nissen, P. E., Asplund, M., Hill, V., & D'Odorico, S. 2000, A&A, 357, L49
In the text
NASA ADS
-
Pilachowski, C. A., Sneden, C., & Booth, J. 1993, ApJ, 407, 699
In the text
NASA ADS
-
Richard, O., Vauclair, S., Charbonnel, C., & Dziembowski, W. A. 1996, A&A,
312, 1000
In the text
NASA ADS
-
Ryan, S. G., Beers, T. C., Deliyannis, C. P., & Thorburn, J. A. 1996, ApJ,
458, 543
In the text
NASA ADS
-
Ryan, S. G., Kajino, T., Beers, T. C., et al. 2001, ApJ, 549, 55
In the text
NASA ADS
-
Ryan, S. G., Norris, J. E., & Beers, T. C. 1999, ApJ, 523, 654
In the text
NASA ADS
-
Salaris, M., Degl'Innocenti, S., & Weiss, A. 1997, ApJ, 479, 665
In the text
NASA ADS
-
Salaris, M., Groenewegen, M. A. T., & Weiss, A. 2000, A&A, 355, 299
In the text
NASA ADS
-
Salaris, M., & Weiss, A. 1998, A&A, 335, 943
In the text
NASA ADS
-
Spite, F., & Spite, M. 1982, A&A, 115, 357
In the text
NASA ADS
-
Spite, M., Francois, P., Nissen, P. E., & Spite, F. 1996, A&A, 307, 172
In the text
NASA ADS
-
Thorburn, J. A. 1994, ApJ, 421, 318
In the text
NASA ADS
-
Vangioni-Flam, E., Cassé, M., Cayrel, R., et al. 1999, New Astron., 4, 245
In the text
NASA ADS
-
Vangioni-Flam, E., Coc, A., & Cassé, M. 2000, A&A, 360, 15
In the text
NASA ADS
-
Vauclair, S. 1999, A&A, 351, 973
In the text
NASA ADS
-
Vauclair, S., & Charbonnel, C. 1995, A&A, 295, 715
In the text
NASA ADS
-
Vauclair, S., & Charbonnel, C. 1998, ApJ, 502, 372
In the text
NASA ADS
-
Vazdekis, A., Salaris, M., Arimoto, N., & Rose, J. A. 2001, ApJ, 549, 274
In the text
NASA ADS
-
Weiss, A., Denissenkov, P. A., & Charbonnel, C. 2000, A&A, 356, 181
In the text
NASA ADS
-
Weiss, A., & Schlattl, H. 2000, A&AS, 144, 487
In the text
NASA ADS
Copyright ESO 2001









