The procedure described in the previous section yields the components'
masses. For instance, in the IKLup system
(Fig. 5) the components have masses of
and
with respect to the Baraffe et al. (1998)
tracks. The resulting masses derived for the components from all three sets
of PMS tracks used are given in Table 2. For some systems
(indicated with question marks in Table 2) the primary
is located in a region of the HRD that is not covered by the respective
tracks. The Swenson et al. (1994) model does only cover a
mass range above
,
so for some secondaries only
upper mass limits can be derived from that model. The errors
given in Table 2 reflect the range of tracks that is
covered by the stars' locations in the HRD. These uncertainties are
20-30% for most stars and thus quite large. However, all error sources
discussed so far are random and not systematic. Therefore in a
statistical analysis of these masses that we will do in
Sects. 6.2 and 6.3, these uncertainties
will partially cancel and have less influence to the results.
There are however additional uncertainties
within the PMS models theirselves. One can see from
Table 2 that there are discrepancies in masses obtained
for the same stars from different PMS models that can be much larger
than the indicated errors which trace the uncertainty
of our measurements. The components' mass functions derived from
the three models (see Fig. 6) are different at a 99%
confidence level which indicates that these mass differences are systematic.
There is now some evidence that the Baraffe et al. (1998) tracks could be preferrable among the current PMS models: White et al. (1999) have placed the four components of GGTau into the HRD and compared their positions with different sets of PMS tracks. They found that the Baraffe et al. (1998) model is best consistent with the assumption that all components are coeval. Simon et al. (2000) and Steffen et al. (2000) presented first results of empirical mass determinations from orbital motion around T Tauri stars that are also comparable with the predictions of the Baraffe et al. (1998) model. It would however be premature to consider these results as a final solution of the problem of inconsistent PMS models, mainly because the mentioned observations do not cover the whole range of masses and ages expected for T Tauri stars. Therefore in this paper we will - as we have already done in Sect. 4.4 - rely on the three PMS models given by D'Antona & Mazzitelli (1998), Swenson et al. (1994) and Baraffe et al. (1998) and compare the respective results. It can be seen that the uncertainties inherent in the evolutionary model predictions often surpass the uncertainties resulting from the measurement errors.
| System |
![$M_1[M_{\odot}]$](/articles/aa/full/2001/36/aa9681/img64.gif){kind=small} |
![$M_2[M_{\odot}]$](/articles/aa/full/2001/36/aa9681/img65.gif){kind=small} |
|
|
|
|
| DM98 | Swenson | Baraffe | ||||
| HBC 351 | 0.85 
0.1 |
0.25
0.1 |
1.0
0.1 |
0.4
0.1 |
1.0
0.1 |
0.4
0.1 |
| HBC 352/353 | 1.0
0.05 |
0.9
0.05 |
? | ? | ? | ? |
| HBC 358Aa | 0.35
0.1 |
0.35
0.1 |
0.7
0.05 |
0.7
0.05 |
0.4
0.1 |
0.4
0.1 |
| HBC 358 B | 0.4
0.1 |
0.7
0.05 |
0.5
0.1 |
|||
| HBC 360/361 | 0.2
0.05 |
0.2
0.05 |
0.5
0.1 |
0.5
0.1 |
0.3
0.1 |
0.3
0.1 |
| FO Tau | 0.35
0.05 |
0.14
0.04 |
0.5
0.1 |
0.35
0.1 |
0.6
0.1 |
0.3
0.1 |
| DD Tau | 0.5
0.1 |
0.4
0.1 |
0.7
0.1 |
0.65
0.1 |
0.7
0.1 |
0.6
0.1 |
| CZ Tau | 0.4
0.1 |
0.04
0.04 |
0.7
0.1 |
<0.15 | 0.6
0.1 |
0.10
0.05 |
| FQ Tau | 0.4
0.05 |
0.4
0.05 |
0.7
0.05 |
0.7
0.05 |
0.5
0.1 |
0.5
0.1 |
| V 819 Tau | 0.45
0.05 |
0.04
0.04 |
0.7
0.05 |
<0.15 | 1.1
0.1 |
0.08
0.02 |
| LkCa 7 | 0.5
0.1 |
0.2
0.05 |
0.85
0.15 |
0.45
0.1 |
1.1
0.1 |
0.6
0.1 |
| FS Tau | 0.5
0.1 |
0.12
0.04 |
0.75
0.05 |
0.15
0.10 |
0.7
0.1 |
0.2
0.05 |
| FV Tau | 0.65
0.15 |
0.35
0.15 |
1.15
0.15 |
0.7
0.15 |
1.3
0.1 |
1.0
0.1 |
| UX TauAC | 1.2
0.2 |
0.16
0.05 |
1.4
0.2 |
0.25
0.1 |
1.3
0.1 |
0.4
0.1 |
| UX TauBb | 0.25
0.05 |
0.20
0.05 |
0.5
0.1 |
0.4
0.1 |
0.6
0.1 |
0.5
0.1 |
| FX Tau | 0.35
0.05 |
0.35
0.05 |
0.55
0.1 |
0.55
0.1 |
0.8
0.2 |
0.8
0.2 |
| DK Tau | 0.50
0.05 |
0.15
0.05 |
0.8
0.15 |
0.35
0.1 |
1.1
0.1 |
0.4
0.1 |
LkH
331 |
0.16
0.03 |
0.12
0.02 |
0.4
0.05 |
0.15
0.05 |
0.20
0.05 |
0.15
0.05 |
| HK Tau | 0.5
0.1 |
0.04
0.02 |
0.6
0.1 |
<0.15 | 0.7
0.1 |
0.08
0.02 |
| V 710 Tau | 0.4
0.1 |
0.35
0.1 |
0.55
0.1 |
0.45
0.1 |
0.65
0.15 |
0.5
0.15 |
| HK Tau G2 | 0.35
0.05 |
0.35
0.05 |
0.6
0.1 |
0.45
0.1 |
0.9
0.1 |
0.7
0.1 |
| GG Tau Aa | 0.4
0.05 |
0.2
0.05 |
0.65
0.05 |
0.4
0.05 |
0.9
0.1 |
0.5
0.1 |
| GG Tau Bb | 0.09
0.02 |
0.04
0.02 |
<0.15 | <0.15 | 0.2
0.05 |
0.04
0.02 |
| UZ Tau w | 0.20
0.05 |
0.18
0.05 |
0.45
0.1 |
0.35
0.1 |
0.35
0.15 |
0.30
0.15 |
| GH Tau | 0.35
0.1 |
0.35
0.1 |
0.55
0.1 |
0.55
0.1 |
0.6
0.15 |
0.5
0.15 |
| Elias 12 | 0.4
0.05 |
0.3
0.05 |
0.7
0.1 |
0.35
0.05 |
1.2
0.1 |
0.9
0.1 |
| IS Tau | 1.1
0.1 |
0.4
0.1 |
1.05
0.15 |
0.7
0.1 |
0.9
0.1 |
0.7
0.1 |
| GK Tau / GI Tau | 0.55
0.1 |
0.4
0.1 |
0.95
0.2 |
0.75
0.2 |
1.2
0.1 |
1.0
0.1 |
| HN Tau | 0.7
0.1 |
0.35
0.1 |
0.75
0.1 |
0.45
0.1 |
0.7
0.1 |
0.4
0.1 |
| CoKu Tau 3 | 0.4
0.1 |
0.16
0.03 |
0.75
0.05 |
0.35
0.1 |
0.6
0.1 |
0.3
0.1 |
| HBC 412 | 0.35
0.1 |
0.3
0.1 |
0.6
0.1 |
0.5
0.1 |
0.55
0.15 |
0.50
0.15 |
| Haro 6-28 | 0.20
0.05 |
0.04
0.04 |
0.55
0.1 |
<0.15 | 0.25
0.15 |
0.06
0.04 |
| VY Tau | 0.60
0.1 |
0.25
0.05 |
0.85
0.1 |
0.35
0.1 |
0.8
0.1 |
0.4
0.1 |
| IW Tau | 0.7
0.1 |
0.6
0.1 |
0.95
0.05 |
0.85
0.05 |
0.9
0.1 |
0.8
0.1 |
| LkH
332 G1 |
0.4
0.05 |
0.18
0.03 |
0.55
0.1 |
0.35
0.1 |
0.8
0.2 |
0.4
0.1 |
| LkH
332 G2 |
0.45
0.05 |
0.20
0.05 |
0.75
0.1 |
0.3
0.05 |
1.2
0.1 |
0.7
0.1 |
| LkH
332 |
0.7
0.1 |
0.6
0.1 |
0.95
0.05 |
0.8
0.05 |
1.0
0.1 |
0.8
0.1 |
| Haro 6-37 Aa | 0.7
0.1 |
0.09
0.05 |
1.05
0.1 |
0.2
0.1 |
1.1
0.1 |
0.3
0.1 |
| Haro 6-37 /c | 0.35
0.1 |
0.65
0.1 |
0.7
0.1 |
|||
| RW Aur | 1.1
0.1 |
0.4
0.1 |
1.4
0.1 |
0.7
0.1 |
1.3
0.1 |
0.9
0.1 |
| NTTS 155203-2338 | 1.7
0.1 |
0.7
0.1 |
1.85
0.2 |
0.9
0.1 |
? | ? |
| NTTS 155219-2314 | 0.16
0.04 |
0.09
0.04 |
0.375
0.075 |
<0.15 | 0.2
0.05 |
0.1
0.05 |
| NTTS 160735-1857 | 0.20
0.05 |
0.16
0.04 |
0.35
0.05 |
0.3
0.05 |
0.4
0.1 |
0.3
0.1 |
| NTTS 160946-1851 | 1.7
0.1 |
0.6
0.1 |
1.9
0.2 |
0.75
0.15 |
? | ? |
| WX Cha | 0.5
0.1 |
0.1
0.04 |
0.75
0.1 |
0.15
0.1 |
1.0
0.1 |
0.35
0.1 |
| VW Cha AB | 0.6
0.1 |
0.4
0.1 |
1.05
0.2 |
0.7
0.2 |
? | ? |
| HM Anon | 1.3
0.1 |
0.7
0.1 |
1.35
0.2 |
0.85
0.05 |
1.2
0.1 |
0.9
0.1 |
| LkH
332-17 |
1.75
0.1 |
0.3
0.05 |
1.9
0.2 |
0.45
0.1 |
? | ? |
| IK Lup | 0.35
0.1 |
0.14
0.04 |
0.5
0.15 |
0.2
0.1 |
0.9
0.2 |
0.3
0.1 |
| HT Lup | 1.3
0.4 |
0.2
0.15 |
1.9
0.5 |
0.23
0.1 |
? | ? |
| HN Lup | 0.25
0.05 |
0.25
0.05 |
0.4
0.1 |
0.4
0.1 |
0.7
0.1 |
0.6
0.1 |
| HBC 604 | 0.11
0.02 |
0.05
0.02 |
0.23
0.05 |
<0.15 | ? | ? |
| HO Lup | 0.35
0.05 |
0.14
0.02 |
0.5
0.1 |
0.2
0.1 |
0.7
0.1 |
0.3
0.1 |
| System | DM98 | Swenson | Baraffe | d[arcsec] |
| HBC351 | 0.29
0.15 |
0.40
0.14 |
0.40
0.14 |
0.61
0.03 |
| HBC352/353 | 0.90
0.10 |
8.6
0.8 |
||
| HBC358Aa | 1.0
0.57 |
1.0
0.14 |
1.0
0.5 |
0.15 |
| HBC360/361 | 1.0
0.5 |
1.0
0.4 |
1.0
0.67 |
7.2
0.8 |
| FOTau | 0.40
0.17 |
0.70
0.34 |
0.50
0.25 |
0.165
0.005 |
| DDTau | 0.80
0.36 |
0.93
0.28 |
0.86
0.27 |
0.57
0.03 |
| CZTau | 0.10
0.13 |
<0.21 | 0.17
0.11 |
0.33
0.01 |
| FQTau | 1.00
0.25 |
1.0
0.14 |
1.0
0.4 |
0.79
0.01 |
| V819Tau | 0.09
0.10 |
<0.21 | 0.07
0.02 |
10.5
0.3 |
| LkCa7 | 0.40
0.18 |
0.53
0.21 |
0.55
0.14 |
1.05
0.01 |
| FSTau | 0.24
0.13 |
0.20
0.15 |
0.29
0.11 |
0.265
0.005 |
| FVTau | 0.54
0.36 |
0.61
0.21 |
0.77
0.14 |
0.72
0.10 |
| UXTauAC | 0.13
0.06 |
0.18
0.10 |
0.31
0.10 |
2.7
0.1 |
| UXTauBb | 0.80
0.36 |
0.80
0.36 |
0.83
0.31 |
0.138 |
| FXTau | 1.00
0.29 |
1.00
0.36 |
1.00
0.50 |
0.91
0.01 |
| DKTau | 0.30
0.13 |
0.44
0.21 |
0.36
0.13 |
2.8
0.3 |
| LkH331 |
0.75
0.27 |
0.38
0.17 |
0.75
0.44 |
0.30
0.01 |
| HKTau | 0.08
0.06 |
<0.25 | 0.11
0.05 |
2.4
0.1 |
| V710Tau | 0.88
0.47 |
0.82
0.33 |
0.77
0.41 |
3.24
0.10 |
| HKTauG2 | 1.00
0.29 |
0.75
0.29 |
0.78
0.20 |
0.18
0.01 |
| GGTauAa | 0.50
0.19 |
0.62
0.12 |
0.56
0.17 |
0.26
0.01 |
| GGTauBb | 0.44
0.32 |
0.20
0.15 |
1.4
0.2 |
|
| UZTau w | 0.90
0.48 |
0.78
0.40 |
0.86
0.80 |
0.34
0.06 |
| GHTau | 1.00
0.57 |
1.00
0.36 |
0.83
0.46 |
0.35
0.01 |
| Elias12 | 0.75
0.22 |
0.50
0.14 |
0.75
0.15 |
0.41
0.01 |
| ISTau | 0.36
0.12 |
0.67
0.19 |
0.78
0.20 |
0.21
0.02 |
| GKTau / GITau | 0.73
0.31 |
0.79
0.37 |
0.83
0.15 |
12.2
0.2 |
| HNTau | 0.50
0.21 |
0.60
0.21 |
0.57
0.22 |
3.1
0.1 |
| CoKuTau3 | 0.40
0.18 |
0.47
0.16 |
0.50
0.25 |
2.04
0.07 |
| HBC412 | 0.86
0.53 |
0.83
0.31 |
0.91
0.52 |
0.70
0.01 |
| Haro6-28 | 0.20
0.25 |
<0.27 | 0.24
0.30 |
0.66
0.02 |
| VYTau | 0.42
0.15 |
0.41
0.17 |
0.50
0.19 |
0.66
0.02 |
| IWTau | 0.86
0.27 |
0.89
0.10 |
0.89
0.21 |
0.27
0.02 |
| LkH332G1 |
0.45
0.13 |
0.64
0.30 |
0.50
0.25 |
0.23
0.02 |
| LkH332G2 |
0.44
0.16 |
0.40
0.12 |
0.58
0.13 |
0.30
0.01 |
| LkH332 |
0.86
0.27 |
0.84
0.10 |
0.80
0.18 |
0.33
0.03 |
| Haro6-37Aa | 0.13
0.09 |
0.19
0.11 |
0.27
0.12 |
0.331
0.005 |
| RWAur | 0.36
0.12 |
0.50
0.11 |
0.69
0.13 |
1.50
0.01 |
| NTTS155203-2338 | 0.41
0.08 |
0.49
0.11 |
0.758
0.007 |
|
| NTTS155219-2314 | 0.56
0.39 |
<0.40 | 0.50
0.38 |
1.485
0.003 |
| NTTS160735-1857 | 0.80
0.40 |
0.86
0.27 |
0.75
0.44 |
0.299
0.003 |
| NTTS160946-1851 | 0.35
0.08 |
0.39
0.12 |
0.203
0.006 |
|
| WXCha | 0.20
0.12 |
0.20
0.16 |
0.35
0.14 |
0.79
0.04 |
| VWChaAB | 0.67
0.28 |
0.67
0.32 |
0.66
0.03 |
|
| HMAnon | 0.54
0.12 |
0.63
0.13 |
0.75
0.15 |
0.27
0.03 |
| LkH332-17 |
0.17
0.04 |
0.24
0.08 |
5.3
0.2 |
|
| IKLup | 0.40
0.23 |
0.40
0.32 |
0.33
0.19 |
6.5
0.3 |
| HTLup | 0.15
0.16 |
0.12
0.08 |
2.8
0.1 |
|
| HNLup | 1.00
0.40 |
1.00
0.50 |
0.86
0.27 |
0.24
0.01 |
| HBC604 | 0.45
0.26 |
<0.65 | 1.99
0.09 |
|
| HOLup | 0.40
0.11 |
0.40
0.28 |
0.43
0.20 |
1.49
0.07 |
In six of our systems the mass determination from the D'Antona & Mazzitelli
(1998) tracks leads to companion masses
that are below the hydrogen burning mass limit of
(see Oppenheimer et al. 2000 and
references therein). This is the case for CZ Tau B,
V 819 Tau B, HK Tau/c, GG Tau b,
Haro 6-28 B and HBC 604 B. With respect to the
Swenson et al. (1994) model that does not cover the
region close above and below the hydrogen burning mass limit all six
mentioned objects have masses below
.
The Baraffe
et al. (1998) tracks yield masses of
for V819Tau B, HKTau/c, GGTau B
and Haro6-28 B. The primary of HBC604 could not
be reliably compared to the Baraffe et al. (1998) tracks,
so we cannot give a Baraffe mass for the secondary.
We emphasize that a definitive classification of a companion as a substellar object is not possible on the basis of our data and requires spatially resolved spectra of the components. It has already been mentioned (Sect. 3.2) that based on NIR colors we cannot distinguish between stars with very late spectral types and deeply embedded objects. HK Tau/c definitely belongs to the latter class of objects, because it has an edge-on seen disk detected by Stapelfeldt et al. (1998). For two of the other mentioned objects, namely the companions of CZTau and Haro6-28, we have detected unusually large NIR color excesses by placing them into a color-color diagram (see Fig. 1) which makes them good candidates for heavily extincted objects. V819Tau B may be a chance projected background star as has been mentioned in Sect. 4.4. The apparent low luminosity would in this case be the result of underestimating its distance.
Substellar companions to young stars probably do exist. GG Tau b has
been placed into the HRD based on spatially resolved spectroscopy by White
et al. (1999). They derived a mass of
which is in line with our mass estimate of
for this
object derived from the D'Antona & Mazzitelli (1998) and the
Baraffe et al. (1998) models. Meyer et al. (1997)
have estimated a mass of 
for the companion of
DI Tau that has been detected by Ghez et al. (1993).
This system is not within our object list because its projected separation of
0
12 is below the diffraction limit of a 3.5 m telescope in the K-band.
There are no strong substellar companion candidates among the
components covered by our study.
Among T Tauri stars in the Taurus-Auriga association there is a significant overabundance of binaries compared to main sequence stars in the solar neighbourhood (see Köhler & Leinert 1998 and references therein). If the binary excess detected with lunar occultation observations, speckle interferometry and direct imaging is extra-polated towards the whole range of projected separations one comes to the conclusion that nearly all stars in this SFR belong to multiple systems. It is therefore interesting to derive the components' mass function for the Taurus-Auriga association, because this should be a better representation of the mass function in this SFR than the systems' mass function - including unresolved binaries - that has been given by Kenyon & Hartmann (1995).
The mass functions for the components of young multiple systems in
Taurus-Auriga for which we have given masses in Table 2 are
plotted in Fig. 6 for the three sets of PMS tracks used.
We have now to ask to what degree these mass functions can be representative
of the whole binary population in this SFR. Our sample is taken from
Leinert et al. (1993). It is restricted to systems with projected
separations from 0
13 to
13
and apparent magnitudes
.
For the first restriction one has to assume that the components' masses
are not a function of their separation. The latter restriction means that we
can detect all primaries with
(for a flux ratio
I2/I1 = 1) while the secondaries are complete
to a magnitude of K = 12 mag. After transforming the theoretical evolutionary
model from the HRD to a diagram where the luminosity is indicated by the
K-band magnitude (see Sect. 4.1) one can determine which mass
range is completely above the K = 10.25 mag brightness limit
for ages less than
.
This leads to completeness limits of
(D'Antona & Mazzitelli 1998 tracks),
(Baraffe
et al. 1998 tracks) and
(Swenson et al.
1994 tracks). The first incomplete bins
are indicated with arrows in Fig. 6. It is thus not
possible based on our data to answer the question if and where the
components' mass function has a maximum and how it continues into the
substellar regime. For this purpose deep imaging surveys for low luminosity
young stars and follow up high angular resolution observations will be
necessary. Concerning mass ratios, our sample is much less subject
to incompleteness.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms9681.fig6.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/img80.gif) |
Figure 6:
Mass function for the components of
young binary systems in Taurus-Auriga from Table 2
derived using the PMS evolutionary models from D'Antona & Mazzitelli
(1998), Swenson et al. (1994) and Baraffe et al.
(1998). The bins indicated with arrows and all bins left of
them only represent lower limits, because of the incompleteness of our
sample (see Sect. 6.2). The objects represented by the
shaded bin in the upper right panel can also have lower masses than
indicated here, because the Swenson et al. (1994) model
does only cover masses with
 . |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms9681.fig7.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/img81.gif) |
Figure 7: Distribution of mass ratios for the young binary systems from Table 2 derived with respect to three sets of PMS evolutionary models. The open histograms represent all 51 binaries from that table, the shaded histograms show a restricted sample (45 binaries) for which all companions can be detected with the applied observational techniques (see Sect. 6.3). In the lower right panel also the distribution of K band flux ratios is given. |
The distribution of mass ratios of binary components and their dependence on
other parameters are of special interest, because they can be compared
to predictions of theoretical models for multiple star formation
(see Sect. 7). To place reliable constraints on this quantity
one has to define a complete sample that is unaffected by
biases caused by the observational techniques. Köhler et al.
(2000) have come to the conclusion that using speckle
interferometry at a 3.5 m-telescope in the K-band![[*]](/icons/foot_motif.gif){kind=icon}
will detect any companion
with a projected separation above 0
13 and a magnitude difference
to the primary of
.
The first condition
is fulfilled for all components in Table 2. By applying
the second restriction and obtaining a homogeneous data set we exclude six
systems from the following discussion, namely V819Tau,
UXTauAC, HKTau, HNTau, WXCha
and LkH332-17. They have very faint companions that have
been detected using direct imaging.
The mass ratios derived from three sets of PMS tracks are shown
in Table 3. For triple and quadruple systems we have only
given them for close pairs in hierarchical systems.
The errors indicated in Table 3 are
formally derived from the mass errors given in Table 2.
This is a conservative estimate, since distance errors affect the components
of a binary in a similar way and therefore do not fully influence the
mass ratio. To take the uncertainties that are within the PMS models into account
we compare the mass ratio distributions derived from the
D'Antona & Mazzitelli (1998), Swenson et al. (1994)
and Baraffe et al. (1998) models (Fig. 7).
The shaded histograms show the restricted sample, the open histograms
represent all pairs from Table 2. The distributions
derived from the D'Antona & Mazzitelli (1998) and
Swenson et al. (1994) tracks are flat for
within the uncertainties. The apparent deficit in the first bin is
probably due to incomplete detections in this regime. Actually we have
found more pairs with mass ratios below 0.2.
The Baraffe et al. (1998)
model suggests a rising of the mass ratio distribution towards unity,
but this may also be caused by incompletes of the sample at low mass
ratios and is not very significant. The distribution for
is still compatible with being flat on a 57%
confidence level. In discussing the mass ratio distributions given
in Fig. 7 one has to take into account
that the mean error of the individual mass ratios (Table 3)
is about one binsize. This effect will cause a flattening of any
given distribution. We will conclude this discussion with the statement
that our data does not support the preference of any mass ratios. On the
other hand we admit that it would be premature to say that the mass
ratio distribution is definetely flat taking into account the large
differences between the distributions shown in Fig. 7.
A flat distribution of mass ratios is supported by the distribution of K-band
flux ratios (Fig. 7, lower right panel). For low-mass PMS
stars there is a K-band mass-luminosity relation of about 
(e.g.
Simon et al. 1992), so the distribution of this quantity should in
a good approximation resemble that of the mass ratios. There is again no
clustering towards
M2/M1 = 1. If also the systems with
,
i.e.
F2(K)/F1(K) < 0.1 are included there seems to appear even
a slight overabundance of low mass ratios.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms9681.fig8.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/img85.gif) |
Figure 8: Distribution of mass ratios as a function of the projected separation for the three sets of PMS models used in this paper. |
 |
 |
|
| D'Antona & Mazzitelli (1998) | ||
| M2/M1 > 0.5 | 14
3.7 |
9
3.0 |
 |
12
3.5 |
10
3.2 |
| Swenson et al. (1994) | ||
| M2/M1 > 0.5 | 16
4.0 |
9
3.0 |
|
|
10
3.2 |
8
2.8 |
| Baraffe et al. (1998) | ||
| M2/M1 > 0.5 | 17
4.1 |
8
2.8 |
|
|
8
2.8 |
6
2.5 |
First, we want to examine a possible
correlation of mass ratios and the components'
separations. For this purpose it is useful to convert the measured
projected angular separations to physical separations. This allows us
to discuss binaries in SFRs with different distances
(see Table 1) simultaneously.
Moreover this yields a comparison between mass ratios and characteristic
length scales like the radii of circumstellar disks.
Applying this conversion one has to consider that values for the projected
distance obtained with "snap-shot'' observations can be very different
from the semimajor axis A. This cannot be corrected for individual systems.
Leinert et al. (1993) have however calculated that the
relationship between the projected separation
and the
semimajor axis A is on average
 |
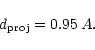(2) |
will
resemble the distribution of semimajor axes in a good approximation.
In Fig. 8 the mass ratios derived from three sets
of PMS evolutionary tracks are plotted as a function of
.
To present the results more clearly we have divided
these scatter plots into four fields (Table 4) and have
particularly discriminated between separations
that are larger or lower than a typical circumstellar disk radius that
is
(e.g. Hartmann 1998).
With respect to the D'Antona & Mazzitelli (1998) and the
Swenson et al.(1994) models, in both regions the numbers of
systems with low and high mass ratios are comparable within the uncertainties.
The result obtained from the Baraffe et al. (1998) model
suggests a slight preference of larger mass ratios at lower separations,
but this is significant only at the 1
level.
| D'Antona & Mazzitelli (1998) | ||
 |
 |
|
| M2/M1 > 0.5 | 15
3.9 |
8
2.8 |
|
|
11
3.3 |
11
3.3 |
| Swenson et al.(1994) | ||
 |
 |
|
| M2/M1 > 0.5 | 13
3.6 |
11
3.3 |
|
|
5
2.2 |
13
3.6 |
| Baraffe et al.(1998) | ||
|
|
|
|
| M2/M1 > 0.5 | 10
3.2 |
15
3.9 |
|
|
6
2.5 |
8
2.8 |
Finally, we ask for a correlation between the mass ratio and the primary mass. The result is shown in Fig. 9 and Table 5. The threshold between "low'' and "high'' primary masses is arbitrarily chosen to have a comparable number of objects in both groups for each theoretical PMS model considered. With regard to the Baraffe et al. (1998) model the behaviour of both groups is the same. The D'Antona & Mazzitelli (1998) and Swenson et al. (1994) models suggest a preference of higher mass ratios for lower primary masses. The latter result has also been mentioned by Leinert et al. (1993) on the basis of K band magnitudes and flux ratios.
We conclude that correlations between mass ratio and other binary parameters are weak if they exist at all.
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms9681.fig9.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/img93.gif)