and implications for multiple star formation
A&A 376, 982-996 (2001)
DOI: 10.1051/0004-6361:20011034
J.Woitas1, 2 - Ch.Leinert2 - R.Köhler3, 2
1 - Thüringer Landessternwarte Tautenburg, Sternwarte 5,
07778 Tautenburg, Germany
2 - Max-Planck-Institut für Astronomie, Königstuhl 17,
69117 Heidelberg, Germany
3 - Center for Astrophysics and Space Sciences, University of California,
San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0424, USA
Received 25 February 2000 / Accepted 12 July 2001
Abstract
Using near-infrared speckle interferometry we have obtained
resolved JHK-photometry for the components of 58 young binary systems.
From these measurements, combined with other data taken from literature,
we derive masses and particularly mass ratios of the components.
We use the J-magnitude as an indicator for the stellar luminosity and assign
the optical spectral type of the system to the primary.
On the assumption that the components within a binary are coeval we can then
also place the secondaries into the HRD and derive masses and mass ratios
for both components by comparison with different sets of current theoretical
pre-main sequence evolutionary tracks. The resulting distribution of mass
ratios is comparatively flat for
![]() ,
but depends on assumed
evolutionary tracks. The mass ratio is neither correlated with the primary's
mass or the components' separation. These findings are in line with the
assumption that for most multiple systems in T associations the components'
masses are principally determined by fragmentation during formation and
not by the following accretion processes.
Only very few unusually red objects were newly found among the detected
companions.This finding shows that the observed overabundance of binaries
in the Taurus-Auriga association compared to nearby main sequence stars
should be real and not the outcome of observational biases related to
infrared observing.
,
but depends on assumed
evolutionary tracks. The mass ratio is neither correlated with the primary's
mass or the components' separation. These findings are in line with the
assumption that for most multiple systems in T associations the components'
masses are principally determined by fragmentation during formation and
not by the following accretion processes.
Only very few unusually red objects were newly found among the detected
companions.This finding shows that the observed overabundance of binaries
in the Taurus-Auriga association compared to nearby main sequence stars
should be real and not the outcome of observational biases related to
infrared observing.
Key words: binaries: general - stars: pre-main sequence - stars: formation - stars: fundamental parameters - techniques: interferometric - infrared: stars
Most stars in the solar neighbourhood are members of multiple systems (e.g. Duquennoy & Mayor 1991; Fischer & Marcy 1992). This raises the question of whether most of these systems were formed as binaries or whether they are the result of later capture processes. After high angular resolution techniques in the near infrared (NIR) had been developed at the beginning of the 1990s this problem became an issue of observational astronomy.
A large number of multiplicity surveys in star-forming regions (SFRs) and clusters has now been done (see Mathieu et al. 2000 and references therein). It is still a matter of debate if different environmental conditions of star formation lead to different degrees of multiplicity. One can however conclude that there is at this time no sample of young stars that shows a significant binary deficit compared to nearby main sequence stars. In some SFRs even a strong binary excess is observed. The consequence of these results is that multiplicity must be already established in very early phases of stellar evolution and that star formation to a large extent has to be considered as formation of multiple stars. Multiplicity has to be taken into account if one asks for stellar properties. If this question is addressed to the systems instead of the components, misleading results may be obtained.
In this paper we will discuss the young binary systems in the nearby SFRs Taurus-Auriga, Upper Scorpius, ChamaeleonI and Lupus that have been detected by Leinert et al. (1993), Ghez et al. (1997a) and Köhler et al. (2000). We present resolved photometry of the components in the NIR spectral bands J, H and K (Sect. 2). Based on these data we discuss the components in a color-color diagram (Sect. 3) and in a color-magnitude diagram (Sect. 4). Using the J-band magnitude as an indicator for the stellar luminosity and published spectral types for the primaries, we place the components pairwise into the Hertzsprung-Russell diagram (HRD, Sect. 5) and derive masses and in particular mass ratios from a comparison with theoretical PMS evolutionary models (Sect. 6). Implications of the results for theoretical concepts of multiple star formation and for binary statistics are discussed in Sect. 7.
If not stated otherwise we take the systems' magnitudes, interstellar extinction coefficients AV and spectral types from the literature. The references are Kenyon & Hartmann (1995) for Taurus-Auriga, Walter et al. (1994) and also Köhler et al. (2000) for Upper Scorpius, Gauvin & Strom (1992) for Chamaeleon I and Hughes et al. (1994) for Lupus. Possible effects of variability are discussed in Sect. 4.2.2.
Data for the objects in Taurus-Auriga were obtained during several observing runs with the NIR camera MAGIC at the 3.5 m-telescope on Calar Alto from 1993 to 1998. Measurements at this telescope before September 1993 were done with a device for one-dimensional speckle-interferometry that has been described by Leinert & Haas (1989). Observations of multiple systems in southern SFRs were carried out in May 1998 at the ESO New Technology Telescope (NTT) on La Silla that is also a 3.5 m-telescope, using the SHARP camera of the Max-Planck-Institute for Extraterrestrial Physics (Hofmann et al. 1992).
Since most binaries of our sample have projected separations of less than
![]() ,
a high angular resolution technique is needed to overcome the
effects of atmospheric turbulence and to reach the diffraction limit which is
,
a high angular resolution technique is needed to overcome the
effects of atmospheric turbulence and to reach the diffraction limit which is
![]() for a 3.5 m-telescope at
for a 3.5 m-telescope at
![]() .
We have mostly used two-dimensional speckle interferometry.
Sequences of typically 1000 images with exposure times of
.
We have mostly used two-dimensional speckle interferometry.
Sequences of typically 1000 images with exposure times of
![]()
![]() were taken for the object and a
nearby reference star. After background subtraction, flatfielding and badpixel
correction these data cubes are Fourier-transformed.
were taken for the object and a
nearby reference star. After background subtraction, flatfielding and badpixel
correction these data cubes are Fourier-transformed.
We determine the modulus of the complex visibility (i.e. the Fourier transform of the object brightness distribution) from power spectrum analysis. The phase is recursively reconstructed using two different methods: The Knox-Thompson algorithm (Knox & Thompson 1974) and the bispectrum analysis (Lohmann et al. 1983). A detailed description of this data reduction process has been given by Köhler et al. (2000, Appendix A). Modulus and phase show characteristic strip patterns for a binary. In the case of a triple or quadruple star these patterns will be overlayed by similar structures that belong to the additional companion(s).
Fitting a binary model to the complex visibility yields the binary parameters position angle, projected separation and flux ratio. The errors of these parameters are estimated by doing this fit for different subsets of the data. The comparison of our position angles and projected separations with those obtained by other authors that has been done in another paper (Woitas et al. 2001) has shown that systematic differences in relative astrometry are negligible. Differences in resolved K-band photometry have an order of magnitude that can be explained by the variability of T Tauri stars.
Together with the system brightness that is taken from the literature, in most cases the flux ratio determines the components' magnitudes. We present the results of our individual measurements in Table A.1. To reduce the effect of the variability of T Tauri stars we calculate the mean of all resolved photometric observations in one filter obtained by us and other authors (see Appendix A).
Our sample grew out of surveys for multiplicity in star forming regions. With a total of 119 individual components it is of reasonable size. By construction it is largely independent of biases due to duplicity. This makes it well suited for statistical discussions.
From the resolved photometry alone we can check for circumstellar excess emission, search for possible infrared companions, detect contamination by background stars and have some check on whether the components of a binary system are coeval. In the last point we encounter the limitations of our method: the large uncertainty in color, resulting mainly from variability, seriously degrades possible age determinations.
Therefore we use in the HRD known spectral types to derive masses for the components dominating the visual region, and derived masses for the companions on the assumption of coevality. The reliability of these mass determinations profit from our explicit knowledge of duplicity. The presentation of the results starts with those resulting from resolved photometry alone.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms9681.fig1a.eps}\hspace*{10mm}
\includegraphics[width=7.5cm,clip]{ms9681.fig1b.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/Timg27.gif) |
Figure 1: Color-color diagram for the components of weak-lined T Tauri stars (WTTS, left panel) and classical T Tauri stars (CTTS, right panel). The almost vertical solid line denotes the main sequence, with the giant branch to the right (Bessell & Brett 1988). The dotted lines are parallel to the reddening vector (indicated for AV = 5 in the lower right of both panels). The cross gives the typical error bars of our observations (see Sect. 4.2). Only in the region labeled "A'' and on the main sequence the observed colors are consistent with photospheric emission, whereas for objects located right to this region circumstellar excess emission is present. The numbers in the right panel denote Haro6-28B (1), CZTauB (2), the infrared companion of XZTau (3), the components of FSTau (4, 5), HNTauA (6) and the infrared companion of UYAur (7). |
| Open with DEXTER | |
The resulting dereddened colors are not necessarily
stellar colors, because infrared excess emission caused by circumstellar
disks is a common phenomenon in T Tauri stars (e.g. Beckwith et al.
1990). For this reason we first consider a subsample of
systems that consist of weak-lined T Tauri stars (WTTS). The adopted
classification criterion for WTTS is that their H![]() equivalent width
is less than
equivalent width
is less than
![]() (Herbig & Bell 1988). WTTS are not
expected to have prominent disks and their mean excess emission in J, H and
K is zero (Hartigan et al. 1995). Almost all components of these
systems have colors comparable to main sequence stars (Fig. 1,
left panel), as is expected. The only exceptions are the two components
of UXTauB and the companion of V773Tau.
For components of systems with classical T Tauri stars (CTTS) where
significant circumstellar excess emission is expected, the positions in the
color-color diagram are much more spread around (Fig. 1,
right panel). These colors cannot be referred to stellar photospheres
in a simple way.
(Herbig & Bell 1988). WTTS are not
expected to have prominent disks and their mean excess emission in J, H and
K is zero (Hartigan et al. 1995). Almost all components of these
systems have colors comparable to main sequence stars (Fig. 1,
left panel), as is expected. The only exceptions are the two components
of UXTauB and the companion of V773Tau.
For components of systems with classical T Tauri stars (CTTS) where
significant circumstellar excess emission is expected, the positions in the
color-color diagram are much more spread around (Fig. 1,
right panel). These colors cannot be referred to stellar photospheres
in a simple way.
It is interesting to look for companions with extreme red colors, because these can be candidates for infrared companions (IRCs). IRCs are objects that are very weak or have even not been detected at optical wavelengths, but dominate the system's brightness in the infrared. They are somewhat puzzling for star formation theory, because some of them appear to be more massive than the optical "primary'' but are at the same time more embedded and less evolved.
At this time 8 IRCs are known (Koresko et al. 1997; Ressler & Barsony 2001). Two of these objects - XZTauB and UYAurB - do indeed show unusual red colors in the color-color diagram (Fig. 1, right panel). Two other known IRCs that belong to our sample - TTauB and Haro6-10 B - are not discussed here, because we could not detect those objects in the J-band. In Fig. 1 we have also indicated CZTauB, Haro6-28B, both components of FSTau and HNTauA as unsually red objects. For these systems additional spatially resolved observations at longer and shorter wavelengths will be necessary to decide if they really contain IRCs.
The best candidate for a new IRC is the companion of FVTau/c
that we have observed in H and K, but failed to detect in the J-band.
Ghez et al. (1997a) have proposed HBC603B and
VWChaC to be IRCs, because these objects were found by
their K-band survey, but missed at
![]() by
Reipurth & Zinnecker (1993). We have observed these systems
in J and H and did not detect any companion either, which calls
for additional observations at longer wavelengths.
by
Reipurth & Zinnecker (1993). We have observed these systems
in J and H and did not detect any companion either, which calls
for additional observations at longer wavelengths.
Extinction by circumstellar envelopes or edge-on disks is not the only possible explanation for extremely red colors. The objects mentioned in this section may also have a very late spectral type and may even be young brown dwarfs. We will discuss the topic of possible substellar companions in Sect. 6.1.
In any case extremely red objects are not frequent among the companions detected by Leinert et al. (1993) in Taurus-Auriga. This indicates that the observed overabundance of binaries in this SFR compared to nearby main sequence stars is real and not the result of using infrared wavelengths for multiplicity surveys among young stars.
For comparison with the data, we convert
luminosity L and
![]() for distinct masses and ages from
the theoretical atmosphere models to near-infrared colors
and magnitudes. To this purpose we use relationships
that give the bolometric correction BCV and several colors
as a function of spectral type or the corresponding
for distinct masses and ages from
the theoretical atmosphere models to near-infrared colors
and magnitudes. To this purpose we use relationships
that give the bolometric correction BCV and several colors
as a function of spectral type or the corresponding
![]() .
These
relations are tabulated by Bessell (1991), Bessell &
Brett (1988) and Schmidt-Kaler (1982).
To interpolate between the datapoints given in these tables we use
polynomial fits that have been done by Meyer (1996).
The apparent J-band magnitude is derived from L and
.
These
relations are tabulated by Bessell (1991), Bessell &
Brett (1988) and Schmidt-Kaler (1982).
To interpolate between the datapoints given in these tables we use
polynomial fits that have been done by Meyer (1996).
The apparent J-band magnitude is derived from L and
![]() using the following equation:
using the following equation:
The magnitude errors that are given in Table A.2 are the errors of the mean magnitude that result from averaging over all spatially resolved measurements in a given spectral band. If only one observation has been done the error is calculated from the uncertainties of measured system photometry and flux ratio, as given in Table A.1. For the comparison of colors and magnitudes to theoretical PMS models additional error sources have to be taken into account.
To obtain the distance modulus m - M used in Eq. (1)
we adopt distances to the SFRs that are the mean of all
Hipparcos distances derived for members of the respective association.
The values and references are given in Table 1.
However, distances to individual objects
may be different from these mean values. To take this into account, we
assume that the radial diameters of the SFRs are as large as their
projected diameters on the sky. The latter quantity can be estimated
to be ![]()
![]() for Taurus-Auriga (see Fig. 1 in Köhler
& Leinert 1998) as well as for Scorpius-Centaurus (see Fig. 1
in Köhler et al. 2000). Concerning the mean distances
from Table 1 this corresponds to a diameter of 50 pc.
We assume here
for Taurus-Auriga (see Fig. 1 in Köhler
& Leinert 1998) as well as for Scorpius-Centaurus (see Fig. 1
in Köhler et al. 2000). Concerning the mean distances
from Table 1 this corresponds to a diameter of 50 pc.
We assume here
![]() as uncertainty for the
distance of an individual system which is a very conservative
estimate: more than two thirds of the stars will be within
as uncertainty for the
distance of an individual system which is a very conservative
estimate: more than two thirds of the stars will be within ![]() 15 pc
for an even spatial distribution.
15 pc
for an even spatial distribution.
| SFR | distance[pc] | reference |
| Taurus-Auriga | 142 |
Wichmann et al. (1998) |
| Upper Scorpius | 145 |
de Zeeuw et al. (1999) |
| ChamaeleonI | 160 |
Wichmann et al. (1998) |
| Lupus | 190 |
Wichmann et al. (1998) |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ms9681.fig2.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/Timg36.gif) |
Figure 2: Distribution of variability amplitudes for components of young binary systems in the NIR spectral bands J, H and K. They contain all of the systems discussed in this paper for which repeated spatially resolved observations in one filter exist (see Table A.1 for our observations and caption of Table A.2 for references to other published data). |
| Open with DEXTER | |
T Tauri stars are variable. Although this effect is much less in the
infrared compared to optical wavelengths (Nurmanova
1983), it cannot be neglected. We use those components for
which there are observations in the same filter at different epochs to
estimate the influence of variability on the magnitudes. The distribution of
variability amplitudes is given in Fig. 2. The mean
amplitudes that we consider as variability errors are
![]() ,
,
![]() and
and
![]() .
These variations, as derived from our data set,
are similar to those in the tabulation of Rydgren et al. (1984)
but smaller than those found by Skrutskie et al. (1996).
Therefore our estimate of variability may be somewhat optimistic.
.
These variations, as derived from our data set,
are similar to those in the tabulation of Rydgren et al. (1984)
but smaller than those found by Skrutskie et al. (1996).
Therefore our estimate of variability may be somewhat optimistic.
Kenyon & Hartmann (1995) have given for the extinction an error of
![]() for the systems in
Taurus-Auriga. We adopt this error also for the systems in other SFRs.
for the systems in
Taurus-Auriga. We adopt this error also for the systems in other SFRs.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{ms9681.fig3.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/Timg43.gif) |
Figure 3:
Components of young binary systems placed
into a NIR color-magnitude diagram together with the theoretical PMS model
by D'Antona & Mazzitelli (1998). The solid lines are evolutionary
tracks for different stellar masses (0.9 to 0.017 |
| Open with DEXTER | |
The following two error sources do not affect colors or magnitudes, but the transformation of theoretical PMS models to observable quantities. By this way they also enter into the error discussion:
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{ms9681.fig4a.eps}\includegraphics[width=9cm,clip]{ms9681.fig4b.eps} }\end{figure}](/articles/aa/full/2001/36/aa9681/Timg48.gif) |
Figure 4:
Examples of colour-magnitude diagrams for two WTTS systems.
Left: V819Tau, the putative companion appears to be a background object.
Right: HBC351: an example for coevality of the components.
The data are overplotted with the PMS model by
D'Antona & Mazzitelli (1998). The dashed lines denote
evolutionary tracks for masses from 0.02 to
|
| Open with DEXTER | |
In Fig. 3 the placement of the components into a J/(H-K) color-magnitude diagram is shown. The PMS evolutionary model by D'Antona & Mazzitelli (1998) is also indicated in the figure. The distribution of objects in a J/(J-K) color-magnitude diagram would look quite similar.
Almost all components are above the lower main sequence, as they are expected to be. But many stars lie in a region that is not covered by the evolutionary tracks. This cannot be corrected by further dereddening, but must be due to the presence of circumstellar color excesses that we have already mentioned above. E.g., nearly all stars that have an unusually large H-K are CTTS (represented by triangles) and the only WTTS in this region are the components of V773Tau and UXTau where we have noticed excess emission already in Sect. 3.1.
Since there is no resolved spectroscopy of the components, we cannot correct for the color excesses mentioned in the previous section. For this reason we restrict the discussion of the components in the color-magnitude diagram to a subsample of 17 systems that consist of WTTS where no significant circumstellar excess emission is expected.
The placement of the individual components into a J/(J-K) color-magnitude
diagram is shown in Fig. 4. Object by object, the positons of
the components in these plots are compared to the PMS evolutionary model by
D'Antona & Mazzitelli (1998) to check for coevality and validity of
the association. We have also used the sets of PMS
tracks and isochrones given by Swenson et al. (1994) and
Baraffe et al.(1998) and have obtained similar results.
With respect to the D'Antona & Mazzitelli (1998) tracks in 14 out of
17 cases the components appear to be coeval. Unfortunately, this finding
has not much weight because of the large errors in color.
Nevertheless some useful checks can be performed.
The three problematic cases are V773Tau, UXTau and
V819Tau. For the first two systems we have already noticed
the presence of excess emission (Sects. 3.1 and 4.3).
Duchêne et al. (1999b) have proposed
to reclassify UXTau as a CTTS, because
its H![]() equivalent width is
equivalent width is
![]() and thus above the
upper limit for WTTS with spectral type K that is
and thus above the
upper limit for WTTS with spectral type K that is
![]() according to Martín (1998). The companion of
V819Tau lies far below the main sequence in the color-magnitude
diagram. This indicates that V819TauB is in fact not a binary
companion, but a chance projected background star.
according to Martín (1998). The companion of
V819Tau lies far below the main sequence in the color-magnitude
diagram. This indicates that V819TauB is in fact not a binary
companion, but a chance projected background star.
For HBC 352/353 Fig. B.1 yields an age range
of about
![]() yr
which is problematic because this age is larger than the age spread found
for the Taurus SFR (e.g. Kenyon & Hartmann 1995).
Also, Martín et al. (1994) called into question that these
are young stars because they do not show significant Lithium line
absorption.
yr
which is problematic because this age is larger than the age spread found
for the Taurus SFR (e.g. Kenyon & Hartmann 1995).
Also, Martín et al. (1994) called into question that these
are young stars because they do not show significant Lithium line
absorption.
With the mentioned exceptions, our data are compatible with the assumption that the components of the T Tauri binaries are coeveal. There are other studies that better prove that this assumption is valid: Brandner & Zinnecker (1997) have obtained spatially resolved spectroscopy for the components of eight young binary systems and placed them into the HRD. In all cases the components are coeval. Particularly well this has been shown in the case of the quadruple system GGTau (White et al. 1999) from resolved spectroscopy with the HST Faint Object Spectrograph. Below we will use the assumption of coevality to estimate masses for the companions and mass ratios for the components in binary systems.
In this section we will place the components of young binary systems into the HRD and compare their positions in this diagram with theoretical PMS evolutionary models to derive masses and mass ratios. For this purpose one has to know their luminosities and spectral types. Since these quantities are not known as directly measured values we have to make some assumptions to estimate them from our resolved NIR photometry and the system properties that are given in the literature.
As described in Sect. 4.1 for the colour-magnitude diagrams,
we transform the theoretical atmosphere models that give
![]() and L as functions of mass and age into a diagram in which the luminosity
is represented by a NIR magnitude.
and L as functions of mass and age into a diagram in which the luminosity
is represented by a NIR magnitude.
Circumstellar excess emission is minimal around
![]() (e.g. Kenyon & Hartmann 1995). For this reason we prefer
the J-band magnitudes of the components to H and K as luminosity indicator.
It is however not clear if this excess emission is negligible in the J-band.
Hartigan et al. (1995) have measured the veiling in optical
spectra of T Tauri stars. Assuming that the excess emission in the J-band
is
(e.g. Kenyon & Hartmann 1995). For this reason we prefer
the J-band magnitudes of the components to H and K as luminosity indicator.
It is however not clear if this excess emission is negligible in the J-band.
Hartigan et al. (1995) have measured the veiling in optical
spectra of T Tauri stars. Assuming that the excess emission in the J-band
is
![]() ,
where
,
where
![]() ,
they come to the conclusion
that for a sample of 19 CTTS and 10 WTTS the mean value is consistent with
,
they come to the conclusion
that for a sample of 19 CTTS and 10 WTTS the mean value is consistent with
![]() .
Folha & Emerson (1999) determined the
NIR excess emission directly using infrared spectra of 50 T Tauri stars.
Their result is that
.
Folha & Emerson (1999) determined the
NIR excess emission directly using infrared spectra of 50 T Tauri stars.
Their result is that
![]() for the CTTS in their sample
and thus much larger than expected. To take this into account, we apply an
excess correction of
for the CTTS in their sample
and thus much larger than expected. To take this into account, we apply an
excess correction of
![]() corresponding to this
<rJ>, if we use J magnitudes as an indicator for CTTS stellar
luminosities. For the WTTS in their sample Folha & Emerson (1999)
find values of rJ that are compatible with zero, so for the
components of WTTS systems no excess correction is necessary.
corresponding to this
<rJ>, if we use J magnitudes as an indicator for CTTS stellar
luminosities. For the WTTS in their sample Folha & Emerson (1999)
find values of rJ that are compatible with zero, so for the
components of WTTS systems no excess correction is necessary.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms9681.fig5.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/Timg60.gif) |
Figure 5:
The components of the young binary system
IKLup placed into the HRD as an example for the method
described in Sect. 5. The cross gives the position of the
primary, the horizontal dashed lines the locus for the secondary
and the respective error. The theoretical model is by
Baraffe et al. (1998). The evolutionary tracks are given
for masses of 0.04, 0.06, 0.08, 0.10, 0.15, 0.20, 0.25, 0.30, 0.40,
0.50, 0.60, 0.70, 0.80, 0.90, 1.00 and 1.20 |
| Open with DEXTER | |
For nearly all of the systems discussed here we know the combined optical spectral type from the literature (see Sect. 2.1 and Table A.2). We assume that these combined spectra represent to a good approximation those of the optical primary components, and we assign the optical spectral type of the system to the brightest component in the J-band. The spectral type and effective temperature of the companion is estimated using the assumption that all components within a system are coeval. We are now ready to place the components into the HRD. The procedure is shown in Fig. 5 using the T Tauri binary system IKLup as an example. For 48 more systems the placement of the components into the HRD is shown in Fig. C.1, available in electronic form. The theoretical PMS evolutionary model used is by Baraffe et al. (1998). The position of the primary is determined by its J-band magnitude and the system's spectral type. For the latter quantity we assume an error of one spectral subclass as given by Kenyon & Hartmann (1995) for the systems in Taurus-Auriga. The companion's J-band magnitude and the respective error define a locus for the companion in the HRD. If we assume that both components are coeval the companion is situated at the point of intersection between this locus and the isochrone of the primary. In the same way we also defined the loci of the components in the HRD for the evolutionary tracks of Swenson et al. (1994) and D'Antona & Mazzitelli (1998).
The procedure described in the previous section yields the components'
masses. For instance, in the IKLup system
(Fig. 5) the components have masses of
![]() and
and
![]() with respect to the Baraffe et al. (1998)
tracks. The resulting masses derived for the components from all three sets
of PMS tracks used are given in Table 2. For some systems
(indicated with question marks in Table 2) the primary
is located in a region of the HRD that is not covered by the respective
tracks. The Swenson et al. (1994) model does only cover a
mass range above
with respect to the Baraffe et al. (1998)
tracks. The resulting masses derived for the components from all three sets
of PMS tracks used are given in Table 2. For some systems
(indicated with question marks in Table 2) the primary
is located in a region of the HRD that is not covered by the respective
tracks. The Swenson et al. (1994) model does only cover a
mass range above
![]() ,
so for some secondaries only
upper mass limits can be derived from that model. The errors
given in Table 2 reflect the range of tracks that is
covered by the stars' locations in the HRD. These uncertainties are
20-30% for most stars and thus quite large. However, all error sources
discussed so far are random and not systematic. Therefore in a
statistical analysis of these masses that we will do in
Sects. 6.2 and 6.3, these uncertainties
will partially cancel and have less influence to the results.
There are however additional uncertainties
within the PMS models theirselves. One can see from
Table 2 that there are discrepancies in masses obtained
for the same stars from different PMS models that can be much larger
than the indicated errors which trace the uncertainty
of our measurements. The components' mass functions derived from
the three models (see Fig. 6) are different at a 99%
confidence level which indicates that these mass differences are systematic.
,
so for some secondaries only
upper mass limits can be derived from that model. The errors
given in Table 2 reflect the range of tracks that is
covered by the stars' locations in the HRD. These uncertainties are
20-30% for most stars and thus quite large. However, all error sources
discussed so far are random and not systematic. Therefore in a
statistical analysis of these masses that we will do in
Sects. 6.2 and 6.3, these uncertainties
will partially cancel and have less influence to the results.
There are however additional uncertainties
within the PMS models theirselves. One can see from
Table 2 that there are discrepancies in masses obtained
for the same stars from different PMS models that can be much larger
than the indicated errors which trace the uncertainty
of our measurements. The components' mass functions derived from
the three models (see Fig. 6) are different at a 99%
confidence level which indicates that these mass differences are systematic.
There is now some evidence that the Baraffe et al. (1998) tracks could be preferrable among the current PMS models: White et al. (1999) have placed the four components of GGTau into the HRD and compared their positions with different sets of PMS tracks. They found that the Baraffe et al. (1998) model is best consistent with the assumption that all components are coeval. Simon et al. (2000) and Steffen et al. (2000) presented first results of empirical mass determinations from orbital motion around T Tauri stars that are also comparable with the predictions of the Baraffe et al. (1998) model. It would however be premature to consider these results as a final solution of the problem of inconsistent PMS models, mainly because the mentioned observations do not cover the whole range of masses and ages expected for T Tauri stars. Therefore in this paper we will - as we have already done in Sect. 4.4 - rely on the three PMS models given by D'Antona & Mazzitelli (1998), Swenson et al. (1994) and Baraffe et al. (1998) and compare the respective results. It can be seen that the uncertainties inherent in the evolutionary model predictions often surpass the uncertainties resulting from the measurement errors.
| System |
|
|
|
|
|
|
| DM98 | Swenson | Baraffe | ||||
| HBC 351 | 0.85 |
0.25 |
1.0 |
0.4 |
1.0 |
0.4 |
| HBC 352/353 | 1.0 |
0.9 |
? | ? | ? | ? |
| HBC 358Aa | 0.35 |
0.35 |
0.7 |
0.7 |
0.4 |
0.4 |
| HBC 358 B | 0.4 |
0.7 |
0.5 |
|||
| HBC 360/361 | 0.2 |
0.2 |
0.5 |
0.5 |
0.3 |
0.3 |
| FO Tau | 0.35 |
0.14 |
0.5 |
0.35 |
0.6 |
0.3 |
| DD Tau | 0.5 |
0.4 |
0.7 |
0.65 |
0.7 |
0.6 |
| CZ Tau | 0.4 |
0.04 |
0.7 |
<0.15 | 0.6 |
0.10 |
| FQ Tau | 0.4 |
0.4 |
0.7 |
0.7 |
0.5 |
0.5 |
| V 819 Tau | 0.45 |
0.04 |
0.7 |
<0.15 | 1.1 |
0.08 |
| LkCa 7 | 0.5 |
0.2 |
0.85 |
0.45 |
1.1 |
0.6 |
| FS Tau | 0.5 |
0.12 |
0.75 |
0.15 |
0.7 |
0.2 |
| FV Tau | 0.65 |
0.35 |
1.15 |
0.7 |
1.3 |
1.0 |
| UX TauAC | 1.2 |
0.16 |
1.4 |
0.25 |
1.3 |
0.4 |
| UX TauBb | 0.25 |
0.20 |
0.5 |
0.4 |
0.6 |
0.5 |
| FX Tau | 0.35 |
0.35 |
0.55 |
0.55 |
0.8 |
0.8 |
| DK Tau | 0.50 |
0.15 |
0.8 |
0.35 |
1.1 |
0.4 |
| LkH |
0.16 |
0.12 |
0.4 |
0.15 |
0.20 |
0.15 |
| HK Tau | 0.5 |
0.04 |
0.6 |
<0.15 | 0.7 |
0.08 |
| V 710 Tau | 0.4 |
0.35 |
0.55 |
0.45 |
0.65 |
0.5 |
| HK Tau G2 | 0.35 |
0.35 |
0.6 |
0.45 |
0.9 |
0.7 |
| GG Tau Aa | 0.4 |
0.2 |
0.65 |
0.4 |
0.9 |
0.5 |
| GG Tau Bb | 0.09 |
0.04 |
<0.15 | <0.15 | 0.2 |
0.04 |
| UZ Tau w | 0.20 |
0.18 |
0.45 |
0.35 |
0.35 |
0.30 |
| GH Tau | 0.35 |
0.35 |
0.55 |
0.55 |
0.6 |
0.5 |
| Elias 12 | 0.4 |
0.3 |
0.7 |
0.35 |
1.2 |
0.9 |
| IS Tau | 1.1 |
0.4 |
1.05 |
0.7 |
0.9 |
0.7 |
| GK Tau / GI Tau | 0.55 |
0.4 |
0.95 |
0.75 |
1.2 |
1.0 |
| HN Tau | 0.7 |
0.35 |
0.75 |
0.45 |
0.7 |
0.4 |
| CoKu Tau 3 | 0.4 |
0.16 |
0.75 |
0.35 |
0.6 |
0.3 |
| HBC 412 | 0.35 |
0.3 |
0.6 |
0.5 |
0.55 |
0.50 |
| Haro 6-28 | 0.20 |
0.04 |
0.55 |
<0.15 | 0.25 |
0.06 |
| VY Tau | 0.60 |
0.25 |
0.85 |
0.35 |
0.8 |
0.4 |
| IW Tau | 0.7 |
0.6 |
0.95 |
0.85 |
0.9 |
0.8 |
| LkH |
0.4 |
0.18 |
0.55 |
0.35 |
0.8 |
0.4 |
| LkH |
0.45 |
0.20 |
0.75 |
0.3 |
1.2 |
0.7 |
| LkH |
0.7 |
0.6 |
0.95 |
0.8 |
1.0 |
0.8 |
| Haro 6-37 Aa | 0.7 |
0.09 |
1.05 |
0.2 |
1.1 |
0.3 |
| Haro 6-37 /c | 0.35 |
0.65 |
0.7 |
|||
| RW Aur | 1.1 |
0.4 |
1.4 |
0.7 |
1.3 |
0.9 |
| NTTS 155203-2338 | 1.7 |
0.7 |
1.85 |
0.9 |
? | ? |
| NTTS 155219-2314 | 0.16 |
0.09 |
0.375 |
<0.15 | 0.2 |
0.1 |
| NTTS 160735-1857 | 0.20 |
0.16 |
0.35 |
0.3 |
0.4 |
0.3 |
| NTTS 160946-1851 | 1.7 |
0.6 |
1.9 |
0.75 |
? | ? |
| WX Cha | 0.5 |
0.1 |
0.75 |
0.15 |
1.0 |
0.35 |
| VW Cha AB | 0.6 |
0.4 |
1.05 |
0.7 |
? | ? |
| HM Anon | 1.3 |
0.7 |
1.35 |
0.85 |
1.2 |
0.9 |
| LkH |
1.75 |
0.3 |
1.9 |
0.45 |
? | ? |
| IK Lup | 0.35 |
0.14 |
0.5 |
0.2 |
0.9 |
0.3 |
| HT Lup | 1.3 |
0.2 |
1.9 |
0.23 |
? | ? |
| HN Lup | 0.25 |
0.25 |
0.4 |
0.4 |
0.7 |
0.6 |
| HBC 604 | 0.11 |
0.05 |
0.23 |
<0.15 | ? | ? |
| HO Lup | 0.35 |
0.14 |
0.5 |
0.2 |
0.7 |
0.3 |
| System | DM98 | Swenson | Baraffe | d[arcsec] |
| HBC351 | 0.29 |
0.40 |
0.40 |
0.61 |
| HBC352/353 | 0.90 |
8.6 |
||
| HBC358Aa | 1.0 |
1.0 |
1.0 |
0.15 |
| HBC360/361 | 1.0 |
1.0 |
1.0 |
7.2 |
| FOTau | 0.40 |
0.70 |
0.50 |
0.165 |
| DDTau | 0.80 |
0.93 |
0.86 |
0.57 |
| CZTau | 0.10 |
<0.21 | 0.17 |
0.33 |
| FQTau | 1.00 |
1.0 |
1.0 |
0.79 |
| V819Tau | 0.09 |
<0.21 | 0.07 |
10.5 |
| LkCa7 | 0.40 |
0.53 |
0.55 |
1.05 |
| FSTau | 0.24 |
0.20 |
0.29 |
0.265 |
| FVTau | 0.54 |
0.61 |
0.77 |
0.72 |
| UXTauAC | 0.13 |
0.18 |
0.31 |
2.7 |
| UXTauBb | 0.80 |
0.80 |
0.83 |
0.138 |
| FXTau | 1.00 |
1.00 |
1.00 |
0.91 |
| DKTau | 0.30 |
0.44 |
0.36 |
2.8 |
| LkH |
0.75 |
0.38 |
0.75 |
0.30 |
| HKTau | 0.08 |
<0.25 | 0.11 |
2.4 |
| V710Tau | 0.88 |
0.82 |
0.77 |
3.24 |
| HKTauG2 | 1.00 |
0.75 |
0.78 |
0.18 |
| GGTauAa | 0.50 |
0.62 |
0.56 |
0.26 |
| GGTauBb | 0.44 |
0.20 |
1.4 |
|
| UZTau w | 0.90 |
0.78 |
0.86 |
0.34 |
| GHTau | 1.00 |
1.00 |
0.83 |
0.35 |
| Elias12 | 0.75 |
0.50 |
0.75 |
0.41 |
| ISTau | 0.36 |
0.67 |
0.78 |
0.21 |
| GKTau / GITau | 0.73 |
0.79 |
0.83 |
12.2 |
| HNTau | 0.50 |
0.60 |
0.57 |
3.1 |
| CoKuTau3 | 0.40 |
0.47 |
0.50 |
2.04 |
| HBC412 | 0.86 |
0.83 |
0.91 |
0.70 |
| Haro6-28 | 0.20 |
<0.27 | 0.24 |
0.66 |
| VYTau | 0.42 |
0.41 |
0.50 |
0.66 |
| IWTau | 0.86 |
0.89 |
0.89 |
0.27 |
| LkH |
0.45 |
0.64 |
0.50 |
0.23 |
| LkH |
0.44 |
0.40 |
0.58 |
0.30 |
| LkH |
0.86 |
0.84 |
0.80 |
0.33 |
| Haro6-37Aa | 0.13 |
0.19 |
0.27 |
0.331 |
| RWAur | 0.36 |
0.50 |
0.69 |
1.50 |
| NTTS155203-2338 | 0.41 |
0.49 |
0.758 |
|
| NTTS155219-2314 | 0.56 |
<0.40 | 0.50 |
1.485 |
| NTTS160735-1857 | 0.80 |
0.86 |
0.75 |
0.299 |
| NTTS160946-1851 | 0.35 |
0.39 |
0.203 |
|
| WXCha | 0.20 |
0.20 |
0.35 |
0.79 |
| VWChaAB | 0.67 |
0.67 |
0.66 |
|
| HMAnon | 0.54 |
0.63 |
0.75 |
0.27 |
| LkH |
0.17 |
0.24 |
5.3 |
|
| IKLup | 0.40 |
0.40 |
0.33 |
6.5 |
| HTLup | 0.15 |
0.12 |
2.8 |
|
| HNLup | 1.00 |
1.00 |
0.86 |
0.24 |
| HBC604 | 0.45 |
<0.65 | 1.99 |
|
| HOLup | 0.40 |
0.40 |
0.43 |
1.49 |
In six of our systems the mass determination from the D'Antona & Mazzitelli
(1998) tracks leads to companion masses
that are below the hydrogen burning mass limit of
![]() (see Oppenheimer et al. 2000 and
references therein). This is the case for CZ Tau B,
V 819 Tau B, HK Tau/c, GG Tau b,
Haro 6-28 B and HBC 604 B. With respect to the
Swenson et al. (1994) model that does not cover the
region close above and below the hydrogen burning mass limit all six
mentioned objects have masses below
(see Oppenheimer et al. 2000 and
references therein). This is the case for CZ Tau B,
V 819 Tau B, HK Tau/c, GG Tau b,
Haro 6-28 B and HBC 604 B. With respect to the
Swenson et al. (1994) model that does not cover the
region close above and below the hydrogen burning mass limit all six
mentioned objects have masses below
![]() .
The Baraffe
et al. (1998) tracks yield masses of
.
The Baraffe
et al. (1998) tracks yield masses of
![]() for V819Tau B, HKTau/c, GGTau B
and Haro6-28 B. The primary of HBC604 could not
be reliably compared to the Baraffe et al. (1998) tracks,
so we cannot give a Baraffe mass for the secondary.
for V819Tau B, HKTau/c, GGTau B
and Haro6-28 B. The primary of HBC604 could not
be reliably compared to the Baraffe et al. (1998) tracks,
so we cannot give a Baraffe mass for the secondary.
We emphasize that a definitive classification of a companion as a substellar object is not possible on the basis of our data and requires spatially resolved spectra of the components. It has already been mentioned (Sect. 3.2) that based on NIR colors we cannot distinguish between stars with very late spectral types and deeply embedded objects. HK Tau/c definitely belongs to the latter class of objects, because it has an edge-on seen disk detected by Stapelfeldt et al. (1998). For two of the other mentioned objects, namely the companions of CZTau and Haro6-28, we have detected unusually large NIR color excesses by placing them into a color-color diagram (see Fig. 1) which makes them good candidates for heavily extincted objects. V819Tau B may be a chance projected background star as has been mentioned in Sect. 4.4. The apparent low luminosity would in this case be the result of underestimating its distance.
Substellar companions to young stars probably do exist. GG Tau b has
been placed into the HRD based on spatially resolved spectroscopy by White
et al. (1999). They derived a mass of
![]() which is in line with our mass estimate of
which is in line with our mass estimate of
![]() for this
object derived from the D'Antona & Mazzitelli (1998) and the
Baraffe et al. (1998) models. Meyer et al. (1997)
have estimated a mass of
for this
object derived from the D'Antona & Mazzitelli (1998) and the
Baraffe et al. (1998) models. Meyer et al. (1997)
have estimated a mass of ![]()
![]() for the companion of
DI Tau that has been detected by Ghez et al. (1993).
This system is not within our object list because its projected separation of
0
for the companion of
DI Tau that has been detected by Ghez et al. (1993).
This system is not within our object list because its projected separation of
0
![]() 12 is below the diffraction limit of a 3.5 m telescope in the K-band.
There are no strong substellar companion candidates among the
components covered by our study.
12 is below the diffraction limit of a 3.5 m telescope in the K-band.
There are no strong substellar companion candidates among the
components covered by our study.
Among T Tauri stars in the Taurus-Auriga association there is a significant overabundance of binaries compared to main sequence stars in the solar neighbourhood (see Köhler & Leinert 1998 and references therein). If the binary excess detected with lunar occultation observations, speckle interferometry and direct imaging is extra-polated towards the whole range of projected separations one comes to the conclusion that nearly all stars in this SFR belong to multiple systems. It is therefore interesting to derive the components' mass function for the Taurus-Auriga association, because this should be a better representation of the mass function in this SFR than the systems' mass function - including unresolved binaries - that has been given by Kenyon & Hartmann (1995).
The mass functions for the components of young multiple systems in
Taurus-Auriga for which we have given masses in Table 2 are
plotted in Fig. 6 for the three sets of PMS tracks used.
We have now to ask to what degree these mass functions can be representative
of the whole binary population in this SFR. Our sample is taken from
Leinert et al. (1993). It is restricted to systems with projected
separations from 0
![]() 13 to
13
13 to
13
![]() and apparent magnitudes
and apparent magnitudes
![]() .
For the first restriction one has to assume that the components' masses
are not a function of their separation. The latter restriction means that we
can detect all primaries with
.
For the first restriction one has to assume that the components' masses
are not a function of their separation. The latter restriction means that we
can detect all primaries with
![]() (for a flux ratio
I2/I1 = 1) while the secondaries are complete
to a magnitude of K = 12 mag. After transforming the theoretical evolutionary
model from the HRD to a diagram where the luminosity is indicated by the
K-band magnitude (see Sect. 4.1) one can determine which mass
range is completely above the K = 10.25 mag brightness limit
for ages less than
(for a flux ratio
I2/I1 = 1) while the secondaries are complete
to a magnitude of K = 12 mag. After transforming the theoretical evolutionary
model from the HRD to a diagram where the luminosity is indicated by the
K-band magnitude (see Sect. 4.1) one can determine which mass
range is completely above the K = 10.25 mag brightness limit
for ages less than
![]() .
This leads to completeness limits of
.
This leads to completeness limits of
![]() (D'Antona & Mazzitelli 1998 tracks),
(D'Antona & Mazzitelli 1998 tracks),
![]() (Baraffe
et al. 1998 tracks) and
(Baraffe
et al. 1998 tracks) and
![]() (Swenson et al.
1994 tracks). The first incomplete bins
are indicated with arrows in Fig. 6. It is thus not
possible based on our data to answer the question if and where the
components' mass function has a maximum and how it continues into the
substellar regime. For this purpose deep imaging surveys for low luminosity
young stars and follow up high angular resolution observations will be
necessary. Concerning mass ratios, our sample is much less subject
to incompleteness.
(Swenson et al.
1994 tracks). The first incomplete bins
are indicated with arrows in Fig. 6. It is thus not
possible based on our data to answer the question if and where the
components' mass function has a maximum and how it continues into the
substellar regime. For this purpose deep imaging surveys for low luminosity
young stars and follow up high angular resolution observations will be
necessary. Concerning mass ratios, our sample is much less subject
to incompleteness.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms9681.fig6.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/Timg80.gif) |
Figure 6:
Mass function for the components of
young binary systems in Taurus-Auriga from Table 2
derived using the PMS evolutionary models from D'Antona & Mazzitelli
(1998), Swenson et al. (1994) and Baraffe et al.
(1998). The bins indicated with arrows and all bins left of
them only represent lower limits, because of the incompleteness of our
sample (see Sect. 6.2). The objects represented by the
shaded bin in the upper right panel can also have lower masses than
indicated here, because the Swenson et al. (1994) model
does only cover masses with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms9681.fig7.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/Timg81.gif) |
Figure 7: Distribution of mass ratios for the young binary systems from Table 2 derived with respect to three sets of PMS evolutionary models. The open histograms represent all 51 binaries from that table, the shaded histograms show a restricted sample (45 binaries) for which all companions can be detected with the applied observational techniques (see Sect. 6.3). In the lower right panel also the distribution of K band flux ratios is given. |
| Open with DEXTER | |
The distribution of mass ratios of binary components and their dependence on
other parameters are of special interest, because they can be compared
to predictions of theoretical models for multiple star formation
(see Sect. 7). To place reliable constraints on this quantity
one has to define a complete sample that is unaffected by
biases caused by the observational techniques. Köhler et al.
(2000) have come to the conclusion that using speckle
interferometry at a 3.5 m-telescope in the K-band![]() will detect any companion
with a projected separation above 0
will detect any companion
with a projected separation above 0
![]() 13 and a magnitude difference
to the primary of
13 and a magnitude difference
to the primary of
![]() .
The first condition
is fulfilled for all components in Table 2. By applying
the second restriction and obtaining a homogeneous data set we exclude six
systems from the following discussion, namely V819Tau,
UXTauAC, HKTau, HNTau, WXCha
and LkH
.
The first condition
is fulfilled for all components in Table 2. By applying
the second restriction and obtaining a homogeneous data set we exclude six
systems from the following discussion, namely V819Tau,
UXTauAC, HKTau, HNTau, WXCha
and LkH![]() 332-17. They have very faint companions that have
been detected using direct imaging.
332-17. They have very faint companions that have
been detected using direct imaging.
The mass ratios derived from three sets of PMS tracks are shown
in Table 3. For triple and quadruple systems we have only
given them for close pairs in hierarchical systems.
The errors indicated in Table 3 are
formally derived from the mass errors given in Table 2.
This is a conservative estimate, since distance errors affect the components
of a binary in a similar way and therefore do not fully influence the
mass ratio. To take the uncertainties that are within the PMS models into account
we compare the mass ratio distributions derived from the
D'Antona & Mazzitelli (1998), Swenson et al. (1994)
and Baraffe et al. (1998) models (Fig. 7).
The shaded histograms show the restricted sample, the open histograms
represent all pairs from Table 2. The distributions
derived from the D'Antona & Mazzitelli (1998) and
Swenson et al. (1994) tracks are flat for
![]() within the uncertainties. The apparent deficit in the first bin is
probably due to incomplete detections in this regime. Actually we have
found more pairs with mass ratios below 0.2.
The Baraffe et al. (1998)
model suggests a rising of the mass ratio distribution towards unity,
but this may also be caused by incompletes of the sample at low mass
ratios and is not very significant. The distribution for
within the uncertainties. The apparent deficit in the first bin is
probably due to incomplete detections in this regime. Actually we have
found more pairs with mass ratios below 0.2.
The Baraffe et al. (1998)
model suggests a rising of the mass ratio distribution towards unity,
but this may also be caused by incompletes of the sample at low mass
ratios and is not very significant. The distribution for
![]() is still compatible with being flat on a 57%
confidence level. In discussing the mass ratio distributions given
in Fig. 7 one has to take into account
that the mean error of the individual mass ratios (Table 3)
is about one binsize. This effect will cause a flattening of any
given distribution. We will conclude this discussion with the statement
that our data does not support the preference of any mass ratios. On the
other hand we admit that it would be premature to say that the mass
ratio distribution is definetely flat taking into account the large
differences between the distributions shown in Fig. 7.
is still compatible with being flat on a 57%
confidence level. In discussing the mass ratio distributions given
in Fig. 7 one has to take into account
that the mean error of the individual mass ratios (Table 3)
is about one binsize. This effect will cause a flattening of any
given distribution. We will conclude this discussion with the statement
that our data does not support the preference of any mass ratios. On the
other hand we admit that it would be premature to say that the mass
ratio distribution is definetely flat taking into account the large
differences between the distributions shown in Fig. 7.
A flat distribution of mass ratios is supported by the distribution of K-band
flux ratios (Fig. 7, lower right panel). For low-mass PMS
stars there is a K-band mass-luminosity relation of about ![]() (e.g.
Simon et al. 1992), so the distribution of this quantity should in
a good approximation resemble that of the mass ratios. There is again no
clustering towards
M2/M1 = 1. If also the systems with
(e.g.
Simon et al. 1992), so the distribution of this quantity should in
a good approximation resemble that of the mass ratios. There is again no
clustering towards
M2/M1 = 1. If also the systems with
![]() ,
i.e.
F2(K)/F1(K) < 0.1 are included there seems to appear even
a slight overabundance of low mass ratios.
,
i.e.
F2(K)/F1(K) < 0.1 are included there seems to appear even
a slight overabundance of low mass ratios.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms9681.fig8.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/Timg85.gif) |
Figure 8: Distribution of mass ratios as a function of the projected separation for the three sets of PMS models used in this paper. |
| Open with DEXTER | |
|
|
|
|
| D'Antona & Mazzitelli (1998) | ||
| M2/M1 > 0.5 | 14 |
9 |
|
|
12 |
10 |
| Swenson et al. (1994) | ||
| M2/M1 > 0.5 | 16 |
9 |
|
|
10 |
8 |
| Baraffe et al. (1998) | ||
| M2/M1 > 0.5 | 17 |
8 |
|
|
8 |
6 |
First, we want to examine a possible
correlation of mass ratios and the components'
separations. For this purpose it is useful to convert the measured
projected angular separations to physical separations. This allows us
to discuss binaries in SFRs with different distances
(see Table 1) simultaneously.
Moreover this yields a comparison between mass ratios and characteristic
length scales like the radii of circumstellar disks.
Applying this conversion one has to consider that values for the projected
distance obtained with "snap-shot'' observations can be very different
from the semimajor axis A. This cannot be corrected for individual systems.
Leinert et al. (1993) have however calculated that the
relationship between the projected separation
![]() and the
semimajor axis A is on average
and the
semimajor axis A is on average
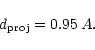 |
(2) |
With respect to the D'Antona & Mazzitelli (1998) and the
Swenson et al.(1994) models, in both regions the numbers of
systems with low and high mass ratios are comparable within the uncertainties.
The result obtained from the Baraffe et al. (1998) model
suggests a slight preference of larger mass ratios at lower separations,
but this is significant only at the 1![]() level.
level.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms9681.fig9.eps}
\end{figure}](/articles/aa/full/2001/36/aa9681/Timg93.gif) |
Figure 9: Distribution of mass ratios as function of the primary mass. |
| Open with DEXTER | |
| D'Antona & Mazzitelli (1998) | ||
|
|
|
|
| M2/M1 > 0.5 | 15 |
8 |
|
|
11 |
11 |
| Swenson et al.(1994) | ||
|
|
|
|
| M2/M1 > 0.5 | 13 |
11 |
|
|
5 |
13 |
| Baraffe et al.(1998) | ||
|
|
|
|
| M2/M1 > 0.5 | 10 |
15 |
|
|
6 |
8 |
Finally, we ask for a correlation between the mass ratio and the primary mass. The result is shown in Fig. 9 and Table 5. The threshold between "low'' and "high'' primary masses is arbitrarily chosen to have a comparable number of objects in both groups for each theoretical PMS model considered. With regard to the Baraffe et al. (1998) model the behaviour of both groups is the same. The D'Antona & Mazzitelli (1998) and Swenson et al. (1994) models suggest a preference of higher mass ratios for lower primary masses. The latter result has also been mentioned by Leinert et al. (1993) on the basis of K band magnitudes and flux ratios.
We conclude that correlations between mass ratio and other binary parameters are weak if they exist at all.
It is now widely believed that fragmentation during protostellar collapse is the major process for forming multiple stars in low-density SFRs as discussed here (e.g. Clarke et al. 2000). Our results generally are in line with this assumption:
For this purpose Bate (1997, 1998) and Bate & Bonnell (1997) have simulated the behaviour of a "binary'' formed out of two point masses that are situated in a cavity within a surrounding gas sphere. The mass ratio of the binary and the angular momentum of the infalling material are variable initial conditions. The result of these simulations is that in the course of the accretion process the system's mass ratio increases and approaches unity if the total cloud mass is accreted. Mass ratios close to unity should be more probable in close systems than for wide pairs.
This is not in agreement with our result (Sect. 6.3) that there is no significant preference of mass ratios close to unity and that the mass ratio is probably independent of the components' separation. So it seems that the initial conditions used by Bate & Bonnell are somehow unrealistic and that the "final'' stellar masses are more dependent on the fragment masses than on the following accretion processes. One explanation for this could be that in the course of protobinary evolution most of the initial mass is condensed into fragments, before accretion becomes important. Another idea is that there is some process that halts accretion before a large amount of the remaining cloud mass is accreted onto the fragments. In any case, our knowledge about this issue is preliminary and additional theoretical and observational effort is necessary to decide what physical processes determine stellar masses.
Multiplicity surveys by Leinert et al. (1993) and Ghez et al. (1993) led to the surprising result that there is a significant overabundance of binaries in the Taurus-Auriga SFR compared to main sequence stars in the solar neighbourhood. This result was further proved by the follow-up studies done by Simon et al. (1995) and Köhler & Leinert (1998). Although this paper is not directly concerned with binary statistics, we can draw some conclusions that further support the idea that this binary excess is real and not a result of observational biases.
If one compares the binary frequency among young and evolved stars one has to take into account that due to evolutionary effects companions can be relatively bright in their PMS phase, but invisible on the main sequence stage. This is particularly the case for substellar companions. One has further to consider that the multiplicity surveys were done at infrared wavelengths in SFRs, but in the optical range for main sequence stars. So there might be a bias that supports the detection of very red "infrared companions'' (IRCs, see Sect. 3.2) in the vicinity of PMS stars. Another problem is that the surveys in Taurus-Auriga and the solar neighbourhood could be not directly comparable if they were sensitive to a different range of mass ratios and thus stellar masses.
If the presence of substellar companions or IRCs in the vicinity of T Tauri
stars in Taurus-Auriga were a common phenomenon, this could at least partially
explain the observed binary excess in this SFR. Our results presented in
Sects. 3.2 and 6.1 show that this is not the case:
Köhler & Leinert (1998) have found that after applying
a statistical correction for chance projected background stars there
are
![]() companions per 100 primaries (including single stars)
in Taurus-Auriga. We have denoted only 5 out of 40 companions (for which we
have given masses in Table 2) as candidates
for substellar objects based on masses derived from the D'Antona &
Mazzitelli (1998) PMS evolutionary tracks (Sect. 6.1).
With respect to the Baraffe et al. (1998) model this number
is even lower. If we take the mentioned 5 out of 40 companions as an estimate
for the real number of brown dwarf companions in Taurus-Auriga
and subtract this from the companion frequency given by Köhler &
Leinert (1998) this value diminishes to
companions per 100 primaries (including single stars)
in Taurus-Auriga. We have denoted only 5 out of 40 companions (for which we
have given masses in Table 2) as candidates
for substellar objects based on masses derived from the D'Antona &
Mazzitelli (1998) PMS evolutionary tracks (Sect. 6.1).
With respect to the Baraffe et al. (1998) model this number
is even lower. If we take the mentioned 5 out of 40 companions as an estimate
for the real number of brown dwarf companions in Taurus-Auriga
and subtract this from the companion frequency given by Köhler &
Leinert (1998) this value diminishes to
![]() .
This is still far above the value of
.
This is still far above the value of
![]() that was given by
Duquennoy & Mayor (1991) for G-dwarfs in the solar
neighbourhood. Furthermore we have found that only 3 out of 51 companions in Taurus-Auriga
are detectable in the H-band and at longer wavelengths, but were missed
at
that was given by
Duquennoy & Mayor (1991) for G-dwarfs in the solar
neighbourhood. Furthermore we have found that only 3 out of 51 companions in Taurus-Auriga
are detectable in the H-band and at longer wavelengths, but were missed
at
![]() ,
so IRCs are probably not a frequent phenomenon.
The binary frequency does not have to be corrected for IRCs, because their
successors in the main sequence phase will be "normal'' stellar companions
(see Koresko et al. 1997 for estimates of IRCs' masses).
,
so IRCs are probably not a frequent phenomenon.
The binary frequency does not have to be corrected for IRCs, because their
successors in the main sequence phase will be "normal'' stellar companions
(see Koresko et al. 1997 for estimates of IRCs' masses).
Duquennoy & Mayor (1991) have claimed that their sample
is complete for mass ratios
![]() .
It has already been mentioned
by Köhler & Leinert (1998, Sect. 5.2) that the
completeness limit of the binary surveys in Taurus-Auriga is in any case
not lower, the actual value dependent on the mass-luminosity relation used.
We can further prove this result, because there are only 2 out of 51 systems
with mass ratios less than 0.1 with respect to the D'Antona & Mazzitelli
(1998) PMS model and 1 out of 50 considering the Baraffe et al.
(1998) tracks (Table 3).
We conclude that the observed binary excess in Taurus-Auriga compared
to nearby main sequence stars is neither the result of a higher sensitivity
in mass ratio nor a consequence of a large frequency of substellar or
infrared companions. The strange overabundance of binaries in
Taurus-Auriga remains a fact also after this more detailed analysis of the
systems found by Leinert et al. (1993).
.
It has already been mentioned
by Köhler & Leinert (1998, Sect. 5.2) that the
completeness limit of the binary surveys in Taurus-Auriga is in any case
not lower, the actual value dependent on the mass-luminosity relation used.
We can further prove this result, because there are only 2 out of 51 systems
with mass ratios less than 0.1 with respect to the D'Antona & Mazzitelli
(1998) PMS model and 1 out of 50 considering the Baraffe et al.
(1998) tracks (Table 3).
We conclude that the observed binary excess in Taurus-Auriga compared
to nearby main sequence stars is neither the result of a higher sensitivity
in mass ratio nor a consequence of a large frequency of substellar or
infrared companions. The strange overabundance of binaries in
Taurus-Auriga remains a fact also after this more detailed analysis of the
systems found by Leinert et al. (1993).
From speckle interferometry and direct imaging we have derived resolved JHK photometry for the individual components of T Tauri binary systems in nearby star forming regions. These measurements are combined with other data taken from literature (resolved JHK photometry from other authors, system magnitudes and spectral types, extinction coefficients) to study properties of the components in young binary systems. The main results are:
Acknowledgements
We are grateful to Andreas Eckart and Klaus Bickert for their support in observing with the SHARP camera. We also thank the staff at ESO La Silla and Calar Alto for their support during several observing runs. The authors appreciate fruitful discussions with Michael Meyer, Monika Petr, Matthew Bate and Coryn Bailer-Jones, and they thank an anonymous referee for pointed and productive comments. This research has made use of the SIMBAD database, operated at CDS, France.
The spatially resolved observations of T Tauri binary systems obtained by the authors are listed in Table A.1. Column 1 gives the most common name of the object, Cols. 2 and 3 the wavelength band and the date of observation, Col. 4 the brightness ratio (secondary/primary, usually but not always <1), Cols. 5 through 7 the magnitude of system, primary and secondary components in the respective wavelength band.
Table A.2 contains the adopted near-infrared magnitudes of the components of the young binary systems which compose our sample. The values given here are the mean of all spatially resolved photometric observations, i.e. our data from Table A.1 and measurements published by Chelli et al. (1995), Duchêne (1999a), Ghez et al. (1993, 1997a, 1997b), Haas et al. (1990), Hartigan et al. (1994), Köhler et al. (2000), Moneti & Zinnecker(1991), Richichi et al. (1999), Roddier et al. (1996) and Simon et al. (1992). The values for visual extinction AV and the spectral type given with the primaries, belong to the systems (see Sect. 2.1 for references). The numbers in the last column denote the star forming region: Taurus-Auriga (1), Upper Scorpius (2), ChamaeleonI (3) and Lupus (4).
These two tables are available in electronic form at the CDS only. To demonstrate their contents, very much shortened versions, each containing only a typical one of the first few entries, are given below.
| System | Filter | Date | I2/I1 |
|
|
|
| HBC 351 | J | 30Sep1993 | 0.165 |
9.92 |
10.09 |
12.04 |
| H | 8.Jan1993 | 0.190 |
9.30 |
9.49 |
11.29 |
|
| K | 16.Feb1992 | 0.22 |
9.15 | 9.37 |
11.01 |
| System | Component | J | H | K | AV | Spectral type | SFR |
| LkCa3 | A | 8.99 |
8.34 |
8.11 |
0.42 | M1 | 1 |
| B | 9.51 |
8.68 |
8.48 |