

Up: Line ratios for helium-like plasmas
3 Schematic model
We illustrate the relevant processes in the formation of the resonance, intercombination, and
forbidden lines with a simplified level scheme (cf. Mewe & Schrijver 1978a) consisting of the
following levels denoted by short labels: g: ground level 1
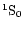 ;
;
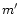 :
upper metastable
level 21S0 of the two-photon transition; 1
:
upper metastable
level 21S0 of the two-photon transition; 1 :
upper level 21P1 of the resonance line; m:
upper metastable level 23S1 of the forbidden (f) line; pk (k=1,2,3: levels
2
:
upper level 21P1 of the resonance line; m:
upper metastable level 23S1 of the forbidden (f) line; pk (k=1,2,3: levels
2
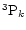 (2
(2
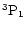 is the upper level of the by far the strongest component (y) of the
intercombination line i, and 2
is the upper level of the by far the strongest component (y) of the
intercombination line i, and 2
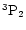 is the upper level of the weaker component (x)); c: continuum
level which lumps together all higher levels to represent the cascades from excitation and recombination
processes.
is the upper level of the weaker component (x)); c: continuum
level which lumps together all higher levels to represent the cascades from excitation and recombination
processes.
The electron collisional rate coefficient (in cm3 s-1) for transition 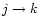 is written as:
is written as:
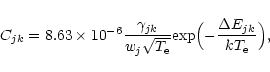 |
(3) |
where
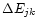 is the excitation energy,
is the excitation energy, 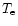 is the electron temperature in K,
is the electron temperature in K,
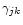 the
collision strength averaged over a Maxwellian electron energy distribution, and wj the statistical weight of
the initial level j.
the
collision strength averaged over a Maxwellian electron energy distribution, and wj the statistical weight of
the initial level j.
The total rate coefficients for the formation of the forbidden (f or z notation)
and intercombination (i or x+y)
line can be written as (e.g., Mewe & Schrijver 1978a, Eqs. (18-30)):
If = ![$\displaystyle BR_{mg} \Bigl[ C_{gm} + \sum_{k=0}^2 BR_{p_km} C_{gp_k}\Bigr],$](/articles/aa/full/2001/36/aa1442/img34.gif) |
(4) |
Ii = ![$\displaystyle \sum_{k=1}^2 BR_{p_kg} \Bigl[ C_{gp_k} + BR_{mp_k} C_{gm} \Bigr],$](/articles/aa/full/2001/36/aa1442/img35.gif) |
(5) |
with the various branching ratios:
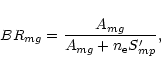 |
(6) |
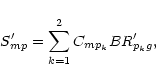 |
(7) |
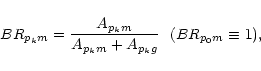 |
(8) |
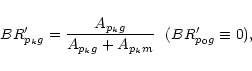 |
(9) |
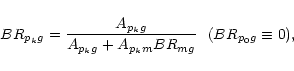 |
(10) |
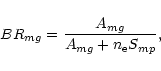 |
(11) |
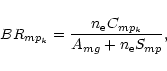 |
(12) |
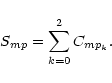 |
(13) |
Analogously, we can derive
the total rate coefficients for the formation of the resonance (r or w) line or two-photon radiation
(2ph) by substituting
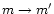 ,
,
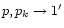 and performing no summation:
and performing no summation:
![\begin{displaymath}%
I_r = BR_{1^{\prime}g} \Bigl[ C_{g1^{\prime}} + BR_{m^{\prime}1^{\prime}} C_{gm^{\prime}} \Bigr],
\end{displaymath}](/articles/aa/full/2001/36/aa1442/img46.gif) |
(14) |
![\begin{displaymath}%
I_{2ph} = BR_{m^{\prime}g} \Bigl[ C_{gm^{\prime}} + BR_{1^{\prime}m} C_{g1^{\prime}}\Bigr],
\end{displaymath}](/articles/aa/full/2001/36/aa1442/img47.gif) |
(15) |
and changing all BR's etc. appropriately.
We note that the collision coefficients Cjk include also the n > 2 cascades.
The radiative transition probabilities are tabulated in the Table 2 of PaperI and the
effective collision strengths 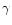 in their Tables 9-13 and in their Fig. 4.
We assume in this section that the electron density is so low that the collision de-excitation rate
in their Tables 9-13 and in their Fig. 4.
We assume in this section that the electron density is so low that the collision de-excitation rate
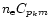 can be
neglected with respect to the spontaneous radiative rate Apkm (e.g., for C V
can be
neglected with respect to the spontaneous radiative rate Apkm (e.g., for C V
 for
for
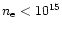 cm-3).
This can be easily taken into account by the substitution
cm-3).
This can be easily taken into account by the substitution
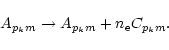 |
(16) |
Further, all collision processes that couple the singlet and triplet system are neglected in this schematic model.
It turns out that at high density the coupling
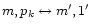 cannot be
neglected.
cannot be
neglected.
In the full calculations used in this work (see Sect. 5),
the coupling between the singlet and triplet system has been taken into account,
as well as the collisional de-excitation.
If we take also into account the contribution from radiative and dielectronic recombinations of the
hydrogen-like ion we substitute
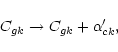 |
(17) |
where k = m or k = pk, respectively, and
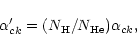 |
(18) |
where
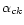 is the total radiative and dielectronic recombination rate coefficient including cascades
and
is the total radiative and dielectronic recombination rate coefficient including cascades
and
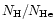 is the abundance ratio of hydrogen-like to helium-like ions (e.g. taken from Arnaud & Rothenflug
1985; Mazzotta et al. 1998). The recombination coefficients are given in Tables 3-8 in Paper I.
However, for a collision-dominated plasma, the recombination generally gives
only a minor effect (i.e. far less than few percents),
but are nevertheless introduced in the full calculations in Sect. 5.
is the abundance ratio of hydrogen-like to helium-like ions (e.g. taken from Arnaud & Rothenflug
1985; Mazzotta et al. 1998). The recombination coefficients are given in Tables 3-8 in Paper I.
However, for a collision-dominated plasma, the recombination generally gives
only a minor effect (i.e. far less than few percents),
but are nevertheless introduced in the full calculations in Sect. 5.
Mewe & Schrijver (1978a) took also into account the effect
of a stellar radiation field (also called photo-excitation) with effective radiation
temperature
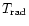 .
This can be done by substituting in the above equations:
.
This can be done by substituting in the above equations:
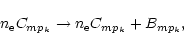 |
(19) |
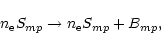 |
(20) |
where
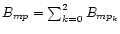 and
and
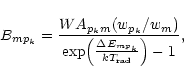 |
(21) |
is the rate (in s-1) of absorption
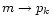 and W is the dilution factor of the radiation
field (as a special case we take
and W is the dilution factor of the radiation
field (as a special case we take
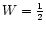 close to the stellar surface).
We have checked that the radiation field is so low
that the induced emission rate
close to the stellar surface).
We have checked that the radiation field is so low
that the induced emission rate
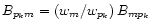 is negligible respect to the
spontaneous radiative rate Apkm.
Nevertheless, in the full calculations used in this work (see Sect. 5),
we have taken into account induced emission as well as photo-excitation.
is negligible respect to the
spontaneous radiative rate Apkm.
Nevertheless, in the full calculations used in this work (see Sect. 5),
we have taken into account induced emission as well as photo-excitation.
Mewe & Schrijver (1978a) considered also inner-shell ionization of the Lithium-like ion which can give
an important contribution to the forbidden line in a transient plasma (Mewe & Schrijver 1978b) such as a supernova remnant.
However, in the present calculations we neglect this because we consider plasmas in ionization equilibrium.
Finally, Mewe & Schrijver (1978a, 1978c) have considered
also excitation 23S 23P by proton collisions
using approximations of Coulomb-Born results from Blaha (1971).
In a new version (SPEX90) of our spectral code SPEX (Kaastra et al. 1996), which contains for the
H- and He-like ions an improvement of the known MEKAL code (Mewe et al. 1985, 1995a), proton collisions are
taken into account based on Blaha's results. Test calculations with SPEX90 show that for an equilibrium plasma
in all practical cases proton excitation is negligible compared to electron excitation.
23P by proton collisions
using approximations of Coulomb-Born results from Blaha (1971).
In a new version (SPEX90) of our spectral code SPEX (Kaastra et al. 1996), which contains for the
H- and He-like ions an improvement of the known MEKAL code (Mewe et al. 1985, 1995a), proton collisions are
taken into account based on Blaha's results. Test calculations with SPEX90 show that for an equilibrium plasma
in all practical cases proton excitation is negligible compared to electron excitation.
In the case where
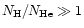 ,
recombination is dominant e.g., for photo-ionized plasmas it turns
out that the ratios
,
recombination is dominant e.g., for photo-ionized plasmas it turns
out that the ratios
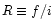 are for collisional and photo-ionized plasmas comparable in the
same density range (cf. also Mewe 1999), but the ratios
are for collisional and photo-ionized plasmas comparable in the
same density range (cf. also Mewe 1999), but the ratios
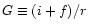 are very different,
e.g.,
are very different,
e.g., 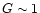 for a collisional plasma and a factor
for a collisional plasma and a factor
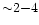 larger for a
photo-ionized plasma where the resonance line is relatively much weaker.
larger for a
photo-ionized plasma where the resonance line is relatively much weaker.


Up: Line ratios for helium-like plasmas
Copyright ESO 2001
![]() ;
;
![]() :
upper metastable
level 21S0 of the two-photon transition; 1
:
upper metastable
level 21S0 of the two-photon transition; 1![]() :
upper level 21P1 of the resonance line; m:
upper metastable level 23S1 of the forbidden (f) line; pk (k=1,2,3: levels
2
:
upper level 21P1 of the resonance line; m:
upper metastable level 23S1 of the forbidden (f) line; pk (k=1,2,3: levels
2
![]() (2
(2
![]() is the upper level of the by far the strongest component (y) of the
intercombination line i, and 2
is the upper level of the by far the strongest component (y) of the
intercombination line i, and 2
![]() is the upper level of the weaker component (x)); c: continuum
level which lumps together all higher levels to represent the cascades from excitation and recombination
processes.
is the upper level of the weaker component (x)); c: continuum
level which lumps together all higher levels to represent the cascades from excitation and recombination
processes.
![]() is written as:
is written as:
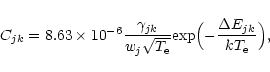
![$\displaystyle BR_{mg} \Bigl[ C_{gm} + \sum_{k=0}^2 BR_{p_km} C_{gp_k}\Bigr],$](/articles/aa/full/2001/36/aa1442/img34.gif)
![$\displaystyle \sum_{k=1}^2 BR_{p_kg} \Bigl[ C_{gp_k} + BR_{mp_k} C_{gm} \Bigr],$](/articles/aa/full/2001/36/aa1442/img35.gif)
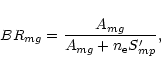
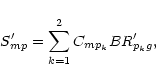
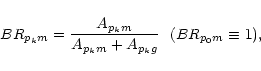
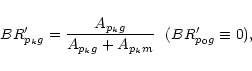
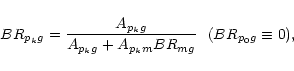
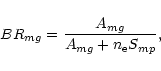
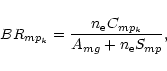
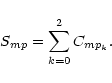
![\begin{displaymath}%
I_r = BR_{1^{\prime}g} \Bigl[ C_{g1^{\prime}} + BR_{m^{\prime}1^{\prime}} C_{gm^{\prime}} \Bigr],
\end{displaymath}](/articles/aa/full/2001/36/aa1442/img46.gif)
![\begin{displaymath}%
I_{2ph} = BR_{m^{\prime}g} \Bigl[ C_{gm^{\prime}} + BR_{1^{\prime}m} C_{g1^{\prime}}\Bigr],
\end{displaymath}](/articles/aa/full/2001/36/aa1442/img47.gif)
![]() in their Tables 9-13 and in their Fig. 4.
We assume in this section that the electron density is so low that the collision de-excitation rate
in their Tables 9-13 and in their Fig. 4.
We assume in this section that the electron density is so low that the collision de-excitation rate
![]() can be
neglected with respect to the spontaneous radiative rate Apkm (e.g., for C V
can be
neglected with respect to the spontaneous radiative rate Apkm (e.g., for C V
![]() for
for
![]() cm-3).
This can be easily taken into account by the substitution
cm-3).
This can be easily taken into account by the substitution
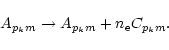
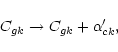
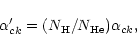
![]() .
This can be done by substituting in the above equations:
.
This can be done by substituting in the above equations:
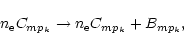
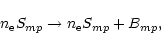
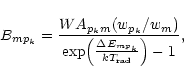
![]() 23P by proton collisions
using approximations of Coulomb-Born results from Blaha (1971).
In a new version (SPEX90) of our spectral code SPEX (Kaastra et al. 1996), which contains for the
H- and He-like ions an improvement of the known MEKAL code (Mewe et al. 1985, 1995a), proton collisions are
taken into account based on Blaha's results. Test calculations with SPEX90 show that for an equilibrium plasma
in all practical cases proton excitation is negligible compared to electron excitation.
23P by proton collisions
using approximations of Coulomb-Born results from Blaha (1971).
In a new version (SPEX90) of our spectral code SPEX (Kaastra et al. 1996), which contains for the
H- and He-like ions an improvement of the known MEKAL code (Mewe et al. 1985, 1995a), proton collisions are
taken into account based on Blaha's results. Test calculations with SPEX90 show that for an equilibrium plasma
in all practical cases proton excitation is negligible compared to electron excitation.
![]() ,
recombination is dominant e.g., for photo-ionized plasmas it turns
out that the ratios
,
recombination is dominant e.g., for photo-ionized plasmas it turns
out that the ratios
![]() are for collisional and photo-ionized plasmas comparable in the
same density range (cf. also Mewe 1999), but the ratios
are for collisional and photo-ionized plasmas comparable in the
same density range (cf. also Mewe 1999), but the ratios
![]() are very different,
e.g.,
are very different,
e.g., ![]() for a collisional plasma and a factor
for a collisional plasma and a factor
![]() larger for a
photo-ionized plasma where the resonance line is relatively much weaker.
larger for a
photo-ionized plasma where the resonance line is relatively much weaker.