to collision-dominated plasmas
A&A 376, 1113-1122 (2001)
DOI: 10.1051/0004-6361:20010959
D. Porquet1,2 - R. Mewe3 - J. Dubau4,5 - A. J. J. Raassen3,6 - J. S. Kaastra3
1 -
CEA/DSM/DAPNIA, Service d'Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
2 -
DAEC, Observatoire de Paris, Section Meudon, 92195 Meudon Cedex, France
3 -
Space Research Organization Netherlands (SRON),
Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
4 -
LSAI, U.M.R. 8624, CNRS, Université de Paris Sud, 91405 Orsay Cedex, France
5 -
DARC, Observatoire de Paris, Section Meudon, 92195 Meudon Cedex, France
6 -
Astronomical Institute "Anton Pannekoek", Kruislaan 403,
1098 SJ Amsterdam, The Netherlands
Received 4 May 2001 / Accepted 21 June 2001
Abstract
The line ratios R and G of the three main lines of He-like ions (triplet: resonance,
intercombination,
forbidden lines) are calculated for C V, N VI, O VII,
Ne IX, Mg XI,
and Si XIII. These ratios can be used to derive electron density
![]() and temperature
and temperature ![]() of hot late-type stellar coronae and O, B stars from high-resolution spectra obtained with
Chandra (LETGS, HETGS) and XMM-Newton (RGS). All excitation and radiative processes between the
levels and the effect of upper-level cascades from collisional electronic excitation
and from dielectronic and radiative
recombination have been considered. When possible the best experimental values for radiative transition
probabilities are used. For the higher-Z ions (i.e. Ne IX, Mg XI, Si XIII) possible
contributions from blended dielectronic satellite lines to each line of the triplets were included in the
calculations of the line ratios R and G for four specific spectral resolutions:
RGS, LETGS, HETGS-MEG, HETGS-HEG. The influence of an external stellar radiation field on the
coupling of the 23S (upper level of the forbidden line) and 23P levels (upper levels of the
intercombination lines) is taken into account.
This process is mainly important for the lower-Z ions
(i.e. C V, N VI, O VII) at moderate radiation temperature (
of hot late-type stellar coronae and O, B stars from high-resolution spectra obtained with
Chandra (LETGS, HETGS) and XMM-Newton (RGS). All excitation and radiative processes between the
levels and the effect of upper-level cascades from collisional electronic excitation
and from dielectronic and radiative
recombination have been considered. When possible the best experimental values for radiative transition
probabilities are used. For the higher-Z ions (i.e. Ne IX, Mg XI, Si XIII) possible
contributions from blended dielectronic satellite lines to each line of the triplets were included in the
calculations of the line ratios R and G for four specific spectral resolutions:
RGS, LETGS, HETGS-MEG, HETGS-HEG. The influence of an external stellar radiation field on the
coupling of the 23S (upper level of the forbidden line) and 23P levels (upper levels of the
intercombination lines) is taken into account.
This process is mainly important for the lower-Z ions
(i.e. C V, N VI, O VII) at moderate radiation temperature (
![]() ).
These improved calculations were done for plasmas in collisional ionization equilibrium,
but will be later extended to
photo-ionized plasmas and to transient ionization plasmas.
The values for R and G are given in extensive tables,
for a large range of parameters, which could be used
directly to compare to the observations.
).
These improved calculations were done for plasmas in collisional ionization equilibrium,
but will be later extended to
photo-ionized plasmas and to transient ionization plasmas.
The values for R and G are given in extensive tables,
for a large range of parameters, which could be used
directly to compare to the observations.
Key words: X-rays: stars - atomic processes - stars: coronae - stars: late-type - stars: activity - early-type stars: activity
The new generation of X-ray satellites (Chandra, XMM-Newton)
enables us to obtain unprecedented high
spectral resolution and high S/N spectra. The wavelength ranges of the RGS![]() (6-35 Å),
of the LETGS
(6-35 Å),
of the LETGS![]() (2-175 Å),
and of the HETGS
(2-175 Å),
and of the HETGS![]() (MEG range: 2.5-31 Å; HEG range: 1.2-15 Å)
contain the helium-like line "triplets'' from C V
(or N VI for the RGS, and for the HETGS-HEG) to Si XIII. The triplet consists of three close lines: the resonance
line, the intercombination line and the forbidden line. The helium-like triplets provide electron
density (
(MEG range: 2.5-31 Å; HEG range: 1.2-15 Å)
contain the helium-like line "triplets'' from C V
(or N VI for the RGS, and for the HETGS-HEG) to Si XIII. The triplet consists of three close lines: the resonance
line, the intercombination line and the forbidden line. The helium-like triplets provide electron
density (
![]() cm-3) as well as electron temperature (
cm-3) as well as electron temperature (
![]() MK) as first
shown by Gabriel & Jordan (1969). The line ratios of these He-like triplets enable also the
determination of the ionization processes (photo-ionization and/or collisional ionization) which prevail
in the plasma (Porquet & Dubau 2000; Liedahl 1999).
MK) as first
shown by Gabriel & Jordan (1969). The line ratios of these He-like triplets enable also the
determination of the ionization processes (photo-ionization and/or collisional ionization) which prevail
in the plasma (Porquet & Dubau 2000; Liedahl 1999).
The ratios of these lines are already widely used for collisional solar plasma diagnostics (e.g., Gabriel & Jordan 1969; Doyle 1980; Keenan et al. 1987; McKenzie & Landecker 1982).
Recently, also theoretical calculations for photo-ionized plasmas or "hybrid'' plasmas (photo-ionization plus collisional ionization) have been given by Porquet & Dubau (2000) (hereafter referred to as Paper I). Their calculations have been already applied to spectra of Seyfert galaxies (e.g. NGC5548, Kaastra et al. 2000; Mkn3, Sako et al. 2000; NGC4151, Ogle et al. 2000; NGC4051, Collinge et al. 2001, etc.).
We present here calculations of these ratios, from C V to Si XIII, which could be applied
directly for the first time to Chandra and XMM-Newton observations of extra-solar collisional
plasmas such as stellar coronae. These calculations have been done to apply an improved model to the density
analysis of the RGS, the LETGS and the HETGS spectra of various
late-type stars such as Capella, Procyon,
and ![]() Centauri (e.g., Audard et al. 2001; Ness et al. 2001a;
Mewe et al. 2001) and also to O stars such as
Centauri (e.g., Audard et al. 2001; Ness et al. 2001a;
Mewe et al. 2001) and also to O stars such as ![]() Puppis (Kahn et al. 2001).
Our model is to
be considered as an improvement of various previous calculations for solar plasmas such as done by e.g.,
Gabriel & Jordan (1969), Blumenthal et al. (1972), Mewe (1972),
Mewe & Schrijver (1978a, 1978b, 1978c),
Pradhan & Shull (1981), Mewe & Gronenschild (1981),
Mewe et al. (1985), and Pradhan (1982, 1985).
The calculations are partly based on recent work by Porquet & Dubau (2000).
Puppis (Kahn et al. 2001).
Our model is to
be considered as an improvement of various previous calculations for solar plasmas such as done by e.g.,
Gabriel & Jordan (1969), Blumenthal et al. (1972), Mewe (1972),
Mewe & Schrijver (1978a, 1978b, 1978c),
Pradhan & Shull (1981), Mewe & Gronenschild (1981),
Mewe et al. (1985), and Pradhan (1982, 1985).
The calculations are partly based on recent work by Porquet & Dubau (2000).
In the next three sections, we introduce the plasma diagnostics and the atomic processes and atomic data taken into
account in the calculations. In Sect. 5, we display the results for R and G calculated for four specific spectral resolutions (Full Width at Half Maximum: FWHM): RGS, LETGS, HETGS-MEG,
HETGS-HEG, over a broad range of physical parameters: ![]() ,
,
![]() ,
radiation temperature (
,
radiation temperature (
![]() ),
and radiation dilution factor (W).
),
and radiation dilution factor (W).
In the X-ray range, the three most intense lines of helium-like ions ("triplet'') are: the
resonance line (w, also called r: 1s21S0-1s2p1P1),
the intercombination lines (x+y, also called i: 1s21S0-1s2p3P2,1) and
the forbidden line (z, also called f: 1s2
![]() -1s2s
-1s2s
![]() ).
They correspond to transitions between the n=2 shell and the n=1 ground-state shell
(see Fig. 1).
The wavelengths in Å of each line from C V (Z=6) to Si XIII (Z=14)
are reported in Table 1.
).
They correspond to transitions between the n=2 shell and the n=1 ground-state shell
(see Fig. 1).
The wavelengths in Å of each line from C V (Z=6) to Si XIII (Z=14)
are reported in Table 1.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{MS1442f1.eps}}\par\end{figure}](/articles/aa/full/2001/36/aa1442/Timg15.gif) |
Figure 1: Simplified level scheme for helium-like ions. w (or r), x, y (or i), and z (or f): resonance, intercombination, and forbidden lines, respectively. Full upward arrows: collisional excitation transitions, broken arrows: radiative transitions (including photo-excitation from 23S1 to 23P0,1,2 levels, and 2-photon continuum from 21S0 to the ground level), and thick skew arrows: recombination (radiative and dielectronic) plus cascade processes. |
| Open with DEXTER | |
line |
label | C V | N VI | O VII | Ne IX | Mg XI | Si XIII |
| resonance | w (r) | 40.279 | 28.792 | 21.603 | 13.447 | 9.1681 | 6.6471 |
| inter- | x | 40.711 | 29.074 | 21.796 | 13.548 | 9.2267 | 6.6838 |
| combination | y | 40.714 | 29.076 | 21.799 | 13.551 | 9.2298 | 6.6869 |
| forbidden | z (f) | 41.464 | 29.531 | 22.095 | 13.697 | 9.3134 | 6.7394 |
As shown by Gabriel & Jordan (1969), the ratios defined below are sensitive to the electron density and
to the electron temperature:
In the low-density limit, all n=2 states are populated directly
or via upper-level radiative cascades by electron impact
from the He-like ground state and/or by (radiative and dielectronic)
recombination of H-like ions (see Fig. 2).
These states decay radiatively directly or by cascades to the ground level. The relative intensities of the
three intense lines are then independent of density. As ![]() increases from the low-density
limit, some of these states (1s2s3S1 and 1S0) are depleted by collisions to the nearby
states where
increases from the low-density
limit, some of these states (1s2s3S1 and 1S0) are depleted by collisions to the nearby
states where
![]() C
C![]() A, with C being the collisional coefficient rate, A being the
radiative transition probability from n=2 to n=1 (ground state), and
A, with C being the collisional coefficient rate, A being the
radiative transition probability from n=2 to n=1 (ground state), and
![]() being the
critical density. Collisional excitation depopulates first the 1s2s 3S1 level
(upper level of the forbidden line) to the 1s2p 3P0,1,2 levels (upper levels of
the intercombination lines). The intensity of the forbidden line decreases while those of the
intercombination lines increase, hence implying a reduction of the ratio R (according to
Eq. (1)), over approximately two or three decades of density (see Fig. 8 in Paper I).
For much higher densities, 1s2s1S0 is also depopulated to 1s2p1P1, and the
resonance line becomes sensitive to the density (this has been nicely illustrated by Gabriel & Jordan 1972 in their Fig. 4.6.9).
being the
critical density. Collisional excitation depopulates first the 1s2s 3S1 level
(upper level of the forbidden line) to the 1s2p 3P0,1,2 levels (upper levels of
the intercombination lines). The intensity of the forbidden line decreases while those of the
intercombination lines increase, hence implying a reduction of the ratio R (according to
Eq. (1)), over approximately two or three decades of density (see Fig. 8 in Paper I).
For much higher densities, 1s2s1S0 is also depopulated to 1s2p1P1, and the
resonance line becomes sensitive to the density (this has been nicely illustrated by Gabriel & Jordan 1972 in their Fig. 4.6.9).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{MS1442f2.eps}}\par\end{figure}](/articles/aa/full/2001/36/aa1442/Timg22.gif) |
Figure 2: Simplified diagram showing the different contributions to the population of a given n=2 shell level. (1): direct contribution due to collisional excitation from the ground level (1s2) of He-like ions; (2)+(2'): collisional excitation plus upper-level radiative cascade contribution; (3): direct radiative recombination or direct dielectronic recombination from H-like ions; and (4)+(4'): radiative recombination or dielectronic recombination plus upper-level radiative cascade contribution. |
| Open with DEXTER | |
However, caution should be applied for low-Z ions (i.e. C V, N VI, O VII) since in the case of an intense UV radiation field, the photo-excitation between the 3S term and the 3P term is not negligible. This process has the same effect on the forbidden line and on the intercombination line as the collisional coupling, i.e. lowering of the ratio R, and thus could mimic a high-density plasma. It should be taken into account to avoid any confusion between a high-density plasma and a high radiation field (see Sect. 4.4 for more details).
The ratio G (see Eq. (2)) is sensitive to the electron temperature since the collisional
excitation rates do not have the same dependence on temperature for the resonance line as for the
forbidden and intercombination lines.
In addition, as detailed in Paper I (see also Mewe 1999; Liedahl 1999), the relative intensity of the
resonance w (or r) line, compared to the forbidden z (or f) and the intercombination x+y (or i) lines, contains
information about the ionization processes that occur: a strong resonance line compared to the
forbidden or the intercombination lines corresponds to collision-dominated plasmas.
It leads to a ratio of
![]() (or
(or
![]() ).
On the contrary, a weak resonance line corresponds to plasmas dominated
by photo-ionization (
G=(z+(x+y))/w>4, or (f+i)/r>4).
).
On the contrary, a weak resonance line corresponds to plasmas dominated
by photo-ionization (
G=(z+(x+y))/w>4, or (f+i)/r>4).
We illustrate the relevant processes in the formation of the resonance, intercombination, and
forbidden lines with a simplified level scheme (cf. Mewe & Schrijver 1978a) consisting of the
following levels denoted by short labels: g: ground level 1
![]() ;
;
![]() :
upper metastable
level 21S0 of the two-photon transition; 1
:
upper metastable
level 21S0 of the two-photon transition; 1![]() :
upper level 21P1 of the resonance line; m:
upper metastable level 23S1 of the forbidden (f) line; pk (k=1,2,3: levels
2
:
upper level 21P1 of the resonance line; m:
upper metastable level 23S1 of the forbidden (f) line; pk (k=1,2,3: levels
2
![]() (2
(2
![]() is the upper level of the by far the strongest component (y) of the
intercombination line i, and 2
is the upper level of the by far the strongest component (y) of the
intercombination line i, and 2
![]() is the upper level of the weaker component (x)); c: continuum
level which lumps together all higher levels to represent the cascades from excitation and recombination
processes.
is the upper level of the weaker component (x)); c: continuum
level which lumps together all higher levels to represent the cascades from excitation and recombination
processes.
The electron collisional rate coefficient (in cm3 s-1) for transition ![]() is written as:
is written as:
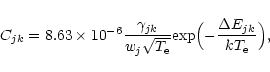 |
(3) |
The total rate coefficients for the formation of the forbidden (f or z notation)
and intercombination (i or x+y)
line can be written as (e.g., Mewe & Schrijver 1978a, Eqs. (18-30)):
If = ![$\displaystyle BR_{mg} \Bigl[ C_{gm} + \sum_{k=0}^2 BR_{p_km} C_{gp_k}\Bigr],$](/articles/aa/full/2001/36/aa1442/img34.gif) |
(4) |
Ii = ![$\displaystyle \sum_{k=1}^2 BR_{p_kg} \Bigl[ C_{gp_k} + BR_{mp_k} C_{gm} \Bigr],$](/articles/aa/full/2001/36/aa1442/img35.gif) |
(5) |
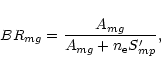 |
(6) |
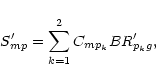 |
(7) |
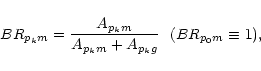 |
(8) |
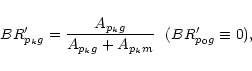 |
(9) |
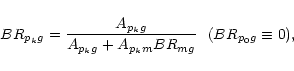 |
(10) |
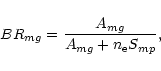 |
(11) |
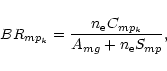 |
(12) |
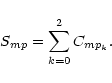 |
(13) |
![\begin{displaymath}%
I_r = BR_{1^{\prime}g} \Bigl[ C_{g1^{\prime}} + BR_{m^{\prime}1^{\prime}} C_{gm^{\prime}} \Bigr],
\end{displaymath}](/articles/aa/full/2001/36/aa1442/img46.gif) |
(14) |
![\begin{displaymath}%
I_{2ph} = BR_{m^{\prime}g} \Bigl[ C_{gm^{\prime}} + BR_{1^{\prime}m} C_{g1^{\prime}}\Bigr],
\end{displaymath}](/articles/aa/full/2001/36/aa1442/img47.gif) |
(15) |
We note that the collision coefficients Cjk include also the n > 2 cascades.
The radiative transition probabilities are tabulated in the Table 2 of PaperI and the
effective collision strengths ![]() in their Tables 9-13 and in their Fig. 4.
We assume in this section that the electron density is so low that the collision de-excitation rate
in their Tables 9-13 and in their Fig. 4.
We assume in this section that the electron density is so low that the collision de-excitation rate
![]() can be
neglected with respect to the spontaneous radiative rate Apkm (e.g., for C V
can be
neglected with respect to the spontaneous radiative rate Apkm (e.g., for C V
![]() for
for
![]() cm-3).
This can be easily taken into account by the substitution
cm-3).
This can be easily taken into account by the substitution
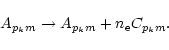 |
(16) |
In the full calculations used in this work (see Sect. 5), the coupling between the singlet and triplet system has been taken into account, as well as the collisional de-excitation.
If we take also into account the contribution from radiative and dielectronic recombinations of the
hydrogen-like ion we substitute
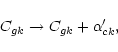 |
(17) |
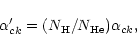 |
(18) |
Mewe & Schrijver (1978a) took also into account the effect
of a stellar radiation field (also called photo-excitation) with effective radiation
temperature
![]() .
This can be done by substituting in the above equations:
.
This can be done by substituting in the above equations:
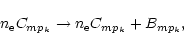 |
(19) |
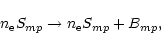 |
(20) |
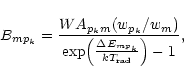 |
(21) |
Mewe & Schrijver (1978a) considered also inner-shell ionization of the Lithium-like ion which can give an important contribution to the forbidden line in a transient plasma (Mewe & Schrijver 1978b) such as a supernova remnant. However, in the present calculations we neglect this because we consider plasmas in ionization equilibrium.
Finally, Mewe & Schrijver (1978a, 1978c) have considered
also excitation 23S![]() 23P by proton collisions
using approximations of Coulomb-Born results from Blaha (1971).
In a new version (SPEX90) of our spectral code SPEX (Kaastra et al. 1996), which contains for the
H- and He-like ions an improvement of the known MEKAL code (Mewe et al. 1985, 1995a), proton collisions are
taken into account based on Blaha's results. Test calculations with SPEX90 show that for an equilibrium plasma
in all practical cases proton excitation is negligible compared to electron excitation.
23P by proton collisions
using approximations of Coulomb-Born results from Blaha (1971).
In a new version (SPEX90) of our spectral code SPEX (Kaastra et al. 1996), which contains for the
H- and He-like ions an improvement of the known MEKAL code (Mewe et al. 1985, 1995a), proton collisions are
taken into account based on Blaha's results. Test calculations with SPEX90 show that for an equilibrium plasma
in all practical cases proton excitation is negligible compared to electron excitation.
In the case where
![]() ,
recombination is dominant e.g., for photo-ionized plasmas it turns
out that the ratios
,
recombination is dominant e.g., for photo-ionized plasmas it turns
out that the ratios
![]() are for collisional and photo-ionized plasmas comparable in the
same density range (cf. also Mewe 1999), but the ratios
are for collisional and photo-ionized plasmas comparable in the
same density range (cf. also Mewe 1999), but the ratios
![]() are very different,
e.g.,
are very different,
e.g., ![]() for a collisional plasma and a factor
for a collisional plasma and a factor
![]() larger for a
photo-ionized plasma where the resonance line is relatively much weaker.
larger for a
photo-ionized plasma where the resonance line is relatively much weaker.
The intensities of the three lines (resonance, forbidden and intercombination) are calculated mainly from atomic data presented in Paper I (Porquet & Dubau 2000). In this work (as well as in Paper I) for all temperatures (low and high), radiative recombination contributions (direct + upper-level radiative cascades), and collisional excitations inside the n=2 shell were included in the line ratio calculations. For high temperatures, the collisional excitation contribution (direct + near-threshold resonance + cascades) from the ground level (n=1 shell, 1s2) are important as well as dielectronic recombination (direct + cascades).
Excitation collisional data are also taken from Paper I, which are based on the calculations from Zhang & Sampson (1987) plus the contribution of the upper-level (n>2) radiative cascades calculated in Paper I (see Paper I for more details).
The ionization balance is from Mazzotta et al. (1998) and the data for radiative and dielectronic recombinations are from Paper I. Various new data for the transition probabilities (e.g., forbidden and intercombination lines) have been selected (see Sect. 4.1).
In the following paragraphs we describe the several differences between Paper I and this work: Aki, optical depth, contribution of the blended dielectronic satellite lines, and radiation field.
| ion | forbidden line | intercombination line |
| (z, |
(y, |
|
| C V | 4.857(+1) (S94) | 2.90(+7) (H85) |
| N VI | 2.538(+2) (N00) | 1.38(+8) (H85) |
| O VII | 1.046(+3) (C98) | 5.800(+8) (E81) |
| Ne IX | 1.09(+4) (T99) | 5.400(+9) * |
| Mg XI | 7.347(+4) (S95) | 3.448(+10) (A81) |
| Si XIII | 3.610(+5) * | 1.497(+11) (A79) |
(A79): Armour et al. (1979)
(A81): Armour et al. (1981)
(C98): Crespo López-Urrutia et al. (1998)
(E81): Engström et al. (1981)
(H85): Hutton et al. (1985)
(N00): Neill et al. (2000)
(S94): Schmidt et al. (1994)
(S95): Stefanelli et al. (1995)
(T99): Träbert et al. (1999)
*: Theoretical values taken from Lin et al. (1977), see text (Sect. 4.1).
We have updated the transition probabilities Aki reported in Paper I
for the intercombination (y, ![]() )
and the forbidden (z,
)
and the forbidden (z, ![]() )
line by published experimental values (see Table 2, and references therein). In some cases, no published
experimental values have been found and then we used the theoretical values from Lin et al. (1977).
Indeed, comparisons of their theoretical values with the experimental values reported in
Table 2 seem to show good agreement in other cases.
)
line by published experimental values (see Table 2, and references therein). In some cases, no published
experimental values have been found and then we used the theoretical values from Lin et al. (1977).
Indeed, comparisons of their theoretical values with the experimental values reported in
Table 2 seem to show good agreement in other cases.
For C V, the ratio R is reduced by about 20![]() comparing the calculations using the values of
Aki reported in Paper I, while for N VI the reduction is
less than
comparing the calculations using the values of
Aki reported in Paper I, while for N VI the reduction is
less than ![]() .
For O VII, Ne IX, Mg XI, and Si XIII, the differences
between the current calculations using these new values of Aki and those reported in Paper I are negligible.
.
For O VII, Ne IX, Mg XI, and Si XIII, the differences
between the current calculations using these new values of Aki and those reported in Paper I are negligible.
Schrijver et al. (1995) and Mewe et al. (1995b) have investigated the possibility that
resonance photons are scattered out of the line of sight in late-type stellar coronae (see also Acton 1978).
Indeed, in this process, a resonance line photon is absorbed by an ion in the ground state and then re-emitted,
generally in a different direction. So, the total photon intensity integrated over 4![]() remains unchanged
but the photon distribution with respect to a given direction is altered. This absorption and re-emission is
indistinguishable from scattering and depends on the geometry of the region being observed. In general,
photons would be scattered preferentially out of the line of sight for active regions (relatively dense areas)
and into the line of sight for the surrounding quiet Sun (less dense area), see Schmelz et al.
(1997) and Mewe et al. (2001). The effect is smaller for instruments with a
larger field of view.
remains unchanged
but the photon distribution with respect to a given direction is altered. This absorption and re-emission is
indistinguishable from scattering and depends on the geometry of the region being observed. In general,
photons would be scattered preferentially out of the line of sight for active regions (relatively dense areas)
and into the line of sight for the surrounding quiet Sun (less dense area), see Schmelz et al.
(1997) and Mewe et al. (2001). The effect is smaller for instruments with a
larger field of view.
This could have an impact on the temperature diagnostic, the so-called G=(z+x+y)/w or (f+i)/r ratio. If the optical depth of the line is not taken into account, the calculated intensity ratio G can be overestimated and the inferred temperature from the G ratio is underestimated.
As detailed in Mewe et al. (2001), branching ratios can be used to check the assumption of the
optical thin model because effects of resonance scattering would affect the measured branching ratio. From
the fact that the intensities of e.g., the strong resonance lines Fe XVIII![]() 93.92 and
Fe XIX
93.92 and
Fe XIX![]() 108.307 are in good agreement with the intensities of other lines sharing the same
upper level, one can derive a constraint on the optical depth taking into account the systematic
uncertainties of the theoretical transition probabilities A (typical 25
108.307 are in good agreement with the intensities of other lines sharing the same
upper level, one can derive a constraint on the optical depth taking into account the systematic
uncertainties of the theoretical transition probabilities A (typical 25![]() for each A, hence 35
for each A, hence 35![]() for
the branching ratio) which dominate over the statistical errors (typically 10
for
the branching ratio) which dominate over the statistical errors (typically 10![]() ). If we rule out a
reduction in the resonance line intensity larger than about 30
). If we rule out a
reduction in the resonance line intensity larger than about 30![]() ,
then on the basis of a simple
"escape-factor'' model with
,
then on the basis of a simple
"escape-factor'' model with
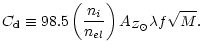 |
(24) |
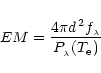 |
(25) |
Since
![]() (
(
![]() and
and
![]() corresponding respectively to the optical depth of
the resonance and the intercombination lines), we can write
corresponding respectively to the optical depth of
the resonance and the intercombination lines), we can write
![]() ,
where
,
where ![]() is the value of the ratio taken into account the optical depth of the resonance line,
G is the value without resonant scattering (such as in Paper I and Sect. 5), and
is the value of the ratio taken into account the optical depth of the resonance line,
G is the value without resonant scattering (such as in Paper I and Sect. 5), and
![]() is the escape probability for the resonance line (Eq. (22)).
One should note that
is the escape probability for the resonance line (Eq. (22)).
One should note that ![]() is not strictly exact when the contribution of the blended dielectronic satellite lines are
introduced in the calculations (see Sect. 4.3).
is not strictly exact when the contribution of the blended dielectronic satellite lines are
introduced in the calculations (see Sect. 4.3).
The intensity of a dielectronic satellite line arising from a doubly excited state with principal quantum number n
in a Lithium-like ion produced by dielectronic recombination of a He-like ion is given by:
| (26) |
The rate coefficient (in cm3s-1) for dielectronic recombination is given by (Bely-Dubau et al. 1979):
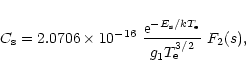 |
(27) |
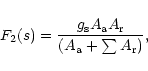 |
(28) |
For a group of satellites with the same principal quantum
number n, ![]() can be approximated by
can be approximated by
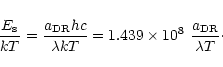 |
(30) |
For the n=2, 3, 4 blended dielectronic satellite lines we use the atomic data reported in the Appendix.
For the higher-n blended dielectronic satellite lines we use the results from Karim and co-workers.
For Z=10 (Ne IX) we use the data from Karim (1993) who gives the intensity factor
![]() for
the strongest (
F*2 > 1012s-1) dielectronic satellite lines with n=5-8. For Z=14 (Si XIII),
we take the calculations from Karim & Bhalla (1992) who report the intensity factor
F*2 for the strongest (
F*2 > 1012s-1) dielectronic satellite lines
with n=5-8. For Z=12 (Mg XI) we have interpolated between the calculations from Karim (1993) for
Z=10, and from
Karim & Bhalla (1992) for Z=14.
for
the strongest (
F*2 > 1012s-1) dielectronic satellite lines with n=5-8. For Z=14 (Si XIII),
we take the calculations from Karim & Bhalla (1992) who report the intensity factor
F*2 for the strongest (
F*2 > 1012s-1) dielectronic satellite lines
with n=5-8. For Z=12 (Mg XI) we have interpolated between the calculations from Karim (1993) for
Z=10, and from
Karim & Bhalla (1992) for Z=14.
Including the contribution of the blended dielectronic satellite lines, we write for the ratios R and G:
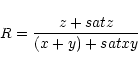 |
(31) |
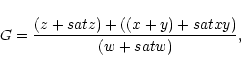 |
(32) |
At the temperature at which the ion fraction is maximum for the He-like ion
(see e.g. Arnaud & Rothenflug 1985; Mazzotta et al. 1998), the differences between the
calculations for R (for G) with or without taking into account the blended dielectronic satellite lines are only
of about 1![]() (9
(9![]() ),
), ![]() (5
(5![]() ), and 5
), and 5![]() (3
(3![]() )
for Ne IX, Mg XI, and
Si XIII at the low-density limit and for
)
for Ne IX, Mg XI, and
Si XIII at the low-density limit and for
![]() K, respectively. On the other hand, for much
lower electron temperatures, the effect is bigger since the intensity of
the dielectronic satellite lines is proportional to
K, respectively. On the other hand, for much
lower electron temperatures, the effect is bigger since the intensity of
the dielectronic satellite lines is proportional to
![]() .
As well, for high values of density
(
.
As well, for high values of density
(![]() )
at which the intensity of the forbidden line is very weak (i.e. tends to zero), the
contribution of the blended dielectronic satellite lines to the forbidden line leads to a ratio R which decreases much
slower with
)
at which the intensity of the forbidden line is very weak (i.e. tends to zero), the
contribution of the blended dielectronic satellite lines to the forbidden line leads to a ratio R which decreases much
slower with ![]() than in the case where the contribution of the blended dielectronic satellite lines is not taken
into account.
than in the case where the contribution of the blended dielectronic satellite lines is not taken
into account.
Recently, Kahn et al. (2001) have found with the RGS on XMM-Newton
that for ![]() Puppis, the forbidden to
intercombination line ratios within the helium-like triplets are abnormally low for N VI,
O VII, and Ne IX. While this is sometimes indicative of a high electron density,
they have shown that
in the case of
Puppis, the forbidden to
intercombination line ratios within the helium-like triplets are abnormally low for N VI,
O VII, and Ne IX. While this is sometimes indicative of a high electron density,
they have shown that
in the case of ![]() Puppis, it is instead caused by the intense radiation field of this star. This constrains
the location of the X-ray emitting shocks relative to the star, since the emitting regions should be close enough
to the star in order that the UV radiation is not diluted too much.
A strong radiation field can mimic a high density if the upper (3S) level of the forbidden line
is significantly depopulated via photo-excitation to the upper (3P) levels
of the intercombination lines,
analogously to the effect of electronic collisional excitation (Fig. 1).
The result is an increase of the intercombination
lines and a decrease of the forbidden line.
Puppis, it is instead caused by the intense radiation field of this star. This constrains
the location of the X-ray emitting shocks relative to the star, since the emitting regions should be close enough
to the star in order that the UV radiation is not diluted too much.
A strong radiation field can mimic a high density if the upper (3S) level of the forbidden line
is significantly depopulated via photo-excitation to the upper (3P) levels
of the intercombination lines,
analogously to the effect of electronic collisional excitation (Fig. 1).
The result is an increase of the intercombination
lines and a decrease of the forbidden line.
Equation (21) gives the expression for photo-excitation from level m to level pk in a radiation field
with effective blackbody temperature
![]() from a hot star underlying the X-ray line emitting plasma. As pointed
out by Mewe & Schrijver (1978a) the radiation is diluted by a factor W given by
from a hot star underlying the X-ray line emitting plasma. As pointed
out by Mewe & Schrijver (1978a) the radiation is diluted by a factor W given by
![\begin{displaymath}%
W=\frac{1}{2}~\left[1-\left(1-\left(\frac{r_{*}}{r}\right)\right)^{1/2}\right],
\end{displaymath}](/articles/aa/full/2001/36/aa1442/img123.gif) |
(33) |
In their Table 8, Mewe & Schrijver (1978a) give for information the radiation temperature for a
solar photospheric field for Z=6, 7, and 8. In Table 3, we report the wavelengths at
which the radiation temperature should be estimated for Z=6, 7, 8, 10, 12, 14.
These wavelengths correspond to the transitions between the 3S and 3P levels (
![]() )
and the
1S and 1P levels (
)
and the
1S and 1P levels (
![]() ).
).
| C V | N VI | O VII | Ne IX | Mg XI | Si XIII | |
|
|
2280 | 1906 | 1637 | 1270 | 1033 | 864 |
|
|
3542 | 2904 | 2454 | 1860 | 1475 | 1200 |
The photo-excitation from the 3S level and 3P levels is very important for low-Z ions C V,
N VI, O VII. For higher-Z ions, this process is only important for very high radiation temperature
(![]() few 10000 K).
few 10000 K).
One can note that the photo-excitation between the levels 1S0 and 1P1 is negligible compared
to the photo-excitation between the 3S1 and 3P0,1,2 levels. For example, for a very high
value of
![]() K the difference between the calculations taken or not taken into account the
photo-excitation between 1S0 and 1P1 is smaller than 20
K the difference between the calculations taken or not taken into account the
photo-excitation between 1S0 and 1P1 is smaller than 20![]() for C V, where this effect
is expected to be maximum.
for C V, where this effect
is expected to be maximum.
Using the above-mentioned atomic data, we have calculated the line intensity ratios R and G
for C V, N VI, O VII, Ne IX, Mg XI,
and Si XIII![]() The wavelengths of these three (four) lines for each He-like ion treated in this paper
are reported in Table 1.
The wavelengths of these three (four) lines for each He-like ion treated in this paper
are reported in Table 1.
All the relevant processes detailed in Sects. 3 and 4 between the seven levels are taken into account (full resolution): radiative de-excitation, collisional electronic excitation and de-excitation, radiative and dielectronic recombination, photo-excitation and induced emission (between 3S1 and 3P levels).
We considered a broad range of densities (![]() )
and radiation temperatures (
)
and radiation temperatures (
![]() )
calculated
for photo-excitation between the 3S level and the 3P levels and a number of electron temperatures (
)
calculated
for photo-excitation between the 3S level and the 3P levels and a number of electron temperatures (![]() ).
As well, we considered different values of the dilution factor of the radiation field (W)
which could be used either for hot late-type stars or O, B stars.
).
As well, we considered different values of the dilution factor of the radiation field (W)
which could be used either for hot late-type stars or O, B stars.
We display the
![]() line intensity ratios, from Tables 4 to 9,
for the six ions, for five values
of electron temperature (
line intensity ratios, from Tables 4 to 9,
for the six ions, for five values
of electron temperature (![]() )
including the temperature of maximum line formation for the He-like
lines (cf. Mewe et al. 1985); and for two or more values of the radiation temperature (
)
including the temperature of maximum line formation for the He-like
lines (cf. Mewe et al. 1985); and for two or more values of the radiation temperature (
![]() ), and
several values of
), and
several values of ![]() .
As one can note the ratio G is as expected to be sensitive to
.
As one can note the ratio G is as expected to be sensitive to ![]() ,
while
it is almost insensitive to the exact values of
,
while
it is almost insensitive to the exact values of ![]() and
and
![]() .
The resonance line becomes sensitive at high density due to the depopulation of the
1s2s1S0 level to the 1s2p1P1 level (see Gabriel & Jordan 1972).
Since the sum z+(x+y) is a constant or almost constant,
the value of G is independent of the exact value of the dilution factor (W). Here the calculations were done for dilution factor W=1/2.
.
The resonance line becomes sensitive at high density due to the depopulation of the
1s2s1S0 level to the 1s2p1P1 level (see Gabriel & Jordan 1972).
Since the sum z+(x+y) is a constant or almost constant,
the value of G is independent of the exact value of the dilution factor (W). Here the calculations were done for dilution factor W=1/2.
Finally, we display the
![]() line intensity ratios for the six ions,
in Tables 10 to 69,
for the same values of electron temperature (
line intensity ratios for the six ions,
in Tables 10 to 69,
for the same values of electron temperature (![]() )
and much more values of radiation temperature
(
)
and much more values of radiation temperature
(
![]() ), and for three values of the dilution factor of the radiation field W=0.5, 0.1, 0.01.
), and for three values of the dilution factor of the radiation field W=0.5, 0.1, 0.01.
Since as said previously in Sect. 4.3, the contribution of the blended dielectronic satellite lines depends
on the spectral resolution, we give the values of R and G for Ne IX, Mg XI, and Si XIII, for four specific values of spectral resolutions (FWHM):
RGS-1 at the first order
(i.e.
![]() ,
0.075 and 0.078 Å for Ne IX, Mg XI and Si XIII respectively),
LETGS (i.e.
,
0.075 and 0.078 Å for Ne IX, Mg XI and Si XIII respectively),
LETGS (i.e.
![]() Å), HETGS-MEG (i.e.
Å), HETGS-MEG (i.e.
![]() Å), and HETGS-HEG
(i.e.
Å), and HETGS-HEG
(i.e.
![]() Å). In the cases where the differences (
Å). In the cases where the differences (![]() )
are negligible
between two or more spectral resolutions, we display the results together (e.g. RGS and LETGS).
)
are negligible
between two or more spectral resolutions, we display the results together (e.g. RGS and LETGS).
For the first time, thanks to the new generation of X-ray satellites, Chandra and XMM-Newton, the diagnostics based on the line ratios of He-like ions could be used for powerful extra-solar plasma diagnostics (Warm Absorber in AGNs, stellar coronae, ...). These diagnostics are one of the keys for a better understanding of the solar-stellar connection: heating of the coronae, magnetic activity, etc. In this work, we have calculated the line ratio R and G which allow, respectively, electron density and temperature diagnostics. These calculations are based partly on the previous work of Porquet & Dubau (2000) and on different improvements of atomic data (see Sect. 4).
We have tabulated the results adapted for the different spectral resolutions of the spectrometers on board of Chandra and XMM-Newton for parameter ranges which correspond as much as possible to most cases of stellar coronae (hot-late type star, O B stars...).
Acknowledgements
The Space Research Organization Netherlands (SRON) is supported financially by NWO.
We report in this Appendix the atomic data related to the dielectronic satellite lines, calculated in this work for Z=10, 12, and 14, blended with one of their parent lines: forbidden, intercombination, and resonance.
The satellite line wavelengths and intensities have been obtained using
a set of computer codes developed partly in University-College-London
(SUPERSTRUCTURE: Eissner, Jones, Nussbaumer 1974) and in Meudon Observatory
(AUTOLSJ: TFR group, Dubau J., Loulergue M. 1981). Multiconfigurational-wavefunctions are
calculated in a "scaled" Thomas-Fermi-Dirac-Amaldi potentials, depending
on linear scaling parameters (
![]() ,
,
![]() ,
,
![]() ...) different
for l-orbitals, which are obtained through a self-consistent variational
procedure on the energy sum of the first lowest (SL) terms. In
SUPERSTRUCTURE, the level energies and the radiative probabilities are
calculated in the relativistic Breit-Paul hamiltonian approach, which gives
fine-structure bound and autoionizing levels. In the AUTOLSJ code, the
autoionization probabilities are derived in the Distorted-wave
approximation, using the same wavefunctions as in SUPERSTRUCTURE.
For the present calculations, the following configuration were used:
...) different
for l-orbitals, which are obtained through a self-consistent variational
procedure on the energy sum of the first lowest (SL) terms. In
SUPERSTRUCTURE, the level energies and the radiative probabilities are
calculated in the relativistic Breit-Paul hamiltonian approach, which gives
fine-structure bound and autoionizing levels. In the AUTOLSJ code, the
autoionization probabilities are derived in the Distorted-wave
approximation, using the same wavefunctions as in SUPERSTRUCTURE.
For the present calculations, the following configuration were used:
![]() ,
,
![]() ,
and
,
and
![]() for
for
![]() and
and
![]() .
.
The wavelengths of the dielectronic satellite lines calculated here should be
compared to the "reference'' wavelengths used in the Jacques Dubau's calculations
respectively for Ne IX, Mg XI, and Si XIII,
![]() ,
9.1740, 6.6482 Å,
,
9.1740, 6.6482 Å,
![]() ,
9.2395, 6.6903 Å,
,
9.2395, 6.6903 Å,
![]() ,
9.2358, 6.6865 Å,
,
9.2358, 6.6865 Å,
![]() ,
9.3219, 6.7420 Å.
One can notice that these wavelengths are not identical to the wavelengths of
Vainshtein & Safronova (1978) used in the calculation
of the line ratios R and G, tabulated in Table 1.
Then in order to determine which dielectronic satellite lines are blended
with one of the parent lines (forbidden, intercombination,
and resonance), one should take into account the shift of the
satellite line compared to the wavelengths chosen for the parent lines
in the calculation of R and G.
,
9.3219, 6.7420 Å.
One can notice that these wavelengths are not identical to the wavelengths of
Vainshtein & Safronova (1978) used in the calculation
of the line ratios R and G, tabulated in Table 1.
Then in order to determine which dielectronic satellite lines are blended
with one of the parent lines (forbidden, intercombination,
and resonance), one should take into account the shift of the
satellite line compared to the wavelengths chosen for the parent lines
in the calculation of R and G.
The values of ![]() ,
which is the energy of the satellite level s,
used in this calculation are well reproduced using formula (29).
,
which is the energy of the satellite level s,
used in this calculation are well reproduced using formula (29).
In Tables![]() A.1, A.2, and A.3,
the dielectronic satellite lines n=2, for Z=10, 12, and 14, respectively
are reported. In Tables A.4, A.5, and A.6, the dielectronic satellite lines n=3,
and 4, for Z=10, 12, and 14, respectively are reported.
A.1, A.2, and A.3,
the dielectronic satellite lines n=2, for Z=10, 12, and 14, respectively
are reported. In Tables A.4, A.5, and A.6, the dielectronic satellite lines n=3,
and 4, for Z=10, 12, and 14, respectively are reported.