A&A 376, 1064-1072 (2001)
DOI: 10.1051/0004-6361:20011032
C. Vastel1 - M. Spaans2 - C. Ceccarelli3,4 - A. G. G. M. Tielens2 - E. Caux1
1 -
CESR CNRS-UPS, BP 4346, 31028 Toulouse Cedex 04, France
2 -
Kapteyn Astronomical Institute, PO Box 800, 9700 AV Groningen, The Netherlands
3 -
Observatoire de Bordeaux, 2 rue de l'Observatoire, BP 89, 33270 Floirac,
France
4 -
Observatoire de Grenoble, BP 53, 38041 Grenoble Cedex 09, France
Received 24 April 2001 / Accepted 12 July 2001
Abstract
We present ISO-LWS and ground-based SEST observations which probe the
Photo Dissociation Region (PDR) of W49N. The ISO-LWS observations consist of low
resolution (![]() 200) grating spectra between 43
200) grating spectra between 43 ![]() m and 197
m and 197 ![]() m, and high
resolution (
m, and high
resolution (![]() 104) Fabry-Pérot spectra of the [CII] 158
104) Fabry-Pérot spectra of the [CII] 158 ![]() m and
[OI] 63 and 145
m and
[OI] 63 and 145 ![]() m lines. The SEST observations consist of C16O
m lines. The SEST observations consist of C16O
![]() and C18O
and C18O
![]() maps of the region.
Using all these observations and with the help of a detailed PDR model,
we have determined the physical and chemical structure of the PDR of W49N.
We find that only a tiny fraction, 2.5%, of the cloud gas is in the atomic form.
This gas has an average density n=104 cm-3 and a temperature
maps of the region.
Using all these observations and with the help of a detailed PDR model,
we have determined the physical and chemical structure of the PDR of W49N.
We find that only a tiny fraction, 2.5%, of the cloud gas is in the atomic form.
This gas has an average density n=104 cm-3 and a temperature ![]() K.
The PDR is created by a FUV field
K.
The PDR is created by a FUV field
![]() times brighter than the average
FUV interstellar field, which is emitted by the stars associated with the several
HII regions inside the cloud. The photoelectric heating efficiency is very low,
times brighter than the average
FUV interstellar field, which is emitted by the stars associated with the several
HII regions inside the cloud. The photoelectric heating efficiency is very low,
![]() 10-4, relative to other known PDRs, probably because of the relatively
high G0/n ratio. Overall, W49N seems to be one of the youngest giant molecular
clouds actively forming stars in the Galaxy, since most of the cloud material is
still molecular and dense and not yet dispersed by the several embedded newly formed
massive protostars.
10-4, relative to other known PDRs, probably because of the relatively
high G0/n ratio. Overall, W49N seems to be one of the youngest giant molecular
clouds actively forming stars in the Galaxy, since most of the cloud material is
still molecular and dense and not yet dispersed by the several embedded newly formed
massive protostars.
Key words: ISM: abundances - ISM: molecules - ISM: atoms - HII regions - ISM: individual: W49N
Several kinematical models have been proposed to explain the origin of the burst
of star formation in the W49N complex. Mufson & Liszt (1977) first proposed a
"two cloud collision'' model, in which star formation has occurred at the
interacting region between two massive molecular clouds. Their CO (2.6 mm),
H2CO (2 cm) and hot ionized gas (H76![]() )
observations are consistent
with a picture where a large HII region lies between two massive molecular clouds
at velocities of
)
observations are consistent
with a picture where a large HII region lies between two massive molecular clouds
at velocities of ![]() 4 and 12 kms-1.
Welch et al. (1987) proposed an alternative scenario based on 6 cm continuum,
H76
4 and 12 kms-1.
Welch et al. (1987) proposed an alternative scenario based on 6 cm continuum,
H76![]() and HCO+ (1-0) observations, in which a single collapsing molecular
cloud leads to a rotating ring of at least ten ultracompact HII regions.
However, de Pree et al. (1997) complemented these studies with
observations of H92
and HCO+ (1-0) observations, in which a single collapsing molecular
cloud leads to a rotating ring of at least ten ultracompact HII regions.
However, de Pree et al. (1997) complemented these studies with
observations of H92![]() ,
H66
,
H66![]() and H52
and H52![]() and found no evidence of
any ordered motions indicating rotation. In addition, Serabyn et al. (1993) detected
three dense molecular clumps (two at 12 kms-1 and one at 4 kms-1) in the
W49N core with their CS and C34S observations, and re-proposed that star formation
has been triggered by a cloud-cloud collision, and not by a free-fall collapse.
and found no evidence of
any ordered motions indicating rotation. In addition, Serabyn et al. (1993) detected
three dense molecular clumps (two at 12 kms-1 and one at 4 kms-1) in the
W49N core with their CS and C34S observations, and re-proposed that star formation
has been triggered by a cloud-cloud collision, and not by a free-fall collapse.
In this paper, we report observations of several far-infrared and millimeter emission
lines in W49N and use the fluxes from these lines to examine the physical properties of the
emitting region. The FIR lines of [OI] (63 and 145 ![]() m), [CII] (158
m), [CII] (158 ![]() m), and the
rotational lines of CO provide important diagnostic tools for investigation of the
physical conditions in Photo-Dissociation Regions (PDR; Tielens & Hollenbach 1985a).
These regions of the interstellar medium are chemically affected by the strong far-ultraviolet
(91 nm-240 nm; FUV) radiation emitted by nearby stars, which dissociates molecules and ionizes
atoms. Luminous PDRs (such as W49N) are signposts of massive newly formed stars and PDR observations
can be used to determine the conditions associated with active massive star formation. Moreover,
as argued by Tielens & Hollenbach (1999), PDRs are interesting in themselves because they
contain all of the atomic gas and at least 90% of the molecular
gas in the Galaxy. Furthermore, PDRs are the origin of much of the IR radiation
from the ISM (Tielens & Hollenbach 1999). From luminosity considerations, the PDR emission
in W49N is powered by the photon energy from the newly formed massive stars which are
also responsible for ionizing the HII regions.
m), and the
rotational lines of CO provide important diagnostic tools for investigation of the
physical conditions in Photo-Dissociation Regions (PDR; Tielens & Hollenbach 1985a).
These regions of the interstellar medium are chemically affected by the strong far-ultraviolet
(91 nm-240 nm; FUV) radiation emitted by nearby stars, which dissociates molecules and ionizes
atoms. Luminous PDRs (such as W49N) are signposts of massive newly formed stars and PDR observations
can be used to determine the conditions associated with active massive star formation. Moreover,
as argued by Tielens & Hollenbach (1999), PDRs are interesting in themselves because they
contain all of the atomic gas and at least 90% of the molecular
gas in the Galaxy. Furthermore, PDRs are the origin of much of the IR radiation
from the ISM (Tielens & Hollenbach 1999). From luminosity considerations, the PDR emission
in W49N is powered by the photon energy from the newly formed massive stars which are
also responsible for ionizing the HII regions.
The outline of this paper is as follows. In Sect. 2 we present observations of
the continuum and the [OI] and [CII] fine structure lines towards W49N obtained
with the ISO-LWS spectrometer, and the C16O (J = 1
![]() 0) and C18O
(J = 2
0) and C18O
(J = 2
![]() 1) rotational lines obtained with the SEST telescope. In Sect. 3,
the ensemble of these observations is used to characterize the PDR of W49N,
namely the average dust temperature, gas density and temperature as well
as the illuminating UV field intensity.
Section 4 presents the chemical and physical structure of such a PDR,
as derived by a detailed PDR model.
We finally compare the W49N case to other studied PDRs.
1) rotational lines obtained with the SEST telescope. In Sect. 3,
the ensemble of these observations is used to characterize the PDR of W49N,
namely the average dust temperature, gas density and temperature as well
as the illuminating UV field intensity.
Section 4 presents the chemical and physical structure of such a PDR,
as derived by a detailed PDR model.
We finally compare the W49N case to other studied PDRs.
We present observations towards W49N obtained with the
Long Wavelength Spectrometer (LWS: Clegg et al. 1996)
on board the Infrared Space Observatory (ISO).
We obtained spectra between 43 and 197 ![]() m in grating mode
(
m in grating mode
(![]() /
/
![]() )
and high resolution spectra in Fabry-Pérot mode
(
)
and high resolution spectra in Fabry-Pérot mode
(![]() /
/
![]() )
of the fine structure lines
[CII] 158
)
of the fine structure lines
[CII] 158 ![]() m and [OI] 63 and 145
m and [OI] 63 and 145 ![]() m.
The
m.
The ![]() 80
80
![]() ISO-LWS beam (LWS handbook, Gry et al.
2000) was centred on the W49N HII region, namely at:
ISO-LWS beam (LWS handbook, Gry et al.
2000) was centred on the W49N HII region, namely at:
![]() ,
,
![]() .
The data were processed
using the Off-Line-Processing pipeline version 7, and the latest improvements
of the LIA (LWS Interactive Analysis version 7.3). A final analysis was made
using the latest version of the standard package ISAP (version 2.0).
Each spectrum was carefully deglitched scan by scan. The continuum level of
the FP data was calibrated against observations of the same line of sight
with LWS in the grating mode (L01 during revolution 527).
L01 spectra are flux calibrated using Uranus, and the absolute accuracy is
estimated to be better than 30% (Swinyard et al. 1998).
.
The data were processed
using the Off-Line-Processing pipeline version 7, and the latest improvements
of the LIA (LWS Interactive Analysis version 7.3). A final analysis was made
using the latest version of the standard package ISAP (version 2.0).
Each spectrum was carefully deglitched scan by scan. The continuum level of
the FP data was calibrated against observations of the same line of sight
with LWS in the grating mode (L01 during revolution 527).
L01 spectra are flux calibrated using Uranus, and the absolute accuracy is
estimated to be better than 30% (Swinyard et al. 1998).
To separate instrumental effects from real features, we have determined the
instrumental response at 158 ![]() m of the LWS-FP in the same way as
for the 63 and 145
m of the LWS-FP in the same way as
for the 63 and 145 ![]() m lines described in Vastel et al. (2000),
i.e. using the observations towards NGC 7023.
m lines described in Vastel et al. (2000),
i.e. using the observations towards NGC 7023.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{158.eps}\end{figure}](/articles/aa/full/2001/36/aa1417/Timg18.gif) |
Figure 1:
ISO-LWS FP's instrumental profile (solid line) obtained at
157.741 |
| Open with DEXTER | |
The derived instrumental profile is shown in Fig. 1:
it has a FWHM of 37.1 kms-1,
slightly larger than the 33.4 kms-1 predicted by the instrument
optical model. This is probably due to transient effects, as discussed
in Vastel et al. (2000).
![\begin{figure}
\par\includegraphics[width=7.7cm,height=9.5cm,clip]{OI_CIIspectra.eps}\end{figure}](/articles/aa/full/2001/36/aa1417/Timg19.gif) |
Figure 2:
Observed high resolution spectra of the lines at 63, 145 and
158 |
| Open with DEXTER | |
Figure 2 presents the [OI] 63 ![]() m, 145
m, 145 ![]() m and
[CII] 158
m and
[CII] 158 ![]() m line profiles observed in the high spectral resolution mode.
Both 145 and 158
m line profiles observed in the high spectral resolution mode.
Both 145 and 158 ![]() m lines are fitted, before convolution,
by a 16 kms-1 Gaussian.
Note that the 63
m lines are fitted, before convolution,
by a 16 kms-1 Gaussian.
Note that the 63 ![]() m line contains a strong absorption feature,
whose origin is discussed in Vastel et al. (2000) and which
affects the emission component at 8 kms-1.
Vastel et al. (2000) separated this emission component from the
absorption component, which is due to cold molecular clouds and diffuse HI clouds in the velocity range
[35 kms-1, 70 kms-1] along the line of sight.
In this paper, we focus on the emission component modeled by a 16 kms-1 Gaussian linewidth, associated with
the HII region of W49N. We disentangled the emission component at 63
m line contains a strong absorption feature,
whose origin is discussed in Vastel et al. (2000) and which
affects the emission component at 8 kms-1.
Vastel et al. (2000) separated this emission component from the
absorption component, which is due to cold molecular clouds and diffuse HI clouds in the velocity range
[35 kms-1, 70 kms-1] along the line of sight.
In this paper, we focus on the emission component modeled by a 16 kms-1 Gaussian linewidth, associated with
the HII region of W49N. We disentangled the emission component at 63 ![]() m from the absorption due to diffuse
and molecular clouds between -10 kms-1 and 100 kms-1 with the method described in Vastel et al. (2000).
The total absorption component is modeled by the absorption from molecular clouds traced by CO and from diffuse
HI clouds where we used a spin temperature of 50 K in the HI clouds (see Brogan & Troland 2001).
The corrected line flux at 63
m from the absorption due to diffuse
and molecular clouds between -10 kms-1 and 100 kms-1 with the method described in Vastel et al. (2000).
The total absorption component is modeled by the absorption from molecular clouds traced by CO and from diffuse
HI clouds where we used a spin temperature of 50 K in the HI clouds (see Brogan & Troland 2001).
The corrected line flux at 63 ![]() m and the measured fluxes of the 145 and 158
m and the measured fluxes of the 145 and 158 ![]() m lines are listed in
Table 1. Note that the absorption of atomic oxygen from the HI clouds between 0 and 20 kms-1 is
less than 10% of the total flux of atomic oxygen in emission modeled by Gaussian.
We also checked the line fluxes in the grating mode and found that the [OI] 145
m lines are listed in
Table 1. Note that the absorption of atomic oxygen from the HI clouds between 0 and 20 kms-1 is
less than 10% of the total flux of atomic oxygen in emission modeled by Gaussian.
We also checked the line fluxes in the grating mode and found that the [OI] 145 ![]() m and [CII] 158
m and [CII] 158 ![]() m lines are similar to the Fabry-Pérot ones at better than 30%.
m lines are similar to the Fabry-Pérot ones at better than 30%.
| Line | Transition | Flux |
| ( |
(10-10 ergs-1cm-2) | |
|
|
3P
|
3.7 |
|
|
3P
|
0.54 |
|
|
2P
|
1.27 |
We observed the C16O J = 1
![]() 0 and C18O
J = 2
0 and C18O
J = 2
![]() 1 lines in May and November 1999 with the
15 meter SEST telescope (ESO - La Silla, Chile).
We simultaneously used two SIS receivers at 115 GHz and
230 GHz connected to an
Acousto-Optic Spectrometer that provided a spectral resolution of 43 kHz
in the two bands (0.105 kms-1 and 0.217 kms-1 respectively).
Typical SSB system temperatures during the observations were 190-250 K
and 250-380 K in the
two bands respectively. The beam size is 45
1 lines in May and November 1999 with the
15 meter SEST telescope (ESO - La Silla, Chile).
We simultaneously used two SIS receivers at 115 GHz and
230 GHz connected to an
Acousto-Optic Spectrometer that provided a spectral resolution of 43 kHz
in the two bands (0.105 kms-1 and 0.217 kms-1 respectively).
Typical SSB system temperatures during the observations were 190-250 K
and 250-380 K in the
two bands respectively. The beam size is 45
![]() at 115 GHz and 23
at 115 GHz and 23
![]() at 230 GHz. Pointing and focus were
monitored regularly, and pointing corrections were always found smaller
than
at 230 GHz. Pointing and focus were
monitored regularly, and pointing corrections were always found smaller
than ![]() 3
3
![]() .
We performed a five point cross around the
nominal position of the W49N HII region, with a 30
.
We performed a five point cross around the
nominal position of the W49N HII region, with a 30
![]() spacing
between the points. The goal was to obtain the emission line spectra averaged
over the ISO-LWS beam in order to compare C16O, C18O, [OI] and [CII] observations.
The CO spectra were therefore convolved with a Gaussian weighting function to degrade the
resolution of the SEST beam to 80
spacing
between the points. The goal was to obtain the emission line spectra averaged
over the ISO-LWS beam in order to compare C16O, C18O, [OI] and [CII] observations.
The CO spectra were therefore convolved with a Gaussian weighting function to degrade the
resolution of the SEST beam to 80
![]() .
Figure 3 shows the smoothed spectra.
The temperatures quoted in this paper are main beam temperatures.
It can be noticed that the lines appear in the five point cross around the central position.
.
Figure 3 shows the smoothed spectra.
The temperatures quoted in this paper are main beam temperatures.
It can be noticed that the lines appear in the five point cross around the central position.
![\begin{figure}
\par\includegraphics[width=8cm,height=8.3cm,clip]{CO_C18O.eps}\end{figure}](/articles/aa/full/2001/36/aa1417/Timg26.gif) |
Figure 3:
C16O
|
| Open with DEXTER | |
The goal of this section is to determine the average physical conditions in the PDR of W49N, using simple models to analyze the observed cooling lines. In the following, we will assume that the [OI] and [CII] lines are emitted in the same region dominated by the PDR.
Given the relatively low spectral and spatial resolution of ISO-LWS we need first to infer indirectly the value
of two key parameters, namely the sizes and the linewidth of the line emitting region.
Harvey et al. (1977) mapped W49N at 53 ![]() m with a 25
m with a 25
![]() (FWHM) beam. Their
cross-section scans in the directions SE-NW and NE-SW gives a continuum source size around 50
(FWHM) beam. Their
cross-section scans in the directions SE-NW and NE-SW gives a continuum source size around 50
![]() .
Comparison between the [CII] line emission and the FIR continuum emission in another similar PDR, namely towards
the L1630/NGC2024/Orion B cloud (Jaffe et al. 1994; Mookerjea et al. 2000), shows that the C+ region has sizes
similar or slightly larger than the continuum region. Assuming therefore that the [OI] and [CII] line extent is
similar or larger than the continuum extent, the W49N line emitting region is somewhat larger than 50
.
Comparison between the [CII] line emission and the FIR continuum emission in another similar PDR, namely towards
the L1630/NGC2024/Orion B cloud (Jaffe et al. 1994; Mookerjea et al. 2000), shows that the C+ region has sizes
similar or slightly larger than the continuum region. Assuming therefore that the [OI] and [CII] line extent is
similar or larger than the continuum extent, the W49N line emitting region is somewhat larger than 50
![]() but the emission originates from a region smaller than the LWS beam (80
but the emission originates from a region smaller than the LWS beam (80
![]() ). This is equivalent to a linear size between 2.8 and 4.5 pc.
). This is equivalent to a linear size between 2.8 and 4.5 pc.
The other key observational parameter to constrain is the intrinsic linewidth.
In Sect. 2.1 we showed that the [OI] 145 ![]() m and [CII] 158
m and [CII] 158 ![]() m lines have
linewidths equal to 16 kms-1.
Given the large LWS beam, it is likely that such relatively
large linewidth is due to the presence of several components in the beam.
As mentioned in the Introduction, the radio continuum map of
Welch et al. (1987) shows a 2-parsec ring of at
least 10 distinct ultracompact HII regions, each associated with at least one
O star.
From their H76
m lines have
linewidths equal to 16 kms-1.
Given the large LWS beam, it is likely that such relatively
large linewidth is due to the presence of several components in the beam.
As mentioned in the Introduction, the radio continuum map of
Welch et al. (1987) shows a 2-parsec ring of at
least 10 distinct ultracompact HII regions, each associated with at least one
O star.
From their H76![]() recombination line observations, they found that
the radial velocities of the HII regions are between 14.5 and -2.5 kms-1.
Therefore, the combination of this ring of spots can give
rise to the observed linewidth of 16 kms-1 (see Sect. 2.1).
Actually, the C18O spectrum of Fig. 3 confirms
the presence of several components in the cloud, whose total
velocity dispersion is about 16 kms-1.
In the following, we will assume that the observed FIR line emission originates
in these components and that each cloud component is micro-turbulent pressure
supported.
We adopt a Doppler b parameter equal to 3.5 kms-1, but we remark that the
calculated line intensities are not too sensitive to this value.
recombination line observations, they found that
the radial velocities of the HII regions are between 14.5 and -2.5 kms-1.
Therefore, the combination of this ring of spots can give
rise to the observed linewidth of 16 kms-1 (see Sect. 2.1).
Actually, the C18O spectrum of Fig. 3 confirms
the presence of several components in the cloud, whose total
velocity dispersion is about 16 kms-1.
In the following, we will assume that the observed FIR line emission originates
in these components and that each cloud component is micro-turbulent pressure
supported.
We adopt a Doppler b parameter equal to 3.5 kms-1, but we remark that the
calculated line intensities are not too sensitive to this value.
From the continuum observations in the grating mode, we can estimate the
average dust temperature. As usual, the continuum dust emission from
a homogeneous slab can be written in the form:
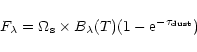 |
(1) |
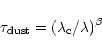 |
(2) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{w49N-continuum.eps}\end{figure}](/articles/aa/full/2001/36/aa1417/Timg35.gif) |
Figure 4:
Comparison between the LWS observed spectrum in the
grating mode (dotted line) and the best-fit greybody spectrum (solid line).
Units are 10-8 ergs-1cm-2 |
| Open with DEXTER | |
The total far-infrared flux of W49N can be calculated by integrating
Eq. (1) and with results
![]() ergs-1cm-2.
At a distance of 11.4 kpc, this corresponds to a total IR luminosity of
ergs-1cm-2.
At a distance of 11.4 kpc, this corresponds to a total IR luminosity of
![]() ,
in excellent agreement with the
previous estimate (
,
in excellent agreement with the
previous estimate (
![]() )
by Buckley & Ward-Thompson (1996), obtained using observations in
a larger wavelength range and with a larger beam size
(
)
by Buckley & Ward-Thompson (1996), obtained using observations in
a larger wavelength range and with a larger beam size
(
![]() ).
).
We have used a Large Velocity Gradient (LVG) code to model the flux of the [OI] lines as functions of the source physical conditions. The details of the code are
reported in Ceccarelli et al. (1998). For the present computations, we included
also photon pumping by the FIR dust continuum (see Sect. 3.2). The free parameters
of the LVG model are: the gas density and temperature, the size of the line emission
region, and the column density of atomic oxygen.
The dust temperature (43.5 K) and the linewidth (16 kms-1)
have been derived in the previous sections.
The line emitting region will be assumed to be between 50
![]() and 80
and 80
![]() in size, as discussed in Sect. 3.1.
The results of our computations are shown in Fig. 5, where we present the
63
in size, as discussed in Sect. 3.1.
The results of our computations are shown in Fig. 5, where we present the
63 ![]() m and 145
m and 145 ![]() m line emission for three column densities of atomic oxygen, as functions
of the gas temperature and density.
m line emission for three column densities of atomic oxygen, as functions
of the gas temperature and density.
![\begin{figure}
\par\includegraphics[width=14.6cm,clip]{plot_contour.eps}\end{figure}](/articles/aa/full/2001/36/aa1417/Timg39.gif) |
Figure 5:
Temperature versus density plots from our LVG model for a source size
of 50
|
| Open with DEXTER | |
In order to simultaneously account for the observed [OI] 63 ![]() m and 145
m and 145 ![]() m line fluxes,
the gas temperature has to be
m line fluxes,
the gas temperature has to be ![]() 130 K and the O column density has to be
130 K and the O column density has to be
![]() cm-2,
for a source extent of 50
cm-2,
for a source extent of 50
![]() ,
and a factor 2.5 lower for
a source extent of 80
,
and a factor 2.5 lower for
a source extent of 80
![]() .
.
In the optically thin limit, the column density of ionized carbon can be
derived from the observed line flux with a simple analytic expression as
a function of the gas temperature and density. Figure 6 shows
the column density of C+ computed assuming a beam size of 50
![]() and 80
and 80
![]() and a density equal to
104 cm-3 for a range of temperatures between 100 and 1000 K.
Within this range of temperatures N(C+) varies between 1.5
and a density equal to
104 cm-3 for a range of temperatures between 100 and 1000 K.
Within this range of temperatures N(C+) varies between 1.5
![]() and 4
and 4
![]() cm-2 if the source size is 50
cm-2 if the source size is 50
![]() and
it is a factor 2 lower for 80
and
it is a factor 2 lower for 80
![]() .
A higher gas density would give
the same results since the 158
.
A higher gas density would give
the same results since the 158 ![]() m line thermalizes at
m line thermalizes at ![]()
![]() cm-3 for
hydrogen impact excitation, whereas a lower density gas would require larger C+ column
densities.
Assuming a minimum gas temperature of 130 K, as estimated in Sect. 3.3,
the C+ column density is (0.8-2)
cm-3 for
hydrogen impact excitation, whereas a lower density gas would require larger C+ column
densities.
Assuming a minimum gas temperature of 130 K, as estimated in Sect. 3.3,
the C+ column density is (0.8-2)![]() 1018 cm-2.
Note that O/C+
1018 cm-2.
Note that O/C+ ![]() 2.5 if the line is emitted in a 50
2.5 if the line is emitted in a 50
![]() region, whereas O/C+
region, whereas O/C+ ![]() 1 if the emitting sizes are rather 80
1 if the emitting sizes are rather 80
![]() .
The measured gas phase elemental abundance ratio of O/C is 2.3 in the diffuse ISM (Cardelli et al. 1996; Meyer et al. 1998).
Since C+ and O are the dominant reservoir of carbon and oxygen in a PDR, this
would favor a 50
.
The measured gas phase elemental abundance ratio of O/C is 2.3 in the diffuse ISM (Cardelli et al. 1996; Meyer et al. 1998).
Since C+ and O are the dominant reservoir of carbon and oxygen in a PDR, this
would favor a 50
![]() source size.
source size.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{flux157.eps}\end{figure}](/articles/aa/full/2001/36/aa1417/Timg45.gif) |
Figure 6:
Computed flux of the [CII] line at 157.741 |
| Open with DEXTER | |
In this section we discuss how the [CII], [OI] and CO line emission
and line-to-continuum ratio can constrain the
physical conditions in the PDR; i.e., the average density and the intensity of
the incident FUV radiation field. A method of parameterizing
the FUV field incident on a cloud is through G0,
the strength of the 91-240 nm UV radiation field in units of the local
interstellar radiation field (Tielens & Hollenbach 1985a). A value of
G0 = 1 corresponds to a FUV
radiation field of
![]() ergs-1cm-2sr-1.
Assuming that the FUV is the main heating source of the dust,
the observed integrated infrared intensity toward W49N
(33.5 ergs-1cm-2sr-1) implies
ergs-1cm-2sr-1.
Assuming that the FUV is the main heating source of the dust,
the observed integrated infrared intensity toward W49N
(33.5 ergs-1cm-2sr-1) implies
![]() ,
in excellent agreement with the UV flux
of the HII regions in W49N, derived from radio observations by
De Pree et al. (2000).
,
in excellent agreement with the UV flux
of the HII regions in W49N, derived from radio observations by
De Pree et al. (2000).
Taking the value of
![]() ,
we can estimate the density of the PDR
using the predictions by the Wolfire et al. (1990; hereinafter
WTH90) PDR model. They presented especially useful contour plots of the
fine-structure emission and line ratios predicted as a function of G0 and n.
Using the observed [CII] 158
,
we can estimate the density of the PDR
using the predictions by the Wolfire et al. (1990; hereinafter
WTH90) PDR model. They presented especially useful contour plots of the
fine-structure emission and line ratios predicted as a function of G0 and n.
Using the observed [CII] 158 ![]() m/[OI] 63
m/[OI] 63 ![]() m line ratio, we derive a density
m line ratio, we derive a density
![]() cm-3 and a G0/n ratio
cm-3 and a G0/n ratio ![]() 30. In these conditions,
the [OI] 63 and 145
30. In these conditions,
the [OI] 63 and 145 ![]() m and [CII] 158
m and [CII] 158 ![]() m lines are expected to be the dominant
cooling lines (WTH90). Then the ratio between the derived total line intensity and the
FIR continuum intensity yields the grain photoelectric heating efficiency
m lines are expected to be the dominant
cooling lines (WTH90). Then the ratio between the derived total line intensity and the
FIR continuum intensity yields the grain photoelectric heating efficiency ![]() which is
the fraction of FUV photon energy which is converted to gas heating. This value is equal to
which is
the fraction of FUV photon energy which is converted to gas heating. This value is equal to
![]() in W49N and is relatively low
when compared to that of other studied PDRs, where
in W49N and is relatively low
when compared to that of other studied PDRs, where ![]() is typically
is typically
![]() (see Table 4 and the discussion in Sect. 4.3) and implies a
relatively large positive grain charge, in agreement with the relatively large G0/n ratio. In fact a large grain charge implies a high Coulomb barrier
that has to be overcome by the photo-ejected electrons and consequently a relatively
small fraction of the photon energy carried away by the electrons, reducing the
efficiency of the heating mechanism.
(see Table 4 and the discussion in Sect. 4.3) and implies a
relatively large positive grain charge, in agreement with the relatively large G0/n ratio. In fact a large grain charge implies a high Coulomb barrier
that has to be overcome by the photo-ejected electrons and consequently a relatively
small fraction of the photon energy carried away by the electrons, reducing the
efficiency of the heating mechanism.
Finally, we can estimate the mass in warm atomic gas, ![]() ,
from the observed [CII]
158
,
from the observed [CII]
158 ![]() m line flux, following the formalism by WTH90. Taking the values
m line flux, following the formalism by WTH90. Taking the values
![]() and
and
![]() cm-3, we derive an atomic hydrogen column
density of
cm-3, we derive an atomic hydrogen column
density of ![]()
![]() cm-2 from WTH90 Fig. 6 and an atomic gas
mass
cm-2 from WTH90 Fig. 6 and an atomic gas
mass
![]() .
Using our C18O observations we
can also estimate the mass of the molecular gas
.
Using our C18O observations we
can also estimate the mass of the molecular gas
![]() in the same beam of the
[CII] 158 observations. Assuming that the C18O line is optically thin and a
16O/18O ratio equal to 500, we find
in the same beam of the
[CII] 158 observations. Assuming that the C18O line is optically thin and a
16O/18O ratio equal to 500, we find
![]() = (1-2.5)
= (1-2.5)
![]() (e.g. Eqs. (14.115) by Rohlfs & Wilson 1999).
This value is in good agreement with previous estimates of the cloud mass
(
(e.g. Eqs. (14.115) by Rohlfs & Wilson 1999).
This value is in good agreement with previous estimates of the cloud mass
(
![]() ), obtained from 1300
), obtained from 1300 ![]() m continuum emission,
C18O (2
m continuum emission,
C18O (2
![]() 1) and CS (2
1) and CS (2
![]() 1)
observations in a beam larger that our 80
1)
observations in a beam larger that our 80
![]() (Schloerb et al. 1987; Miyawaki et al. 1986).
In practice, we find that between 2.4% and 6.2% of the gas mass resides
in the warm atomic surface layers of the molecular cloud heated by the newly formed
massive stars.
(Schloerb et al. 1987; Miyawaki et al. 1986).
In practice, we find that between 2.4% and 6.2% of the gas mass resides
in the warm atomic surface layers of the molecular cloud heated by the newly formed
massive stars.
Here we use a detailed PDR model to determine the physical structure of the
PDR whose parameters have been previously derived, namely
![]() and n= 104 cm-3. The physical and chemical properties
of a PDR depend on several parameters that may vary over a wide range of possible
values; i.e., the molecular hydrogen gas density and pressure, the intensity of the incident
FUV radiation field, the absorption and scattering properties of the dust grains,
the gas-phase elemental abundances, and the clumpiness of the cloud.
The code, described in Spaans (1996) and Spaans & van Dishoeck (1997), has been
adopted to a static, plane-parallel, semi-infinite slab which is exposed to an
isotropic FUV radiation field in a face-on configuration.
In our calculations we assume a constant hydrogen particle density throughout the
cloud of 104 cm-3 and adopt an incident FUV field equal to
and n= 104 cm-3. The physical and chemical properties
of a PDR depend on several parameters that may vary over a wide range of possible
values; i.e., the molecular hydrogen gas density and pressure, the intensity of the incident
FUV radiation field, the absorption and scattering properties of the dust grains,
the gas-phase elemental abundances, and the clumpiness of the cloud.
The code, described in Spaans (1996) and Spaans & van Dishoeck (1997), has been
adopted to a static, plane-parallel, semi-infinite slab which is exposed to an
isotropic FUV radiation field in a face-on configuration.
In our calculations we assume a constant hydrogen particle density throughout the
cloud of 104 cm-3 and adopt an incident FUV field equal to
![]() .
.
The chemical structure depends on the total gas-phase abundances of the heavy
elements. For the volatile elements, carbon and oxygen, we adopt
[C] = 1.4 ![]() 10-4 (Cardelli et al. 1996),
[O] = 3.2
10-4 (Cardelli et al. 1996),
[O] = 3.2 ![]() 10-4 (Meyer et al. 1998), and
[PAH] = 4
10-4 (Meyer et al. 1998), and
[PAH] = 4 ![]() 10-7 (Désert et al. 1990) relative to
hydrogen.
The photo-destruction rates depend on the incident FUV radiation field and on
the cloud depth z, while the cosmic-ray destruction rates depend on the
cosmic-ray hydrogen ionization rate. In our model we adopt an interstellar
cosmic-ray H2 ionization rate of
10-7 (Désert et al. 1990) relative to
hydrogen.
The photo-destruction rates depend on the incident FUV radiation field and on
the cloud depth z, while the cosmic-ray destruction rates depend on the
cosmic-ray hydrogen ionization rate. In our model we adopt an interstellar
cosmic-ray H2 ionization rate of
![]() s-1
(van der Tak & van Dishoeck 2000).
Table 2 lists the set of adopted model parameters.
s-1
(van der Tak & van Dishoeck 2000).
Table 2 lists the set of adopted model parameters.
| Parameter | Symbol | Value |
| Hydrogen particle density |
|
104 |
| FUV intensity | G0 | 3 |
| Turbulent Doppler width | b (kms-1) | 3.5 |
| Carbon abundance | [C] | 1.4 |
| Oxygen abundance | [O] | 3.2 |
| PAH abundance | [PAH] | 4 |
Given all these parameters, the model computes the emergent intensities of
the dominant cooling lines including the [CII] 158 ![]() m, [OI] 63 and
145
m, [OI] 63 and
145 ![]() m fine structure transitions. The emission of other lines like CO rotational lines,
[SiII] 35
m fine structure transitions. The emission of other lines like CO rotational lines,
[SiII] 35 ![]() m, [CI] 609
m, [CI] 609 ![]() m are predicted.
The model results are compared to the observations in Table 3.
m are predicted.
The model results are compared to the observations in Table 3.
| Observations | Model | |
| G0=3 |
||
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
no |
|
|
|
no |
|
| CO(
|
|
|
|
|
|
The lower limit of the observed [OI] 145 ![]() m and [CII] 158
m and [CII] 158 ![]() m
lines compares favorably with the model which is consistent with the assumption
that the size of the line emitting region is of the order of 80
m
lines compares favorably with the model which is consistent with the assumption
that the size of the line emitting region is of the order of 80
![]() .
In contrast, comparison between the upper limit of the observed [OI] 63
.
In contrast, comparison between the upper limit of the observed [OI] 63 ![]() m
line and the model would imply a smaller emitting region of 50
m
line and the model would imply a smaller emitting region of 50
![]() .
Assuming this 50
.
Assuming this 50
![]() extend for the cooling lines, the optically thin
[CII] 158
extend for the cooling lines, the optically thin
[CII] 158 ![]() m and [OI] 145
m and [OI] 145 ![]() m lines are somewhat low but still consistent
within a factor of two with the observations. This discrepancy is quite common in
detailed model fits (cf. Tielens & Hollenbach 1985b) and may reflect geometry effects
and/or different dust extinction properties. For example, a viewing angle of 60
m lines are somewhat low but still consistent
within a factor of two with the observations. This discrepancy is quite common in
detailed model fits (cf. Tielens & Hollenbach 1985b) and may reflect geometry effects
and/or different dust extinction properties. For example, a viewing angle of 60![]() rather than face-on would result in a factor 2 increase in the
intensity of optically thin lines without affecting much the intensity of optically
thick lines (i.e. [OI] 63
rather than face-on would result in a factor 2 increase in the
intensity of optically thin lines without affecting much the intensity of optically
thick lines (i.e. [OI] 63 ![]() m and CO
m and CO
![]() ).
Alternatively, a 20% change in the ratio of FUV dust absorption over visual
extinction changes the column density of warm gas (
).
Alternatively, a 20% change in the ratio of FUV dust absorption over visual
extinction changes the column density of warm gas (![]() 100 K at
100 K at
![]() mag) that emits these lines by a factor of 2.
mag) that emits these lines by a factor of 2.
Figure 7 displays the computed chemical structure of the PDR. The atomic and molecular abundances are sensitive to the cloud depth and many species show distinct abundance peaks at several locations through the cloud. The ionized carbon abundance decreases steadily with depth into the cloud as the FUV flux responsible for the ionization of carbon is attenuated. The CO abundance increases to a level at which most carbon is in the form of CO due to enhanced shielding of CO molecules deeper into the PDRs.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{ab_n1e4.ps}\end{figure}](/articles/aa/full/2001/36/aa1417/Timg78.gif) |
Figure 7:
Abundances of O, C+, C, CO and OH relative to hydrogen as a function of the depth
into the cloud parametrized by the total visual extinction, |
| Open with DEXTER | |
Figure 8 shows the gas temperature as a function of depth into the
cloud. The gas temperature initially increases with depth from
![]() K at
the cloud surface to a maximum of
K at
the cloud surface to a maximum of
![]() K at
K at
![]() .
The existence
of this temperature peak depends on the decrease of the grain charge with depth into
the cloud and on the increase of the optical depth in the main [OI] 63
.
The existence
of this temperature peak depends on the decrease of the grain charge with depth into
the cloud and on the increase of the optical depth in the main [OI] 63 ![]() m cooling
line. Once the grains are largely neutral deeper into the cloud, further FUV
attenuation leads to a decrease in the photo-electric heating rate and hence in the
temperature. The predicted temperature profile compares well with the average gas
temperature derived by the LVG model, i.e. between 250 K and 350 K (see
Fig. 5) with a density equal to 104 cm-3.
m cooling
line. Once the grains are largely neutral deeper into the cloud, further FUV
attenuation leads to a decrease in the photo-electric heating rate and hence in the
temperature. The predicted temperature profile compares well with the average gas
temperature derived by the LVG model, i.e. between 250 K and 350 K (see
Fig. 5) with a density equal to 104 cm-3.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{temp_n1e4.ps}\end{figure}](/articles/aa/full/2001/36/aa1417/Timg82.gif) |
Figure 8:
Thermal profile of the cloud as a function of depth into
the cloud parametrized by the total visual extinction, |
| Open with DEXTER | |
The column densities predicted by the PDR model are:
in the warm (![]() 100 K) surface layers
100 K) surface layers
![]() cm-2 and
cm-2 and
![]() cm-2,
while
cm-2,
while
![]() cm-2 and
cm-2 and
![]() cm-2 integrating up to
cm-2 integrating up to
![]() mag.
We remark that the column densities of the atomic oxygen and ionized carbon
computed by the detailed PDR model are in excellent agreement
with the estimates of the simpler LVG model.
mag.
We remark that the column densities of the atomic oxygen and ionized carbon
computed by the detailed PDR model are in excellent agreement
with the estimates of the simpler LVG model.
To summarize, our LVG model in combination with the WTH90 model give estimates of the main parameters of the PDR of W49N, which are confirmed by a detailed PDR model which takes the physics and chemistry of such region fully into account.
We now compare the PDR of W49N to other studied PDRs associated with HII
regions (30 Doradus, M 17, M 42), PDRs associated
with reflection nebulae and planetary nebulae (NGC 2068, NGC 7023, NGC 2023,
NGC 7027), PDRs associated with the nuclei of a starburst galaxy (M 82), and
PDRs associated with the nucleus of our Galaxy.
Table 4 lists the observed line fluxes of [OI] 63 ![]() m,
[OI] 145
m,
[OI] 145 ![]() m, [CII] 158
m, [CII] 158 ![]() m, CO (1
m, CO (1
![]() 0), the integrated
far infrared continuum intensity (FIR) and the computed UV field intensity G0.
0), the integrated
far infrared continuum intensity (FIR) and the computed UV field intensity G0.
| Sources | Distance | I(63) | I(145) | I(158) | I(CO(1-0)) | I(FIR) | Log(G0) | References | |
| (kpc) | 10-4 | 10-4 | 10-4 | 10-7 | 10-4 | ||||
| W49N | 11.4 | 31-80 | 4.6-12 | 11-28 | 4.6 | 33.5 | 5.5 | 1.4-3.6 | 1 |
| NGC 2023 | 0.48 | 36 | 2.3 | 6.8 | 1.5 | 1.1 | 4.2 | 41 | 2 |
| NGC 7027 | 1.1 | 1200 | 45 | 130 | 3.1 | 60 | 5.7 | 23 | 3 |
| M 82 | 3300 | 120 | 5.3 | 17 | 2.7 | 50 | 4.7 | 33 | 4 |
| Orion Bar | 0.47 | 400 | 20 | 60 | 4 | 5 | 4.6 | 110 | 5 |
| M17 SW | 2.5 | 150 | 19 | 26 | 7 | 6.7 | 4.7 | 47 | 6 |
| 30 Doradus | 49 | 4.9 | 0.4 | 5 | 0.1 | 0.6 | 3.7 | 17 | 7 |
| M 42 | 0.47 | 400-600 | 30-60 | 40-70 | 5.8 | 12 | 5 | 25 | 8 |
| NGC 7023 | 0.43 | 7.5 | 0.9 | 2.8 | 0.6 | 0.6 | 3.7 | 19 | 9 |
| NGC 2068 | 0.48 | 2.3 | 0.9 | 8.1 | 1.1 | 0.3 | 3.4 | 39 | 10 |
| Galactic centre 1 | 8.1 | 240 | 6.9 | 15 | 2.2-3.0 | 48 | 5.6 | 9.5 | 11 |
| Galactic centre 2 | 8.1 | 40 | 2.8 | 8.3 | 2.2-3.0 | 17 | 5.1 | 4 | 12 |
1) This paper. 2) Steiman-Cameron (1997); Milman et al. (1975). 3) Telesco & Harper (1977); Ellis & Werner (1984); Burton et al. (1990).
4) Telesco & Harper (1977); Stacey et al. (1991); WTH90. 5) Tauber et al. (1994).
6) Meixner et al. (1992). 7) Stacey et al. (1991), Poglitsch et al. (1995).
8) Crawford et al. (1985); WTH90. 9) Chokshi et al. (1988), Fuente et al. (2000).
10) Milman et al. (1975); Young Owl et al. (in preparation). 11
and 12) offset of ![]() = 0,
= 0, ![]() = 20
= 20
![]() for
position 1, and
for
position 1, and ![]() = 0,
= 0,
![]() for position
2, from
for position
2, from
![]() = 17h 44m 25.52s and
= 17h 44m 25.52s and
![]() = 28
= 28![]() 58
58![]() 1.7
1.7
![]() (WTH90).
(WTH90).
As already mentioned, the UV field in W49N is consistent with the O-5 to O-8 type
stars illuminating the several HII regions in the W49N core (De Pree et al. 2000).
W49N appears to be one of the most luminous and massive galactic HII regions
reflecting an enhanced star formation rate.
The compact HII region W49N is a very peculiar source in terms of its heating
efficiency which is a factor of ![]() 10 less than most others PDRs (in
Table 4) except for the position 2 in the direction of the Galactic
Centre, which has very similar characteristics to W49N.
The low photoelectric heating efficiency (
10 less than most others PDRs (in
Table 4) except for the position 2 in the direction of the Galactic
Centre, which has very similar characteristics to W49N.
The low photoelectric heating efficiency (![]() )
determined for W49N has been
explained in the previous sections by a relatively high UV field with respect to the
illuminated gas density (G0/n of
)
determined for W49N has been
explained in the previous sections by a relatively high UV field with respect to the
illuminated gas density (G0/n of ![]() 30).
30).
The ratio between the mass of atomic gas and the molecular gas in W49N, between 2% and 6%, can be compared with the 16% computed for the entire Orion Molecular Cloud (OMC-1)
and for the galactic centre (WTH90), and 40% for 30 Doradus which is the most luminous
and massive star-forming region in the Large Magellanic Cloud (Poglitsch et al. 1995). This ratio
reaches 10% within the central 330 pc for the starburst galaxy M 82 (WTH90), 20% in the
reflection nebula NGC 2023 and 30% in the planetary nebula NGC 7027 (Tielens & Hollenbach 1999).
The comparison between Orion and W49N is particularly instructive, being both galactic massive
star forming regions. Since they lie at about the same galactocentric distance they are likely
exposed to approximately similar external physical conditions. Therefore, their difference may
correspond to a different evolutionary stage. The molecular mass of the gas in the dense star
forming core OMC-1 in Orion (![]() 250
250 ![]() )
is 100 times smaller than in W49N
(
)
is 100 times smaller than in W49N
(![]()
![]() )
(WTH90; De Pree et al. 1997). The total number of Lyman continuum photons is
ten times larger in W49N than in Orion although the mass of ionized gas is 6 times larger in Orion
than in W49N (Churchwell & Goss 1999; De Pree et al. 1997). A simple explanation
is that the O-type stars formed in W49N have only just started to excavate their environment.
Moreover, Orion is the classic example of sequential massive star formation where the winds and supernova
explosion of one generation of massive stars triggers the formation of the next one (Elmegreen & Lada
1977). W49N seems to be in the earliest stage of this process where the first generation of massive stars
has just formed, possibly triggered by the collision of two giant molecular clouds.
In conclusion, the W49N complex is one of the youngest star-forming region in the Galaxy since
the surrounding molecular cloud has not yet been dispersed by the several embedded
newly formed massive protostars.
)
(WTH90; De Pree et al. 1997). The total number of Lyman continuum photons is
ten times larger in W49N than in Orion although the mass of ionized gas is 6 times larger in Orion
than in W49N (Churchwell & Goss 1999; De Pree et al. 1997). A simple explanation
is that the O-type stars formed in W49N have only just started to excavate their environment.
Moreover, Orion is the classic example of sequential massive star formation where the winds and supernova
explosion of one generation of massive stars triggers the formation of the next one (Elmegreen & Lada
1977). W49N seems to be in the earliest stage of this process where the first generation of massive stars
has just formed, possibly triggered by the collision of two giant molecular clouds.
In conclusion, the W49N complex is one of the youngest star-forming region in the Galaxy since
the surrounding molecular cloud has not yet been dispersed by the several embedded
newly formed massive protostars.
We report observations of [OI] and [CII] lines obtained with LWS on board the ISO
satellite in the high resolution spectral mode combined with grating observations.
We also present C16O 1
![]() 0 and C18O 2
0 and C18O 2
![]() 1
observations obtained with the SEST telescope in the same region encompassed by the
ISO-LWS beam.
1
observations obtained with the SEST telescope in the same region encompassed by the
ISO-LWS beam.
Using a LVG model and a more sophisticated PDR model we were able to determine the
physical structure of the PDR in W49N. This PDR is illuminated by an intense UV field
(
![]() )
created by the several massive protostars in the cloud.
The average gas density of the PDR is 104 cm-3. The gas temperature reaches a
peak of 360 K at
)
created by the several massive protostars in the cloud.
The average gas density of the PDR is 104 cm-3. The gas temperature reaches a
peak of 360 K at
![]() and decreases to
and decreases to ![]() 22 K in the shielded layers of
the cloud.
22 K in the shielded layers of
the cloud.
The photoelectric heating efficiency is very low,
![]() ,
when compared with the value of other similar PDRs,
,
when compared with the value of other similar PDRs, ![]() 10-3.
This is probably due to the relatively large UV field with respect to the
illuminated gas density, which creates highly charged grains making the
photoelectric ejection of the electrons more difficult.
10-3.
This is probably due to the relatively large UV field with respect to the
illuminated gas density, which creates highly charged grains making the
photoelectric ejection of the electrons more difficult.
Finally the fraction of the atomic gas in the cloud seems to be smaller than other PDRs, despite the presence of several O stars. This fact suggests that W49N is a relatively young star forming region, where the massive protostars did not yet have time to disperse the cloud.
Acknowledgements
We are grateful to D. Jansen for his assistance with some aspects of the PDR's thermal balance. We acknowledge the dedication of the LWS team which made these observations possible.