A&A 376, 1135-1146 (2001)
DOI: 10.1051/0004-6361:20010996
E. Athanassoula - Ch. L. Vozikis![]() - J. C. Lambert
- J. C. Lambert
Observatoire de Marseille, 2 place Le Verrier, 13248 Marseille Cedex 4, France
Received 22 February 2001 / Accepted 5 July 2001
Abstract
In this paper we measure the two-body relaxation time from the angular
deflection of test particles launched in a rigid configuration of field
particles. We find that centrally concentrated configurations have
relaxation times that can be shorter than those of the corresponding
homogeneous
distributions by an order of magnitude or more. For homogeneous
distributions we confirm that the relaxation time is proportional to
the number of particles. On the other hand centrally concentrated
configurations have a much shallower dependence, particularly for
small values of the softening. The relaxation time increases with the
inter-particle velocities and with softening. The latter dependence is
not very strong, of the order of a factor of two when the softening is
increased by an order of magnitude. Finally we show that relaxation
times are the same on GRAPE-3 and GRAPE-4, dedicated computer boards
with limited and high precision respectively.
Key words: celestial mechanics - stellar dynamics - galaxies: kinematics and dynamics - methods: N-body simulations
The relaxation time will obviously increase with the number of particles in the configuration, and tend to infinity as the number of particles tends to infinity, in which limit the evolution of the system will follow the collisionless Boltzmann equation. Thus the relaxation time of simulations will be much shorter than that of galaxies, which is much longer than the age of the universe. Relaxation leads to a loss of memory of the initial conditions and an evolution of the system towards a state of higher entropy. It is thus necessary to have good estimates of the relaxation times of N-body simulations, since we can trust their results only for times considerably shorter than that.
In the early times of N-body simulations, when the number of particles used was of the order of a few hundred, the authors by necessity gave estimates of relaxation times in order to enhance the credibility of their results. Unfortunately in most cases only simple analytical estimates were used and the corresponding relaxation times were found to be comfortably, although perhaps unrealistically, high. As computers became faster, the number of particles used in simulations was increased. Authors using several tens or hundreds of thousands particles deemed it unnecessary to include such simple estimates of the relaxation times, since it was well known that the simple analytical estimates would give reassuringly high relaxation times. Nevertheless, it is not clear whether the simple analytical estimates are in all cases sufficiently near the true values. This could well be doubted since the simple analytical estimates rely on a number of approximations, which are not in all cases valid.
Since different N-body methods may lead to different relaxation rates, it is of interest to discuss relaxation times when introducing a new method. It could thus have been feared that in a tree code (Barnes & Hut 1986) the relaxation time would not be determined by the number of particles, but by the number of nodes, which would then act as "super-particles''. Since the number of nodes is always much smaller than the number of particles, this would entail considerably shorter relaxation times than direct summation with the same number of particles, and thus constitute a major disadvantage of the tree code. This fear was put to rest by Hernquist (1987) who showed that the relaxation for tree code calculations does not differ greatly from that obtained by direct summation provided the tolerance parameter is less than 1.2. Similarly Hernquist & Barnes (1990) compare relaxation rates in direct summation, tree and spherical harmonic N-body codes, while Weinberg (1996) introduces a modification of the orthogonal function potential solver that minimises relaxation.
Several methods have been used to measure two-body relaxation. Standish & Aksnes (1969), Lecar & Cruz-Conzález (1972) and Hernquist (1987) have measured the angular deflection of test particles moving in a configuration of N field particles. Although this method has the disadvantage of not including collective effects, it has the advantage that all the parameters can be changed independently of each other, and that the results are easy to interpret. Theis (1998) performed semi-analytical calculations, assuming a homogeneous medium and also ignoring cumulative effects. The most widely used approach is to monitor the energy conservation of individual particles in systems in which, had it not been for the individual encounters, the individual energies would have been conserved. This method, which includes collective effects, is well suited for testing relaxation rates introduced by different codes, but can only be used with systems in equilibrium. It has been used e.g. by Hernquist & Barnes (1990), Hernquist & Ostriker (1992), Huang et al. (1993) and Weinberg (1996). Theuns (1996) measured the diffusion coefficients as a function of the energy in a direct summation N-body simulation by studying the properties of the random walk in energy space for particles of given energy and found very good agreement with theoretically calculated diffusion coefficients. Finally a number of studies (e.g. Farouki & Salpeter 1982, 1994; Smith 1992) rely on a measurement of the mass segregation, i.e. on the fact that, due to two-body encounters, high mass particles lose energy and spiral towards the center, while light ones gain energy and move to larger radii. Thus the configuration of the high mass particles contracts, while that of the light particles expands, and from the rate at which this happens we can calculate the two-body relaxation time.
In this paper we will calculate the relaxation times in a large number of cases, using the first of the methods mentioned above, i.e. by measuring deflection angles of individual trajectories of test particles in a configuration of rigid field particles. We will cover a much larger part of the parameter space than was done so far, and we will also extend to larger number of particles. All the calculations presented in this paper were made on the Marseille GRAPE-3, GRAPE-4 and GRAPE-5 systems. The Marseille GRAPE-3 systems have been described by Athanassoula et al. (1998), while a general description of the GRAPE-4 systems and their PCI interfaces has been given by Makino et al. (1997) and Kawai et al. (1997) respectively. A description of the GRAPE-5 board can be found in Kawai et al. (2000). Opting for a GRAPE system restricts us to a single type of softening, the standard Plummer softening, but has the big advantage of allowing us to make a very large number of trials, covering well the relatively large parameter space. Theis (1998) compared the relaxation rates obtained with the standard Plummer softening to those given by a spline (Hernquist & Katz 1989) and showed that the differences between the two are only of the order of 20-40%.
This paper is organised as follows: in Sect. 2 we briefly summarise the simple analytical estimates of the relaxation time. In Sect. 3 we describe the numerical methods used in this paper and discuss the validity of their approximations. Here we also introduce the mass models which will be used throughout this paper. The values of the parameters to be used, and in particular the values of the softening, are derived and discussed in Sect. 4. In Sect. 5 we give results for the relaxation time. We specifically discuss the effect of number of particles, of the velocity and of the softening, and compare results obtained with GRAPE-3 and GRAPE-4. We also give a prediction for the relaxation time in an N-body simulation. We summarise in Sect. 6.
The relaxation time for a single star can be defined as the time
necessary for two-body encounters to change its velocity, or energy, by
an amount of the same order as the initial velocity, or energy,
i.e. the time in which the memory of the initial values is lost. Thus
for the velocity we have
 |
(5) |
The appropriate values of
![]() and
and
![]() in
the above equations have
been discussed at length in the literature. Chandrasekhar (1942)
argued that
in
the above equations have
been discussed at length in the literature. Chandrasekhar (1942)
argued that
![]() is the value of b for which the
angular deflection
of the star is equal to
is the value of b for which the
angular deflection
of the star is equal to
![]() .
The value of
.
The value of
![]() has been subject to considerable controversy. Chandrasekhar (1942),
Kandrup (1980) and Smith (1992) have opted for a
has been subject to considerable controversy. Chandrasekhar (1942),
Kandrup (1980) and Smith (1992) have opted for a
![]() of
the order of the mean inter-particle distance, while others
(e.g. Spitzer & Hart 1971; Farouki & Salpeter
1982; Spitzer 1987)
used for
of
the order of the mean inter-particle distance, while others
(e.g. Spitzer & Hart 1971; Farouki & Salpeter
1982; Spitzer 1987)
used for
![]() a characteristic radius of the system. The
numerical simulations of Farouki & Salpeter (1994) argue
in favour of the latter. This is further corroborated by the
results of Theis (1998).
a characteristic radius of the system. The
numerical simulations of Farouki & Salpeter (1994) argue
in favour of the latter. This is further corroborated by the
results of Theis (1998).
Using the estimates
![]() ,
,
![]() and
assuming virial equilibrium, so that we can use for the velocity the
estimate
and
assuming virial equilibrium, so that we can use for the velocity the
estimate
![]() ,
we find
(Binney & Tremaine 1987)
,
we find
(Binney & Tremaine 1987)
It is clear that, for the number of particles used in present-day
simulations of collisionless systems and the appropriate values of the
softening, N is considerably larger than
![]() .
Since,
however, only the logarithms of these quantities enter in Eqs. (6) and (7), the differences in the estimates of the relaxation
times differ, for commonly used values of N, by less than a factor of
2. Equation (7)
is more appropriate, since it includes the softening. Often a
coefficient g is introduced in the Coulomb logarithm,
i.e.
.
Since,
however, only the logarithms of these quantities enter in Eqs. (6) and (7), the differences in the estimates of the relaxation
times differ, for commonly used values of N, by less than a factor of
2. Equation (7)
is more appropriate, since it includes the softening. Often a
coefficient g is introduced in the Coulomb logarithm,
i.e.
![]() .
Giersz & Heggie (1994) estimated
that the most appropriate value of g is 0.11. They also
compiled in their Table 2 the values given by several other
authors. They are all between 0.11 and 0.4. Independent of what is
chosen for the Coulomb logarithm, equations such as (6)
or (7) argue that even for a moderately low number
of particles, of the order of say a few thousands, the relaxation time
is comfortably high, of the order of, or higher than, 40 crossing
times.
.
Giersz & Heggie (1994) estimated
that the most appropriate value of g is 0.11. They also
compiled in their Table 2 the values given by several other
authors. They are all between 0.11 and 0.4. Independent of what is
chosen for the Coulomb logarithm, equations such as (6)
or (7) argue that even for a moderately low number
of particles, of the order of say a few thousands, the relaxation time
is comfortably high, of the order of, or higher than, 40 crossing
times.
Following Standish & Aksnes (1969), Lecar & Cruz-Conzález (1972) and Hernquist (1987) we will measure relaxation using the angular deflection suffered by a test particle moving in a configuration of N field particles fixed in space.
Let us consider a sphere of a given density profile represented by N fixed
particles, which we will hereafter refer to as field particles, and
let us place a test particle of zero mass at the edge of
this sphere either at rest, or with a radial velocity v. In the
limit of
![]() its trajectory
will be a straight line passing through the center of the sphere,
which we will hereafter call the theoretical trajectory. For
a finite N, however, the test particle will be
deflected by a number of encounters with the field particles and
thus it will cross the surface of the sphere at an angle
its trajectory
will be a straight line passing through the center of the sphere,
which we will hereafter call the theoretical trajectory. For
a finite N, however, the test particle will be
deflected by a number of encounters with the field particles and
thus it will cross the surface of the sphere at an angle ![]() from
the corresponding theoretical point. Following Standish & Aksnes
(1969), or Lecar & Cruz-Conzález (1972), we can
measure the relaxation time as
from
the corresponding theoretical point. Following Standish & Aksnes
(1969), or Lecar & Cruz-Conzález (1972), we can
measure the relaxation time as
We will repeat such calculations here, extending them to non-homogeneous density distributions, different initial velocities of the test particle and a larger range of field particle numbers N. This will allow us to discuss the effect of central concentration, of initial test particle velocities, of softening and of particle number on the relaxation time.
To find the effect of central concentration on the relaxation time we
use three different
mass distributions, namely the homogeneous sphere (hereafter model H),
the Plummer model (hereafter model P) and the Dehnen sphere (Dehnen
1993 - hereafter model D). For the Plummer model the density is
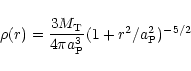 |
(10) |
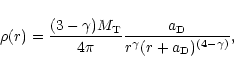 |
(11) |
These three models span a large range of central concentrations. They have the same cut-off radius, but the radius containing 1/10 of the total mass is for model D roughly one fourth of the corresponding radius for model P and roughly an order of magnitude smaller than that of model H. Similarly the radius containing half the mass for model D is roughly half of that of model P and a third of that of model H. These models will thus allow us to explore fully the effect of central concentration on the relaxation time.
We start 1000 test particles from random positions on the surface
of a sphere of radius 20 and with initial radial velocities equal to
![]() times
their theoretical escape velocity (hereafter
times
their theoretical escape velocity (hereafter
![]() ), calculated
from the model. The particles were advanced using a
leap-frog scheme with a fixed time-step of
), calculated
from the model. The particles were advanced using a
leap-frog scheme with a fixed time-step of
![]() .
We made sure this gives a sufficient accuracy by
calculating orbits without the use of GRAPE and with this
time-step. This showed that the energy is
conserved to 8 or 9 digits. We then repeated the exercise using a
Bulirsch-Stoer scheme (Press et al. 1992) and found that the
energy was conserved to 10 digits. Since an accuracy of 8 or 9 digits
is ample for our work, we adopted the leap-frog integrator and the
afore-mentioned time-step.
.
We made sure this gives a sufficient accuracy by
calculating orbits without the use of GRAPE and with this
time-step. This showed that the energy is
conserved to 8 or 9 digits. We then repeated the exercise using a
Bulirsch-Stoer scheme (Press et al. 1992) and found that the
energy was conserved to 10 digits. Since an accuracy of 8 or 9 digits
is ample for our work, we adopted the leap-frog integrator and the
afore-mentioned time-step.
The forces between particles were calculated using one of the Marseille GRAPE-3AF systems, except for the results given in Sects. 5.4 and 5.5, where we used the Marseille GRAPE-4 system.
For each model we take 10 different field particles distributions
and for each we calculate the 1000 test particles trajectories.
For simplicity the test particles are the same in each of the 10 field
particles distributions.
For each of the test particles we calculate ![]() and
the deflection angle from the theoretical (straight line)
orbit,
and
the deflection angle from the theoretical (straight line)
orbit, ![]() .
Then the relaxation time is calculated using Eqs. (8) and (9). The errors are obtained using
the bootstrap method (Press et al. 1992). In Figs. 3 to 5 error bars are plotted only when
.
Then the relaxation time is calculated using Eqs. (8) and (9). The errors are obtained using
the bootstrap method (Press et al. 1992). In Figs. 3 to 5 error bars are plotted only when
![]() .
.
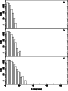 |
Figure 1:
Distribution of the number of test particles orbits that have a given
deflection angle, |
| Open with DEXTER | |
Equations (8) and (9) were derived
assuming small deflection angles. There could, however, be
cases in which a test particle comes very near a given field particle
and is very strongly deviated from its initial trajectory, so that the
deflection angle is greater than
90
![]() .
In that case Eqs. (8) and (9) are certainly not valid, particularly since for a
deflection of 180
.
In that case Eqs. (8) and (9) are certainly not valid, particularly since for a
deflection of 180
![]() they will give the same result as for 0
they will give the same result as for 0
![]() .
It is not easy to treat such deflections accurately, so what
we will do here is to keep track of their number and make sure that
it is sufficiently small so as not to influence our results. We have
thus monitored the number of orbits whose velocity component along the
axis which includes the initial radial velocity changes sign. We will
hereafter for brevity call such orbits looping orbits. None
were found for the homogeneous sphere distribution, and very
few, 3 in 10000 at the most, for the case of the Plummer sphere,
and that for the smallest of the softenings used here
(cf. Sect. 5.3 and Fig. 5). The largest
number of looping orbits was found, as expected, for model D
and the smallest
softening, i.e.
.
It is not easy to treat such deflections accurately, so what
we will do here is to keep track of their number and make sure that
it is sufficiently small so as not to influence our results. We have
thus monitored the number of orbits whose velocity component along the
axis which includes the initial radial velocity changes sign. We will
hereafter for brevity call such orbits looping orbits. None
were found for the homogeneous sphere distribution, and very
few, 3 in 10000 at the most, for the case of the Plummer sphere,
and that for the smallest of the softenings used here
(cf. Sect. 5.3 and Fig. 5). The largest
number of looping orbits was found, as expected, for model D
and the smallest
softening, i.e.
![]() .
For this case,
.
For this case,
![]() and N = 64000, we find of the
order of 30 such orbits in 10000. Although this is considerably
larger than the corresponding number for homogeneous and Plummer
spheres, it is still low enough not to influence much our statistics,
particularly if we take into account that it refers to an exceedingly
small softening. For the more reasonable value
and N = 64000, we find of the
order of 30 such orbits in 10000. Although this is considerably
larger than the corresponding number for homogeneous and Plummer
spheres, it is still low enough not to influence much our statistics,
particularly if we take into account that it refers to an exceedingly
small softening. For the more reasonable value
![]() ,
we
find that there are no looping orbits at all. We can thus safely
conclude that the number
of particles with looping orbits is too low to influence our results.
,
we
find that there are no looping orbits at all. We can thus safely
conclude that the number
of particles with looping orbits is too low to influence our results.
We still have to make sure that the remaining orbits have sufficiently
small deflection angles for Eqs. (8) and (9) to be valid. Figure 1 shows a
histogram of the number of test particles orbits that have a given
deflection angle, ![]() ,
as a function of that angle,
,
as a function of that angle, ![]() ,
for
model D, i.e. the one that should have the largest deflection
angles, with
,
for
model D, i.e. the one that should have the largest deflection
angles, with
![]() ,
,
![]() .
The upper panel
corresponds to N=4000, the middle one to N=2000 and the lower
one to N=1000. Note that we have used a logarithmic scale for the
ordinate, because otherwise the plot would show in all cases only a few
bins near
.
The upper panel
corresponds to N=4000, the middle one to N=2000 and the lower
one to N=1000. Note that we have used a logarithmic scale for the
ordinate, because otherwise the plot would show in all cases only a few
bins near
![]() .
.
For N=1000 there is one particle with deviation of
![]() ,
one
with
,
one
with
![]() and two with
and two with
![]() .
Furthermore only 30
trajectories, of a total of 10000, have a deflection angle larger
than
.
Furthermore only 30
trajectories, of a total of 10000, have a deflection angle larger
than
![]() .
The
numbers are even more comforting for N=2000, where only two
trajectories have a deflection angle larger than
.
The
numbers are even more comforting for N=2000, where only two
trajectories have a deflection angle larger than
![]() ,
and even
more so
for N=4000, where no particles reach that deflection angle. We can
thus conclude that in all but very few cases the small deflection
angle hypothesis leading to Eqs. (8) and (9) is valid.
,
and even
more so
for N=4000, where no particles reach that deflection angle. We can
thus conclude that in all but very few cases the small deflection
angle hypothesis leading to Eqs. (8) and (9) is valid.
We will calculate the values of the relaxation time as a function of three free parameters, namely the number of field particles, the initial velocity of the test particles and the softening. In this section we will discuss what the relevant ranges for these parameters are.
The question for the initial velocity is more convoluted. The simple
analytical approaches leading to Eqs. (6) and (7),
instead of taking a spectrum of velocities for the individual
encounters and then integrating over these velocities, introduce an
effective or average velocity and assume that all interactions are
made at this velocity. In our numerical calculations individual
encounters occur at different velocities, depending on their position
on the trajectory of the test particle and on the initial velocity of
this particle. We can, nevertheless, introduce
![]() ,
an
average or effective velocity, in a similar way as the analytical
approximation. A simple and straightforward, albeit not
unique, such definition can be obtained as follows:
let us assume that the test particle moves on a straight line. At each
point of its trajectory we can define a thin sheet going through this
point and locally perpendicular to the trajectory. It will contain all
field particles which have this point as their closest approach with
the test particle.
Let dr be the thickness of
this sheet and
,
an
average or effective velocity, in a similar way as the analytical
approximation. A simple and straightforward, albeit not
unique, such definition can be obtained as follows:
let us assume that the test particle moves on a straight line. At each
point of its trajectory we can define a thin sheet going through this
point and locally perpendicular to the trajectory. It will contain all
field particles which have this point as their closest approach with
the test particle.
Let dr be the thickness of
this sheet and
![]() the fraction of the total mass of the field
particles that is in it. Then we can define the effective velocity
the fraction of the total mass of the field
particles that is in it. Then we can define the effective velocity
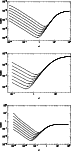 |
Figure 2:
MASE as a function of the softening |
| Open with DEXTER | |
The third free parameter in our calculations is the softening. Merritt
(1996; hereafter M96) and Athanassoula et al. (2000; hereafter
AFLB)
showed that, for a given mass distribution and a given number
of particles N, there is a value of the softening, called optimal
softening
![]() ,
which gives the most accurate
representation of the gravitational forces within the N-body
representation of the mass distribution. For values of the softening
smaller than
,
which gives the most accurate
representation of the gravitational forces within the N-body
representation of the mass distribution. For values of the softening
smaller than
![]() the error in
the force calculation is mainly due to noise, because of the
graininess of the configuration. For values of the softening larger than
the error in
the force calculation is mainly due to noise, because of the
graininess of the configuration. For values of the softening larger than
![]() the error is mainly due to the biasing, since the
force is heavily softened and therefore far from Newtonian.
Since the two-body
relaxation is also a result of graininess it makes sense to consider
softening values for which it is the noise and not the bias that
dominates, i.e. to concentrate our calculations mainly on values
of the softening which are smaller than or of the
order of
the error is mainly due to the biasing, since the
force is heavily softened and therefore far from Newtonian.
Since the two-body
relaxation is also a result of graininess it makes sense to consider
softening values for which it is the noise and not the bias that
dominates, i.e. to concentrate our calculations mainly on values
of the softening which are smaller than or of the
order of
![]() ,
keeping in mind that too small values of
the softening have no practical significance. The value of the optimal
softening
decreases with N and can be well approximated by a power law
,
keeping in mind that too small values of
the softening have no practical significance. The value of the optimal
softening
decreases with N and can be well approximated by a power law
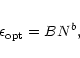
M96 and AFLB have calculated
![]() using the
mean average square error (MASE) of the force, which
measures how well the forces in an N-body representation of a given
mass distribution represent the true forces in this distribution. The average
square error (ASE) is defined as
using the
mean average square error (MASE) of the force, which
measures how well the forces in an N-body representation of a given
mass distribution represent the true forces in this distribution. The average
square error (ASE) is defined as
Figure 2 shows values of MASE as a function of ![]() for
the three models considered in Sects. 5.1 to 5.4 and seven values of N, in
the range of values considered here
(cf. Sect. 4.1). The general form of the curves is
as expected. There is in all cases a minimum error between the
region dominated by the noise (small values of the softening) and the
region dominated by the bias (large values of the softening). This
minimum - marked with a
for
the three models considered in Sects. 5.1 to 5.4 and seven values of N, in
the range of values considered here
(cf. Sect. 4.1). The general form of the curves is
as expected. There is in all cases a minimum error between the
region dominated by the noise (small values of the softening) and the
region dominated by the bias (large values of the softening). This
minimum - marked with a ![]() in Fig. 2 - gives the
value of
in Fig. 2 - gives the
value of
![]() .
For all three models a larger number of
particles corresponds to a smaller error and a smaller value of
.
For all three models a larger number of
particles corresponds to a smaller error and a smaller value of
![]() ,
as expected (M96, AFLB).
,
as expected (M96, AFLB).
The more concentrated configurations give smaller values of
![]() ,
as already discussed in AFLB. Thus for
,
as already discussed in AFLB. Thus for
![]() the optimum softening for model H is less than twice that of model P,
while the ratio between the softenings of models P and D is more than 10.
the optimum softening for model H is less than twice that of model P,
while the ratio between the softenings of models P and D is more than 10.
Comparing our results to those of AFLB we can get insight on the
effect of the truncation radius. For this it is best to compare our
results obtained with
![]() with those given by AFLB for
with those given by AFLB for
![]() ,
since these two N values are very close and we do not have
to make corrections for particle number. For our model P
and
,
since these two N values are very close and we do not have
to make corrections for particle number. For our model P
and
![]() we find an optimum softening of 0.52, or,
equivalently, 0.057
we find an optimum softening of 0.52, or,
equivalently, 0.057![]() ,
where
,
where ![]() is the scale
length of the Plummer sphere. This is smaller than the value
of 0.063
is the scale
length of the Plummer sphere. This is smaller than the value
of 0.063![]() found for the AFLB Plummer model and the
difference is due to the
different truncation radii of the two models. AFLB truncated their
Plummer sphere at a radius of 38.71
found for the AFLB Plummer model and the
difference is due to the
different truncation radii of the two models. AFLB truncated their
Plummer sphere at a radius of 38.71![]() ,
which encloses
0.999 of the total mass of the untruncated sphere, while model P is
truncated at 2.2
,
which encloses
0.999 of the total mass of the untruncated sphere, while model P is
truncated at 2.2![]() ,
which contains only 75% of total mass. The difference in the values
of
,
which contains only 75% of total mass. The difference in the values
of
![]() is in good agreement with the discussion in
Sect. 5.2 of AFLB. When the truncation radius is large, the model
includes a relatively high fraction of low density regions, where the
inter-particle distances are large. This is not the case if the
truncation radius is much smaller, as it is here. Thus the mean
inter-particle distance is larger in the former case and, as can
be seen from Fig. 11 of AFLB, the corresponding optimal softening
also. This predicts that the optimal softening should be smaller in
models with smaller truncation radius, and it is indeed what we
find here.
is in good agreement with the discussion in
Sect. 5.2 of AFLB. When the truncation radius is large, the model
includes a relatively high fraction of low density regions, where the
inter-particle distances are large. This is not the case if the
truncation radius is much smaller, as it is here. Thus the mean
inter-particle distance is larger in the former case and, as can
be seen from Fig. 11 of AFLB, the corresponding optimal softening
also. This predicts that the optimal softening should be smaller in
models with smaller truncation radius, and it is indeed what we
find here.
Our model H is the same as that of AFLB, except for the difference in
the cut-off radii. Thus the values of the optimum softening are the
same, after the appropriate rescaling with the cut-off radii has been
applied. Our model D differs in two ways from the corresponding model of
AFLB. We use here
![]() ,
while AFLB used
,
while AFLB used ![]() = 0. We also truncated our model at 6.5
= 0. We also truncated our model at 6.5![]() ,
while
AFLB truncated theirs at 2998
,
while
AFLB truncated theirs at 2998![]() .
It is thus not possible to make any qualitative or quantitative comparisons.
.
It is thus not possible to make any qualitative or quantitative comparisons.
| Model | A1 | B1 |
|
|
||
| H | 0.78 | 1.00 | 0.05 | 0.01 | ||
| P | 1.5 | 0.01 | 0.76 | 0.98 | 0.04 | 0.01 |
| D | 0.63 | 0.78 | 0.04 | 0.01 | ||
| H | 0.87 | 1.01 | 0.05 | 0.01 | ||
| P | 1.5 | 0.03 | 0.80 | 1.00 | 0.11 | 0.03 |
| D | 0.86 | 0.77 | 0.11 | 0.03 | ||
| H | 0.99 | 1.01 | 0.06 | 0.01 | ||
| P | 1.5 | 0.10 | 0.94 | 1.00 | 0.11 | 0.03 |
| D | 0.75 | 0.89 | 0.07 | 0.02 | ||
| H | 1.13 | 1.02 | 0.08 | 0.02 | ||
| P | 1.5 | 0.50 | 1.24 | 0.98 | 0.07 | 0.02 |
| D | 1.29 | 0.94 | 0.07 | 0.02 | ||
| H | 1.17 | 1.01 | 0.04 | 0.01 | ||
| P | 2.0 | 0.03 | 0.98 | 1.01 | 0.08 | 0.02 |
| D | 0.78 | 0.87 | 0.12 | 0.03 | ||
| P | 3.0 | 0.01 | 1.40 | 0.97 | 0.04 | 0.01 |
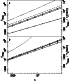 |
Figure 3:
Relaxation time as a function of the number of field
particles, for
|
| Open with DEXTER | |
Figure 3 shows the relaxation time as a function of the number
of particles for the models H, P and D described in the
previous section. The upper panel was
obtained for
![]() and
and
![]() and the lower one for
and the lower one for
![]() and
and
![]() .
As can be seen from Fig. 2, for the
first value of the softening
noise dominates over bias for all three models. For the second value noise
dominates for model H, bias dominates for model D, and we are near the
optimum value for model P and the high N values. The left ordinate
in Fig. 3 gives the
relaxation time while the right one gives the ratio of the relaxation
to transit time for the homogeneous sphere and
.
As can be seen from Fig. 2, for the
first value of the softening
noise dominates over bias for all three models. For the second value noise
dominates for model H, bias dominates for model D, and we are near the
optimum value for model P and the high N values. The left ordinate
in Fig. 3 gives the
relaxation time while the right one gives the ratio of the relaxation
to transit time for the homogeneous sphere and
![]() .
The corresponding values of this ratio for the
other two density distributions can be easily obtained if one takes
into account that for
.
The corresponding values of this ratio for the
other two density distributions can be easily obtained if one takes
into account that for
![]() the three theoretical
transit times are 20.35, 17.52 and 16.91, for the H, P and D models respectively.
We fitted straight lines
the three theoretical
transit times are 20.35, 17.52 and 16.91, for the H, P and D models respectively.
We fitted straight lines
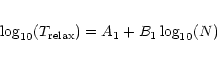
The dependence of
![]() on N is reasonably well represented by a
straight line in the log-log plane and that for all values of the
softening and
on N is reasonably well represented by a
straight line in the log-log plane and that for all values of the
softening and ![]() we tried and for all three models. The
relaxation time for model D
is always smaller than that for models P and H.
The difference is much more important (
we tried and for all three models. The
relaxation time for model D
is always smaller than that for models P and H.
The difference is much more important (![]() dex) for the smaller
value of the softening, than for the larger one
(
dex) for the smaller
value of the softening, than for the larger one
(
![]() dex). Similarly, the relaxation time for Plummer
distributions is somewhat smaller (
dex). Similarly, the relaxation time for Plummer
distributions is somewhat smaller (![]() dex) than that of the homogeneous
one for small values of the softening, while for the larger value the
two relaxation times do not differ significantly.
dex) than that of the homogeneous
one for small values of the softening, while for the larger value the
two relaxation times do not differ significantly.
Figure 3 and Table 1 also show a trend for the slopes of the straight lines. For the small softening the homogeneous model has a relaxation time which is roughly proportional to the number of field particles in the configuration, and that is in good agreement with Eq. (7). This is not true any more for the more centrally concentrated mass distributions, which have a value of B1less than unity. For model P the value of B1 is slightly less than unity, but for model D it is considerably so. Thus when we increase the number of particles in the configuration, we increase the relaxation time relatively less in more centrally concentrated configurations than in less centrally concentrated ones. In other words not only is the relaxation time smaller in the more centrally concentrated configurations, but also it takes more particles to increase it by a given amount.
These trends for the slopes of the straight lines are also present for
the larger value of the softening. The
differences, however, between the slopes, i.e. between the
corresponding values of B1, are much
smaller. Thus for
![]() and
and
![]() there is a
difference of roughly 25%
between the slopes corresponding to models H and D, while this value is
reduced to roughly 8% when
there is a
difference of roughly 25%
between the slopes corresponding to models H and D, while this value is
reduced to roughly 8% when
![]() .
.
Figure 3 also compares the prediction of
Eq. (7)
with the results of our numerical calculations for the homogeneous
sphere. The agreement is fairly good, particularly for the larger
softening, where the difference is of the order of 0.08 dex.
It should be noted that these predictions were obtained with
![]() ,
the cutoff radius of the system. A yet better agreement would have
been possible if one used
,
the cutoff radius of the system. A yet better agreement would have
been possible if one used
![]() ,
where f is a constant
larger than 1. Since, however, this constant is a function of the
softening used and perhaps also of the value of
,
where f is a constant
larger than 1. Since, however, this constant is a function of the
softening used and perhaps also of the value of ![]() ,
it is not very useful to determine its numerical value. The results obtained by
using
,
it is not very useful to determine its numerical value. The results obtained by
using
![]() ,
where l is the mean inter-particle distance, are
given by open squares. We note that they give a bad approximation of
the numerical results, particularly so for a large number of particles
and for the value of the softening
which is nearest to optimal. For the smaller softening the
approximation with
,
where l is the mean inter-particle distance, are
given by open squares. We note that they give a bad approximation of
the numerical results, particularly so for a large number of particles
and for the value of the softening
which is nearest to optimal. For the smaller softening the
approximation with
![]() is still considerably worse than
that obtained with
is still considerably worse than
that obtained with
![]() ,
but the difference is smaller than in the case of
the optimal softening. Whether this
will be reversed for an even smaller value of the softening or not is
not possible to predict from the above calculations. Nevertheless, if
it did happen, it would be for a value of the softening that gave a
very bad representation of the forces within model H.
Thus we can conclude that, at least for collisionless
simulations which have a reasonable softening, the simple analytical estimates
presented in Sect. 2 give a
reasonable approximation of the relaxation time if we use
,
but the difference is smaller than in the case of
the optimal softening. Whether this
will be reversed for an even smaller value of the softening or not is
not possible to predict from the above calculations. Nevertheless, if
it did happen, it would be for a value of the softening that gave a
very bad representation of the forces within model H.
Thus we can conclude that, at least for collisionless
simulations which have a reasonable softening, the simple analytical estimates
presented in Sect. 2 give a
reasonable approximation of the relaxation time if we use
![]() ,
but not if we use
,
but not if we use
![]() .
The latter
gives too high a value of the relaxation time, and is therefore
falsely reassuring.
.
The latter
gives too high a value of the relaxation time, and is therefore
falsely reassuring.
We also compared our results with theoretical estimates using
![]() for the Coulomb logarithm and different
values of g, as tabulated by Giersz & Heggie (1994). We
find that they always fare less well than Eq. (7) with
for the Coulomb logarithm and different
values of g, as tabulated by Giersz & Heggie (1994). We
find that they always fare less well than Eq. (7) with
![]() ,
particularly for
,
particularly for
![]() .
Amongst the
values tried,
g= 0.11, proposed by Giersz & Heggie (1994),
gave the best fit for
.
Amongst the
values tried,
g= 0.11, proposed by Giersz & Heggie (1994),
gave the best fit for
![]() ,
while the value g= 0.4(Spitzer 1987) was best for
,
while the value g= 0.4(Spitzer 1987) was best for
![]() .
The
differences between the results for various values of g are
nevertheless small.
.
The
differences between the results for various values of g are
nevertheless small.
To summarise this section we can say that more centrally concentrated distributions have smaller relaxation times and that the difference is more important for smaller values of the softening. This argues that the relaxation time is more influenced by the maximum rather than by the average density.
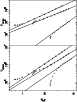 |
Figure 4:
Relaxation time as a function of the effective velocity
of the test
particles, for |
| Open with DEXTER | |
| Model | A2 | B2 |
|
|
|
| H | 4.84 | 2.72 | 0.02 | 0.04 | |
| P | 0.01 | 4.58 | 2.39 | 0.02 | 0.04 |
| D | 2.33 | 4.28 | 0.20 | 0.35 | |
| H | 5.20 | 2.83 | 0.01 | 0.02 | |
| P | 0.5 | 5.02 | 2.53 | 0.02 | 0.04 |
| D | 4.42 | 2.90 | 0.06 | 0.11 |
In order to test the effect of velocity on the relaxation time we have launched test particles with different initial velocities.
Figure 4 shows the relaxation time as a function of the
effective velocity of the particles, defined in
Sect. 4, for the
three density
distributions under consideration. The calculations have been made
with 64000 field particles and a softening of 0.01 for the upper
panel and 0.5 for the lower one. The dependence is linear in the
log-log plane for large values of the effective velocity and deviates
strongly from it for small values. We thus fitted a
straight line in the log-log plane to the higher velocities estimating
for each of the mass models separately the number of points that could
be reasonably fitted by a straight line. We give the constants of the
regression
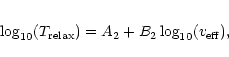
In all cases the relaxation
time increases with the initial velocity of the particles. In order to
compare this with the analytical predictions of
Sect. 2 we note that the deviation of a particle
from its trajectory due to an encounter
should be smaller for larger impact velocities (cf. Eq. (2)), while larger
impact velocities imply smaller crossing times. Thus from Eqs. (6) and (7) we note that
![]() should be proportional to the third power of the
velocity, i.e. that the coefficient B2 in Table 2
should be roughly equal to 3. We note that in the homogeneous case,
which should be nearer to the analytical result, there is a difference
of less than 10%, presumably due to the fact that the
approximations of the analytical approach are too harsh. The
differences with the results of models P and D are on average larger, but
strictly speaking, Eqs. (6) and (7)
do not apply to them.
should be proportional to the third power of the
velocity, i.e. that the coefficient B2 in Table 2
should be roughly equal to 3. We note that in the homogeneous case,
which should be nearer to the analytical result, there is a difference
of less than 10%, presumably due to the fact that the
approximations of the analytical approach are too harsh. The
differences with the results of models P and D are on average larger, but
strictly speaking, Eqs. (6) and (7)
do not apply to them.
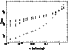 |
Figure 5:
Relaxation time as a function of the softening,
for |
| Open with DEXTER | |
Figure 5 shows the relaxation time
![]() as a function
of the softening
as a function
of the softening ![]() for the case of
for the case of ![]() and
and
![]() .
We note that the relaxation time increases with
softening as expected. There is no simple linear
dependence between the two plotted quantities. In fact the relaxation
time increases much faster with
.
We note that the relaxation time increases with
softening as expected. There is no simple linear
dependence between the two plotted quantities. In fact the relaxation
time increases much faster with
![]() for large values of the
softening than for small ones. The point at which this change of slope
occurs is roughly the same for models H and P,
and much smaller for model D. In fact in all cases
it is roughly at the position of the corresponding optimal softening,
which is roughly the same for models H and P and
considerably smaller for model D (cf. Sect. 4.3). Thus the change of
slope must correspond to a change between a noise dominated regime and
a bias dominated one.
for large values of the
softening than for small ones. The point at which this change of slope
occurs is roughly the same for models H and P,
and much smaller for model D. In fact in all cases
it is roughly at the position of the corresponding optimal softening,
which is roughly the same for models H and P and
considerably smaller for model D (cf. Sect. 4.3). Thus the change of
slope must correspond to a change between a noise dominated regime and
a bias dominated one.
In the noise dominated regime the sequence between the three models is the same as in previous cases. Namely it is model H that has the largest relaxation time, followed very closely by model P, and less closely by model D. It is interesting to note that for high values of the softening the three curves intersect. Such values, however, are too dominated by bias to be relevant to N-body simulations.
Figure 5 shows the only examples in this paper in
which the error bars are large enough to be
plotted, i.e. for which
![]() .
These
occur for the smallest values of the softening,
used here more for reasons of completeness than for their practical
significance.
.
These
occur for the smallest values of the softening,
used here more for reasons of completeness than for their practical
significance.
All results presented so far were made on one of the Marseille GRAPE-3
systems (Athanassoula et al. 1998). Such systems, however,
are known to have limited
accuracy, since they use 14 bits for the masses, 20 bits for the
positions and 56 bits for the forces. One could thus worry whether
this would introduce any extra graininess, which in turn would decrease the
relaxation time.
| N | G3 | G4 | |
| 1000 | 1040 | 1007 | 0.0328 |
| 2000 | 1626 | 1633 | 0.0043 |
| 4000 | 2698 | 2707 | 0.0033 |
| 8000 | 4834 | 4845 | 0.0023 |
| 16000 | 8143 | 8123 | 0.0025 |
| 32000 | 14490 | 14548 | 0.0040 |
| 64000 | 25858 | 25860 | 0.0001 |
In order to test this we repeated on GRAPE-4, which is a high accuracy
machine, some of the calculations made also with GRAPE-3. For this
purpose, we ran 7 configurations of model D with
![]() ,
,
![]() and different number of field
particles. The calculated relaxation time,
and different number of field
particles. The calculated relaxation time,
![]() ,
obtained by the GRAPE-3 and GRAPE-4 runs, together with their
differences, are shown in Table 3. As we can see
the results have, in all but one case, a difference less than 0.5%.
Only in the case of N=1000 does the difference rise to 3%, but as we
mentioned before, this very low number of particles is hardly used
nowadays, even in direct summation simulations on a general purpose computer.
,
obtained by the GRAPE-3 and GRAPE-4 runs, together with their
differences, are shown in Table 3. As we can see
the results have, in all but one case, a difference less than 0.5%.
Only in the case of N=1000 does the difference rise to 3%, but as we
mentioned before, this very low number of particles is hardly used
nowadays, even in direct summation simulations on a general purpose computer.
In the standard version of the angular deflection method we have used
so far all the test
particles start from the same radius with the same initial velocity. On the
other hand in any N-body realisation of a
given model the particles have different apocenters. It is thus
necessary to extend this method somewhat in order to obtain
an estimate of how long a given N-body
simulation will remain unaffected by two-body relaxation. Let us
consider a simple model consisting of a Plummer sphere of total mass
20 and scale length 9.2, truncated at
a radius equal to 30.125, i.e. at a radius containing roughly 7/8 of the total
mass. As an example we wish to estimate the relaxation time of a
74668-body![]() realisation of this model which will be evolved with
a softening of 0.5, a value near the optimal softening for
model P. For this we will somewhat modify the standard angular
deflection method in order to
consider several groups, starting each at a given radius. We first calculate
the relaxation time from each group separately. The relaxation time of
the model will be a weighted average of the relaxation times of the
individual groups. The weights have to be calculated in such a way
that the mean velocities with which the test particles encounter the
field particles at any given radius represent fairly well the encounter
velocities between any two particles in the N-body realisation,
which is not far from the dispersion of velocities. We found we could
achieve this reasonably well by considering 18 groups, of 10000 test
particles each, with apocenters
realisation of this model which will be evolved with
a softening of 0.5, a value near the optimal softening for
model P. For this we will somewhat modify the standard angular
deflection method in order to
consider several groups, starting each at a given radius. We first calculate
the relaxation time from each group separately. The relaxation time of
the model will be a weighted average of the relaxation times of the
individual groups. The weights have to be calculated in such a way
that the mean velocities with which the test particles encounter the
field particles at any given radius represent fairly well the encounter
velocities between any two particles in the N-body realisation,
which is not far from the dispersion of velocities. We found we could
achieve this reasonably well by considering 18 groups, of 10000 test
particles each, with apocenters
![]() .
Each group starts from a distance such that
.
Each group starts from a distance such that
![]() and
we weight the results of each by
3-i, i = 1,..18. These weighting factors
were just found empirically after a few trials and deemed adequate
since they give
an approximation of the velocity dispersion of the Plummer sphere of
the order of 10 per cent. It would of course be
possible to get a better representation by using a larger number of
groups and e.g. some linear programming technique, but since we only
need to have a rough approximation of the
encounter velocities and the fit we obtained is adequate, we did not
deem it necessary to complicate the problem unnecessarily.
and
we weight the results of each by
3-i, i = 1,..18. These weighting factors
were just found empirically after a few trials and deemed adequate
since they give
an approximation of the velocity dispersion of the Plummer sphere of
the order of 10 per cent. It would of course be
possible to get a better representation by using a larger number of
groups and e.g. some linear programming technique, but since we only
need to have a rough approximation of the
encounter velocities and the fit we obtained is adequate, we did not
deem it necessary to complicate the problem unnecessarily.
As expected, we find that the relaxation time and the transit time are
larger for groups with larger initial radius. The range of values we
find is rather large. Thus for the innermost group we find a
relaxation time of
![]() and a transit time of 4, while
for the outermost group the corresponding values are
and a transit time of 4, while
for the outermost group the corresponding values are
![]() and 51. The
weighted average of the relaxation time, taken over all orbits in
the representation, is
and 51. The
weighted average of the relaxation time, taken over all orbits in
the representation, is
![]() ,
and that of the transit
time 4.9, i.e. nearer to those of the inner groups due to their larger
weights.
,
and that of the transit
time 4.9, i.e. nearer to those of the inner groups due to their larger
weights.
A comparison with the estimates of the simple analytical formula given
in Eq. (7) is not straightforward, since one has to adopt a
characteristic radius, and the result is heavily dependent on
that. Thus if we adopt an outer radius, where the virial velocity is
small and therefore the crossing time large, we obtain very large
values of the relaxation time, like those we find for the outer parts
of our model Plummer sphere. On the other hand if we take the half
mass radius then we obtain
![]() ,
in good
agreement with our estimate obtained from the weighted average of all
groups.
,
in good
agreement with our estimate obtained from the weighted average of all
groups.
Our model P is sufficiently similar to the
![]() King model used by Huang et al. (1993) to
allow comparisons. These authors obtain the relaxation time by
monitoring the change of energy of
individual particles in a simulation. They consider only particles which at
the end of the
simulation are near the half mass radius and find a
relaxation time which, rescaled to our units, is
King model used by Huang et al. (1993) to
allow comparisons. These authors obtain the relaxation time by
monitoring the change of energy of
individual particles in a simulation. They consider only particles which at
the end of the
simulation are near the half mass radius and find a
relaxation time which, rescaled to our units, is
![]() .
Thus this estimate is based on a
group of particles which have their apocenters at or beyond the half mass
radius. Applying our own method only to such particles also we
obtain a relaxation time of
.
Thus this estimate is based on a
group of particles which have their apocenters at or beyond the half mass
radius. Applying our own method only to such particles also we
obtain a relaxation time of
![]() ,
which is in excellent agreement
with the value of Huang et al. (1993).
,
which is in excellent agreement
with the value of Huang et al. (1993).
In this paper we have calculated two-body relaxation times for different mass distributions, number of particles, softenings and particle velocities. For this we launched test particles in a configuration of rigid field particles and measured the relaxation time from the deflection angles (measured from the theoretical trajectory of the same particles) and the transit times.
We first determine the range of softening values for which the error in the force calculation is dominated by noise, rather than by bias. These extend to larger values of the softening for smaller number of particles and for less centrally concentrated configurations, in good agreement with what was found by AFLB. We also find them to be somewhat larger for models with a larger cut-off radius.
We confirm that the relaxation time increases with the number of particles. Indeed a larger number of particles entails a lesser graininess and thus a smaller effect of two-body encounters. In particular for homogeneous density distributions we confirm the analytical result that the relaxation time is proportional to the number of particles. We find, however, that this dependence does not hold for all mass distributions.
We find that the relaxation time depends strongly on how centrally concentrated the mass distribution is, in the sense that more centrally concentrated configurations have considerably shorter relaxation times. This can be understood if we make an N-body realisation not by distributing particles of equal masses in such a way as to follow the density, but by distributing the particles homogeneously in space and attributing to each one of them an appropriate mass. Our effect then simply follows from the fact that the deviation of a particle trajectory by a single very massive particle is larger than that due to a sum of low mass particles of the same total mass.
This dependence of relaxation time on central concentration is
strong. E.g. for a softening
![]() and a
and a ![]() of 1.5 the relaxation times of
models D and H (or P) differ by roughly an order of magnitude. In order to
achieve this difference by changing the number of particles one has to
increase them by a factor of 10 also. I.e. in order to avoid two-body
relaxation ten times more particles are necessary for a simulation
of model D than for one of model H, provided one
uses the same softening. The difference is even larger if the
softening is chosen to be optimal in each configuration, since the
optimal softenings differ by more than an order of magnitude, so an
extra factor of two is introduced to the necessary particle number.
of 1.5 the relaxation times of
models D and H (or P) differ by roughly an order of magnitude. In order to
achieve this difference by changing the number of particles one has to
increase them by a factor of 10 also. I.e. in order to avoid two-body
relaxation ten times more particles are necessary for a simulation
of model D than for one of model H, provided one
uses the same softening. The difference is even larger if the
softening is chosen to be optimal in each configuration, since the
optimal softenings differ by more than an order of magnitude, so an
extra factor of two is introduced to the necessary particle number.
Also the dependence of the relaxation time on the number of particles changes with the central concentration of the configuration. We find a shallower dependence for our more concentrated models, the difference being more important for smaller values of the softening. For a softening of 0.01 the difference in the exponent of the power law dependence is of the order of 20%.
We find that the relaxation time increases with velocity, as
expected. The reason is that the deflections in two-body encounters
are larger when the relative velocity is smaller. The dependence of
the relaxation time on the effective velocity is linear in a log-log
plane for the larger values of the effective velocity we have
considered and deviates
strongly from linear for smaller velocities. In the simple analytical
estimates of
Sect. 2,
![]() is proportional to the third
power of the velocity. Our more precise numerical estimates argue that
these estimates are only about 10% off for the case of the
homogeneous sphere, to which they apply.
is proportional to the third
power of the velocity. Our more precise numerical estimates argue that
these estimates are only about 10% off for the case of the
homogeneous sphere, to which they apply.
The strong decrease of relaxation time with encounter velocities entails that two-body relaxation has little effect in simulations of "violent'' events as collapses or mergings. On the other hand it may, depending on the configuration, the number of particles and the softening, play a role in simulations of quasi-equilibrium configurations. Furthermore two-body relaxation will be less of a menace in simulations of objects with high velocity dispersions, like giant ellipticals which are largely pressure supported, than in cases with less pressure and more rotational support, like small ellipticals or discs, putting aside of course the effects of shape and rotation, which we have not addressed here.
We have also examined the dependence of the relaxation time on softening. We find that, as expected, the relaxation time increases with softening. The dependence, however, is complicated, and not given by a simple mathematical formula. Nevertheless for the not too centrally concentrated models the increase is not too large. Thus for our models H and P we increase the relaxation time by a factor of the order of 2 if we increase the softening by a factor of 10. In this we agree well with Theis (1998). The only case where the increase is more pronounced is for model D and particularly for high values of the softening. It should, however, be remembered that this is a bias dominated regime. We can thus conclude that in the noise dominated regime the increase of the relaxation time with the softening is relatively small.
Finally we compared results obtained using GRAPE-3 with those found by GRAPE-4, and found they are similar. From the above results we can deduce that the relaxation times of the two types of GRAPE systems are essentially the same. This can be understood as follows. Athanassoula et al. (1998) argued that the limited precision of GRAPE-3 does not influence the accuracy with which the force is calculated since the error in the calculation of the pairwise forces can be considered as random (cf. their Fig. 5). This is in good agreement with what was initially argued by Hernquist et al. (1993) and Makino (1994), who pointed out that the two-body relaxation dominates the error and that the effect of the error in the force calculation is practically negligible, provided this error is random.
Our results for the relaxation time are always smaller than those
given by the simple analytical formula. The differences are relatively
small if one uses
![]() in the formula, but quite large
if one uses
in the formula, but quite large
if one uses
![]() .
Thus our results argue strongly that
the former is the right value to use, at least for collisionless
simulations. In this we agree with Spitzer & Hart (1971),
Farouki & Salpeter (1982), Spitzer (1987) and
Theis (1998). It should also be
noted that the analytical estimate obtained with
.
Thus our results argue strongly that
the former is the right value to use, at least for collisionless
simulations. In this we agree with Spitzer & Hart (1971),
Farouki & Salpeter (1982), Spitzer (1987) and
Theis (1998). It should also be
noted that the analytical estimate obtained with
![]() is
always considerably larger that the numerical result, and thus is falsely
reassuring.
is
always considerably larger that the numerical result, and thus is falsely
reassuring.
By extending somewhat the standard method based on the angular deflections we obtained an estimate for the relaxation time of an N-body simulation of a Plummer sphere. Comparing it with the results found by Huang et al. (1993) we find excellent agreement. This is very interesting since Huang et al. (1993) obtain their estimate of the relaxation time directly from an N-body simulation, i.e. include collective effects. This agreement could argue that such effects are not very large, and thus gives more weight to the results obtained with our simple and straightforward method.
It is often stressed that galaxies have so many stars that their relaxation times are far longer than the age of the universe, and thus that N-body simulations extending to long periods of time should have a very large number of particles to also achieve sufficiently large relaxation times. As a counter-argument one could say that real galaxies are not only composed of individual stars, but also of star clusters and gaseous clouds, which, being considerably more massive than individual stars, will introduce two-body relaxation and change the dynamics from that of a collisionless system. This, however, is no argument in favour of N-body simulations with short relaxation times, since the deviations from the evolution of a smooth stellar fluid brought by the graininess of the N-body system need not be the same as those brought by the compact objects, star clusters or gaseous clouds. It is thus necessary in N-body simulations to strive for high relaxation times and believe the results only for times considerably shorter than that. If desired, the effects of the compact objects, star clusters or gaseous clouds can then be studied separately.
Acknowledgements
We would like to thank A. Bosma for many useful discussions. We would also like to thank IGRAP, the INSU/CNRS, the region PACA and the University of Aix-Marseille I for funds to develop the computing facilities used for the calculations in this paper. C. Vozikis acknowledges the European Commission ERBFMBI-CT95-0384 T.M.R. postdoctoral grant and the hospitality of the Observatoire de Marseille.