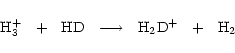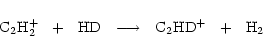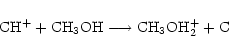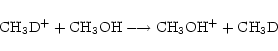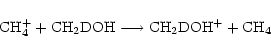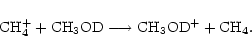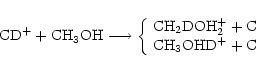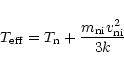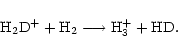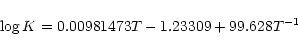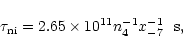A&A 376, 1054-1063 (2001)
DOI: 10.1051/0004-6361:20011022
Deuterium fractionation along the TMC-1 ridge
A. J. Markwick1 - S. B. Charnley2 - T. J. Millar1
1 -
Department of Physics, UMIST,
PO Box 88, Manchester M60 1QD, UK
2 -
Space Science Division, NASA Ames Research Center,
MS 245-3, Moffett Field, CA 94035, USA
Received 6 February 2001 / Accepted 12 July 2001
Abstract
In this paper, we present a model to predict and explain the observed gradients in deuterium fractionation and molecular abundance along the TMC-1 ridge. In TMC-1, gradients in the level of deuterium fractionation are observed for all the molecular species for which the measurement has been made;
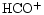 ,
,
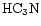 ,
,
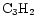 and HNC. The model is based on the assumption that the chemical evolution of the TMC-1 ridge has been affected by Alfvén waves. The structure of the model and its comparison with observations are discussed. We find that the model qualitatively and somewhat quantitatively reproduces the observations of the aforementioned molecular species. We present predictions of the fractionation gradients along the TMC-1 ridge for other molecules of observational interest.
and HNC. The model is based on the assumption that the chemical evolution of the TMC-1 ridge has been affected by Alfvén waves. The structure of the model and its comparison with observations are discussed. We find that the model qualitatively and somewhat quantitatively reproduces the observations of the aforementioned molecular species. We present predictions of the fractionation gradients along the TMC-1 ridge for other molecules of observational interest.
Key words: MHD: waves - ISM: abundances - ISM: molecules -
ISM: individual: Taurus Molecular Cloud - molecular processes
The cold, dark, interstellar cloud TMC-1 is most notable as a rich source of emission from complex organic molecules, particularly of carbon-chain species such as the polyacetylenes and cyanopolyynes, and for the strong spatial abundance gradients exhibited by them and other, simpler, molecules like SO,  and CCS (e.g. Olano et al. 1988; Pratap et al. 1997; see Fig. 1). For almost 20 years it has been the testbed for many theories of interstellar chemistry and yet no concensus has been reached as to the correct explanation of the apparently distinctive organic chemistry and its associated spatial differentiation. TMC-1 displays large enhancements in the deuterium enrichment of many molecules (Table 1), and also spatial gradients in the associated deuterium fractionation ratios along the ridge (Guélin et al. 1982; Bell et al. 1988; Howe et al. 1994; Hirota & Yamamoto 1998; Butner & Charnley 2001). These ratios, R(XD), are defined as quotients of number densities i.e. n(XD)/n(XH). Apart from the well-known cyanopolyyne peak (CP) and ammonia peak (AP), there is the
and CCS (e.g. Olano et al. 1988; Pratap et al. 1997; see Fig. 1). For almost 20 years it has been the testbed for many theories of interstellar chemistry and yet no concensus has been reached as to the correct explanation of the apparently distinctive organic chemistry and its associated spatial differentiation. TMC-1 displays large enhancements in the deuterium enrichment of many molecules (Table 1), and also spatial gradients in the associated deuterium fractionation ratios along the ridge (Guélin et al. 1982; Bell et al. 1988; Howe et al. 1994; Hirota & Yamamoto 1998; Butner & Charnley 2001). These ratios, R(XD), are defined as quotients of number densities i.e. n(XD)/n(XH). Apart from the well-known cyanopolyyne peak (CP) and ammonia peak (AP), there is the
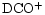 peak (DP). The DP is almost spatially coincident with the AP and
peak (DP). The DP is almost spatially coincident with the AP and
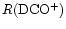 is seen to increase as one moves along the ridge from CP to AP (Guélin et al. 1982).
is seen to increase as one moves along the ridge from CP to AP (Guélin et al. 1982).
 |
Figure 1:
Schematic diagram of the TMC-1 ridge, adapted from Fig. 6 of Olano et al. (1988). The solid contours trace HC7N emission and the dotted contours show NH3. The distance shown is calculated assuming that the CP and AP are at the same distance from Earth. |
Table 1:
Deuteration at the CP position (04 38 38, +25 35 45).
| Species |
R(XD) |
f(XD) |
f(XH) |
Refs. |
| C3HD |
0.08 |
1.2(-9) |
1.5(-8) |
(1) |
| CH3CCD |
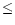 0.013 0.013 |
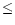 2(-10) 2(-10) |
1.7(-8) (2) |
|
| CH2DCCH |
0.054 |
9.2(-10) |
1.7(-8) |
(2) |
| CCD |
<0.03 |
<1.2(-11) |
4(-9) |
(3) |
| C4D |
0.004 |
2.3(-10) |
5.6(-8) |
(4) |
| HDCS |
0.02 |
1.2(-10) |
6.1(-9) |
(5) |
| DC3N |
0.03 |
6.6(-11) |
2.2(-9) |
(6) |
| DC5N |
0.016 |
- |
- |
(7) |
| DCO+ |
0.013 |
1.2(-10) |
8.4(-9) |
(8) |
References: (1) Bell et al. (
1988); (2) Gerin et al. (
1992); (3) Vrtilek et al. (
1985); (4) Turner (
1989); (5) Minowa et al. (
1997); (6) Langer et al. (
1979); (7) Schloerb et al. (
1981); (8) Butner & Charnley (
2001).
Gas phase deuteration is driven by the molecular ions
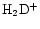 ,
,
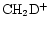 and
and
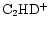 ,
which, because of the zero-point energy difference between
,
which, because of the zero-point energy difference between 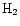 and HD, can persist at the temperatures (
and HD, can persist at the temperatures ( 10 K) of dark clouds. The R(XD) produced by ion-molecule reactions are sensitive to the gas temperature T, and the models of Millar et al. (1989) demonstrate that, as T increases, the deuteration due to each of these ions becomes less efficient. Temperatures of about 20 K are sufficient to to drive the reverse reaction of the primary deuteration process
10 K) of dark clouds. The R(XD) produced by ion-molecule reactions are sensitive to the gas temperature T, and the models of Millar et al. (1989) demonstrate that, as T increases, the deuteration due to each of these ions becomes less efficient. Temperatures of about 20 K are sufficient to to drive the reverse reaction of the primary deuteration process
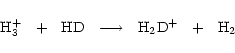 |
(1) |
and render it ineffective. However, even at 70 K, the reaction
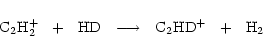 |
(2) |
produces enough
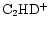 to maintain some enhanced, though residual, deuterium fractionation (Millar et al. 1989). Observations place the current gas temperature along the TMC-1 ridge to be in the range 10-15 K or less. This is insufficient to account for the spatial D/H gradients as being due to corresponding temperature gradients. Reaction (1) could be driven nonthermally by ambipolar diffusion caused by MHD wave motions cause ionized material to move relative to the neutral component (Charnley & Roberge 1991). Based on a crude treatment of the CO cooling, and associated uncertainties in the precise kinetics of reaction (1), Charnley (1998) showed that low wave amplitudes, and hence sufficiently low ion-neutral drift speeds,
to maintain some enhanced, though residual, deuterium fractionation (Millar et al. 1989). Observations place the current gas temperature along the TMC-1 ridge to be in the range 10-15 K or less. This is insufficient to account for the spatial D/H gradients as being due to corresponding temperature gradients. Reaction (1) could be driven nonthermally by ambipolar diffusion caused by MHD wave motions cause ionized material to move relative to the neutral component (Charnley & Roberge 1991). Based on a crude treatment of the CO cooling, and associated uncertainties in the precise kinetics of reaction (1), Charnley (1998) showed that low wave amplitudes, and hence sufficiently low ion-neutral drift speeds,
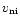 ,
such that there is negligible heating of the gas,
,
such that there is negligible heating of the gas,
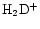 production could be suppressed to significant levels. Hence, the declining D/H ratios running NW
production could be suppressed to significant levels. Hence, the declining D/H ratios running NW
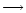 SE down the TMC-1 ridge (i.e. from the DP/AP region to the CP) could simply be due to a corresponding increase in
SE down the TMC-1 ridge (i.e. from the DP/AP region to the CP) could simply be due to a corresponding increase in
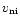 .
Of the D/H gradients that have been determined, namely those in DCO+, C3HD, DC3N, N2D+ (Butner & Charnley 2001) and DNC (Hirota & Yamamoto 1998), all are consistent with this interpretation.
.
Of the D/H gradients that have been determined, namely those in DCO+, C3HD, DC3N, N2D+ (Butner & Charnley 2001) and DNC (Hirota & Yamamoto 1998), all are consistent with this interpretation.
Markwick et al. (2000; hereafter Paper I) have modeled the spatial abundance gradients of TMC-1 as being due to the propagation of MHD waves along the ridge. The source of these waves could either be relative clump motions or, as favoured in Paper I, the embedded IRAS source IRAS 04381+2580. Markwick et al. showed that many of the molecular gradients observed by Pratap et al., including those of the large carbon-chain compounds, could be explained if simple hydrocarbons, such as methane and acetylene, were rapidly injected from dust grain mantles. Grain heating due to the relative drift of charged and neutral grains (at speed 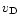 ), induced by MHD waves, was assumed to lead either to thermal evaporation of the most volatile species, or to complete mantle removal in an explosive event.
), induced by MHD waves, was assumed to lead either to thermal evaporation of the most volatile species, or to complete mantle removal in an explosive event.
In this paper we combine the work described in Paper I with that in Charnley (1998) to model the deuterium chemistry of TMC-1 in which gas phase deuteration through
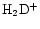 is largely suppresed in the vicinity of the CP, and simultaneously, enhanced abundances of heavily deuterated neutral molecules have been released from grain mantles into the gas. The deuterium fractionation in these mantles could have been set either by surface reactions or by a previous epoch of gas phase chemistry in which the products condensed out on to the dust (Tielens 1983; Brown & Millar 1989). Since little is known about the deuterium content of grain ice mantles, we assume throughout this work that the ratios in the ice are the same as the ratios in the gas. We are particularly interested in the injection of deuterated
is largely suppresed in the vicinity of the CP, and simultaneously, enhanced abundances of heavily deuterated neutral molecules have been released from grain mantles into the gas. The deuterium fractionation in these mantles could have been set either by surface reactions or by a previous epoch of gas phase chemistry in which the products condensed out on to the dust (Tielens 1983; Brown & Millar 1989). Since little is known about the deuterium content of grain ice mantles, we assume throughout this work that the ratios in the ice are the same as the ratios in the gas. We are particularly interested in the injection of deuterated
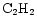 ,
,
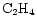 and
and 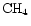 since these molecules are mainly responsible for the gradients seen in more complex organics and ions derived from them,
since these molecules are mainly responsible for the gradients seen in more complex organics and ions derived from them,
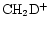 and
and
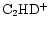 ,
can enhance specific gas phase deuteration pathways. In this scenario the D/H ratios observed in
,
can enhance specific gas phase deuteration pathways. In this scenario the D/H ratios observed in 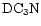 ,
,
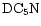 ,
CCD,
,
CCD,
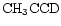 and
and
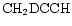 should reflect the competition between their production from the surface reservoir of D in
should reflect the competition between their production from the surface reservoir of D in 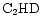 and
and 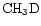 and deuteron-hydrogen exchange in gas-phase reactions.
and deuteron-hydrogen exchange in gas-phase reactions.
For example, deuterated acetylene should form deuterated cyanoacetylene through
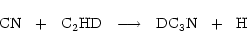 |
(3) |
and we wish to see if the observed gradient in R(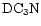 )
(Howe et al. 1994) can be produced in spite of D atom exchanges. Furthermore, as it has two detectable deuterated isotopomers,
)
(Howe et al. 1994) can be produced in spite of D atom exchanges. Furthermore, as it has two detectable deuterated isotopomers,
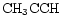 is a potentially important molecule. Methyl acetylene is understood to take up D in structurally different sites through gas phase reactions whose rates will be enhanced by the injection of deuterated mantles, e.g.
is a potentially important molecule. Methyl acetylene is understood to take up D in structurally different sites through gas phase reactions whose rates will be enhanced by the injection of deuterated mantles, e.g.
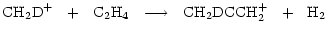 |
|
|
(4) |
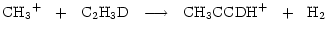 |
|
|
(5) |
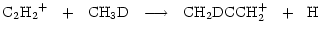 |
|
|
(6) |
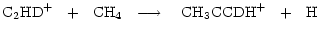 |
|
|
(7) |
where we have listed only those channels incorporating a D atom into protonated methyl acetylene.
The ability to reproduce the
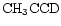 /
/
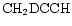 ratio in spite of gas phase D atom exchange reactions offers a detailed test of the theory proposed in Paper I.
ratio in spite of gas phase D atom exchange reactions offers a detailed test of the theory proposed in Paper I.
The aims of this paper are to model the deuterium chemistry under the constraints imposed by the observed fractionation ratios, R(XD), as well as their spatial gradients, and to predict associated values for potentially detectable species like C3D, DC7N and DCS+. In Sect. 2, we briefly review the relevant observations of deuterated molecules in TMC-1. The modification of our model of the chemistry along the TMC-1 ridge to include the effects of non-zero
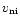 on the gas phase chemistry is described in Sect. 3. The extension of the chemical network to include deuterium and the initial conditions of the problem are also addressed in Sect. 3. The results of the study are presented in Sect. 4, and their sensitivity to model parameters is discussed in Sect. 5. The model itself can be applied to any cold dark interstellar clouds which support low-velocity Alfvén waves.
on the gas phase chemistry is described in Sect. 3. The extension of the chemical network to include deuterium and the initial conditions of the problem are also addressed in Sect. 3. The results of the study are presented in Sect. 4, and their sensitivity to model parameters is discussed in Sect. 5. The model itself can be applied to any cold dark interstellar clouds which support low-velocity Alfvén waves.
2 Observations of deuterated molecules in TMC-1
Compared to previous studies on nondeuterated species (e.g. Olano et al. 1988; Pratap et al. 1997), there is far less detailed information on the spatial gradients in R(XD) and for many species the level of fractionation has only been determined at TMC-1:CP. Exceptions are the 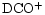 map of the entire ridge by Guélin et al. (1982) and the partial map in DC3N around the CP by Howe et al. (1994). Hirota & Yamamoto (1998) report a DNC map with the conclusion that the DNC/
map of the entire ridge by Guélin et al. (1982) and the partial map in DC3N around the CP by Howe et al. (1994). Hirota & Yamamoto (1998) report a DNC map with the conclusion that the DNC/
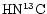 ratio increases as one moves from the CP to the DP/AP. A similar conclusion is reached by Butner & Charnley (2001) who also find that the
ratio increases as one moves from the CP to the DP/AP. A similar conclusion is reached by Butner & Charnley (2001) who also find that the
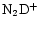 /
/
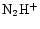 ratio increases more rapidly than that of
ratio increases more rapidly than that of 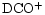 /
/
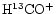 .
This information is summarised in Table 2. To convert the numbers into a test for the model presented here, we must consider the positions along the ridge at which the measurements were made. These positions are shown in Fig. 2. This spatial information, together with the values of fractionation allow us to estimate the fractionation gradients. From the data in Table 2, we see that
.
This information is summarised in Table 2. To convert the numbers into a test for the model presented here, we must consider the positions along the ridge at which the measurements were made. These positions are shown in Fig. 2. This spatial information, together with the values of fractionation allow us to estimate the fractionation gradients. From the data in Table 2, we see that
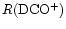 increases from 0.013 to about 0.040 between the CP and AP;
increases from 0.013 to about 0.040 between the CP and AP;
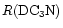 goes from 0.03 to at least 0.11 (this value is about halfway along the ridge, see Fig. 2);
goes from 0.03 to at least 0.11 (this value is about halfway along the ridge, see Fig. 2);
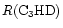 increases from 0.08 to 0.12. For all the molecules for which spatial information is available, a positive gradient in fractionation from CP to AP is seen.
increases from 0.08 to 0.12. For all the molecules for which spatial information is available, a positive gradient in fractionation from CP to AP is seen.
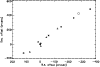 |
Figure 2:
Positions of mapping observations in DC3N (triangles), C3HD (squares) and DCO+ (stars). The (0,0) position is the CP (04 38 38, +25 35 45); (-276, 420) is the AP. |
Table 2:
Deuterium fractionation along the ridge. The offsets are in arcsec relative to the CP position (04 38 38, +25 35 45).
| DCO+ |
DC3N |
| Offset |
R(XD) |
Offset |
R(XD) |
| (120, -120) |
0.010 |
(75, -105) |
0.03 |
| (0, 0) |
0.013 |
(-4, 15) |
0.03 |
| (-60, 120) |
0.015 |
(-44, 95) |
0.06 |
| (-150, 240) |
0.030 |
(-124, 215) |
0.11 |
| (-240, 360) |
0.040 |
|
|
| (-360, 480) |
0.037 |
|
|
| |
|
|
|
| C3HD |
DNC |
| Offset |
R(XD) |
Offset |
R(XD) |
| (0, 0) |
0.08 |
(0, 0) |
0.028 |
| (-276, 420) |
0.12 |
(-276, 420) |
0.042 |
References: Butner & Charnley (2001); Howe et al. (1994); Bell et al. (1988); Hirota (2000).
To study the deuteration gradients, the model in Paper I has to be augmented in three ways.
Firstly, the reaction set obviously needs to include deuterated species, not a trivial process but
one which can be accomplished algorithmically if care is used.
Secondly, the level of the ion-neutral drift attained in the Alfvén wave gives ion-neutral
reaction rates a non-thermal component, so we need to follow the wave profile in real time, recalculating these rates as we go.
Finally, because we are following the wave profile properly, the grain ice mantles can be exploded at exactly the right time, i.e. when
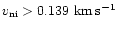 (see Paper I). The species desorbed are the same as in Paper I, with the addition of their deuterated counterparts. This introduces a new parameter in the model - the level of fractionation in grain ice mantles, but as noted above, we assume the ratios to be the same as in the gas phase.
(see Paper I). The species desorbed are the same as in Paper I, with the addition of their deuterated counterparts. This introduces a new parameter in the model - the level of fractionation in grain ice mantles, but as noted above, we assume the ratios to be the same as in the gas phase.
We now consider the first two modifications in more detail.
3.1 Fractionating a chemical network
The method described in this section is applied to hydrogen isotope fractionation, but could equally well be
applied to carbon, oxygen, or nitrogen for example.
There is not enough experimental data to create a deuterated ratefile by a literature search alone, so
some iterative procedure must be used. Such procedures have been discussed previously (e.g.
Bennett 1988) - the method used here is as follows.
Deuterating a ratefile can greatly increase the number of species and reactions it contains.
On investigation, it is found that the number of species will typically increase by 75% and the
number of reactions by a factor of three. From a computational point of view, the important
number to watch is the number of species, since this determines the number of ordinary
differential equations which have to be integrated. Therefore, for this study, we chose to start from a
smaller chemistry than that used in Paper I, with 250 species instead of 390. Briefly, all the species
involving phosphorus, chlorine and silicon, and some of the larger
organic molecules were removed from the Paper I chemical network. This returned a ratefile of around
2900 reactions. However, because in this study
we are particularly interested in, for example, CH3CCD and CH2DCCH, many of the species which
were previously designated by empirical formulae like CxHy had to be split up to allow us to
follow the abundances of the different isomers separately.
In general, the deuteration process is performed in a series of steps:
- 1.
- isolate individual species and work out the deuterated analogues;
- 2.
- totally deuterate the ratefile;
- 3.
- filter the result;
- 4.
- work out the rates assuming statistical branching ratios;
- 5.
- add fractionation reactions.
Taking methanol as an example species, we see from step (1) that there are 2 possible analogues, CH3OD and CH2DOH (we don't consider double deuteration yet). In step (2), the ratefile is fractionated by brute force, that is, for a reaction involving n (m) distinct groups of reactant (product) hydrogen atoms respectively, there will be 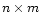 new reactions, e.g. for the reaction
new reactions, e.g. for the reaction
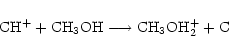 |
(8) |
in which n=3 and m=2, there will be 6 new reactions,
Some of the reactions resulting from this are removed, either because they do not preserve the reaction type, or because of the way the deuteron moves in the reaction. In the above set, for example, reactions (12) and (13) will be rejected, because we assume that a deuterium atom will not end up in the same molecule but in a different functional group. For the reaction
 |
(15) |
though there are 9 possible deuterium reactions, only the ones which preserve the charge transfer nature of the original reaction will be kept, that is, only
The last stage is to work out the branching ratios, which we take as statistical, except where there is experimental evidence to the contrary. Therefore, the reactions
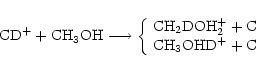 |
(16) |
have rates
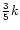 and
and
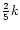 respectively, where the undeuterated reaction rate is k. This simply reflects the probability of the deuteron finishing in either group, assuming it has an equal chance of replacing any hydrogen atom.
respectively, where the undeuterated reaction rate is k. This simply reflects the probability of the deuteron finishing in either group, assuming it has an equal chance of replacing any hydrogen atom.
The whole chemistry is deuterated in this manner, including experimental reaction rates and branching ratios wherever such data exists. The fractionation reactions (reactions with no undeuterated analogue) are well known and can be found in Millar et al. (1989). The result is a reaction scheme with 8969 reactions connecting 434 species.
There is almost certainly a great deal of inaccuracy in the statistical branching ratio approach, especially given that there are some reactions whose rates are unstatistical and that not many of the reactions have been studied experimentally.
3.2 Ambipolar diffusion
The effect of ambipolar diffusion or ion-neutral drift induced by the Alfvén waves
is to increase the rates at which all the ion-neutral reactions occur. The non-thermal
rate can be calculated from the ion-neutral velocity
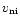 using an
"effective temperature'',
using an
"effective temperature'',
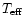 ,
given by
,
given by
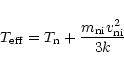 |
(17) |
(Draine 1980; Flower et al. 1985), where
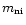 is the reduced mass of the reactants
and k is Boltzmann's constant. The ion-neutral velocity
is the reduced mass of the reactants
and k is Boltzmann's constant. The ion-neutral velocity
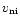 was taken from a model
of MHD disturbances in dense clouds developed by Roberge and co-workers (Roberge &
Hanany 1990; Roberge et al. 1995) and which was kindly made
available to us. These numerical values of
was taken from a model
of MHD disturbances in dense clouds developed by Roberge and co-workers (Roberge &
Hanany 1990; Roberge et al. 1995) and which was kindly made
available to us. These numerical values of
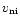 are presented in terms of the
dissipation time of Alfvén waves due to ion-neutral damping,
are presented in terms of the
dissipation time of Alfvén waves due to ion-neutral damping,
 .
Therefore,
given the physical conditions of the cloud, we can work out what the ion-neutral
velocity is at any time in the model, and hence calculate the rate coefficients for
that time step. The method as described only applies to reactions which have a
temperature dependence, a relatively small number of reactions, as it turns out. Furthermore, some of the reactions affected in this way have such severe energy barriers that they will still not proceed. Some do however, and these are precisely the reactions which are most important for fractionation, for example, the reaction
.
Therefore,
given the physical conditions of the cloud, we can work out what the ion-neutral
velocity is at any time in the model, and hence calculate the rate coefficients for
that time step. The method as described only applies to reactions which have a
temperature dependence, a relatively small number of reactions, as it turns out. Furthermore, some of the reactions affected in this way have such severe energy barriers that they will still not proceed. Some do however, and these are precisely the reactions which are most important for fractionation, for example, the reaction
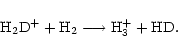 |
(18) |
Normally at 10 K this reaction does not happen as it has an energy barrier. It is this fact which
allows species to get chemically fractionated in the interstellar medium at all. However, when the temperature
(effective or actual) is above 20 K, the reaction rate increases dramatically. The rate for this particular
reaction is obtained from a polynomial fit to the equilibrium constant calculated by Sidhu et al. (1992).
The equilibrium constant is approximated by
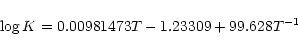 |
(19) |
and then the rate coefficient comes from
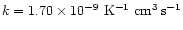 .
.
The higher reaction rate coefficient decreases the amount of H2D+ and
therefore the level of fractionation in all species which are fractionated through this ion. A similar thing
occurs for the other fractionating reactions. The net effect of all this is that deuterium fractionation is
heavily suppressed during the passage of the Alfvén wave. After the wave has passed, the reaction rate
returns to its normal 10 K value and fractionation has a chance to recover.
As in Paper I, the chemistry is evolved for 108 yr using the initial
abundances in Table 3. In this study, we took more representative values of the density and cosmic ray ionisation rate along the TMC-1 ridge, of
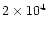 cm-3 and
cm-3 and
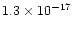 s-1 respectively (see Sect. 5 below). After 108 yr, the effects of the Alfvén wave propagation were introduced and followed.
s-1 respectively (see Sect. 5 below). After 108 yr, the effects of the Alfvén wave propagation were introduced and followed.
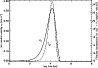 |
Figure 3:
The variation of the ion-neutral velocity
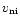 (solid line) and the effective temperature of the reaction (18) (dashed line) in the model.
(solid line) and the effective temperature of the reaction (18) (dashed line) in the model. |
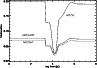 |
Figure 4:
The level of fractionation in certain important ions throughout the Alfvén wave model. |
Figure 3 shows the variation of the ion-neutral velocity and the effective temperature of
reaction (18) given by Eq. (17), starting from the steady state cloud composition. The rate of this reaction
increases by 6 orders of magnitude during
the wave passage - the effect of this on the abundance of H2D+, and of derivative fractionating
ions is shown in Fig. 4. How the fractionation suppression effect is passed
on to other deuterated species in the network depends on the formation routes of these species. The primary fractionating ions are H2D+, CH2D+ and C2HD+, but at 10 K, the most significant ion is by far H2D+. For example, we see that H2D+/H3+ is roughly a factor of three greater than DCO+/HCO+, as expected (e.g. Millar et al. 1989). We return to a detailed explanation of Fig. 4 below.
In Fig. 5, the variation of the fractionation in certain other species is shown. The curves show some interesting behaviour, with the fractionation
increasing and decreasing in seemingly arbitrary ways, and in different ways for different species. This is due to the combination of the effects of the mantle desorption and the fractionation suppression. The behaviour of the fractionation is much simpler if the two effects are treated separately.
In general, the fractionation goes through several changes, described below and briefly in Table 4.
Table 4:
Evolution towards steady-state.
| Epoch |
Time (yr) |
Comments |
| 1 |
t<103 |
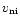 too low to cause effects
too low to cause effects |
| 2 |
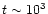 |
wave triggers mantle explosions |
| 3 |
103<t<105 |
ion-neutral reaction rates affected |
| 4 |
105<t<106 |
fractionation recovers |
| 5 |
t>106 |
steady state |
Consider the curve of
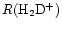 in Fig. 4 as an example. When t<103 yr, the ion-neutral velocity is too low to cause any of the effects on the chemistry considered here. In this region,
in Fig. 4 as an example. When t<103 yr, the ion-neutral velocity is too low to cause any of the effects on the chemistry considered here. In this region,
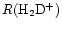 remains at its steady state value. Then, at
remains at its steady state value. Then, at
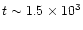 yr,
yr,
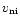 is large enough to trigger wave mantle explosions, and through the instantaneous desorption of mantle species, the fractionation is hit quite dramatically. Whether the fractionation goes up or down depends on how significant a mantle species is for the formation of either the species or its deuterated analogue.
is large enough to trigger wave mantle explosions, and through the instantaneous desorption of mantle species, the fractionation is hit quite dramatically. Whether the fractionation goes up or down depends on how significant a mantle species is for the formation of either the species or its deuterated analogue.
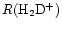 drops because the introduction into the gas-phase of the mantle species H2O is more significant for the destruction of H2D+ than for the destruction of H3+.
drops because the introduction into the gas-phase of the mantle species H2O is more significant for the destruction of H2D+ than for the destruction of H3+.
At times between
103<t<105 yr, the ion-neutral reactions are affected most, causing severe fractionation suppression. In fact, most of the deuterated ions depend on H2D+ for their formation, and the suppression takes longer to occur for derivative ions. This effect means that the fractionation troughs are not coincident, reflecting the distance in the network of the species from H2D+. That is why the curves of
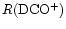 and
and
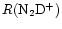 in Fig. 4 are almost coincident with that of
in Fig. 4 are almost coincident with that of
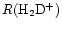 ,
but the curve of DC7N in Fig. 5 is not.
,
but the curve of DC7N in Fig. 5 is not.
The next epoch starts when
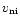 drops back to a level where the ion-neutral reaction rates return to their normal 10 K values. This happens at
drops back to a level where the ion-neutral reaction rates return to their normal 10 K values. This happens at
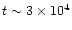 yr, and the chemical fractionation recovers as H2D+ now survives. After this point the chemistry is dominated by the addition of mantle species (as in Paper I) and eventually a steady state is reached. It is worth noting that the final steady state reached by the chemistry is not the same steady state as when the model began, because through the desorption of ice mantle species, the chemical composition of the gas has been altered.
yr, and the chemical fractionation recovers as H2D+ now survives. After this point the chemistry is dominated by the addition of mantle species (as in Paper I) and eventually a steady state is reached. It is worth noting that the final steady state reached by the chemistry is not the same steady state as when the model began, because through the desorption of ice mantle species, the chemical composition of the gas has been altered.
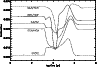 |
Figure 5:
The level of fractionation throughout the model for some species of interest. The complicated variation of the fractionation is due to the combined effects of mantle disruption and ion-neutral reaction rate alteration. |
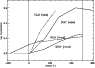 |
Figure 6:
The observed fractionation compared to the model results for DC3N and DCO+. The offsets have been calculated assuming that the AP and CP are equidistant from Earth. Although the sense of the gradients is correct, we significantly underestimate them. |
The time ordinate in the models can be converted into a spatial ordinate corresponding to distance along the TMC-1 ridge, and from this, a spatial gradient can be determined. The observed data on deuteration in TMC-1 was shown in Tables 1 and 2. As was previously discussed in Paper I, the limiting factor in choosing the times which correspond to the endpoints of the ridge is just the wave speed, which at 2 km s-1 gives the age difference of the CP and AP as
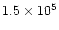 yr. The choice of the absolute age at the CP position is arbitrary, but since we wish to retain the result of Paper I, namely the production of molecular abundance gradients, we choose the time at the CP to be when HC7N is at a maximum. The spatial gradients in the level of deuterium fractionation produced by the model are shown in Table 5. The molecular abundance gradients are shown in Table 8 and will be discussed below.
yr. The choice of the absolute age at the CP position is arbitrary, but since we wish to retain the result of Paper I, namely the production of molecular abundance gradients, we choose the time at the CP to be when HC7N is at a maximum. The spatial gradients in the level of deuterium fractionation produced by the model are shown in Table 5. The molecular abundance gradients are shown in Table 8 and will be discussed below.
All the molecular species exhibit a gradient in the correct sense and of comparable magnitude to the observations. However, the model underestimates the gradients, sometimes significantly. This is most apparent in Fig. 6, which shows the model results compared to the observational measurements of DC3N and DCO+ along the ridge. Of the species for which mapping observations have been made, C3HD and DC3N achieve levels of fractionation in TMC-1 which continue to remain unexplained by gas phase chemistry. While Table 6 shows that both the model presented here and the model of Roberts & Millar (2000) produce a level of fractionation in HC3N comparable to the observed value at TMC-1:CP, the difference lies away from the cyanopolyyne peak where the fractionation rises sharply. Compared to the observed fractionation at TMC-1:CP, where many more species have been observed, the agreement is quite good.
Table 5:
Comparison of the model results with observations of fractionation gradients along the TMC-1 ridge.
The gradients are the change in log (fractionation) between TMC-1:CP (0,0) and the point indicated.
| Species |
Endpoint |
Observed |
Model |
| DCO+ |
(-240, 360) |
0.50 |
0.25 |
| DC3N |
(-124, 215) |
0.56 |
0.22 |
| C3HD |
(-276, 420) |
0.18 |
0.10 |
| DNC |
AP |
0.18 |
0.16 |
Table 6:
Comparison of the model with the observed deuteration at TMC-1:CP. The column RM2000 shows the steady state fractionation obtained by Roberts & Millar (2000). * Only CH2DCCH is included in model RM2000, not CH3CCD.
| Species |
Observed |
Model |
RM2000 |
| C3HD |
0.08 |
0.017 |
0.020 |
| CH3CCD |
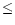 0.013 0.013 |
0.008 |
- |
| CH2DCCH |
0.054 |
0.070 |
0.099* |
| CCD |
<0.03 |
0.020 |
0.027 |
| C4D |
0.004 |
0.017 |
0.029 |
| HDCS |
0.02 |
0.050 |
0.046 |
| DC3N |
0.03 |
0.014 |
0.026 |
| DC5N |
0.016 |
0.010 |
0.026 |
| DCO+ |
0.013 |
0.056 |
0.087 |
| DNC |
0.028 |
0.022 |
0.015 |
| DCN |
0.023 |
0.022 |
0.025 |
| HDCO |
0.005-0.11 |
0.046 |
0.055 |
| N2D+ |
0.08 |
0.056 |
0.052 |
| NH2D |
0.009-0.014 |
0.020 |
0.028 |
Table 7 presents predicted gradients from the model for various molecular species. The species which are most interesting from the point of view of this study are species which have already been observed in TMC-1 and for which mapping observations may be possible, and species which have not yet been observed but which could be in the future. Deuterated methyl acetylene (CH2DCCH) is particularly interesting as it has one of the highest known levels of fractionation in TMC-1 (see Table 1). From Table 7 we see that it is predicted to have one of the steepest gradients. An observed value of the spatial fractionation gradient for this molecule would be a good test of the model presented here.
Table 7:
Predicted gradients for some species of potential observational interest. The gradients are given as the change in log fractionation along the ridge from TMC-1:CP to TMC-1:AP.
| Species |
Gradient |
Species |
Gradient |
| CD |
0.23 |
CH2DCCH |
0.27 |
| OD |
0.14 |
DC5N |
0.40 |
| N2D+ |
0.24 |
DC7N |
0.20 |
| DCS+ |
0.30 |
C3D |
0.07 |
| CCD |
0.12 |
C4D |
0.19 |
| HDCS |
0.30 |
HDCO |
0.20 |
| NH2D |
0.13 |
DCN |
0.21 |
Table 8 shows the molecular abundance gradients obtained in the same way as Table 4 in Paper I, for comparison. The "goodness'' of each model, shown in the Table, is defined as the number of abundance gradients which the model places inside the observed constraints from Pratap et al. (1997). In terms of this quantity, the models presented in this paper and in Paper I are identical. However, while some species gradients are produced better in this new model than before (e.g. CN, HCN), some are not, most noteably methanol. The chemistry of methanol in a mantle desorption model was discussed in Paper I, in the context of the formation of cumulenone molecules (H2CnO, n>2). In this sense, and because of the results shown in Table 8, the chemistry of methanol in TMC-1 is very interesting indeed, and will be the subject of a future paper.
The model presented here has a high number of adjustable parameters, not only physical, such as T, n, 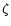 and Av, but chemical as well. These include the ionisation fraction x, the composition of ice mantles, and the level of fractionation therein. Because of the sheer number of adjustable parameters and the lack of data available to constrain them, the problem of fitting the observational data correctly could degenerate into a simple problem of optimisation. However, it is appropriate to examine the parameter space a little further.
and Av, but chemical as well. These include the ionisation fraction x, the composition of ice mantles, and the level of fractionation therein. Because of the sheer number of adjustable parameters and the lack of data available to constrain them, the problem of fitting the observational data correctly could degenerate into a simple problem of optimisation. However, it is appropriate to examine the parameter space a little further.
In the model presented here and in Paper I, the temperature has always been 10 K and the visual extinction 15 mag. The density and cosmic ray ionisation rate have a special role in the fractionation gradients model, because they determine the wave profile. Recall that the dissipation time is given by
where n4 is the molecular hydrogen density in units of 104molecules cm-3 and x-7 is the fractional abundance of
electrons in units of 10-7 (see Paper I). Throughout the model, the ionisation fraction is calculated as the sum of all the abundances of gaseous ions. A higher value for 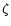 increases this value and therefore decreases
increases this value and therefore decreases
 ,
as does a higher value of the density. Because
,
as does a higher value of the density. Because
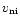 is obtained from a profile which depends on
is obtained from a profile which depends on
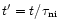 ,
a lower dissipation time means that the gas is less affected by the propagation of the wave. This is particularly important for the fractionation gradients, because it determines the length of time that the ion-neutral reaction rates are influenced, which in turn controls the suppression of the fractionation process. Therefore, the gradients can be directly influenced by changing n and
,
a lower dissipation time means that the gas is less affected by the propagation of the wave. This is particularly important for the fractionation gradients, because it determines the length of time that the ion-neutral reaction rates are influenced, which in turn controls the suppression of the fractionation process. Therefore, the gradients can be directly influenced by changing n and 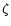 .
It is this fact which prompted the change of the values of these parameters from the values quoted in Paper I, although, as noted above, this makes little difference to those results.
.
It is this fact which prompted the change of the values of these parameters from the values quoted in Paper I, although, as noted above, this makes little difference to those results.
Table 9:
Assumed ice mantle composition prior to explosive desorption.
| Species |
A |
B |
| H2O |
100 |
100 |
| CH4 |
10 |
2 |
| C2H2 |
5 |
- |
| C2H4 |
0.5 |
- |
| CH3OH |
- |
20 |
| CO2 |
- |
15 |
| H2CO |
- |
5 |
| HCOOH |
- |
5 |
| NH3 |
- |
15 |
| OCS |
- |
0.2 |
What is of more interest is whether the results can be obtained using a lower value of the ion-neutral speed. Currently, the maximum value attained is
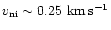 .
The wave mantles explode when
.
The wave mantles explode when
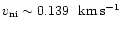 ,
just over half the current maximum value. Therefore we can afford a wave which is roughly half as severe to still obtain mantle explosions. The effect of reducing the maximum velocity goes as the square of
,
just over half the current maximum value. Therefore we can afford a wave which is roughly half as severe to still obtain mantle explosions. The effect of reducing the maximum velocity goes as the square of
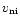 for the ion-neutral rate change (Eq. (17)), so a 50% reduction in
for the ion-neutral rate change (Eq. (17)), so a 50% reduction in
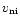 translates to a 75% reduction in
translates to a 75% reduction in
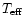 .
.
The level of fractionation in the ice mantles has been assumed to be the same as in the gas phase. The only available measurement of a deuterated ice mantle species is of HDO, observed in W33A and NGC 7538 IRS9 by Teixeira et al. (1999). The observations, however, are based on a tentative ISO detection of the O-D stretching mode at 4.1 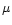 m, and so are not conclusive. Ignoring this, the value reported corresponds to a ratio
m, and so are not conclusive. Ignoring this, the value reported corresponds to a ratio
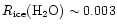 ,
a factor of ten lower than the gas phase value at the time of mantle desorption in our model. Also, it appears that there is little observational evidence for either acetylene or ethlyene in ice mantles, outside the indirect evidence inferred from models like those presented here.
,
a factor of ten lower than the gas phase value at the time of mantle desorption in our model. Also, it appears that there is little observational evidence for either acetylene or ethlyene in ice mantles, outside the indirect evidence inferred from models like those presented here.
To study the effect of varying the species desorbed, and how sensitive the results are to these species, a model was run which adheres strictly to observations of mantle species. Gibb et al. (2000) present an inventory of interstellar ices towards infrared sources, reproduced here as Col. B in Table 9. (Note that methanol appears as a 20% fraction of water, cf. Paper I.) The results of this model run for our species of interest are shown in Fig. 7 for comparison with the original model, labelled column A in the table. It can be seen that for the species in the figure, the qualitative behaviour of the curves is similar, reflecting the fact that it is only the possibility of extra carbon that creates the gradient effects - it does not make much difference which species are desorbed, as long as these are able to provide reactive carbon. Species containing sulphur are greatly affected in this run of the model however, because of the large amount of sulphur which is desorbed in the form of OCS.
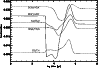 |
Figure 7:
The level of fractionation throughout the model for some species of interest where the desorbed mantle species adhere strictly to observations. The marked difference in the DCS+ curve is due to the desorption of OCS. |
In this paper, we have described an investigation into the effects of Alfvén waves on interstellar dark cloud chemistry, specifically applied to fractionation gradients observed along the TMC-1 ridge. We considered the explosive desorption of grain ice mantles and the alteration of ion-neutral reaction rates by ambipolar diffusion as a means for producing the molecular abundance and deuterium fractionation gradients observed along the TMC-1 ridge.
In Paper I, the Alfvén wave hypothesis was shown to be
capable of explaining the molecular abundance gradients along the TMC-1 ridge, and in this paper, we have extended the model naturally to attempt to account for the fractionation gradients as well. We find that the model qualitatively and somewhat quantitatively reproduces the observations, although there is only relevant published data for four molecular species. More observations of deuterated molecules at positions other than the cyanopolyyne peak would be good tests of this model, and we presented predicted gradients for this purpose.
The model presented here underestimates the fractionation gradients, which suggests that there is a process which contributes to the increase of levels of deuteration which we have not included. This could be one of the following. First, it is well known that accretion of gas-phase material onto dust grains can increase fractionation (Roberts & Millar 2000 and references therein). At present we do not allow material to accrete back onto the grains after it is desorbed, although the timescale for accretion is similar to the time in the model at which our results are produced. Second, the assumption of statistical branching ratios in the process of creating a deuterium chemistry is demonstrably incorrect for some species, where dissociatve recombination favours the retention of deuterons (e.g. Jensen et al. 2000). Where experimental data exists it has been used, but this is only the case for a small number of species. Finally, the effect of periodically sweeping the gas with Alfvén waves has not been considered here and could have important consequences for deuterium fractionation in interstellar clouds. These topics will be discussed further in a future paper.
Acknowledgements
Research in Astrophysics at UMIST is supported by PPARC. A. J. M. acknowledges the support of the SETI Institute for a visit to NASA Ames in July 1999. Theoretical astrochemistry at NASA Ames
is supported by NASA's Origins of Solar Systems and Exobiology Programs. A. J. M thanks the referee for making suggestions which improved the paper.
- Bell, M. B., Avery, L. W., Matthews, H. E., et al. 1988, ApJ, 326, 924
In the text
NASA ADS
- Bennett, A. 1988, in Rate Coefficients in Astrochemistry, ed. T. J. Millar, & D. A. Williams (Kluwer Boston), 339
In the text
- Brown, P. D., & Millar, T. J. 1989, MNRAS, 240, 25
In the text
- Butner, H., & Charnley, S. B. 2001, in preparation
In the text
- Charnley, S. B. 1998, MNRAS, 298, L25
In the text
NASA ADS
- Charnley, S. B., & Roberge, W. G. 1991, in Molecular Clouds, ed. R. A. James, & T. J. Millar (Cambridge University Press), 246
In the text
- Draine, B. T. 1980, ApJ, 241, 1021
In the text
NASA ADS
- Flower, D., Pineau des Forêts, G., & Hartquist, T. W. 1985, MNRAS, 216, 775
In the text
NASA ADS
- åGerin, M., Combes, F., Wlodarczak, G., Encrenaz, P., & Laurent, C. 1992a25329
In the text
- Gibb, E. L., et al. 2000, ApJ, 536, 347
In the text
NASA ADS
- åGuélin, M., Langer, W. D., & Wilson, R. W. 1982107107
In the text
- Hirota, T. 2000, Ph.D. Thesis
In the text
- Hirota, T., & Yamamoto, S. 1998, in Star Formation 1999, ed. T. Nakamoto (Nobeyama Radio Observatory), 171
In the text
- Howe, D. A., Millar, T. J., Schilke, P., & Walmsley, C. M. 1994, MNRAS, 267, 59
In the text
NASA ADS
- Langer, W. D., Frerking, M. A., Linke, R. A., & Wilson, R. W. 1979, ApJ, 232, 169
In the text
- Langer, W. D., Graedel, T. E., Frerking, M. A., & Anmentrout, P. B. 1984, ApJ, 277, 581
NASA ADS
- Markwick, A. J., Millar, T. J., & Charnley, S. B. 2000, ApJ, 535, 256
In the text
NASA ADS
- Millar, T. J., Bennett, A., & Herbst, E. 1989, ApJ, 340, 906
In the text
NASA ADS
- Minowa, H., Satake, M., Hirota, T., et al. 1997, ApJ, 491, L63
In the text
NASA ADS
- åOlano, C., Walmsley, C. M., & Wilson, T. L. 1988196194
In the text
- Pratap, P., Dickens, J. E., Snell, R. L., et al. 1997, ApJ, 486, 862
In the text
NASA ADS
- Roberge, W. G., & Hanany, S. 1990, BAAS, 22, 862
In the text
- Roberge, W. G., Hanany, S., & Messinger, D. W. 1995, ApJ, 435, 238
In the text
- åRoberts, H., & Millar, T. J. 2000361388
In the text
- Schloerb, F. P., Snell, R. L., Young, J. S., & Langer, W. D. 1981, ApJ, 251, L37
In the text
NASA ADS
- åSidhu, K. S., Miller, S., & Tennyson, J. 1992255453
In the text
- åTeixeira, T. C., Devlin, J. P., Buch, V., & Emerson, J. P. 199934719
In the text
- åTielens, A. G. G. M. 1983119177
In the text
- Turner, B. E. 1989, ApJ, 347, 39
In the text
- Vrtilek, J. M., Gottlieb, C. A., Langer, W. D., Thaddeus, P., & Wilson, R. W. 1985, ApJ, 296, 35
In the text
Copyright ESO 2001