A&A 376, 518-531 (2001)
DOI: 10.1051/0004-6361:20010968
K.-H. Hofmann1 - Y. Balega2 - M. Scholz3,4 - G. Weigelt1
1 - Max-Planck-Institut
für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
2 -
Special Astrophysical Observatory, Nizhnij Arkhyz, Zelenchuk region, Karachai-Cherkesia,
357147, Russia
3 -
Institut für Theoretische Astrophysik der Universität Heidelberg, Tiergartenstr. 15,
69121 Heidelberg, Germany
4 -
Chatterton Department of Astronomy, School of Physics, University of Sydney NSW 2006, Australia
Received 14 May 2001 / Accepted 28 June 2001
Abstract
We present diffraction-limited (30 mas resolution) bispectrum
speckle interferometry of the Mira
star R Leo with the 6 m
SAO telescope.
The speckle interferograms were recorded through narrow-band interference
filters with centre wavelength/bandwidth of 673 nm/8 nm
(strong TiO absorption band), 656 nm/10 nm, 699 nm/6 nm and 781 nm/14 nm (moderate TiO absorption),
754 nm/6 nm (weak TiO absorption), and 1045 nm/9 nm (continuum).
The reconstructed images show that the average uniform-disk diameters of
R Leo are 60.6 mas ![]() 3.0 mas at 656 nm, 75.6 mas
3.0 mas at 656 nm, 75.6 mas ![]() 3.7 mas at 673 nm,
52.5 mas
3.7 mas at 673 nm,
52.5 mas ![]() 2.5 mas at 699 nm, 48.7 mas
2.5 mas at 699 nm, 48.7 mas ![]() 2.3 mas at 754 nm,
55.0 mas
2.3 mas at 754 nm,
55.0 mas ![]() 2.7 mas at 781 nm, and 37.9 mas
2.7 mas at 781 nm, and 37.9 mas ![]() 4.0 mas at 1045 nm.
In all six observed wavelength bands the shape of R Leo shows no significant asymmetry.
We compare
our observations with Mira star models and check the
ability of monochromatic linear diameters for discriminating between
model representations of the observed star. Monochromatic
4.0 mas at 1045 nm.
In all six observed wavelength bands the shape of R Leo shows no significant asymmetry.
We compare
our observations with Mira star models and check the
ability of monochromatic linear diameters for discriminating between
model representations of the observed star. Monochromatic
![]() radii were derived from the observed visibilities
by application of
model-predicted center-to-limb variations of the intensity.
Adopting the HIPPARCOS parallax
we derived from the 1045 nm-observation a photospheric radius
(Rosseland
radii were derived from the observed visibilities
by application of
model-predicted center-to-limb variations of the intensity.
Adopting the HIPPARCOS parallax
we derived from the 1045 nm-observation a photospheric radius
(Rosseland
![]() radius) of R Leo
of 417
radius) of R Leo
of 417
![]() (19.2 mas
(19.2 mas ![]() 2.0 mas)
indicating pulsation in the first-overtone mode.
From JHKL photometry and the angular photospheric radius an effective
temperature of
2.0 mas)
indicating pulsation in the first-overtone mode.
From JHKL photometry and the angular photospheric radius an effective
temperature of
![]() K at near maximum phase was obtained.
K at near maximum phase was obtained.
Key words: techniques: interferometric - methods: observational - stars: AGB and post-AGB - stars: imaging - stars: late-type - stars: variables: general - stars: individual: R Leo
High-resolution
interferometric observations of Mira stars allow the study of the size of the stellar disk,
photospheric asymmetries, surface inhomogenities, and the wavelength, pulsation phase
and pulsation cycle dependence of the diameter
(see, e.g., Pease 1931; Bonneau & Labeyrie 1973; Labeyrie et al. 1977;
Bonneau et al. 1982; Karovska et al. 1991; Haniff et al. 1992; Quirrenbach et al. 1992;
Wilson et al. 1992; Tuthill et al. 1994; Danchi et al. 1994; Haniff et al. 1995; Hofmann et al. 1995a;
Weigelt et al. 1996; van Belle et al. 1996; Burns et al. 1998; Perrin et al. 1999; Hofmann et al. 2000a;
Hofmann et al. 2000b; Weigelt et al. 2000).
Theoretical studies (e.g. Watanabe & Kodaira 1979; Scholz 1985; Bessell et al. 1989; Bessell et al. 1996 = BSW96)
show that accurate monochromatic diameter measurements can improve our understanding of M giant atmospheres.
Previous interferometric single-dish observations of R Leo at optical wavelengths were reported by
Labeyrie et al. (1977),
Tuthill et al. (1994, 1999) and Haniff et al. (1995).
Di Giacomo et al. (1991) reported high-resolution lunar occultation observations
of R Leo in the near infrared, Danchi et al. (1994) interferometric 11.5 ![]() m measurements,
Burns et al. (1998) observations at optical wavelengths with the COAST interferometer,
and Perrin et al. (1999) K-band observations with the IOTA interferometer.
m measurements,
Burns et al. (1998) observations at optical wavelengths with the COAST interferometer,
and Perrin et al. (1999) K-band observations with the IOTA interferometer.
In this paper we present diffraction-limited 2-dimensional images of R Leo reconstructed by the bispectrum speckle interferometry method and comparisons of the observations with Mira star models.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2880.f1.eps}\end{figure}](/articles/aa/full/2001/35/aah2880/Timg18.gif) |
Figure 1:
Typical model-predicted Mira star spectrum |
| Open with DEXTER | |
| Data set | Epoche | Visual cycle | Exposure time | Photons/frame | Frames | FOV | Pixel size |
| and phase | per frame | ||||||
| 656/10 | 1996.255 | 0+0.20 | 5 ms | 53800 | 516 | 2
|
4.69 mas |
| 673/8 | " | " | 10 ms | 23400 | 2310 | " | " |
| 699/6 | " | " | 5 ms | 71100 | 130 | " | " |
| 754/6 | " | " | " | 94500 | 200 | " | " |
| 781/14 | " | " | " | 120600 | 1940 | " | " |
| 1045/9 | " | " | 70 ms | 260 | 3
|
14.53 mas |
The R Leo speckle interferograms were obtained with the Russian 6 m telescope at the Special Astrophysical Observatory on April 4, 1996 (see Table 1). The data were recorded through narrow-band interference filters with center wavelength (nm)/bandwidth (nm) of 656/10, 673/8, 699/6, 754/6, 781/14 and 1045/9 (filter width of the 6 filters at 10% transmission level: 12 nm, 9 nm, 8 nm, 6 nm, 16 nm, 13 nm; 1% level: 16 nm, 11 nm, 10 nm, 9 nm, 21 nm, 19 nm, respectively). Figure 1 shows the transmission curves of the filters. Due to the narrow bandwidth and the nearly rectangle-shaped transmission curve of our filters, specific regions of the molecular band structure of the Mira star spectrum can be selected which is important for sound physical interpretation (cf. Hofmann & Scholz 1998 = HS98; Hofmann et al. 1998 = HSW98). With these narrow-band filters quasi-monochromatic radii of R Leo can be measured in the strong TiO absorption band at 673 nm, at the moderate TiO absorption bands at 656 nm, 699 nm and 781 nm, in the weak TiO absorption band at 754 nm, and in the continuum at 1045 nm, suited for the comparison with predictions of Mira star models.
The observational parameters are listed in Table 1.
Seeing was approximately 1
![]() 6.
The plate scale error is
6.
The plate scale error is ![]() 1.5% and the error of detector orientation
1.5% and the error of detector orientation ![]() 0.7
0.7![]() (derived from speckle observations of calibration binaries).
The optical speckle interferograms were recorded with the speckle camera described
by Baier & Weigelt (1983).
The detector used was an image intensifier
(gain 500000, quantum efficiency: 9% at 600 nm, 8% at 700 nm, and
less than 1% at 900 nm) coupled optically
to a fast CCD camera (5122 pixels/frame, frame rate 4 framess-1,
digital correlated double sampling).
The near-infrared speckle raw data
(1045 nm continuum)
were recorded with our NICMOS-3 camera.
(derived from speckle observations of calibration binaries).
The optical speckle interferograms were recorded with the speckle camera described
by Baier & Weigelt (1983).
The detector used was an image intensifier
(gain 500000, quantum efficiency: 9% at 600 nm, 8% at 700 nm, and
less than 1% at 900 nm) coupled optically
to a fast CCD camera (5122 pixels/frame, frame rate 4 framess-1,
digital correlated double sampling).
The near-infrared speckle raw data
(1045 nm continuum)
were recorded with our NICMOS-3 camera.
![\begin{figure}
\par\includegraphics[width=5.72cm,clip]{h2880.f2a.eps}\hspace*{2m...
...\par\includegraphics[width=5.72cm,clip]{h2880.f2g.eps}\hspace*{3cm}
\end{figure}](/articles/aa/full/2001/35/aah2880/Timg21.gif) |
Figure 2: Diffraction-limited bispectrum speckle interferometry images of R Leo at 656 nm, 673 nm, 699 nm, 754 nm, 781 nm and 1045 nm, and for comparison of the unresolved star HIC 49637 at 673 nm (the filter widths are described in Sect. 2.1). In each panel the contour levels are plotted from 7 to 98% of peak intensity in steps of 7%. North is at the top and east to the left. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{h2880.f3a.eps}\hspace*{3mm...
....eps}\hspace*{3mm}
\includegraphics[width=6.7cm,clip]{h2880.f3f.eps}\end{figure}](/articles/aa/full/2001/35/aah2880/Timg22.gif) |
Figure 3: Azimuthally averaged visibilities (diamonds) of R Leo and fitted visibilities of the artificial spherical symmetric UD, FDD and Gaussian CLV functions. From top left to right bottom: R Leo at 656 nm, 673 nm, 699 nm, 754 nm, 782 nm and 1045 nm. The solid line corresponds to the best fitting Gaussian CLV function, the dashed line to the best-fitting UD CLV function, and the small dashed line to the best-fitting FDD CLV function. The visibility data are plotted up to the telescope cut-off frequency (44.1, 43.2, 41.6, 38.6, 37.2, and 27.8 cycles/arcsec for 656 nm, 673 nm, 699 nm, 754 nm, 782 nm, and 1045 nm, respectively). |
| Open with DEXTER | |
Diffraction-limited images
were reconstructed from the speckle interferograms
by the
bispectrum speckle interferometry method (Weigelt 1977; Lohmann et al. 1983;
Hofmann et al. 1995b). The visibilities of R Leo were determined with the
speckle interferometry method (Labeyrie 1970).
The speckle
transfer function was derived from speckle interferograms of
unresolved stars (HIC 49637, HIC 49669). The correct speckle transfer function
was determined by comparison of the
object-independent spectral ratio function (von der Lühe 1984)
of object and reference star.
The bispectrum of each frame consisted of ![]() 37 million
elements.
37 million
elements.
Figure 2 presents the reconstructed diffraction-limited R Leo images and for comparison the
673 nm reconstruction of the unresolved star HIC 49637.
These diffraction-limited
images of R Leo
(April 1996 at cycle+phase of 0+0.20)
show no significant asymmetry in all six filters, i.e. in the continuum at 1.04 ![]() m
and in the TiO absorption bands showing the upper atmosphere.
Note, however, the weak asymmetry reported by Lattanzi et al. (1997; November 1995
at cycle+phase of -1+0.71) and
Tuthill et al. (1999; January 1992 at cycle+phase of -5+0.27, June 1993 at
cycle+phase of -4+0.88).
In contrast to R Leo, R Cas
shows a strong asymmetry of its shape in all TiO absorption band filters (see Hofmann et al. 2000a).
m
and in the TiO absorption bands showing the upper atmosphere.
Note, however, the weak asymmetry reported by Lattanzi et al. (1997; November 1995
at cycle+phase of -1+0.71) and
Tuthill et al. (1999; January 1992 at cycle+phase of -5+0.27, June 1993 at
cycle+phase of -4+0.88).
In contrast to R Leo, R Cas
shows a strong asymmetry of its shape in all TiO absorption band filters (see Hofmann et al. 2000a).
| Data set | Diameter/ |
| FWHM (mas) | |
| UD | |
| 656/10 | 60.6 |
| 673/8 | 75.6 |
| 699/6 | 52.5 |
| 754/6 | 48.7 |
| 781/14 | 55.0 |
| 1045/9 | 37.9 |
| Gaussian | |
| 656/10 | 38.1 |
| 673/8 | 47.6 |
| 699/6 | 32.7 |
| 754/6 | 30.5 |
| 781/14 | 34.6 |
| 1045/9 | 23.6 |
| FDD | |
| 656/10 | 68.3 |
| 673/8 | 85.3 |
| 699/6 | 59.0 |
| 754/6 | 54.8 |
| 781/14 | 62.1 |
| 1045/9 | 42.7 |
Figure 3 shows the reconstructed diffraction-limited visibilities from which we derived the disk parameters of R Leo by fitting the following artificial (i.e. non-physical) center-to-limb variations (=CLV) of emitted intensity: uniform disk (UD), fully darkened disk (FDD) and Gaussian function (Gauss). Inspection of the 2-dimensional visibilities of R Leo in all six wavelength bands used yields axis ratios of the stellar disk ranging between 0.93 and 0.98. However, these axis ratios do not indicate any significant asymmetry of the shape of R Leo as the uncertainty of the axis ratios is approximately 10%. Hence, the disk parameters were derived from the azimuthally averaged 2-dimensional visibilities by fitting spherical symmetric CLVs.
| Data set | UD | Gaussian | FDD |
| 656/10 | 660 |
415 |
744 |
| 673/8 | 823 |
518 |
929 |
| 699/6 | 572 |
356 |
642 |
| 754/6 | 530 |
332 |
597 |
| 781/14 | 599 |
377 |
676 |
| 1045/9 | 413 |
257 |
465 |
In Fig. 3 the azimuthally averaged visibilities at 656 nm, 673 nm, 699 nm, 754 nm, 782 nm and 1045 nm
together with the visibilities of the fitted spherical symmetric uniform disk and
Gaussian functions are shown.
Note, that the Gaussian function fits the reconstructed visibilities at optical wavelengths
much better than FDD and UD, and that all three artificial CLVs fit the 1045 nm visibility
equally well. Table 2 lists the fitted disk parameters of R Leo.
Table 3 contains the
diameters of Table 2
converted to linear radii (in solar radii ![]() )
using R Leo's HIPPARCOS parallax
of 9.87 mas
)
using R Leo's HIPPARCOS parallax
of 9.87 mas ![]() 2.07 mas
(ESA 1997, Whitelock & Feast 2000).
Note, that Gaussian FWHM values are not directly comparable to diameter
quantities.
2.07 mas
(ESA 1997, Whitelock & Feast 2000).
Note, that Gaussian FWHM values are not directly comparable to diameter
quantities.
| Feature | FDD |
| diameter ratio | |
| (754/6) / (1045/9) | 1.28 |
| (699/6) / (1045/9) | 1.38 |
| (781/14) / (1045/9) | 1.46 |
| (656/10) / (1045/9) | 1.60 |
| (673/8) / (1045/9) | 2.00 |
| (699/6) / (754/6) | 1.08 |
| (781/14) / (754/6) | 1.14 |
| (656/10) / (754/6) | 1.25 |
| (673/8) / (754/6) | 1.56 |
| (781/14) / (699/6) | 1.06 |
| (656/10) / (699/6) | 1.16 |
| (673/8) / (699/6) | 1.45 |
| (656/10) / (781/14) | 1.09 |
| (673/8) / (781/14) | 1.36 |
| (673/8) / (656/10) | 1.25 |
Table 4 presents the ratios of the R Leo diameters at different wavelengths. We only list the FDD diameter ratios since the FDD approximation provides reasonable fits to the CLV in near-continuum filters and many other filters (HS98, HSW98), and since UD and Gaussian fits yield almost identical ratios. Note, however, that real diameter ratios can be different from those based on these artificial CLVs because, in particular, the shape of the physical CLV may be angle-dependent (e.g. occurrence of hot or cool spots). The UD diameter is approximately two times larger in the TiO absorption band head at 673 nm than in the 1045 nm continuum. The UD diameters at 656 nm, 699 nm and 781 nm (moderate TiO absorption band) are about 1.60, 1.38 and 1.46 times larger than at 1045 nm, respectively. The UD diameter at the weak TiO absorption band (754 nm) is about 1.28 times larger than at 1045 nm.
In this section we compare our monochromatic radius observations with monochromatic radii predicted by Mira models. Since the wavelength dependence of the stellar radius sensitively depends on the model-predicted structure of the Mira atmosphere (Bessell et al. 1989, BSW96, HSW98), this comparison should give some hint whether any of the models is a fair representation of R Leo. We discuss the linear radii and the pulsation mode obtained by adopting R Leo's HIPPARCOS parallax and the effective temperature derived from the 1045/9 measurement and the bolometric flux.
All Mira star models used in this paper are from BSW96 (D and E series)
and from HSW98 (P, M and O series).
They are meant
as possible representations of the prototype Mira variable o Ceti, and hence have periods Pvery close to the 332 day period of this star; they differ in pulsation mode, assumed mass M and
assumed luminosity L; and the BSW96 models differ from the (more advanced) HSW98 models
with respect to the pulsation modelling technique. Solar abundances were assumed
for all models.
The five models represent stars pulsating in the fundamental mode (f; D, P and M models) or
in the first-overtone mode (o; E and O models).
Table 5 lists the properties of these Mira model series (![]() = Rosseland radius,
i.e., distance from the non-pulsating "parent star's" center at which the Rosseland optical depth
= Rosseland radius,
i.e., distance from the non-pulsating "parent star's" center at which the Rosseland optical depth
![]() equals
unity;
equals
unity;
![]() = effective
temperature).
We compare predictions of these models at different phases and cycles with
our observations (Table 6; arbitrary numbering of model cycles).
The correlation of bolometric model phases with
visual phases was taken from Lockwood & Wing (1971) and Lockwood (1972) who
discuss the observed light curves of Mira variables in their 104 filter (1035 nm/13 nm) which
closely matches the bolometric light curve.
= effective
temperature).
We compare predictions of these models at different phases and cycles with
our observations (Table 6; arbitrary numbering of model cycles).
The correlation of bolometric model phases with
visual phases was taken from Lockwood & Wing (1971) and Lockwood (1972) who
discuss the observed light curves of Mira variables in their 104 filter (1035 nm/13 nm) which
closely matches the bolometric light curve.
| Series | Mode | P/day |
|
|
|
|
| D | f | 330 | 1.0 | 3470 | 236 | 2900 |
| E | o | 328 | 1.0 | 6310 | 366 | 2700 |
| P | f | 332 | 1.0 | 3470 | 241 | 2860 |
| M | f | 332 | 1.2 | 3470 | 260 | 2750 |
| O | o | 320 | 2.0 | 5830 | 503 | 2250 |
| Model | cycle+
|
|
|
|
Abscissa |
| D27360 | 0 + 0.8 | 0.90 | 0.90 | 3050 | 1 |
| D27520 | 1 + 0.0 | 1.04 | 1.04 | 3020 | 2 |
| D27600 | 1 + 0.2 | 1.09 | 1.10 | 3010 | 3 |
| D27760 | 1 + 0.5 | 0.91 | 0.90 | 2710 | 4 |
| D28320 | 1 + 0.8 | 0.90 | 0.90 | 3050 | 5 |
| D28760 | 2 + 0.0 | 1.04 | 1.05 | 3030 | 6 |
| D28847 | 2 + 0.2 | 1.09 | 1.09 | 3000 | 7 |
| D28960 | 2 + 0.5 | 0.91 | 0.90 | 2690 | 8 |
| E8300 | 0 + 0.83 | 1.16 | 1.07 | 2330 | 9 |
| E8380 | 1 + 0.0 | 1.09 | 1.09 | 2620 | 10 |
| E8460 | 1 + 0.1 | 1.12 | 1.11 | 2760 | 11 |
| E8560 | 1 + 0.21 | 1.17 | 1.15 | 2610 | 12 |
| P71800 | 0 + 0.5 | 1.20 | 0.90 | 2160 | 13 |
| P73200 | 1 + 0.0 | 1.03 | 1.04 | 3130 | 14 |
| P73600 | 1 + 0.5 | 1.49 | 0.85 | 1930 | 15 |
| P74200 | 2 + 0.0 | 1.04 | 1.04 | 3060 | 16 |
| P74600 | 2 + 0.5 | 1.17 | 0.91 | 2200 | 17 |
| P75800 | 3 + 0.0 | 1.13 | 1.14 | 3060 | 18 |
| P76200 | 3 + 0.5 | 1.13 | 0.81 | 2270 | 19 |
| P77000 | 4 + 0.0 | 1.17 | 1.16 | 2870 | 20 |
| M96400 | 0 + 0.5 | 0.93 | 0.84 | 2310 | 21 |
| M97600 | 1 + 0.0 | 1.19 | 1.18 | 2750 | 22 |
| M97800 | 1 + 0.5 | 0.88 | 0.83 | 2460 | 23 |
| M98800 | 2 + 0.0 | 1.23 | 1.20 | 2650 | 24 |
| O64210 | 0 + 0.5 | 1.12 | 1.00 | 2050 | 25 |
| O64530 | 0 + 0.8 | 0.93 | 0.91 | 2150 | 26 |
| O64700 | 1 + 0.0 | 1.05 | 1.01 | 2310 | 27 |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{h2880.f4.eps}\end{figure}](/articles/aa/full/2001/35/aah2880/Timg32.gif) |
Figure 4: Linear Rosseland observed and model radii. The observed linear Rosseland radii are based on the 1045/9 measurements for each model/phase combination; the model radii are calculated for the transmission curve of each filter used; Table 6 gives the link between the abscissa values and the models and their phases. |
| Open with DEXTER | |
In this paper we use the conventional stellar radius definition where
the monochromatic radius
![]() of a star
at wavelength
of a star
at wavelength ![]() is given by the distance from the star's
center at which the optical depth equals unity (
is given by the distance from the star's
center at which the optical depth equals unity (
![]() ).
In analogy, the photospheric stellar radius R is given by the
distance from the star's center at which the Rosseland optical depth
equals unity (
).
In analogy, the photospheric stellar radius R is given by the
distance from the star's center at which the Rosseland optical depth
equals unity (
![]() ).
This radius has the advantage of agreeing well (see Table 6 and the discussion
in HSW98 for deviations sometimes occurring in very cool stars)
with measurable near-infrared continuum radii
and with the standard boundary radius of pulsation models with parameter
).
This radius has the advantage of agreeing well (see Table 6 and the discussion
in HSW98 for deviations sometimes occurring in very cool stars)
with measurable near-infrared continuum radii
and with the standard boundary radius of pulsation models with parameter
![]() .
.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{h2880.f5a.eps}\hspace*{3mm...
...}\par\includegraphics[width=6.6cm,clip]{h2880.f5e.eps}\hspace*{3mm}
\end{figure}](/articles/aa/full/2001/35/aah2880/Timg35.gif) |
Figure 5:
Linear observed and model stellar filter radii |
| Open with DEXTER | |
For each of our six filters (656/10, 673/8, 699/6, 754/6, 781/14 and 1045/9)
we calculated the theoretical CLVs
corresponding to the above mentioned five Mira models at different phases and cycles.
The stellar radius
for filter transmission
![]() is the intensity and filter weighted radius
is the intensity and filter weighted radius
![]() which we call stellar filter radius
which we call stellar filter radius ![]() after the definition of Scholz & Takeda (1987). In this equation
after the definition of Scholz & Takeda (1987). In this equation
![]() denotes the above monochromatic
denotes the above monochromatic
![]() radius,
radius,
![]() the central intensity spectrum and
the central intensity spectrum and
![]() the transmission of the filter.
Owing to the chosen positions and narrow widths of our filters f, the
the transmission of the filter.
Owing to the chosen positions and narrow widths of our filters f, the ![]() radii are almost monochromatic
radii are almost monochromatic
![]() radii if the molecular line structure of the TiO bands is neglected.
radii if the molecular line structure of the TiO bands is neglected.
The observed angular stellar filter radius
![]() of R Leo corresponding to a certain
filter f and
model-phase combination m, was derived by a least-squares fit between the
azimuthally averaged measured visibility and the visibility of the corresponding theoretical CLV.
For a detailed description of the visibility fitting procedure we refer to HS98.
of R Leo corresponding to a certain
filter f and
model-phase combination m, was derived by a least-squares fit between the
azimuthally averaged measured visibility and the visibility of the corresponding theoretical CLV.
For a detailed description of the visibility fitting procedure we refer to HS98.
In the following subsections we apply CLVs predicted from all five models at phases both near our R Leo observations (phase 0.20) and, for comparison, also at other phases.
Since R Leo is located in our neighborhood, the radii of the Mira star
can be directly compared with the predictions of Mira star models.
Linear stellar R Leo radii can be obtained if we use
its HIPPARCOS parallax of
![]() mas
(ESA 1997, Whitelock & Feast 2000;
see discussion in this paper on the parallax errors in the case
of stars with large extended shapes).
mas
(ESA 1997, Whitelock & Feast 2000;
see discussion in this paper on the parallax errors in the case
of stars with large extended shapes).
The 1045 nm model CLV visibility was fitted to the measured 1045 nm visibility of R Leo yielding
the linear monochromatic
![]() radius R1045 and, as predicted by the specific model, the associated
linear Rosseland radius R (Fig. 4).
We see that
the derived linear Rosseland radius values are nearly the same for all model-phase combinations,
that is they depend very little on differences of CLVs of our models.
The average measured R1045 radius is
radius R1045 and, as predicted by the specific model, the associated
linear Rosseland radius R (Fig. 4).
We see that
the derived linear Rosseland radius values are nearly the same for all model-phase combinations,
that is they depend very little on differences of CLVs of our models.
The average measured R1045 radius is
![]() (
(
![]() mas),
and the average Rosseland radius is
mas),
and the average Rosseland radius is
![]() (
(
![]() mas)
(average
over all model-phase combinations).
The Rosseland radii of the E model series at all available phases (0.83, 1.0, 1.1, 1.21),
of the M model series at near-maximum phases (1.0, 2.0), and of the O model
at near-maximum phases (0.8, 1.0)
are very close or close (within the error bars) to the
Rosseland radii derived from the measured 1045 nm visibility at phase 0.20.
All other model-phase combinations
yield large differences (larger than the error bars).
mas)
(average
over all model-phase combinations).
The Rosseland radii of the E model series at all available phases (0.83, 1.0, 1.1, 1.21),
of the M model series at near-maximum phases (1.0, 2.0), and of the O model
at near-maximum phases (0.8, 1.0)
are very close or close (within the error bars) to the
Rosseland radii derived from the measured 1045 nm visibility at phase 0.20.
All other model-phase combinations
yield large differences (larger than the error bars).
The 1045 nm continuum model radius R1045 and the Rosseland model radius Raveraged over all
available E model phases is
404 ![]() and 416
and 416 ![]() ,
respectively, and the measured value (using the E model CLVs)
is
,
respectively, and the measured value (using the E model CLVs)
is
![]() and
and
![]() ,
respectively.
The E model at phase 1.21 (closest to our observed phase 0.20) has
,
respectively.
The E model at phase 1.21 (closest to our observed phase 0.20) has
![]() (
(
![]() ), and data reduction by means of this CLV yields for R Leo the observed value of
), and data reduction by means of this CLV yields for R Leo the observed value of
![]() (
(
![]() ).
Hence, the difference between model and star is smaller than the error bar.
).
Hence, the difference between model and star is smaller than the error bar.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2880.f6a.eps}\hspace*{3mm...
....eps}\hspace*{3mm}
\includegraphics[width=6.8cm,clip]{h2880.f6f.eps}\end{figure}](/articles/aa/full/2001/35/aah2880/Timg51.gif) |
Figure 6:
Linear observed and model stellar filter radii |
| Open with DEXTER | |
In Fig. 6, we compare our observed linear stellar filter radii with
the model radii of all 27 model-phase combinations m. Clearly the
three fundamental-mode model stars are systematically too small
(by ![]() 20 to
50%), whereas most model radii of the overtone E and O series coincide within
the error bars with the measured values. We see that the TiO forming layers of
the Mira atmosphere may extend as far as 4 to 6 AU from the star's center.
We also see from the figure that the model atmospheres are systematically more
compact than the observed Mira atmosphere, i.e. the distance-independent ratio
20 to
50%), whereas most model radii of the overtone E and O series coincide within
the error bars with the measured values. We see that the TiO forming layers of
the Mira atmosphere may extend as far as 4 to 6 AU from the star's center.
We also see from the figure that the model atmospheres are systematically more
compact than the observed Mira atmosphere, i.e. the distance-independent ratio
![]() is too small in the
here considered models (see Appendix for details).
is too small in the
here considered models (see Appendix for details).
After the period-radius relation of Miras from Feast (1996) a fundamental mode
pulsator with a period of 310 days (R Leo) and with a mass ranging between 1.0 and 1.5 ![]() should have a linear photospheric radius ranging from 220-270
should have a linear photospheric radius ranging from 220-270 ![]() ,
and
a first overtone pulsator should have a linear photospheric radius ranging from 390-450
,
and
a first overtone pulsator should have a linear photospheric radius ranging from 390-450 ![]() .
Therefore, the measured linear Rosseland radius of 417
.
Therefore, the measured linear Rosseland radius of 417
![]() (derived from the 1045 nm-visibility measurement and the E-model at phase close to our
observation) places R Leo among the first-overtone pulsators.
The question why the period-radius relation of M-type Miras indicates first-overtone pulsation
whereas MACHO observations (Wood et al. 1999) and pulsation velocities (Scholz & Wood 2000)
favor fundamental mode pulsation, remains open.
(derived from the 1045 nm-visibility measurement and the E-model at phase close to our
observation) places R Leo among the first-overtone pulsators.
The question why the period-radius relation of M-type Miras indicates first-overtone pulsation
whereas MACHO observations (Wood et al. 1999) and pulsation velocities (Scholz & Wood 2000)
favor fundamental mode pulsation, remains open.
Effective temperatures of R Leo were derived from its angular
Rosseland radii
![]() (derived from the 1045/9-observation with
all 27 above discussed models)
and its bolometric flux using the relation
(derived from the 1045/9-observation with
all 27 above discussed models)
and its bolometric flux using the relation
![]() where
where
![]() is the apparent bolometric flux in units of 10-8 ergcm-2s-1and
is the apparent bolometric flux in units of 10-8 ergcm-2s-1and
![]() is the apparent angular photospheric diameter in mas.
Figure 7 (top) displays the angular Rosseland radii obtained from the 1045/9 observation
by fitting all 27 theoretical model-phase CLV visibilities to the measured 1045/9 visibility.
The average measured angular Rosseland radius is 19.4 mas (average over all model-phase
combinations).
Figure 7 (top) also shows that inaccuracies
caused by adopting incorrect continuum limb-darkening from
inadequate models rarely
exceed
is the apparent angular photospheric diameter in mas.
Figure 7 (top) displays the angular Rosseland radii obtained from the 1045/9 observation
by fitting all 27 theoretical model-phase CLV visibilities to the measured 1045/9 visibility.
The average measured angular Rosseland radius is 19.4 mas (average over all model-phase
combinations).
Figure 7 (top) also shows that inaccuracies
caused by adopting incorrect continuum limb-darkening from
inadequate models rarely
exceed ![]() 10% (i.e. 5% in
10% (i.e. 5% in
![]() ).
).
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{h2880.f7a.eps}\par\include...
...{h2880.f7b.eps}\par\includegraphics[width=6.9cm,clip]{h2880.f7c.eps}\end{figure}](/articles/aa/full/2001/35/aah2880/Timg58.gif) |
Figure 7: Top: Angular Rosseland radii (in mas) derived for each model-phase combination m from the 1045/9 measurements. Middle: Linear Rosseland observed and model radii. The observed linear Rosseland radii were derived for each model-phase combination m from the 1045/9 observations. Bottom: Effective model temperatures for all model-phase combinations m and effective temperatures derived from the above angular Rosseland radii (top) and the the bolometric flux of R Leo measured around phase 0.20. Table 6 gives the link between the abscissa values and the models and their phases (diamonds: observations reduced with model CLVs with phases close to the phase of the observation; crosses:observations reduced with model CLVs with phases far from the phase of the observation; squares: theoretical model values). |
| Open with DEXTER | |
For cool stars such as LPV's, where most
of the luminosity is emitted at near-infrared wavelengths, a convenient method
for calculating bolometric magnitudes is to use a blackbody function
to interpolate between photometric measurements in the J, H, K and L bands.
For estimating the bolometric flux we have used JHKL-flux measurements from P. Whitelock's
(1997, private communication)
R Leo observations of April 6, 1996.
These observations were carried out at nearly the same variability phase (0.20) and cycle as our
1045/9 observation of April 4, 1996.
The bolometric magnitude of R Leo, calculated by P. Whitelock (1997, private communication)
yields
![]() and, assuming that
a zero magnitude star has a flux of
and, assuming that
a zero magnitude star has a flux of
![]() ergcm-2s-1,
yields
ergcm-2s-1,
yields
![]() ergcm-2s-1.
As a by-product we determined the luminosity of R Leo near maximum phase 0.20 from its
bolometric magnitude and HIPPARCOS parallax to
ergcm-2s-1.
As a by-product we determined the luminosity of R Leo near maximum phase 0.20 from its
bolometric magnitude and HIPPARCOS parallax to
![]() ,
which is close to the near-maximum luminosity of the E and O model series (BSW96, HSW98).
,
which is close to the near-maximum luminosity of the E and O model series (BSW96, HSW98).
Figure 7 (bottom) presents
![]() values derived for each of the 27 model-phase combinations from
the bolometric flux and the angular Rosseland radii
values derived for each of the 27 model-phase combinations from
the bolometric flux and the angular Rosseland radii
![]() measured at near-maximum phase 0.20.
Fortunately, this value depends little on the model-phase combination CLV
and is about
measured at near-maximum phase 0.20.
Fortunately, this value depends little on the model-phase combination CLV
and is about
![]() K
(average over all model-phase combinations).
The
K
(average over all model-phase combinations).
The
![]() values of the E model series at all near-maximum phases (1.0, 1.1, 1.21)
and of the M model series at all near-maximum phases (1.0, 2.0) are very close
(within the error bars) to the
values of the E model series at all near-maximum phases (1.0, 1.1, 1.21)
and of the M model series at all near-maximum phases (1.0, 2.0) are very close
(within the error bars) to the
![]() values derived from the 1045 nm
visibility observation
and the JHKL photometric measurement performed at the near-maximum phase 0.20.
All other models (i.e. D, P and O) yield at all available near-maximum phases
large differences between theoretical and measured
values derived from the 1045 nm
visibility observation
and the JHKL photometric measurement performed at the near-maximum phase 0.20.
All other models (i.e. D, P and O) yield at all available near-maximum phases
large differences between theoretical and measured
![]() values.
The closest E model with phase 1.21 has an effective temperature of 2610 K. Application
of its CLV and
values.
The closest E model with phase 1.21 has an effective temperature of 2610 K. Application
of its CLV and
![]() (measured at phase
(measured at phase ![]() 0.20) to our
1045/9 observation
yields for R Leo an angular Rosseland radius of 19.1 mas
0.20) to our
1045/9 observation
yields for R Leo an angular Rosseland radius of 19.1 mas ![]() 2.0 mas
and an effective temperature of 2600 K
2.0 mas
and an effective temperature of 2600 K ![]() 180 K.
The average theoretical effective temperature of all near-maximum phases (1.0, 2.0) of the
M model is 2700 K. The average measured effective temperature derived from the
1045/9 observation by application of the M model CLVs
at the near-maximum phases 1.0 and 2.0 has a value of 2650 K
180 K.
The average theoretical effective temperature of all near-maximum phases (1.0, 2.0) of the
M model is 2700 K. The average measured effective temperature derived from the
1045/9 observation by application of the M model CLVs
at the near-maximum phases 1.0 and 2.0 has a value of 2650 K ![]() 180 K.
180 K.
From our speckle observations of R Leo at near maximum phase (phase 0.20) we derived UD diameters of
Tuthill et al. (1994) derived UD diameters of
![]() mas and
mas and
![]() mas at
833 nm/41 nm and 902 nm/50 nm, respectively and
derived Rosseland diameters of
mas at
833 nm/41 nm and 902 nm/50 nm, respectively and
derived Rosseland diameters of
![]() mas and
mas and
![]() mas, respectively.
These measurements agree well with our angular Rosseland diameter of
mas, respectively.
These measurements agree well with our angular Rosseland diameter of
![]() mas
at phase 0.20 (April 4, 1996).
Haniff et al. (1995) reported on R Leo observations
through their 700 nm/10 nm filter comparable to our 699 nm/6 nm filter.
They derived an UD diameter of
mas
at phase 0.20 (April 4, 1996).
Haniff et al. (1995) reported on R Leo observations
through their 700 nm/10 nm filter comparable to our 699 nm/6 nm filter.
They derived an UD diameter of
![]() mas at cycle+phase of -4+0.88which is approximately
20% larger than our near-maximum phase (0.20) 699 nm/6 nm UD diameter of
mas at cycle+phase of -4+0.88which is approximately
20% larger than our near-maximum phase (0.20) 699 nm/6 nm UD diameter of
![]() mas.
This difference might be explained by UD diameter variations with the
variability phase reported by Burns et al. (1998).
Di Giacomo et al. (1991) derived an UD diameter of
mas.
This difference might be explained by UD diameter variations with the
variability phase reported by Burns et al. (1998).
Di Giacomo et al. (1991) derived an UD diameter of
![]() mas from their lunar occultation
measurements (May 1990, cycle+phase of -7+0.2)
in the Br
mas from their lunar occultation
measurements (May 1990, cycle+phase of -7+0.2)
in the Br![]() line of atomic hydrogen at 2.16
line of atomic hydrogen at 2.16 ![]() m.
Tej et al. (1999) obtained UD diameters of
m.
Tej et al. (1999) obtained UD diameters of ![]() mas and
mas and ![]() mas from their lunar occultation
observations through a narrowband filter at 3.36
mas from their lunar occultation
observations through a narrowband filter at 3.36 ![]() m (December 1997, cycle+phase of 2+0.17)
and a broadband filter at 2.2
m (December 1997, cycle+phase of 2+0.17)
and a broadband filter at 2.2 ![]() m (March 1998, cycle+phase of 2+0.44),
respectively.
K-band observations with the IOTA interferometer by
Perrin et al. (1999) yielded UD diameters of
m (March 1998, cycle+phase of 2+0.44),
respectively.
K-band observations with the IOTA interferometer by
Perrin et al. (1999) yielded UD diameters of
![]() mas
at cycle+phase of 0+0.24 (April 17-18, 1996)
and
mas
at cycle+phase of 0+0.24 (April 17-18, 1996)
and
![]() mas at cycle+phase of 1+0.28 (March 3-10, 1997).
Note that the 1996 measurement of Perrin et al. was done at nearly
the same phase of the same pulsation cycle as the here presented observations.
mas at cycle+phase of 1+0.28 (March 3-10, 1997).
Note that the 1996 measurement of Perrin et al. was done at nearly
the same phase of the same pulsation cycle as the here presented observations.
The difference between our 1045 nm/9 nm UD diameter (at cycle+phase of 0+0.20)
and the K-Band UD diameter of
Perrin et al. (1999; at cycle+phase of 0+0.24)
is larger than expected and
may indicate that there exists an additional near-infrared extinction,
not included in the BSW96 and HSW98 models, which blankets the 1 ![]() m
region more strongly than the K bandpass.
No such opacity source is known so far, but Bedding et al. (2001) noticed that
dust particles condensating in the uppermost atmospheric layers may produce
this type of effect by generating a two-component appearance of the CLV which
is more pronounced at shorter
m
region more strongly than the K bandpass.
No such opacity source is known so far, but Bedding et al. (2001) noticed that
dust particles condensating in the uppermost atmospheric layers may produce
this type of effect by generating a two-component appearance of the CLV which
is more pronounced at shorter ![]() .
Danchi et al. (1994) claim that R Leo belongs to a class of stars whose
inner dust-shell radii are very close to the photosphere (3 to 5 photospheric radii), i.e. dust might be formed in the uppermost atmospheric
layers.
Therefore, we cannot exclude that our
measured radius has to be scaled to the true-continuum radius resulting in a
smaller stellar radius and in a higher effective temperature. A similar
1
.
Danchi et al. (1994) claim that R Leo belongs to a class of stars whose
inner dust-shell radii are very close to the photosphere (3 to 5 photospheric radii), i.e. dust might be formed in the uppermost atmospheric
layers.
Therefore, we cannot exclude that our
measured radius has to be scaled to the true-continuum radius resulting in a
smaller stellar radius and in a higher effective temperature. A similar
1 ![]() m vs. K-band discrepancy was reported for the Mira variable R Cas
(Weigelt et al. 2000).
m vs. K-band discrepancy was reported for the Mira variable R Cas
(Weigelt et al. 2000).
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{h2880.f8a.eps}\hspace*{4mm...
...}\par\includegraphics[width=6.4cm,clip]{h2880.f8e.eps}\hspace*{4cm}
\end{figure}](/articles/aa/full/2001/35/aah2880/Timg77.gif) |
Figure 8:
Observed and model radius ratios |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{h2880.f9a.eps}\hspace*{1.5...
...ps}\hspace*{1.5mm}
\includegraphics[width=5.1cm,clip]{h2880.f9o.eps}\end{figure}](/articles/aa/full/2001/35/aah2880/Timg78.gif) |
Figure 9: Observed and model radius ratios Ri/Rjof stellar filter radii Ri and Rj (i and j denote filters). The 15 plots show all possible filter combinations. Table 6 gives the link between the abscissa values and the models and their phases. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{h2880.f10.eps}\end{figure}](/articles/aa/full/2001/35/aah2880/Timg79.gif) |
Figure 10: Normalized distance Dm between measured and model diameter ratio vectors (see text; diamonds: observations reduced with model CLVs with phases close to the phase of the observation; crosses: observations reduced with model CLVs with phases far from the phase of the observation; squares: theoretical model radii). Table 6 gives the link between the abscissa values and the 27 model-phase combinations m. |
| Open with DEXTER | |
When measured visibility data are reduced with limb-darkening profiles
predicted by recent
Mira models (BSW96, HSW98), we find that strong-TiO
![]() diameters depend substantially on the adopted model, whereas the continuum
diameter does not. Since these models are
taylored to the parameters of o Ceti which has nearly the same period
and
luminosity as R Leo (310 days,
diameters depend substantially on the adopted model, whereas the continuum
diameter does not. Since these models are
taylored to the parameters of o Ceti which has nearly the same period
and
luminosity as R Leo (310 days,
![]() ),
they should predict also quantitatively
the basic properties of R Leo.
The predictions of the E model series
are in good agreement with (i) the stellar filter radii measured through five of
six filters (however, the stellar filter radii measured in the strong TiO
absorption
band at 673 nm are about 50% larger than the model-predicted values,
i.e. the models of the E series
as well as the other models considered here are systematically too compact;
see Appendix);
(ii) the measured
Rosseland radius and the derived pulsation mode; and (iii) the measured
effective temperature of 2590 K
),
they should predict also quantitatively
the basic properties of R Leo.
The predictions of the E model series
are in good agreement with (i) the stellar filter radii measured through five of
six filters (however, the stellar filter radii measured in the strong TiO
absorption
band at 673 nm are about 50% larger than the model-predicted values,
i.e. the models of the E series
as well as the other models considered here are systematically too compact;
see Appendix);
(ii) the measured
Rosseland radius and the derived pulsation mode; and (iii) the measured
effective temperature of 2590 K ![]() 180 K at near-maximum phase 0.20.
We obtain a Rosseland
180 K at near-maximum phase 0.20.
We obtain a Rosseland
![]() 1 radius of
1 radius of
![]() (based on the E-model at phase 1.21 close to the phase of our observations)
with an accuracy of about 23% (the error of the HIPPARCOS parallax of
(based on the E-model at phase 1.21 close to the phase of our observations)
with an accuracy of about 23% (the error of the HIPPARCOS parallax of
![]() 20% is the largest
fraction of the total error; the speckle error is
20% is the largest
fraction of the total error; the speckle error is ![]() 10%).
10%).
Acknowledgements
We thank P. Whitelock for sending us her JHKL photometric observations of R Leo and for calculating the bolometric flux.
We have also compared the model stellar filter radii
![]() as predicted by each model-phase combination m with our measured angular stellar filter radii
as predicted by each model-phase combination m with our measured angular stellar filter radii
![]() by comparing the observed and model diameter ratios at
different wavelengths (filter f: 656/10, 673/8, 699/6, 754/6, 781/14 and 1045/9).
By confronting a large variety of Mira models
with the here presented narrow-bandpass observations, we may test
how sensitively monochromatic radius measurements probe model structures and
whether they are indeed reliable tools of Mira diagnostics.
Since different models predict, at different phases, both different stellar filter radii
by comparing the observed and model diameter ratios at
different wavelengths (filter f: 656/10, 673/8, 699/6, 754/6, 781/14 and 1045/9).
By confronting a large variety of Mira models
with the here presented narrow-bandpass observations, we may test
how sensitively monochromatic radius measurements probe model structures and
whether they are indeed reliable tools of Mira diagnostics.
Since different models predict, at different phases, both different stellar filter radii ![]() and different filter CLV curves, we expect better agreement between
model-predicted ratios and observed ratios (based upon the corresponding
model-phase combination of CLV) for models that represent R Leo well and for
model phases that are close to the observed phases than for other models and
phases. Since our five models are taylored to the parameters of o Ceti
which roughly has the same period and luminosity as R Leo (310 days,
and different filter CLV curves, we expect better agreement between
model-predicted ratios and observed ratios (based upon the corresponding
model-phase combination of CLV) for models that represent R Leo well and for
model phases that are close to the observed phases than for other models and
phases. Since our five models are taylored to the parameters of o Ceti
which roughly has the same period and luminosity as R Leo (310 days,
![]() :
derived
from its bolometric flux measured at phase 0.20 close to our observations and its HIPPARCOS parallax),
this comparison should give some hint as to whether any of the models is a fair representation of R Leo.
We must be aware, however,
that model
phases are close to but not identical with observed phases, and cycle-to-cycle
variations may be substantial (BSW96, HSW98).
:
derived
from its bolometric flux measured at phase 0.20 close to our observations and its HIPPARCOS parallax),
this comparison should give some hint as to whether any of the models is a fair representation of R Leo.
We must be aware, however,
that model
phases are close to but not identical with observed phases, and cycle-to-cycle
variations may be substantial (BSW96, HSW98).
For illustration, Fig. 8 presents
the observed and model ratios ![]() /
/
![]() of the stellar filter radii
of the stellar filter radii ![]() and
and
![]() as a function of wavelength
as a function of wavelength ![]() for all applied model series (D, E, P, M and O)
and phases close to our observations (since nearly all model series consist of
several cycles, a best fit selection was applied).
Figure 9 displays the observed and theoretical
ratios for all
model-phase combinations m and all filter pairs.
Figure 10 presents
the distance Dm between the measured and model
stellar filter radius ratios (between all possible pairs of filters)
for each model-phase combination.
The distance Dm is defined as
for all applied model series (D, E, P, M and O)
and phases close to our observations (since nearly all model series consist of
several cycles, a best fit selection was applied).
Figure 9 displays the observed and theoretical
ratios for all
model-phase combinations m and all filter pairs.
Figure 10 presents
the distance Dm between the measured and model
stellar filter radius ratios (between all possible pairs of filters)
for each model-phase combination.
The distance Dm is defined as
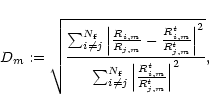 |
(1) |
Inspection of Figs. 8, 9 and 10 shows that from the point of view of diameter
ratios,
some of the model-phase combinations are acceptable as representations
of the here presented observations of R Leo but none is completely satisfactory.
Nearly all models are too compact in the strong TiO absorption band at 673 nm,
i.e. the distance-independent ratio
![]() is too small compared with the observations.
For the model-phase combinations at phases close to the observation, the P model
series which exhibits the most
pronounced atmospheric extension of the BSW96/HSW98 studies
has in most cases (i.e., in 11 out of all 15 filter ratio combinations) model
diameter ratios which are identical (within the error bars) to the measured ones. The order
of ranking
after the P model is: E model (6/15), D model (6/15), M model (3/15) and O model (1/15).
is too small compared with the observations.
For the model-phase combinations at phases close to the observation, the P model
series which exhibits the most
pronounced atmospheric extension of the BSW96/HSW98 studies
has in most cases (i.e., in 11 out of all 15 filter ratio combinations) model
diameter ratios which are identical (within the error bars) to the measured ones. The order
of ranking
after the P model is: E model (6/15), D model (6/15), M model (3/15) and O model (1/15).