A&A 376, 667-671 (2001)
DOI: 10.1051/0004-6361:20011013
G. Micha![]() ek
ek
1 - Center for Solar Physics and Space Weather, Department of Physics, The Catholic University of America, Washington, DC 20064, USA
2 -
Obserwatorium Astronomiczne, Uniwersytet Jagiellonski,
ul. Orla 171, 30-244 Kraków, Poland
Received 8 February 2001 / Accepted 12 June 2001
Abstract
The cross-field diffusion coefficient of charged particles
in the presence of pure isotropic
Alfvén waves, pure isotropic magnetosonic waves and their mixture
is considered using Monte Carlo particle simulations.
We show that the cross-field diffusion coefficient
![]() strongly depends on the assumed spectrum and amplitude of MHD turbulence
but much less on the type of waves considered. It is demonstrated that
transport perpendicular to the average magnetic field is mostly determined
by compound diffusion which combines the effects of scattering off
magnetic irregularities with magnetic braiding. The ratio
strongly depends on the assumed spectrum and amplitude of MHD turbulence
but much less on the type of waves considered. It is demonstrated that
transport perpendicular to the average magnetic field is mostly determined
by compound diffusion which combines the effects of scattering off
magnetic irregularities with magnetic braiding. The ratio
![]() is independent of rigidity
over the wide range considered.
is independent of rigidity
over the wide range considered.
Key words: cosmic rays - magnetohydrodynamics (MHD) - turbulence - solar wind
Observations of solar energetic particle events confirm that
energetic particle transport in the heliosphere must be considered
as a diffusive process. Understanding the mechanism by which particles
are scattered in cosmic plasma continues to be one of the most
important problems of modern cosmic-ray physics. The main physical
process underlying the diffusive propagation is assumed to be pitch-angle
scattering by magnetic fluctuations imposed on the large-scale magnetic
field. It is usually analyticly
described by the quasi-linear theory (QLT; cf. Jokipii 1966;
Hasselman & Wibberenz 1968; Schlickeiser 1989).
The quasi-linear theory for the parallel diffusion (
![]() )
of cosmic rays (CR) appears to be reasonably well developed, in contrast to
the perpendicular diffusion coefficient (
)
of cosmic rays (CR) appears to be reasonably well developed, in contrast to
the perpendicular diffusion coefficient (
![]() ). That coefficient
is one of the most crucial parameters influencing the solar modulation
of CR. In spite of its importance, there is no fundamental theory
of perpendicular transport. It was only well established for hard-sphere
scattering in a magnetized plasma (Gleeson 1969).
Other analytical considerations
based on Foker-Planck theory (Forman et al. 1974; Jokipii & Parker 1969)
were limited
to a weak perturbed slab magnetic turbulence. However, recent results
indicate that in the case of solar wind we encounter complex high-amplitude
turbulence (Bieber et al. 1996). What is more, Giacalone
& Jokipii (1994) proved that diffusion across the
mean magnetic field needs a three
dimensional structure for the turbulent magnetic field. Similarly, Jokipii & Kota (1999)
showed that the method based on the velocity correlation function,
developed by
Kubo in 1957 to evaluate spatial diffusion coefficients, cannot be used
for compound diffusion, in which the particles are scattered back and forth along spreading
magnetic field lines. In two papers (Micha
). That coefficient
is one of the most crucial parameters influencing the solar modulation
of CR. In spite of its importance, there is no fundamental theory
of perpendicular transport. It was only well established for hard-sphere
scattering in a magnetized plasma (Gleeson 1969).
Other analytical considerations
based on Foker-Planck theory (Forman et al. 1974; Jokipii & Parker 1969)
were limited
to a weak perturbed slab magnetic turbulence. However, recent results
indicate that in the case of solar wind we encounter complex high-amplitude
turbulence (Bieber et al. 1996). What is more, Giacalone
& Jokipii (1994) proved that diffusion across the
mean magnetic field needs a three
dimensional structure for the turbulent magnetic field. Similarly, Jokipii & Kota (1999)
showed that the method based on the velocity correlation function,
developed by
Kubo in 1957 to evaluate spatial diffusion coefficients, cannot be used
for compound diffusion, in which the particles are scattered back and forth along spreading
magnetic field lines. In two papers (Micha![]() ek & Ostrowski 1997, 1998)
it was shown
that particle transport across magnetic field is a very complex process.
It depends,
in very complicated
way, on resonant interaction with MHD turbulence, diffusion of magnetic
field lines and drifts due to gradients and curvature of magnetic irregularities.
Recently, Giacalone & Jokipii (1999,
ek & Ostrowski 1997, 1998)
it was shown
that particle transport across magnetic field is a very complex process.
It depends,
in very complicated
way, on resonant interaction with MHD turbulence, diffusion of magnetic
field lines and drifts due to gradients and curvature of magnetic irregularities.
Recently, Giacalone & Jokipii (1999, ![]() GJ99)
presented numerical simulations of perpendicular and parallel diffusion
coefficients in the presence of a stationary irregular magnetic field.
They showed that the cross-field diffusion could be larger than
the prediction of classical scattering but smaller than the
prediction of the quasi-linear theory. The transport of charged particles
across the average magnetic field must be considered as the
superposition of two
fundamental effects. The first is scattering at an irregular magnetic field, the
second is caused by wandering or braiding of the magnetic field lines. Depending
on the efficiency of these processes the transport of charged particles normal to the
mean magnetic field may be described by ballistic motion, sub-diffusive motion or
compound diffusion (Duffy et al. 1995). A Markovian process involving diffusion along
a magnetic field, that is itself wandering, is regarded as compound diffusion.
In many astrophysical circumstances transport across the mean magnetic field
could be controlled by this process.
GJ99)
presented numerical simulations of perpendicular and parallel diffusion
coefficients in the presence of a stationary irregular magnetic field.
They showed that the cross-field diffusion could be larger than
the prediction of classical scattering but smaller than the
prediction of the quasi-linear theory. The transport of charged particles
across the average magnetic field must be considered as the
superposition of two
fundamental effects. The first is scattering at an irregular magnetic field, the
second is caused by wandering or braiding of the magnetic field lines. Depending
on the efficiency of these processes the transport of charged particles normal to the
mean magnetic field may be described by ballistic motion, sub-diffusive motion or
compound diffusion (Duffy et al. 1995). A Markovian process involving diffusion along
a magnetic field, that is itself wandering, is regarded as compound diffusion.
In many astrophysical circumstances transport across the mean magnetic field
could be controlled by this process.
The aim of the present paper is to study
![]() in the heliosphere at 1 AU. We consider the particle transport in the
presence of different amplitude MHD turbulence
models involving pure isotropic Alfvén waves,
pure isotropic magnetosonic waves or their mixture.
The influence of the wave amplitude and the wave spectrum on charged
particle transport is also considered. The
Monte Carlo simulations performed involve derivations of particle trajectories
are described in Sect. 2.
Next, in Sect. 3 we present results of simulations and in
Sect. 4 summarize the results.
in the heliosphere at 1 AU. We consider the particle transport in the
presence of different amplitude MHD turbulence
models involving pure isotropic Alfvén waves,
pure isotropic magnetosonic waves or their mixture.
The influence of the wave amplitude and the wave spectrum on charged
particle transport is also considered. The
Monte Carlo simulations performed involve derivations of particle trajectories
are described in Sect. 2.
Next, in Sect. 3 we present results of simulations and in
Sect. 4 summarize the results.
Let us consider an infinite region of tenuous plasma with
a uniform mean magnetic field along the z-axis (
![]() ),
perturbed with propagating MHD waves. In this respect our model
substantially diverges from the solar wind spiral-like configuration
of the mean magnetic field. Test particles (protons) are injected
into turbulent magnetized plasma and their trajectories are
followed by integrating particle equations of motion in space and momentum.
By averaging over a large number of trajectories
one derives the cross field diffusion coefficient
field
),
perturbed with propagating MHD waves. In this respect our model
substantially diverges from the solar wind spiral-like configuration
of the mean magnetic field. Test particles (protons) are injected
into turbulent magnetized plasma and their trajectories are
followed by integrating particle equations of motion in space and momentum.
By averaging over a large number of trajectories
one derives the cross field diffusion coefficient
field
![]() .
In simulations we usually used 200 particles with the same initial velocity
.
In simulations we usually used 200 particles with the same initial velocity
![]() in an individual run. The 4th-order Runge-Kutta
integration code with a constant integration step was used.
The number of particles engaged into simulations is
limited due to extensive integration time for individual trajectories.
Simulations with much bigger number of particles for a few particular
cases did not reveal any significant difference. A number
of tests of the code were performed. They included
standard checks of the applied random number generator.
The accuracy of a long time integration was checked by repeating
computations with shorter time steps. Also, for static perturbations,
the particle energy was conserved within the required accuracy.
in an individual run. The 4th-order Runge-Kutta
integration code with a constant integration step was used.
The number of particles engaged into simulations is
limited due to extensive integration time for individual trajectories.
Simulations with much bigger number of particles for a few particular
cases did not reveal any significant difference. A number
of tests of the code were performed. They included
standard checks of the applied random number generator.
The accuracy of a long time integration was checked by repeating
computations with shorter time steps. Also, for static perturbations,
the particle energy was conserved within the required accuracy.
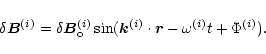 |
(1) |
![\begin{displaymath}\left[ \sum_{i = 1}^{768}\left(\delta B_{\rm o}^{(i)}\right)^2 \right]^{1/2} \equiv \delta
B.
\end{displaymath}](/articles/aa/full/2001/35/aa1118/img18.gif) |
(2) |
We consider three types of wave spectra.
In the first "wide range spectrum''
(hereafter referred to as the "wide spectrum'' ![]() W) the wave vectors are
drawn in a random manner (on a logarithmic scale)
from the broad wave vector range
W) the wave vectors are
drawn in a random manner (on a logarithmic scale)
from the broad wave vector range
![]() ,
where
,
where
![]() and
and
![]() are respectively the resonant wave vectors in the
mean magnetic field (
are respectively the resonant wave vectors in the
mean magnetic field (
![]() )
for
the fastest and slowest particles considered in simulations.
This spectrum seems to be the most reasonable for turbulence in a solar wind.
The second one is a "cutoff spectrum'' (hereafter referred to as a "cutoff
spectrum''
)
for
the fastest and slowest particles considered in simulations.
This spectrum seems to be the most reasonable for turbulence in a solar wind.
The second one is a "cutoff spectrum'' (hereafter referred to as a "cutoff
spectrum'' ![]() C) with the wave vectors
drown from the range
C) with the wave vectors
drown from the range
![]() ,
where
,
where
![]() is the resonance wave vector for particles
with a rigidity of 1 GV. Such a cutoff in the turbulence spectrum, near
the gyroresonance for protons, was postulated by Ragot (1999).
By choosing such a spectrum we can study
the influence of nonresonant scattering on particle transport.
Finally we introduce
a "narrow range spectrum'' (hereafter this spectrum is referred to as a
"narrow spectrum''
is the resonance wave vector for particles
with a rigidity of 1 GV. Such a cutoff in the turbulence spectrum, near
the gyroresonance for protons, was postulated by Ragot (1999).
By choosing such a spectrum we can study
the influence of nonresonant scattering on particle transport.
Finally we introduce
a "narrow range spectrum'' (hereafter this spectrum is referred to as a
"narrow spectrum'' ![]() N) with turbulence power concentrated in the
resonance range for each particle energy.
In this case the wave vectors
are drown in a random manner from a narrow band near the resonant
wave vector for a given initial particle velocity
N) with turbulence power concentrated in the
resonance range for each particle energy.
In this case the wave vectors
are drown in a random manner from a narrow band near the resonant
wave vector for a given initial particle velocity
![]() ,
,
![]() ,
where
,
where
![]() is the resonant wave vector for particles
with the given velocity
is the resonant wave vector for particles
with the given velocity
![]() .
It must be stressed
that spectrum of this last type is used for comparison only.
For illustration, in
the Fig. 1 simulated power spectra of
waves versus respective particle rigidity
are presented.
.
It must be stressed
that spectrum of this last type is used for comparison only.
For illustration, in
the Fig. 1 simulated power spectra of
waves versus respective particle rigidity
are presented.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1118f1r.eps}\end{figure}](/articles/aa/full/2001/35/aa1118/Timg35.gif) |
Figure 1: Simulated wave power spectra versus respective resonant particle rigidity. The results for a wide spectrum, a cutoff spectrum and an example of a narrow spectrum for particles with rigidity about 4 MV are presented by dashed, thick solid and thin solid lines respectively. |
| Open with DEXTER | |
In Fig. 2, simulated values of the cross field diffusion coefficient
versus rigidity
for all considered models are shown. From top to bottom of
the picture, in the respective panels, the results for the pure
Alfvén waves,
for mixture of waves and for magnetosonic waves are presented.
From left to right
the simulated values of
![]() for the N, C and W spectra
are given. One should remember that the results for N spectra
are obtained with a different spectrum for each point,
and they are provided for comparison only.
Additionally, the diffusion coefficients of
the magnetic field
for the N, C and W spectra
are given. One should remember that the results for N spectra
are obtained with a different spectrum for each point,
and they are provided for comparison only.
Additionally, the diffusion coefficients of
the magnetic field
![]() (where L is separation of adjacent
field lines and s is the distance measured along the field line)
for all considered models (for
(where L is separation of adjacent
field lines and s is the distance measured along the field line)
for all considered models (for
![]() )
are given by thin solid lines.
In the figure one may observe that simulated values of
)
are given by thin solid lines.
In the figure one may observe that simulated values of
![]() for C and W spectra are constant in the low and middle rigidity range
and increase
in the high rigidity range. For models with the N spectrum a clear increase
of the cross field diffusion coefficient is
observed over the whole considered rigidity range.
These general trends do not depend
on the type of MHD waves used for simulations.
The second obvious feature seen in the picture are much bigger
cross field diffusion coefficients for the models with larger
wave amplitude of
for C and W spectra are constant in the low and middle rigidity range
and increase
in the high rigidity range. For models with the N spectrum a clear increase
of the cross field diffusion coefficient is
observed over the whole considered rigidity range.
These general trends do not depend
on the type of MHD waves used for simulations.
The second obvious feature seen in the picture are much bigger
cross field diffusion coefficients for the models with larger
wave amplitude of
![]() in comparison
to the ones with
in comparison
to the ones with
![]() .
.
![\begin{figure}
\par\includegraphics[width=16.2cm,height=10cm,clip]{1118f2.eps}\end{figure}](/articles/aa/full/2001/35/aa1118/Timg40.gif) |
Figure 2:
The simulated values of the cross field diffusion coefficient
versus particle rigidity
for all considered models. From top to bottom of the picture,
in the respective panels we have
pure Alfvén waves, mixture of waves and pure magnetosonic waves.
From left to right in the respective panels we have the N,
C and W spectra. The results for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.2cm,height=10cm,clip]{1118f3.eps}\end{figure}](/articles/aa/full/2001/35/aa1118/Timg41.gif) |
Figure 3:
The simulated values of the parallel diffusion coefficient
versus particle rigidity for all considered models. From top to bottom
of the picture,
in the respective panels we have
pure Alfvén waves, mixture of waves and pure magnetosonic waves.
From left to right in the respective panels we have the N,
C and W spectra. The results for
|
| Open with DEXTER | |
The most striking feature emerging from the both pictures are that
the cross field diffusion
coefficient is smaller by about two orders of magnitude with respect to
the parallel diffusion coefficients but strictly follows their behaviour over
the wide rigidity range considered. It seems that parallel transport could
be the most
important parameter determining
![]() .
Such a tendency
could appear
when the transport across
magnetic fields is controlled by compound diffusion. In such a Markovian
process, particles diffuse along a magnetic field which is itself wandering.
In contrast to sub-diffusive motion a particle can escape and restart motion
in a new coherent patch of field lines. In this collisional transport
regime
.
Such a tendency
could appear
when the transport across
magnetic fields is controlled by compound diffusion. In such a Markovian
process, particles diffuse along a magnetic field which is itself wandering.
In contrast to sub-diffusive motion a particle can escape and restart motion
in a new coherent patch of field lines. In this collisional transport
regime
![]() ,
where
,
where
![]() is the Lyapunov length
describing the exponential separation of adjacent field lines (Duffy et al. 1995).
So then, if the cross field diffusion is described by compound
diffusion, the ratio
is the Lyapunov length
describing the exponential separation of adjacent field lines (Duffy et al. 1995).
So then, if the cross field diffusion is described by compound
diffusion, the ratio
![]() should
be
should
be ![]() const. The values of
const. The values of
![]() received for the models W, C and N
are almost independent of rigidity.
received for the models W, C and N
are almost independent of rigidity.
For models with the C spectrum,
where in the low rigidity range particles could propagate without
resonant interactions (more effective transport parallel to the average magnetic field),
![]() is more than
an order of magnitude larger in comparison to the models N and W
and results presented by GJ99.
The same situation could appear for model W in the low rigidity
range, causing an enhancement in diffusion above predictions of the model
N and the results presented by GJ99. It is clear that at a given value of
is more than
an order of magnitude larger in comparison to the models N and W
and results presented by GJ99.
The same situation could appear for model W in the low rigidity
range, causing an enhancement in diffusion above predictions of the model
N and the results presented by GJ99. It is clear that at a given value of ![]() an increase in the particle parallel transport must
cause a similar increase in the cross field diffusion.
In the high rigidity range, transport for all the considered wave
spectra models (W, C and N)
is to a similar degree controlled by
resonant interactions and differences between the simulated
an increase in the particle parallel transport must
cause a similar increase in the cross field diffusion.
In the high rigidity range, transport for all the considered wave
spectra models (W, C and N)
is to a similar degree controlled by
resonant interactions and differences between the simulated
![]() disappear.
disappear.
We must stress that at the lowest particle velocities (
![]() ), where the Coulomb scattering
becomes more effective,
the models could be unrealistic. However, our considerations
could be useful for comparison with some published results
(especially for
), where the Coulomb scattering
becomes more effective,
the models could be unrealistic. However, our considerations
could be useful for comparison with some published results
(especially for
![]() )
and to test models of turbulence.
)
and to test models of turbulence.
Propagation of protons in the solar wind
at a wide range of rigidities was studied for a few models of MHD waves.
A choice of the turbulence model composed of Alfvén or fast magnetosonic
waves relies upon the fact that these particular waves are less
effectively damped in plasma with the parameter
![]() and constitute a big part of the observed solar turbulence (Stix 1992;
Goldstein et al. 1995).
Summarizing, our simulations show that the global form of the
curves of "cross field diffusion'' versus rigidity is sensitive
to the spectrum and
amplitude of waves, but only depends to a small degree on the type of
MHD waves considered. The transport across the average
magnetic field could be
controlled by compound diffusion to
a large degree.
It is shown that the field-lines random
walk,
together with the effective particle transport along the mean magnetic field,
in the absence of resonant interactions, leads to a large enhancement of the cross
field diffusion coefficient, above the results obtained by GJ99 and quasi-linear theory.
It is interesting to note that the ratio
and constitute a big part of the observed solar turbulence (Stix 1992;
Goldstein et al. 1995).
Summarizing, our simulations show that the global form of the
curves of "cross field diffusion'' versus rigidity is sensitive
to the spectrum and
amplitude of waves, but only depends to a small degree on the type of
MHD waves considered. The transport across the average
magnetic field could be
controlled by compound diffusion to
a large degree.
It is shown that the field-lines random
walk,
together with the effective particle transport along the mean magnetic field,
in the absence of resonant interactions, leads to a large enhancement of the cross
field diffusion coefficient, above the results obtained by GJ99 and quasi-linear theory.
It is interesting to note that the ratio
![]() is roughly independent of energy.
is roughly independent of energy.
Acknowledgements
The work was supported by foundation of Prof. A. Krzyzanowskiego and Komitet Badan Naukowych through the grant PB 258/P03/99/17.