A&A 376, 713-726 (2001)
DOI: 10.1051/0004-6361:20011041
M. Ossendrijver1 - M. Stix1 - A. Brandenburg2,3
1 - Kiepenheuer-Institut für Sonnenphysik,
Schöneckstraße 6, 79104 Freiburg, Germany
2 - Department of Mathematics, University of Newcastle upon Tyne, NE1 7RU, UK
3 - Nordita, Blegdamsvej 17, 2100 Copenhagen Ø, Denmark
Received 24 October 2000 / Accepted 12 July 2001
Abstract
We present numerical simulations of three-dimensional compressible magnetoconvection
in a rotating rectangular box that represents a section of the solar convection zone.
The box contains a convectively unstable layer, surrounded by stably
stratified layers with overshooting convection. The magnetic Reynolds number,
Rm, is chosen subcritical, thus excluding spontaneous growth of the magnetic
field through dynamo action, and the magnetic energy is maintained by
introducing a constant magnetic field into the box, once convection has attained
a statistically stationary state. Under the influence of the Coriolis force,
the advection of the magnetic field results in
a non-vanishing contribution to the mean electric
field, given by
![]() .
From this electric field, we calculate
the
.
From this electric field, we calculate
the ![]() -effect, separately for the stably and the unstably stratified
layers, by averaging over time and over suitably defined volumes. From the
variation of
-effect, separately for the stably and the unstably stratified
layers, by averaging over time and over suitably defined volumes. From the
variation of ![]() we derive an error estimate, and the dependence of
we derive an error estimate, and the dependence of
![]() on rotation and magnetic field strength is studied. Evidence is
found for rotational quenching of the vertical
on rotation and magnetic field strength is studied. Evidence is
found for rotational quenching of the vertical ![]() effect, and
for a monotonic increase of the horizontal
effect, and
for a monotonic increase of the horizontal ![]() effect with
increasing rotation. For
effect with
increasing rotation. For
![]() ,
our results for both
vertical and horizontal
,
our results for both
vertical and horizontal ![]() effect are consistent with magnetic
quenching by a factor
effect are consistent with magnetic
quenching by a factor
![]() .
The signs
of the small-scale current helicity and of the vertical component of
.
The signs
of the small-scale current helicity and of the vertical component of
![]() are found to be opposite to those for isotropic turbulence.
are found to be opposite to those for isotropic turbulence.
Key words: convection - magnetic fields
Magnetic fields are observed on a wide variety of cosmical bodies, among which are planets, stars and galaxies. With the exception of a few types of objects whose magnetic fields are thought to be frozen-in relic fields, cosmical magnetic fields are attributed to dynamo action. Dynamo theory concerns the generation of magnetic fields in electrically conducting fluids. In stars and planets, dynamo action is the result of an interplay between convection and rotation. The present simulations focus on dynamo action in late-type stars, which are characterized by an outer convective zone on top of a stably stratified radiative interior. Many late-type stars are magnetically active, and some exhibit magnetic cycles, as does the Sun.
A successful solar model was first proposed by Parker (1955) who recognized
that shear and helicity cooperate in such a way that the mean magnetic field
oscillates in a migratory manner; later Yoshimura (1975) has shown that the
field generally propagates along the surfaces of constant angular velocity.
Since then, magnetic cycles and butterfly diagrams have been produced by
mean-field models using spherical
geometry (Steenbeck & Krause 1969), with depth-dependent magnetic
diffusivity (Roberts & Stix 1972), and with the character of an
interface wave at the base of the convection zone (Parker 1993;
Charbonneau & MacGregor 1997). As an alternative to the helical effect of
convection (the ![]() effect), the systematic tilt of flux tubes that
become unstable and erupt to the solar surface has been employed
as a regenerative agent for the mean poloidal field (Leighton 1969;
Durney 1995, 1997; Schmitt et al. 1996; Dikpati & Charbonneau 1999), with
equal success regarding the existence of Sun-like cycles and butterfly
diagrams. In all cases, however, the regenerative terms in the mean-field
equations were based either on approximations such as first-order
smoothing, or on the limited available knowledge about the behavior of
magnetic flux tubes in the convection zone; the review of Stix (2001)
summarizes some of the current problems.
effect), the systematic tilt of flux tubes that
become unstable and erupt to the solar surface has been employed
as a regenerative agent for the mean poloidal field (Leighton 1969;
Durney 1995, 1997; Schmitt et al. 1996; Dikpati & Charbonneau 1999), with
equal success regarding the existence of Sun-like cycles and butterfly
diagrams. In all cases, however, the regenerative terms in the mean-field
equations were based either on approximations such as first-order
smoothing, or on the limited available knowledge about the behavior of
magnetic flux tubes in the convection zone; the review of Stix (2001)
summarizes some of the current problems.
In principle, the problem can be attacked by direct numerical integration
of the equations of magnetohydrodynamics (MHD) for the star's convection
zone (for a review, see e.g. Nordlund et al. 1994).
But severe problems are encountered.
Firstly, a stellar convection zone is a highly turbulent plasma
(
![]() ), so that the kinetic energy spectrum encompasses a very
wide range of length scales. If these were all to be resolved, a prohibitive
number of mesh points would be required. Secondly, since the magnetic
Reynolds number is also large (
), so that the kinetic energy spectrum encompasses a very
wide range of length scales. If these were all to be resolved, a prohibitive
number of mesh points would be required. Secondly, since the magnetic
Reynolds number is also large (
![]() ), a similar argument holds
for the length scales of the magnetic field. For these reasons
three-dimensional MHD simulations often have been restricted to a
rectangular box that represents only a small section of a stellar
convection zone. In the present work we do this, too. Thirdly, the Prandtl
number, the ratio of the kinematic viscosity to the radiative diffusivity,
is very small in the solar convection zone (
), a similar argument holds
for the length scales of the magnetic field. For these reasons
three-dimensional MHD simulations often have been restricted to a
rectangular box that represents only a small section of a stellar
convection zone. In the present work we do this, too. Thirdly, the Prandtl
number, the ratio of the kinematic viscosity to the radiative diffusivity,
is very small in the solar convection zone (
![]() -10-7),
so that the flow can vary on much smaller scales than the temperature.
This is known to have consequences for the topology and temporal
behavior of convective turbulence
(Cattaneo et al. 1991; Brandenburg et al. 1996;
Brummell et al. 1996), but
in the present simulations, we ignore such effects, and set
-10-7),
so that the flow can vary on much smaller scales than the temperature.
This is known to have consequences for the topology and temporal
behavior of convective turbulence
(Cattaneo et al. 1991; Brandenburg et al. 1996;
Brummell et al. 1996), but
in the present simulations, we ignore such effects, and set
![]() .
Fourthly, the Mach number,
.
Fourthly, the Mach number,
![]() ,
decreases with depth in the
solar convection zone from about 0.1 in the photosphere to less than
0.001 near the base. The corresponding high sound speed in the lower
convection zone necessitates the use of very small time steps in order to
fulfill the CFL condition for compressible hydrodynamics
(
,
decreases with depth in the
solar convection zone from about 0.1 in the photosphere to less than
0.001 near the base. The corresponding high sound speed in the lower
convection zone necessitates the use of very small time steps in order to
fulfill the CFL condition for compressible hydrodynamics
(
![]() ), while it is often desirable to continue
simulations for at least several convective turnover times. One possibility
to circumvent this problem is to adopt the anelastic approximation
whereby sound waves are excluded, so that larger time steps can be
used (Ogura & Charney 1962; Lantz & Fan 1999).
Here we maintain full compressibility, and attain a mean Mach number
of the order 0.1; in a subsequent paper we shall study effects of a
smaller Mach number.
), while it is often desirable to continue
simulations for at least several convective turnover times. One possibility
to circumvent this problem is to adopt the anelastic approximation
whereby sound waves are excluded, so that larger time steps can be
used (Ogura & Charney 1962; Lantz & Fan 1999).
Here we maintain full compressibility, and attain a mean Mach number
of the order 0.1; in a subsequent paper we shall study effects of a
smaller Mach number.
Brandenburg et al. (1990) extended a 3D hydrodynamical
code to the case of magnetoconvection, including the effect of rotation.
Subsequently, a spontaneous dynamo instability was observed in the
simulations (Nordlund et al. 1992; Brandenburg et al.
1996). Recent simulations of isotropically forced helical
turbulence (Brandenburg 2001) have verified the
existence of large scale dynamo action, and it was possible to identify
this as the result of an ![]() effect (in the sense of a
non-local inverse cascade). However, the large scale
field generated possesses magnetic helicity and, since for closed or
periodic boundaries the magnetic helicity can change only resistively,
the growth of the large scale field is slowed down as the magnetic
Reynolds number increases. This translates inevitably to a
magnetic-Reynolds-number dependent
effect (in the sense of a
non-local inverse cascade). However, the large scale
field generated possesses magnetic helicity and, since for closed or
periodic boundaries the magnetic helicity can change only resistively,
the growth of the large scale field is slowed down as the magnetic
Reynolds number increases. This translates inevitably to a
magnetic-Reynolds-number dependent ![]() effect and
turbulent magnetic diffusivity, as suggested by Vainshtein
& Cattaneo (1992). The argument of
Vainshtein & Cattaneo is however only phenomenological, not based
upon the fundamental concept of magnetic helicity conservation, and
hence their conclusion that strong large-scale fields are
impossible is not borne out by the simulations of
Brandenburg (2001). Furthermore, in that paper it
was shown that the
effect and
turbulent magnetic diffusivity, as suggested by Vainshtein
& Cattaneo (1992). The argument of
Vainshtein & Cattaneo is however only phenomenological, not based
upon the fundamental concept of magnetic helicity conservation, and
hence their conclusion that strong large-scale fields are
impossible is not borne out by the simulations of
Brandenburg (2001). Furthermore, in that paper it
was shown that the ![]() obtained by imposing a magnetic field is
indeed a reasonable approximation to the
obtained by imposing a magnetic field is
indeed a reasonable approximation to the ![]() that results
naturally even if no field is imposed.
that results
naturally even if no field is imposed.
In the present simulations we do not calculate box dynamos, but rather
concentrate on the dynamo coefficients that occur in mean-field theory.
Therefore, all simulations are performed with an imposed magnetic field,
and the magnetic Reynolds number is chosen subcritical, so that the
magnetic field is not self-sustained. We think that progress in stellar
dynamo theory can be made through a combination of exact MHD simulation
and mean-field dynamo theory. Furthermore, the existence of
systematic, large-scale magnetic fields and stellar cycles with periods
far in excess of convective time scales suggests that a mean-field
description is possible in some form. Also, we argue that mean-field
theory (in the wide sense that includes the above-mentioned models
such as Leighton's) is the only current model that reproduces
large-scale magnetic fields and cycles, including such an outstanding
feature as the solar butterfly diagram, even though the diverse
approximations made for calculating the dynamo coefficients may not
be valid under stellar conditions.
The case of self-excited dynamo action would of course be very
interesting too, especially in view of the question of whether
![]() -quenching depends on the magnetic Reynolds number, as suggested
by Vainshtein & Cattaneo (1992). However, we postpone this
until a later study, partly because the measurement of the dynamo
coefficients in the presence of a large-scale field
that is different from the imposed one is less straightforward.
-quenching depends on the magnetic Reynolds number, as suggested
by Vainshtein & Cattaneo (1992). However, we postpone this
until a later study, partly because the measurement of the dynamo
coefficients in the presence of a large-scale field
that is different from the imposed one is less straightforward.
The present investigation is limited to the regime where
the coefficients are determined directly by the flow, and
we do not address the question of whether the large-scale magnetic
field of late-type stars is in fact generated by such an ordinary
![]() effect in the convection zone, or by a magnetic instability
in an underlying stably stratified layer
(e.g., Brandenburg & Schmitt 1998).
We do include a stably stratified
layer with overshooting convection, but its main purpose here is to
provide realistic conditions for the flow in the unstable region.
In most runs, the strength of the imposed field is set to a value which
amounts to typically
effect in the convection zone, or by a magnetic instability
in an underlying stably stratified layer
(e.g., Brandenburg & Schmitt 1998).
We do include a stably stratified
layer with overshooting convection, but its main purpose here is to
provide realistic conditions for the flow in the unstable region.
In most runs, the strength of the imposed field is set to a value which
amounts to typically ![]() of the equipartition field with respect
to the kinetic energy density. During the subsequent evolution
the field strength also remains small compared to the equipartition value.
Furthermore we shall explore the influence of the imposed magnetic field
by increasing its strength up to values somewhat in excess of the
equipartition value.
Therefore the results may have relevance for the solar convection zone,
where the magnetic field is no stronger than the equipartition value.
The
of the equipartition field with respect
to the kinetic energy density. During the subsequent evolution
the field strength also remains small compared to the equipartition value.
Furthermore we shall explore the influence of the imposed magnetic field
by increasing its strength up to values somewhat in excess of the
equipartition value.
Therefore the results may have relevance for the solar convection zone,
where the magnetic field is no stronger than the equipartition value.
The ![]() effect produced in the galactic
gas by supernova explosions has been calculated by Ziegler et al.
(1996), in a similar spirit as in the present work.
effect produced in the galactic
gas by supernova explosions has been calculated by Ziegler et al.
(1996), in a similar spirit as in the present work.
The relevance of the transport coefficients for mean-field dynamo theory
becomes clear from the equation for the mean magnetic field,
![\begin{displaymath}\frac{\partial\langle\vec{B}\rangle}{\partial t}=\nabla\times...
...es\vec{b}\rangle-\eta\nabla\times\langle\vec{B}\rangle\big]\,,
\end{displaymath}](/articles/aa/full/2001/35/aa10386/img48.gif) |
(1) |
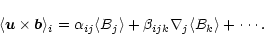 |
(2) |
The remainder of the paper is structured as follows. After introducing the model and
the equations, we focus on the dependence of ![]() on rotation.
In the following section, effects of the strength and orientation of the imposed field
are studied. In the final section, a discussion of the results is presented.
on rotation.
In the following section, effects of the strength and orientation of the imposed field
are studied. In the final section, a discussion of the results is presented.
![\begin{figure}
\par\includegraphics[width=6.15cm,clip]{fig1.eps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg59.gif) |
Figure 1: Geometry of the simulation domain. The layer boundaries are at z1=-0.15, z2=0, z3=1, and z4=2.85, except for run 10 that has no stable regions, so that z1=z2=0 and z3=z4=1. The horizontal extent is 4. |
| Open with DEXTER | |
The governing equations are those describing magnetic induction, mass
continuity, and the balance of momentum and energy:
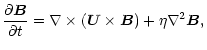 |
(3) | ||
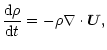 |
(4) | ||
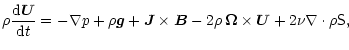 |
(5) | ||
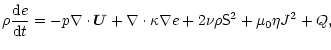 |
(6) |
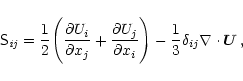 |
(7) |
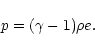 |
(8) |
All quantities are made dimensionless by setting
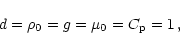 |
(11) |
On several occasions we shall consider the energy balance,
which is governed by a conservation law,
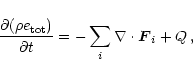 |
(12) |
| (13) | |||
| (14) | |||
| (15) | |||
| (16) | |||
| (17) |
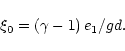 |
(19) |
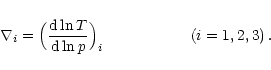 |
(20) |
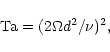 |
(22) |
All other parameters are secondary. The Coriolis number, or inverse Rossby number, measures
the importance of the Coriolis force and is defined as
| (23) |
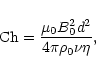 |
(24) |
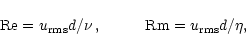 |
(27) |
| run | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ta | 2 | 10 | 30 | 100 | 300 | 2000 | ||||
| T (
|
206 | 822 | 206 | 841 | 698 | 545 | 940 | 362 | 376 | 554 |
| T (
|
- | - | - | 564 | 564 | 456 | 508 | 346 | 290 | 521 |
| Ma | 0.089 | 0.088 | 0.088 | 0.084 | 0.091 | 0.089 | 0.080 | 0.070 | 0.056 | 0.10 |
| Re | 34 | 34 | 34 | 34 | 35 | 34 | 30 | 30 | 20 | 38 |
| Co | 0.042 | 0.093 | 0.16 | 0.30 | 0.50 | 1.3 | 3.3 | 5.4 | 11 | 2.6 |
We employ a finite difference scheme, according to which spatial derivatives are calculated with 6th-order accuracy (Lele 1992). Time-stepping is done using a third-order Hyman predictor-corrector method. Table 1 gives a list of the parameters used for a first series of runs in which the influence of rotation is investigated by varying the Taylor number.
![\begin{figure}
\par\includegraphics[width=6.25cm,clip]{fig2a.ps}\\ [1cm]
\includegraphics[width=6.25cm,clip]{fig2b.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg139.gif) |
Figure 2:
Averaging procedure (run 6). Top: at each time step,
|
| Open with DEXTER | |
Essentially, the ![]() effect amounts to a proportionality between the
mean electromotive force,
effect amounts to a proportionality between the
mean electromotive force,
![]() ,
and the mean magnetic field.
Magnetoconvection in a rotating, stratified medium provides the necessary
anisotropies for a non-zero
,
and the mean magnetic field.
Magnetoconvection in a rotating, stratified medium provides the necessary
anisotropies for a non-zero ![]() .
In the present case, with the rotation
axis chosen parallel to the direction of gravity, the most elementary,
non-isotropic form of the expression for the
.
In the present case, with the rotation
axis chosen parallel to the direction of gravity, the most elementary,
non-isotropic form of the expression for the ![]() effect is one that
distinguishes vertical and horizontal components:
effect is one that
distinguishes vertical and horizontal components:
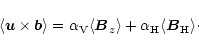 |
(28) |
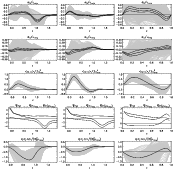 |
Figure 3:
Row 1: vertical |
| Open with DEXTER | |
It is well known from other numerical simulations that ![]() is an
extremely noisy quantity, so that one should do as much averaging as
possible in order to optimize the statistics.
is an
extremely noisy quantity, so that one should do as much averaging as
possible in order to optimize the statistics.
For this paper we have chosen two averaging procedures. The first,
which is considered in the present section, consists of an average over
the horizontal coordinates and over time (Fig. 2, upper
panel). The time average is initiated from the moment when the
magnetoconvection has attained a statistically stationary state, i.e.
when the kinetic and magnetic energy densities are more or less constant.
The second is an additional average over two suitably chosen depth ranges
(Fig. 2, lower panel): since the
![]() effect depends on
depth, and is expected to change sign near the bottom of the unstable layer,
the averaging over depth is performed separately for the unstably and the
stably stratified layers. This second procedure will be used mainly
in later sections.
effect depends on
depth, and is expected to change sign near the bottom of the unstable layer,
the averaging over depth is performed separately for the unstably and the
stably stratified layers. This second procedure will be used mainly
in later sections.
The statistical deviation of ![]() from its mean value generally
is large, often larger than the difference between that mean and zero,
as illustrated in Fig. 3. Therefore, extended simulations
are necessary in order to obtain a significant result. In the present
paper the error estimate is based on the assumption that a single
simulation can be divided into a number of time intervals containing
independent realizations of the small-scale flow and magnetic field.
The length
from its mean value generally
is large, often larger than the difference between that mean and zero,
as illustrated in Fig. 3. Therefore, extended simulations
are necessary in order to obtain a significant result. In the present
paper the error estimate is based on the assumption that a single
simulation can be divided into a number of time intervals containing
independent realizations of the small-scale flow and magnetic field.
The length ![]() of those time intervals should then exceed the
correlation time, which is
of those time intervals should then exceed the
correlation time, which is ![]() 20 (in dimensionless units), as
determined from the width of the autocorrelation function. To be on
the safe side, we smoothed curves of
20 (in dimensionless units), as
determined from the width of the autocorrelation function. To be on
the safe side, we smoothed curves of
![]() and
and
![]() for several runs by performing a box
average, and then calculated the autocorrelation function. This
procedure yields a typical coherence time
for several runs by performing a box
average, and then calculated the autocorrelation function. This
procedure yields a typical coherence time ![]() ,
which is several
times longer than the value derived from the unsmoothed curves.
,
which is several
times longer than the value derived from the unsmoothed curves.
Our procedure of estimating errors is more primitive than that applied
earlier to results of numerical simulations (Pulkkinen et al. 1993).
Moreover, the errors of the mean values determined in this manner can
only be crude estimates because firstly we cannot be sure that we deal
with Gaussian statistics (although inspection of the examples of Fig.
3 suggests that ![]() varies in a nearly symmetric manner
around its mean), and secondly the number
varies in a nearly symmetric manner
around its mean), and secondly the number ![]() of time intervals
is not very large. Nevertheless we think that the procedure indicates
whether or not the obtained mean values are significantly different
form zero. Test simulations with identical parameters but different
initializations confirm this indication. Of course, the resulting
error bars do not imply anything about the physical assumptions made.
In particular, we cannot expect that models based on different
assumptions, such as ours and that of Rüdiger & Kitchatinov
(1993), will yield results that lie within error bars
obtained from statistics (these bars shrink to zero for
of time intervals
is not very large. Nevertheless we think that the procedure indicates
whether or not the obtained mean values are significantly different
form zero. Test simulations with identical parameters but different
initializations confirm this indication. Of course, the resulting
error bars do not imply anything about the physical assumptions made.
In particular, we cannot expect that models based on different
assumptions, such as ours and that of Rüdiger & Kitchatinov
(1993), will yield results that lie within error bars
obtained from statistics (these bars shrink to zero for
![]() ). In contrast, we must see whether we can
find qualitatively similar or dissimilar results from different
models, especially as none of the models yet meets the real Sun.
). In contrast, we must see whether we can
find qualitatively similar or dissimilar results from different
models, especially as none of the models yet meets the real Sun.
The existence of the ![]() effect is attributed to the helical
nature of convective flows in a rotating medium. Figure 3
shows
effect is attributed to the helical
nature of convective flows in a rotating medium. Figure 3
shows
![]() ,
,
![]() and several quantities that,
as is shown below, have a relation to the
and several quantities that,
as is shown below, have a relation to the ![]() effect.
Three different runs are selected in order to demonstrate
the effects of rotation and boundary conditions.
effect.
Three different runs are selected in order to demonstrate
the effects of rotation and boundary conditions.
The ![]() coefficients are depth-dependent,
and undergo a sign change within the unstable layer.
For
coefficients are depth-dependent,
and undergo a sign change within the unstable layer.
For
![]() ,
the vertical alpha coefficient exceeds the
horizontal coefficient, and has the opposite sign. If rotation is
stronger, the vertical
,
the vertical alpha coefficient exceeds the
horizontal coefficient, and has the opposite sign. If rotation is
stronger, the vertical ![]() effect is strongly reduced.
effect is strongly reduced.
For isotropic turbulence, the first-order smoothing approximation
(FOSA) yields that ![]() can be described by a single scalar
can be described by a single scalar
The kinetic helicity is positive at the top of the convective layer (Fig. 3, row 3), as
is expected for the southern hemisphere based on the direction of the Coriolis force for contracting
sinking parcels, or expanding rising parcels. Brummell et al. (1998) find kinetic
helicity with the same sign for a box on the northern
hemisphere, but their coordinate system turns out to have a left-handed orientation. Near the center
of the convective layer, the sign of the kinetic helicity reverses if rotation is sufficiently strong,
because below a certain point sinking parcels expand laterally while
approaching the level z=1 (i.e., the stably stratified overshoot layer or
the impenetrable lower boundary if an overshoot layer is absent),
while rising parcels contract while moving away from it. For
![]() ,
no reverse-helicity region seems to exist. Nevertheless, in these cases
alpha still changes its sign near the bottom of the convective layer. For
comparison we have calculated a case (run 10) with the same Taylor number as
in run 7, but where the stably stratified layers are replaced by impenetrable
boundaries at z=0 and z=1. In this case the kinetic helicity near the
bottom of the unstable layer is more strongly negative, and has a magnitude
comparable to that in the upper part of the unstable layer (Fig. 3,
row 3, Col. 3). This can be attributed to the fact that an impenetrable
boundary forces a sinking parcel to diverge more strongly than does a
stably stratified layer. Thus, except for the stable region in some cases,
the sign of
,
no reverse-helicity region seems to exist. Nevertheless, in these cases
alpha still changes its sign near the bottom of the convective layer. For
comparison we have calculated a case (run 10) with the same Taylor number as
in run 7, but where the stably stratified layers are replaced by impenetrable
boundaries at z=0 and z=1. In this case the kinetic helicity near the
bottom of the unstable layer is more strongly negative, and has a magnitude
comparable to that in the upper part of the unstable layer (Fig. 3,
row 3, Col. 3). This can be attributed to the fact that an impenetrable
boundary forces a sinking parcel to diverge more strongly than does a
stably stratified layer. Thus, except for the stable region in some cases,
the sign of ![]() as predicted by Eq. (29) roughly agrees with
that of
as predicted by Eq. (29) roughly agrees with
that of
![]() ,
while it is opposite to that of
,
while it is opposite to that of
![]() .
The deviating sign of
.
The deviating sign of
![]() was explained by Brandenburg et al.
(1990). We note that the same unconventional sign of
was explained by Brandenburg et al.
(1990). We note that the same unconventional sign of
![]() was also found by Ferrière (1992), and
Rüdiger & Kitchatinov (1993), although not for the same
values of the Coriolis parameter as in our simulations.
was also found by Ferrière (1992), and
Rüdiger & Kitchatinov (1993), although not for the same
values of the Coriolis parameter as in our simulations.
The gradient of
![]() is positive at the top of the
convective layer and changes sign at a point near the bottom of the
unstable layer in the runs with an overshoot layer (Fig. 3,
row 4, Cols. 1, 2). Hence the sign of
is positive at the top of the
convective layer and changes sign at a point near the bottom of the
unstable layer in the runs with an overshoot layer (Fig. 3,
row 4, Cols. 1, 2). Hence the sign of ![]() as predicted by (31)
agrees with that of
as predicted by (31)
agrees with that of
![]() in the simulations, also if rotation
is weak. In this respect,
in the simulations, also if rotation
is weak. In this respect,
![]() agrees qualitatively
more closely than does the kinetic or the current helicity. In the upper
region,
agrees qualitatively
more closely than does the kinetic or the current helicity. In the upper
region,
![]() is positive because the density
gradient dominates, while near the bottom of the unstable domain the
influence of the convective stability is felt, resulting in a reduction
of the turbulent velocity sufficient to produce a negative sign.
With regard to
is positive because the density
gradient dominates, while near the bottom of the unstable domain the
influence of the convective stability is felt, resulting in a reduction
of the turbulent velocity sufficient to produce a negative sign.
With regard to
![]() ,
the sign and the dependence on Co
differ strongly from (31).
Also, in the run without the stably stratified layer, the
gradient of the density dominates throughout the box, and no sign change of
,
the sign and the dependence on Co
differ strongly from (31).
Also, in the run without the stably stratified layer, the
gradient of the density dominates throughout the box, and no sign change of
![]() is observed (Fig. 3, row 4, Col. 3).
Both components of
is observed (Fig. 3, row 4, Col. 3).
Both components of ![]() do exhibit a sign change, though. This
inconsistency may be a result of the impenetrable boundary condition at
z=1, which causes a transfer of kinetic energy from the vertical
to the horizontal components, an effect which is not accounted for by
Eq. (31). A detailed comparison of the rotational dependence of
do exhibit a sign change, though. This
inconsistency may be a result of the impenetrable boundary condition at
z=1, which causes a transfer of kinetic energy from the vertical
to the horizontal components, an effect which is not accounted for by
Eq. (31). A detailed comparison of the rotational dependence of
![]() and
and
![]() with Eq. (31), and with the
analytical results of Rüdiger & Kitchatinov (1993), will
be presented in Sect. 4.2.
with Eq. (31), and with the
analytical results of Rüdiger & Kitchatinov (1993), will
be presented in Sect. 4.2.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{fig4.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg169.gif) |
Figure 4:
Solid: kinetic helicity,
|
| Open with DEXTER | |
The current helicity is negative in the upper part of the unstable layer
for a vertical imposed magnetic field (Fig. 3, row 5), which
confirms earlier results of Brandenburg et al. (1990). A
reverse-polarity layer is not observed, except in run 10 with the
impenetrable boundary at z=1. Thus, the sign of ![]() in the unstable layer as predicted
by Eq. (30) is the same as that of
in the unstable layer as predicted
by Eq. (30) is the same as that of
![]() .
The negative
sign of
.
The negative
sign of
![]() ,
which corresponds to a positive sign
in the bulk of the convection zone on the northern hemisphere, is at odds
with forced isotropic turbulence calculations by Brandenburg
(2001) as well as with observations of the solar surface
(Seehafer 1990; Low 1996) and mean-field calculations (Rädler &
Seehafer 1990; Rüdiger et al. 2001). For a
horizontal imposed magnetic field, the current helicity is about one order
of magnitude smaller than in the case of a vertical imposed field. It is
highly fluctuating, and its mean value can have either sign (not shown).
The smaller amplitude is consistent with the smaller amplitude of the
magnetic fluctuations (Fig. 6).
,
which corresponds to a positive sign
in the bulk of the convection zone on the northern hemisphere, is at odds
with forced isotropic turbulence calculations by Brandenburg
(2001) as well as with observations of the solar surface
(Seehafer 1990; Low 1996) and mean-field calculations (Rädler &
Seehafer 1990; Rüdiger et al. 2001). For a
horizontal imposed magnetic field, the current helicity is about one order
of magnitude smaller than in the case of a vertical imposed field. It is
highly fluctuating, and its mean value can have either sign (not shown).
The smaller amplitude is consistent with the smaller amplitude of the
magnetic fluctuations (Fig. 6).
In this section we investigate the dependence of the
![]() effect
on the angular velocity
effect
on the angular velocity ![]() .
The relevant dimensionless parameters
are the Taylor number and the Coriolis number, as defined by (22) and (23). Averages are calculated over time, and separately over the unstable
region and the stable region, as explained above.
.
The relevant dimensionless parameters
are the Taylor number and the Coriolis number, as defined by (22) and (23). Averages are calculated over time, and separately over the unstable
region and the stable region, as explained above.
Figure 4 shows the rotational dependence of the kinetic
helicity and the current helicity (for the vertical imposed magnetic
field). The kinetic helicity and the current helicity
have been multiplied with
![]() and
and
![]() ,
respectively, in order to allow a comparison with
,
respectively, in order to allow a comparison with
![]() ,
as suggested by Eqs. (29) and (30) if one sets
,
as suggested by Eqs. (29) and (30) if one sets
![]() .
The kinetic helicity in the unstable layer
increases with the rotation rate up to
.
The kinetic helicity in the unstable layer
increases with the rotation rate up to
![]() ;
its value
in the stable layer is much smaller. Hence the general trend and
the correct sign of
;
its value
in the stable layer is much smaller. Hence the general trend and
the correct sign of
![]() (Fig. 5, bottom) are
recovered by (29) in the unstable layer, but not in the stable layer.
The current helicity for the vertical imposed magnetic field increases
with rotation up to
(Fig. 5, bottom) are
recovered by (29) in the unstable layer, but not in the stable layer.
The current helicity for the vertical imposed magnetic field increases
with rotation up to
![]() -300, while it decreases for
stronger rotation, as do the magnetic fluctuations (Fig. 6).
It seems that
-300, while it decreases for
stronger rotation, as do the magnetic fluctuations (Fig. 6).
It seems that
![]() in the unstable layer roughly traces the
current helicity (Figs. 4 and 5).
Note however that both the normalized kinetic helicity,
in the unstable layer roughly traces the
current helicity (Figs. 4 and 5).
Note however that both the normalized kinetic helicity,
![]() ,
and the
normalized current helicity,
,
and the
normalized current helicity,
![]() ,
increase monotonically with
,
increase monotonically with ![]() (not shown).
This reflects an increasing degree of alignment of vorticity with velocity,
and of current with magnetic field, respectively.
(not shown).
This reflects an increasing degree of alignment of vorticity with velocity,
and of current with magnetic field, respectively.
The main conclusion to be drawn with regard to the validity of (29)-(31) is that qualitative agreement exists only
between
![]() , (29), and (31) on the one hand,
and between
, (29), and (31) on the one hand,
and between
![]() and (30) in the unstable layer on
the other hand.
For
and (30) in the unstable layer on
the other hand.
For
![]() ,
such qualitative similarities are no longer evident,
but in the following sub-section we shall compare
the behavior of
,
such qualitative similarities are no longer evident,
but in the following sub-section we shall compare
the behavior of
![]() and
and
![]() with mean-field
results that were derived for the case of arbitrary rates of rotation.
with mean-field
results that were derived for the case of arbitrary rates of rotation.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{fig5a.ps}\\ [2mm]
\includegraphics[width=7cm,clip]{fig5b.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg181.gif) |
Figure 5:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.52cm,clip]{fig6.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg182.gif) |
Figure 6:
Strength of the velocity and magnetic field perturbations as a
function of Ta, in units of |
| Open with DEXTER | |
Figure 5 shows
![]() and
and
![]() ,
normalized
by
,
normalized
by
![]() ,
as a function of Ta (or Co). For zero rotation the
,
as a function of Ta (or Co). For zero rotation the
![]() effect vanishes. For weak rotation
effect vanishes. For weak rotation
![]() increases with increasing rotation rate. It reaches a maximum near
increases with increasing rotation rate. It reaches a maximum near
![]() (
(
![]() ); for stronger rotation
it is quenched. The decrease of
); for stronger rotation
it is quenched. The decrease of
![]() occurs in
spite of the monotonic increase of the kinetic helicity, and in spite of
the decrease of
occurs in
spite of the monotonic increase of the kinetic helicity, and in spite of
the decrease of
![]() with increasing rotation rate (Fig. 6).
The horizontal
with increasing rotation rate (Fig. 6).
The horizontal ![]() effect sets in at a higher rotation rate.
Its magnitude increases monotonically with the rotation rate,
and exceeds that of the vertical
effect sets in at a higher rotation rate.
Its magnitude increases monotonically with the rotation rate,
and exceeds that of the vertical
![]() effect if
effect if
![]() .
For
.
For
![]() ,
Coriolis forces
are so strong that they stifle the convection (see below), and hence also
alpha. Two effects that are not shown in detail appear to be responsible
for the reduction of
,
Coriolis forces
are so strong that they stifle the convection (see below), and hence also
alpha. Two effects that are not shown in detail appear to be responsible
for the reduction of
![]() :
an increasing number of sign changes
of
:
an increasing number of sign changes
of
![]() ,
resulting in cancelations when the volume average
is calculated, and a decreasing amplitude of the magnetic fluctuations
(Fig. 6). Both effects are absent in the case of
,
resulting in cancelations when the volume average
is calculated, and a decreasing amplitude of the magnetic fluctuations
(Fig. 6). Both effects are absent in the case of
![]() .
.
Clearly, the alpha effect is highly anisotropic, and its dependence on
rotation is more complicated than suggested by Eqs. (29) and (31). Rüdiger & Kichatinov (1993)
present analytical expressions for the rotational dependence of
![]() and
and
![]() ,
based on the first-order smoothing
approximation (FOSA), but for arbitrary rotation rates.
They employ a linearized equation of motion for the fluctuating quantities
which includes a random driving force with prescribed spectral properties
to model turbulence, and which takes into account a stratification of the
density and of the turbulent velocity. Due to the stratification as well
as rotation, the electromotive force becomes anisotropic. In the simplest
case of a driving force with zero frequency and containing a single
wavelength (the case designated mixing-length approximation by the authors),
and for a weak magnetic field, a manageable expression can be derived.
For the present geometry, i.e., a local Cartesian grid situated at the
south pole, one obtains
,
based on the first-order smoothing
approximation (FOSA), but for arbitrary rotation rates.
They employ a linearized equation of motion for the fluctuating quantities
which includes a random driving force with prescribed spectral properties
to model turbulence, and which takes into account a stratification of the
density and of the turbulent velocity. Due to the stratification as well
as rotation, the electromotive force becomes anisotropic. In the simplest
case of a driving force with zero frequency and containing a single
wavelength (the case designated mixing-length approximation by the authors),
and for a weak magnetic field, a manageable expression can be derived.
For the present geometry, i.e., a local Cartesian grid situated at the
south pole, one obtains
| = | ![$\displaystyle \frac{1}{x^3}\left[\frac{1}{2}x^2-\frac{23}{2}
-\frac{(x^2-1)^2}{2(x^2+1)}+2\frac{x^2+6}{x}\arctan x \right]$](/articles/aa/full/2001/35/aa10386/img198.gif) |
(34) | |
| = | ![$\displaystyle \frac{1}{x^3}\left[ x^2-17-\frac{(x^2-1)^2}
{x^2+1}+2\frac{x^2+9}{x}\arctan x\right],$](/articles/aa/full/2001/35/aa10386/img200.gif) |
(35) |
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{fig7.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg207.gif) |
Figure 7:
Functions
|
| Open with DEXTER | |
| run | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
|
2 | 10 | 30 | 100 | 300 | 2000 | 104 |
|
|
| eddy size | 2.5 | 2.5 | 2.5 | 2.5 | 2.0 | 1.5 | 1.3 | 1.0 | 0.8 |
|
|
2.8 | 2.8 | 2.7 | 2.4 | 2.1 | 1.5 | 1.1 | 1.0 | 0.82 |
![\begin{figure}
\par\includegraphics[width=6.35cm,clip]{fig8a.ps}\\ [3mm]
\includegraphics[width=6.35cm,clip]{fig8b.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg217.gif) |
Figure 8: Snapshot of the vertical velocity (connected lanes: downward, isolated patches: upward). Top: run 6, moderate rotation. Bottom: run 9, strong rotation. The white curve denotes the zero level of the vertical velocity. The top and bottom surfaces correspond to z=0.09 and z=1.81, respectively. |
| Open with DEXTER | |
In order to shed further light on the influence of rotation, Fig. 8 shows snapshots of
the vertical velocity for two simulations with different rotation rates.
Clearly, stronger rotation causes the eddies to have a smaller diameter in the horizontal plane
(i.e. perpendicular to the rotation axis). Hence the number of eddies within the simulation domain
increases with the rotation rate, and this leads to a more accurate result for ![]() ,
as is obvious
from the length of the error bars in Fig. 5, taking into account the duration of the
runs (Table 1). In the simpler case of Boussinesq convection in a rotating layer,
the scale at which the instability sets in also decreases with increasing Taylor number
(Chandrasekhar 1961). Although the present simulations are done at supercritical Rayleigh
numbers whereas the analysis of Chandrasekhar applies to the marginally stable case, we may
for the moment set aside this difference, as well as possible effects of compressibility and
different boundary conditions. In fact, the smallest value of the local Rayleigh number in the
unstable layer was found to be typically 104, so that the actual supercriticality is less than assumed.
The present runs, which are characterized by
,
as is obvious
from the length of the error bars in Fig. 5, taking into account the duration of the
runs (Table 1). In the simpler case of Boussinesq convection in a rotating layer,
the scale at which the instability sets in also decreases with increasing Taylor number
(Chandrasekhar 1961). Although the present simulations are done at supercritical Rayleigh
numbers whereas the analysis of Chandrasekhar applies to the marginally stable case, we may
for the moment set aside this difference, as well as possible effects of compressibility and
different boundary conditions. In fact, the smallest value of the local Rayleigh number in the
unstable layer was found to be typically 104, so that the actual supercriticality is less than assumed.
The present runs, which are characterized by
![]() and
and
![]() ,
belong to a regime
where the onset of instability occurs in the form of non-oscillatory convection.
Since the value of the critical Rayleigh number depends on the horizontal wavenumber, k, there
is a critical wavenumber,
,
belong to a regime
where the onset of instability occurs in the form of non-oscillatory convection.
Since the value of the critical Rayleigh number depends on the horizontal wavenumber, k, there
is a critical wavenumber, ![]() ,
corresponding to a preferred eddy size
,
corresponding to a preferred eddy size
![]() ,
for which the critical Rayleigh number attains a minimal value,
,
for which the critical Rayleigh number attains a minimal value,
![]() .
The eddy sizes observed in the simulations are in quite good agreement with the analytical
values of
.
The eddy sizes observed in the simulations are in quite good agreement with the analytical
values of
![]() for convection between two free boundary surfaces
(Table 2). The results suggest that the preferred mode of convection
is the same as that pertaining to the onset of convection.
The critical Rayleigh number increases with
for convection between two free boundary surfaces
(Table 2). The results suggest that the preferred mode of convection
is the same as that pertaining to the onset of convection.
The critical Rayleigh number increases with ![]() from 661 for
from 661 for
![]() up to
up to
![]() for
for
![]() .
This explains why for a fixed
value of
.
This explains why for a fixed
value of ![]() the intensity of convection, as measured by
the intensity of convection, as measured by
![]() ,
decreases with
increasing rotation rate. Since the actual Rayleigh number in the unstable layer has a local
minimum of about 104, this also explains why no convection was observed for
,
decreases with
increasing rotation rate. Since the actual Rayleigh number in the unstable layer has a local
minimum of about 104, this also explains why no convection was observed for
![]() .
.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{fig9a.ps}\\ [4mm]
\includegraphics[width=6.6cm,clip]{fig9b.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg223.gif) |
Figure 9:
Energy fluxes. Top: run 6; Bottom: run 9.
Only the three most important contributions are shown, the viscous
and electromagnetic fluxes being negligible. The total flux
|
| Open with DEXTER | |
As the scale of the individual eddies decreases, the corresponding
decrease of the effective Coriolis number,
![]() ,
may
be interpreted as a readjustment of the convection in response to
increased Coriolis forces, which tend to hamper the convective energy
transport. Still the convective flux of the run with the strongest
rotation (run 9) is reduced by a factor of about two compared to runs
with weak rotation. Apart from a possible effect of the increased
Coriolis force, the reduced flux may result from the fact that smaller
eddies lead to larger temperature gradients in horizontal planes, and this
causes increased horizontal radiative transport between adjacent eddies
which reduces the efficiency of convective energy transport in the
vertical direction (Fig. 9).
,
may
be interpreted as a readjustment of the convection in response to
increased Coriolis forces, which tend to hamper the convective energy
transport. Still the convective flux of the run with the strongest
rotation (run 9) is reduced by a factor of about two compared to runs
with weak rotation. Apart from a possible effect of the increased
Coriolis force, the reduced flux may result from the fact that smaller
eddies lead to larger temperature gradients in horizontal planes, and this
causes increased horizontal radiative transport between adjacent eddies
which reduces the efficiency of convective energy transport in the
vertical direction (Fig. 9).
If the strength of the imposed magnetic field is increased, effects of the Lorentz force become more noticeable. Moreover, these effects depend on the orientation of the imposed field, i.e. vertical or horizontal. From the previously discussed runs, a representative case (run 7) was selected as the starting point for runs with increasingly strong imposed magnetic fields of both orientations (Table 3). A comprehensive study of the mode structure of magnetoconvection for different imposed magnetic fields is beyond the scope of the present paper, though. Various cases for a vertical imposed field, without rotation, are treated by Matthews et al. (1995). Wissink et al. (2000) consider the breakup of a horizontal magnetic layer into a number of flux tubes, thereby including the effect of rotation.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{fig10a.ps}\\ [6.8mm]
\includegraphics[width=6.4cm,clip]{fig10b.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg225.gif) |
Figure 10:
Top: rms velocity perturbations as a function of the
strength of the imposed magnetic field (normalized to the value
of
|
| Open with DEXTER | |
| run | 7 | 7a | 7b | 7c | 7d | 7e |
| B0 | 0.001 | 0.01 | 0.02 | 0.04 | 0.06 | 0.08 |
| T (
|
940 | 205 | 203 | 200 | 414 | 96 |
| T (
|
508 | 280 | 278 | 559 | 381 | 268 |
![\begin{figure}
\par\includegraphics[width=6.55cm,clip]{fig11a.ps}\\ [7mm]
\includegraphics[width=6.55cm,clip]{fig11b.ps}\end{figure}](/articles/aa/full/2001/35/aa10386/Timg227.gif) |
Figure 11:
Top:
|
| Open with DEXTER | |
For an imposed magnetic field in the vertical direction, convection is
increasingly hampered
with increasing field strength, as is indicated by a decrease of the rms turbulent velocity
(Fig. 10, top) and of the convective energy flux. Since the magnetic energy is enhanced
by advection of the imposed field, while the kinetic energy decreases as a result of the Lorentz
force, after a while the rms magnetic field can be much larger than the
equipartition field strength (Fig. 10, bottom).
Moreover, if the initial magnetic field is too strong, then convection
dies out completely. This in fact occured during
run 7e (
![]() ). After 100 time units, the
volume-averaged energy density of the velocity and magnetic-field
perturbations had both fallen by about 2 orders of magnitude.
The decrease of
). After 100 time units, the
volume-averaged energy density of the velocity and magnetic-field
perturbations had both fallen by about 2 orders of magnitude.
The decrease of
![]() is more rapid than that of
is more rapid than that of
![]() ,
because advection of the imposed field by convection is stifled; this
explains why alpha decreases also when measured in dynamical units
(i.e., when divided by
,
because advection of the imposed field by convection is stifled; this
explains why alpha decreases also when measured in dynamical units
(i.e., when divided by
![]() ).
).
A debate is ongoing in the literature about how and whether the magnetic
Reynolds number affects the magnetic quenching of the ![]() effect.
The dependence of
effect.
The dependence of ![]() on the magnetic field strength is often
schematically represented in the form
on the magnetic field strength is often
schematically represented in the form
![]() .
While some numerical and analytical results suggest that
.
While some numerical and analytical results suggest that
![]() (Kraichnan 1979a, 1979b;
Brandenburg & Donner 1997),
others suggest
(Kraichnan 1979a, 1979b;
Brandenburg & Donner 1997),
others suggest
![]() (Cattaneo & Vainshtein
1991; Vainshtein & Cattaneo 1992;
Tao et al. 1993; Cattaneo 1994; Cattaneo & Hughes 1996;
Vainshtein 1998; Brandenburg 2001).
Although the present set of simulations is not well-suited to answer this
question because of the relatively small Reynolds numbers
(
(Cattaneo & Vainshtein
1991; Vainshtein & Cattaneo 1992;
Tao et al. 1993; Cattaneo 1994; Cattaneo & Hughes 1996;
Vainshtein 1998; Brandenburg 2001).
Although the present set of simulations is not well-suited to answer this
question because of the relatively small Reynolds numbers
(
![]() ), the results for both
), the results for both
![]() and
and
![]() are consistent with
are consistent with
![]() (Fig. 11).
Blackman & Field (2000) argued that the quenching with
(Fig. 11).
Blackman & Field (2000) argued that the quenching with
![]() observed in simulations with periodic boundaries may in
fact be a consequence of the boundary conditions rather than a dynamic
effect, and that p=0 should be possible if a flux of magnetic helicity
through the
boundaries is allowed. Our conditions (10) do allow for a flux
of magnetic helicity through the top and bottom boundaries. Thus, the fact
that
observed in simulations with periodic boundaries may in
fact be a consequence of the boundary conditions rather than a dynamic
effect, and that p=0 should be possible if a flux of magnetic helicity
through the
boundaries is allowed. Our conditions (10) do allow for a flux
of magnetic helicity through the top and bottom boundaries. Thus, the fact
that ![]() quenching sets in when
quenching sets in when
![]() suggests that an Rm-dependence of the
suggests that an Rm-dependence of the ![]() quenching is possible
in the present case; such quenching could be dynamic according to the
reasoning of Blackman and Field. However, this conclusion may change if one
allows for shear near the surface. This is the case between the solar surface
and the corona, and so a strong helicity flux is possible in that case
(Berger & Ruzmaikin 2000).
quenching is possible
in the present case; such quenching could be dynamic according to the
reasoning of Blackman and Field. However, this conclusion may change if one
allows for shear near the surface. This is the case between the solar surface
and the corona, and so a strong helicity flux is possible in that case
(Berger & Ruzmaikin 2000).
It appears that for boundaries that allow for a flux of helicity
diverse Rm dependencies of the ![]() quenching are possible,
depending, e.g., on the character of the forcing of the flow.
Brandenburg & Dobler (2001) report a case where
quenching are possible,
depending, e.g., on the character of the forcing of the flow.
Brandenburg & Dobler (2001) report a case where
![]() .
We also note that even with the strong
.
We also note that even with the strong
![]() -quenching of
-quenching of
![]() a large-scale field may build up because of an equally strong
quenching of the turbulent magnetic diffusivity (Brandenburg
2001).
a large-scale field may build up because of an equally strong
quenching of the turbulent magnetic diffusivity (Brandenburg
2001).
The magnetic-field dependence of the ![]() coefficients is essentially
the same for the cases of the vertical and horizontal imposed fields,
even though convection is hampered less in the case of a horizontal
imposed field (Fig. 11, top). For field strengths comparable to
the equipartition value, the convective pattern becomes very different. If
coefficients is essentially
the same for the cases of the vertical and horizontal imposed fields,
even though convection is hampered less in the case of a horizontal
imposed field (Fig. 11, top). For field strengths comparable to
the equipartition value, the convective pattern becomes very different. If
![]() ,
convection exhibits a pattern of
irregular oblique elongated cells that make an angle with the direction
of the imposed magnetic field, and a small horizontal
,
convection exhibits a pattern of
irregular oblique elongated cells that make an angle with the direction
of the imposed magnetic field, and a small horizontal ![]() effect
is still measured. For runs with field strengths
effect
is still measured. For runs with field strengths
![]() and
and
![]() respectively, longitudinal rolls are formed that are increasingly aligned
along the x-direction, and the coefficient
respectively, longitudinal rolls are formed that are increasingly aligned
along the x-direction, and the coefficient
![]() is
practically zero. For still stronger fields
(
is
practically zero. For still stronger fields
(
![]() ), convection assumes the form of highly
regular oblique lanes, and a small
), convection assumes the form of highly
regular oblique lanes, and a small ![]() effect is again measured.
effect is again measured.
The following discussion of our results in the solar context may be considered
as complimentary to that of Brandenburg et al. (1990).
First-order smoothing is a justified approximation if either the magnetic
Reynolds number is small, or if the flow is slow in the sense
![]() .
In our dimensionless variables, the latter condition would mean
.
In our dimensionless variables, the latter condition would mean
![]() but, with the rms velocities and coherence times
obtained in our simulations, we rather have
but, with the rms velocities and coherence times
obtained in our simulations, we rather have
![]() .
Our magnetic Reynolds
number (20-35) is quite moderate but not small. Hence the simulations clearly
go beyond first-order smoothing, although we are far from the conditions met
in the solar convection zone. The large fluctuations that occur at large
Reynolds number are evident in our calculations. In particular we see that
the components of the
.
Our magnetic Reynolds
number (20-35) is quite moderate but not small. Hence the simulations clearly
go beyond first-order smoothing, although we are far from the conditions met
in the solar convection zone. The large fluctuations that occur at large
Reynolds number are evident in our calculations. In particular we see that
the components of the ![]() tensor undergo large fluctuations. Only
after averaging over many coherence times and over the horizontal coordinates
of the box a significant depth variation is obtained. With this variation
we confirm some results obtained in the case of weakly anisotropic
turbulence, and extend them beyond the limits of first-order smoothing:
in the southern hemisphere
the horizontal
tensor undergo large fluctuations. Only
after averaging over many coherence times and over the horizontal coordinates
of the box a significant depth variation is obtained. With this variation
we confirm some results obtained in the case of weakly anisotropic
turbulence, and extend them beyond the limits of first-order smoothing:
in the southern hemisphere
the horizontal ![]() coefficient (Fig. 3, row 2) is
negative (positive) in the upper (lower) part of the box, as is plausible
from the rotational effect on convergent and divergent velocities that arise
as the flow is forced into the horizontal direction. On the other hand we
find the opposite sign for the vertical
coefficient (Fig. 3, row 2) is
negative (positive) in the upper (lower) part of the box, as is plausible
from the rotational effect on convergent and divergent velocities that arise
as the flow is forced into the horizontal direction. On the other hand we
find the opposite sign for the vertical ![]() coefficient (Figs. 2
and 3, row 1). Also of opposite sign is the small-scale
current helicity. Indeed, both the sign and the rotational dependence of
coefficient (Figs. 2
and 3, row 1). Also of opposite sign is the small-scale
current helicity. Indeed, both the sign and the rotational dependence of
![]() in the unstable layer roughly agree with that predicted
by the simple FOSA-expression which relates
in the unstable layer roughly agree with that predicted
by the simple FOSA-expression which relates ![]() to the current
helicity (30).
to the current
helicity (30).
For cases with convective overshooting in the lower part of the box the
components of ![]() reverse their sign near the transition to the
stable stratification. For an
reverse their sign near the transition to the
stable stratification. For an
![]() dynamo the horizontal component
dynamo the horizontal component
![]() is the essential ingredient; possibly the sign change of
is the essential ingredient; possibly the sign change of
![]() has interesting implications for a dynamo that operates
as an interface wave at the base of the convection zone. In the layer of
convective overshooting the sign of
has interesting implications for a dynamo that operates
as an interface wave at the base of the convection zone. In the layer of
convective overshooting the sign of
![]() is appropriate for
the equatorward migration of the mean field, if the positive shear
is appropriate for
the equatorward migration of the mean field, if the positive shear
![]() ,
as inferred from helioseismology for the depth
range around
,
as inferred from helioseismology for the depth
range around
![]() and the lower heliographic latitudes (Kosovichev
et al. 1997), is used as the other essential ingredient.
These conclusions are drawn from simulations with an imposed magnetic
field
B0=10-3, and may still be valid for
B0=10-2, as the
results of run 7a, shown in Fig. 11, suggest. The latter field
strength corresponds to
and the lower heliographic latitudes (Kosovichev
et al. 1997), is used as the other essential ingredient.
These conclusions are drawn from simulations with an imposed magnetic
field
B0=10-3, and may still be valid for
B0=10-2, as the
results of run 7a, shown in Fig. 11, suggest. The latter field
strength corresponds to ![]() 10 T, which is the strength of the
field in the stable layer below the convection zone, as deduced from
the properties of rising flux tubes (Caligari et al. 1995).
For stronger fields we obtain a marked quenching of
10 T, which is the strength of the
field in the stable layer below the convection zone, as deduced from
the properties of rising flux tubes (Caligari et al. 1995).
For stronger fields we obtain a marked quenching of ![]() consistent with a factor
consistent with a factor
![]() ,
although
we have checked this only for
,
although
we have checked this only for
![]() .
The simulations have also revealed a striking difference between the
convective patterns for a vertical and a horizontal orientation of the
imposed magnetic field, with rolls being formed for strong horizontal fields.
In view of a strong toroidal field at the base of the convection zone a
magnetic Rayleigh-Taylor instability
(Brandenburg & Schmitt 1998) or an instability
of toroidal flux tubes (Ferriz-Mas et al. 1994)
should be employed to obtain an
.
The simulations have also revealed a striking difference between the
convective patterns for a vertical and a horizontal orientation of the
imposed magnetic field, with rolls being formed for strong horizontal fields.
In view of a strong toroidal field at the base of the convection zone a
magnetic Rayleigh-Taylor instability
(Brandenburg & Schmitt 1998) or an instability
of toroidal flux tubes (Ferriz-Mas et al. 1994)
should be employed to obtain an ![]() effect. Nevertheless, since the sign
of
effect. Nevertheless, since the sign
of
![]() follows plausible arguments, we may hope to obtain the
same sign for such a dynamically determined
follows plausible arguments, we may hope to obtain the
same sign for such a dynamically determined ![]() (Brandenburg & Schmitt 1998).
(Brandenburg & Schmitt 1998).
As far as the dependence of ![]() on rotation is concerned, the simulation
may yield more reliable results than for the other parameters. In the solar
convection zone the Coriolis number is small near the surface, and increases to
values around 1 or somewhat larger near its base. This is the regime shown
in Fig. 5. The rotational quenching of
on rotation is concerned, the simulation
may yield more reliable results than for the other parameters. In the solar
convection zone the Coriolis number is small near the surface, and increases to
values around 1 or somewhat larger near its base. This is the regime shown
in Fig. 5. The rotational quenching of
![]() and the
saturation of
and the
saturation of
![]() (Fig. 5, top) may therefore just
begin in the depth region where the dynamo operates, but in solar-type stars
which are younger and therefore rotating faster, these effects may be
important. We have observed some agreement between the numerical results for
(Fig. 5, top) may therefore just
begin in the depth region where the dynamo operates, but in solar-type stars
which are younger and therefore rotating faster, these effects may be
important. We have observed some agreement between the numerical results for
![]() and the predictions of Rüdiger & Kichatinov (1993),
as far as the dependence on rotation and on depth is concerned.
In both the unstable and the stable layer, the approximate Coriolis number
dependence and the correct sign for
and the predictions of Rüdiger & Kichatinov (1993),
as far as the dependence on rotation and on depth is concerned.
In both the unstable and the stable layer, the approximate Coriolis number
dependence and the correct sign for
![]() are reproduced. The
main discrepancies concern the amplitude of
are reproduced. The
main discrepancies concern the amplitude of ![]() (the scaling factors
of the theoretical curves in Fig. 5) and the sign of
(the scaling factors
of the theoretical curves in Fig. 5) and the sign of
![]() in the unstable layer, as well as the sign of the
small-scale current helicity.
in the unstable layer, as well as the sign of the
small-scale current helicity.
Even within the limited range accessible to numerical simulation, the
parameter space is enormous. We have not yet considered the latitude
dependence of ![]() (although some earlier work of Brandenburg
1994 indicates that
(although some earlier work of Brandenburg
1994 indicates that ![]() is maximum at about
is maximum at about
![]() of latitude), and we have not yet explored the dependencies
on the Reynolds and Rayleigh numbers.
This must be done by further simulations.
of latitude), and we have not yet explored the dependencies
on the Reynolds and Rayleigh numbers.
This must be done by further simulations.