A&A 376, 194-212 (2001)
DOI: 10.1051/0004-6361:20010937
Ch. Helling 1 - M. Oevermann 2 - M. J. H. Lüttke 1 - R. Klein 2,3 - E. Sedlmayr 1
1 - Zentrum für Astronomie und Astrophysik, Technische
Universität Berlin, Hardenbergstraße 36,
10623 Berlin, Germany
2 - Konrad-Zuse-Zenrum für Informationstechnik Berlin,
Takustraße 7, 14195 Berlin, Germany
3 - Fachbereich Mathematik und Informatik, Freie Universität Berlin, Takustraße 7, 14195 Berlin, Germany
Received 3 May 2001 / Accepted 27 June 2001
Abstract
Dust formation in turbulent media is studied adopting the
example of brown dwarf atmospheres. By combining asymptotic techniques
and time-dependent, multi-dimensional numerical simulations, we show
that acoustic waves originating from convective motions provide a
mechanism to initiate dust nucleation in otherwise dust-hostile
environments. The subsequently growing particles cause a radiative
cooling strong enough to re-initiate efficient dust formation resulting
in a strongly inhomogeneous distribution of dust in such
environments. Recent observations bear indications for such cloudy
dust distributions in brown dwarf atmospheres.
Brown dwarfs are star-like objects with masses below the stable hydrogen
burning limit (![]() 7.5%
7.5% ![]() for solar metallicity
for solar metallicity
![]() ;
see Chabrier & Baraffe 2000) and electron
degeneracy balances the gravitational collapse keeping the interior in
hydrostatic equilibrium. The objects are very faint and the radiation
pressure is negligible in their atmospheres. The interior of brown
dwarfs is entirely convective. Chabrier & Baraffe (1997)
found the upper limit of fully convective stars to be
;
see Chabrier & Baraffe 2000) and electron
degeneracy balances the gravitational collapse keeping the interior in
hydrostatic equilibrium. The objects are very faint and the radiation
pressure is negligible in their atmospheres. The interior of brown
dwarfs is entirely convective. Chabrier & Baraffe (1997)
found the upper limit of fully convective stars to be
![]() (
(
![]() )
based on the mixing
length theory. The top of the interior's convective zone lies only a few
pressure scale heights (
)
based on the mixing
length theory. The top of the interior's convective zone lies only a few
pressure scale heights (![]() )
below the photosphere
(Chabrier et al. 2000). The convective transport of
energy, momentum, and material reaches into the brown dwarf atmosphere
(Chabrier & Baraffe 1997; Burrows et al. 1997; Burrows & Sharp 1999;
Allard et al. 1999; Tsuji et al. 1999) and can be
important for the replenishment of the atmosphere by heavy elements
which might have been previously depleted by incorporation into dust
particles and their gravitational settling
(Chabrier et al. 2000;
Helling et al. 2000).
)
below the photosphere
(Chabrier et al. 2000). The convective transport of
energy, momentum, and material reaches into the brown dwarf atmosphere
(Chabrier & Baraffe 1997; Burrows et al. 1997; Burrows & Sharp 1999;
Allard et al. 1999; Tsuji et al. 1999) and can be
important for the replenishment of the atmosphere by heavy elements
which might have been previously depleted by incorporation into dust
particles and their gravitational settling
(Chabrier et al. 2000;
Helling et al. 2000).
Indeed, the CO molecule has been observed in the brown dwarf Gl 229B in atmospheric regions too cool for CO to be present according to chemical equilibrium calculations (Noll et al. 1997; Oppenheimer et al. 1998). The cause may be: i) Hot, CO containing gas reaches into the atmosphere due to convective material transport. The CO molecule is not destroyed during the subsequent cooling since the chemical composition is determined by non-equilibrium effects; ii) convection transports warm, CO containing gas into the cooler atmosphere and a pattern of warm and dense regions results. Therefore the CO molecule sustains inside the warm regions while chemical equilibrium holds; or iii) The interstellar UV field is strong enough to initiate in situ CO formation by photo reactions. However, the chemical non-equilibrium hypothesis (i) is rather unlikely due to the high density of the atmospheric gas (see e.g. Patzer et al. 1999b) and only the last possibility (iii) can omit the presents of convective energy transport. Oppenheimer et al. (1998) suggested also that the observation of the atomic Cs line in Gl 229B (also GD 165B) might indicate the existence of an convective material transport since Cs should be bound in some molecules at these low temperatures according to chemical equilibrium arguments.
Furthermore, according to estimates based on static model atmospheres,
the Reynolds number - a measure of the viscous damping capability of the
gas - exceeds unity by orders of magnitude already on microscopic scales
(
![]() ,
,
![]() density scale height).
Consequently, disturbances e.g. introduced by the interior convective
overshooting into the atmosphere can not be damped efficiently.
Therefore, a brown dwarf atmosphere may be expected to consist of a
turbulent fluid field fed by the interior's convection which also may
influence the distribution of a possible solid component.
density scale height).
Consequently, disturbances e.g. introduced by the interior convective
overshooting into the atmosphere can not be damped efficiently.
Therefore, a brown dwarf atmosphere may be expected to consist of a
turbulent fluid field fed by the interior's convection which also may
influence the distribution of a possible solid component.
Bailer-Jones & Mundt (2001a,b; see also Bailer-Jones &
Mundt 1999) found 11 of a sample of 21 brown dwarfs (see their Table 2)
to be variable on time scales of a few minutes and to a few tens of
hours with a confidence level of 99%. Eight of these show small
amplitude variations between 0.01 and 0.03 mag not correlated with a
rotation period. It was suggested by the authors that these variations
might well result from an inhomogeneous distribution of dust in the
atmosphere. Martín et al. (2001) follow this
interpretation for their observations of the ultracool, very inactive
dwarf BRI 0021-0214. Oppenheimer et al. (1998) found evidence for
variability in the brown dwarf Gl 229B of a maximum of ![]() on
time scales from several minutes over a few days to one year in the
1.6
on
time scales from several minutes over a few days to one year in the
1.6 ![]() m CH4 absorption line. Gelino et al. (2001) argue that
magnetic spots are unlikely to be responsible for such variability since
the magnetic Reynolds number of the atmospheric gas is very small on the
mesoscopic scales (
m CH4 absorption line. Gelino et al. (2001) argue that
magnetic spots are unlikely to be responsible for such variability since
the magnetic Reynolds number of the atmospheric gas is very small on the
mesoscopic scales (
![]() )
considered.
)
considered.
Brown Dwarf atmospheres provide favorable conditions for the gas-solid
phase transition due to their low temperatures and high
densities. Stevenson (1986) and
Lunine et al. (1989) were the first to point out the
importance of dust as opacity source in the brown dwarf's evolution.
Tsuji et al. (1996b) suggested dust containing
photospheres (
![]() K) as the only reasonable fit to the
observed spectral energy distribution (SED) of the brown dwarf GD 165B
observed by Tinney et al. (1993) and to the infrared
H2O bands observed by Jones et al. (1994). Kirkpatrick
et al. (1999a) provide a comparable fit by static
model atmospheres considering the existence of power-law-sized solid
particles in order to account for the unexpectedly weak molecular
absorption bands. But still, too strong VO and TiO bands are predicted
from the models.
K) as the only reasonable fit to the
observed spectral energy distribution (SED) of the brown dwarf GD 165B
observed by Tinney et al. (1993) and to the infrared
H2O bands observed by Jones et al. (1994). Kirkpatrick
et al. (1999a) provide a comparable fit by static
model atmospheres considering the existence of power-law-sized solid
particles in order to account for the unexpectedly weak molecular
absorption bands. But still, too strong VO and TiO bands are predicted
from the models.
Liebert et al. (2000) argue that a correct treatment of the line wings (more advanced than Lorenzian profile) of the alkali absorption lines (Na I and K I doublets) could make the necessity to include dust in brown dwarfs atmospheres obsolete.
The present interpretation of the observed brown dwarf spectra relies exclusively on static model atmospheres with elaborate treatments of frequency dependent radiative transport including a large body of atomic and molecular line data. Encouraged by extensive theoretical investigations of possible compounds in the cool and dense environment of brown dwarfs (and gas planets; Burrows & Sharp 1999; Lodders 1999), dust has been included in the static model atmospheres as an opacity source. The dust caused a strong backwarming and element depletion, resulting in weaker molecular absorption (Tsuji et al. 1996a, 1996b; Jones & Tsuji 1997; Pavlenko et al. 2000; Chabrier et al. 2000; Leinert et al. 2000; Basri et al. 2000; Allard et al. 2001) and a better agreement with observation could be achieved. Depending on the purpose of the models, dust has been taken out or taken into account as opacity source. The easy access of the dust complex in the static model atmospheres must be payed for by various simplifications:
- The compounds are assumed to be in phase equilibrium with the gas (e.g. Burrows & Sharp 1999; Chabrier et al. 2000; Leinert et al. 2000; Allard et al. 2001) as introduced by Grossmann (1972) and Lunine et al. (1989). If, however, the supersaturation ratio S equals 1 (phase equilibrium), and therefore the formation and destruction rates equilibrate, no solid particle can form. A sufficient supersaturation is needed to form non-plane solids, therefore, a much lower temperature than T(S=1) is required (see e.g. Rossow 1978; Gail et al. 1984).
- Adopting phase equilibrium, the description of the formation of the
compounds is omitted. Therefore it appears the inconsistence that the
monomer molecules from which the compounds are meant to form are often
not present in the gas phase or only in very small amounts
(e.g. Al2O3, CaTiO3, MgAl2O4, CaMgSi2O7 ![]() ).
).
- The grain size distribution had to be prescribed. The interstellar
power law has been adopted for grain sizes of
![]() m in
order to derive the spectral characteristics of the dust for the opacity
calculation.
m in
order to derive the spectral characteristics of the dust for the opacity
calculation.
Lunine et al. (1989) were the first to point out the influence of the grain size on the resulting grey atmosphere structure in brown dwarfs following time-scale arguments of Rossow (1978).
The gas-solid phase transition is in fact a non-equilibrium process and the grain size distribution is not known a priori. Furthermore, the formation of dust particles is a time dependent process and a consistent treatment with hydro- and thermodynamics is therefore required. One example, where the implications of such a consistent treatment due to non-linear interactions have been shown by numerical simulations, are circumstellar dust shells of long periodic variables (Gail & Sedlmayr 1987; Dominik et al. 1990; Fleischer et al. 1992; Höfner et al. 1994; Helling et al. 2000; Winters et al. 2000). Here, the non-linear coupling between dust and hydro-/thermodynamics causes the creation of dust induced shock waves due to the high luminosity of the star and the large opacity of the dust, the occurrence of an onion-like distribution of dust around the star due to backwarming, and in a time dependent size distribution of the dust grains due to time-dependent thermodynamic conditions.
In brown dwarfs, dust-free convective cells originating from the
interior convective zone travel upward and decay into smaller and
smaller eddies at some point in the atmosphere. Following Kolmogoroff's
assumption (e.g. Frisch 1995), energy is transfered
from the largest scales, comparable to the system's size, by non-linear
processes into smaller and smaller scales until the energy is finally
dissipated on the Kolmogoroff scale![]() by the
viscosity of the gas. The smaller the scale, the smaller the influence
of large scale flow structures. Then, the resulting turbulent
fluctuations can be considered homogeneous and isotropic on microscopic
scales. Considering that the large scale turbulent motions have a
characteristic Mach number of the order of unity, resulting acoustic
waves (Fig. 1, l.h.s.) create a turbulent
temperature and density field in the atmosphere which influences the
dust complex due to its high temperature and density sensitivity.
Indications for such a turbulent atmosphere may be the observations of
CO (and possibly Cs) in Gl 229B (Oppenheimer et al. 1998) but also the
non-periodic variability observed by Bailer-Jones & Mundt
(2001a,b) and Martín et al. (2001). The aim of this
paper is therefore to study the complex, non-linear interactions between
dust formation, chemistry and turbulence at first on microscopic scales.
by the
viscosity of the gas. The smaller the scale, the smaller the influence
of large scale flow structures. Then, the resulting turbulent
fluctuations can be considered homogeneous and isotropic on microscopic
scales. Considering that the large scale turbulent motions have a
characteristic Mach number of the order of unity, resulting acoustic
waves (Fig. 1, l.h.s.) create a turbulent
temperature and density field in the atmosphere which influences the
dust complex due to its high temperature and density sensitivity.
Indications for such a turbulent atmosphere may be the observations of
CO (and possibly Cs) in Gl 229B (Oppenheimer et al. 1998) but also the
non-periodic variability observed by Bailer-Jones & Mundt
(2001a,b) and Martín et al. (2001). The aim of this
paper is therefore to study the complex, non-linear interactions between
dust formation, chemistry and turbulence at first on microscopic scales.
Our approach is to combine asymptotic techniques and numerical simulations. The asymptotic techniques will allow us to consider the long term behavior of the dust forming system by the use of a reduced model. It also serves as an independent method to test our numerical results. The numerical simulations of the full model problem are performed in order to consistently study dust formation in a strongly fluctuating environment.
In Sect. 2, the full model problem containing hydro-, thermodynamics and the dust complex is outlined. Typical time scales and the characteristic numbers of the system - the brown dwarf atmosphere - are discussed in order to justify our model approach.
Section 3 contains the asymptotic analysis of a reduced model problem and the study of the long term behavior of the dust complex for a typical brown dwarf atmosphere situation.
Section 4 starts with the validation of the multi-dimensional code on the basis of a zero dimensional test problem. In two scenarios, 1D and 2D, the appearance of an intermittent dust distribution caused by acoustics-induced thermodynamic fluctuations in the microscopic regime of the turbulent brown dwarf atmosphere is shown.
In Sect. 5 we discuss the problem of the grain size distribution, the gap between T(S=1) and the threshold temperature for efficient nucleation, the possible rain out, the problem of cloud formation in the framework of our studies and the site of the dust in the atmosphere.
Section 6 contains our conclusions.
The model problem is twofold:
Complex A: The hydro- and thermodynamics which are described following the classical approach for an inviscid, compressible fluid.
Complex B: The chemistry and dust formation. The dust formation is a two step process - nucleation and growth (Rossow 1978; Gail et al. 1984; Gail & Sedlmayr 1988) - and depends by the amount of condensible species on the local temperature and density of the gas which are determined by Complex A. Dust formation is initiated by the clustering of molecular species from the gas phase into clusters consisting of roughly 100 molecules on which irreversible growth of gas phase species becomes possible. Since aggregates of this size are usually less tightly bound than the bulk condensate, considerable supercooling below the stability limit of the corresponding solid material is required before the seed nuclei can form. These nuclei serve as centers for subsequent growth to macroscopic sizes. The material initiating dust formation does not need to be identical to the main dust material formed during subsequent growth on the initial seed nuclei, since even a rare component of the gas mixture can provide the required seed nuclei if these are formed at higher temperatures than all other material from which seed nuclei might be formed.
The description of the dust nucleation is based on the modified classical nucleation theory. The dust growth is described by the momentum method (Gail & Sedlmayr 1986, 1988; Dominik et al. 1993) in combination with the differential equations describing the element conservation.
The model equations have been transformed into their dimensionless form
by substituting
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (
(
![]() ),
),
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and dimensionless
numbers have been identified. (All symbols will be explained shortly.)
and dimensionless
numbers have been identified. (All symbols will be explained shortly.)
Complex A:
The following relations hold (Gail & Sedlmayr 1988;
![]() cmj cm-3):
cmj cm-3):
The system of partial differential equations is closed by various material quantities and equations of state which are partly expressed by non-linear algebraic equations:
| Name | Characteristic | Value | ||||
| Number | inside | outside | ||||
| Reynolds number |
|
|||||
|
|
108 | 106 | ||||
Mach number |
|
|||||
Froude number |
|
140 | 80 | (**) | ||
| Radiation number |
|
|
|
|
||
| 1.0 | 10-2 |
|
||||
| Damköhler number of nucleation |
|
0 | 107 | |||
Damköhler number of growth |
|
0 | 103 | |||
| j=0: 1 | ||||||
| Sedlmaÿr number
|
|
j=1: 0.21 | ||||
| j=2: 0.046 | ||||||
| j=3: 10-2 | ||||||
| Element Consumption number |
|
10-3 | ||||
| Name | Reference Value | Value | ||||
| inside | outside | |||||
| temperature |
|
[K] | 2000 | 1000 | ||
| density |
|
[g/cm3] | 10-4 | 10-6 | ||
| thermal pressure |
|
[dyn/cm2] | 107 |
|
||
| velocity of sound |
|
[cm/s] |
|
|
||
| velocity |
|
[cm/s] | ||||
| length |
|
[cm] | 104 | |||
| hydrodyn. time |
|
[s] | 0.0267 | 0.0357 | ||
| gravitational acceleration |
|
[cm/s2] | 105 | |||
| total absorption coefficient |
|
[1/cm] |
|
|
|
|
|
|
|
|
||||
| nucleation rate |
|
[1/s] | 0 |
|
||
| 0 |
|
[1/g] |
|
|||
| heterog. growth velocity |
|
[cm/s] |
|
10-2 | ||
| mean particle radius |
|
[cm] | 10-6 | |||
| element abundance |
|
[-] | 10-6 | |||
| total hydrogen density |
|
[1/cm3] |
|
|
||
(*) For a hydrogen rich gas.
(**) Fr = 1 if
![]() ,
, ![]() = density scale hight
(
= density scale hight
(![]() 106cm).
106cm).
![]() gas only,
gas only,
![]() dust and gas,
dust and gas,
![]() Gail & Sedlmayr (1999).
Gail & Sedlmayr (1999).
The related estimations of typical time and length scales are summarized
in Table 1 and have been performed in order to
characterize the physical and chemical situation in the atmospheres of
brown dwarfs. The choice of the thermodynamical values has been guided
by a hydrostatic brown dwarf model atmosphere developed by
Tsuji et al. (1999) which is considered as a representative
state of the art model of brown dwarf atmospheres![]() .
.
The dimensionless numbers characterizing our problem are the Mach number
M, the Froude number Fr, and the Reynolds number Re. Assuming the turbulence velocity to be of the order of the
velocity of sound leads to
![]() ,
indicating the strong
influence of the fluid's compressibility. In fact, in classical
1D stellar atmosphere simulations an additional line broadening
component is needed in order to fit observed spectra. This component in
generally chosen to be of the order of the velocity of sound (see
e.g. Allard et al. 1995; Tsuji et al. 1999)
and might be understood as the mean value of a turbulent background
velocity field
,
indicating the strong
influence of the fluid's compressibility. In fact, in classical
1D stellar atmosphere simulations an additional line broadening
component is needed in order to fit observed spectra. This component in
generally chosen to be of the order of the velocity of sound (see
e.g. Allard et al. 1995; Tsuji et al. 1999)
and might be understood as the mean value of a turbulent background
velocity field![]() .
.
The Froude number, which relates the hydrodynamic and the gravitational
acceleration, equals one if the density scale height is considered as
reference length. If smaller reference lengths (
![]() )
are considered, gravitation becomes negligible for the hydrodynamic
behavior since
)
are considered, gravitation becomes negligible for the hydrodynamic
behavior since ![]() .
Therefore, turbulent mixing and
relative velocities between dust and gas (drift) are negligible which is
characteristic for microscopic scales. The reference length
.
Therefore, turbulent mixing and
relative velocities between dust and gas (drift) are negligible which is
characteristic for microscopic scales. The reference length
![]() is chosen much smaller than a typical atmosphere's
extension of a few
is chosen much smaller than a typical atmosphere's
extension of a few ![]() (
(
![]() cm). The estimate
of the Reynolds number,
cm). The estimate
of the Reynolds number,
![]() ,
for a typical brown
dwarf atmosphere situation indicates that the viscosity of the gas is
too small to damp hydrodynamical perturbations and a turbulent
hydrodynamic field can be expected.
,
for a typical brown
dwarf atmosphere situation indicates that the viscosity of the gas is
too small to damp hydrodynamical perturbations and a turbulent
hydrodynamic field can be expected.
In radiatively influenced environments like stellar atmospheres, a
characteristic number for the radiative heating / cooling,
![]() ,
can be identified which relates the radiative energy contents
and the thermal energy contents of the gas. Depending on typical
absorption coefficients, it changes by orders of magnitude, if the
absorption coefficient
,
can be identified which relates the radiative energy contents
and the thermal energy contents of the gas. Depending on typical
absorption coefficients, it changes by orders of magnitude, if the
absorption coefficient ![]() changes, e.g. due to dust formation (see
Table 1). Even without dust, Rd varies between the
inner and the outer layers of the atmosphere because of varying gas
absorption coefficients.
changes, e.g. due to dust formation (see
Table 1). Even without dust, Rd varies between the
inner and the outer layers of the atmosphere because of varying gas
absorption coefficients.
The scaling of the dust moment equations provides two dust Damköhler
numbers![]() and a characteristic number for the grain size distribution:
and a characteristic number for the grain size distribution:
The Damköhler numbers of dust nucleation,
![]() ,
and dust
growth,
,
and dust
growth,
![]() ,
are both large in contrast to the Damköhler
number of element consumption, El, inside the dust
formation window (
,
are both large in contrast to the Damköhler
number of element consumption, El, inside the dust
formation window (
![]() K). The reason is that usually the
nucleation process is much faster than the growth process (
K). The reason is that usually the
nucleation process is much faster than the growth process (
![]() large
large
![]() ), and the growth velocity is usually large enough
that macroscopic particles (
), and the growth velocity is usually large enough
that macroscopic particles (
![]() )
are formed (
)
are formed (
![]() large
large
![]() ). The small El indicates that only a relatively
large amount of dust can significantly affect the elemental abundances
which determines the amount of the gaseous species not trapped in dust
grains (compare Figs. 3 and 5).
). The small El indicates that only a relatively
large amount of dust can significantly affect the elemental abundances
which determines the amount of the gaseous species not trapped in dust
grains (compare Figs. 3 and 5).
The time scales,
The large difference between
![]() and
and
![]() justifies the separate treatment of seed formation (nucleation) and
growth. We thereby confirm the corresponding time scale estimate in
Rossow (1978).
justifies the separate treatment of seed formation (nucleation) and
growth. We thereby confirm the corresponding time scale estimate in
Rossow (1978).
The cooling time scale
The analysis of the characteristic numbers shows that the governing equations of our model problem are those of an inviscid, compressible fluid which are coupled to stiff dust moment equations and a singular radiative energy relaxation if dust is present. The dominant interactions in the model Eqs. (1)-(3) occur in the energy equation (Eq. (3)) and in the dust moment equations (Eq. (7)).
Our investigations are led by the following model:
In the atmosphere of a brown dwarf, acoustic expansion
waves are continuously generated by turbulence. The local temperature
might fall below the temperature threshold ![]() for effective dust
nucleation by the superposition of acoustic expansion waves carrying
negative temperature disturbances. During the time of the interaction
seed nuclei will form. The temperature increases again after the
superposition, and nucleation stops, but the seeds are not destroyed. As
the seeds subsequently grow to macroscopic sizes, radiative cooling
intensifies, the temperature decreases, and nucleation proceeds
further. Thus, dust formation can be initiated by the interaction
of acoustic waves in the microscopic scale regime.
for effective dust
nucleation by the superposition of acoustic expansion waves carrying
negative temperature disturbances. During the time of the interaction
seed nuclei will form. The temperature increases again after the
superposition, and nucleation stops, but the seeds are not destroyed. As
the seeds subsequently grow to macroscopic sizes, radiative cooling
intensifies, the temperature decreases, and nucleation proceeds
further. Thus, dust formation can be initiated by the interaction
of acoustic waves in the microscopic scale regime.
This model is used to investigate possible mechanisms to initiate dust formation. It further serves to define a test problem for numerical simulation since analytical, approximate solutions can be obtained by asymptotic techniques.
In the following, we consider an observer co-moving with the local fluid
velocity. Such an observer recognizes the interaction of acoustic waves
as a fast process leaving local spots of dust nuclei with an initial
value for L0. The different time scales of the fast acoustic wave
interactions and the comparably slow dust growth justifies the following
separate treatment of dust nucleation and growth.
We consider a temperature and pressure regime close to effective dust
forming conditions. The supersaturation ratio
![]() can be approximated by introducing material constants A and
B for
can be approximated by introducing material constants A and
B for
![]() (
(![]() ):
):
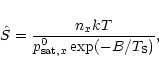 |
(28) |
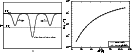 |
Figure 1:
Left: two interacting waves with identical wavelength and amplitudes. Right: evaluation of the seed formation integral
|
| Open with DEXTER | |
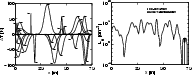 |
Figure 2: Left: stochastic interaction of 86 Gaussian acoustic waves. Right: resulting spatial distribution of dust nuclei of 86 Gaussian acoustic waves. |
| Open with DEXTER | |
A key observation for the analysis is that the nucleation rate J*strongly depends on temperature with a reverse activation energy type
characteristic. The number of dust nuclei formed in a time interval
![]() is given by the time integral
is given by the time integral
![]() ,
where
,
where ![]() is the time of
interaction between two waves (Fig. 1,
l.h.s.). Under typical dust forming conditions the parameter
is the time of
interaction between two waves (Fig. 1,
l.h.s.). Under typical dust forming conditions the parameter ![]() in
Eq. (29) is very large, here
in
Eq. (29) is very large, here
![]() .
This allows
an asymptotic approximation of the integral in the form
.
This allows
an asymptotic approximation of the integral in the form
To study the effects of multiple stochastic interactions of this type,
we consider 86 Gaussian-shaped acoustic waves with random amplitudes
![]() [K]
[K]
![]() ,
wavelengths
,
wavelengths ![]() [cm]
[cm]
![]() ,
and propagation directions (Fig. 2,
l.h.s.). Since every wave travels with the same speed of sound here,
only waves moving in opposite directions interact. If two waves with a
negative temperature fluctuation collide, seed formation occurs during
the time of interaction. Figure 2 (r.h.s.) displays the
spatial distribution of dust nuclei, represented by the zeroeth dust
moment L0 (Eq. (10)), after the interaction of all the
acoustic waves. For the computation of the spatial nuclei distribution
we used the asymptotic Eq. (30) assuming linear
superposition of the waves.
,
and propagation directions (Fig. 2,
l.h.s.). Since every wave travels with the same speed of sound here,
only waves moving in opposite directions interact. If two waves with a
negative temperature fluctuation collide, seed formation occurs during
the time of interaction. Figure 2 (r.h.s.) displays the
spatial distribution of dust nuclei, represented by the zeroeth dust
moment L0 (Eq. (10)), after the interaction of all the
acoustic waves. For the computation of the spatial nuclei distribution
we used the asymptotic Eq. (30) assuming linear
superposition of the waves.
Even with short interaction times of the order
![]() s), we see locally
s), we see locally
![]() dust nuclei per unit
volume in Fig. 2. Comparing the time scales of seed
nucleation by interaction of turbulence generated acoustic waves and the
time scales for a complete dust growth process in Fig. 3,
the separate investigation of the nucleation process alone here is fully
justified.
For the long term evolution of a complete grain growth process we
investigate the time evolution of a single gas cell in Lagrangian space
after the initiation of the dust growth cycle by stochastic acoustic
waves. This corresponds to following a gas cell along particle
trajectories with initial conditions on L0 given by one point in
Fig. 2. For an observer moving with the gas cell, the
flow is governed to leading order by the equations for low Mach numbers.
Assuming a constant background pressure, the energy equation in
Lagrangian space can be reduced to the the following equation:
dust nuclei per unit
volume in Fig. 2. Comparing the time scales of seed
nucleation by interaction of turbulence generated acoustic waves and the
time scales for a complete dust growth process in Fig. 3,
the separate investigation of the nucleation process alone here is fully
justified.
For the long term evolution of a complete grain growth process we
investigate the time evolution of a single gas cell in Lagrangian space
after the initiation of the dust growth cycle by stochastic acoustic
waves. This corresponds to following a gas cell along particle
trajectories with initial conditions on L0 given by one point in
Fig. 2. For an observer moving with the gas cell, the
flow is governed to leading order by the equations for low Mach numbers.
Assuming a constant background pressure, the energy equation in
Lagrangian space can be reduced to the the following equation:
The long term evolution of dust formation has been set up as a test problem in order to validate the code solving the full Eulerian model problem (Eqs. (1)-(8)) against the presented simplified model. The results will be discussed in comparison to the solution of the full model problem in Sect. 4.2.
The fully time-dependent solution of the model equations has been obtained by applying a multi-dimensional Euler solver for compressible fluids which has been extended in order to treat the complex of dust formation (Eqs. (6)-(7)) and elemental conservation (Eq. (8)) consistently coupled to the hydro- and thermodynamics (Eqs. (1)-(4)). The hydro-/thermodynamics code has already been the subject of several studies in computational science (Klein 1995; Smiljanovski et al. 1997; Schneider et al. 1999).
In the following example calculation we assume that TiO2 and SiO are
the most abundant molecules which contain Ti and Si, respectively.
According to the equilibrium chemistry used (based on the electronic
version of JANAF tables 1985), this assumption is well justified for SiO
in the ![]() range considered here. The situation is not as clear
for TiO2 but it is the most abundant Ti-bearing molecule for the
following situations considered. Taking advantage of this, we adopted a
simple algebraic equation,
range considered here. The situation is not as clear
for TiO2 but it is the most abundant Ti-bearing molecule for the
following situations considered. Taking advantage of this, we adopted a
simple algebraic equation,
![]() ,
for
calculating the number density of TiO2 and SiO in order to be able to
obtain some long-term behavior of the dust complex. Thereby, we can
abandon the chemical equilibrium calculation and save half of the
computing time.
,
for
calculating the number density of TiO2 and SiO in order to be able to
obtain some long-term behavior of the dust complex. Thereby, we can
abandon the chemical equilibrium calculation and save half of the
computing time.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{Vergleich.eps}\end{figure}](/articles/aa/full/2001/34/aah2848/Timg238.gif) |
Figure 3:
Long term behavior of the dust formation process according to a result of asymptotic techniques (asterisks; a)) and numerical simulation of the full model problem (solid line; b)). The
calculations considere the nucleation of (TiO2)N clusters and
their growth by TiO2 and SiO addition. Initial conditions:
T(x,0) =
1900K (
|
| Open with DEXTER | |
Figure 3 compares the long term evolution of the grain
growth process computed with
a) a simplified zero dimensional
incompressible flow model where a single Lagrangian gas cell after the
initiation of nucleation by stochastic wave interaction is considered in
the incompressible limit (asterisks, Fig. 3; see
also Sect. 3), and
b) the numerical simulation
of the full set of equations (Eqs. (1)-(8);
solid line, Fig. 3).
The density is kept constant in this test calculation. Both
calculations consider (TiO2)N nuclei and SiO/TiO2 growth. As
radiative equilibrium temperature,
![]() K is considered
which is well below the critical temperature for dust nucleation. A
corresponding radiation field is thereby assumed to be present.
K is considered
which is well below the critical temperature for dust nucleation. A
corresponding radiation field is thereby assumed to be present.
At the same time when new dust particles have been formed, the radiative
cooling has again intensified (steeper temperature slope) and the
radiative equilibrium temperature has been reached. It should, however,
be noticed that the time scales considered are very long in the
framework of microscopic scales. A typical reference time is the time
for an acoustic waves to cross a path of 1/10 of the density scale
hight, which is ![]() 0.03s (compare Table 1).
0.03s (compare Table 1).
The results can be summarized as follows:
![]() s: initially present grains (seed particles) grow;
s: initially present grains (seed particles) grow;
![]() s: temperature low enough to initiate further nucleation;
s: temperature low enough to initiate further nucleation;
2s
![]() 2.8s: radiative cooling intensifies due to dust formation;
2.8s: radiative cooling intensifies due to dust formation;
![]() 2.8s: gaseous Ti and Si are consumed and nucleation and growth stops radiative equilibrium is reached.
2.8s: gaseous Ti and Si are consumed and nucleation and growth stops radiative equilibrium is reached.
The long-term behavior of the dust component has been simultaneously
described by the full Eulerian description of the multi-dimensional code
and the Lagrangian description of a simplified model. The agreement of
the results gives us confidence in the successful coupling between the full
fluid dynamics (Eqs. (1)-(4)) and the dust
complex (Eqs. (6)-(8)) carried out in the
dimensionless formulation. We proceed therefore to study the interaction
between turbulent motion and dust formation in the framework of more
complex scenarios in 1D and in 2D on microscopic scales.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1D_T1900_TRE1800_accustics_initial.ps}\end{figure}](/articles/aa/full/2001/34/aah2848/Timg248.gif) |
Figure 4:
Initial condition for one-dimensional acoustic waves creating temperature disturbances of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1D_T1900_TRE1800_accustics...
...8cm,clip]{1D_T1900_TRE1800_accustics_offen_1700_5500_8800_10600.eps}\end{figure}](/articles/aa/full/2001/34/aah2848/Timg253.gif) |
Figure 5:
Left: four snapshots of two interacting acoustic expansion waves and their influence on the dust complex (solid =
|
| Open with DEXTER | |
The initiation of dust formation in hot atmospheric regions needs a cooling scenario in order to provide appropriately low temperatures to enter the dust formation window. Intense convective motion creates interacting acoustic waves which may cause local temperature decreases low enough to initiate dust nucleation. A first study of this scenario in a zero-dimensional approach has been used as test problem for the full model code in the previous section.
In the following, the influence of interacting acoustic waves on the dust formation shall be studied in 1D and in 2D. The understanding of the one-dimensional simulations (Sect. 4.3.1) is seen as necessary for the understanding of the more complex multi-dimensional simulations (Sect. 4.3.2). The 2D simulation will provide insight into the spatial distribution of the dust component as a result of multiple interacting acoustic waves.
The following two scenarios have been set up:
The first scenario, where we study an one-dimensional setup, investigates the interaction of acoustic expansion waves which cause a disturbance of the initially homogeneous temperature and density field.
Figure 5 (l.h.s.) depicts the time evolution of two
interacting acoustic waves and their influence on dust formation until a
stationary situation is reached. Stationarity is reached after ![]() 0.01s (dotted line) when the sound waves have propagated through the
1D test volume, characterized by a homogeneous temperature, density, gas
pressure distribution and a zero hydrodynamic velocity. During the time
interval depicted on the l.h.s. of Fig. 5, the
interacting sound waves cause the appearance of an inhomogeneous
distribution of dust observable from the dust particle number density
0.01s (dotted line) when the sound waves have propagated through the
1D test volume, characterized by a homogeneous temperature, density, gas
pressure distribution and a zero hydrodynamic velocity. During the time
interval depicted on the l.h.s. of Fig. 5, the
interacting sound waves cause the appearance of an inhomogeneous
distribution of dust observable from the dust particle number density
![]() which is preserved as long as the stationary state of T,
which is preserved as long as the stationary state of T,
![]() ,
,
![]() ,
and u is conceived.
,
and u is conceived.
The initial pressure pulses are already large enough to reach a
temperature where dust nucleation is possible but on a very low rate
(solid line, l.h.s.), i.e. still outside the window of efficient dust
formation. At the time when (
![]() s) and the site where
(x=0.25) the acoustic expansion waves constructively interfere, the
temperature decreases considerably (solid line). This causes the
nucleation rate per hydrogen atom
s) and the site where
(x=0.25) the acoustic expansion waves constructively interfere, the
temperature decreases considerably (solid line). This causes the
nucleation rate per hydrogen atom
![]() to increase by 7
orders of magnitude due to its high temperature sensitivity. The dust
particle number
to increase by 7
orders of magnitude due to its high temperature sensitivity. The dust
particle number ![]() increases accordingly. Meanwhile, the mean
grain size
increases accordingly. Meanwhile, the mean
grain size
![]() has slightly increased but is smaller
where the dust nucleation has efficiently taken place during the wave
interaction.
has slightly increased but is smaller
where the dust nucleation has efficiently taken place during the wave
interaction.
As the propagating sound wave solution suggests, the waves penetrate
each other and continue to travel in their initial direction. Ideally,
they should maintain their original amplitudes. Since the temperature
disturbances are still large enough for some dust nucleation (compare
![]() in Fig. 5, l.h.s.), the dust
particle number distribution broadens its shoulders which do, however,
not reach the high value of the constructive interference event at
in Fig. 5, l.h.s.), the dust
particle number distribution broadens its shoulders which do, however,
not reach the high value of the constructive interference event at
![]() s and x=0.25 (solid line). While the waves
continue to pass the 1D test volume, the growth process continues,
too. Again, at sites and times of highest J*, the mean particle
radius is smallest because the growth material is distributed over more
and more particles.
s and x=0.25 (solid line). While the waves
continue to pass the 1D test volume, the growth process continues,
too. Again, at sites and times of highest J*, the mean particle
radius is smallest because the growth material is distributed over more
and more particles.
As soon as the disturbances have left the domain, temperature, density,
and gas pressure become homogeneous and u=0. Consequently, the
temperature is again too high to allow dust nucleation, therefore
![]() and no further increase of the dust particle number
density occurs. But the growth velocity is non-zero, therefore, the dust
complex is now governed by a steady increase of the dust particle sizes
by the grow of the dust mantel until radiative cooling becomes efficient
enough.
and no further increase of the dust particle number
density occurs. But the growth velocity is non-zero, therefore, the dust
complex is now governed by a steady increase of the dust particle sizes
by the grow of the dust mantel until radiative cooling becomes efficient
enough.
Radiative cooling by dust sets in after the grains have grown to a mean
size of about 10-4cm (=![]() m) in the calculation
(Fig. 5). While the gas pressure stays constant, the
temperature decrease causes a corresponding increase of the density
which will support the dust formation process, too. Now, the same
run-away effect sets in as outlined in our model in
Sect. 4.2: the more dust particles are formed the faster
the temperature decreases by radiative cooling. This in turn causes more
dust to form. The gas temperature has reached the radiative equilibrium
temperature and the run-away is stopped (Fig. 5,
r.h.s., dashed line).
m) in the calculation
(Fig. 5). While the gas pressure stays constant, the
temperature decrease causes a corresponding increase of the density
which will support the dust formation process, too. Now, the same
run-away effect sets in as outlined in our model in
Sect. 4.2: the more dust particles are formed the faster
the temperature decreases by radiative cooling. This in turn causes more
dust to form. The gas temperature has reached the radiative equilibrium
temperature and the run-away is stopped (Fig. 5,
r.h.s., dashed line).
As time proceeds, the available material is consumed by dust nucleation
and growth and the degrees of condensation of Ti and Si,
![]() and
and
![]() ,
approach unity. As
,
approach unity. As
![]() increases, the
nucleation rate decreases (compare dashed and dash-doted line, r.h.s,
Fig. 5) due to less and less material being available
to form seed nuclei. Consequently, the growth by SiO is more efficient
after
increases, the
nucleation rate decreases (compare dashed and dash-doted line, r.h.s,
Fig. 5) due to less and less material being available
to form seed nuclei. Consequently, the growth by SiO is more efficient
after ![]()
![]() s inside the wave interaction zone and the mean
particle size increases. The abundance of Si decreases faster,
i.e.
s inside the wave interaction zone and the mean
particle size increases. The abundance of Si decreases faster,
i.e.
![]() approaches 1 faster than
approaches 1 faster than
![]() (dash-dot,
r.h.s, Fig. 5). After the dust formation is
completed in the wave interaction zone (
(dash-dot,
r.h.s, Fig. 5). After the dust formation is
completed in the wave interaction zone (
![]() ),
),
![]() .
Nevertheless, TiO2 and SiO are still present
in the gas phase but only with a partial pressure equal to the
saturation vapor pressure.
.
Nevertheless, TiO2 and SiO are still present
in the gas phase but only with a partial pressure equal to the
saturation vapor pressure.
Meanwhile, also the temperature of the shoulders has decreased and
nucleation has been re-initiated. Again, a run-away effect drives the
temperature towards
![]() and the dust formation stops if
and the dust formation stops if
![]() is reached.
is reached.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{pap_initial2D_pv_400x400.ps}\par\end{figure}](/articles/aa/full/2001/34/aah2848/Timg266.gif) |
Figure 6:
Initial pressure and velocity field (
|
| Open with DEXTER | |
It has been shown in the last section that acoustic expansion waves may allow the initiation of efficient dust nucleation for a short time. This model scenario shall now be studied in the framework of two-dimensional simulations of the full model problem. The initial values are set up such that a time-evolution of 2D isentropic, acoustic waves and their influence on the dust formation in the microscopic scale regime are considered.
Figures 7-9 depict the time evolution of the temperature, density, and velocity distributions (Fig. 7), the nucleation rate (Fig. 8), the dust particle number density and mean particle radius (Fig. 9) as results of interaction of various acoustic waves moving randomly in a 2D test volume. The instants of time illustrate the system's evolution until a quasi-stationary state is reached (compare Sect. 4.3.1).
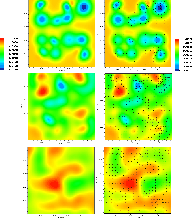 |
Figure 7:
Time evolution (top to bottom) of the temperature ( left) and the density ( right). The scaler density field superimposed is the velocity vector field. The interval of temperature and density plotted is given beside the plots left and right, respectively. The values are plotted dimensionless.
( Top:
|
| Open with DEXTER | |
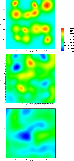 |
Figure 8:
Time evolution (top to bottom) of the nucleation rate
|
| Open with DEXTER | |
The temperature and density distributions in the 2D test volume seem
very similar during the whole time interval depicted. Note, that both
values and the velocity are plotted dimensionless and the different
scales are plotted next to the graphs and are given in the caption,
respectively. As it is characteristic for acoustic waves, an increase of
density corresponds to an increase in temperature which can be observed
in the colliding (red) zones at
![]() or
or
![]() in Fig. 7, middle panels. The
net direction of the velocity vector indicates the colliding course of
the gas at these sites (Fig. 7, the velocity vector
field is superimposed to the scalar density field) and it directly
results in an inhibition of dust nucleation (Fig. 8,
middle panel, blue regions). The particle number density and the mean
grain radius are not much affected since the temperature increases to
such moderate values that evaporation does not set in
(Fig. 9, top and middle panels). However, such
interruptions of dust nucleation due to local temperature increases will
support the formation of an inhomogeneously distributed dust component
on a longer time scale.
in Fig. 7, middle panels. The
net direction of the velocity vector indicates the colliding course of
the gas at these sites (Fig. 7, the velocity vector
field is superimposed to the scalar density field) and it directly
results in an inhibition of dust nucleation (Fig. 8,
middle panel, blue regions). The particle number density and the mean
grain radius are not much affected since the temperature increases to
such moderate values that evaporation does not set in
(Fig. 9, top and middle panels). However, such
interruptions of dust nucleation due to local temperature increases will
support the formation of an inhomogeneously distributed dust component
on a longer time scale.
In the middle panel (l.h.s.) of Fig. 7 deep
blue/black (
![]() )
regions can be
identified which at that time of the simulation have low temperatures
due to the constructively interfering expansion waves. The comparison
with earlier instants of time (top panels) supports this since no
pressure pulses have been initially present at these sites. This pattern
of temperature minima is directly mapped by the nucleation rate
(Fig. 8, middle panel): J* is highest where the
temperature is lowest (
)
regions can be
identified which at that time of the simulation have low temperatures
due to the constructively interfering expansion waves. The comparison
with earlier instants of time (top panels) supports this since no
pressure pulses have been initially present at these sites. This pattern
of temperature minima is directly mapped by the nucleation rate
(Fig. 8, middle panel): J* is highest where the
temperature is lowest (
![]() )
indicating an efficient dust formation process. During these events of
efficient nucleation, the mean particle radius decreases while the dust
number density increases (Fig. 9, middle panels).
)
indicating an efficient dust formation process. During these events of
efficient nucleation, the mean particle radius decreases while the dust
number density increases (Fig. 9, middle panels).
As time proceeds, the temperature minima are gone and instead, large regions of temperatures too high for dust formation appear. Consequently, the nucleation rate drops and reaches its minimum (Figs. 7 and 8, last panels).
From now on, the hydro-/thermodynamic quantities return to their (initial) equilibrium levels until radiative cooling becomes effective. The dust complex is governed only by continuous growth of the existing particles. This can be observed from the evolution of the mean particle radius in the two last time steps depicted in Fig. 9 (r.h.s., middle and bottom panels). Here, an increase of the mean particle size occurs in the whole test volume uniformly (compare color changes).
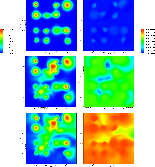 |
Figure 9:
Time evolution (top to bottom) of the dust particle number density
|
| Open with DEXTER | |
The results presented in the last sections have been outlined utilizing
a typical ![]() tuple for the hot and dust-hostile regions of a brown
dwarf atmosphere. Asymptotic analysis have been performed and one- and
two-dimensional test cases have been considered applying numerical
simulations in order to study the effects of turbulent disturbances of
the T-,
tuple for the hot and dust-hostile regions of a brown
dwarf atmosphere. Asymptotic analysis have been performed and one- and
two-dimensional test cases have been considered applying numerical
simulations in order to study the effects of turbulent disturbances of
the T-, ![]() ,
and
,
and ![]() field on the formation of
solid compounds from the gas phase.
field on the formation of
solid compounds from the gas phase.
Extending the parameter space along a typical ![]() trajectory of a
static model atmosphere shows that dust formation at low temperatures
(
trajectory of a
static model atmosphere shows that dust formation at low temperatures
(
![]() K) consumes almost instantaneously the available
material until S=1 is reached. Here, many small particles form due
to high nucleation rates. The investigations of the hotter and denser
regions reveal the necessity of a cooling mechanism as it has been
investigated and proposed in this paper. The higher the temperatures the
larger amplitudes and wavelengths of the expansion waves are needed
to create a first appropriate amount of seed nuclei. For temperatures
low enough to assure the stability of the seeds, the seed particles grow
to large particles since the density inside the atmosphere is higher
than at higher altitudes where the temperatures are small.
K) consumes almost instantaneously the available
material until S=1 is reached. Here, many small particles form due
to high nucleation rates. The investigations of the hotter and denser
regions reveal the necessity of a cooling mechanism as it has been
investigated and proposed in this paper. The higher the temperatures the
larger amplitudes and wavelengths of the expansion waves are needed
to create a first appropriate amount of seed nuclei. For temperatures
low enough to assure the stability of the seeds, the seed particles grow
to large particles since the density inside the atmosphere is higher
than at higher altitudes where the temperatures are small.
Figure 10 depicts the stability limits S=1 in the (T,
![]() )
plane for various oxygen bearing solid materials
disregarding element depletion by dust formation for a solar element
composition gas. Below these curves the respective solids are
thermodynamically stable which suggests a "condensation'' sequence
)
plane for various oxygen bearing solid materials
disregarding element depletion by dust formation for a solar element
composition gas. Below these curves the respective solids are
thermodynamically stable which suggests a "condensation'' sequence![]() for decreasing
temperature. This conclusion is not as straightforward as it might
seem. Regarding the first condensate, the stability of macroscopic dust
grains is a necessary, but not a sufficient condition for
the dust formation process. The formation of solid particles has to
proceed via the formation of seed particles (nucleation) followed by
grain growth towards macroscopic sizes
(Eqs. (6), (7)). Thereby, a large supersaturation
has to be achieved which results in a considerable gap between
typical nucleation and stability (i.e. sublimation) temperatures of
plane solids.
for decreasing
temperature. This conclusion is not as straightforward as it might
seem. Regarding the first condensate, the stability of macroscopic dust
grains is a necessary, but not a sufficient condition for
the dust formation process. The formation of solid particles has to
proceed via the formation of seed particles (nucleation) followed by
grain growth towards macroscopic sizes
(Eqs. (6), (7)). Thereby, a large supersaturation
has to be achieved which results in a considerable gap between
typical nucleation and stability (i.e. sublimation) temperatures of
plane solids.
It has, however, been pointed out by Rossow (1978) that the supersaturation needed for nucleation might be smaller for heterogeneous nucleation processes (also refered to as chemical nucleation in Rossow 1978). Presently, heterogeneous nucleation has only been studied in carbon-rich environments regarding the formation of polycyclic aromatic hydrocarbons (PAHs, Keller 1987; Goeres & Sedlmayr 1991; Cherchneff & Glassgold 1993) and no definite answer is available for the oxygen-rich case. However, quantum mechanical calculations performed by Patzer et al. (1998, see also Patzer et al. 1999a) have shown that homogeneous nucleation of molecular Al2O3 seems not to be the favorable process for the formation of corundum ((Al2O3)N) nuclei. If corundum nuclei form, they need to result from a heterogeneous nucleation process but no applicable description is at hand.
Promising astrophysical seed candidates are titanium oxides and iron
clusters, which appear in appropriate amounts in cold oxygen-rich gases;
iron seeds might be even more favorable in the most dense atmospheres
(
![]() cm-3) or in regions of high iron
concentration (John & Sedlmayr 1997). Other possible high
temperature condensates, such as silicon monoxide (SiO)N, are almost
negligible since their nucleation rates are very low. They may rather
serve as growth species than as first nuclei.
cm-3) or in regions of high iron
concentration (John & Sedlmayr 1997). Other possible high
temperature condensates, such as silicon monoxide (SiO)N, are almost
negligible since their nucleation rates are very low. They may rather
serve as growth species than as first nuclei.
Burrows & Sharp (1999) argue that dust particles in brown dwarf
atmospheres should have a mean size of ![]()
![]() m (
m (![]()
![]() m
for Gl 229B in Chabrier & Baraffe 2000) in order to fit the optical
spectra reasonably without too much influence on the near-IR. This
estimate is somewhat uncertain since also the wings of alkali resonance
lines (K I, Na I) are sources of absorption in this spectral region. It
is not quite clear which composition of the dust particles the two above
mentioned papers had in mind. Since the composition of the grains might
well depend on T and
m
for Gl 229B in Chabrier & Baraffe 2000) in order to fit the optical
spectra reasonably without too much influence on the near-IR. This
estimate is somewhat uncertain since also the wings of alkali resonance
lines (K I, Na I) are sources of absorption in this spectral region. It
is not quite clear which composition of the dust particles the two above
mentioned papers had in mind. Since the composition of the grains might
well depend on T and ![]() by the stability of the compounds,
differently composed grains might exhibit different sizes at different
sites in the atmosphere. However, the large grains might have already
gravitationally settled and only smaller particles are left floating in
the atmosphere. But if one assumes that an infinite amount of time is
available (as in static model atmospheres), even the smallest grains
would have been gravitationally settled (rain out).
by the stability of the compounds,
differently composed grains might exhibit different sizes at different
sites in the atmosphere. However, the large grains might have already
gravitationally settled and only smaller particles are left floating in
the atmosphere. But if one assumes that an infinite amount of time is
available (as in static model atmospheres), even the smallest grains
would have been gravitationally settled (rain out).
Lunine et al. (1989) argue that grains up to ![]() m
form by coalescence; our calculations show that they may easily be
formed by single particle grow. Such large particles would even less
sustain in the brown dwarf atmosphere.
m
form by coalescence; our calculations show that they may easily be
formed by single particle grow. Such large particles would even less
sustain in the brown dwarf atmosphere.
The sedimentation process (rain out) is known as the "drift problem'' in astrophysics describing relative velocities of dust and gas due to frictional decoupling. The drifting particle will enter hotter regions where still condensible material is present without being destroyed due to the gap between the temperature of efficient nucleation and stability of the compounds. The particles will grow during their descent into the deep atmosphere if considerable material is available (S>1) in this region. A competition between the increased drift velocity of the growing particle and the deceleration due to the inward decreasing gas density determines if the particle continues to fall. However, even with a very little drift velocity a static atmosphere will be completely dust free since an infinite amount of time is available in these model approaches. Since there is good observational evidence that brown dwarfs are not dust free, we conclude that brown dwarf atmospheres are not static but influenced by hydro-/thermodynamical processes, e.g. by convection. Convective material transport reaches into the atmosphere (see models by e.g. Burrows et al. 1997) and thereby replenishes these previously depleted zones. It thereby provides material for the formation of new dust. The appearance of associated acoustic waves will cause inhomogeneous distributions of dust (in size and site) in the brown dwarf atmosphere.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Tsubl.eps_NEU}\end{figure}](/articles/aa/full/2001/34/aah2848/Timg291.gif) |
Figure 10:
Sublimation temperature T(S=1) of various solid compounds as a
function of the total hydrogen density
|
| Open with DEXTER | |
Gl 229B could be a brown dwarf example where dust formation might take
place in layers below
![]() ,
i.e. at
,
i.e. at
![]() inside the photosphere. Shallower regions should than already
be emptied by gravitational settling. In such objects, dust formation
could be influenced by convection relatively high in the
atmosphere. Note that Lunine et al. (1989) show that buoyancy might be
large enough to sustain convective plums of refractory condensates due
to the release of latent heat. Guillot (1995),
however, argue that the latent heat release of refractory materials may
be too small to sustain a moist convective instability due to the
small abundances of the elements involved.
inside the photosphere. Shallower regions should than already
be emptied by gravitational settling. In such objects, dust formation
could be influenced by convection relatively high in the
atmosphere. Note that Lunine et al. (1989) show that buoyancy might be
large enough to sustain convective plums of refractory condensates due
to the release of latent heat. Guillot (1995),
however, argue that the latent heat release of refractory materials may
be too small to sustain a moist convective instability due to the
small abundances of the elements involved.
Els et al. (2001) argue that the brown dwarf Gl 86B
seems to fall in between the two aforementioned extreme cases. This
possibly might indicate that either the dust is formed at regions
![]() or the object is observed in the state of
gravitational settling when only the upper atmosphere is already
dust-free.
or the object is observed in the state of
gravitational settling when only the upper atmosphere is already
dust-free.
Brown dwarf atmospheres are influenced by the convective interior which results in the initiation of turbulent motions and thereby in the creation of acoustic waves. The existence of a non-static fluid field can also be inferred from the indirect observation of dust in brown dwarfs like Kelu 1 since all the dust would have settled and thereby removed from the atmosphere in a static situation.
The study of the interaction of dust formation and turbulent motion has been restricted to the microscopic scale regime in this paper since only here a direct simulation of the model equations (hydro-/thermodynamics, dust formation, element conservation) is possible. For any increase of the scale regime a model for the smallest scales will be needed in order to properly take into account all scales which influence the system. Our work involves:
formation initially took place.
Regarding the dust to be formed under conditions typical for a brown dwarf atmosphere we have worked out that
Acknowledgements
The referee is thanked for the useful advises to the manuscript. We thank Prof. T. Tsuji for providing us with his 1D models of static model atmospheres of brown dwarfs. Discussions and valuable comments on the manuscript by Dr. P. Woitke and Dr. C. Bailer-Jones are greatly acknowledged. We thank Prof. U. G. Jørgensen for the careful reading of the manuscript. Dipl.-Ing. H. Schmidt is thanked for providing his hydro-code and for the support in setting up the computations. This work has been supported by the DFG (grants SE 420/19-1, Kl 611/7-1, Kl 611/9-1).