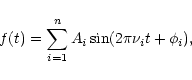6 Time-series analysis

As noted in the previous section, two independent time-series studies of the BN and BV Cnc photometry have been carried out. The objective is to find the best solution of the type

$$f(t) = \sum_{i=1}^n A_i\sin(2\pi\nu_i t + \phi_i),$$ (1)

which defines the amplitudes A_i, the frequencies $\nu_i$ and the phases $\phi_i$.

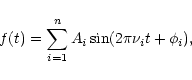6.1 Analysis 1

After cleaning the data with method 1, of the order of 7200 data points remained for BN Cnc and around 6800 for BV Cnc. To this we added about 620 points for BN Cnc and 680 for BV Cnc from 1997 obtained by Arentoft et al. (1998). The data from both seasons were combined together at the final stage of our analysis.

Periods, amplitudes and phases for a set of modes have been derived using the code Period98 (Sperl 1998) in its standard version and also in a version with a different weigthing scheme (see Sect. 5.1). In principle, Period98 uses Fourier periodogram and non-linear least-squares within its prewhitening process. In addition, the results from Period98 have been checked and special weighting procedures applied earlier by Frandsen et al. (1996) have been used.

Figure 6: Selected nights of the 1998 photometry of BN and BV Cnc. The data were prepared according to method 1, the solid line corresponds to the fit taken from analysis 1 and given in Tables 2 and 3 for BN and BV Cnc, respectively. The number in each panel presents the HJD with 2450800 subtracted for the origin of the X-axis. Short tick marks are spaced 0.02 d. The tick marks on the Y-axis are separated by 5 mmag. The second label indicates the site(s) from which the data come: Bia - Biaków, open circles, Kon - Konkoly, plus signs, Sut - Sutherland, crosses, Ten - Tenerife, dots, and LaP - La Palma, squares.

6.2 Analysis 2

The data merged and weighted in a way described in Sect. 5.2 were used in analysis 2. Because in this approach some observations from the campaign were not used, the 1998 input dataset consisted of about 5000 data points for BN Cnc and rougly 4500 for BV Cnc. For 1997, the numbers were approximately the same as in analysis 1. In analysis 2, the least-squares (LS) periodogram allowing different weights was applied. In principle, the $p(f) = 1 - V_{\rm post}/V_{\rm pre}$parameter plotted against the sample frequency f was used as a periodogram. The $V_{\rm pre}$ and $V_{\rm post}$ are the variances calculated prior to ( $V_{\rm pre}$) and after ( $V_{\rm post}$) fitting a sinusoid with a given frequency f to the data. In addition, the amplitude of a fitted sinusoid with frequency f was plotted as a second periodogram (hereafter, this will be called the LS amplitude periodogram). A detection of consecutive frequencies was done, like in analysis 1, by prewhitening with all previously found frequencies.

6.3 Comparison

The consecutive steps of the prewhitening with both kinds of time-series analysis are shown in Figs. 7 and 8 for BN Cnc and BV Cnc 1998 data, respectively.

Figure 7: Frequencies detected in the 1998 photometry of BN Cnc. The triangles indicate which frequencies were subtracted in the consecutive steps. Left: prewhitening process within analysis 1. These are Fourier periodograms. The spectral window is shown at the top panel. Right: the consecutive steps of prewhitening within analysis 2. The periodograms are the LS amplitude periodograms. The high peak at frequency 1 d-1 is an artifact produced by the method.

Figure 8: The same as in Fig. 7, but for the 1998 BV Cnc data.

The final results seem to be fairly robust in terms of a good agreement between the sets of oscillating modes for each variable derived using different weights and different programs. Although there are 1 d^-1 differences in case of BV Cnc, the frequencies are derived in the same sequence by both methods. There are, however, small differences which need to be commented.

For BN Cnc (Fig. 7) the two methods yield, within the errors, the same frequencies F1 to F5. Although in analysis 2 the alias peak at F1-1 d^-1 is higher than F1, the analysis of the combined 1997 and 1998 data (as well as the results from the STEPHI campaign, which had a better spectral window, Belmonte et al. 1994) leaves no doubt that the true frequency is F1 $\approx$ 25.76 d^-1, found as highest by analysis 1. Consequently, a sinusoid with frequency F1 was subtracted in the first step of prewhitening in analysis 2 as well. The largest difference ( $\Delta \approx$ 0.044 d^-1) was obtained for the last frequency we derive, that is, F6. Again, combined 1997 and 1998 data indicate that F6 = 25.4351 d^-1 is the correct one. We note that these different F6 frequencies are 1/ $\Delta \approx$ 23-day aliases, and 23 d is the average time difference between our 1998 January/February, late February and March groups of data (see Fig. 1). The amplitudes found in analysis 1 and 2 agree within the 3$\sigma$ error, although, on average, analysis 2 gives them higher by 0.13 mmag.

For BV Cnc (Fig. 8) the situation is more confusing. As can be seen in Fig. 8, there is a strong aliasing problem for all three frequencies we find in the 1998 data. Like for BN Cnc, analysis 2 gives slightly higher amplitudes.

Because the results of analysis 1 and 2 are quite consistent (within the errors), we decided to present in a tabular form only the results of analysis 1. The differences we indicated above give an evaluation of the systematic errors which can be introduced at the subjective stage of merging and weighting the data of different quality.

To illustrate the data, selected nights are displayed in Fig. 6 together with the best fit found. On some dates data come from two sites.