A&A 376, 302-309 (2001)
DOI: 10.1051/0004-6361:20010935
M. Kaasalainen
Observatory, PO Box 14, 00014 University of Helsinki, Finland
Received 23 April 2001 / Accepted 26 June 2001
Abstract
I show that the lightcurves of freely precessing asteroids can be analyzed
using basically the same methods as with objects in relaxed rotation. At
least two different observation geometries (with respect to the angular
momentum vector) are needed for a unique full solution; an informative
basic model can be constructed at only one geometry, if the observations
span several precession cycles. Even noisy data yield a good estimate of the
dynamical parameters, whereas accurate data are required for a good shape
solution.
Key words: methods: numerical - techniques: photometric - minor planets, asteroids - celestial mechanics
Most asteroid lightcurves are single-periodic and thus imply that the rotational state of the object is relaxed, i.e., that the asteroid rotates about the axis corresponding to its maximum moment of inertia, and this axis is aligned with the angular momentum vector. Several lightcurves, however, exhibit double-periodic behaviour. In most of these cases the object has been shown to be a binary asteroid either by lightcurve analysis (Pravec & Hahn 1997; Mottola & Lahulla 2000) or by direct imaging. So far, few asteroids have been suspected or found to be in an excited state of rotation, i.e., precessing. This is a direct consequence of the fact that no real object is completely rigid: tumbling motion causes the asteroid to lose rotational energy and thus reach the relaxed state in a relatively short time interval (Harris 1994). Indeed, to date, the only complete analysis of a tumbling asteroid is that of 4179 Toutatis based on radar images (Hudson & Ostro 1998). However, collisions and other fast perturbative events ensure that the supply of precessing asteroids is never exhausted. With the growing number of observations, lightcurves of potential precessing targets are certain to be measured every now and then. Small Near-Earth Objects are natural candidates for such observations: as the body size decreases, relaxation time increases while the time intervals between significant collisions decrease. The major bonus in observing a precessing asteroid is that only a short observation span is needed to construct a model since, due to the complicated motion, the dynamical parameters leave strong fingerprints on the lightcurve, and all parts of the target are usually seen and illuminated within a short period of time.
The lightcurves of asteroids in relaxed rotation contain a wealth of information on the objects' shapes, scattering properties, and rotational states, well extractable with suitable optimization techniques (Kaasalainen et al. 2001a,b). In principle, precessing objects are no exception: the parameter space only contains a few more dynamical parameters. However, they have some idiosyncratic properties, so care must be taken in extending the scheme for principal-axis rotators to include excited states of rotation. I describe the general aspects of the dynamical parameters in Sect. 2 (a detailed account of some necessary concepts is given in the Appendix). The inversion procedure is discussed in Sect. 3, and examples are presented in Sect. 4. Section 5 presents a summary.
A total of eight parameters are needed for a complete description of the
motion of the inertia ellipsoid in force-free precession. The body shape is
described in the coordinate frame defined by the inertia ellipsoid, so the
shape/scattering parameter
part of the problem is exactly the same as in
relaxed rotation (including the possible straightforward use of the
computed inertia tensor in a regularizing function). Many eight-parameter
sets are possible; I use the set
![]() ,
where
,
where ![]() denotes the constant angular momentum vector (its size given
by L and its direction by the ecliptic
latitude
denotes the constant angular momentum vector (its size given
by L and its direction by the ecliptic
latitude ![]() and longitude
and longitude ![]() ), while
), while
![]() are the standard Euler angles of, respectively,
precession, nutation (or tilt), and rotation at some epoch t0.
I give these three angles in the so-called x-convention,
used in, e.g., Goldstein (1980), Samarasinha & A'Hearn (1991),
and Kryszczynska et al. (1999).
are the standard Euler angles of, respectively,
precession, nutation (or tilt), and rotation at some epoch t0.
I give these three angles in the so-called x-convention,
used in, e.g., Goldstein (1980), Samarasinha & A'Hearn (1991),
and Kryszczynska et al. (1999).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2821f1.eps} \end{figure}](/articles/aa/full/2001/34/aah2821/Timg7.gif) |
Figure 1: Synthetic lightcurve of an asteroid in short-axis mode. |
| Open with DEXTER | |
The time evolution of the ellipsoid's orientation in space is given by the
equations of motion for ![]() ,
,
![]() ,
and
,
and ![]() (see the Appendix for this and
other details of the concepts discussed in the main text).
If
(see the Appendix for this and
other details of the concepts discussed in the main text).
If
![]() denotes a vector
in the ecliptic coordinate system, the same vector seen from the asteroid's
coordinate system,
denotes a vector
in the ecliptic coordinate system, the same vector seen from the asteroid's
coordinate system,
![]() ,
is
,
is
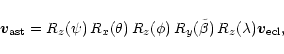 |
(1) |
The tumbling motion is governed by two periods: one, ![]() ,
for the
rotation about the extremal axis, and the other,
,
for the
rotation about the extremal axis, and the other, ![]() ,
for the
precession about
,
for the
precession about ![]() .
The nutation period is exactly one half of the
rotation period. While
.
The nutation period is exactly one half of the
rotation period. While ![]() is a real period and a constant of the
motion,
is a real period and a constant of the
motion, ![]() is not an actual period but rather defined through
another constant
is not an actual period but rather defined through
another constant
![]() :
:
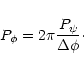 |
(2) |
The two characteristic periods are just as important as the single period in
relaxed rotation, since they define the power spectrum of a lightcurve.
Constraining these periods is of great value in constraining the parameter
space of the inverse problem. The (main) peaks of the spectrum are located
at frequencies that are linear combinations of ![]() and
and ![]() ,
where f=1/P. Prominent peaks are usually found at
,
where f=1/P. Prominent peaks are usually found at ![]() and
and
![]() ,
where the plus sign holds for LAMs and the
minus sign for SAMs; other low harmonics and combinations are
typically seen as well. The factor two is the same shape-related phenomenon
as in double-sinusoidal ordinary lightcurves. The
combination of the frequencies
is perhaps best understood when one considers the apparent frequency in the
limiting case of principal-axis rotation
(i.e., when the nutation angle is
,
where the plus sign holds for LAMs and the
minus sign for SAMs; other low harmonics and combinations are
typically seen as well. The factor two is the same shape-related phenomenon
as in double-sinusoidal ordinary lightcurves. The
combination of the frequencies
is perhaps best understood when one considers the apparent frequency in the
limiting case of principal-axis rotation
(i.e., when the nutation angle is ![]() ): the two frequencies
are still present, but they are seen only as the single frequency
): the two frequencies
are still present, but they are seen only as the single frequency
![]() .
When the body is slightly tilted, an additional
spectrum peak corresponding to the precession frequency will make its
appearance.
As an example, Fig. 1
shows a simulated lightcurve of an object (the same as
in Fig. 6) in SAM (the nutation angle wobbles between
.
When the body is slightly tilted, an additional
spectrum peak corresponding to the precession frequency will make its
appearance.
As an example, Fig. 1
shows a simulated lightcurve of an object (the same as
in Fig. 6) in SAM (the nutation angle wobbles between
![]() and
and ![]() ),
and the power spectrum is plotted in Fig. 2.
),
and the power spectrum is plotted in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2821f2.eps} \end{figure}](/articles/aa/full/2001/34/aah2821/Timg32.gif) |
Figure 2: The power spectrum of the lightcurve of Fig. 1. |
| Open with DEXTER | |
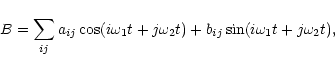 |
(3) |
A convenient parameter set for the inverse problem is
![]() ,
where the symmetric
,
where the symmetric
![]() and
the antisymmetric
and
the antisymmetric
![]() .
Using the search region
.
Using the search region
![]() ,
,
![]() automatically takes into account
the triangle inequalities fulfilled by the moments of inertia of all real
bodies. This diagonal strip in the (I1,I2)-plane is further reduced by
using only one sign for
automatically takes into account
the triangle inequalities fulfilled by the moments of inertia of all real
bodies. This diagonal strip in the (I1,I2)-plane is further reduced by
using only one sign for ![]() (the other sign describing the same
situation with indices 1 and 2 interchanged) and dropping out the redundant
region where I1 and I2 are on different sides of unity value. The
resulting sections - one for LAMs and one for SAMs - in which I1
is always an extremal axis and I2
the intermediate one are shown in Fig. 3.
(the other sign describing the same
situation with indices 1 and 2 interchanged) and dropping out the redundant
region where I1 and I2 are on different sides of unity value. The
resulting sections - one for LAMs and one for SAMs - in which I1
is always an extremal axis and I2
the intermediate one are shown in Fig. 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2821f3.eps} \end{figure}](/articles/aa/full/2001/34/aah2821/Timg44.gif) |
Figure 3:
The boundaries of the allowed regions in |
| Open with DEXTER | |
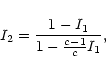 |
(4) |
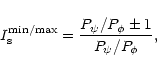 |
(5) |
Some further limiting factors apply as well. One is the lightcurve amplitude,
another the expected maximum elongations of the body dimensions. If, for
example, one deems an elongation ratio of more than three between any two
axes unlikely,
![]() for LAMs,
while
for LAMs,
while
![]() for SAMs
(i.e., any state with
for SAMs
(i.e., any state with
![]() would be declared LAM
outright), and
would be declared LAM
outright), and
![]() .
Amplitude is not an
important constraint as it is geometry-dependent, and the other constraints
already bound the search region well. For example, a
rough guess for a SAM near opposition would be
.
Amplitude is not an
important constraint as it is geometry-dependent, and the other constraints
already bound the search region well. For example, a
rough guess for a SAM near opposition would be
![]() ,
where A is the
relative intensity difference between maxima and minima. Since the tilt
angle
,
where A is the
relative intensity difference between maxima and minima. Since the tilt
angle ![]() of an axisymmetric body is given by
of an axisymmetric body is given by
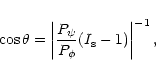 |
(6) |
It is useful first to scan the dynamical parameter space by using an
ellipsoid whose dimensions are consistent with the current moments of
inertia so that, the scattering law aside, eight parameters describe the
whole problem. The scanning be done on a relatively loose grid, choosing
a starting point from each grid cell and homing in on the local minimum
with a gradient algorithm (such as Levenberg-Marquardt - see
Kaasalainen et al. 2001a,b). Only a few sampling
values are needed for each angle (
![]() ).
Sparse sampling is usually sufficient for
).
Sparse sampling is usually sufficient for ![]() ,
,
![]() as well,
though there may be raggedness in
as well,
though there may be raggedness in ![]() along the
along the
![]() - parameter axis in places. Genetic algorithms, though slower
than gradient ones, usually clear the possible unsmooth bits well.
The two periods behave just as the single period of a principal-axis rotator,
i.e., the sampling interval for the period P should be smaller than
- parameter axis in places. Genetic algorithms, though slower
than gradient ones, usually clear the possible unsmooth bits well.
The two periods behave just as the single period of a principal-axis rotator,
i.e., the sampling interval for the period P should be smaller than
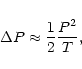 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2821f4.eps} \end{figure}](/articles/aa/full/2001/34/aah2821/Timg62.gif) |
Figure 4: Synthetic lightcurve of an asteroid in long-axis mode (crosses) and the corresponding curve of the obtained convex model (solid line). |
| Open with DEXTER | |
The main bonus of observing a precessing target is that only one observing
geometry (with respect to the angular momentum vector ![]() )
is already
sufficient for a preliminary model if the lightcurve covers several cycles.
Two geometries are needed for a unique solution. If the solar phase angle
)
is already
sufficient for a preliminary model if the lightcurve covers several cycles.
Two geometries are needed for a unique solution. If the solar phase angle
![]() at the one observing geometry is nonzero, there are always two
possible mirror solutions for
at the one observing geometry is nonzero, there are always two
possible mirror solutions for ![]() ,
with corresponding mirror-image shape
solutions. One solution is the correct
,
with corresponding mirror-image shape
solutions. One solution is the correct ![]() ,
while the other one is the
reflection of
,
while the other one is the
reflection of ![]() with respect to the Sun-Earth-asteroid plane. If the
one geometry is at opposition (or close to it), there is an infinite number
of
with respect to the Sun-Earth-asteroid plane. If the
one geometry is at opposition (or close to it), there is an infinite number
of ![]() -solutions, all on a cone around the line of sight, its surface
defined by the angle between the viewer and
-solutions, all on a cone around the line of sight, its surface
defined by the angle between the viewer and ![]() .
The shape solutions
and other dynamical parameters can still be correct (within a possible
reflection). If at least one more geometry is available (sufficiently
different from the first one, and the asteroid is not moving in the plane
of the ecliptic), the symmetry breaks and there is only one solution.
.
The shape solutions
and other dynamical parameters can still be correct (within a possible
reflection). If at least one more geometry is available (sufficiently
different from the first one, and the asteroid is not moving in the plane
of the ecliptic), the symmetry breaks and there is only one solution.
In the case of short-period observations (e.g., only two lightcurves a few days apart), we are attempting a feat that would be strictly impossible for principal-axis rotators. This is why the quality of the data now plays an especially important role. As shown in Kaasalainen et al. (2001a,b), noise is not a significant factor in the case of relaxed rotators, because there always must be lightcurves from a relatively long time span and various geometries. Inversion of a few short lightcurves of a precessing object is obviously more vulnerable to noise and especially outliers. Also, the difference between models obtained with different scattering laws may now be more noticeable.
Inversion results of long-spanned observations of precessing asteroids are
similar to those of principal-axis rotators, so I concentrate here on the
case of minimal observations. A synthetic noisy
lightcurve of a LAM asteroid, produced by the same object (shown
in Fig. 6) and scattering law as before, and
observed at the solar phase angle
![]() ,
is shown in Fig. 4,
and the corresponding power spectrum in Fig. 5.
,
is shown in Fig. 4,
and the corresponding power spectrum in Fig. 5.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2821f5.eps} \end{figure}](/articles/aa/full/2001/34/aah2821/Timg65.gif) |
Figure 5: The power spectrum of the lightcurve of Fig. 4. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{h2821f6.eps} \end{figure}](/articles/aa/full/2001/34/aah2821/Timg69.gif) |
Figure 6: The object used in generating the synthetic lightcurves. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{h2821f7.eps} \end{figure}](/articles/aa/full/2001/34/aah2821/Timg70.gif) |
Figure 7: The convex shape model obtained from the lightcurve of Fig. 4. |
| Open with DEXTER | |
An obvious example of real observations is 4179 Toutatis. The main problem with the data set of Spencer et al. (1995) is poor calibration combined with the slowness of the precession/rotation. Fitting relative brightnesses is not possible since the observing geometry changes considerably during the basic cycles. Significant new parts of rotational cycles cannot be obtained during one night, so the absolute magnitude should be calibrated very accurately. As the lightcurve fit of Hudson & Ostro (1998) (based on radar observations) shows, this is not the case, and we should expect the corresponding noise to be of order 0.1 mag. Lightcurve analysis without prior information confirms this.
Figure 8 presents two fits
to the data set of Dec. 1992-Jan. 1993, obtained
with the Hapke scattering model.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2821f8.eps} \end{figure}](/articles/aa/full/2001/34/aah2821/Timg74.gif) |
Figure 8: Two model fits to the observed magnitudes of 4179 Toutatis (crosses): the solid line is produced by a consistent ellipsoid, and the dashed line by a general convex shape. |
| Open with DEXTER | |
Gaps and outliers cause the general shape result to drift far away from the correct one. This is quite evident even without the information from the radar images, since the discrepancy between the shape and the obtained moments of inertia is considerable. The lightcurve fit is much better (0.08 mag if albedo variegation allowed, 0.09 mag if not) than it ought to be (0.12 mag for the radar model). A consistent ellipsoid fits the data as well as the radar solution, and it is evident that no more details can be obtained from the lightcurve; myriads of different shape solutions fit the data within 0.12 mag, and many better than that. The dynamical parameters, however, are good, so the Toutatis data set confirms the implications of numerical simulations.
Lightcurves of precessing bodies (spanning a number of both characteristic periods) have quite distinct appearances and should usually be distinguishable - after either a preliminary or a full analysis - from other two-period lightcurves, viz. those of binary asteroids in non-synchronous rotation. The fingerprints of the rotational state are quite strong, so the dynamical parameters can usually be well inferred even from noisy data, if the observations cover at least two sufficiently different observing geometries. Some basic precession parameters can be obtained already at one geometry. If the observation span is short, the shape model is more sensitive to noise; thus, a detailed shape model requires accurate measurements and/or at least a few (long) lightcurves.
We may expect the observed tumbling bodies to be more often slow (such as Toutatis) rather than fast rotators since the lifetime of slow tumbling motion is longer. In such cases, accurate calibration of absolute brightnesses is of primary importance.
Acknowledgements
I would like to thank Stefano Mottola for valuable comments and discussions.
Free precession has been well discussed by many authors (see, e.g., Samarasinha & A'Hearn 1991 and references therein). However, some subjects needed in the inverse problem require special attention, so I give a concise account of the dynamical problem here.
The time evolution of the Euler angles
![]() is easy to derive
from the basic kinematic equations (see, e.g., Goldstein 1980)
that can be written as
is easy to derive
from the basic kinematic equations (see, e.g., Goldstein 1980)
that can be written as
| = | |||
| = | (A.1) | ||
| = |
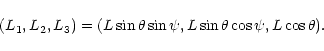 |
(A.2) |
The semiaxes a,b,c and the corresponding principal moments of inertia
of an ellipsoid are related by (setting
c=1, Ic=1)
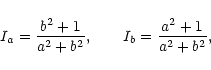 |
(A.4) |
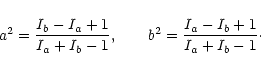 |
(A.5) |
Using the angular momentum ![]() and the energy E,
and the energy E,
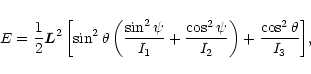 |
(A.6) |
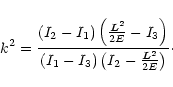 |
(A.8) |
| = | |||
| = | (A.9) | ||
| = |
Using the constant
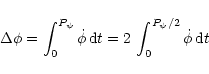 |
(A.10) |
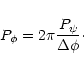 |
(A.11) |
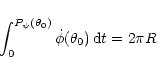 |
(A.12) |
![]() when either k2=1, i.e.,
when either k2=1, i.e.,
![]() ,
or
,
or
![]() .
In terms of the nutation angle
.
In terms of the nutation angle
![]() ,
this happens when
,
this happens when
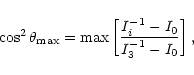 |
(A.13) |
Knowing ![]() enables one to jump easily over the gaps between
lightcurves, thus keeping the integration time short (for maximal saving of
integration time, all epochs can be projected within one time
interval of
enables one to jump easily over the gaps between
lightcurves, thus keeping the integration time short (for maximal saving of
integration time, all epochs can be projected within one time
interval of ![]() ).
Thus
).
Thus