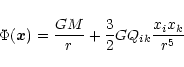 |
(1) |
A&A 376, 165-174 (2001)
DOI: 10.1051/0004-6361:20010938
A. F. Lanza1 - M. Rodonò1,2
1 -
Osservatorio Astrofisico di Catania, Via Santa Sofia, 78, Città Universitaria,
95125 Catania, Italy
2 -
Dipartimento di Fisica e Astronomia dell'Università degli Studi,
Via Santa Sofia, 78, Città Universitaria,
95125 Catania, Italy
Received 7 February 2001 / Accepted 27 June 2001
Abstract
Density fluctuations in convective stars produce small variations
of their outer gravitational field that give rise to a very small, though
finite, orbital eccentricity in close binaries with convective components. We revisit the theory for such an effect, originally presented by Phinney (1992), and propose a new approach to compute the fluctuations of the outer gravitational field based on Chandrasekhar's virial theorem. It is applied to compute the eccentricities of binaries with a millisecond pulsar component in the framework of a simplified model of their evolution. The comparison with the observations allows us to test the models proposed for the formation of such systems, giving
support to the evolutionary scenarios that connect them
with low-mass X-ray binaries, and to provide a
new test for turbulent convection models of giant stars.
Key words: stars: close binaries - binary pulsars - celestial mechanics - stellar convection - extrasolar planets
Tidal interactions are particularly effective in close binaries with convective components and lead to orbit circularization and spin-orbit synchronization over time scales much shorter than the evolutionary time scales of the components. However, perfect circularization and synchronization is never attained, as noticed by Phinney (1992). He pointed out that convection produces random fluctuations of the density inside a star, associated with rising and falling turbulent plasma columns, that induce, in turn, fluctuations of the star's outer gravitational field. The random radial force acting between the components excites small oscillations of their separation with the period of the unperturbed orbit. The resulting orbital eccentricity grows proportionally to t1/2, where t is time, in a random walk process, analogue to the resonant excitation of a linear oscillator by a random force. However, its indefinite increase is prevented by tidal dissipation, which grows linearly with the eccentricity itself, until a statistical equilibrium is reached between the stochastic excitation by the convective fluctuations and the tidal dumping.
Phinney noticed that the measurement of the small residual eccentricity produced by this process gives information on the response of the orbit to the tidal dissipation, thus introducing an analogue of the fluctuation-dissipation theorem in statistical physics (cf., e.g., Reichl 1980). The most interesting application is the prediction of the final eccentricities of binaries containing millisecond pulsars, which can actually be measured thanks to the very accurate timing that is now achievable for such systems (cf. Phinney & Kulkarni 1994). The comparison between theory and observations thus provides a powerful test of the evolutionary scenarios proposed for the formation of these binaries.
In the present paper we revisit Phinney's suggestion that convective motions can induce fluctuations of the gravitational field of a convective star and show how, by applying Chandrasekhar's virial theorem, the power spectrum of such fluctuations can be computed. The effects of these fluctuations on the orbital dynamics are evaluated using the methods of general perturbation theory. Only the fluctuations of the quadrupole term in the multipole expansion of the gravitational potential are relevant because higher order multipoles decay very rapidly with the distance from the baricentre of the star. An illustrative application of our approach supports Phinney's conjecture and shows how the distribution of the final eccentricities depends on the assumed properties of convection and tidal dissipation efficiency. Conversely, this provides a novel method to test stellar convection and tidal dissipation.
Phinney (1992) showed that the gravitational quadrupole moment of a star with a convective envelope is not constant, being subject to fluctuations related to the density fluctuations in the convective envelope. He estimated the amplitude and the power spectrum of the fluctuations of the quadrupole moment in a simplified way. In this Section, we present a more rigorous treatment based on an application of the tensor virial theorem in magnetohydrodynamics after Chandrasekhar (1961). The main advantage of the present approach is that the fluctuations of the quadrupole moment tensor are directly related to the kinetic energy fluctuations produced by convective motions.
In order to study the fluctuations due to convection, we shall consider an inertial reference frame with the origin at the baricentre of the star, the z axis along its rotation axis and the x and y axes lying in the equatorial plane.
The external gravitational field produced by the convective component
can be expanded up to the quadrupole term as:
The centrifugal and tidal distortions induce a static quadrupole moment, which can be neglected for the present purposes although it may be slowly modulated over time scales of several decades in stars with intense magnetic activity (cf., e.g., Applegate 1992; Lanza & Rodonò 1999).
The tensorial virial theorem in our inertial reference frame is expressed by the relationship (Chandrasekhar 1961):
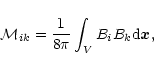 |
(6) |
From the definition of the gravitational quadrupole moment
(Eq. (2)), Eq. (4) implies:
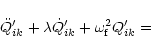
In order to study the fluctuations of the energy terms, we express the instantaneous density and velocity
at a given position ![]() inside the star as:
inside the star as:
In view of Eq. (15), the only non-trivial
components in Eq. (11) are those with i=k.
The fluctuations of the gravitation quadrupole moment tensor
can be characterized
by means of its power spectrum
PQik (see, e.g., Panter 1965 for a definition of
the power spectrum and its basic properties). Substituting Eq.
(15) into Eq. (11) and considering that
the statistical properties of the fluctuations are spherically symmetric, we find:
The determination of
![]() calls for a model of the
convective turbulence in stellar interiors. The Reynolds and the Rayleigh
numbers in stellar convection are many orders of magnitude larger than
in laboratory experiments or in detailed
numerical simulations, thus significant uncertainties remain on the
statistical properties of stellar convective flows (cf., e.g.,
Schatzman & Praderie 1993; Rüdiger 1989). Nevertheless, we shall assume a simplified
model for stellar convection in order to estimate the power spectrum of
the kinetic energy fluctuations. For simplicity sake, we subdivide the
convective envelope into domains whose fluctuations are statistically
uncorrelated; as a consequence the power spectrum of the entire convection zone
is simply the sum of the power spectra of the single domains
(cf. Panter 1965). Moreover, we shall assume that the density is
constant within a given domain, which is a fairly good assumption
since the typical length scale of the largest convective eddies is assumed
to be comparable with the local pressure (and density) scale height, according to the standard mixing-length treatment.
calls for a model of the
convective turbulence in stellar interiors. The Reynolds and the Rayleigh
numbers in stellar convection are many orders of magnitude larger than
in laboratory experiments or in detailed
numerical simulations, thus significant uncertainties remain on the
statistical properties of stellar convective flows (cf., e.g.,
Schatzman & Praderie 1993; Rüdiger 1989). Nevertheless, we shall assume a simplified
model for stellar convection in order to estimate the power spectrum of
the kinetic energy fluctuations. For simplicity sake, we subdivide the
convective envelope into domains whose fluctuations are statistically
uncorrelated; as a consequence the power spectrum of the entire convection zone
is simply the sum of the power spectra of the single domains
(cf. Panter 1965). Moreover, we shall assume that the density is
constant within a given domain, which is a fairly good assumption
since the typical length scale of the largest convective eddies is assumed
to be comparable with the local pressure (and density) scale height, according to the standard mixing-length treatment.
In convection models based on the mixing length approach, the
energy is injected in the largest eddies and then it
goes down along a turbulent cascade, until the smallest eddies reach the dimension at which viscosity effects become important.
The energy cascade produces a spectrum which is of the Kolmogorov's type
(e.g., Goldreich & Keeley 1977; Goldreich & Kumar 1988).
If we denote ![]() and u0 as the length scale and the velocity of the largest
eddies, the velocity
and u0 as the length scale and the velocity of the largest
eddies, the velocity ![]() of an eddy of turnover frequency
of an eddy of turnover frequency
![]() is
is
![]() ,
where
,
where
![]() .
The ratio of the mixing length
.
The ratio of the mixing length
![]() of that eddy to the length of the largest eddies
of that eddy to the length of the largest eddies ![]() scales as:
scales as:
![]() and its kinetic energy
and its kinetic energy
![]() - not to be confused with the power spectrum
of the kinetic energy - as
- not to be confused with the power spectrum
of the kinetic energy - as
![]() ,
where
e0 is the kinetic energy of the largest eddies.
The fluctuations of the kinetic energy of the largest eddies of dimension
,
where
e0 is the kinetic energy of the largest eddies.
The fluctuations of the kinetic energy of the largest eddies of dimension ![]() due to the eddies of dimension
due to the eddies of dimension
![]() scale as
scale as
![]() because the largest eddies contain
because the largest eddies contain
![]() uncorrelated smaller eddies of dimension
uncorrelated smaller eddies of dimension
![]() and
energy
and
energy ![]() .
Therefore, the power spectrum of the kinetic energy
fluctuations in the inertial range,
where the Kolmogorov spectrum applies, scales as
.
Therefore, the power spectrum of the kinetic energy
fluctuations in the inertial range,
where the Kolmogorov spectrum applies, scales as
![]() .
.
The Kolmogorov spectrum can not be extended
to very low frequencies (
![]() because that would
imply an infinite total energy per unit volume. Therefore, for
because that would
imply an infinite total energy per unit volume. Therefore, for
![]() we shall assume that the fluctuations of the total kinetic energy can be
regarded as hydrodynamics fluctuations (cf., e.g., Lifshitz & Pitaevskii
1980), with a characteristic relaxation time
we shall assume that the fluctuations of the total kinetic energy can be
regarded as hydrodynamics fluctuations (cf., e.g., Lifshitz & Pitaevskii
1980), with a characteristic relaxation time
![]() equal to the
turbulent dissipation time of the layer:
equal to the
turbulent dissipation time of the layer:
![]() .
.
In the light of these hypotheses, the power spectrum of the
kinetic energy fluctuations can be written as:

The power spectrum of the quadrupole moment fluctuations produced by a
layer of mixing length ![]() can be easily found by substituting Eq. (17)
into Eq. (16).
The power spectrum of the
quadrupole moment fluctuations of the whole star is obtained by summing all the contributions
coming from the uncorrelated convective layers, into which the convection zone was divided.
can be easily found by substituting Eq. (17)
into Eq. (16).
The power spectrum of the
quadrupole moment fluctuations of the whole star is obtained by summing all the contributions
coming from the uncorrelated convective layers, into which the convection zone was divided.
The mean square fluctuation of the quadrupole moment produced by
a convective layer can be computed by integrating Eq. (16):
In a close binary system,
the fluctuations of the stellar quadrupole moment of the convective
component produce fluctuating
forces that act on the companion, which in turn induces
a perturbation of the orbital motion. The variations of the orbital elements
under the action of a random force have already been studied in other
contexts and a general formalism has been developed in the framework of
Hamiltonian mechanics (cf., e.g., Barge et al. 1982). For the present problem,
however, we shall make use of the simplest formalism based on Lagrange
planetary equations for the variation of the orbital elements in the
formulation of Gauss (e.g.,
Roy 1978). In that approach the gradient of the perturbing function,
the so-called perturbing force, associated with the
fluctuating quadrupole moment is decomposed into
three components: S, directed outward along the radius vector, T in the orbital plane at right angle to S, such that it makes an angle less than
![]() with the velocity vector, and W, perpendicular to
the orbital plane and positive towards the north side of the plane. Starting from Eq. (1) and assuming a reference frame with the x-axis directed
along the line joining the centers of the two stars
from the convective component to its companion,
the only component of the quadrupole moment tensor which contributes to the
perturbing acceleration is Qxx and the perturbing force is:
with the velocity vector, and W, perpendicular to
the orbital plane and positive towards the north side of the plane. Starting from Eq. (1) and assuming a reference frame with the x-axis directed
along the line joining the centers of the two stars
from the convective component to its companion,
the only component of the quadrupole moment tensor which contributes to the
perturbing acceleration is Qxx and the perturbing force is:
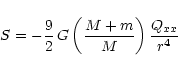
Therefore, the
only two Lagrange equations that do not reduce to an identity are:
We shall consider long time
intervals with respect to those characteristic of the fluctuations of Qxx, so that the
stochastic variations of the perturbing force can be regarded as a Markovian
process, i.e., with an autocorrelation function of the form:
![]() ,
where
,
where ![]() is the Dirac delta function.
By applying the theory outlined by, e.g., Rytov et al. (1987), we can write the
Fokker-Planck equations ruling the probability density distributions
is the Dirac delta function.
By applying the theory outlined by, e.g., Rytov et al. (1987), we can write the
Fokker-Planck equations ruling the probability density distributions
![]() and
and
![]() .
We find:
.
We find:
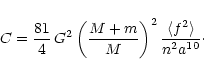 |
(28) |
We are interested in the solution of Eq. (25) in a short time interval
compared to the time needed by ![]() to change by
to change by ![]() by random walk fluctuations. Therefore, its solution is that typical of
a diffusion process:
by random walk fluctuations. Therefore, its solution is that typical of
a diffusion process:
In the case of Eq. (27), we are interested in the stationary
probability density for the residual eccentricity, that is attained
after a sufficiently long time with respect to
![]() .
By assuming that the l.h.s. of Eq. (27) vanishes and imposing the boundary condition, we find:
.
By assuming that the l.h.s. of Eq. (27) vanishes and imposing the boundary condition, we find:
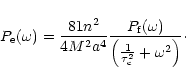 |
(33) |
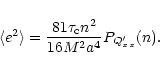 |
(36) |
In this section, an application of the theory outlined above will be presented dealing with the residual eccentricity of binaries containing millisecond pulsars. Moreover, we shall compute the order of magnitude of the fluctuations of the mean longitude at the epoch and show that they are too small to be observed.
As reviewed by Verbunt (1990, 1993) and van den Heuvel (1992), binary millisecond pulsars are believed to have been spun-up by mass transfer and their progenitors should have been X-ray binaries. According to Phinney (1992) and Phinney & Kulkarni (1994), the observed small eccentricities of their orbits are fossil residuals of their spin-up phase.
The evolutionary channels
that may produce binary millisecond pulsars have been recently reviewed by Taam et al. (2000) and we refer the reader to that paper for more details.
For our purposes it is interesting to
consider the systems that may be formed through two of the proposed
channels: a) late evolution of a low-mass secondary, in which the donor star
during the mass transfer phase was a red giant with a degenerate helium core
and ended its evolution
as a helium white dwarf (initial mass
![]() ); b)
early massive Case B evolution, in which the donor star was massive
enough to ignite helium under non-degenerate conditions; if the initial mass
ratio of the binary was smaller than a critical value (which depends
on the initial orbital separation,
see King & Ritter 1999), the final phase of mass transfer
took place after the end of the central helium
burning, when the star had approached the AGB branch. At this stage it has
an extended outer convective envelope. The donor star ends its
evolution as a CO white dwarf, after having depleted its
envelope (cf. Tauris et al. 2000).
); b)
early massive Case B evolution, in which the donor star was massive
enough to ignite helium under non-degenerate conditions; if the initial mass
ratio of the binary was smaller than a critical value (which depends
on the initial orbital separation,
see King & Ritter 1999), the final phase of mass transfer
took place after the end of the central helium
burning, when the star had approached the AGB branch. At this stage it has
an extended outer convective envelope. The donor star ends its
evolution as a CO white dwarf, after having depleted its
envelope (cf. Tauris et al. 2000).
In both scenarios the final phase of
mass transfer is characterized by a secondary
with a deep convective envelope.
The matter flowing through the
inner Lagrangian point to the primary pulsar is responsible for its spin-up
and X-ray emission so that the system is observable as a
low-mass X-ray binary.
That phase comes to an end when the mass of the secondary's envelope
falls below
![]() and the
star starts to shrink and detaches from its Roche lobe.
It is during this stage of the secondary evolution that the
residual eccentricity is produced, according to the model
proposed by Phinney (1992). The shrinking secondary still retains
a convective envelope which is responsible for the fluctuations
of the gravitational quadrupole moment of the star, thus inducing
a residual eccentricity of the orbit. The contraction
occurs on a time scale ranging from
and the
star starts to shrink and detaches from its Roche lobe.
It is during this stage of the secondary evolution that the
residual eccentricity is produced, according to the model
proposed by Phinney (1992). The shrinking secondary still retains
a convective envelope which is responsible for the fluctuations
of the gravitational quadrupole moment of the star, thus inducing
a residual eccentricity of the orbit. The contraction
occurs on a time scale ranging from
![]() to
to
![]() yr in the case of a degenerate helium core secondary, thus,
when the secondary
radius is close to the radius of its Roche lobe
yr in the case of a degenerate helium core secondary, thus,
when the secondary
radius is close to the radius of its Roche lobe ![]() ,
the circularization time
,
the circularization time
![]() yr is much shorter than
the evolutionary time and the
mean square value of the eccentricity is given by Eq. (38).
However, once the radius of the secondary R becomes
yr is much shorter than
the evolutionary time and the
mean square value of the eccentricity is given by Eq. (38).
However, once the radius of the secondary R becomes
![]() ,
the timescale for pumping and dumping the eccentricity becomes longer than
the time scale on which the envelope is contracting, because
,
the timescale for pumping and dumping the eccentricity becomes longer than
the time scale on which the envelope is contracting, because
![]() .
The eccentricity is then
"frozen" at its value when
.
The eccentricity is then
"frozen" at its value when
![]() .
.
The radius of the Roche lobe is given with a good approximation by:
![]() ,
where a is the semi-major axis of the
orbit and q=M/m is the mass ratio (Eggleton 1983). For
simplicity, we shall assume that the mass of the pulsar is
,
where a is the semi-major axis of the
orbit and q=M/m is the mass ratio (Eggleton 1983). For
simplicity, we shall assume that the mass of the pulsar is
![]() in all systems.
The radius of the secondary star
is primarily a function of its core mass (cf. Refsdal & Weigert 1970;
Ritter 1999) and
at the end of the mass transfer phase it
equals the maximum radius corresponding to the mass of its core, that
is the white dwarf companion of the millisecond
pulsar. Refsdal & Weigert (1971)
gave a simple relationship between the maximum radius of the secondary
and its core mass:
in all systems.
The radius of the secondary star
is primarily a function of its core mass (cf. Refsdal & Weigert 1970;
Ritter 1999) and
at the end of the mass transfer phase it
equals the maximum radius corresponding to the mass of its core, that
is the white dwarf companion of the millisecond
pulsar. Refsdal & Weigert (1971)
gave a simple relationship between the maximum radius of the secondary
and its core mass:
![]() ,
valid
for stars of solar chemical composition and neglecting the small difference
between the mass of the secondary and that of its helium core (
,
valid
for stars of solar chemical composition and neglecting the small difference
between the mass of the secondary and that of its helium core (![]() 5%).
Since the maximum radius
is equal to the Roche lobe radius at the end of mass transfer,
we can express the semi-major axis and the orbital period as a function
of M. More accurate expressions of the mass-period relation are
given by King & Ritter (1999) and Tauris & Savonije (1999).
5%).
Since the maximum radius
is equal to the Roche lobe radius at the end of mass transfer,
we can express the semi-major axis and the orbital period as a function
of M. More accurate expressions of the mass-period relation are
given by King & Ritter (1999) and Tauris & Savonije (1999).
Such a mass-period relation is a consequence of the proposed evolutionary scenario and its validity may be used to distinguish between binary pulsars that were formed through stable mass transfer from a donor star with a core-envelope structure, and binary pulsars that had a different origin (cf. Phinney & Kulkarni 1994; King & Ritter 1999; Taam et al. 2000).
We have applied this criterium to the systems listed by Taam et al.
(2000) considering only those systems with a measured residual eccentricity
or a significant upper limit for it (which excludes J1435-60, J1232-6501, J1453-58 and
J1810-2005). The orbital period P of these 30 systems
is plotted versus the most probable value of their secondary's mass M in Fig.
1, together with the theoretical P-M relationships
derived by King & Ritter (1999) and Refsdal & Weigert (1971), respectively.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2694f1.ps}\end{figure}](/articles/aa/full/2001/34/aah2694/Timg129.gif) |
Figure 1:
The orbital period P of the millisecond binary pulsars
listed in Table 1 of Taam et al. (2000) versus their secondary's mass, together with the theoretical P-M relationships given by King & Ritter
(1999) ( solid line) and Refsdal & Weigert (1971) ( dashed line).
The filled circles with error bars give the
most probable values of their mass (corresponding to the median inclination
|
| Open with DEXTER | |
It is important to note that systems with an orbital period smaller than about 1-2 days, although in several cases appear to agree with the theoretical P-M relationship, should have had a different evolution because the mass transfer started when their secondaries were still on the main sequence (Ergma et al. 1998; Taam et al. 2000).
In conclusion, the comparison with the theoretical P-M relationship
and the requirement that P > 2 days lead us to exclude 13 systems.
For the remaining 17 systems we can compare, as done by
Phinney & Kulkarni (1994), the observed residual eccentricity
with the mean square value predicted according to the evolutionary scenario
outlined above.
In the present paper we do not perform a detailed comparison, but
make an illustrative application in order to show how the
approach developed in Sects. 2 and 3 is applicable to a stellar model.
We adopt the models calculated by Driebe et al. (1998) for the
evolution of secondaries with a degenerate He core from the
red giant branch to the white dwarf sequence and final mass ranging from
![]() to 0.414
to 0.414
![]() .
The luminosity L and the radius Rare derived from their evolutionary tracks,
whereas the mass of the convective envelope
.
The luminosity L and the radius Rare derived from their evolutionary tracks,
whereas the mass of the convective envelope
![]() and the
radius at the base of the convective envelope
and the
radius at the base of the convective envelope ![]() are assumed to be constant
for a given model. The values of
are assumed to be constant
for a given model. The values of
![]() and
and ![]() are listed in Table 1.
are listed in Table 1.
| M |
|
|
| ( |
(
|
( |
| 0.179 | 48.289 | 0.0261 |
| 0.195 | 30.768 | 0.0246 |
| 0.234 | 13.098 | 0.0219 |
| 0.259 | 7.232 | 0.0208 |
| 0.300 | 4.746 | 0.0192 |
| 0.331 | 3.744 | 0.0181 |
| 0.414 | 2.175 | 0.0159 |
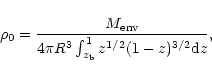 |
(40) |
The pressure scale height is given by:
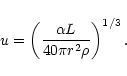 |
(42) |
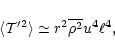 |
(43) |
The final residual eccentricity of the binary comes out as the result of
random excitations and dumpings due to the fluctuating gravitational field of
the secondary and to tidal dissipation, respectively. The contribution to
the final eccentricity produced
during a small time interval
![]() (with
(with
![]() )
is:
)
is:
![\begin{displaymath}\Delta \langle e^{2}_{\rm res} \rangle \simeq
\langle e^{2} \rangle (t) \exp[-2\theta(t)] \Delta t/\tau_{\rm c}(t),
\end{displaymath}](/articles/aa/full/2001/34/aah2694/img158.gif) |
(45) |
Therefore, the mean square value of the
residual eccentricity is approximately given by:
The coefficient B appearing in the distribution
of the mean longitude at the epoch (Eq. (29)) can be computed according to Eq. (30)
using Eqs. (16) and (18), where the contributions
coming from the different convective layers of the star are to be added.
The contribution of
each layer can be evaluated numerically for the secondaries
considered above and we find that B is in any case extremely small
(
![]() yr-1 for
2 < P < 1000 days). Therefore, there is no possibility of observing the
fluctuations of the mean longitude
yr-1 for
2 < P < 1000 days). Therefore, there is no possibility of observing the
fluctuations of the mean longitude ![]() during the phase when the
system was a LMXB since the accuracy with which we can measure the variations
of
during the phase when the
system was a LMXB since the accuracy with which we can measure the variations
of ![]() is of the order of
10-4-10-3 rad for eclipsing systems
observed over several tens of years.
is of the order of
10-4-10-3 rad for eclipsing systems
observed over several tens of years.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{h2694f2.ps}\end{figure}](/articles/aa/full/2001/34/aah2694/Timg174.gif) |
Figure 2:
The observed eccentricities
|
| Open with DEXTER | |
The application of the virial theorem allows us to derive an expression
which relates the fluctuations of the gravitational quadrupole moment
of the star with the kinetic energy
fluctuations of the convective motions. This provides a rigorous theoretical
base to the dissipation-fluctuation theorem proposed by Phinney (1992)
and supports the interpretation he proposed for the residual eccentricities
of binaries containing millisecond pulsars.
Our illustrative calculations show that the mean square value of the residual eccentricity is a function of the secondary's mass only, i.e., of the orbital
period, given the mass-period relationship for binary millisecond pulsars.
The agreement between our theoretical predictions and the observations is good for orbital periods in the range 2-10 d,
but significant deviations of a factor of ![]() appear for systems with
periods longer than 20 days. This discrepancy may be possibly
ascribed to the limitations of the adopted secondary star models.
Specifically, Driebe's et al. models are characterized by
maximum radii which are significantly smaller than the Roche lobe
radii of long period systems.
This may be due to the assumptions made
on the mass loss rate during the evolution of the secondaries, which was
not derived from a detailed physical model. As a matter of fact, the
evolutionary calculations by Tauris & Savonije (1999), who included a more
sophisticated treatment of mass loss, yield larger maximum radii
for the secondaries.
It is interesting to note that our assumption of constant envelope mass
is not critical because the dependencies on
appear for systems with
periods longer than 20 days. This discrepancy may be possibly
ascribed to the limitations of the adopted secondary star models.
Specifically, Driebe's et al. models are characterized by
maximum radii which are significantly smaller than the Roche lobe
radii of long period systems.
This may be due to the assumptions made
on the mass loss rate during the evolution of the secondaries, which was
not derived from a detailed physical model. As a matter of fact, the
evolutionary calculations by Tauris & Savonije (1999), who included a more
sophisticated treatment of mass loss, yield larger maximum radii
for the secondaries.
It is interesting to note that our assumption of constant envelope mass
is not critical because the dependencies on
![]() cancels
each other in the expression for
cancels
each other in the expression for
![]() .
Such a conclusion is also confirmed by some exploratory computation
with
.
Such a conclusion is also confirmed by some exploratory computation
with
![]() .
Moreover, the adopted values for
.
Moreover, the adopted values for ![]() do not
significantly influence our results, provided that
do not
significantly influence our results, provided that
![]() in the relevant
evolutionary phases.
in the relevant
evolutionary phases.
Assuming that the tidal circularization process is properly described,
the distribution of the residual eccentricities may be used to test
models of the secondary's evolution and to probe the
properties of stellar convection, in particular the kinetic energy spectrum,
in the phases
following the end of mass transfer. The approach presented above is
simply illustrative, also in view of the limitations of the present
evolutionary models.
The development of detailed models of the secondary's evolution,
which are capable of following its radius and luminosity variations in a realistic
way during all of the relevant phases,
will allow us to make accurate predictions
by numerically solving the initial value problem posed by Eq. (31)
with a time varying coefficient C and computing the change of the
distribution
![]() versus time. We wish to apply such a more rigorous
approach in a forthcoming paper.
versus time. We wish to apply such a more rigorous
approach in a forthcoming paper.
The proposed method to compute quadrupole moment fluctuations is interesting also for other problems that involve binary systems with a convective component and a circularization
time
![]() long enough to allow a random walk growth of the residual
eccentricity to significant values. The recently discovered extrasolar
planets may be relevant in this respect. In those systems,
the much smaller mass of the planet, with respect to the star,
makes
long enough to allow a random walk growth of the residual
eccentricity to significant values. The recently discovered extrasolar
planets may be relevant in this respect. In those systems,
the much smaller mass of the planet, with respect to the star,
makes
![]() very long, thus allowing
the residual eccentricity to grow. However, an exploratory calculation we
performed by assuming the central star to have the same structure of
the present Sun and a 4.0 d orbital period for the planet,
indicates that the attained residual eccentricities are in the range
very long, thus allowing
the residual eccentricity to grow. However, an exploratory calculation we
performed by assuming the central star to have the same structure of
the present Sun and a 4.0 d orbital period for the planet,
indicates that the attained residual eccentricities are in the range
![]() ,
even if the tidal circularization time may well
exceed the star main sequence life-time (cf. Trilling 2000). However, the situation
may be significantly different if the planet is orbiting a red giant
because in that case the amplitude of the convective fluctuations is
much more pronounced and effective.
,
even if the tidal circularization time may well
exceed the star main sequence life-time (cf. Trilling 2000). However, the situation
may be significantly different if the planet is orbiting a red giant
because in that case the amplitude of the convective fluctuations is
much more pronounced and effective.
Acknowledgements
The authors wish to thank an anonymous Referee for a careful reading of the manuscript and stimulating comments. Research on stellar physics at Catania Astrophysical Observatory and at the Dept. of Physics and Astronomy of Catania University is funded by MURST (Ministero dell'Università e della Ricerca Scientifica e Tecnologica) and Regione Sicilia, whose financial support is gratefully acknowledged.
In this Appendix the relation between the variation of the tensor ![]() and the gravitational quadrupole moment Qik is discussed.
The variation of the gravitational energy tensor due to the density fluctuations can be written as:
and the gravitational quadrupole moment Qik is discussed.
The variation of the gravitational energy tensor due to the density fluctuations can be written as:
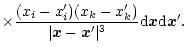 |
(48) |
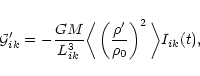 |
(50) |
We define the characteristic frequency
![]() as:
as:
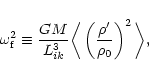 |
(51) |
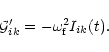 |
(52) |
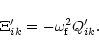 |
(53) |
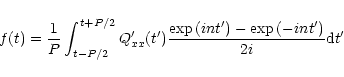 |
(54) |
f(t)=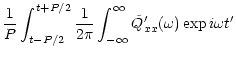 |
|
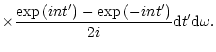 |
(55) |
f(t)=![$\displaystyle \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{1}{P} \left[\tilde{Q}_{xx}^{\prime}(\omega-n)
-\tilde{Q}_{xx}^{\prime}(\omega + n) \right]$](/articles/aa/full/2001/34/aah2694/img204.gif) |
|
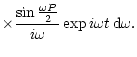 |
(56) |
![\begin{displaymath}\tilde{f}(\omega) = \frac{1}{P} \left[\tilde{Q}_{xx}^{\prime}...
...e}(\omega + n) \right] \frac{\sin \frac{\omega P}{2}}{i\omega}
\end{displaymath}](/articles/aa/full/2001/34/aah2694/img206.gif) |
(57) |