A&A 376, 69-76 (2001)
DOI: 10.1051/0004-6361:20010921
The spectral energy distribution of AO 0235+164 during
two
active optical phases
Y. J. Chen1,2 - D. R. Jiang1,2
1 - Shanghai Astronomical Observatory, Chinese Academy of
Sciences, Shanghai
200030, PR China
2 - National Astronomical Observatory, Chinese Academy of
Sciences, Beijing 100012, PR China
Received 2 August 2000 / Accepted 21 June 2001
Abstract
We investigate the spectral variability of the source AO 0235+164
during two active phases. We find that the peak frequencies in
the Spectral Energy Distributions (SED) are variable with time
within a range of an order of magnitude, which does not cause the
source to make a transition from Low-energy peaked BL Lac objects
to High-energy peaked BL Lac objects. The correlation of peak
frequency and peak flux either for an individual outburst or the
combination of several individual outbursts is significant. Our
research reveals that in many physical properties AO 0235+164 is
much closer to flat-spectrum radio quasars, rather than to High-energy
peaked BL Lacs, which in turn implies that Comptonization of external
radiation may play quite an important role in 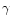 -ray emission.
There are indications that the observed variability may be due to
superposition of intrinsic and propagation effects, which is in
agreement with the conclusion of Kraus et al. (1999).
We also explore the possible origin of the two outbursts and suggest
that intrinsic variability, not including the shock effect, probably
accounts for the two outbursts.
-ray emission.
There are indications that the observed variability may be due to
superposition of intrinsic and propagation effects, which is in
agreement with the conclusion of Kraus et al. (1999).
We also explore the possible origin of the two outbursts and suggest
that intrinsic variability, not including the shock effect, probably
accounts for the two outbursts.
Key words: galaxies: active - galaxies: BL Lacertae objects:
individual: AO 0235+164 - radiation mechanisms: non-thermal
BL Lacertae objects are extragalactic radio sources
characterized by strong and rapidly variable nonthermal emission
extending from radio to gamma-ray band. The nonthermal continuum
is commonly attributed to synchrotron radiation at low frequencies,
and inverse Compton radiation at high frequencies emitted in a
relativistic jet pointing towards the observer (e.g. Urry et al.
1995). BL Lacs can be divided into two subclasses depending on
their Spectral Energy Distribution (SED), namely low-energy peaked BL Lacs (LBL) for objects with synchrotron emission peaking at
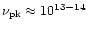 Hz and high-energy peaked BL Lacs
(HBLs) peaking at
Hz and high-energy peaked BL Lacs
(HBLs) peaking at  1017-18 Hz (Padovani & Giommi 1995).
A large sample of blazars was collected by Fossati et al. (1999)
to further investigate their spectral energy distributions, from which
they found that the correlations between synchrotron peak frequency and
luminosity (
1017-18 Hz (Padovani & Giommi 1995).
A large sample of blazars was collected by Fossati et al. (1999)
to further investigate their spectral energy distributions, from which
they found that the correlations between synchrotron peak frequency and
luminosity ( vs.
vs. 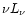 ), peak frequency and optical
luminosity, and peak frequency and
), peak frequency and optical
luminosity, and peak frequency and 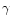 -ray luminosity
are significant. Furthermore, with increasing luminosity the
synchrotron peak moves to lower frequencies, which implies that radiation
losses may play an important role in the radiative process.
In contrast, in the present paper we study the changes in the
SED of a single source during different outbursts and try to
correlate them with the changes in other properties; i.e.
rather than sampling a large number of sources once, we sample
one source many times.
-ray luminosity
are significant. Furthermore, with increasing luminosity the
synchrotron peak moves to lower frequencies, which implies that radiation
losses may play an important role in the radiative process.
In contrast, in the present paper we study the changes in the
SED of a single source during different outbursts and try to
correlate them with the changes in other properties; i.e.
rather than sampling a large number of sources once, we sample
one source many times.
The radio source AO 0235+164 was
identified by Spinrad & Smith (1975) as a BL Lac object
(a subclass of blazar). The object shows pronounced variability
at almost all wavelengths (including strong GeV 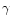 -ray
emission). These variations are often seen as fast, very intensive
flares (Webb & Smith 1989), of which the two most prominent
outbursts took place from late 1975 to early 1976 and from
late 1986 to early 1987 (hereafter we refer to them as the 1975
outburst and the 1987 outburst). Takalo et al. (1998) and Kraus et.
al. (1999) all suggested that a single physical process
cannot explain the observed variability; the former suggested that the
effects of microlensing by a foreground galaxy plays an important
role and the latter suggested that the observed variability is due to a
superposition of intrinsic variability and propagation effects.
-ray
emission). These variations are often seen as fast, very intensive
flares (Webb & Smith 1989), of which the two most prominent
outbursts took place from late 1975 to early 1976 and from
late 1986 to early 1987 (hereafter we refer to them as the 1975
outburst and the 1987 outburst). Takalo et al. (1998) and Kraus et.
al. (1999) all suggested that a single physical process
cannot explain the observed variability; the former suggested that the
effects of microlensing by a foreground galaxy plays an important
role and the latter suggested that the observed variability is due to a
superposition of intrinsic variability and propagation effects.
In this paper, we use the available multifrequency flux density
data from radio to optical wavelength mostly for the two active
phases to study the spectral variability of AO 0235+164. In Sect. 2, we
give a summary of the multifrequency data and describe the data
analysis procedures. We calculate the parameters of simple synchrotron
spectra: the peak frequency
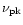 ,
and the peak flux
,
and the peak flux
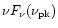 for all these epochs. The correlation results of the spectral
parameters will be presented in Sect. 3. The general results and
discussion can be found in Sect. 4. We conclude with a summary in Sect. 5.
for all these epochs. The correlation results of the spectral
parameters will be presented in Sect. 3. The general results and
discussion can be found in Sect. 4. We conclude with a summary in Sect. 5.
Since the discovery of the radio source AO 0235+164 in 1972 (Argue et
al. 1973), it has undergone rapid, high amplitude variations
several times. There are so far five detected outbursts for which
observational results have been published. Except for the two
outbursts mentioned in Sect. 1, further outbursts occurred in 1979, in
1991 and in 1998 (Roy et al. 2000); of these only three epochs
of multifrequency data sets observed during the 1991 outburst were
suitable for inclusion in our data analysis. Data sets for two
additional epochs, viz. in optical quiescent periods in late 1987 are
also included, together with the above three data sets, as a
supplement to our further data analysis. We have 33 epochs of
different data sets in all for simulation, including 18 collected in
1975, 10 in 1987, 3 in 1991 and 2 in quiescent stage. There are
usually 6-9 observational wavebands for each epoch. Each epoch
includes data in at least two radio bands, and two bands in the
infrared and optical regions to insure that the peak frequency of
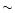 1013 Hz (Ghisellini et al. 1998) lies within the
available wavebands, and that the acquired peak frequencies and
energies are more reasonable.
1013 Hz (Ghisellini et al. 1998) lies within the
available wavebands, and that the acquired peak frequencies and
energies are more reasonable.
The optical and infrared data came from the observations by Rieke
et al. (1976) for the 1975 outburst, Webb & Smith
(1989) for the 1987 outburst, Mead et al. (1990)
and Takalo et al. (1998) for the other 5 epoch. The KPNO
1.3-m telescope (Sitko & Sitko 1991) also made some
contribution of infrared and optical data to the 1987 outburst.
All of the collected data in infrared and optical wavebands were
corrected for galactic extinction as can be found in the
corresponding references. In the radio wavebands at 5 GHz, 8.0
GHz and 14.5 GHz the data were obtained within the Michigan
Monitoring Program. As for the data at 22.2 GHz and 36.8 GHz, the
source has been monitored with the Metsähovi radio telescope
since 1980 (Valtaoja et al. 1992). In addition, we
obtained data at 10.8 GHz from the Algonquin Radio Observatory
(MacLeod et al. 1976), 31.4 GHz data and 85 GHz data from
the NRAO 36-foot antenna (Ledden & Aller 1976). The
amount of data at 90 GHz and 230 GHz is relatively small, mainly
originating from the 30-m telescope at Pico Veleta (Steppe et
al. 1988; Steppe et al. 1993). Above all, we
collected data in as many wavebands as possible for each epoch to
improve the quality of the fits.
Infrared and optical magnitudes are converted to flux densities
for spectral fitting. The optical and infrared flux densities are
obtained from the corresponding magnitude using the following
expression (Clements et al. 1995),
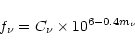 |
(1) |
where the coefficient 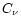 is the standard Johnson flux density
at
is the standard Johnson flux density
at 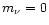 .
.
Before carrying out the spectral energy fitting, we first grouped
the collected multifrequency data according to the observational
date, in such a way that due to the rapid variability in optical
and infrared wavebands, all multifrequency data for each epoch
are grouped to be simultaneous to make sure that the spectral
energy distribution truly reflect the intrinsic radiative
properties of AO 0235+164. This has to be done due to the rapid
variability in optical and infrared wavebands. At radio
wavebands, the variation becomes much slower, and therefore the
simultaneity requirement is less stringent (Marscher & Gear
1985). Centered at the observational date of the optical
wavebands, we selected the radio data as close to the center as
possible. If the time interval between the observational dates of
radio and optical wavebands was over 10 days, the radio data were
discarded. If the time interval between two adjacent radio data
was less than 20 days at the same frequency, we took the
intermediate value using linear interpolation. Above all, the
purpose is to make the multifrequency data for each epoch as
nearly as possible simultaneous. The specific observing epochs,
and the wavebands for each epoch are listed in Table 1.
Table 1:
The observational epochs and observational wavebands for
each epoch.
| Epoch |
Observed Wavebands |
| 75.10.3 |
8.0 GHz, 14.5 GHz, 31.4 GHz, 85.0 GHz, V, B, U |
| 75.10.4 |
8.0 GHz, 14.5 GHz, 31.4 GHz, 85.0 GHz, V, B, U |
| 75.10.8 |
8.0 GHz, 14.5 GHz, 31.4 GHz, 85.0 GHz, L, K, J, B |
| 75.10.10 |
8.0 GHz, 14.5 GHz, L, K, J, B |
| 75.10.11 |
8.0 GHz, 14.5 GHz, L, K, J, B |
| 75.10.12 |
8.0 GHz, 14.5 GHz, L, K, J, B |
| 75.10.26 |
8.0 GHz, 14.5 GHz, 2.4e13 Hz, 2.7e13 Hz, 3.6e13 Hz, L, K,
H, J, B |
| 75.10.27 |
8.0 GHz, 14.5 GHz, K, H, J, V, B, U |
| 75.10.28 |
8.0 GHz, 14.5 GHz, K, H, J, V, B, U |
| 75.11.8 |
4.9 GHz, 8.0 GHz, 14.5 GHz, 1.43e13 Hz, N, M, K, H, J |
| 75.11.9 |
8.0 GHz, 14.5 GHz, 1.43e13 Hz, N, M, L, K, H, J |
| 75.11.11 |
8.0 GHz, 14.5 GHz, M, L, K, H, J |
| 75.11.14 |
8.0 GHz, 14.5 GHz, M, L, K, H, J, B |
| 75.11.24 |
5.0 GHz, 8.0 GHz, 10.8 GHz, 14.5 GHz, 90.0 GHz, V, B, U |
| 75.11.27 |
8.0 GHz, 10.8 GHz, 14.5 GHz, 140.0 GHz, 1.58e13 Hz,
2.73e13 Hz, 3.57e13 Hz, L, M, K, H, J |
| 75.12.1 |
8.0 GHz, 14.5 GHz, 140.0 GHz, 1.43e13 Hz, 2.83e13 Hz, K,
H, J |
| 75.12.2 |
8.0 GHz, 10.8 GHz, 14.5 GHz, 1.43e13 Hz, H, J, B |
| 76.1.3 |
8.0 GHz, 14.5 GHz, V, B, U |
| 86.11.28 |
4.8 GHz, 8.0 GHz, 14.5 GHz, L, K, H, J, I, R, V, B, U |
| 86.12.1 |
4.8 GHz, 8.0 GHz, 14.5 GHz, L, K, H, J |
| 86.12.2 |
4.8 GHz, 8.0 GHz, 14.5 GHz, L, K, H, J |
| 87.1.23 |
4.8 GHz, 8.0 GHz, 14.5 GHz, 22.2 GHz, 36.8 GHz, 90.0 GHz,
230.0 GHz, V, B, U |
| 87.1.24 |
4.8 GHz, 14.5 GHz, 22.2 GHz, 36.8 GHz, V, B |
| 87.1.26 |
4.8 GHz, 8.0 GHz, 14.5 GHz, 36.8 GHz, B, U |
| 87.1.28 |
8.0 GHz, 14.5 GHz, 36.8 GHz, 230.0 GHz, V, B, U |
| 87.1.29 |
8.0 GHz, 14.5 GHz, 36.8 GHz, 230.0 GHz, B, U |
| 87.2.1 |
4.8 GHz, 8.0 GHz, 14.5 GHz, 22.2 GHz, 36.8 GHz, 230.0
GHz, V, B, U |
| 87.2.22 |
4.8 GHz, 8.0 GHz, 14.5 GHz, 22.2 GHz, 36.8 GHz, 90.0 GHz,
L, K, H, J |
| 87.7.28 |
4.8 GHz, 8.0 GHz, 14.5 GHz, K, H, J, I, R, V, B, U |
| 87.9.20 |
4.8 GHz, 14.5 GHz, 22.2 GHz, R, V, B |
| 90.11.22 |
4.8 GHz, 8.0 GHz, 14.5 GHz, 36.8 GHz, I, R, V, B |
| 91.1.9 |
4.8 GHz, 8.0 GHz, 36.8 GHz, 90.0 GHz, I, R, V, B, U |
| 91.1.12 |
4.8 GHz, 8.0 GHz, 36.8 GHz, I, R, V, B, U |
We constructed the rest-frame spectral energy distributions using
the flux densities 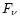 of all observational wavebands
multiplied by the observed frequency
of all observational wavebands
multiplied by the observed frequency 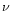 and plot
and plot 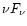 against
against
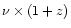 (Sambruna & Urry 1996). It is
known that SEDs clearly show a broad peak between radio and UV-X
rays (Fossati et al. 1999). Thus, in order to determine
the peak frequency of the synchrotron component for each epoch
with an objective procedure, we tried to fit the data points for
each epoch using two type of functions, viz., a second degree
polynomial (Sambruna & Urry 1996) and a third degree
polynomial (Fossati et al. 1999) respectively to
determine which gives the better results. By comparing the results
from these two methods, we find that the parabolic fits are not
very good, while the fits using a third degree polynomial are much
more satisfactory. The reasons may lie in the fact that the
optical spectral index is very steep (
(Sambruna & Urry 1996). It is
known that SEDs clearly show a broad peak between radio and UV-X
rays (Fossati et al. 1999). Thus, in order to determine
the peak frequency of the synchrotron component for each epoch
with an objective procedure, we tried to fit the data points for
each epoch using two type of functions, viz., a second degree
polynomial (Sambruna & Urry 1996) and a third degree
polynomial (Fossati et al. 1999) respectively to
determine which gives the better results. By comparing the results
from these two methods, we find that the parabolic fits are not
very good, while the fits using a third degree polynomial are much
more satisfactory. The reasons may lie in the fact that the
optical spectral index is very steep (
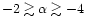 )
(Smith et al. 1987) and
the radio spectral index is flatter (Chu et al. 1996);
This makes it unlikely that the second degree polynomial fitting
result should be very satisfactory. In the following we present
all of the spectral fitting results (Fig. 1), of which
the left-hand side shows the SEDs of the 1975 outburst and the
right-hand one shows the spectral fitting results of the 1987
outburst and the other 5 epochs of data sets.
)
(Smith et al. 1987) and
the radio spectral index is flatter (Chu et al. 1996);
This makes it unlikely that the second degree polynomial fitting
result should be very satisfactory. In the following we present
all of the spectral fitting results (Fig. 1), of which
the left-hand side shows the SEDs of the 1975 outburst and the
right-hand one shows the spectral fitting results of the 1987
outburst and the other 5 epochs of data sets.
![\begin{figure}
\par {
\includegraphics[width=8.8cm,clip]{h2659f1a.ps}\hspace*{3mm}
\includegraphics[width=8.8cm,clip]{h2659f1b.ps} }
\end{figure}](/articles/aa/full/2001/34/aah2659/Timg20.gif) |
Figure 1:
The intrinsic power (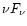 ,
in ,
in
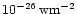 )
is plotted vs. the rest-frame frequency, )
is plotted vs. the rest-frame frequency,
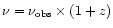 .
Left map: fitting results for all epochs of the 1975
outburst; right map: fitting results for all epochs of the 1987
outburst as
well as the other 5 epoch of multi-frequency data. .
Left map: fitting results for all epochs of the 1975
outburst; right map: fitting results for all epochs of the 1987
outburst as
well as the other 5 epoch of multi-frequency data. |
| Open with DEXTER |
For an individual source, the luminosity distance for all
observational epochs is constant so that using 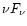 instead
of luminosity
instead
of luminosity 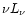 will not change the correlation results.
Throughout this paper, we refer to the quantity
will not change the correlation results.
Throughout this paper, we refer to the quantity 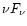 as
peak flux. In addition, all the correlations of physical quantity
pairs refer to the linear correlations of the logarithmic values
of the corresponding physical quantities.
as
peak flux. In addition, all the correlations of physical quantity
pairs refer to the linear correlations of the logarithmic values
of the corresponding physical quantities.
We obtained peak frequency and peak flux in the course of spectral
fitting for each epoch. The distribution of peak flux with peak
frequency in SEDs for the 1975 outburst is displayed with the
symbol of "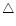 '' in the left map of Fig. 2, as we
can see, the correlation between
'' in the left map of Fig. 2, as we
can see, the correlation between
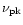 and
and
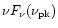 is apparent. The specific values of
correlation coefficient and confidence level are listed in Table
2. A significant correlation of
is apparent. The specific values of
correlation coefficient and confidence level are listed in Table
2. A significant correlation of
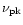 and the
luminosity at 8 GHz also exists for the 1975 outburst.
Furthermore, there may exist a slight correlation for
and the
luminosity at 8 GHz also exists for the 1975 outburst.
Furthermore, there may exist a slight correlation for
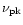 and optical luminosity at B waveband (
and optical luminosity at B waveband (
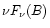 ), but this is not certain.
), but this is not certain.
Except for the pair of
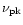 vs.
vs.
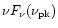 that shows anti-correlation, all the other combinations show
positive correlations. A detailed discussion is given in the next
section.
that shows anti-correlation, all the other combinations show
positive correlations. A detailed discussion is given in the next
section.
In comparison with the 1975 outburst, the number of epochs for
which observations were available was smaller, but the
observations give a more complete, if somewhat sparse, coverage of
the whole outburst.
For the 1987 outburst, the physical quantities of peak frequency
and peak flux are well correlated (displayed with symbol "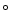 '' in the left map of Fig. 2), yet the correlation
of
'' in the left map of Fig. 2), yet the correlation
of
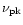 vs.
vs.
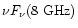 is worse. The
optical energy in the B waveband is strongly correlated with
peak frequency. The detailed correlation parameters are also
shown in Table 2.
is worse. The
optical energy in the B waveband is strongly correlated with
peak frequency. The detailed correlation parameters are also
shown in Table 2.
As was the case for the 1975 outburst, the physical quantities of
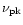 vs.
vs.
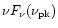 show
anti-correlation, but the peak frequency and optical luminosity
are significantly correlated. On the other hand, luminosity at 8 GHz and peak frequency do not seem to be correlated at all. It
should be noted that the correlation of
show
anti-correlation, but the peak frequency and optical luminosity
are significantly correlated. On the other hand, luminosity at 8 GHz and peak frequency do not seem to be correlated at all. It
should be noted that the correlation of
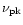 vs. radio
energy at 8 GHz is strong for the 1975 outburst, but weak for
the 1987 outburst.
vs. radio
energy at 8 GHz is strong for the 1975 outburst, but weak for
the 1987 outburst.
We combined the fitting results of all epochs, including the 1975
and 1987 outbursts together with the other 5 epochs, and then
present the general results (see Fig. 2).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{h2659f2a.ps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{h2659f2b.ps} \end{figure}](/articles/aa/full/2001/34/aah2659/Timg23.gif) |
Figure 2:
Left map: distribution of peak frequency and peak flux
for all epochs: "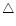 '' stands for the 1975 outburst,
" '' stands for the 1975 outburst,
"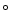 ''
stands for the 1987 outburst, " ''
stands for the 1987 outburst, "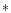 '' for the other
epochs; right
map: distribution of optical energy in the B waveband with peak
frequency
(symbols are the same as on the left). '' for the other
epochs; right
map: distribution of optical energy in the B waveband with peak
frequency
(symbols are the same as on the left). |
| Open with DEXTER |
We can see from Table 2 that the correlation of
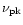 vs. optical luminosity in the B waveband is very strong,
and there appears to be no correlation of
vs. optical luminosity in the B waveband is very strong,
and there appears to be no correlation of
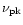 vs.
vs.
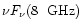 .
.
After combination, the correlation of
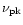 vs.
vs.
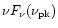 becomes weaker but it still remains fairly
strong, let alone the correlation for both individual outbursts.
In short, the peak frequency in SEDs is well correlated with the
optical flux in the B band and the peak flux. Yet the correlation
between peak frequency and luminosity at 8 GHz is not significant.
becomes weaker but it still remains fairly
strong, let alone the correlation for both individual outbursts.
In short, the peak frequency in SEDs is well correlated with the
optical flux in the B band and the peak flux. Yet the correlation
between peak frequency and luminosity at 8 GHz is not significant.
Blazars are characterized by large amplitude and fast variability,
indicating that the electron distribution is rapidly changing or
the orientation of the emitting jet is varying with time. There
appears to be a more or less continuous sequence of spectral
properties of different objects, HBL
 LBL
LBL
 FSRQs (flat spectrum radio quasars), characterized
by increasing
FSRQs (flat spectrum radio quasars), characterized
by increasing 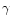 -ray luminosity, increasing dominance of
the energy output in the
-ray luminosity, increasing dominance of
the energy output in the 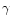 -ray component over the
synchrotron component, and a shift of the peaks in the
-ray component over the
synchrotron component, and a shift of the peaks in the 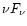 spectra of both components towards lower energies. This sequence
can be understood in terms of increasing dominance of the
external comptonization(EC) over the synchrotron
self-Compton(SSC) mechanism (e.g., Fossati et al. 1997).
These different types of object may show different behaviour in
the evolution of the synchrotron peak in their SEDs, and therefore
can be used as a diagnostic to determine the dominant radiation
mechanism in these objects (Böttcher 1999). Moreover
the changes of the electron spectrum, and physical parameters
such as magnetic field strength inside the jet can also affect the
evolution behaviour of the synchrotron peak in SEDs (Mastichiadis
& Kirk 1997; Petry et al. 2000). In addition,
spectral variability may also involve some other factors such as
the size of the emitting region, the orientation variation of the
emitting jet and possible shock formation in jet as well
(Chiaberge & Ghisellini 1999; Villata & Raiteri
1999; Kirk et al. 1998). Obviously a shock
forming in the jet will change the particle energy distributions
and the orientation variation of the emitting region will change
beaming factor so that the spectral variability will show
different behaviour in both cases (Villata & Raiteri
1999; Kirk et al. 1998).
spectra of both components towards lower energies. This sequence
can be understood in terms of increasing dominance of the
external comptonization(EC) over the synchrotron
self-Compton(SSC) mechanism (e.g., Fossati et al. 1997).
These different types of object may show different behaviour in
the evolution of the synchrotron peak in their SEDs, and therefore
can be used as a diagnostic to determine the dominant radiation
mechanism in these objects (Böttcher 1999). Moreover
the changes of the electron spectrum, and physical parameters
such as magnetic field strength inside the jet can also affect the
evolution behaviour of the synchrotron peak in SEDs (Mastichiadis
& Kirk 1997; Petry et al. 2000). In addition,
spectral variability may also involve some other factors such as
the size of the emitting region, the orientation variation of the
emitting jet and possible shock formation in jet as well
(Chiaberge & Ghisellini 1999; Villata & Raiteri
1999; Kirk et al. 1998). Obviously a shock
forming in the jet will change the particle energy distributions
and the orientation variation of the emitting region will change
beaming factor so that the spectral variability will show
different behaviour in both cases (Villata & Raiteri
1999; Kirk et al. 1998).
In terms of the correlation coefficients and corresponding
confidence values in Table 2, for the radio source of AO
0235+164, there is a significant inverse correlation of peak
frequency and peak flux both for individual outbursts and for the
combination of the two outbursts with the other 5 epoch of SEDs.
The synchrotron peak frequencies of about
1013-14 Hz (see
Fig. 2) of the source are much closer to those of
FSRQs (about
1012-13 Hz; Böttcher 1999) than
to those of HBLs (about
1017-18 Hz). Böttcher
(1999) pointed out that if the 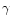 -ray emission of
FSRQs is produced by Comptonization of external radiation which
dominates the radiative energy loss rate of relativistic
electrons in blobs, then the observed peak of the synchrotron
spectrum component depends on the bulk Lorentz factor
-ray emission of
FSRQs is produced by Comptonization of external radiation which
dominates the radiative energy loss rate of relativistic
electrons in blobs, then the observed peak of the synchrotron
spectrum component depends on the bulk Lorentz factor 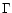 and the external photon density
and the external photon density
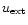 as
as
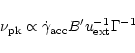 |
(2) |
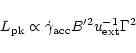 |
(3) |
where B' and
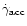 are the magnetic field
strength in the comoving frame and electron acceleration rate
respectively. From the above two equations we can have the
expression as
are the magnetic field
strength in the comoving frame and electron acceleration rate
respectively. From the above two equations we can have the
expression as
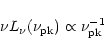 |
(4) |
if B' remains constant or independent of the other quantities.
The synchrotron peak is therefore expected to shift toward lower
frequencies with increasing Lorentz factor while the peak density
generally increases in the 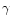 -ray flaring stage. AO
0235+164 is a low-peaked BL Lac, located at intermediate
position in the sequence of subclasses of Blazar mentioned above.
Nuclear emission features were detected by Cohen et al.
(1987) in the optical spectrum of the source, showing
broad permitted Mg II and narrow forbidden lines, which is a
sign of the presence of an ambient medium. This may indicate that
AO 0235+164 fulfills the prerequisite of producing enough soft
photons as seeds for inverse Compton scattering. Madejski et al.
(1996) also pointed out that AO 0235+164 has all the
characteristics of optically violent variable (OVV) quasars
(including the GeV emission), except that it shows weaker
emission lines. They suggested that the SSC interpretation of
-ray flaring stage. AO
0235+164 is a low-peaked BL Lac, located at intermediate
position in the sequence of subclasses of Blazar mentioned above.
Nuclear emission features were detected by Cohen et al.
(1987) in the optical spectrum of the source, showing
broad permitted Mg II and narrow forbidden lines, which is a
sign of the presence of an ambient medium. This may indicate that
AO 0235+164 fulfills the prerequisite of producing enough soft
photons as seeds for inverse Compton scattering. Madejski et al.
(1996) also pointed out that AO 0235+164 has all the
characteristics of optically violent variable (OVV) quasars
(including the GeV emission), except that it shows weaker
emission lines. They suggested that the SSC interpretation of
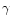 -ray production may be challenged by the fact that the
fast variability in the soft X-ray band is not accompanied by
variability in
-ray production may be challenged by the fact that the
fast variability in the soft X-ray band is not accompanied by
variability in 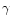 -rays. All these points mentioned above
imply that AO 0235+164 in many physical properties is much closer
to FSRQs rather than HBLs, which in turn indicates that
Comptonization of external radiation may play a quite important
role in
-rays. All these points mentioned above
imply that AO 0235+164 in many physical properties is much closer
to FSRQs rather than HBLs, which in turn indicates that
Comptonization of external radiation may play a quite important
role in 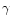 -ray emission in the source. Therefore it is
feasible to interpret the evolution behaviour of synchrotron peak
of AO 0235+164 by a change of Lorentz factor.
-ray emission in the source. Therefore it is
feasible to interpret the evolution behaviour of synchrotron peak
of AO 0235+164 by a change of Lorentz factor.
In the course of linear fitting to the distribution of peak
frequency and peak flux, we also obtained the coefficients of all
polynomials. For the 1975 outburst, we have
![\begin{displaymath}
\log{[\nu F_\nu (\nu_{\rm pk})]}\approx
29.43-1.18\log{\nu_{\rm pk}}.
\end{displaymath}](/articles/aa/full/2001/34/aah2659/img36.gif) |
(5) |
And for the 1987 outburst, the relation can be expressed as
![\begin{displaymath}
\log{[\nu F_\nu (\nu_{\rm pk})]}\approx
26.75-1.00\log{\nu_{\rm pk}}.
\end{displaymath}](/articles/aa/full/2001/34/aah2659/img37.gif) |
(6) |
By comparing Eq. (5) with Eq. (6), we find that the
values of the coefficient of the second term are very close to
each other in the above two equations, essentially within the
range of fitting errors. Therefore from Eqs. (5) and (6) we could have the same expression as Eq. (4),
that is,
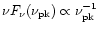 .
This
may in turn be a strong support for the conclusion by
Böttcher (1999), and also indicates that
Comptonization of external photons probably plays an important
role in
.
This
may in turn be a strong support for the conclusion by
Böttcher (1999), and also indicates that
Comptonization of external photons probably plays an important
role in 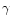 -ray emission in the two outbursts.
-ray emission in the two outbursts.
It is noticeable that an opposite correlation behavior was found
in the BL Lac object Mkn 501 (e.g. Petry et al. 2000) and
Mkn 421 (Fossati et al. 2000), in which peak flux
increases with peak frequency. Both of the two sources belong to
HBLs that peak at X-ray bands. As pointed out by Böttcher
(1999), the broad-line regions of these objects
surrounding the central engine are weak or absent and the
isotropic luminosity of the central accretion disk is generally
weaker than in quasars, implying that the external soft photon
field is much weaker than in FSRQs and hence negligible
compared to the intrinsic synchrotron radiation field; Moreover,
the Compton scattering events near the 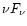 peak of the
peak of the
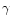 -ray spectrum most probably occur in the extreme
klein-Nishina regime, thus rendering Compton cooling rather
inefficient. However, the fact that the emission lines, although
not very strong, are present and that GeV rather than TeV
-ray spectrum most probably occur in the extreme
klein-Nishina regime, thus rendering Compton cooling rather
inefficient. However, the fact that the emission lines, although
not very strong, are present and that GeV rather than TeV
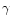 -ray emission is detected in AO 0235+164, at least implies
that an external comptonization interpretation of
-ray emission is detected in AO 0235+164, at least implies
that an external comptonization interpretation of 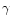 -ray
emission is possible. In Mkn 421 and Mkn 501 the hardening of the
electron spectrum and/or the change of the maximum energy of the
electron injection spectrum could effectively explain
the evolution behaviour of the synchrotron peak of these objects
(Petry et al. 2000; Mastichiadis & Kirk 1997).
-ray
emission is possible. In Mkn 421 and Mkn 501 the hardening of the
electron spectrum and/or the change of the maximum energy of the
electron injection spectrum could effectively explain
the evolution behaviour of the synchrotron peak of these objects
(Petry et al. 2000; Mastichiadis & Kirk 1997).
Another of the most common used interpretations for Mkn 501 is
the change of jet orientation probably due to the orbital motion
of the parent black hole in a binary black hole system (BBHS) and
hence leading to a change of the relativistic beaming factor,
which causes a large shift of the X-ray peak of the SED from
10-20 keV in 1996 to 100-200 keV in 1997 (Villata & Raiteri
1999; Rieger & Mannheim 2000). Phenomena in Mkn
501 such as a discontinuity of the synchrotron spectrum, or
exceptional brightening and hardening of the X-ray spectrum
without a substantial change at lower frequencies have not been
observed in AO 0235+164. In addition small-scale distortions such
as are seen in the VLBI map of Mkn 501 (Giovannini et al.
1998) which is further evidence for BBHS model are also
not observed in high-resolution images of AO 0235+164. This may
merely imply that it is not the change of jet orientation which
is mainly responsible for the spectral variability in AO
0235+164.
A peculiar consequence of the shock model is that the turnover
flux density increases or essentially remain constant while the
turnover frequency decreases in the rising and peaking stage
(Marscher 1985; Valtaoja et al. 1992). This
property can be used to decide if the two outbursts can be caused
by the formation and propagation of shock waves. We used the
method proposed by Landau et al. (1986) to fit a continuous curve
to the spectral flux density distribution with a second degree
polynomial. The final result is shown in Fig. 3, in
which the flux density at the turnover frequency generally
increases with turnover frequency. Since most of the obtained data
lie in the peaking and rising stage (see Fig. 4), It
seems that the shock model doesn't correspond to the scenario of
the two outbursts in AO 0235+164.
In addition, we can see from Fig. 2 that the peaking
frequency and peaking energy in SEDs are variable within a range
of no more than an order of magnitude. This implies that for a low
energy peaked BL Lac object, the peak frequency, although
variable, will not leave this range, and the object will not
appear to be a high energy-peaked BL Lac object.
From Table 2 we can find that for the 1975 outburst, the
peak frequency shows a positive correlation with radio energy at
8 GHz and with optical energy in the B waveband (although not a
very strong one for
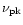 vs.
vs.
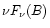 due
to the fact that most epochs lie near to the peaking stage), yet
the peak frequency shows an inverse correlation with peak flux.
For the 1987 outburst, the situation is similar. The difference
lies in this that the peak frequency is well correlated with
optical energy, but essentially not correlated with radio energy.
There is some difficulty in explaining such a scenario
satisfactorily. Since the spectral shape - the spectral index,
changes with time, it is not necessary that flux densities at all
frequencies of synchrotron component are increasing or decreasing
in concert, and one can even have cases in which at certain
frequencies the fluxes decrease while at other frequencies the
fluxes increase. Different sources may show different behavior,
as is seen in objects PKS 0528+134 and 3C 273 (see Figs. 1 and 2 in Böttcher 1999). This will be the subject of
further study.
due
to the fact that most epochs lie near to the peaking stage), yet
the peak frequency shows an inverse correlation with peak flux.
For the 1987 outburst, the situation is similar. The difference
lies in this that the peak frequency is well correlated with
optical energy, but essentially not correlated with radio energy.
There is some difficulty in explaining such a scenario
satisfactorily. Since the spectral shape - the spectral index,
changes with time, it is not necessary that flux densities at all
frequencies of synchrotron component are increasing or decreasing
in concert, and one can even have cases in which at certain
frequencies the fluxes decrease while at other frequencies the
fluxes increase. Different sources may show different behavior,
as is seen in objects PKS 0528+134 and 3C 273 (see Figs. 1 and 2 in Böttcher 1999). This will be the subject of
further study.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{h2659f3.ps}
\end{figure}](/articles/aa/full/2001/34/aah2659/Timg39.gif) |
Figure 3:
The distribution of turnover flux density with turnover
frequency.
Symbols are the same as Fig. 2. |
| Open with DEXTER |
Ghisellini et al. (1998) pointed out that the different
SEDs may reflect different predominant electron cooling
mechanisms. As mentioned above AO 0235+164 is an EGRET source,
and most of its power may be emitted in the 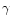 -ray band
through inverse Compton Scattering, especially during the stage
of
-ray band
through inverse Compton Scattering, especially during the stage
of 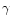 -ray flaring (probably due to the change of Lorentz
factor). At this point the two outbursts seem to be very similar.
However, distinctions are also present. The correlation
difference between peak frequency and flux density at 8 GHz for
the two outbursts implies that there must be something else that
works for one or both of them. Furthermore, since the acquired
turnover frequency distribution for the 1975 outburst is
relatively higher than that for the 1987 outburst (see Fig.
3), we suggest that the emitting region for the 1975
outburst is more compact than that for the 1987 outburst so that
the peak frequency distribution for the 1975 outburst may shift
slightly to a lower frequency and become relatively lower than
that for the 1987 outburst (see the left map of Fig. 2).
In addition, we also find that the 1975 outburst has a larger
amplitude of variation both in optical and in radio bands (see Fig.
4 in our present paper and also Fig. 4 in Chen et al.
1999), which probably means a more violent flaring in
the 1975 outburst.
-ray flaring (probably due to the change of Lorentz
factor). At this point the two outbursts seem to be very similar.
However, distinctions are also present. The correlation
difference between peak frequency and flux density at 8 GHz for
the two outbursts implies that there must be something else that
works for one or both of them. Furthermore, since the acquired
turnover frequency distribution for the 1975 outburst is
relatively higher than that for the 1987 outburst (see Fig.
3), we suggest that the emitting region for the 1975
outburst is more compact than that for the 1987 outburst so that
the peak frequency distribution for the 1975 outburst may shift
slightly to a lower frequency and become relatively lower than
that for the 1987 outburst (see the left map of Fig. 2).
In addition, we also find that the 1975 outburst has a larger
amplitude of variation both in optical and in radio bands (see Fig.
4 in our present paper and also Fig. 4 in Chen et al.
1999), which probably means a more violent flaring in
the 1975 outburst.
The broadband (radio - 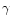 -ray) emission from blazars is
most probably emitted via nonthermal synchrotron radiation and
Comptonization of soft photons by energetic particles in
relativistic jet, and the total emitted power for a single
electron is proportional to the square of its energy, that is,
-ray) emission from blazars is
most probably emitted via nonthermal synchrotron radiation and
Comptonization of soft photons by energetic particles in
relativistic jet, and the total emitted power for a single
electron is proportional to the square of its energy, that is,
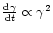 ,
for both radiative
processes. Therefore it is easy to turn high-energy electrons
into low energy electrons, and this will lead to softening of the
particle spectrum. This will facilitate the movement of
synchrotron peaks in SEDs to lower waveband, and hence more
easily result in an inverse correlation between the two physical
quantities. Since photons produced in different parts of the
source have different travel times, the observed spectrum is
produced by the electron distribution at different stages of
evolution. The shape of the light curve in the optical band (see
Fig. 4) and in X-ray band observed in 1993 (see Fig. 1
in Madejski et al. 1996), showing quasi-symmetric
behaviour, suggests that the cooling time of the emitting
electrons is shorter than the light crossing time (Chiaberge &
Ghisellini 1999). This probably implies that the observed
variability is due to superposition of intrinsic and propagation
effects which is consistent with Kraus et al. (1999).
,
for both radiative
processes. Therefore it is easy to turn high-energy electrons
into low energy electrons, and this will lead to softening of the
particle spectrum. This will facilitate the movement of
synchrotron peaks in SEDs to lower waveband, and hence more
easily result in an inverse correlation between the two physical
quantities. Since photons produced in different parts of the
source have different travel times, the observed spectrum is
produced by the electron distribution at different stages of
evolution. The shape of the light curve in the optical band (see
Fig. 4) and in X-ray band observed in 1993 (see Fig. 1
in Madejski et al. 1996), showing quasi-symmetric
behaviour, suggests that the cooling time of the emitting
electrons is shorter than the light crossing time (Chiaberge &
Ghisellini 1999). This probably implies that the observed
variability is due to superposition of intrinsic and propagation
effects which is consistent with Kraus et al. (1999).
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{h2659f4.ps}
\end{figure}](/articles/aa/full/2001/34/aah2659/Timg41.gif) |
Figure 4:
Flux density variation with time for the 1975 outburst
and the 1987 outburst. |
| Open with DEXTER |
In addition, since flux is generally thought to come from
progressively larger regions as frequency falls, a lag is
expected between the optical and the radio variations. For this
reason, we use the method of discrete correlation function (DCF)
(Edelson & Krolik 1989) and find that the radio flux
density variation at 8 GHz and optical variation in the B waveband
are correlated with a delay of 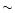 20 days for the 1975
outburst and
20 days for the 1975
outburst and 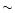 80 days for the 1987 outburst, which can
well explain the correlation results shown in Table 2 viz.
that peak frequency is well correlated with flux density at 8 GHz
for the 1975 outburst but not for the 1987 outburst.
80 days for the 1987 outburst, which can
well explain the correlation results shown in Table 2 viz.
that peak frequency is well correlated with flux density at 8 GHz
for the 1975 outburst but not for the 1987 outburst.
In this paper we collect 33 epochs of multifrequency data sets of
the radio source AO 0235+164, including 18 sets for the 1975
outburst and 10 for the 1987 outburst together with 5 data sets
at other times. A third degree polynomial fitting to all these
data sets is carried out to obtain the peak frequency and energy
in SEDs. By analysing the correlation of peak frequency with peak
flux, we find that:
- 1.
- The peak frequency of AO 0235+164 is variable
with time within a range of an order of magnitude. All the peak
frequencies for the 33 SEDs are within the peak frequency range of LBL,
which is used to define the subclass of BL Lacs (Padovani &
Giommi 1995);
- 2.
- The correlation of peak frequency and peak flux
either for an individual outburst or the combination of several
individual outbursts is significant and is well represented by
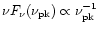 .
This can be interpreted
well by a change of Lorentz factor in objects, in which
Comptonization of external radiation dominates
.
This can be interpreted
well by a change of Lorentz factor in objects, in which
Comptonization of external radiation dominates  -ray emission
(Böttcher 1999). AO 0235+164 in many physical properties
is much closer to FSRQs rather than HBLs, which in turn implies that
Comptonization of external radiation may play important role in
-ray emission
(Böttcher 1999). AO 0235+164 in many physical properties
is much closer to FSRQs rather than HBLs, which in turn implies that
Comptonization of external radiation may play important role in
 -ray emission in the source. Intrinsic variability not
including the shock effect is probably the primary origin of the
two outbursts. Some observational results indicate that the observed
variability is probably due to superposition of intrinsic and
propagation effects which is consistent with the conclusion of
Kraus et al. (1999);
-ray emission in the source. Intrinsic variability not
including the shock effect is probably the primary origin of the
two outbursts. Some observational results indicate that the observed
variability is probably due to superposition of intrinsic and
propagation effects which is consistent with the conclusion of
Kraus et al. (1999);
- 3.
- A comparison between the 1975 outburst and the 1987 outburst
reveals that the two outbursts have a similar flaring time scale,
and the 1975 outburst has a larger amplitude of variation and
relatively higher turnover frequency distribution than that for the
1987 outburst. This may indicate that the 1975 outburst is more violent
and the corresponding emitting region is more compact.
Acknowledgements
We would like to thank the anonymous referee(s) for useful
suggestions and opinions for correction. Also we shall appreciate a
lot
of help in english writing from Dr. J. Katgert and Dr. W. P. Lin.
This
research has made use of data from the University of Michigan Radio
Astronomy
Observatory which is supported by the National Science Foundation and
by funds
the University of Michigan. The work is supported by Chinese NKBRSF
grant G19990754.
-
Argue, A. N., Kenworthy, C. M., & Stewart, P. M. 1973, ApJ, 14, L99
In the text
-
Böttcher, M. 1999, ApJ, 515, L21
In the text
NASA ADS
-
Chiaberge, M., & Ghisellini, G. 1999, MNRAS, 306, 551
In the text
NASA ADS
-
Chen, Y. J., Zhang, F. J., & Sjouwerman, L. O. 1999, ApSS, 266, 495
In the text
-
Chu, H. S., Bååth, L. B., Zhang, F. J., Nicholson, G., &
Rantakyrö, F. T. 1996, A&A, 307, 15
In the text
NASA ADS
-
Cohen, R. D., Smith, H. E., Junkkarinen, V. T., & Burbidge, E. M. 1987,
ApJ, 318, 577
In the text
NASA ADS
-
Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646
In the text
NASA ADS
-
Fossati, G., Celotti, A., Ghisellini, G., & Maraschi, L. 1997, ApJ, 289,
136
In the text
-
Fossati, G., Maraschi, L., Celotti, A., et al. 1999, MNRAS, 299, 433
In the text
NASA ADS
-
Fossati, G., Celotti, A., Chiaberge, M., et al. 2000, ApJ, 541,
166
In the text
NASA ADS
-
Ghisellini, G., Celotti, A., Fossati, G., Maraschi, L., &
Comastri, A. 1998, MNRAS, 301, 451
In the text
NASA ADS
-
Giovannini, G., Cotton, W. D., Feretti, L., Lara, L., & Venturi, T.
1998, in Proc. 32nd COSPAR Scientific Assembly. Adv.
Space Res., in press
In the text
-
Kirk, J. G., Rieger, F. M., & Mastichiadis, A. 1998, A&A, 333, 452
In the text
NASA ADS
-
Kraus, A., Quirrenbach, A., Lobanov, A. P., et al. 1999, A&A,
344, 807
In the text
NASA ADS
-
Ledden, J. E., & Aller, H. D. 1976, Nature, 260, 752
In the text
NASA ADS
-
MacLeod, J. M., Andrew, B. H., & Harvey, G. A. 1976, Nature, 260, 751
In the text
NASA ADS
-
Madejski, G., Takahashi, T., Tashiro, M., et al. 1996, ApJ, 459, 156
In the text
NASA ADS
-
Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114
In the text
NASA ADS
-
Mastichiadis, A., & Kirk, J. G. 1997, A&A, 320, 19
In the text
NASA ADS
-
Mead, A. R. G., Ballard, K. R., Brand, P. W. J. L., et al. 1990, A&AS, 83, 183
In the text
NASA ADS
-
Padovani, P., & Giommi, P. 1995, ApJ, 444, 567
In the text
NASA ADS
-
Petry, D., Böttcher, M., Connaughton, V., et al. 2000,
ApJ, 536, 742
In the text
NASA ADS
-
Rieger, F. M., & Mannheim, K. 2000, A&A, 359, 948
In the text
NASA ADS
-
Rieke, G. H., Grasdalen, G. L., Kinman, T. D., et al. 1976, Nature,
160, 754
In the text
-
Roy, M., Papadakis, I. E., Ramos-Colóm, E., et al. 2000, ApJ, 545, 758
In the text
NASA ADS
-
Sambruna, R. M., Maraschi, L., & Urry, C. M. 1996, ApJ, 463, 444
In the text
NASA ADS
-
Sitko, M., & Sitko, A. 1991, PASP, 103, 160
In the text
NASA ADS
-
Smith, P. X., Balonek, T. J., Elston, R., & Heckert, P. A. 1987, ApJS,
64, 459
In the text
NASA ADS
-
Spinrad, H., & Smith, H. E. 1975, ApJ, 201, 275
In the text
NASA ADS
-
Steppe, H., Salter, C. J., Chini, R., et al. 1988, A&AS, 75, 317
In the text
NASA ADS
-
Steppe, H., Paubert, G., Sievers, A., et al. 1993, A&AS, 102, 611
In the text
NASA ADS
-
Takalo, L. O., Sillanpää, A., Valtaoja, E., et al. 1998, A&AS,
129, 577
In the text
NASA ADS
-
Valtaoja, E., Teräsranta, H., Urpo, S., et al. 1992, A&A, 254
71
In the text
NASA ADS
-
Villata, M., & Raiteri, C. M. 1999, A&A, 347, 30
In the text
NASA ADS
-
Webb, J. R., & Smith, A. G. 1989, A&A, 220, 65
In the text
NASA ADS
Copyright ESO 2001
![\begin{figure}
\par {
\includegraphics[width=8.8cm,clip]{h2659f1a.ps}\hspace*{3mm}
\includegraphics[width=8.8cm,clip]{h2659f1b.ps} }
\end{figure}](/articles/aa/full/2001/34/aah2659/Timg20.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{h2659f2a.ps}\hspace*{4mm}
\includegraphics[width=8.5cm,clip]{h2659f2b.ps} \end{figure}](/articles/aa/full/2001/34/aah2659/Timg23.gif)
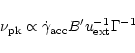
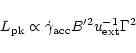
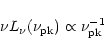
![\begin{displaymath}
\log{[\nu F_\nu (\nu_{\rm pk})]}\approx
29.43-1.18\log{\nu_{\rm pk}}.
\end{displaymath}](/articles/aa/full/2001/34/aah2659/img36.gif)
![\begin{displaymath}
\log{[\nu F_\nu (\nu_{\rm pk})]}\approx
26.75-1.00\log{\nu_{\rm pk}}.
\end{displaymath}](/articles/aa/full/2001/34/aah2659/img37.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{h2659f3.ps}
\end{figure}](/articles/aa/full/2001/34/aah2659/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{h2659f4.ps}
\end{figure}](/articles/aa/full/2001/34/aah2659/Timg41.gif)