A&A 376, 325-332 (2001)
DOI: 10.1051/0004-6361:20010928
M. Rapaport - J.-F. Le Campion - C. Soubiran - G. Daigne - J.-P. Périé - F. Bosq - J. Colin -
J.-M. Desbats -
C. Ducourant - J.-M. Mazurier - G. Montignac - N. Ralite - Y. Réquième - B. Viateau
Observatoire de Bordeaux, CNRS UMR 5804, BP 89, 33270 Floirac, France
Received 28 May 2001 / Accepted 26 June 2001
Abstract
During four years, systematic observations have been conducted in drift scan mode with the
Bordeaux automated meridian circle in the declination band
![]() .
The resulting astrometric catalog
includes about
.
The resulting astrometric catalog
includes about
![]() stars down to the magnitude limit
stars down to the magnitude limit
![]() .
Nearly all stars (96%) have been
observed at least 6 times, the catalog being complete down to
.
Nearly all stars (96%) have been
observed at least 6 times, the catalog being complete down to
![]() .
The median internal standard error
in position is
.
The median internal standard error
in position is
![]() mas in the magnitude range
mas in the magnitude range
![]() ,
which degrades to
,
which degrades to ![]() mas when the faintest stars are considered. M2000 also provides one band
photometry
with a median internal standard error of
mas when the faintest stars are considered. M2000 also provides one band
photometry
with a median internal standard error of
![]() mag. Comparisons with the Hipparcos
and bright part of Tycho-2 catalogs have enabled us to estimate external errors in position to be lower
than 40 mas. In this zone and at epoch 1998, the faint part of Tycho-2 is found to have an accuracy
of 116 mas in
mag. Comparisons with the Hipparcos
and bright part of Tycho-2 catalogs have enabled us to estimate external errors in position to be lower
than 40 mas. In this zone and at epoch 1998, the faint part of Tycho-2 is found to have an accuracy
of 116 mas in
![]() instead of 82 mas deduced from the model-based standard errors given in the catalog.
instead of 82 mas deduced from the model-based standard errors given in the catalog.
Key words: astrometry - catalogs
Accurate proper motions for large samples of stars are of considerable interest for both the
maintenance and extension of optical reference frames and for the understanding of the structure
and evolution of the Galaxy. At present
the largest and most precise all-sky catalogs of proper motions are Hipparcos (ESA 1997), very precise but
concerning only 120000 bright stars, and the recent Tycho-2
(Høg et al. 2000) which is complete down to V=11 with
![]() stars. In 2003, the USNO CCD
Astrograph catalog (UCAC) will be available with an all-sky coverage down to V=16 and a precision similar
to Tycho-2 in positions and proper motions (Zacharias et al. 2000). This will provide a valuable
database
for galactic studies but until then there is a lack of large and complete samples of stars with
accurate proper motions at intermediate magnitude 11-16.
stars. In 2003, the USNO CCD
Astrograph catalog (UCAC) will be available with an all-sky coverage down to V=16 and a precision similar
to Tycho-2 in positions and proper motions (Zacharias et al. 2000). This will provide a valuable
database
for galactic studies but until then there is a lack of large and complete samples of stars with
accurate proper motions at intermediate magnitude 11-16.
The accuracy of proper motions depends on the accuracy of individual positions at different epochs
and the time
baseline which separate them. An invaluable source of old epoch positions is the Carte du Ciel,
an international program conducted at the beginning of the century. It was the first
photographic survey of the entire sky. In this
ambitious program, fields of
![]() were observed twice, to limiting blue magnitudes of
were observed twice, to limiting blue magnitudes of
![]() and
and
![]() respectively. The bright part, the Astrographic Catalog (AC),
was entirely measured and produced a positional catalog of
respectively. The bright part, the Astrographic Catalog (AC),
was entirely measured and produced a positional catalog of
![]() stars, the AC 2000 (Urban et al.
1998), which was combined to the recent Tycho catalog into the ACT catalog (Urban
et al. 1998) and which was also used to produce the Tycho-2 catalog. While the AC positions
have been used to a large extent, it is not the case for the faint survey of the Carte du Ciel, which
has only been used in punctual studies.
stars, the AC 2000 (Urban et al.
1998), which was combined to the recent Tycho catalog into the ACT catalog (Urban
et al. 1998) and which was also used to produce the Tycho-2 catalog. While the AC positions
have been used to a large extent, it is not the case for the faint survey of the Carte du Ciel, which
has only been used in punctual studies.
As one of the participants of the Carte du Ciel,
in charge of the declination band
![]() ,
the Bordeaux Observatory owns
511 Carte du Ciel plates covering this band. It was decided to digitize them in order to salvage
this astronomical treasure before its deterioration and
to conduct at the same time a scientific program. The Bordeaux Observatory is also one of the last
urban observatories where astrometric observations are still possible thanks to its meridian circle
which has been equipped with a CCD camera. Fully automatic and of a great stability,
the Bordeaux meridian
circle has been proved to be very efficient with an internal precision better than 40 mas in
both
coordinates, in the magnitude range
9 < V < 14 (Viateau et al. 1999). The M2000 program aims at
producing a
catalog of positions and proper motions from the cross-identification between today's meridian observations
and the digitized Bordeaux Carte du Ciel plates. The first observations for the
M2000 project began in December 1996 and the programme was completed in December 2000 with a median number of
7 observations per star. Unfortunatly, the digitization of
the Carte du Ciel was delayed due to the lack of an available scanner. The plate processing started in
December 2000
at the APM measuring machine in Cambridge (UK), and should be finished in July 2001. In this first paper,
the meridian catalog of
positions is presented. The Bordeaux meridian
circle, its CCD drift scan camera and image processing
are briefly presented in Sect. 2. Section 3 concerns the global reduction technique in astrometry and
photometry. Section 4
presents some tests performed in order to evaluate the internal and external errors of the catalog.
Section 5 describes the content of the catalog.
,
the Bordeaux Observatory owns
511 Carte du Ciel plates covering this band. It was decided to digitize them in order to salvage
this astronomical treasure before its deterioration and
to conduct at the same time a scientific program. The Bordeaux Observatory is also one of the last
urban observatories where astrometric observations are still possible thanks to its meridian circle
which has been equipped with a CCD camera. Fully automatic and of a great stability,
the Bordeaux meridian
circle has been proved to be very efficient with an internal precision better than 40 mas in
both
coordinates, in the magnitude range
9 < V < 14 (Viateau et al. 1999). The M2000 program aims at
producing a
catalog of positions and proper motions from the cross-identification between today's meridian observations
and the digitized Bordeaux Carte du Ciel plates. The first observations for the
M2000 project began in December 1996 and the programme was completed in December 2000 with a median number of
7 observations per star. Unfortunatly, the digitization of
the Carte du Ciel was delayed due to the lack of an available scanner. The plate processing started in
December 2000
at the APM measuring machine in Cambridge (UK), and should be finished in July 2001. In this first paper,
the meridian catalog of
positions is presented. The Bordeaux meridian
circle, its CCD drift scan camera and image processing
are briefly presented in Sect. 2. Section 3 concerns the global reduction technique in astrometry and
photometry. Section 4
presents some tests performed in order to evaluate the internal and external errors of the catalog.
Section 5 describes the content of the catalog.
The Bordeaux CCD meridian circle has been extensively described in Viateau et al. (1999). Here we briefly recall the main characteristics of the instrument and image processing.
The Bordeaux meridian circle is a refractor with a Texereau objective (202 mm diameter front lens
and 2368 mm focal length). The detector is a front illuminated 1K CCD Thomson 7896M with
![]() m pixels corresponding to
a 28
m pixels corresponding to
a 28![]() field in declination with a scale of 1.65
field in declination with a scale of 1.65
![]() per pixel. Its dark current is lower than the
sky background of the city of Bordeaux. Two combined filters
(GC495 and BG38) give a
visual passband. With the spectral response of the detector cell, the resulting band
per pixel. Its dark current is lower than the
sky background of the city of Bordeaux. Two combined filters
(GC495 and BG38) give a
visual passband. With the spectral response of the detector cell, the resulting band ![]() is displaced
into the red (520-680 nm).
Due to the large bandwith, the effect of chromatic refraction may be significant, as seen by the comparison
with the
Hipparcos catalog (Sect. 4.2). The instrument works in TDI mode with an
integration time of
is displaced
into the red (520-680 nm).
Due to the large bandwith, the effect of chromatic refraction may be significant, as seen by the comparison
with the
Hipparcos catalog (Sect. 4.2). The instrument works in TDI mode with an
integration time of
![]() .
This process enables the reconstruction of numerical images of
28
.
This process enables the reconstruction of numerical images of
28![]() in declination
and several hours in right ascension. Such images are automatically processed on-line to give a list of detected
objects. First, the sky background is estimated using a median filter, and subtracted from the image.
Then objects are defined by at least 2 consecutive pixels above a
in declination
and several hours in right ascension. Such images are automatically processed on-line to give a list of detected
objects. First, the sky background is estimated using a median filter, and subtracted from the image.
Then objects are defined by at least 2 consecutive pixels above a ![]() threshold. The position and flux
of each
detected object are estimated by fitting a two dimensional gaussian flux distribution on the associated
pixels.
In case of multiple objects, positions and flux are measured independently if the separation is larger
than 5
threshold. The position and flux
of each
detected object are estimated by fitting a two dimensional gaussian flux distribution on the associated
pixels.
In case of multiple objects, positions and flux are measured independently if the separation is larger
than 5
![]() .
The dynamical range for the CCD detector is larger than 7 mag. In the declination range of the
M2000 catalog, the detection limit is about
.
The dynamical range for the CCD detector is larger than 7 mag. In the declination range of the
M2000 catalog, the detection limit is about
![]() .
Objects brighter than V = 9.5 are most often
saturated, with a systematic effect in declination as a
consequence. This effect was easily modeled by fitting polynomials on (Hipparcos minus M2000) residuals, and
all saturated stars were systematically corrected in declination.
.
Objects brighter than V = 9.5 are most often
saturated, with a systematic effect in declination as a
consequence. This effect was easily modeled by fitting polynomials on (Hipparcos minus M2000) residuals, and
all saturated stars were systematically corrected in declination.
In order to observe the whole zone of the Bordeaux Carte du Ciel,
![]() ,
39 strips of
,
39 strips of
![]() h were considered, with their centers
in declination separated
by 13
h were considered, with their centers
in declination separated
by 13![]() .
Thanks to this overlap, the 39 strips could be observed 3 times in order to get 6
observations per star plus a thin zone of 2
.
Thanks to this overlap, the 39 strips could be observed 3 times in order to get 6
observations per star plus a thin zone of 2![]() where stars were observed 9 times. The strips had their
length in
right ascension varying from 1h to 12h depending on the other programs and weather conditions. The
observations for the M2000 program started in December 1996 and ended in December 2000, after 3306
hours of observations in a fully automatic mode. The objective to get at least 6 observations per star
for more than 95% of the catalog was successfully achieved. The last year of observation was used to
fill some gaps in the survey where the
faintest stars could not be observed 6 times due to poor weather conditions.
where stars were observed 9 times. The strips had their
length in
right ascension varying from 1h to 12h depending on the other programs and weather conditions. The
observations for the M2000 program started in December 1996 and ended in December 2000, after 3306
hours of observations in a fully automatic mode. The objective to get at least 6 observations per star
for more than 95% of the catalog was successfully achieved. The last year of observation was used to
fill some gaps in the survey where the
faintest stars could not be observed 6 times due to poor weather conditions.
where ![]() is the measured value of x and
is the measured value of x and
![]() its measurement error.
The quantity
its measurement error.
The quantity
![]() stands for
correlated departures in position measurements of neighbouring stars, mainly
attributed to slow variations of the residual angle-of-arrival due to long-period atmospheric fluctuations.
Variations faster than one minute or so are averaged in the TDI mode, their residuals being included
in
stands for
correlated departures in position measurements of neighbouring stars, mainly
attributed to slow variations of the residual angle-of-arrival due to long-period atmospheric fluctuations.
Variations faster than one minute or so are averaged in the TDI mode, their residuals being included
in
![]() .
As explained by Viateau et al. (1999), the deterministic function S has been taken as a B-spline
which attenuates the oscillations caused by these fluctuations.
For a given strip, or part of a strip, it is written in terms of a set of fitted
parameters:
.
As explained by Viateau et al. (1999), the deterministic function S has been taken as a B-spline
which attenuates the oscillations caused by these fluctuations.
For a given strip, or part of a strip, it is written in terms of a set of fitted
parameters:
![]() ).
).
A similar equation can be written in y:
A similar relation can be written between the true coordinate ![]() and
the image ordinate y:
and
the image ordinate y:
The relation between star image coordinates (
![]() )
in a strip
and the true right ascension is deduced from Eqs. (1) and (3):
)
in a strip
and the true right ascension is deduced from Eqs. (1) and (3):
The solution of these equations are obtained with a global method (Eichhorn 1960; Benevides-Soares
& Teixeira 1992) in which the set of equations is considered as a single system
to be solved by a least-square
procedure. The equations in ![]() can be written in form of a matrix:
can be written in form of a matrix:
This system of equations is singular as can be seen in Eq. (5): the unknowns ![]() and a0
appear
through their difference which means that the origin of right ascensions cannot be determined. Consequently,
the system (6) has an infinity of solutions and some constraints must be imposed to get a unique
solution. We shall see that these constraints correspond to the choice of the reference system.
and a0
appear
through their difference which means that the origin of right ascensions cannot be determined. Consequently,
the system (6) has an infinity of solutions and some constraints must be imposed to get a unique
solution. We shall see that these constraints correspond to the choice of the reference system.
The system (6) is solved by the iterative method of Gauss-Seidel (see Rapaport & Le Campion 1990; Le Campion et al. 1992 for more details). Two reasons have motivated this choice: (1) this method is well adapted to the structure of the matrix of equations where only "small systems" have to be solved, (2) mathematical results have proved the convergence of the iterations toward a solution of the equations.
The successive steps of the process can be described as follows. From any reference catalog (Tycho-2 in the
present case) a linear fit will give
a first estimate of the "instrumental constants", and then a first estimate
of coordinates
![]() for all the stars.
for all the stars.
Starting with
![]() ,
the system is solved in
,
the system is solved in
![]() and
and
![]() by least square fit:
by least square fit:
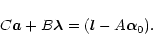 |
(7) |
A single solution is obtained by imposing a constraint:
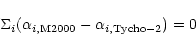 |
(9) |
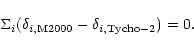 |
(10) |
In what was just described, it must be noted that each star was observed several times at different epochs over four years. Strictly, the proper motions should be introduced in the equations. Except for very high proper motion stars, the 4 years of observations do not enable a correct determination of proper motions. Consequently, we have chosen to temporarily neglect the proper motion displacement over the observing period. The proper motion determination will be possible when data from the scanning of the Carte du Ciel plates will be introduced in the global reduction.
The photometric reduction was performed simultaneously with the astrometric reduction, stellar magnitudes
being entered
as a third unknown parameter after ![]() and
and ![]() .
The flux
.
The flux ![]() of each object is initially converted into a magnitude using the standard formula:
of each object is initially converted into a magnitude using the standard formula:
where V0 is a constant determined by least squares using Tycho-2 ![]() magnitudes. As our
magnitudes. As our ![]() magnitude system is slightly different from the
magnitude system is slightly different from the ![]() system, a color term should be introduced in
Eq. (11). But colors are not available for most stars yet and a more accurate calibration of
magnitudes is not possible. The color effect reaches 0.3 mag for the bluest stars.
In a
second step
the variations of the atmospheric transparency are modeled iteratively by fitting a B-spline on the
residuals of each night:
system, a color term should be introduced in
Eq. (11). But colors are not available for most stars yet and a more accurate calibration of
magnitudes is not possible. The color effect reaches 0.3 mag for the bluest stars.
In a
second step
the variations of the atmospheric transparency are modeled iteratively by fitting a B-spline on the
residuals of each night:
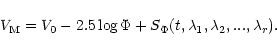 |
(12) |
It was decided to keep in the M2000 catalog all the objects which were observed at least 3 times. The
observing program was stopped when more than 95% of the stars detected in the zone had been observed at least
6 times. Figure 1 shows
the histogram of the number of observations per star. In several fields corresponding to other
observing programmes, stars have been observed up to 31 times. The median number of observations per star is 7.
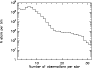 |
Figure 1: Histogram of the number of observations per star. |
| Open with DEXTER | |
After the global reduction, the 3 parameters
![]() could be
recovered for each star at the different epochs of observations, and their standard errors computed.
The median standard error is a good estimate of the internal precision of the catalog. As shown in Fig. 2,
standard errors are larger for stars brigther than V=9.5 due to saturation, and for the faintest
stars of the catalog.
The best results are obtained in right ascension where
standard errors are below 25 mas in the magnitude range
could be
recovered for each star at the different epochs of observations, and their standard errors computed.
The median standard error is a good estimate of the internal precision of the catalog. As shown in Fig. 2,
standard errors are larger for stars brigther than V=9.5 due to saturation, and for the faintest
stars of the catalog.
The best results are obtained in right ascension where
standard errors are below 25 mas in the magnitude range
![]() .
In the same magnitude interval, the
standard errors in declination and magnitude are lower than 30 mas and 0.03 magnitude respectively.
In Fig. 3, the histograms of standard errors in
.
In the same magnitude interval, the
standard errors in declination and magnitude are lower than 30 mas and 0.03 magnitude respectively.
In Fig. 3, the histograms of standard errors in ![]() ,
,
![]() and
and ![]() are presented
for the whole catalog and for stars brighter than 15.
The modes and medians of these 6 histograms are summarized in Table 1.
are presented
for the whole catalog and for stars brighter than 15.
The modes and medians of these 6 histograms are summarized in Table 1.
It is
worth noticing that the standard errors in right ascension and declination are slightly increased by the
fact that no attempt was made to calculate the proper motions in the astrometric reduction. As a matter
of fact,
during 4 years of observations the contribution of the neglected proper motion to the standard error can
reach several mas. The contribution of proper motions in the dispersion of the M2000 measurements is not
easy to estimate as the observations are not uniformly distributed along the time baseline from one strip
to another. The typical time baseline between the first and last observation of a star
is 3 years. The spacing between 2 consecutive observations has 2 typical values: several days
and about 1 year.
If
![]() is the standard deviation of the proper motion distribution of all M2000 stars,
then the maximal contribution of the neglected proper motions is
is the standard deviation of the proper motion distribution of all M2000 stars,
then the maximal contribution of the neglected proper motions is
![]() in the
unfavourable and unprobable case of observations only at the beginning and end of the 4 years baseline. Unfortunatly
in the
unfavourable and unprobable case of observations only at the beginning and end of the 4 years baseline. Unfortunatly
![]() is not known yet. From bright nearby Hipparcos stars,
is not known yet. From bright nearby Hipparcos stars,
![]() was estimated to be 24 masyr-1
for
was estimated to be 24 masyr-1
for
![]() and 16 masyr-1 for
and 16 masyr-1 for
![]() .
To get an idea of the value at fainter magnitudes,
the typical
stellar content of the M2000 catalog has been simulated
with the Besançon model of stellar population synthesis of the Galaxy (Bienaymé et al. 1987;
Robin et al. 1996) in 2 representative fields at
high and low galactic latitudes. This simulation showed that the standard deviation of the proper motion
distribution
reaches 18 masyr-1 at high galactic latitude. We conclude that the contribution of
the neglected proper motions to the standard errors in position is significant, especially for the bright part of
the catalogue (V < 15) where random errors on individual positions have a similar magnitude than
the dispersion due to proper motions. We expect the median standard errors
in equatorial coordinates to improve significantly for bright stars (
.
To get an idea of the value at fainter magnitudes,
the typical
stellar content of the M2000 catalog has been simulated
with the Besançon model of stellar population synthesis of the Galaxy (Bienaymé et al. 1987;
Robin et al. 1996) in 2 representative fields at
high and low galactic latitudes. This simulation showed that the standard deviation of the proper motion
distribution
reaches 18 masyr-1 at high galactic latitude. We conclude that the contribution of
the neglected proper motions to the standard errors in position is significant, especially for the bright part of
the catalogue (V < 15) where random errors on individual positions have a similar magnitude than
the dispersion due to proper motions. We expect the median standard errors
in equatorial coordinates to improve significantly for bright stars (
![]() mas for V < 15)
when the proper motions will be determined from old Carte du Ciel plates.
mas for V < 15)
when the proper motions will be determined from old Carte du Ciel plates.
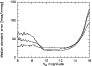 |
Figure 2:
Standard errors in |
| Open with DEXTER | |
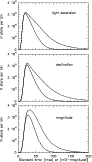 |
Figure 3:
Histogram of standard errors in right ascension, declination and magnitude
for the whole catalog (dotted lines), and for stars with
|
| Open with DEXTER | |
|
|
full catalog | |||
|
|
|
|||
| mode | median | mode | median | |
| 20 | 31 | 20 | 48 | |
| 25 | 34 | 25 | 52 | |
| 28 | 34 | 31 | 47 | |
The first look at the results of the comparison showed that declination measurements were probably
affected with a
significant systematic error. The dispersion of the ![]() differences was 59 mas for the whole sample
and 46 mas for
differences was 59 mas for the whole sample
and 46 mas for
![]() ,
significantly larger than the dispersion in
,
significantly larger than the dispersion in ![]() .
The most
obvious cause is chromatic refraction. As a matter of fact, a correlation was clearly observed
between declination departure and colour index of the stars as seen in Fig. 4.
A linear fit to the data, eliminating outliers, is:
.
The most
obvious cause is chromatic refraction. As a matter of fact, a correlation was clearly observed
between declination departure and colour index of the stars as seen in Fig. 4.
A linear fit to the data, eliminating outliers, is:
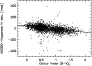 |
Figure 4: Declination departure for Hipparcos stars versus B-V colour. |
| Open with DEXTER | |
| N | |||
| 6372 | -5 | 38 | |
| 6378 | 2 | 46 | |
|
|
2106 | -1 | 37 |
|
|
2108 | 3 | 38 |
In order to estimate exactly the external errors of M2000, the contribution of the errors of Hipparcos
and their propagation from 1991.25
to 1998 were computed. We found the errors of the 6613 Hipparcos stars in the M2000 field
to be on
average 9 mas and 7 mas (medians) respectively in ![]() and
and ![]() at epoch 1998
(12 mas and 10 mas for
at epoch 1998
(12 mas and 10 mas for
![]() ). As the M2000
measurements of bright stars are clearly affected by saturation, from Hipparcos stars with
). As the M2000
measurements of bright stars are clearly affected by saturation, from Hipparcos stars with
![]() ,
the external errors of M2000 are estimated to be 35 mas and 37 mas in
,
the external errors of M2000 are estimated to be 35 mas and 37 mas in ![]() and
and ![]() respectively.
respectively.
Tycho-2 was used as the starting point of the iterative global reduction method.
As explained in Sect. 3.1 the final M2000 catalog is independent, except on the zero point, of the
reference catalog which was used to initialize the reduction. It is then possible
to compare directly M2000 with Tycho-2. M2000 has also been compared with a subsample of Tycho-2 made of
Tycho-1 stars (ESA 1997) because of its higher quality. In order to check the quality of the faint part
of Tycho-2, we have also compared M2000 with a subsample made of Tycho-2 stars not included in Tycho-1.
The limiting magnitude of Tycho-1 is about 11.5,
whereas it reaches 12.5 for Tycho-2.
As for Hipparcos,
an iterative 3![]() rejection was necessary to eliminate from the comparison spurious measurements mainly due
to multiple stars. As B-V colours were available for all these stars, we tried to estimate the chromatic
refraction from Tycho-2 measurements. Due to large random errors, this could not be done in a satisfactory way, but
restrincting the dataset to Tycho-1 stars, the correction was found to be similar, within the error bars, to
Eq. (13) obtained with Hipparcos and it was applied to the declinations. The results are presented
in Table 3, where are also given the Tycho-2 median standard errors (
rejection was necessary to eliminate from the comparison spurious measurements mainly due
to multiple stars. As B-V colours were available for all these stars, we tried to estimate the chromatic
refraction from Tycho-2 measurements. Due to large random errors, this could not be done in a satisfactory way, but
restrincting the dataset to Tycho-1 stars, the correction was found to be similar, within the error bars, to
Eq. (13) obtained with Hipparcos and it was applied to the declinations. The results are presented
in Table 3, where are also given the Tycho-2 median standard errors (
![]() ,
model-based) for
the comparison stars. The standard deviations (
,
model-based) for
the comparison stars. The standard deviations (![]() )
presented in Table 3 result from the convolution of
the external errors of Tycho-2 (
)
presented in Table 3 result from the convolution of
the external errors of Tycho-2 (
![]() )
and M2000 (
)
and M2000 (
![]() ), so we can write:
), so we can write:
| N |
|
|
|||
| 49476 | -1 | 48 | 30 | 33 | |
| 49657 | 4 | 48 | 34 | 31 | |
| 120645 | 0 | 87 | 56 | 80 | |
| 122210 | 2 | 79 | 67 | 70 | |
| 73673 | 1 | 121 | 82 | 116 | |
| 74486 | 0 | 105 | 101 | 98 |
There is no systematic difference between the right ascensions of M2000 and Tycho-2, while there is
an offset of 2 mas in ![]() resulting from the correction of refraction. In Table 3,
resulting from the correction of refraction. In Table 3,
![]() has to be
compared with
has to be
compared with
![]() .
They are in a very good agreement in both coordinates for the sample made of Tycho-1 stars.
The agreement is also satisfactory in
.
They are in a very good agreement in both coordinates for the sample made of Tycho-1 stars.
The agreement is also satisfactory in ![]() for the 2 other samples. But a large difference is observed in
for the 2 other samples. But a large difference is observed in
![]() between the model-based external errors of Tycho-2 and their estimates with M2000.
External errors of M2000 were estimated
in the magnitude range [9-10.5] and in Sect. 4.1 we have shown that M2000
measurements have internal errors lower than 30 mas in the magnitude range [9.5-13.5]. We thus exclude M2000
to be responsible for the resulting high dispersion when compared with Tycho-2.
We conclude that the model-based external errors of Tycho-2 were underestimated in
between the model-based external errors of Tycho-2 and their estimates with M2000.
External errors of M2000 were estimated
in the magnitude range [9-10.5] and in Sect. 4.1 we have shown that M2000
measurements have internal errors lower than 30 mas in the magnitude range [9.5-13.5]. We thus exclude M2000
to be responsible for the resulting high dispersion when compared with Tycho-2.
We conclude that the model-based external errors of Tycho-2 were underestimated in ![]() for the faintest part
of the catalog.
for the faintest part
of the catalog.
The comparison of M2000 with Tycho-1 stars from Tycho-2, has also provided a rough estimate of the external
error in photometry, 0.13 mag, which
is not very significant because the bandpass wave lenght of the 2 instruments are not exactly the same. The dispersion of
the residuals in magnitude reaches 0.20 mag when all Tycho-2 stars are considered, and 0.26 if the faint part
of Tycho-2 is considered.
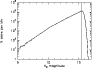 |
Figure 5:
Histogram of the |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{17cm}{!}{\includegraphics[clip]{m2000_fig6.ps}}\end{figure}](/articles/aa/full/2001/34/aa1519/Timg89.gif) |
Figure 6:
The map of density of objects with
|
| Open with DEXTER | |
From comparison with Hipparcos and the bright part of Tycho-2, we have estimated
the external errors to be 35 in ![]() and 37 mas in
and 37 mas in ![]() .
We are aware of a significant
chromatic effect in
.
We are aware of a significant
chromatic effect in ![]() ,
partly due to the atmospheric refraction. External errors reach
50 mas in
,
partly due to the atmospheric refraction. External errors reach
50 mas in ![]() if a correction is not applied. This correction will be possible very soon
for all stars when the
cross-identification with the near-infrared survey 2MASS will be achieved and colours available for
the whole catalog.
if a correction is not applied. This correction will be possible very soon
for all stars when the
cross-identification with the near-infrared survey 2MASS will be achieved and colours available for
the whole catalog.
We have shown that the model based standard errors of the faint part of the Tycho-2-catalog have probably been underestimated.
The measurement of proper motions is now under progress with old Carte du Ciel plates. We expect to obtain
a precison of 2 masyr-1. With colours and accurate proper motions on 2440 square degrees, with
a limit of completness of
![]() ,
M2000
will be a major dataset for galactic structure studies.
,
M2000
will be a major dataset for galactic structure studies.
Acknowledgements
We are very thankful to R. Teixeira and P. Benevides-Soares who are closely associated to the evolution of the Bordeaux meridian circle. We aknowledge with gratitude financial support from the CNRS "Programme National de Physique Stellaire" to maintain the instrument.