A&A 375, 1100-1110 (2001)
DOI: 10.1051/0004-6361:20010854
J. Andries - M. Goossens
Centre for Plasma Astrophysics, K.U. Leuven, Celestijnenlaan 200B, 3001 Heverlee, Belgium
Received 25 April 2001 / Accepted 8 June 2001
Abstract
When a wave is incident on an inhomogeneous boundary layer separating two
plasmas in relative motion, it is often argued that the resonant absorption rate can
become negative when there is a sufficiently large velocity shear, thus giving energy
back to the wave. However such treatment fails to distinguish the two energy exchange
processes that are operative: extraction of wave energy by dissipative processes
around the resonance point and energy exchange between the wave and the flow of the
medium. By aid of the proper wave energy definitions recently discussed by Walker
(2000), rather than by the conventional concept of "negative energy" waves we
reveal the important dependence of the resonant amplification process on the precise
structure of the boundary layer profiles. We conclude that stratification in boundary
layers is very important not only because the resulting wave coupling can cause
resonant instabilities for velocity shears below the Kelvin-Helmholtz threshold, but
also because the coupling can stabilize the Kelvin-Helmholtz instability above this
threshold.
Key words: MHD - instabilities - Sun: oscillations - Sun: magnetic fields
Ryutova (1988) was the first to apply the concept of "negative energy" waves to resonant eigenmodes in stationary flux tubes. She showed that resonant eigenmodes become overstable if they are "negative energy" waves. However according to Hollweg et al. (1990) her work contains an inconsistency.
Hollweg et al. (1990) examined the eigenvalue problem of surface waves on a boundary layer in a plane stratified incompressible plasma (later extended to compressible but cold plasmas by Yang & Hollweg 1991). Assuming that the boundary layer is "thin'' they were able to obtain approximate analytic results. Linear profiles were used and results for different equilibrium parameters were obtained. For certain values of the velocity shear, which are beneath the threshold velocity for Kelvin-Helmholtz instability, overstability of the surface waves occurs.
Tirry et al. (1998) have investigated the same problem in a pressureless plasma. They dropped the assumption of a "thin'' boundary layer and used linear profiles for the Alfvén speed but a discontinuous profile for the streaming velocity. The eigenmodes are damped when coupled to Alfvén waves with parallel longitudinal phase speed, while they are overstable when coupled with Alfvén waves with anti-parallel longitudinal phase speed. The overstabilities, which set in before Kelvin-Helmholtz instability, were explained by the aid of "negative energy'' waves. The amount of energy absorbed by the resonant layer was shown to be negative in the case of overstability, thus giving energy to the wave rather than extracting energy from the wave.
Similar results were obtained analytically in the long wave-length approximation (equivalent to the "thin'' surface approximation) by Ruderman & Wright (1998), who investigated a model of the magnetopause with a discontinuous velocity profile. When the surface waves are "negative energy'' waves they are shown to grow as a result of the dissipation at the resonance point.
Csík et al. (1998) considered the problem of wave-reflection at a smooth boundary. They found that the absorption at resonances in the boundary layer could become negative thus giving energy to the wave which results in overreflection. This resonant overreflection occurred for velocity shears much lower than those needed for overreflection at a discontinuous boundary.
In Andries et al. (2000) we have studied the effect of wave resonances and of the velocity shear on the waves trapped in coronal plumes. We have considered a pressureless plasma with linear profiles for the Alfvén velocity, whereas the flow velocity is discontinuous. Similar results as by Tirry et al. (1998) were obtained. The threshold for resonant overstability becomes lower when the density contrast is increased.
Walker (2000) discussed the reflection and transmission at a discontinuous boundary of two counterstreaming plasmas. The conventional treatment in terms of "negative energy" waves is based on the definition of wave energy and wave energy flux so that wave energy is conserved at the boundary. An overreflected wave then requires a transmitted wave with "negative energy". According to Walker: "such an approach, while producing correct results, obscures the nature and location of the energy interchange". He discusses the proper definitions of energy density and energy flux. The location of the energy exchange is identified as the active boundary and the energy exchange is due to work done by the Reynolds and Maxwell stresses on the gradient of velocity. In this treatment there is no need to invoke "negative energy" waves.
Therefore in Andries & Goossens (2001), where we
have extended the study of Andries et al. (2000) to
![]() ,
we use Walker's approach
and conclude that the resonant layer is always absorbing energy. The gained energy is
due to the velocity gradients. While still using a discontinuous velocity profile we
point out that these considerations make it very likely that the precise velocity
profile might have an important influence on the resonant overstability. In the
discontinuous model used in that paper the threshold for resonant overstability of the
additional slow waves is even smaller than for the fast waves.
,
we use Walker's approach
and conclude that the resonant layer is always absorbing energy. The gained energy is
due to the velocity gradients. While still using a discontinuous velocity profile we
point out that these considerations make it very likely that the precise velocity
profile might have an important influence on the resonant overstability. In the
discontinuous model used in that paper the threshold for resonant overstability of the
additional slow waves is even smaller than for the fast waves.
The aim of this paper is to show that there is indeed an important dependence of the resonant amplification process on the boundary layer profiles. We illustrate this for the driven problem and in the assumption of a "thin" boundary layer since this assumption allows us to distinguish the effects of the profiles itself from other influences.
In Sect. 2 we describe the model and the equations and discuss the solutions, and the associated wave energy flux, in the different regions of the model. The energy exchange process between a global wave (driven oscillation in the asymptotic state) and the background flow is analyzed. Using the approximation of a "thin" boundary layer, we apply these results in Sect. 3 to describe how overreflection is caused. Section 4 describes how to calculate reflection and transmission coefficients. Results are presented which clearly demonstrate the dependence of the resonant amplification process on the boundary layer profiles. Finally these results and their implications are discussed in Sect. 5.
We use a 1-D equilibrium model consisting of two uniform regions separated
by a non-uniform boundary layer (-L<x<0). In the boundary layer the equilibrium
quantities vary continuously from the left to the right value. The equilibrium
magnetic field and the equilibrium flow (V(x)) are oriented in the z-direction. In
the right medium (x>0) the plasma is at rest. Because the medium is uniform in the
y and z directions we can Fourier analyse with respect to these variables.
Furthermore we are interested in the asymptotic state of the driven problem in which
all perturbed quantities vary with the same frequency throughout the whole space. We
thus assume solutions of the form:
![\begin{displaymath}\exp[i(k_y y + k_z z - \omega t)] .\end{displaymath}](/articles/aa/full/2001/33/aah2839/img8.gif)
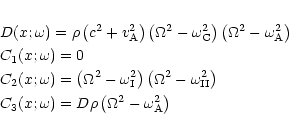
![\begin{eqnarray*}\omega_{\rm I,II} =
\frac{1}{2}\left(k_y^2+k_z^2\right)\left(c^...
...k_y^2+k_z^2)(c^2+v_{\rm A}^2)}\right]^{\frac{1}{2}} \right)\cdot
\end{eqnarray*}](/articles/aa/full/2001/33/aah2839/img14.gif)
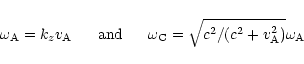
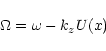
The set of ordinary differential Eqs. (1)-(2) has mobile regular singularities at the positions
![]() and/or
and/or ![]() where D(x) vanishes:
where D(x) vanishes:
By substitution of Eq. (1) into Eq. (2) one second order
differential equation in P' can be derived. In the uniform regions this becomes:
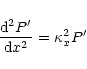
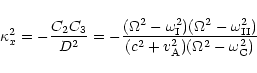
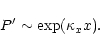
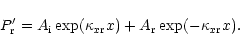
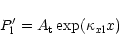
Csík et al. (1998) considered only frequencies with vanishing wave amplitude in the left medium, thus eliminating the possibility of transmission. However there is no difficulty in calculating the reflection coefficients if the wave is partially transmitted. A problem in their paper was the interpretation of this partial transmission. In the absence of transmission they straightforwardly interpreted the part of the energy that is not reflected as the energy absorbed by the resonance. Then if the wave is overreflected the resonance is giving energy to the wave. However this causes problems of interpretation when we have to deal with partially transmitted waves since it is not clear whether the "lost" energy is transmitted or absorbed.
We show that by
using the wave energy flux definitions discussed by Walker (2000) the
solution to these problems is clear and reveals the more detailed structure of the
energy transfer in the boundary layer. We therefore prefer to use Walker's definition
of energy flux to determine the direction of the wave propagation rather than using
the phase velocity and the considerations about its relationship to the group velocity
made by Csík et al. (1998), although in practice the results are equivalent.
The x-component of the wave energy flux (averaged over one cycle) is computed as
(Walker 2000; Adam 1978):
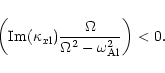
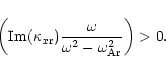
In the boundary layer the set of Eqs. (1), (2) can be integrated numerically. However in the vicinity of a resonance this method fails because of the singularity. This is just a result from the fact that ideal MHD breaks down around the resonance point. Due to the large gradients dissipation becomes important. Sakurai et al. (1991) have included dissipative effects in the resonance layer to remove the singularity and derived connection formulae to connect the solutions to the right and the left of the resonance layer. This can be done because of the very large Reynolds numbers that make sure the resonance layer is very thin (Goossens et al. 1992; Goossens et al. 1995). However these dissipative effects are not essential to the physical result of absorption or amplification of a wave at the resonance. In the ideal initial-value problem the correct connection formulae are obtained by the Landau prescription for going around the pole (Hollweg et al. 1990; Sedlacek 1971). Whether the extracted energy is dissipated into heat or just stored in an infinitely large energy reservoir at the position of the resonance is mathematically unimportant. The important thing is that energy is extracted and thus an energy flux is created.
The jump relations for ![]() and P' at the Alfvén
resonance are (e.g. Goossens et al. 1992):
and P' at the Alfvén
resonance are (e.g. Goossens et al. 1992):
![\begin{eqnarray*}[P']&=& 0 \\ {[} \xi_x ] &=&-i \pi \mbox{sign}(\Omega) \frac{k_y^2
P'}{\rho\vert\Delta\vert}\cdot
\end{eqnarray*}](/articles/aa/full/2001/33/aah2839/img45.gif)
Therefore let us derive in general the
change of energy flux (away from the resonances):
![\begin{eqnarray*}\frac{{\rm d}\left(\frac{F}{\Omega}\right)}{{\rm d}x} =
\frac{{...
...vert P'\vert^2+\frac{C_3}{D}\vert
\xi_x\vert^2\right)\right]= 0.
\end{eqnarray*}](/articles/aa/full/2001/33/aah2839/img52.gif)
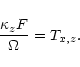
First of all we can apply the findings of the previous section to explain
overreflection for a discontinuous boundary. In that case the effect of the resonances
in the boundary layer is neglected. Since the influence of the resonances is neglected
Tx,z is constant throughout space. If there is no transmission possible
Tx,z=0 in the left region. Thus, the energy flux is zero everywhere, including in
the righthand region where the amplitude of the reflected wave is therefore equal (in
magnitude) to the amplitude of the incoming wave. Nor absorption nor overreflection
occur here. On the other hand suppose there is transmission. In that case the energy
flux in the left medium is negative. The sign of the energy flux in the right medium
is determined by the signs of the right and left hand Dopplershifted frequencies.
Overreflection occurs if and only if:
Notice that the final asymptotic state is reached through the balancing of the stresses. When no transmission is possible the driver is unable to create any resulting stresses in the left region. Thus in the asymptotic state there are no stresses whatsoever. The driving stresses are counteracted by the stresses that are reflected. When transmission is possible, the driver is able to produce stresses that are well defined by the equilibrium parameters in the left region. Although the disturbances are driven in the right medium the asymptotic state is eventually defined by the equilibrium parameters of the left region (and the driving frequency off course).
If resonances are included, the
problem gets more complicated since Tx,z can change at the resonant positions.
Moreover these variations are proportional to
![]() which itself varies.
In order to overcome this last complication we assume that the boundary layer is
"thin". The assumption of a "thin" surface was also made by Hollweg et al.
(1990). They argue that when the surface or boundary layer is "thin" P'remains approximately constant across the boundary layer. In saying so they actually
define what they mean by a "thin" surface. Furthermore under that assumption they also
neglect some contributions to the change of
which itself varies.
In order to overcome this last complication we assume that the boundary layer is
"thin". The assumption of a "thin" surface was also made by Hollweg et al.
(1990). They argue that when the surface or boundary layer is "thin" P'remains approximately constant across the boundary layer. In saying so they actually
define what they mean by a "thin" surface. Furthermore under that assumption they also
neglect some contributions to the change of ![]() across the boundary layer. Indeed,
we call the boundary layer "thin" if it is smaller than the lengthscales on which the
perturbed quantities vary. Under that assumption
across the boundary layer. Indeed,
we call the boundary layer "thin" if it is smaller than the lengthscales on which the
perturbed quantities vary. Under that assumption ![]() and P' are approximately
constant across the boundary layer. However if there is a resonance present the
lengthscales of variation of
and P' are approximately
constant across the boundary layer. However if there is a resonance present the
lengthscales of variation of ![]() and P' become very small near the resonance
point. Thus the variations in these quantities inside the resonance layer can not be
neglected. These variations are given by the jump conditions and correspond exactly to
the term in the variation of
and P' become very small near the resonance
point. Thus the variations in these quantities inside the resonance layer can not be
neglected. These variations are given by the jump conditions and correspond exactly to
the term in the variation of ![]() that is kept by Hollweg et al. (1990).
Outside the resonant layers the variations of the perturbed quantities are
neglected.
that is kept by Hollweg et al. (1990).
Outside the resonant layers the variations of the perturbed quantities are
neglected.
Assume that the conditions are so that transmission is not possible and
that two resonances occur: a forward and a backward Alfvén resonance (therefore
![]() ). The backward resonance occurs further to the left than the forward
resonance. This becomes clear in the next section, where we look at different profiles
and show that no backward resonances can be present without a forward resonance
contrary to what is suggested in Csík et al. (1998), Tirry et al.
(1998), Andries et al. (2000) and Andries & Goossens (2001).
). The backward resonance occurs further to the left than the forward
resonance. This becomes clear in the next section, where we look at different profiles
and show that no backward resonances can be present without a forward resonance
contrary to what is suggested in Csík et al. (1998), Tirry et al.
(1998), Andries et al. (2000) and Andries & Goossens (2001).
Because of the assumption of no
transmission the energy flux in the left medium is zero,
![]() .
In spite of
the velocity gradients the energy flux is also zero at the left side of the backward
resonance region, since Tx,z=0. Then we apply the energy flux jump relation
(7) to obtain the energy flux at the right side of the backward resonance
(subscript b means at the position of the backward resonance, P'0 is the pressure
perturbation which is constant throughout the entire boundary layer):
.
In spite of
the velocity gradients the energy flux is also zero at the left side of the backward
resonance region, since Tx,z=0. Then we apply the energy flux jump relation
(7) to obtain the energy flux at the right side of the backward resonance
(subscript b means at the position of the backward resonance, P'0 is the pressure
perturbation which is constant throughout the entire boundary layer):
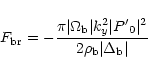
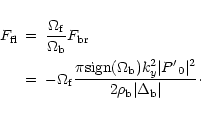
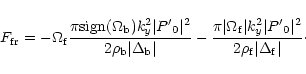
This calculation shows that resonant overreflection only occurs if the contribution of the backward resonance is larger than that of the forward resonance. This depends on several parameters on the resonant positions and thus on the profiles in the boundary layer. We want to emphasize that there is in principle no problem in treating boundary layers that are not "thin". The set of Eqs. (1)-(2) can be integrated numerically in the boundary layer. The reason to confine our interest to "thin" surfaces is that we can focus on the effects of the profiles itself on the two (or more) contributions in (10). If the boundary layer is not thin P'varies through the boundary and affects the relative effect of the two contributions as well. It is then hard to distinguish the effects of the changing amplitude and of the changing equilibrium quantities in the boundary.
We only look at the situation ![]() .
There are several reasons for doing so, while
the treatment of
.
There are several reasons for doing so, while
the treatment of
![]() is not essentially more difficult. First of all the
assumption is made to facilitate the interpretation of the results. When studying fast
incident waves the interesting situations with backward resonances would involve at
least 3 or 4 resonances when
is not essentially more difficult. First of all the
assumption is made to facilitate the interpretation of the results. When studying fast
incident waves the interesting situations with backward resonances would involve at
least 3 or 4 resonances when
![]() .
This would make interpretation very hard
because more terms have to be compared. The results would become even more dependent
on the profiles because there are more parameters defining the profiles (
.
This would make interpretation very hard
because more terms have to be compared. The results would become even more dependent
on the profiles because there are more parameters defining the profiles (![]() determines the relationship between the Alfvén speed profile and the slow speed
profile). Second, there is a problem in analyzing slow waves in the "thin" boundary
approximation. The slow waves behave very an-isotropically and propagate mainly in the
direction of the magnetic field and thus have small perpendicular wavelengths. In the
computation some finite thickness L for the boundary layer has to be used. The
assumption of a thin surface is then satisfied by taking an imposed wavenumber
determines the relationship between the Alfvén speed profile and the slow speed
profile). Second, there is a problem in analyzing slow waves in the "thin" boundary
approximation. The slow waves behave very an-isotropically and propagate mainly in the
direction of the magnetic field and thus have small perpendicular wavelengths. In the
computation some finite thickness L for the boundary layer has to be used. The
assumption of a thin surface is then satisfied by taking an imposed wavenumber
![]() .
.
![]() is of the order of k or smaller except for
slow body waves (
is of the order of k or smaller except for
slow body waves (
![]() )
where it turns out that
)
where it turns out that
![]() becomes very large (infinite) for
becomes very large (infinite) for
![]() .
Thus for all except slow body waves this choice of k assures large perpendicular
wavelengths. In short, putting
.
Thus for all except slow body waves this choice of k assures large perpendicular
wavelengths. In short, putting ![]() facilitates the treatment and it is
sufficient for our purpose: i.e. showing that the profile of the boundary layer has a
strong effect on the modifications made by resonant behaviour to the process of
reflection and transmission.
facilitates the treatment and it is
sufficient for our purpose: i.e. showing that the profile of the boundary layer has a
strong effect on the modifications made by resonant behaviour to the process of
reflection and transmission.
For the computation of the reflection coefficient a
similar treatment as in Sect. 3 is followed. The amplitude reflection and
transmission coefficients are defined as:
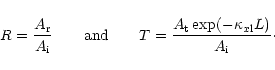
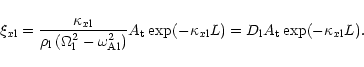
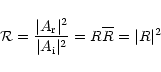
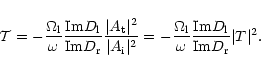
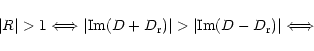
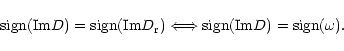
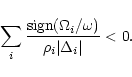
![\begin{figure}
\par\includegraphics[width=7.3cm,height=4.6cm,clip]{h2839f1.ps}\end{figure}](/articles/aa/full/2001/33/aah2839/Timg88.gif) |
Figure 1:
Possible profiles for Alfvén speed
|
| Open with DEXTER | |
In the presentation of the results, velocity is scaled with respect to the right
Alfvén speed. Some different profiles are visualized in Figs. 1 to 7. The horizontal line indicates the z-component of the phase speed
![]() of the imposed incoming wave. The other lines show the profiles of
Dopplershifted Alfvén speed
of the imposed incoming wave. The other lines show the profiles of
Dopplershifted Alfvén speed
![]() (full line) and the Dopplershifted
cut-off speed
(full line) and the Dopplershifted
cut-off speed
![]() (dashed line), which indicates the
distinction between propagating and evanescent waves. Thus resonances are marked by
the intersections between the horizontal line and the full lines. Intersections with
the upper full lines correspond to forward resonances, while intersections with the
lower full line are backward resonances. Since the horizontal line lies above the
upper dashed line in the right medium it first has to intersect the upper full line
before it can intersect the lower full line. Thus backward resonances are impossible
without forward resonances. Also in Csík et al. (1998), Tirry et al.
(1998), Andries et al. (2000) and Andries & Goossens (2001) where backward resonances are
presented without forward resonances, forward resonances occur, but they occur at the
discontinuity and have no effect. This can be seen by rewriting
(dashed line), which indicates the
distinction between propagating and evanescent waves. Thus resonances are marked by
the intersections between the horizontal line and the full lines. Intersections with
the upper full lines correspond to forward resonances, while intersections with the
lower full line are backward resonances. Since the horizontal line lies above the
upper dashed line in the right medium it first has to intersect the upper full line
before it can intersect the lower full line. Thus backward resonances are impossible
without forward resonances. Also in Csík et al. (1998), Tirry et al.
(1998), Andries et al. (2000) and Andries & Goossens (2001) where backward resonances are
presented without forward resonances, forward resonances occur, but they occur at the
discontinuity and have no effect. This can be seen by rewriting
![]() as
follows:
as
follows:
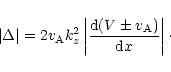
We first present solutions for a model in which the wave is incident from a medium with
higher density and unable to be transmitted through the boundary. The parameters are
set as follows:
![]() ,
L=0.1,
,
L=0.1,
![]() ,
,
![]() and
V=5.5 (Figs. 1, 2) or V=4.6 (Fig. 3). Figure 1
shows a profile in which the velocity and Alfvén speed change linearly over the
entire boundary layer. A forward and a backward resonance occur. The effect of the
backward resonance dominates because the density as well as the derivative of the
Dopplershifted Alfvén profile are smaller at the backward resonance than at the
forward resonance. Thus as indicated, this situation leads to overreflection.
and
V=5.5 (Figs. 1, 2) or V=4.6 (Fig. 3). Figure 1
shows a profile in which the velocity and Alfvén speed change linearly over the
entire boundary layer. A forward and a backward resonance occur. The effect of the
backward resonance dominates because the density as well as the derivative of the
Dopplershifted Alfvén profile are smaller at the backward resonance than at the
forward resonance. Thus as indicated, this situation leads to overreflection.
Now
let us look at the profiles in Fig. 2. They are still piecewise linear
profiles resulting from linear profiles of the Alfvén speed and of the velocity.
However the region where the Alfvén speed varies is located more to the right than
the region where the velocity changes. Moreover the thickness of these regions is
different in the different pictures. Figure 2a shows a profile where the
Alfvén speed changes over a broad distance while the velocity field changes more
abruptly. This situation does not lead to overreflection. The fact that the derivative
of the Alfvén profile is much smaller at the forward resonance seems to overcome the
larger density at the point resulting in the dominance of the forward resonance. In
Fig. 2b the region where the velocity changes is broader, while the Alfvén
speed changes abruptly. This results in a small derivative at the backward resonance,
thereby dominating and causing overreflection. In Fig. 2c an intermediate
region is introduced between the left region where the velocity changes and the right
region where the Alfvén speed changes. Again the smaller derivative makes the
forward resonance dominate. Eventually Fig. 2d shows a situation in which
there is an overlap of the two boundary layers, apparently resulting in
overreflection.
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{h2839f2a.ps}\hspace*{6.7mm...
...c.ps}\hspace*{6.7mm}
\includegraphics[width=5.4cm,clip]{h2839f2d.ps}\end{figure}](/articles/aa/full/2001/33/aah2839/Timg93.gif) |
Figure 2:
Different possible profiles for Alfvén speed
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{h2839f3a.ps}\hspace*{6.7mm...
...c.ps}\hspace*{6.7mm}
\includegraphics[width=5.4cm,clip]{h2839f3d.ps}\end{figure}](/articles/aa/full/2001/33/aah2839/Timg94.gif) |
Figure 3:
Different possible profiles for Alfvén speed
|
| Open with DEXTER | |
We now turn to Fig. 3. In these figures the transition region for the velocity is located on the right and the transition region for the Alfvén speed on the left. This results in a strange behaviour of the backward profile which has a maximum in the boundary layer. If we would have kept all the parameters as in Fig. 2, the third resonance would be absent. In that case the results would be clear (at least for situations a, b, c) and not too exciting: because at both resonances the derivatives are equal and the density is equal, both contributions annihilate each other, thus leading to pure reflection. However we have considered somewhat slower flow speeds to illustrate the situations where the third resonance is present. Since the two first resonances annihilate each other the third resonance, which is a backward one, dominates resulting in overreflection in all cases.
Now let us take a look at Figs. 4 to 6. In these cases the wave is
incident from a medium with lower density. The parameters are
![]() ,
L=0.1,
,
L=0.1,
![]() ,
,
![]() and V=2.4. It is unnecessary to
discuss all of these figures in detail since they are easily interpreted. The
conclusion is that the different profiles of the boundary layer that are shown all
separate the same two homogeneous regions but the calculated reflection coefficients
differ strongly depending on the boundary layer profiles.
and V=2.4. It is unnecessary to
discuss all of these figures in detail since they are easily interpreted. The
conclusion is that the different profiles of the boundary layer that are shown all
separate the same two homogeneous regions but the calculated reflection coefficients
differ strongly depending on the boundary layer profiles.
![\begin{figure}
\par\includegraphics[width=7.05cm,height=4.6cm,clip]{h2839f4.ps}\end{figure}](/articles/aa/full/2001/33/aah2839/Timg96.gif) |
Figure 4:
Possible profiles for Alfvén speed
|
| Open with DEXTER | |
Until now we have restricted our attention to cases in which the resonant
overreflection mechanism is the only overreflection mechanism operative. However we
would also like to know whether the resonant effects can change the KH-type
overreflection significantly or not. The answer is yes, which can be seen immediatelly
from Fig. 7. The situation is essentially the same as in Fig. 2a.
Although, the parameters are slightly different (this is explained below). The
velocity shear is chosen large enough to have wave transmission. If the resonances are
neglected (the boundary is taken to be discontinuous) this results in overreflection
(
![]() ,
,
![]() ). But as can be seen from Fig. 7 the resonances have a strong absorbing effect and overcome the KH-type
overreflection. However it was not easy to find parameters for which the resonant
effects were strong enough to stabilize the non-resonant overreflection. This is
closely related to the assumption of the "thin" boundary. As stated before the
resonant effects vanish in the limit of
). But as can be seen from Fig. 7 the resonances have a strong absorbing effect and overcome the KH-type
overreflection. However it was not easy to find parameters for which the resonant
effects were strong enough to stabilize the non-resonant overreflection. This is
closely related to the assumption of the "thin" boundary. As stated before the
resonant effects vanish in the limit of
![]() .
It is thus not surprising
that in case of a "thin" boundary layer the resonant effects are rather small as can
be seen from the results. In formula (15)
.
It is thus not surprising
that in case of a "thin" boundary layer the resonant effects are rather small as can
be seen from the results. In formula (15) ![]() and
and
![]() depend inversely on k, whereas D0 is roughly proportional to Lthrough the spatial derivative and independent of k. Therefore the resonant effects
will be small as long as
depend inversely on k, whereas D0 is roughly proportional to Lthrough the spatial derivative and independent of k. Therefore the resonant effects
will be small as long as ![]() .
But they can be expected to be much larger when a
"thick" boundary or slowly varying medium is considered. However the overreflecting
and absorbing effects then can not be compared so clearly.
.
But they can be expected to be much larger when a
"thick" boundary or slowly varying medium is considered. However the overreflecting
and absorbing effects then can not be compared so clearly.
In order to obtain
dominant resonant effects we have increased the angle between the wavevector and the
magnetic field to ![]() (
(![]() before). This increases the effect of the
resonances because ky acts as a coupling parameter. The larger ky the stronger
the coupling with local Alfvén waves and thus the stronger the resonant effects.
Analytically this is expressed by the ky/kz factor in D0. The change of the
angle changes the cut-off frequencies as well and thus the z-component of the phase
velocity had to be increased to 2.7 in order to have a propagating wave in the right
medium.
before). This increases the effect of the
resonances because ky acts as a coupling parameter. The larger ky the stronger
the coupling with local Alfvén waves and thus the stronger the resonant effects.
Analytically this is expressed by the ky/kz factor in D0. The change of the
angle changes the cut-off frequencies as well and thus the z-component of the phase
velocity had to be increased to 2.7 in order to have a propagating wave in the right
medium.
Thus from these results we can conclude that stratification in the boundary layers is important, not only because it can introduce overreflection below the KH velocity threshold, but also because it can suppress overreflection above this threshold. Which is the case depends on the precise structure of the boundary layer and may possibly be different for incoming waves with different frequencies.
![\begin{figure}
\par\includegraphics[width=5.3cm,clip]{h2839f5a.ps}\hspace*{7mm}
...
...f5c.ps}\hspace*{7mm}
\includegraphics[width=5.3cm,clip]{h2839f5d.ps}\end{figure}](/articles/aa/full/2001/33/aah2839/Timg103.gif) |
Figure 5:
Different possible profiles for Alfvén speed
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{h2839f6a.ps}\hspace*{7mm}
...
...f6c.ps}\hspace*{7mm}
\includegraphics[width=5.5cm,clip]{h2839f6d.ps}\end{figure}](/articles/aa/full/2001/33/aah2839/Timg104.gif) |
Figure 6:
Different possible profiles for Alfvén speed
|
| Open with DEXTER | |
We have investigated the problem of reflection and transmission at a stratified boundary layer between two homogeneous plasmas. More specifically we addressed the influence of resonant wave coupling in the boundary layer. For sake of simplicity we assumed the boundary layer to be "thin". From the results we can conclude that stratification in the boundary layers can be important, not only because it can introduce overreflection below the KH velocity threshold, but also because it can suppress overreflection above this threshold. Which is the case depends on the precise structure of the boundary layer and may possibly be different for incoming waves with different frequencies. In general waves with large wavelengths are only slightly influenced by the resonant coupling effects in the boundary layer. While waves with small wavelengths are likely to be effected a lot more. More specifically resonant effects are very small if the wavevector of the incoming wave is oriented mainly along the magnetic field. However the resonant effects can become dominant even in the "thin" boundary approximation for oblique waves.
The relevance of this study is mainly due to the relationship between (over)reflection and the (over)stability of waveguide body modes. Waveguide body modes are body waves that are trapped between two boundaries, being reflected each time they reach a boundary. If the conditions are such that in the driven problem overreflection occurs, these waveguide modes grow. Thus in an eigenmode calculation the waveguide modes are overstable. For the stability of surface waves (or surface-type waveguide modes) these calculations are less relevant since they can not be related to a reflection and transmission problem since they are non-propagating. However similar profile dependency can be expected for the surface waves.
Recent studies did already show that the boundary layer and the
occurring resonances may be important (for both surface and body waves) in the sense
that it can lead to overstabilities for velocity shears below the KH threshold
(Ryutova 1988; Hollweg et al. 1990; Tirry et al. 1998;
Ruderman 1998; Andries et al. 2000; Andries & Goossens 2001). However we have shown
that these results can not be straightforwardly generalized. In fact these results are
somewhat weakened by this study because it turns out that overstability was only
obtained because the boundary layer profiles were taken in a way to favour
overstability. However the correspondence between the model profiles and the profiles
that occur in nature is at least uncertain. Thus realistic profiles could possibly
produce very different results.
![\begin{figure}
\par\includegraphics[width=7.4cm,height=4.7cm,clip]{h2839f7.ps}\end{figure}](/articles/aa/full/2001/33/aah2839/Timg105.gif) |
Figure 7:
Possible profiles for Alfvén speed
|
| Open with DEXTER | |
On the other hand this study shows that resonant coupling in the boundary layer is not only important because of the related destabilization mechanism but also because of its possibly stabilizing effect on the KH-istability. To avoid confusion, we repeat that we are talking about KH-instability of trapped waves and not about the classical surface wave KH-instability. However if similar effects are present for the surface waves, wave resonance could possibly provide an explanation for the stabilization of KH-instability by the spreading of the boundary layer. If a boundary is KH-unstable the excited perturbations smear out the boundary layer, eventually reaching a state in which the boundary layer is stable with respect to KH-instability. A thicker boundary layer creates larger derivatives of the above mentioned profiles and thus enhanced influence of the resonant effects which could possibly be damping effects, thereby stabilizing the configuration.
We conclude that effects due to resonant coupling in a stratified boundary layer can not be neglected and can drastically influence the stability of the boundary layer in either way.
Acknowledgements
The authors are grateful to A. D. M. Walker for removing their "negative energy" wave blindfolds. J. A. would like to thank the University of Natal and the Flemish government (BIL97/49) for enabling his visit to the University of Natal, Durban.