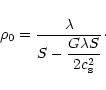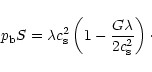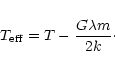A&A 375, 1091-1099 (2001)
DOI: 10.1051/0004-6361:20010857
Boyle's law and gravitational instability
M. Lombardi1 - G. Bertin2
1 - Institüt für Astrophysik und Extraterrestrische Forschung,
Universität Bonn, Auf dem Hügel 71,
53121 Bonn, Germany
2 -
Università degli Studi di Milano, Dipartimento di Fisica, via
Celoria 16, 20133 Milano, Italy
Received 20 April 2001 / Accepted 8 June 2001
Abstract
We have re-examined the classical problem of the macroscopic
equation of state for a hydrostatic isothermal self-gravitating gas
cloud bounded by an external medium at constant pressure. We have
obtained analytical conditions for its equilibrium and stability
without imposing any specific shape and symmetry to the cloud
density distribution. The equilibrium condition can be stated in
the form of an upper limit to the cloud mass; this is found to be
inversely proportional to the power 3/2 of a form factor 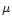 characterizing the shape of the cloud. In this respect, the
spherical solution, associated with the maximum value of the form
factor,
characterizing the shape of the cloud. In this respect, the
spherical solution, associated with the maximum value of the form
factor, 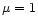 ,
turns out to correspond to the shape that is most
difficult to realize. Surprisingly, the condition that defines the
onset of the Bonnor instability (or gravothermal catastrophe) can be
cast in the form of an upper limit to the density contrast within
the cloud that is independent of the cloud shape. We have then
carried out a similar analysis in the two-dimensional case of
infinite cylinders, without assuming axisymmetry. The results
obtained in this paper generalize well-known results available for
spherical or axisymmetric cylindrical isothermal clouds that have
had wide astrophysical applications, especially in the study of the
interstellar medium.
,
turns out to correspond to the shape that is most
difficult to realize. Surprisingly, the condition that defines the
onset of the Bonnor instability (or gravothermal catastrophe) can be
cast in the form of an upper limit to the density contrast within
the cloud that is independent of the cloud shape. We have then
carried out a similar analysis in the two-dimensional case of
infinite cylinders, without assuming axisymmetry. The results
obtained in this paper generalize well-known results available for
spherical or axisymmetric cylindrical isothermal clouds that have
had wide astrophysical applications, especially in the study of the
interstellar medium.
Key words: equation of state - gravitation -
instabilities - methods: analytical - ISM: clouds
Consider a static isothermal gas cloud embedded in a medium
characterized by an external pressure 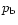 .
Under
equilibrium conditions, it is expected to satisfy the virial
theorem:
.
Under
equilibrium conditions, it is expected to satisfy the virial
theorem:
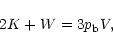 |
(1) |
where K is the total internal kinetic energy associated with the
thermal motions of the gas molecules and W is the total
gravitational energy. From the relation
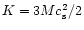 ,
we see that
,
we see that
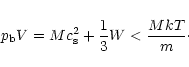 |
(2) |
Here 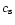 is the thermal speed inside the cloud, given by
is the thermal speed inside the cloud, given by
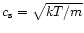 ,
where k is the Boltzmann constant,
T the cloud temperature, and m the mean mass of the gas particles.
Hence, the presence of gravity softens the standard equation of state
,
where k is the Boltzmann constant,
T the cloud temperature, and m the mean mass of the gas particles.
Hence, the presence of gravity softens the standard equation of state
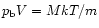 for a gas cloud of volume V (Boyle's
law) into one characterized by an effective temperature
for a gas cloud of volume V (Boyle's
law) into one characterized by an effective temperature
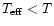 .
Clearly,
.
Clearly,
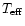 depends on the size,
the shape, and the temperature of the cloud. In particular, for given
values of all other parameters, we could imagine density distributions
for which W is a large negative quantity, so that
depends on the size,
the shape, and the temperature of the cloud. In particular, for given
values of all other parameters, we could imagine density distributions
for which W is a large negative quantity, so that
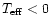 ;
these distributions would not be compatible with the assumed
equilibrium conditions. On the other hand, even when
;
these distributions would not be compatible with the assumed
equilibrium conditions. On the other hand, even when
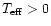 ,
the equilibrium configuration might not be viable because it
could be unstable.
,
the equilibrium configuration might not be viable because it
could be unstable.
Within spherical symmetry, this line of thought has led to the
remarkable discovery (Bonnor 1956; see also Ebert 1955) that a
thermodynamic type of instability takes place when the density
contrast (between the center and the periphery of the cloud) exceeds a
certain threshold value. This relatively simple conclusion has opened
the way to a variety of interesting "applications", best exemplified
by the interpretation of the structure of weakly collisional stellar
systems (globular clusters) in terms of the onset of the so-called
gravitational catastrophe (see Lynden-Bell & Wood 1968 and
following papers; in particular, see Spitzer 1987). The underlying
reason for the instability can be traced to a basic property of
self-gravity, of being associated with a negative specific heat. It
would be conceptually interesting to study whether and how the general
conclusions change for different cloud shapes.
A study of such well-posed mathematical problem appears to be timely.
Indeed, there has been enormous progress in the study of the cloudy
structure of the interstellar medium (e.g., Falgarone et al. 1992;
Falgarone et al. 1998; Lada et al. 1994; Alves et al. 1998).
Curiously, some of the properties that are often considered as
analytically useful in idealized theoretical models have been shown to
be, at least in some cases, also realistic. In particular, while the
possibility of non-trivial shapes for gas clouds is clearly suggested
by observations of the cold interstellar medium (see, e.g., Loren
1989a; Lada et al. 1991), in some cases these observations
quantitatively support a simple interpretation in terms of pure
hydrostatic equilibrium (see, e.g., Alves et al. 2001). Similarly,
it has long been recognized that cold clouds generally conform to the
virial equilibrium conditions (e.g., see Myers 1983; Loren 1989b;
Jijina et al. 1999). Furthermore, although magnetic fields and
rotation are generally accepted to play a significant role in the
dynamics of gas clouds (see Goodman et al. 1995), there is evidence
that cloud shapes are decoupled from the presence of magnetic fields
(compare the case of the Taurus cloud, Heyer et al. 1987; with that
of the 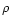 Ophiuchi cloud, Goodman et al. 1990) and that rotation
can often be insignificant (e.g., Walker et al. 1993); moreover,
statistical arguments applied to the distribution of measured axial
ratios for cloud cores suggest that those structures are intrinsically
prolate (David & Verschueren 1987; Myers et al. 1991).
Ophiuchi cloud, Goodman et al. 1990) and that rotation
can often be insignificant (e.g., Walker et al. 1993); moreover,
statistical arguments applied to the distribution of measured axial
ratios for cloud cores suggest that those structures are intrinsically
prolate (David & Verschueren 1987; Myers et al. 1991).
Therefore, we find it natural to address the issue of the stability of
an isothermal cloud in hydrostatic equilibrium, bounded by an external
medium characterized by a specified constant pressure 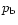 ,
in its most general case, that is beyond the well-known framework of
spherical symmetry. Since we do not consider the role of magnetic
fields and, especially, non-thermal motions, we limit our discussion
to the scale of cloud cores, typically a few tenths of a parsec.
Still, a study on such scales is very important if we wish to
understand the process of star formation. In contrast with previous
analytical investigations, we then let the shape and density
distribution of the cloud deviate significantly from the
spherical shape. The origin of these shapes should be traced to the
presence of external forces (tidal fields and/or other boundary
forces). Here we will not be concerned about how a specific shape can
be realized, appealing to the empirical fact that observations
demonstrate that cloud cores find the way to settle in a variety of
shapes. Note that filamentary structures are very common (e.g., Loren
1989a; Bally et al. 1987), and often each filament contains several
distinct subcondensations, sometimes periodically spaced (Dutrey et al. 1991).
,
in its most general case, that is beyond the well-known framework of
spherical symmetry. Since we do not consider the role of magnetic
fields and, especially, non-thermal motions, we limit our discussion
to the scale of cloud cores, typically a few tenths of a parsec.
Still, a study on such scales is very important if we wish to
understand the process of star formation. In contrast with previous
analytical investigations, we then let the shape and density
distribution of the cloud deviate significantly from the
spherical shape. The origin of these shapes should be traced to the
presence of external forces (tidal fields and/or other boundary
forces). Here we will not be concerned about how a specific shape can
be realized, appealing to the empirical fact that observations
demonstrate that cloud cores find the way to settle in a variety of
shapes. Note that filamentary structures are very common (e.g., Loren
1989a; Bally et al. 1987), and often each filament contains several
distinct subcondensations, sometimes periodically spaced (Dutrey et al. 1991).
By generalizing the study by Bonnor (1956), in this paper we obtain an
expression for the compressibility
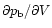 at constant temperature and fixed shape and thus reconstruct the
isothermal curves in the
at constant temperature and fixed shape and thus reconstruct the
isothermal curves in the
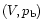 plane. These are
parameterized by a dimensionless form factor
plane. These are
parameterized by a dimensionless form factor 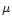 ,
a
quantity that depends only on the shape of the cloud, but otherwise
follow the qualitative behavior characteristic of the self-gravitating
isothermal sphere; in particular, no equilibrium is available above a
certain value of the boundary pressure. Our analysis quantifies how
such equilibrium condition depends on
,
a
quantity that depends only on the shape of the cloud, but otherwise
follow the qualitative behavior characteristic of the self-gravitating
isothermal sphere; in particular, no equilibrium is available above a
certain value of the boundary pressure. Our analysis quantifies how
such equilibrium condition depends on 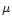 and shows that the sphere,
being associated with the maximum value for the form factor (
and shows that the sphere,
being associated with the maximum value for the form factor (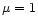 ), corresponds to the shape for which equilibrium is most difficult
to realize. We then proceed to address the condition for the Bonnor
instability and show that it can be cast in a form that is actually
independent of the cloud shape.
), corresponds to the shape for which equilibrium is most difficult
to realize. We then proceed to address the condition for the Bonnor
instability and show that it can be cast in a form that is actually
independent of the cloud shape.
The paper is organized as follows. The relevant basic relations are
introduced in Sect. 2. In
Sect. 3 we derive the equivalent of Boyle's law for
self-gravitating clouds. The implications of the results obtained for
the equilibrium and stability of the cloud are clarified in
Sect. 4 and are summarized in two simple
conditions (Eqs. 34 and 35). In
Sect. 5 we present analogous results for
(infinite) cylinders. Finally, in Sect. 6, we
briefly summarize the main results obtained in this paper.
2 Basic relations
We summarize here the basic relations that will be used through this
paper.
Let us call
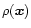 the mass density distribution and
the mass density distribution and 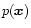 the (scalar) pressure of a cloud at point
the (scalar) pressure of a cloud at point 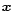 .
If the cloud
is in hydrostatic equilibrium, then
.
If the cloud
is in hydrostatic equilibrium, then
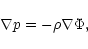 |
(3) |
where
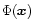 is the Newtonian gravitational potential,
described, inside the cloud, by the Poisson equation
is the Newtonian gravitational potential,
described, inside the cloud, by the Poisson equation
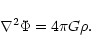 |
(4) |
Furthermore, if the cloud is isothermal we can write
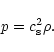 |
(5) |
Taking
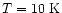 and a cloud made of molecular hydrogen, we
find a typical value of
and a cloud made of molecular hydrogen, we
find a typical value of
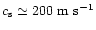 .
.
Equations (3)-(5) combined together lead to
Emden's equation (Emden 1907):
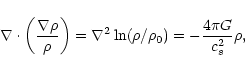 |
(6) |
where 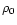 is a characteristic density (e.g., the maximum density
of the cloud). A useful property of Eq. 6 that is the
basis of the following analysis is the homology theorem
(Chandrasekhar 1967): if
is a characteristic density (e.g., the maximum density
of the cloud). A useful property of Eq. 6 that is the
basis of the following analysis is the homology theorem
(Chandrasekhar 1967): if
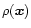 is a solution of this
equation, then
is a solution of this
equation, then
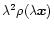 is also a solution.
In fact, we can write Eq. 6 in dimensionless form by
introducing the variables
is also a solution.
In fact, we can write Eq. 6 in dimensionless form by
introducing the variables
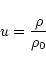 |
(7) |
and
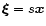 ,
where s-1 is a suitable "Jeans
length'' (cf. Jeans 1929)
,
where s-1 is a suitable "Jeans
length'' (cf. Jeans 1929)
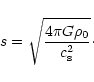 |
(8) |
Hence u is solution of the equation
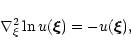 |
(9) |
where
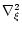 is the Laplacian with respect to the variable
is the Laplacian with respect to the variable
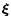 .
In the following we will reserve the subscript b for
quantities measured at the boundary of the cloud.
.
In the following we will reserve the subscript b for
quantities measured at the boundary of the cloud.
3 Boyle's law
In this section we will derive Boyle's law for a self-gravitating
cloud of arbitrary shape subject to a uniform external pressure
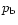 .
In particular, we will obtain an expression for the
derivative
.
In particular, we will obtain an expression for the
derivative
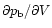 at constant
temperature and fixed shape, for a cloud of given mass. A similar
calculation had been performed by Bonnor (1956; see also Ebert 1955)
in the case of a spherical cloud. Here we imagine that the cloud is
embedded in an external medium in an arbitrary dynamical state. Our
main assumption is that such an arbitrary state enforces a non-trivial
geometry for the cloud, while the cloud has had time to settle into a
hydrostatic equilibrium and is thus described by Eq. 9.
The possibility of such non-trivial shapes is clearly suggested by
observations of the cold interstellar medium (see, e.g., Loren 1989a;
Lada et al. 1991), which in some cases also support the hydrostatic
hypothesis (see, e.g., Alves et al. 2001).
Calculations will be carried out using the following scheme: we will
first calculate the change of the cloud volume corresponding to a
change of the density parameter
at constant
temperature and fixed shape, for a cloud of given mass. A similar
calculation had been performed by Bonnor (1956; see also Ebert 1955)
in the case of a spherical cloud. Here we imagine that the cloud is
embedded in an external medium in an arbitrary dynamical state. Our
main assumption is that such an arbitrary state enforces a non-trivial
geometry for the cloud, while the cloud has had time to settle into a
hydrostatic equilibrium and is thus described by Eq. 9.
The possibility of such non-trivial shapes is clearly suggested by
observations of the cold interstellar medium (see, e.g., Loren 1989a;
Lada et al. 1991), which in some cases also support the hydrostatic
hypothesis (see, e.g., Alves et al. 2001).
Calculations will be carried out using the following scheme: we will
first calculate the change of the cloud volume corresponding to a
change of the density parameter 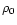 ;
then we will relate the
variation of the density parameter
;
then we will relate the
variation of the density parameter 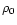 to the variation of the
pressure
to the variation of the
pressure 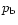 at the boundary of the cloud. The shape of
the cloud is taken to remain unchanged.
at the boundary of the cloud. The shape of
the cloud is taken to remain unchanged.
Since the cloud is in equilibrium with an external pressure
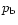 ,
the boundary of the cloud is defined by an iso-density
surface characterized by
,
the boundary of the cloud is defined by an iso-density
surface characterized by
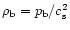 .
When the external pressure changes, the cloud
boundary remains an iso-density surface. In other words, the
transformations considered involve only a change of
.
When the external pressure changes, the cloud
boundary remains an iso-density surface. In other words, the
transformations considered involve only a change of 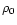 (and thus
of s) in
(and thus
of s) in
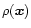 ,
while
,
while
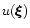 remains unchanged.
Finally, we note that, since the boundary is an iso-density surface,
remains unchanged.
Finally, we note that, since the boundary is an iso-density surface,
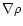 and
and
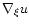 are normal to the cloud boundary.
are normal to the cloud boundary.
3.1 Perturbations at constant mass
Suppose that the density parameter 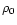 changes by a quantity
changes by a quantity
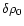 .
Then the cloud density distribution will change by
.
Then the cloud density distribution will change by
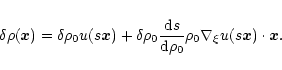 |
(10) |
As a result, the mass inside a given volume V will
change by
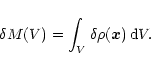 |
(11) |
From Eq. 10 we obtain
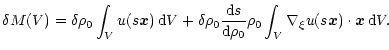 |
|
|
(12) |
The first term on the r.h.s. of the previous equation is simply
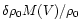 .
For the second term, we can apply the
general relation
.
For the second term, we can apply the
general relation
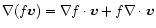 .
Thus we obtain
.
Thus we obtain
where we have used the Gauss theorem (
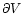 is the boundary of
V,
is the boundary of
V, 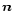 is the unit vector associated with the oriented surface
element). Since
is the unit vector associated with the oriented surface
element). Since 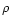 is constant on
is constant on
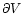 ,
we find
,
we find
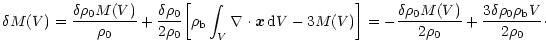 |
|
|
(14) |
Therefore, for perturbations at constant cloud mass a variation
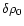 of the "central'' density must be compensated for by a
suitable change of volume
of the "central'' density must be compensated for by a
suitable change of volume 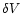 .
Since the change of mass due to
a change of volume
.
Since the change of mass due to
a change of volume 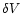 is
is
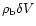 ,
we must
have
,
we must
have
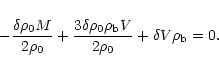 |
(15) |
This equation controls the change of central density
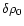 when the volume of the cloud changes.
when the volume of the cloud changes.
3.2 Total mass in virial equilibrium
For the following calculations it is useful to obtain a simple
alternative expression for the total mass applicable to a
self-gravitating isothermal cloud in hydrostatic equilibrium. For the
purpose, we will use Eq. 6 in the integral of the mass:
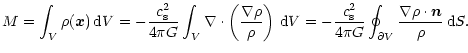 |
|
|
(16) |
This expression can be simplified by noting that 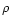 is constant on
is constant on
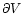 and
and
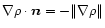 ,
because the boundary is defined as an iso-density surface. [Here
,
because the boundary is defined as an iso-density surface. [Here
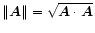 denotes the norm of the vector
denotes the norm of the vector
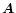 .] Hence, we find
.] Hence, we find
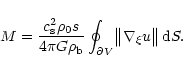 |
(17) |
The use of this relation is equivalent to the use of the equation for
virial equilibrium.
3.3 Compressibility
We now evaluate the change of the external pressure of a cloud as the
cloud volume changes, i.e. the derivative
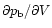 at constant temperature, constant mass, and fixed shape.
at constant temperature, constant mass, and fixed shape.
If we allow for changes of size, at the boundary Eq. 10
becomes
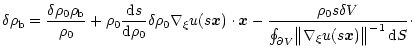 |
|
|
(18) |
The last term on the right-hand-side of this equation can be explained
as follows. Since the cloud can change its size, we expect a related
variation of the external density
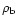 .
Such change can
be written as
.
Such change can
be written as
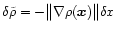 for each point
for each point 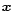 ,
where
,
where 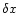 is the
"stretch'' of the boundary at
is the
"stretch'' of the boundary at 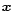 (we recall that this stretch
is always parallel to
(we recall that this stretch
is always parallel to
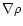 ). We also note that
). We also note that
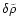 is the same for all points on the boundary of the cloud,
because by definition this quantity can be identified with
is the same for all points on the boundary of the cloud,
because by definition this quantity can be identified with
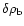 in the case where
in the case where
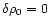 .
Thus the
volume changes by
.
Thus the
volume changes by
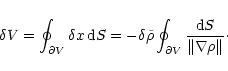 |
(19) |
Inverting this equation, we obtain that the change of density due to a
modification of the size of the cloud is given by
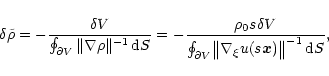 |
(20) |
which is the last term of Eq. 18.
The second term on the r.h.s. of Eq. 18 is constant for
any point 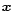 on the boundary
on the boundary
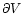 because all the other
terms in the equation are so. Thus we can average this constant term
on the boundary using a convenient weighted mean:
because all the other
terms in the equation are so. Thus we can average this constant term
on the boundary using a convenient weighted mean:
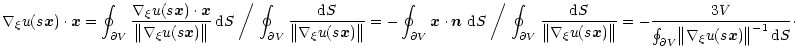 |
|
|
(21) |
With this device the second term is reduced to a form that is similar
to that of the last term of Eq. 18.
3.4 Generalized Boyle's law
Let us briefly summarize the main results obtained so far. We
wish to obtain an expression for
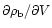 at constant temperature and mass or, equivalently, an expression
for
at constant temperature and mass or, equivalently, an expression
for
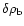 as a function of
as a function of 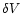 .
Equation 18 is close to our need, but, unfortunately,
it contains the auxiliary quantity
.
Equation 18 is close to our need, but, unfortunately,
it contains the auxiliary quantity
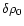 .
On the other hand, we
can use Eq. 15 to express
.
On the other hand, we
can use Eq. 15 to express
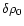 in terms of
in terms of
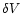 and thus eliminate
and thus eliminate
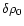 from Eq. 18.
Following this procedure, we obtain the desired
from Eq. 18.
Following this procedure, we obtain the desired
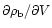 ,
but the resulting expression contains
integrals that are, at first sight, difficult to interpret.
,
but the resulting expression contains
integrals that are, at first sight, difficult to interpret.
We now note that, with the help of Eq. 17, a key term
involving an integration of
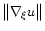 (see
Eqs. 18 and 21) can actually be recognized to be
proportional to
GM/V4/3:
(see
Eqs. 18 and 21) can actually be recognized to be
proportional to
GM/V4/3:
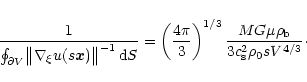 |
(22) |
This expression is reminiscent of what enters in the discussion of the
spherical cloud by Bonnor (1956). For the purpose, we have introduced
the dimensionless form factor as follows:
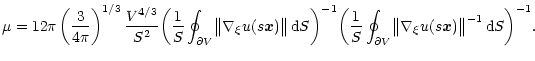 |
|
|
(23) |
In this way, we have isolated the contribution from integrals of
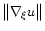 .
We postpone a description of the form
factor to the next subsection, where the reason for the numerical
factors adopted in its definition will become apparent.
.
We postpone a description of the form
factor to the next subsection, where the reason for the numerical
factors adopted in its definition will become apparent.
Using relation 22 in Eq. 21 and combining it
with Eqs. 18 and 15 we find
![\begin{displaymath}
\delta \rho_{\rm b} = -\frac{2 \rho_{\rm b}^2 \delta V}{3
...
...G \mu M^2}{6 c_{\rm s}^2 \rho_{\rm b}
V^{4/3}} \right] \cdot
\end{displaymath}](/articles/aa/full/2001/33/aah2829/img78.gif) |
(24) |
Finally, using Eq. 5 we obtain the desired result:
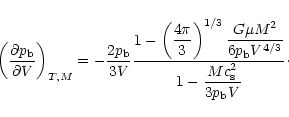 |
(25) |
This expression generalizes Eq. (2.16) in the article by Bonnor
(1956). Before discussing the physical interpretation of the equation
just found and its consequences, the form factor 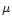 deserves a
special digression.
deserves a
special digression.
3.5 Form factor
The form factor, which plays a key role in the equilibrium and
stability of the cloud, is defined in terms of integrals of
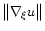 and
and
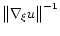 on the
boundary
on the
boundary
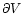 .
Actually, the complex definition 23
has a simple interpretation in terms of general properties of
.
Actually, the complex definition 23
has a simple interpretation in terms of general properties of 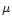 .
.
3.5.1 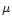 is dimensionless
is dimensionless
As already noted, 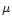 is a dimensionless quantity, which is a choice
that allows us to preserve the scaling of the terms as found in
Bonnor's (1956) derivation. In this respect, note that the term
V4/3 compensates for the two surface integrals in
Eq. 23. As shown below, the introduction of a
dimensionless quantity allows us to characterize and summarize the
properties associated only with the shape of the cloud.
is a dimensionless quantity, which is a choice
that allows us to preserve the scaling of the terms as found in
Bonnor's (1956) derivation. In this respect, note that the term
V4/3 compensates for the two surface integrals in
Eq. 23. As shown below, the introduction of a
dimensionless quantity allows us to characterize and summarize the
properties associated only with the shape of the cloud.
3.5.2 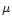 is scale invariant
is scale invariant
It is easily verified that the form factor 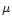 is scale invariant,
i.e. it does not change under the transformation
is scale invariant,
i.e. it does not change under the transformation
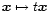 ,
with t > 0. In other words, the form factor depends on the
shape of the cloud but does not depend on its
size. Actually, the scale invariance is directly related to
the fact that
,
with t > 0. In other words, the form factor depends on the
shape of the cloud but does not depend on its
size. Actually, the scale invariance is directly related to
the fact that 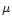 is dimensionless and to the vectorial notation
used in its definition.
is dimensionless and to the vectorial notation
used in its definition.
3.5.3 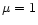 for a sphere
for a sphere
In the case of a sphere, the form factor reduces to unity. In fact,
in this case by symmetry
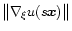 is
constant on the surface of the sphere, so that
is
constant on the surface of the sphere, so that
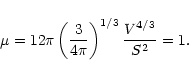 |
(26) |
Here S is the area of the surface of the sphere. Thus, from
Eq. 25, we recover Bonnor's (1956) result for the sphere.
Note that the numerical factors in the definition of
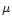 have been chosen precisely to recover
have been chosen precisely to recover 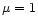 for the sphere.
for the sphere.
3.5.4 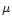 never exceeds unity
never exceeds unity
The form factor can be thought of as the product of two terms,
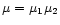 ,
with (cf. Eq. 26)
,
with (cf. Eq. 26)
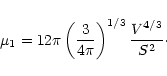 |
(27) |
The first term, 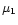 ,
compares the volume V of the cloud with its
surface S. This quantity equals unity when the cloud is a sphere
and is always smaller than unity in the non-spherical case. In fact,
the sphere is the solid which has the largest volume at given surface
(this intuitive theorem has a far from trivial proof, due to De Giorgi
1958). The second term,
,
compares the volume V of the cloud with its
surface S. This quantity equals unity when the cloud is a sphere
and is always smaller than unity in the non-spherical case. In fact,
the sphere is the solid which has the largest volume at given surface
(this intuitive theorem has a far from trivial proof, due to De Giorgi
1958). The second term, 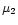 ,
is the ratio between the generalized
harmonic mean of
,
is the ratio between the generalized
harmonic mean of
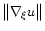 on the boundary
on the boundary
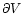 and the generalized simple mean of the same quantity.
The harmonic mean is always smaller than the simple mean, the two
being equal only when all the values involved are constant. Thus
and the generalized simple mean of the same quantity.
The harmonic mean is always smaller than the simple mean, the two
being equal only when all the values involved are constant. Thus
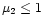 and
and 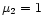 if and only if
if and only if
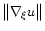 is constant on
is constant on
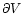 (this happens for the isothermal
sphere). In conclusion,
(this happens for the isothermal
sphere). In conclusion, 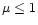 in general and
in general and 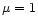 only for
the sphere.
only for
the sphere.
4 The Bonnor instability
Equation 25 allows us to discuss the Bonnor instability
(often known as gravothermal catastrophe; see Lynden-Bell & Wood
1968) for clouds of arbitrary shape. This instability, we recall, is
due to a change in the sign of the derivative of 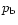 with
respect to V. If this derivative is negative, as normally happens
when gravity can be neglected, a slight decrease of the volume will
produce an increase of the cloud boundary pressure, which would tend
to restore the initial configuration. If, instead, this derivative is
positive, then a small decrease in the volume of the cloud would
correspond to a reduction of the internal boundary pressure and thus
to a collapse of the cloud.
with
respect to V. If this derivative is negative, as normally happens
when gravity can be neglected, a slight decrease of the volume will
produce an increase of the cloud boundary pressure, which would tend
to restore the initial configuration. If, instead, this derivative is
positive, then a small decrease in the volume of the cloud would
correspond to a reduction of the internal boundary pressure and thus
to a collapse of the cloud.
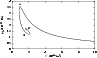 |
Figure 1:
The p-V plot for an isothermal spherical cloud made of
molecular hydrogen at
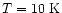 (
(
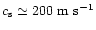 )
with mass )
with mass
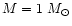 .
The
isothermal lies on a simple .
The
isothermal lies on a simple
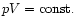 curve at large
volumes, but then at smaller sizes departs from it and the cloud
becomes unstable. The region of stability is on the right side of
point A (which corresponds to the maximum of the boundary
pressure
curve at large
volumes, but then at smaller sizes departs from it and the cloud
becomes unstable. The region of stability is on the right side of
point A (which corresponds to the maximum of the boundary
pressure 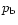 ). The solution spirals into the critical
point C. ). The solution spirals into the critical
point C. |
| Open with DEXTER |
In order to illustrate the instability process in more detail, let us
first refer to the spherical case. We have integrated the
differential Eq. 25 numerically under the boundary
condition
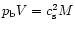 for
for
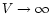 .
Figure 1 shows the case of a spherical cloud of
molecular hydrogen at
.
Figure 1 shows the case of a spherical cloud of
molecular hydrogen at
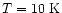 (
(
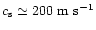 )
with mass
)
with mass
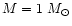 .
The plot
clearly shows that the cloud follows approximately the standard law
.
The plot
clearly shows that the cloud follows approximately the standard law
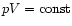 at large volumes, but when sufficiently compressed
it exhibits the Bonnor instability. In particular, the p-V curve
has a maximum and then spirals into a singular point. All points of
the p-V curve where the derivative is positive correspond to
unstable equilibria, since a small decrease of the volume will make
the cloud collapse. Bonnor has shown that actually, in the case of a
spherical cloud, all points in the p-V plot between A and the
critical point correspond to unstable equilibria (below we will
generalize this result to all clouds). The idea is that a spherical
cloud with pressure and volume beyond A will present an instability
for compressions of some internal "core'' (we will discuss this
instability in the general case below).
at large volumes, but when sufficiently compressed
it exhibits the Bonnor instability. In particular, the p-V curve
has a maximum and then spirals into a singular point. All points of
the p-V curve where the derivative is positive correspond to
unstable equilibria, since a small decrease of the volume will make
the cloud collapse. Bonnor has shown that actually, in the case of a
spherical cloud, all points in the p-V plot between A and the
critical point correspond to unstable equilibria (below we will
generalize this result to all clouds). The idea is that a spherical
cloud with pressure and volume beyond A will present an instability
for compressions of some internal "core'' (we will discuss this
instability in the general case below).
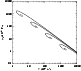 |
Figure 2:
The p-V plot (in logarithmic coordinates) for
isothermal clouds of different shapes made of molecular hydrogen
at
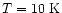 with mass
with mass
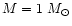 .
The form
factors .
The form
factors 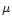 are, from top left to bottom right, 0.125, 0.25,
0.5, and 1. In logarithmic coordinates, a change of
are, from top left to bottom right, 0.125, 0.25,
0.5, and 1. In logarithmic coordinates, a change of 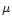 is
described by a simple translation of the isothermal curve.
is
described by a simple translation of the isothermal curve. |
| Open with DEXTER |
In the general case of an arbitrary shape, the situation turns out to
be similar. In fact, going back to Eq. 25, we can see that
the form factor enters the global equation of state together with the
gravitational constant G. In other words, a non-spherical cloud
behaves like a spherical cloud with a reduced gravitational
constant 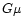 .
As discussed above (see
Sect. 3.5), the isothermal sphere has the largest
admissible value for the form factor,
.
As discussed above (see
Sect. 3.5), the isothermal sphere has the largest
admissible value for the form factor, 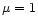 ,
and thus for the
spherical shape the effects introduced by self-gravity are largest.
The
,
and thus for the
spherical shape the effects introduced by self-gravity are largest.
The 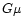 invariance also implies that the isothermal p-V curves
exhibit similar shapes regardless of the value of
invariance also implies that the isothermal p-V curves
exhibit similar shapes regardless of the value of 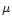 .
In
Fig. 2 we have plotted the integral curves of
Eq. 25 under the assumption that the cloud form factor is
constant as V changes. Figure 2 clearly shows that the
Bonnor instability occurs at any
.
In
Fig. 2 we have plotted the integral curves of
Eq. 25 under the assumption that the cloud form factor is
constant as V changes. Figure 2 clearly shows that the
Bonnor instability occurs at any 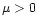 ;
moreover, the effect of
reducing the form factor is to postpone the onset of the
instability to smaller volumes. In the limit of a vanishing form
factor we recover the standard law
;
moreover, the effect of
reducing the form factor is to postpone the onset of the
instability to smaller volumes. In the limit of a vanishing form
factor we recover the standard law
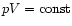 .
From this
figure we also see that in logarithmic coordinates a change of the
form factor
.
From this
figure we also see that in logarithmic coordinates a change of the
form factor 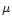 simply results in a simple translation of the
p-V curve. In fact, it is easily checked that, if we define
simply results in a simple translation of the
p-V curve. In fact, it is easily checked that, if we define
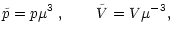 |
|
|
(28) |
then Eq. 25 is transformed back into the equation
appropriate for a sphere, since 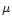 drops out. As a result, a curve
relative to a form factor
drops out. As a result, a curve
relative to a form factor 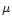 can be obtained from the curve for the
sphere by multiplying the volume by
can be obtained from the curve for the
sphere by multiplying the volume by 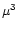 and the pressure by
and the pressure by
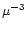 .
.
Point A is a zero of
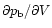 and thus
satisfies
and thus
satisfies
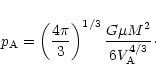 |
(29) |
Using the Emden (1907) solution for the sphere, and taking advantage
of the 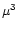 scaling, we can give the position of point A for
arbitrary shapes:
scaling, we can give the position of point A for
arbitrary shapes:
The curves in the p-V plane spiral into the critical point C.
This point is easily obtained by imposing that both the numerator and
the denominator of Eq. 25 vanish. Then we obtain
Let us now complete the discussion of the Bonnor instability for a
general cloud. We have already noted that all clouds for which the
derivative
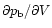 is negative are
unstable. Actually, we can show that all points in the p-V curve
between A and C are unstable. In fact, suppose that the cloud is
in a state represented by a point B between A and C, and let us
consider smaller and smaller portions of the cloud with boundaries
characterized by a constant pressure. Let us call V(p) and M(p),
respectively, the volume and the mass of the part of the cloud with
pressure larger than p. We now observe that a small compression of
this part of the cloud is still described by Eq. 25 with
the obvious replacements
is negative are
unstable. Actually, we can show that all points in the p-V curve
between A and C are unstable. In fact, suppose that the cloud is
in a state represented by a point B between A and C, and let us
consider smaller and smaller portions of the cloud with boundaries
characterized by a constant pressure. Let us call V(p) and M(p),
respectively, the volume and the mass of the part of the cloud with
pressure larger than p. We now observe that a small compression of
this part of the cloud is still described by Eq. 25 with
the obvious replacements
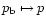 ,
,
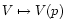 ,
and
,
and
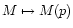 .
As we increase the value of p, we approach
the central part of the cloud. Assuming that the maximum cloud
density
.
As we increase the value of p, we approach
the central part of the cloud. Assuming that the maximum cloud
density 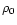 is finite, we have
is finite, we have
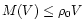 ,
and the
numerator of the last term of Eq. 25 will tend to unity
because
,
and the
numerator of the last term of Eq. 25 will tend to unity
because
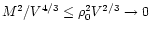 as
as
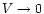 .
As a result, in the central part of the cloud the gas
follows the standard law
.
As a result, in the central part of the cloud the gas
follows the standard law
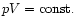 ,
i.e. we are in the
right part of the plot p-V. If we now move back from the central
part to the boundary of the cloud represented by point B we must
travel along the p-V curve (actually, we are moving along
different p-V curves, with respect to the reference one, because
the mass M(V) of the sub-cloud changes while we consider larger and
larger volumes) and we will reach, at a certain boundary pressure
,
i.e. we are in the
right part of the plot p-V. If we now move back from the central
part to the boundary of the cloud represented by point B we must
travel along the p-V curve (actually, we are moving along
different p-V curves, with respect to the reference one, because
the mass M(V) of the sub-cloud changes while we consider larger and
larger volumes) and we will reach, at a certain boundary pressure
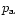 ,
a point of type A. In other words, we have shown
that the sub-cloud characterized by
,
a point of type A. In other words, we have shown
that the sub-cloud characterized by
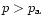 is on a point
of type A of the p-V plot. If this sub-cloud has a small
negative fluctuation of its volume
is on a point
of type A of the p-V plot. If this sub-cloud has a small
negative fluctuation of its volume
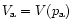 ,
a
decrease of its boundary pressure will occur and this will lead to a
further reduction of its volume. Thus we must conclude that every
cloud characterized by a point in the p-V plot between A and C
is unstable. This is the generalization of the Bonnor instability to
non-spherical clouds.
,
a
decrease of its boundary pressure will occur and this will lead to a
further reduction of its volume. Thus we must conclude that every
cloud characterized by a point in the p-V plot between A and C
is unstable. This is the generalization of the Bonnor instability to
non-spherical clouds.
Point A then defines the boundary of the stability region. If the
external pressure is larger than 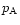 ,
no equilibrium solution exists
for the cloud. This provides an upper limit for the cloud mass:
,
no equilibrium solution exists
for the cloud. This provides an upper limit for the cloud mass:
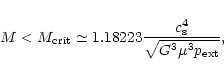 |
(34) |
where
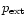 is the external pressure (that we suppose to be
balanced by the cloud boundary pressure
is the external pressure (that we suppose to be
balanced by the cloud boundary pressure 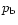 ). Inserting
here a typical value for the pressure of the interstellar medium,
). Inserting
here a typical value for the pressure of the interstellar medium,
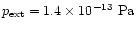 ,
and using
,
and using
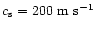 we find
we find
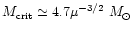 .
.
If condition 34 is met, we can still be in the instability
region if we are in the spiral part of the p-V curve. This
happens if
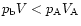 ,
and thus a necessary condition
for stability, independent of
,
and thus a necessary condition
for stability, independent of 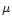 ,
is
,
is
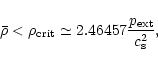 |
(35) |
where
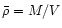 is the mean density of the cloud. Inserting
here the typical values used before, we find
is the mean density of the cloud. Inserting
here the typical values used before, we find
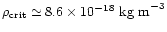 ,
corresponding to about
2600 molecules per
,
corresponding to about
2600 molecules per
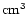 .
Equation 35 can also
be read in terms of a density contrast requirement
.
Equation 35 can also
be read in terms of a density contrast requirement
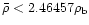 .
Equation 35 proves that
the condition for the Bonnor instability can be cast in a form that
is independent of the shape of the cloud. However, Bonnor's
stability result for spheres, when expressed as a condition
.
Equation 35 proves that
the condition for the Bonnor instability can be cast in a form that
is independent of the shape of the cloud. However, Bonnor's
stability result for spheres, when expressed as a condition
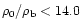 ,
does not hold for clouds of arbitrary shape.
,
does not hold for clouds of arbitrary shape.
Finally, we wish to emphasize that Eqs. 34 and
35 are only necessary conditions for equilibrium
and stability, and not sufficient conditions. In other
words, other kinds of instabilities may occur for clouds that satisfy
Eqs. 34 and 35. Moreover, the presence of
rotation or magnetic fields may qualitatively change these results, as
suggested by recent investigations on the equilibrium of clouds in the
presence of magnetic fields (see Fiege & Pudritz 2000; Curry &
Stahler 2001).
5 Boyle's law for (infinite) cylinders
So far we have assumed that the cloud has finite volume. However,
several observed clouds appear as filaments and can be well modeled by
cylinders. The technique described above, suitably adapted, can be
used also to obtain Boyle's law for (infinite) cylindrical clouds of
arbitrary shape, described by a mass density of the form
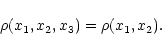 |
(36) |
Note that no assumption on the function
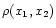 has been
made, and in particular we do not assume a circular
section. We can now calculate the compressibility
has been
made, and in particular we do not assume a circular
section. We can now calculate the compressibility
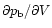 following the steps taken earlier in this
paper. Since the calculations are very similar to the 3D case, we
will just outline the main differences here.
following the steps taken earlier in this
paper. Since the calculations are very similar to the 3D case, we
will just outline the main differences here.
Equations 3 to 10 remain unchanged; however,
since all functions are independent of x3, it is convenient to
define here
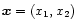 ,
,
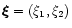 ,
and
,
and
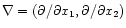 .
The
"total'' mass cannot be defined for infinite cylinders, and hence we
will refer to a linear mass density
.
The
"total'' mass cannot be defined for infinite cylinders, and hence we
will refer to a linear mass density 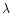 defined as
defined as
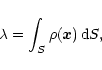 |
(37) |
where S is the section of the cylinder.
5.1 Perturbations at constant mass
Using Eq. 10, which remains unchanged in the 2D case, we can
write the change of "mass''
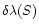 when the central
density changes from
when the central
density changes from 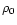 to
to
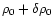 assuming no
variation in the cloud section S. The result obtained is basically
the same as in Sect. 3.1 with the important
difference that now
assuming no
variation in the cloud section S. The result obtained is basically
the same as in Sect. 3.1 with the important
difference that now
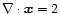 .
As a result,
Eq. 14 now becomes
.
As a result,
Eq. 14 now becomes
![$\displaystyle \delta \lambda(S) = \frac{\delta \rho_0 \lambda(S)}{\rho_0} +
\fr...
...d} S - 2 \lambda(S) \biggr] = \frac{\delta \rho_0 \rho_{\rm b} S}{\rho_0} \cdot$](/articles/aa/full/2001/33/aah2829/img145.gif) |
|
|
(38) |
Note that the two terms involving
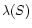 cancel each other. If
we now allow for a change of section
cancel each other. If
we now allow for a change of section 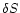 and impose that the
total "mass''
and impose that the
total "mass'' 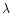 be constant we find the analogue of
Eq. 15:
be constant we find the analogue of
Eq. 15:
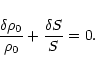 |
(39) |
This equation is independent of
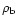 and simply implies
and simply implies
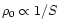 .
.
5.2 Compressibility
Equation 18 rewritten for cylinders is
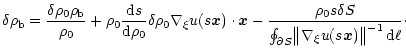 |
|
|
(40) |
Similarly to the 3D case, we can rewrite the second term on the
r.h.s. in a more convenient way by using a suitable average. In this
case we have
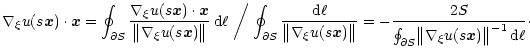 |
|
|
(41) |
Inserting this result in Eq. 40 and using relation
39 we find
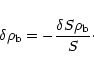 |
(42) |
This simple result should be compared with Eq. 24, valid in
the three-dimensional case. We finally find the analogue of
Eq. 25,
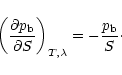 |
(43) |
This equation states that a self-gravitating isothermal
cylinder behaves like a normal gas under compressions, i.e. it
follows the standard law
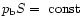 .
However,
we should emphasize that in general the constant that appears on the
r.h.s. of this expression is not equal to
.
However,
we should emphasize that in general the constant that appears on the
r.h.s. of this expression is not equal to
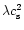 .
In other words, an isothermal cylinder at temperature T follows a
law similar to the one of a perfect gas but at an effective
temperature
.
In other words, an isothermal cylinder at temperature T follows a
law similar to the one of a perfect gas but at an effective
temperature
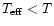 (see Eq. 2; see also
Sect. 5.3 below). The difference
(see Eq. 2; see also
Sect. 5.3 below). The difference
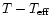 will depend on the particular shape of the cylinder
and on its linear mass density
will depend on the particular shape of the cylinder
and on its linear mass density 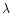 .
Furthermore, for cylinders,
since no form factor needs to be introduced, Eq. 43 can be
integrated exactly without additional assumptions.
.
Furthermore, for cylinders,
since no form factor needs to be introduced, Eq. 43 can be
integrated exactly without additional assumptions.
Since the cylinder follows a law similar to the standard law for
perfect gases, no Bonnor instability is present in this case. Still
we have to make sure that
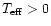 .
From
Eq. 43 we see that this is true as long as an equilibrium
exists with
.
From
Eq. 43 we see that this is true as long as an equilibrium
exists with
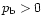 .
In the following subsection we will
consider an axisymmetric cylinder in order to illustrate this point by
means of a simple example.
.
In the following subsection we will
consider an axisymmetric cylinder in order to illustrate this point by
means of a simple example.
5.3 Axisymmetric cylinder
The case of a circular cylinder, with density of the form
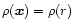 dependent only on the distance r from the axis, has
already been the subject of several investigations (see, e.g.,
Ostriker 1964; Horedt 1986; Bastien et al. 1991). For an
axisymmetric cylinder the exact form of the solution of
Emden's equation is known (Stodo
dependent only on the distance r from the axis, has
already been the subject of several investigations (see, e.g.,
Ostriker 1964; Horedt 1986; Bastien et al. 1991). For an
axisymmetric cylinder the exact form of the solution of
Emden's equation is known (Stodo kiewicz 1963; Ostriker 1964). In our
notation, the solution can be written as
kiewicz 1963; Ostriker 1964). In our
notation, the solution can be written as
![\begin{displaymath}
\rho(r) = \rho_0 \left[ 1 + \frac{(s r)^2}{8} \right]^{-2} \cdot
\end{displaymath}](/articles/aa/full/2001/33/aah2829/img160.gif) |
(44) |
We can integrate this expression out to a certain radius R in order
to get the linear density 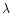 of the cylinder. On the other
hand, if we know the linear density
of the cylinder. On the other
hand, if we know the linear density 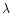 and the radius R of the
cloud, we can obtain the central density
and the radius R of the
cloud, we can obtain the central density 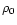 .
A simple
calculation yields
.
A simple
calculation yields
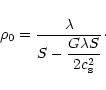 |
(45) |
As anticipated in Eq. 39, we find
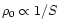 .
Inserting this in Eq. 44 at r = R and using
Eq. 5 we finally find
.
Inserting this in Eq. 44 at r = R and using
Eq. 5 we finally find
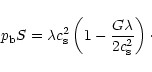 |
(46) |
This is a standard isothermal law, equivalent to Boyle's law, but
characterized by an "effective'' temperature
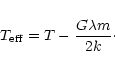 |
(47) |
The term
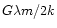 represents the contribution from the
potential energy of the cylinder, as indicated by Eq. 2.
From Eq. 46 we immediately see that when the cloud linear
density is larger than a critical density
represents the contribution from the
potential energy of the cylinder, as indicated by Eq. 2.
From Eq. 46 we immediately see that when the cloud linear
density is larger than a critical density
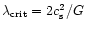 ,
the cloud cannot be in equilibrium (the required boundary
pressure
,
the cloud cannot be in equilibrium (the required boundary
pressure 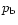 would be negative).
would be negative).
6 Conclusions
The main results obtained in this paper can be summarized as follows.
- 1.
- The generalized Boyle's law for an isothermal self-gravitating
cloud in hydrostatic equilibrium has been studied. No assumption
has been made on the shape of the cloud;
- 2.
- An expression for the compressibility
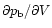 has been obtained and, from that, two conditions for
stable equilibrium have been derived;
has been obtained and, from that, two conditions for
stable equilibrium have been derived;
- 3.
- The equilibrium of the cloud has been shown to be controlled by
one dimensionless form factor. The spherical shape turns out to be
the one for which the effect of self-gravity is largest;
- 4.
- A simple relationship between the isothermal curves in the
p-V plane and the form factor has been obtained;
- 5.
- The actual condition for the Bonnor instability can be written
in a form that does not depend on the shape of the cloud;
- 6.
- For infinite cylinders of arbitrary shape we have shown that the
Bonnor instability is suppressed.
Acknowledgements
We would like to thank João Alves for helpful discussions. Part
of this work has been carried out at the Scuola Normale Superiore,
Pisa, Italy.
- Alves, J., Lada, C. J.,
Lada, E. A., Kenyon, S. J., & Phelps, R. 1998, ApJ, 506, 292
In the text
NASA ADS
- Alves, J., Lada, C. J.,
& Lada, E. A. 2001, Nature, 409, 159
In the text
NASA ADS
-
Bally, J., Stark, A. A., Wilson, R. W., & Langer, W. D. 1987, ApJ, 312, L45
In the text
NASA ADS
- Bastien, P., Arcoragi,
J., Benz, W., Bonnell, I., & Martel, H. 1991, ApJ, 378, 255
In the text
NASA ADS
- Bonnor, W. B. 1956, MNRAS,
116, 351
In the text
NASA ADS
- Chandrasekhar, S. 1967, An Introduction to the
Study of Stellar Structure (Toronto, Dover)
In the text
- Curry, C. L., & Stahler, S. W. 2001, ApJ, in press
[astro-ph/0102477]
In the text
- David, M.,
& Verschueren, W. 1987, A&A, 186, 295
In the text
NASA ADS
- De Giorgi, E. 1958, Atti dell'Accademia Nazionale
dei Lincei, Memorie della Classe di Scienze Matematiche Fisiche e
Naturali, Sezione I (8), 5, 33
In the text
- Dutrey, A., Duvert, G.,
Castets, A., et al. 1991, A&A, 247, L9
In the text
NASA ADS
- Ebert, R. 1955, Zs. Ap., 217
In the text
- Emden, R. 1907, Gaskugeln (Leipzig, Teubner)
In the text
- Falgarone, E.,
Puget, J., & Perault, M. 1992, A&A, 257, 715
In the text
NASA ADS
- Falgarone, E.,
Panis, J., Heithausen, A., et al. 1998, A&A, 331, 669
In the text
NASA ADS
- Fiege, K., & Pudritz, R. E. 2000, ApJ, 534, 291
In the text
NASA ADS
- Goodman, A. A., Bastien,
P., Menard, F., & Myers, P. C. 1990, ApJ, 359, 363
In the text
NASA ADS
- Goodman, A. A.,
Jones, T. J., Lada, E. A., & Myers, P. C. 1995, ApJ, 448, 748
In the text
NASA ADS
- Heyer, M. H., Vrba,
F. J., Snell, R .L., et al. 1987, ApJ, 321, 855
In the text
NASA ADS
- Horedt, G. P. 1986, A&A,
160, 148
In the text
NASA ADS
- Jeans, J. H. 1929, Astronomy and Cosmogony (Cambridge University Press, Cambridge)
In the text
- Jijina, J., Myers,
P. C., & Adams, F. C. 1999, ApJS, 125, 161
In the text
NASA ADS
- Lada, C. J., Lada, E.A.,
Clemens, D. P., & Bally, J. 1994, ApJ, 429, 694
In the text
NASA ADS
- Lada, E. A., Bally, J.,
& Stark, A. A. 1991, ApJ, 368, 432
In the text
NASA ADS
- Loren, R. B. 1989a, ApJ, 338,
902
In the text
NASA ADS
- Loren, R. B. 1989b, ApJ, 338,
925
In the text
NASA ADS
- Lynden-Bell, D.,
& Wood, R. 1968, MNRAS, 138, 495
In the text
NASA ADS
- Myers, P. C. 1983, ApJ, 270,
105
In the text
NASA ADS
- Myers, P. C., Fuller,
G. A., Goodman, A. A., & Benson, P. J. 1991, ApJ, 376, 561
In the text
NASA ADS
- Ostriker, J. 1964, ApJ, 140,
1056
In the text
NASA ADS
- Shu, F. H., Adams, F. C.,
& Lizano, S. 1987, ARA&A, 25, 23
NASA ADS
- Spitzer, L. 1987,
Dynamical Evolution of Globular Clusters (Princeton
University Press, Princeton)
In the text
- Stodo
 kiewicz, J. S. 1963,
Acta Astron., 13, 30
In the text
kiewicz, J. S. 1963,
Acta Astron., 13, 30
In the text
- Walker, C. K., Carlstrom,
J. E., & Bieging, J. H. 1993, ApJ, 402, 655
In the text
NASA ADS
Copyright ESO 2001
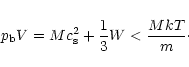
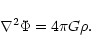
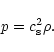
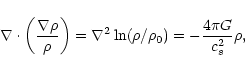
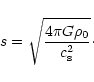
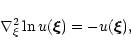
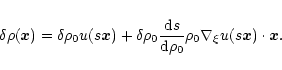
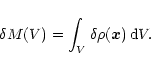
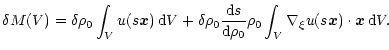
![$\displaystyle \frac{\delta \rho_0 M(V)}{\rho_0} + \delta
\rho_0 \frac{{\rm d} s...
...u(s \vec x) \vec x \bigr) - u(s \vec x) \nabla \cdot \vec x \bigr] \,
{\rm d} V$](/articles/aa/full/2001/33/aah2829/img51.gif)
![$\displaystyle \frac{\delta\rho_0 M(V)}{\rho_0} + \delta \rho_0 \frac{{\rm d}
\l...
... \cdot \vec n \, {\rm d} S - 3 \int_V \rho_0 u(s \vec x) \, {\rm d} V
\biggr] ,$](/articles/aa/full/2001/33/aah2829/img52.gif)
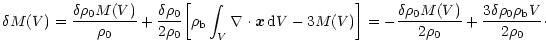
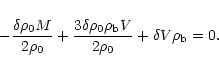
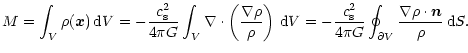
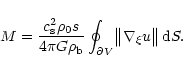
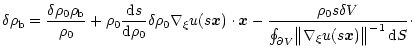
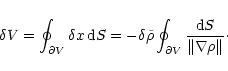
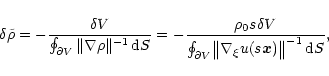
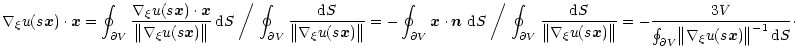
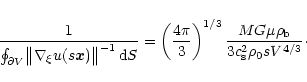
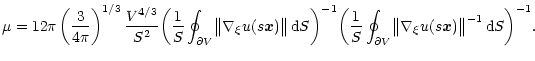
![\begin{displaymath}
\delta \rho_{\rm b} = -\frac{2 \rho_{\rm b}^2 \delta V}{3
...
...G \mu M^2}{6 c_{\rm s}^2 \rho_{\rm b}
V^{4/3}} \right] \cdot
\end{displaymath}](/articles/aa/full/2001/33/aah2829/img78.gif)
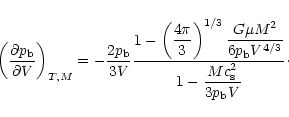
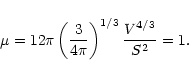
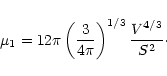


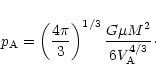
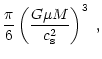
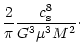
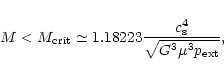
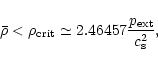
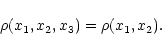
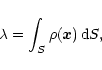
![$\displaystyle \delta \lambda(S) = \frac{\delta \rho_0 \lambda(S)}{\rho_0} +
\fr...
...d} S - 2 \lambda(S) \biggr] = \frac{\delta \rho_0 \rho_{\rm b} S}{\rho_0} \cdot$](/articles/aa/full/2001/33/aah2829/img145.gif)
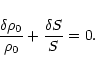
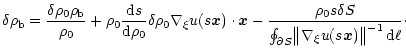
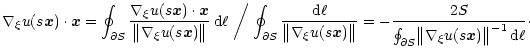
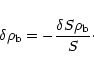
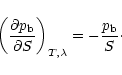
![\begin{displaymath}
\rho(r) = \rho_0 \left[ 1 + \frac{(s r)^2}{8} \right]^{-2} \cdot
\end{displaymath}](/articles/aa/full/2001/33/aah2829/img160.gif)