The galaxies were selected to have an angular diameter greater than 4.2 arcmin and an inclination less than 50 degrees. Our sample covers a wide range of Hubble types, de Vaucouleurs class (T index) as well as form family (SA, SAB and SB). The Elmegreen arm class (Elmegreen & Elmegreen 1987) for the sample spans the entire range, from flocculent types 1-3 to "extreme grand design'' class 12. A discussion of the sample appears in Stedman & Knapen (2001) and in Knapen et al. (in preparation). The latter paper also gives a full description of the data gathering and reduction procedures used.

Table 1 lists the galaxies observed. This sample has the advantage in that it contains many famous spirals whose angular diameters would normally be too large to be included in other 4-m class near-infrared imaging surveys. Included are galaxies such as NGC 4501 (M 88, one of the largest spirals in the Virgo cluster) and Hubble Atlas prototypes such as NGC 628 (M 74), NGC 3351 (M 95) and NGC 4321 (M 100).

A variety of quantitative parameters has been suggested or could be interpreted to represent a measure of the strength of a bar, as discussed by Buta & Block (2001). The simplest is the deprojected bar axis ratio, $(b/a)_{\rm bar}$ , developed by Martin (1995) and listed in his table as $(b/a)_{\it i}$ . (This can be expressed as a bar ellipticity index $\epsilon_{{\rm b}i} = 10[1-(b/a)_{\it i}]$ .) Martin's parameter does not depend on spectroscopic observations, surface photometry, or mass-to-light ratio assumptions, but nevertheless should relate to bar strength based on the analytical models of Athanassoula (1992). This kind of parameter has also been used in a number of other recent papers such as Rozas et al. (1998), Knapen et al. (2000), and Abraham & Merrifield (2000). A K-band Fourier analysis of bar strength is discussed by Regan & Elmegreen (1997). Martin (1995) notes that $(b/a)_{\rm i}$ is not a complete description of bar strength, but merely the most accessible one. The $Q_{\rm b}$ parameter has the advantage in that it is not necessary to rigorously define the bar to measure its strength in this manner (i.e., where the bar begins or ends), while bar axis ratios depend on what we see as the bar.

$\begin{figure} \par\includegraphics[width=6.8cm,clip]{h2815fig1.eps}\end{figure}$

Figure 1: A selection of nine galaxies observed with the 4.2-m William Herschel Telescope. All images have been deprojected. The spirals illustrated here are of class H2 i.e., they are two armed, and have a dominant m=2 Fourier harmonic. Their complete dust penetrated (DP) classifications appear in Col. 4 of Table 1.

$\begin{figure} \par\includegraphics[width=6.8cm,clip]{h2815fig2.eps}\end{figure}$

Figure 2: A sequence of galaxies (deprojected) ranked in terms of increasing bar torque; individual torque classes are listed in Col. 4 of Table 1. The four filled black or yellow dots per image indicate the locations of where the ratio of the tangential force to the mean axisymmetric radial force reaches a maximum (in modulus), per quadrant.

$\begin{figure} \par\includegraphics[width=6.8cm,clip]{h2815fig3.eps}\end{figure}$

Figure 3: A deprojected near-infrared image of the ringed SB(r) galaxy NGC 5921 with inverse Fourier transform contours (m=2harmonic) superimposed. The contours trace out two grand design stellar arms exterior to the bar and inner ring (see also Panel 206 in Sandage & Bedke 1994).

Dust-penetrated classifications, including principal harmonic Hm, arm pitch angle class $P_{\rm c}$ , and bar torque class $B_{\rm c}$ , were derived for each galaxy in Table 1 following Block & Puerari (1999) and Buta & Block (2001), and are listed in Col. 4 in the form $HmP_{\rm c}B_{\rm c}$ . Figure 1 shows our near-infrared tuning prong for nine of the galaxies observed using the WHT; all galaxies illustrated in this figure have been deprojected to appear "face-on''.

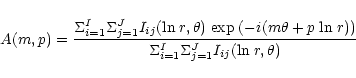
$\begin{displaymath}\displaystyle A(m,p) = \frac{\Sigma_{i=1}^I \Sigma_{j=1}^J I_... ...))}{\Sigma_{i=1}^I \Sigma_{j=1}^J I_{ij} ({\rm ln}\;r,\theta)} \end{displaymath}$

It is important to note that in our formulation, a logarithmic spiral (with a single, well-defined pitch angle independent of radius) may be generated for each mode m (corresponding to the locale where A(m,p)peaks). A set of possibly different pitch angles may be computed, but we bin galaxies in Table 1 according to the "principal'' pitch angle corresponding to the dominant mode. However, we are fully aware that the spiral arms in barred galaxies often depart from a logarithmic shape. The arms may break at a large angle to the bar and then wind back to the other side, as in a "pseudoring''. Also, barred spirals may have two spiral patterns, as in an "inner pseudoring'' and an "outer pseudoring'' (e.g. NGC 3504; see Sandage 1961). These distortions show that the disk structure "feels'' the potential of the bar (Kormendy 1979; Kennicutt 1981). We minimize the impact of rings and pseudorings by excluding from our analysis the bar regions of the galaxies in question. The pitch angles listed in Table 1 correspond to arms outside of the inner bar/bulge or inner pseudoring region.

To illustrate what the Fourier method is extracting in a typical inner-ringed system in Table 1, consider the SB(r) galaxy NGC 5921 (Figs. 1 and 3). Figure 3 shows the m=2 inverse Fourier transform contours superposed on a deprojected image. The contours trace out the two grand design arms extending outward from the ring (see also panel 206 in "The Carnegie Atlas of Galaxies'', Sandage & Bedke 1994). The Fourier method provides a reasonable measure of the openness of the two outer arms in this case. In galaxies with stronger rings, the dominant part of the outer arm pattern should still provide a well-defined pitch angle.

In general, strong outer rings and pseudorings have little impact on our classifications because the relative frequency of such features is fairly low. Only 10% of RC3 disk galaxies within about 20 Mpc have such features (Buta & Combes 1996), therefore the classifications for barred and nonbarred galaxies should have a comparable precision. Our pitch angle classes in Table 1 are in any case a "first order'' approximation, set within the limits imposed by the distortions of the arms in both normal and barred galaxies. As in the case of optical classifications of barred galaxies, we find that from an operational point of view, the dominant degree of openness of the arm pattern for galaxies in Table 1 can be determined, quantified and placed in one of our three broad classes $\alpha$ , $\beta$ or $\gamma$ .

Bar torque classes are derived from the maximum value of the ratio of the tangential force to the mean axisymmetric radial force (Combes & Sanders 1981) using gravitational potentials derived from the near-IR images under the assumptions of a constant mass-to-light ratio and an exponential vertical scale height (Quillen et al. 1994). Bar class $B_{\rm c}=1$ includes galaxies having relative torques $Q_{\rm b}= 0.1\pm0.05$ (meaning the tangential force reaches a maximum of 10% of the axisymmetric background radial force); class 2 involves those with $Q_{\rm b}= 0.2\pm0.05$ , etc., up to class 6 (Buta & Block 2001). Uncertainties introduced in the torque method are fully discussed in Buta & Block (2001). In cases where pitch angles for spiral arms could not be determined due to low S/N for example, only the bar class number is given for the dust penetrated (DP) class in Table 1.

The referee questions whether the bar strength code could be deceived by two strong spiral arms in a nonbarred galaxy, giving a falsely significant bar strength. In general, this is not likely. Two-armed spirals betray their presence by peaks at either p>0or p<0 in the m=2 mode, whereas bars reveal their presence by a peak at p=0 in the m=2 component. A relative maximum in A(2, 0) is the Fourier spectral indicator of the presence of a bar. An independent check to ensure that one never confuses m=2spirals with bars is simply to look at the tangential-to-radial force ratio map: in such a map, the characteristic signature of a bar is the rectangular or parallelogram pattern of the four maxima or minima (see Fig. 1 of Buta & Block 2001). It is always possible to overlay the locations of these points on deprojected images, as in Fig. 2, to make sure that they are not connected with the spiral arms.

The constancy of the mass-to-light ratio has not been explicitly tested for any of the galaxies in Table 1 (e.g., by fitting an observed rotation curve or computing a near-IR color distribution). However, based on discussions by Freeman (1992) and Persic et al. (1996), we believe the assumption should be valid for the galaxies in our sample, whose average luminosity is comparable to the Galaxy. (It would not be valid for dwarf galaxies, none of which we study here.)

Constraints on the dark halo content of barred galaxies may also be deduced from the dynamical friction or drag of bars rotating within dark matter halos. The studies of Debattista & Sellwood (1998, 2000) indicate that bars are only able to maintain their high pattern speeds if the disk itself provides most of the gravitational potential; a high central density, dark matter halo would simply provide too much drag on the bar. Such independent studies suggest that light effectively traces mass within the optical disks of barred spiral galaxies.

The vertical scaleheights of our preferentially face-on galaxies are also not known. As noted by Buta & Block (2001), this is one of the principal uncertainties in the $Q_{\rm b}$ technique. Our run of bar torque determinations in Table 1 assume an exponential scaleheight for each galaxy of 325 parsecs (in other words, equal to the exponential scaleheight of our Galaxy; see Gilmore & Reid 1983). Of course not all galaxies have the same exponential scaleheight: the study by de Grijs (1998) indicates that late-type galaxies on average have a thinner disk than earlier type systems. To account for possible variations in scaleheight based on morphological type, and for the possibility that some bars are thicker than their disks, we have conducted separate potential runs for scaleheights h_z = 225 pc and 425 pc.

The effect of varying the scaleheight from 225 to 425 pc is to move a galaxy by one bar class, at most; many galaxies retain their bar classes with the three different scaleheight runs. When a galaxy does move from one bar class to the next, the effect of decreasing the scaleheight is to increase the bar strength; increasing the scaleheight leads to a decrease in the bar strength. Buta & Block (2001) find that an uncertainty of $\pm$ 100 pc in h_z produces an average uncertainty of $\mp$ 13% in bar strength. In the future, it should be possible to improve our judgment of h_z by scaling from values of the radial scalelength, as done by Quillen et al. (1994).

Finally, in this preliminary analysis, we have assumed that each bulge is as flat as the disk. If the light distribution of a spherical bulge is transformed into a potential assuming it is a thin disk, then the axisymmetric radial forces derived will be too large, especially in the bulge-dominated region where the error can reach a factor of two. However, as discussed by Buta & Block (2001), as long as the bulge-dominated region is well inside the ends of the bar, this effect will have little or no impact on the measured bar strength.

The ratio of the tangential force to the mean axisymmetric radial force reaches a maximum or minimum around or near the ends of the bar. Figure 2 shows a montage of nine WHT $K_{\rm s}$ images wherein galaxies are ranked in terms of increasing gravitational bar torque. The characteristic signature of a bar in each of the images may be seen in Fig. 2 by noting the location of the filled black or yellow dots, where the ratio reaches a maximum or minimum in each quadrant.

2 Dust-penetrated classifications for 45 galaxies