A&A 375, 761-769 (2001)
DOI: 10.1051/0004-6361:20010775
D. L. Block1 - I. Puerari2 - J. H. Knapen3,4 - B. G. Elmegreen5 - R. Buta6 - S. Stedman4 - D. M. Elmegreen7
1 - Department of Computational and Applied Mathematics,
University of the Witwatersrand, 1 Jan Smuts Avenue,
Johannesburg 2001, South Africa
2 - Instituto Nacional de Astrofísica, Optica y Electrónica,
Calle Luis Enrique Erro 1, 72840 Tonantzintla, Puebla, México
3 - Isaac Newton Group of Telescopes, Apartado 321, 38700
Santa
Cruz de La Palma, Spain
4 -
University of Hertfordshire, Dept. of Physical Sciences, Hatfield,
Herts. AL10 9AB, UK
5 -
IBM Research Division, TJ Watson Research Center, Box 218,
Yorktown Heights NY 10598, USA
6 - Dept. of Physics and Astronomy, University of Alabama, Box
870324, Tuscaloosa, Alabama 35487, USA
7 -
Vassar College, Dept. of Physics and Astronomy, Poughkeepsie,
NY
12604-0278, USA
Received 4 March 2001 / Accepted 28 May 2001
Abstract
The relative bar torques for 45 galaxies observed at K-band with the 4.2 m William Herschel Telescope are determined by
transforming the
light distributions into potentials and deriving the maximum ratios of
the tangential forces relative to the radial forces. The results are
combined with the bar torques for 30 other galaxies determined
from our previous K-band survey (Buta & Block 2001). Relative bar
torques determine the degree of spiral arm forcing, gas accretion, and bar evolution. They differ from other measures of bar strength, such as the relative amplitude of
the bar determined photometrically, because they include the bulge and
other disk light that contributes to the radial component of the total force. If
the bulge is strong and the radial forcing large, then even a prominent
bar can have a relatively weak influence on the azimuthal motions in
the disk. Here we find that the relative bar torque correlates only weakly with
the optical bar type listed in the Revised Shapley-Ames and de
Vaucouleurs systems. In fact, some classically barred galaxies have weaker
relative bar torques than classically unbarred galaxies. The optical class is
a poor measure of azimuthal disk forcing for two reasons: some
infrared bars are not seen optically, and some bars with strong bulges have
their azimuthal forces so strongly diluted by the average radial force that
they exert only small torques on their disks. The Hubble
classification scheme poorly recognizes the gravitational influence of bars.
Applications of our bar torque method to the high-redshift universe
are briefly discussed.
Key words: galaxies: spiral - galaxies: structure - galaxies: fundamental parameters - galaxies: kinematics and dynamics - galaxies: general
Bars have been recognized in galaxies since the time of Curtis (1918) and Hubble (1926), but only recently have methods been developed that quantify the impact of these features on galaxy structure. Bar strength is important in galaxy morphological studies because phenomena such as gas inflow, angular momentum transfer, noncircular motions, lack of abundance gradients, nuclear activity, starbursts, and the shapes and morphologies of rings and spirals, may all be tied in various ways to the effectiveness with which a bar potential influences the motions of stars and gas in a galactic disk (e.g., Sellwood & Wilkinson 1993; Buta & Combes 1996; Knapen 1999).
In the past, bar strength was judged visually from galaxy images on blue-sensitive photographic plates. Hubble (1926) divided galaxies into barred (SBa, SBb, ...) and normal (Sa, Sb, ...) spirals along a famous "tuning fork''. This view was revised by de Vaucouleurs (1959), whose classification volume recognized apparent bar strength (SA, SAB, SB) as a continuous property of galaxies called the "family''. De Vaucouleurs' main contribution here was to recognize the existence of galaxies having a bar intermediate in apparent strength between nonbarred and barred spirals. This is the essence of category SAB.
However, neither the Hubble nor the de Vaucouleurs bar classifications can be expected to be accurate measures of bar strength because apparent bar strength is impacted by wavelength, the effects of extinction and star formation, inclination and bar orientation relative to the line of sight, and also on observer interpretations. It is well known that bars are more prominent in near-infrared images than in blue-light images (e.g., Block & Wainscoat 1991; Knapen et al. 2000; Eskridge et al. 2000). Clearly, the near-infrared is the best wavelength regime for judging bar strength.
In the near-infrared, one probes the older, star dominated disk.
This led Block & Puerari (1999) to propose a simple
classification scheme for spirals in the near-IR involving
the dominant Fourier m-mode and the pitch angle of the spiral
arms. Old disks may be grouped into three principal
archetypes: the tightly wound ![]() class, an intermediate
class, an intermediate
![]() class (with pitch angles of
class (with pitch angles of ![]() 25
25![]() ); and the
); and the ![]() class, in which the pitch angles in the near-infrared are
class, in which the pitch angles in the near-infrared are ![]() 40
40![]() .
Flat or falling rotation curves give rise to the tightly
wound
.
Flat or falling rotation curves give rise to the tightly
wound
![]() class; rising rotation curves are associated with the open
class; rising rotation curves are associated with the open
![]() class. Hence, these dust penetrated classes are
inextricably
related to the rate of shear in the stellar disk (Block et al. 1999).
class. Hence, these dust penetrated classes are
inextricably
related to the rate of shear in the stellar disk (Block et al. 1999).
In this paper, we further describe the newest quantitative parameter
in our near-infrared classification
scheme: the gravitational torque of a bar embedded in its disk,
based on the theoretical definition of Combes & Sanders
(1981). This parameter, called ![]() ,
has recently been
developed by Buta & Block (2001). Our goal here is to
build on this study and to evaluate the visual bar classifications
of Hubble and de Vaucouleurs by comparing them with
,
has recently been
developed by Buta & Block (2001). Our goal here is to
build on this study and to evaluate the visual bar classifications
of Hubble and de Vaucouleurs by comparing them with ![]() .
.
The galaxies were selected to have an angular diameter greater than 4.2 arcmin and an inclination less than 50 degrees. Our sample covers a wide range of Hubble types, de Vaucouleurs class (T index) as well as form family (SA, SAB and SB). The Elmegreen arm class (Elmegreen & Elmegreen 1987) for the sample spans the entire range, from flocculent types 1-3 to "extreme grand design'' class 12. A discussion of the sample appears in Stedman & Knapen (2001) and in Knapen et al. (in preparation). The latter paper also gives a full description of the data gathering and reduction procedures used.
Table 1 lists the galaxies observed. This sample has the advantage in that it contains many famous spirals whose angular diameters would normally be too large to be included in other 4-m class near-infrared imaging surveys. Included are galaxies such as NGC 4501 (M 88, one of the largest spirals in the Virgo cluster) and Hubble Atlas prototypes such as NGC 628 (M 74), NGC 3351 (M 95) and NGC 4321 (M 100).
A variety of quantitative parameters has been suggested or could
be interpreted to represent a measure of the strength of a bar,
as discussed by Buta & Block (2001).
The simplest is the deprojected bar axis ratio,
![]() ,
developed by Martin (1995) and listed in his table as
,
developed by Martin (1995) and listed in his table as
![]() .
(This can be expressed as a bar ellipticity index
.
(This can be expressed as a bar ellipticity index
![]() .) Martin's parameter does not
depend on spectroscopic observations, surface photometry, or
mass-to-light ratio assumptions, but nevertheless should relate
to bar strength based on the analytical models of Athanassoula
(1992).
This kind of parameter
has also been used in a number of other recent papers
such as Rozas et al. (1998), Knapen et al. (2000), and Abraham & Merrifield (2000). A K-band Fourier analysis of bar strength is discussed by Regan & Elmegreen
(1997).
Martin (1995) notes that
.) Martin's parameter does not
depend on spectroscopic observations, surface photometry, or
mass-to-light ratio assumptions, but nevertheless should relate
to bar strength based on the analytical models of Athanassoula
(1992).
This kind of parameter
has also been used in a number of other recent papers
such as Rozas et al. (1998), Knapen et al. (2000), and Abraham & Merrifield (2000). A K-band Fourier analysis of bar strength is discussed by Regan & Elmegreen
(1997).
Martin (1995) notes that
![]() is not a complete description
of bar strength, but merely the most accessible one. The
is not a complete description
of bar strength, but merely the most accessible one. The ![]() parameter has the advantage in that it is not necessary to
rigorously
define the bar to measure its strength in this manner (i.e., where the
bar begins or ends), while bar axis ratios depend on what we see
as the bar.
parameter has the advantage in that it is not necessary to
rigorously
define the bar to measure its strength in this manner (i.e., where the
bar begins or ends), while bar axis ratios depend on what we see
as the bar.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2815fig1.eps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg17.gif) |
Figure 1: A selection of nine galaxies observed with the 4.2-m William Herschel Telescope. All images have been deprojected. The spirals illustrated here are of class H2 i.e., they are two armed, and have a dominant m=2 Fourier harmonic. Their complete dust penetrated (DP) classifications appear in Col. 4 of Table 1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2815fig2.eps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg18.gif) |
Figure 2: A sequence of galaxies (deprojected) ranked in terms of increasing bar torque; individual torque classes are listed in Col. 4 of Table 1. The four filled black or yellow dots per image indicate the locations of where the ratio of the tangential force to the mean axisymmetric radial force reaches a maximum (in modulus), per quadrant. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2815fig3.eps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg19.gif) |
Figure 3: A deprojected near-infrared image of the ringed SB(r) galaxy NGC 5921 with inverse Fourier transform contours (m=2harmonic) superimposed. The contours trace out two grand design stellar arms exterior to the bar and inner ring (see also Panel 206 in Sandage & Bedke 1994). |
| Open with DEXTER | |
Dust-penetrated classifications, including principal harmonic Hm,
arm pitch
angle class ![]() ,
and bar torque class
,
and bar torque class ![]() ,
were derived for
each
galaxy in Table 1
following Block & Puerari (1999) and Buta & Block
(2001), and are listed in Col. 4 in the form
,
were derived for
each
galaxy in Table 1
following Block & Puerari (1999) and Buta & Block
(2001), and are listed in Col. 4 in the form
![]() .
Figure 1 shows our near-infrared tuning
prong for nine of the galaxies observed
using the WHT; all galaxies illustrated in this figure have
been deprojected to appear "face-on''.
.
Figure 1 shows our near-infrared tuning
prong for nine of the galaxies observed
using the WHT; all galaxies illustrated in this figure have
been deprojected to appear "face-on''.
The amplitude of each Fourier component is given by
(Schröder et al. 1994):
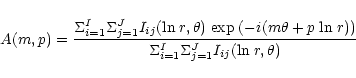
It is important to note that in our formulation, a logarithmic spiral (with a single, well-defined pitch angle independent of radius) may be generated for each mode m (corresponding to the locale where A(m,p)peaks). A set of possibly different pitch angles may be computed, but we bin galaxies in Table 1 according to the "principal'' pitch angle corresponding to the dominant mode. However, we are fully aware that the spiral arms in barred galaxies often depart from a logarithmic shape. The arms may break at a large angle to the bar and then wind back to the other side, as in a "pseudoring''. Also, barred spirals may have two spiral patterns, as in an "inner pseudoring'' and an "outer pseudoring'' (e.g. NGC 3504; see Sandage 1961). These distortions show that the disk structure "feels'' the potential of the bar (Kormendy 1979; Kennicutt 1981). We minimize the impact of rings and pseudorings by excluding from our analysis the bar regions of the galaxies in question. The pitch angles listed in Table 1 correspond to arms outside of the inner bar/bulge or inner pseudoring region.
To illustrate what the Fourier method is extracting in a typical inner-ringed system in Table 1, consider the SB(r) galaxy NGC 5921 (Figs. 1 and 3). Figure 3 shows the m=2 inverse Fourier transform contours superposed on a deprojected image. The contours trace out the two grand design arms extending outward from the ring (see also panel 206 in "The Carnegie Atlas of Galaxies'', Sandage & Bedke 1994). The Fourier method provides a reasonable measure of the openness of the two outer arms in this case. In galaxies with stronger rings, the dominant part of the outer arm pattern should still provide a well-defined pitch angle.
In general, strong
outer rings and pseudorings have little impact on our classifications
because the
relative frequency of such features is fairly low. Only 10% of RC3 disk
galaxies
within about 20 Mpc have such features (Buta & Combes 1996), therefore
the classifications
for barred and nonbarred galaxies should have a comparable precision.
Our pitch angle classes in Table 1 are in any case a "first order''
approximation, set within the limits imposed by the distortions of
the arms in both normal and barred galaxies. As in the case of optical
classifications of barred galaxies, we find that from an operational
point of view, the dominant degree of openness of the arm pattern
for galaxies in Table 1 can be determined,
quantified and placed in one of our three broad classes ![]() ,
,
![]() or
or ![]() .
.
Bar torque classes are derived from
the maximum value of the ratio of the tangential force to the
mean axisymmetric radial force (Combes & Sanders 1981)
using gravitational potentials
derived from the near-IR images under the assumptions of a
constant mass-to-light ratio and an exponential vertical
scale height (Quillen et al. 1994).
Bar class
![]() includes galaxies having relative torques
includes galaxies having relative torques
![]() (meaning the tangential force reaches a
maximum of 10% of the axisymmetric background radial force);
class 2 involves those with
(meaning the tangential force reaches a
maximum of 10% of the axisymmetric background radial force);
class 2 involves those with
![]() ,
etc., up to class 6 (Buta & Block 2001).
Uncertainties introduced in the torque
method are fully discussed in Buta & Block (2001).
In cases where pitch angles for spiral arms could not be
determined due to low S/N for example, only the bar class number
is given for the dust penetrated (DP) class in Table 1.
,
etc., up to class 6 (Buta & Block 2001).
Uncertainties introduced in the torque
method are fully discussed in Buta & Block (2001).
In cases where pitch angles for spiral arms could not be
determined due to low S/N for example, only the bar class number
is given for the dust penetrated (DP) class in Table 1.
The referee questions whether the bar strength code could be deceived by two strong spiral arms in a nonbarred galaxy, giving a falsely significant bar strength. In general, this is not likely. Two-armed spirals betray their presence by peaks at either p>0or p<0 in the m=2 mode, whereas bars reveal their presence by a peak at p=0 in the m=2 component. A relative maximum in A(2, 0) is the Fourier spectral indicator of the presence of a bar. An independent check to ensure that one never confuses m=2spirals with bars is simply to look at the tangential-to-radial force ratio map: in such a map, the characteristic signature of a bar is the rectangular or parallelogram pattern of the four maxima or minima (see Fig. 1 of Buta & Block 2001). It is always possible to overlay the locations of these points on deprojected images, as in Fig. 2, to make sure that they are not connected with the spiral arms.
The constancy of the mass-to-light ratio has not been explicitly tested for any of the galaxies in Table 1 (e.g., by fitting an observed rotation curve or computing a near-IR color distribution). However, based on discussions by Freeman (1992) and Persic et al. (1996), we believe the assumption should be valid for the galaxies in our sample, whose average luminosity is comparable to the Galaxy. (It would not be valid for dwarf galaxies, none of which we study here.)
Constraints on the dark halo content of barred galaxies may also be deduced from the dynamical friction or drag of bars rotating within dark matter halos. The studies of Debattista & Sellwood (1998, 2000) indicate that bars are only able to maintain their high pattern speeds if the disk itself provides most of the gravitational potential; a high central density, dark matter halo would simply provide too much drag on the bar. Such independent studies suggest that light effectively traces mass within the optical disks of barred spiral galaxies.
The vertical scaleheights of our preferentially face-on galaxies are
also not known. As noted by Buta & Block (2001), this is one of
the principal uncertainties in the ![]() technique.
Our run of bar torque determinations in Table 1 assume an
exponential scaleheight for each galaxy of 325 parsecs
(in other words, equal to the exponential scaleheight of
our Galaxy; see Gilmore & Reid 1983).
Of course not all galaxies have the same exponential scaleheight:
the study by de Grijs (1998) indicates that
late-type galaxies on average have a thinner disk than earlier type
systems. To account for possible variations in scaleheight based
on morphological type, and for the possibility that some bars are thicker than their
disks, we have conducted separate potential runs for scaleheights hz
= 225 pc and 425 pc.
technique.
Our run of bar torque determinations in Table 1 assume an
exponential scaleheight for each galaxy of 325 parsecs
(in other words, equal to the exponential scaleheight of
our Galaxy; see Gilmore & Reid 1983).
Of course not all galaxies have the same exponential scaleheight:
the study by de Grijs (1998) indicates that
late-type galaxies on average have a thinner disk than earlier type
systems. To account for possible variations in scaleheight based
on morphological type, and for the possibility that some bars are thicker than their
disks, we have conducted separate potential runs for scaleheights hz
= 225 pc and 425 pc.
The effect of varying the scaleheight from 225 to 425 pc is
to move a galaxy by one bar class, at most;
many galaxies retain their bar
classes with the three different scaleheight runs.
When a galaxy does move from one bar class to the next,
the effect of decreasing the scaleheight is to increase the bar
strength;
increasing the scaleheight leads to a decrease in the bar strength.
Buta & Block (2001) find that an uncertainty of
![]() 100 pc in hz produces an average uncertainty of
100 pc in hz produces an average uncertainty of ![]() 13% in bar strength.
In the future, it should be possible to improve our judgment of hz by scaling from values of the radial scalelength, as done by Quillen et al. (1994).
13% in bar strength.
In the future, it should be possible to improve our judgment of hz by scaling from values of the radial scalelength, as done by Quillen et al. (1994).
Finally, in this preliminary analysis, we have assumed that each bulge is as flat as the disk. If the light distribution of a spherical bulge is transformed into a potential assuming it is a thin disk, then the axisymmetric radial forces derived will be too large, especially in the bulge-dominated region where the error can reach a factor of two. However, as discussed by Buta & Block (2001), as long as the bulge-dominated region is well inside the ends of the bar, this effect will have little or no impact on the measured bar strength.
The ratio of the tangential force to the mean axisymmetric radial
force reaches a maximum
or minimum around or near the ends of the bar.
Figure 2 shows a
montage of nine WHT ![]() images wherein galaxies are ranked
in
terms of increasing gravitational bar torque.
The characteristic signature
of a bar in each of the images may be seen in Fig. 2 by noting
the location of the filled
black or yellow dots, where the ratio reaches a maximum or
minimum in each quadrant.
images wherein galaxies are ranked
in
terms of increasing gravitational bar torque.
The characteristic signature
of a bar in each of the images may be seen in Fig. 2 by noting
the location of the filled
black or yellow dots, where the ratio reaches a maximum or
minimum in each quadrant.
Combining the sample in Table 1 with that in Table 1 of Buta
& Block (2001), we have 75 galaxies for which ![]() is now
available. Six of the galaxies in Table 1 are in common with
the list in Buta & Block (2001). Except for NGC 4548, the values
are in good agreement, with differences attributable
to the quality of the images. We give preference in our analysis to
the Table 1 values, because the INGRID images are superior in signal-to-noise to the images used by Buta & Block (2001). In the case of NGC 4548, a rebinning error caused Buta & Block (2001) to overestimate the
bar strength; the Table 1 value is the actual bar torque in this galaxy.
is now
available. Six of the galaxies in Table 1 are in common with
the list in Buta & Block (2001). Except for NGC 4548, the values
are in good agreement, with differences attributable
to the quality of the images. We give preference in our analysis to
the Table 1 values, because the INGRID images are superior in signal-to-noise to the images used by Buta & Block (2001). In the case of NGC 4548, a rebinning error caused Buta & Block (2001) to overestimate the
bar strength; the Table 1 value is the actual bar torque in this galaxy.
Figure 4 shows ![]() versus the Hubble S and SB classifications,
extracted from the "Revised Shapley-Ames Catalog'' (RSA; Sandage &
Tammann 1981). Figure 5 is a similar
plot, but for the de Vaucouleurs (1963)
classifications
versus the Hubble S and SB classifications,
extracted from the "Revised Shapley-Ames Catalog'' (RSA; Sandage &
Tammann 1981). Figure 5 is a similar
plot, but for the de Vaucouleurs (1963)
classifications![]() .
For a number of galaxies in Table 1, Martin (1995) lists an
estimate of the deprojected visual bar axis ratio,
.
For a number of galaxies in Table 1, Martin (1995) lists an
estimate of the deprojected visual bar axis ratio,
![]() .
Figure 6 shows a
plot of our gravitational bar torque
.
Figure 6 shows a
plot of our gravitational bar torque ![]() vs.
vs.
![]() .
Several points are noteworthy:
.
Several points are noteworthy:
|
Galaxy |
RSA type | Form Family | DP Type |
NGC 0210 |
Sb(rs)I | SAB | H2 |
| NGC 0488 | Sab(rs)I | SA | ...1 |
| NGC 0628 | Sc(s)I | SA | H2 |
| NGC 0864 | Sbc(r)II-III | SAB | H2 |
| NGC 1042 | Sc(rs)I-II | SAB | H2 |
| NGC 1073 | SBc(rs)II | SB | H2 |
| NGC 1169 | SBa(r)I | SAB | H2 |
| NGC 1179 | SBc(rs)I-II | SAB | H2 |
| NGC 1300 | SBb(s)I.2 | SB | H2 |
| NGC 2775 | Sa(r) | SA | ...0 |
| NGC 2805 | --- | SAB | H2 |
| NGC 3184 | Sc(r)II.2 | SAB | H2 |
| NGC 3344 | SBbc(rs)I | SAB | H2 |
| NGC 3351 | SBb(r)II | SB | ...2 |
| NGC 3368 | Sab(s)II | SAB | ...2 |
| NGC 3486 | Sc(r)I-II | SAB | H2 |
| NGC 3631 | Sc(s)I-II | SA | H2 |
| NGC 3726 | Sc(r)I-II | SAB | H2 |
| NGC 3810 | Sc(s)II | SA | H2 |
| NGC 4030 | Sbc(r)I | SA | H2 |
| NGC 4051 | Sbc(s)II | SAB | H2 |
| NGC 4123 | SBbc(rs) | SB | ...4 |
| NGC 4145 | SBc(r)II | SAB | H2 |
| NGC 4254 | Sc(s)I.3 | SA | H2 |
| NGC 4303 | Sc(s)I.2 | SAB | H2 |
| NGC 4314 | SBa(rs) pec | SB | H2 |
| NGC 4321 | Sc(s)I | SAB | H2 |
| NGC 4450 | Sab pec | SA | ...2 |
| NGC 4501 | Sbc(s)II | SA | H2 |
| NGC 4535 | SBc(s)I.3 | SAB | H2 |
| NGC 4548 | SBb(rs)I-II | SB | H2 |
| NGC 4579 | Sab(s)II | SAB | H2 |
| NGC 4618 | SBbc(rs)II.2 pec | SB | H1 |
| NGC 4689 | Sc(s)II.3 | SA | H2 |
| NGC 4725 | Sb/SBb(r)II | SAB | ...3 |
| NGC 5247 | Sc(s)I-II | SA | H2 |
| NGC 5248 | Sbc(s)I-II | SAB | H2 |
| NGC 5371 | Sb(rs)I/SBb(rs)I | SAB | H1 |
| NGC 5850 | SBb(sr)I-II | SB | ...2 |
| NGC 5921 | SBbc(s)I-II | SB | H2 |
| NGC 5964 | --- | SB | H2 |
| NGC 6140 | --- | -- | H1 |
| NGC 6384 | Sb(r)I | SAB | H2 |
| NGC 6946 | Sc(s)II | SA | H2 |
| NGC 7741 | SBc(s)II.2 | SB | ...5 |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{h2815fig4.ps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg33.gif) |
Figure 4: Bar torque versus Hubble Classification as prescribed in the RSA for 64 galaxies, based on the combined sample from Table 1 and the similar table in Block & Buta (2001). Spirals classified as Sa, Sab, Sb, Sbc etc are all grouped into the unbarred "S'' bin; those of type SBa, SBab etc. into the barred SB bin. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{h2815fig5.eps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg34.gif) |
Figure 5: Bar torque versus the de Vaucouleurs (1963) form family for 69 galaxies, again based on the combined sample. The plot excludes 6 galaxies whose form family is from other sources, as well as NGC 4618, classified by de Vaucouleurs as a magellanic barred spiral. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{h2815fig6.eps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg35.gif) |
Figure 6:
A comparison between gravitational bar torques |
| Open with DEXTER | |
(i) Category S in Fig. 4 includes galaxies ranging from bar torque class 0 (e.g., NGC 628) to bar class 3 (e.g., NGC 1042). NGC 4321, a Hubble Sc prototype, has a bar class of 2. Likewise, NGC 4450 (Sab) is of bar class 2. NGC 4450 is illustrated in Panel 110 of Sandage & Bedke (1994), and there is a distinct visual impression of a bar. This is clearly evident in the near-infrared (see Fig. 7).
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2815fig7.ps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg36.gif) |
Figure 7: NGC 4450 is of de Vaucouleurs type SA. In the near- infrared, a bar of class 2 is identified, and our bar torque method finds the locations (indicated by four filled black squares) where the ratio of the tangential to the mean axisymmetric radial force reaches a maximum (in modulus), per quadrant. The hint of a bar is also indicated optically, in Panel 110 of "The Carnegie Atlas of Galaxies'' by Sandage & Bedke (1994). |
| Open with DEXTER | |
Similarly, Hubble category SB in the RSA has a wide range of
bar strengths. This category
commences at
a bar torque of class 1 (NGC 3344) and
reaches bar class 5 (e.g., NGC 7741) in Table 1 and bar class
6 in Table 1 of Buta & Block (2001).
In other words, the bar strengths of some
RSA SB galaxies may be weaker
than those found in
RSA unbarred spirals such as NGC 1042 (Sc; near-infrared
bar class 3). This is not due to the uncertainties in the
![]() method, but instead reflects the difficulties of making
reliable bar strength judgments in the visual Hubble system. The
work of Knapen et al. (2000) reaches this
identical
conclusion, using their independent definition of bar strength.
method, but instead reflects the difficulties of making
reliable bar strength judgments in the visual Hubble system. The
work of Knapen et al. (2000) reaches this
identical
conclusion, using their independent definition of bar strength.
| Classification |
|
N | range |
| RSA S |
|
32 | 0.01-0.33 |
| RSA SB |
|
32 | 0.07-0.63 |
| deV SA |
|
14 | 0.01-0.14 |
| deV SAB |
|
32 | 0.02-0.33 |
| deV SB |
|
23 | 0.16-0.63 |
The gravitational influence of bars is thus poorly recognized
by the Hubble classification scheme.
Table 2 shows that, on average, RSA SB galaxies have relative bar
torques
only 2.5 times as strong as in RSA S galaxies, with a very
large range in ![]() in each class. In this table, two galaxies
of RSA type Sb/SBb have been included in the SB category.
in each class. In this table, two galaxies
of RSA type Sb/SBb have been included in the SB category.
(ii) Figure 5 and Table 2 show that the situation is better for de
Vaucouleurs
classifications. The mean value of ![]() changes smoothly with
de Vaucouleurs
family, and in fact verifies
the continuity in bar strength embodied in de
Vaucouleurs classifications. De Vaucouleurs SB galaxies have
relative
bar torques 5.5 times that of SA galaxies and twice that of SAB
galaxies. However, the scatter is still very large in the SAB and SB
categories.
In Table 1, SAB galaxies
encompass bar torque classes over the wide range 0 (e.g.,
NGC 6946) to 3 (e.g., NGC 4303), while SB galaxies encompass
the
range 2 (e.g., NGC 3351) to 5 (e.g., NGC 1300).
NGC 7479 (Buta & Block 2001) is a type SB galaxy of bar
class 6.
changes smoothly with
de Vaucouleurs
family, and in fact verifies
the continuity in bar strength embodied in de
Vaucouleurs classifications. De Vaucouleurs SB galaxies have
relative
bar torques 5.5 times that of SA galaxies and twice that of SAB
galaxies. However, the scatter is still very large in the SAB and SB
categories.
In Table 1, SAB galaxies
encompass bar torque classes over the wide range 0 (e.g.,
NGC 6946) to 3 (e.g., NGC 4303), while SB galaxies encompass
the
range 2 (e.g., NGC 3351) to 5 (e.g., NGC 1300).
NGC 7479 (Buta & Block 2001) is a type SB galaxy of bar
class 6.
(iii) Figure 6 shows that ![]() correlates fairly well with
Martin's (1995)
correlates fairly well with
Martin's (1995)
![]() parameter, confirming that bar
ellipticity
does provide a measure of bar strength. However, the scatter
at a given bar axis ratio is still large. Buta &
Block (2001) had noted that highly elongated bars (such as in M 83;
an example of Martin's bar ellipticity class 7) may have weak
torques.
At
parameter, confirming that bar
ellipticity
does provide a measure of bar strength. However, the scatter
at a given bar axis ratio is still large. Buta &
Block (2001) had noted that highly elongated bars (such as in M 83;
an example of Martin's bar ellipticity class 7) may have weak
torques.
At
![]() ,
,
![]() ranges from 0.1 to 0.5.
Thus, apparently strong bars with significant ellipiticity
(e.g., with elongations of
ranges from 0.1 to 0.5.
Thus, apparently strong bars with significant ellipiticity
(e.g., with elongations of
![]() )
may
be strong, weak, or intermediate as far as
)
may
be strong, weak, or intermediate as far as ![]() torque values are
concerned.
torque values are
concerned. ![]() does not measure just the shape of an
isolated bar;
it also accounts for the disk in which the bar is embedded.
does not measure just the shape of an
isolated bar;
it also accounts for the disk in which the bar is embedded.
(iv) We suspect that some of the scatter seen in Figs. 4-6 could be due to dilution of the bar torque by a strong bulge. We might expect this because bars that are strong in terms of the m=2 Fourier component of the optical light distribution (Elmegreen & Elmegreen 1985) can have either small or large relative torques, depending on the relative mass of the bulge. If the bulge is weak, then even a weak bar can have a strong torque compared to the radial component of the force (e.g., NGC 1073). Bars that are long can have a strong torque because the end of the bar is far from the bulge (e.g., NGC 1300). This means that the simultaneous decreases in relative bulge strength and bar length with later Hubble type partially offset each other, giving a relative torque that can either go up or down, depending sensitively on the mass distribution.
However, when we replot Fig. 5 separating the points by Hubble type, we find that the galaxy-to-galaxy variation in the bar torque for each bar type is not entirely the result of a varying force dilution from the bulge. This is shown in Fig. 8, which includes the same galaxies as in Fig. 5 but with different symbols for early, intermediate, and late Hubble types. These subtypes reflect a variation in the relative strength of the bulge, with earlier types having stronger bulges in both barred and non-barred galaxies. Even within a subtype, some optically barred galaxies have smaller bar torques than some optically unbarred galaxies. The relative bar torque comes from a mixture of bar amplitude, radial profile and relative length, all combined with the bulge strength. These quantities vary in different ways along the Hubble subtype sequence, producing a wide range in relative bar torques.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{h2815fig8.eps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg46.gif) |
Figure 8: Relative bar torque versus de Vaucouleurs bar type is shown with different symbols and a slight offset for the different Hubble subtypes. The wide range of relative bar torques for each bar type is present for all subtypes. |
| Open with DEXTER | |
Variations in torque with bar type are not obvious from the morphology. If bars drive spirals, particularly in early Hubble types where the presence of a bar correlates well with grand design spiral structure (Elmegreen & Elmegreen 1989), they tend to do so only to the point of saturation, producing very strong arms after only a few revolutions. This is apparently true for both high and low bar torques, because even the low torques are enough to make strong spirals. Thus there is little sensitivity in spiral arm strength to the bar torque, aside from the known sensitivity of arm strength to the relative magnitude of the m=2 component of the infrared light (Elmegreen & Elmegreen 1985).
Several bars in Fig. 2 show a two-component morphology: a broad oval bulge or bar-like structure extending out to about half or two-thirds of the full bar length, and a thin spindle-like structure extending out further. NGC 4314 is an example; the thick component is outside the ILR in this case because there is a small ILR ring much closer to the center. These two bar components generally appear to be from two distinct populations of stars: a warm or hot population to make the thick bar, and a cool population to make the spindle. The two components could also have formed at different times, with the hot component being much older. In this case, it would be interesting to study these galaxies as possible examples where a relatively short bar formed first and dissolved by the instabilities discussed in Hasan et al. (1993), producing the oval we see today, and then another, larger bar formed afterwards out of a younger population of stars and gas, producing the spindle. We also note that some galaxies have the thick oval leading the thin spindle in the direction of rotation (e.g., NGC 1300), and other galaxies have it lagging (e.g., NGC 4123). This variation might indicate some dynamical interaction between the two bars, such as an oscillation about the equilibrium aligned configuration.
Block et al. (2001) have suggested that a physically meaningful classification system for high-redshift galaxies may be more easily devised at rest-frame infrared wavelengths, rather than in the optical regime. Sub-mm observations indicate that at least some of these systems are heavily obscured by dust (Sanders 1999). Lessons from our local Universe are that optical morphologies can be radically different from near-infrared ones; some optically flocculent galaxies, for example, may have beautiful grand design stellar disks when examined at K. The decoupling of gaseous and stellar disks can be dramatic (see e.g., Puerari et al. 2000; Elmegreen et al. 1999; Grosbøl & Patsis 1998; Block et al. 1994). Block et al. (2001) show that Fourier spectra may be generated on simulated Next Generation Space Telescope (NGST) rest-frame Kpost-stamp FITS images which may be as small as 1'' on a side.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2815fig9.eps}\end{figure}](/articles/aa/full/2001/33/aah2815/Timg48.gif) |
Figure 9:
A simulated NGST image of the galaxy NGC 922 as it
would
appear at a redshift of z = 1.2, in its rest-frame K-band. The
square post-stamp
FITS image measures |
| Open with DEXTER | |
With the tremendous importance in attempting to bridge the low and
high-redshift universe from a morphological point of view, it is
natural to enquire how robust our bar torque method
is as we degrade the quality
of the images. First indications are that ![]() is surprisingly robust
in the presence of
noise and limited spatial resolution.
is surprisingly robust
in the presence of
noise and limited spatial resolution.
Recreated rest-frame
K-band NGST images of the galaxies
NGC 2997 and NGC 922 when moved out to
redshifts of z = 0.7 and z = 1.2, are presented in Block et al. (2001).
We have applied our ![]() method to NGC 922,
which may serve as an excellent morphological interface between
the
low and high redshift universe (see Block
et al. 2001 for full details).
method to NGC 922,
which may serve as an excellent morphological interface between
the
low and high redshift universe (see Block
et al. 2001 for full details).
The results are indicated in Fig. 9. Even in the
presence of significant image degradation of NGC 922 when this
galaxy is moved out to
a redshift of z=1.2 (the eye now cannot
easily distinguish the boundaries of a bar, see Fig. 9) -
the four locations where the ratio of the
tangential force to the mean axisymmetric radial force reaches a
maximum (in modulus) may readily be identified. NGC 922 in the
groundbased as well as in the simulated image (Fig. 9) belongs
to bar class 2. Further work on moving each galaxy in Table 1 out
to ![]() (L and
M band imaging) as well as to
(L and
M band imaging) as well as to ![]() (simulated N-band imaging) at rest-frame K-band, with NGST, are in
progress. This would
yield a statistically complete sample upon which to test the
robustness in preservation of bar torque class with increasing z.
(simulated N-band imaging) at rest-frame K-band, with NGST, are in
progress. This would
yield a statistically complete sample upon which to test the
robustness in preservation of bar torque class with increasing z.
We have shown that RSA and de Vaucouleurs bar classifications
correlate
poorly with relative bar torque. It is not unexpected
that there would be some average correlation; as shown in
Table 2,
the S, SA/SAB categories do indeed select weaker bars on
average than
the
SB categories. However, the scatter in any given category is so
large
that
all categories have significant overlap. Some RSA SB galaxies have
much weaker bars than some RSA S galaxies. Deprojected bar
axis
ratios
are a better measure of bar
strength, but even with this more quantitative parameter, the scatter
in ![]() is still large for each axis ratio.
is still large for each axis ratio.
The relative bar torque parameter ![]() provides a logical addition
to the dust-penetrated classification of Block & Puerari (1999). As
noted by Buta & Block (2001), there is still room for improvement that
would involve better estimates of orientation parameters, more quantitative
treatments of the bulge, better tests of the constant M/L assumption using near-IR colors, and a derivation of the vertical scaleheight as
a fraction of the radial scalelength. These issues will be addressed
in more depth in a future paper.
provides a logical addition
to the dust-penetrated classification of Block & Puerari (1999). As
noted by Buta & Block (2001), there is still room for improvement that
would involve better estimates of orientation parameters, more quantitative
treatments of the bulge, better tests of the constant M/L assumption using near-IR colors, and a derivation of the vertical scaleheight as
a fraction of the radial scalelength. These issues will be addressed
in more depth in a future paper.
At least for NGC 922, the ![]() bar torque method is surprisingly
robust in the presence of
noise and limited spatial resolution, when simulated images of this
galaxy are recreated at a redshift of z = 1.2 in the dust-penetrated
rest-frame K-band.
bar torque method is surprisingly
robust in the presence of
noise and limited spatial resolution, when simulated images of this
galaxy are recreated at a redshift of z = 1.2 in the dust-penetrated
rest-frame K-band.
Acknowledgements
We thank the anonymous referee for valuable comments. A note of deep gratitude is expressed by DLB to the entire SASOL Board, including P. Kruger (Chairman) and P. Cox (CEO). SASOL Corporate Affairs Manager Mr S. Motau has been most helpful. We are also most indebted to the Anglo American Chairman's Fund; in particular, we warmly thank the Board of Trustees and CEO Mrs. M. Keeton for the funding of two of us (RJB and IP) to work in South Africa. DLB freely acknowledges the saving grace of God in allowing this research to continue after a motor car accident; "Iam ediximus deum universitatem hanc mundi verbo et ratione et virtute molitum'' (Tertullian). We thank R. S. de Jong and D. M. Bramich for help with the new images. IP would like to express his deep gratitude to E. Athanassoula for interesting discussions on spiral structure. These discussions were made possible in terms of the ECOS/ANUIES exchange project M99-U02, for which IP is most grateful. The groundbased near-infrared image of NGC 922 from which Fig. 9 was created, was kindly secured by Dr. A. Stockton.