A&A 375, L39-L42 (2001)
DOI: 10.1051/0004-6361:20010927
F. Paletou1 - A. López Ariste2 - V. Bommier3 - M. Semel4
1 - Observatoire de la Côte d'Azur, Département G. D. Cassini,
BP 4229, 06304 Nice Cedex 4, France
2 -
High Altitude Observatory, NCAR![]() , PO Box 3000,
Boulder CO 80303, USA
, PO Box 3000,
Boulder CO 80303, USA
3 -
Observatoire de Paris, DAMAp (CNRS/UMR 8588),
92195 Meudon, France
4 -
Observatoire de Paris, DASOP-LPSH (CNRS/UMR 8645),
92195 Meudon, France
Received 18 June 2001 / Accepted 28 June 2001
Abstract
We report on first spectropolarimetric observations of
solar prominences made at THEMIS. Hereafter we shall emphasis on the
preliminary analysis of He I D3 full-Stokes
observations. Our measurements clearly show manifestations of both the
Hanle and Zeeman effects. More generally, we demonstrate the very
favourable performances of the THEMIS multi-line spectropolarimetric
mode for further new investigations of the magnetic field in solar
prominences.
Key words: Sun: prominences - Sun: magnetic fields - polarization
Quoting Einar Tandberg-Hanssen (1974), "the single,
physically most important parameter to study in prominences may be the
magnetic field. Shapes, motions, and in fact the very existence of
prominences depend on the nature of the magnetic field threading the
prominence plasma''. Indeed, being low ![]() structures, the
channeling of plasma motions and of thermal conduction are controlled
by the magnetic field, and it provides also support to the prominence
material against gravity (Démoulin 1998). Details and
further references can be found in the reviews of Leroy
(1989) and Landi Degl'Innocenti (1990), as well as
in Tandberg-Hanssen (1974,1995).
structures, the
channeling of plasma motions and of thermal conduction are controlled
by the magnetic field, and it provides also support to the prominence
material against gravity (Démoulin 1998). Details and
further references can be found in the reviews of Leroy
(1989) and Landi Degl'Innocenti (1990), as well as
in Tandberg-Hanssen (1974,1995).
Polarimetry constitutes a unique tool for the direct
measurement of astrophysical magnetic fields. Up to now, the most
comprehensive observational work on the determination of magnetic
fields in solar prominences was led by J. L. Leroy using the facilities
of the Pic du Midi observatory (France). First measurements,
using the D3 line of He I, were done in 1973-1976 with a
photo-electric polarimeter attached to a 26 cm diameter coronograph
(Leroy et al. 1977; Leroy 1977,1978). This
instrumentation offered a rather high polarimetric sensitivity (better
than 10-3) at the price of a poor spatial resolution (![]()
![]() )
and, no spectral resolution. However, the measured linear
polarization signals could be interpreted further in terms of magnetic
field strength and orientation by use of the Hanle effect theory
(Sahal-Bréchot et al. 1977; Bommier & Sahal-Bréchot
1978).
)
and, no spectral resolution. However, the measured linear
polarization signals could be interpreted further in terms of magnetic
field strength and orientation by use of the Hanle effect theory
(Sahal-Bréchot et al. 1977; Bommier & Sahal-Bréchot
1978).
Shortly after, Bommier et al. (1981) pointed-out the
possibility of a complete determination of the prominence magnetic
field from two simultaneous (linear) polarization measurements made at
two different wavelengths. One solution is indeed to observe two
different spectral lines, such as D3 and the H![]() or H
or H![]() Balmer lines of H I, for instance. This approach was
successfully applied to diagnose new data taken during the 1974-1982
period (Leroy et al. 1983,1984).
Balmer lines of H I, for instance. This approach was
successfully applied to diagnose new data taken during the 1974-1982
period (Leroy et al. 1983,1984).
Another possibility comes from the use of the two components of D3itself, namely the 3d3D
![]() p3P1,2 and
3d3D
p3P1,2 and
3d3D
![]() p3P0 groups of atomic
transitions. However it requires to spectrally resolve those
two components distant of some 34 pm. First profiles of the D3 line
observed in solar prominences were recorded in September 1977 with the
HAO Stokes polarimeter available at the 40 cm coronograph of the NSO Evans
Solar Facility at Sacramento Peak (Baur et al. 1981). Those
new measurements allowed for a complete determination of the magnetic
fields in quiescent prominences (Landi Degl'Innocenti 1982;
Athay et al. 1983; Querfeld et al. 1985).
p3P0 groups of atomic
transitions. However it requires to spectrally resolve those
two components distant of some 34 pm. First profiles of the D3 line
observed in solar prominences were recorded in September 1977 with the
HAO Stokes polarimeter available at the 40 cm coronograph of the NSO Evans
Solar Facility at Sacramento Peak (Baur et al. 1981). Those
new measurements allowed for a complete determination of the magnetic
fields in quiescent prominences (Landi Degl'Innocenti 1982;
Athay et al. 1983; Querfeld et al. 1985).
It was then well assessed from all these works that the mean magnetic
field in quiescent prominences (i) has strength in the 3-15 G range,
(ii) it is almost horizontal and (iii) it makes a small angle (![]() 25
25
![]() )
with the long axis of the structure. However, after the
success of the 70's and 80's, and besides quite recent observations of
filaments (i.e. a prominence as seen on projection against the
solar disk) made in the 1083 nm line of He I by Lin et al. (1998), there has been up to now just very little
"activity'' in the field of the spectropolarimetry of solar
prominences. On the other hand, nowadays instruments provide higher
spatial and spectral resolution observations together with a
)
with the long axis of the structure. However, after the
success of the 70's and 80's, and besides quite recent observations of
filaments (i.e. a prominence as seen on projection against the
solar disk) made in the 1083 nm line of He I by Lin et al. (1998), there has been up to now just very little
"activity'' in the field of the spectropolarimetry of solar
prominences. On the other hand, nowadays instruments provide higher
spatial and spectral resolution observations together with a ![]() 10-3 (or better) polarimetric sensitivity.
10-3 (or better) polarimetric sensitivity.
THEMIS allows for multi-line spectropolarimetric observations at high resolution in the visible, which is definitely critical in order to perform a reliable diagnosis of prominences magnetic fields. The photon collector is large: the primary mirror's diameter is 90 cm, and it was super-polished at REOSC down to a 4 Å roughness (P. Assus, private communication). In combination with a unique multi-line capability, full-Stokes spectropolarimetry gives an opportunity to carry out new observations with the aim of improving our knowledge of the prominences magnetic field.
A 7-days observing run dedicated to the full-Stokes spectropolarimetry
of limb prominences in the He I D3 and H I H![]() spectral lines simultaneously, was conducted in June 2000. We used the
multi-line spectropolarimetric (MTR) observing mode available at
THEMIS. The latter has been described in some details by Paletou &
Molodij (2001).
spectral lines simultaneously, was conducted in June 2000. We used the
multi-line spectropolarimetric (MTR) observing mode available at
THEMIS. The latter has been described in some details by Paletou &
Molodij (2001).
We shall focus on observations made on June 15th, 2000 between 07:18
and 09:40 UT. We selected a low-lying and rather bright prominence
passing at the South-Western limb, at a polar angle of ![]()
![]() .
Synoptic observations made during the previous days showed
that the filament long-axis was oriented
.
Synoptic observations made during the previous days showed
that the filament long-axis was oriented ![]()
![]() respective to
the local meridian. Our observations were made in a sit-and-stare
mode, with the slit oriented parallel to the nearest limb, and at some
respective to
the local meridian. Our observations were made in a sit-and-stare
mode, with the slit oriented parallel to the nearest limb, and at some
![]() above the limb. We recorded a total of
above the limb. We recorded a total of
![]() images in a row, according to the following temporal sequence for the
polarization analysis:
images in a row, according to the following temporal sequence for the
polarization analysis:
![]() (a calcite beam-splitter was used; therefore the 2 orthogonal
states of polarization were measured simultaneously). This took us 31 min with an exposure time of 8 s per image. The scintillometer's
real-time measurement available at THEMIS indicated a very stable and
excellent seeing, of the order of
(a calcite beam-splitter was used; therefore the 2 orthogonal
states of polarization were measured simultaneously). This took us 31 min with an exposure time of 8 s per image. The scintillometer's
real-time measurement available at THEMIS indicated a very stable and
excellent seeing, of the order of
![]() ,
during the whole
observing sequence.
,
during the whole
observing sequence.
At the time of the observation, the sky's transparency was also quite good for the site. In order to evaluate the amount of diffused light contaminating the prominence emission spectra, we recorded a set of images with the slit put off-limb at a neighbouring radial position, although at the same radial distance and with the same relative orientation vs. the nearest limb as in the prominence case. The level of diffused light as compared to the overall signal is shown in Fig. 1. Spectral variations are small but not negligible. A faint chromospheric D3 emission component can be seen. At both ends of the spectral window, small absorption features can be clearly noticed, corresponding to photospheric Fe lines. No significant polarization signal was found from this set of images.
![\begin{figure}
\includegraphics[width=8.1cm]{paletouFig1.eps} \end{figure}](/articles/aa/full/2001/33/aadf183/Timg14.gif) |
Figure 1: The mean D3 emission profile is displayed before having corrected it for diffused light. The thick line (slightly shifted in intensity for comparison) represents the spectral variations of the latter quantity as derived from our observations. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{paletouFig2.eps} \end{figure}](/articles/aa/full/2001/33/aadf183/Timg15.gif) |
Figure 2: Maps of the time-averaged Stokes parameters I, Q, U and V. |
| Open with DEXTER | |
We adopted the numerical procedure first proposed by Trujillo Bueno et al. (2001). We could therefore retrieve a full Stokes
vector with a temporal cadence of ![]() 37 s. Indeed, after each set
of four successive independent measurements, a Stokes vector can be
computed by inverting, for each beam, the "modulation'' scheme which
we may formally write as:
37 s. Indeed, after each set
of four successive independent measurements, a Stokes vector can be
computed by inverting, for each beam, the "modulation'' scheme which
we may formally write as:
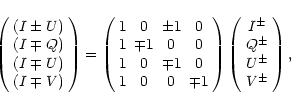 |
(1) |
It is important to bear in mind that, as written above, the modulation
scheme implicitly considers perfect retarders. On the contrary,
the quarter-wave plates we used show some phase chromatism in
the 400-700 nm range; they depart from being
![]() by roughly
by roughly
![]() at 587.6 nm. However, one can easily extend the
above-described reduction scheme in order to take into account for
phase chromatism, and therefore accurately consider crosstalks among
the measured Stokes parameters.
at 587.6 nm. However, one can easily extend the
above-described reduction scheme in order to take into account for
phase chromatism, and therefore accurately consider crosstalks among
the measured Stokes parameters.
Application of this procedure shows that U could be determined with
a
![]() polarimetric sensitivity per pixel, and twice
as much for Q and V, in agreement with previous estimates of
López Ariste et al. (2000). This can be improved by a factor
of
polarimetric sensitivity per pixel, and twice
as much for Q and V, in agreement with previous estimates of
López Ariste et al. (2000). This can be improved by a factor
of ![]() by avering the images of the full temporal sequence
in time, while keeping intact the spatial-spectral multiplex on the
CCD images.
by avering the images of the full temporal sequence
in time, while keeping intact the spatial-spectral multiplex on the
CCD images.
One can clearly see in Fig. 2 a very nice Q signal,
persisting along most of the slit i.e. over a field of view of ![]()
![]() .
The contribution of both "components'' of the D3 line
are detected, although the red component is indeed weaker and more
affected by the noise level; typical values are of the order of
.
The contribution of both "components'' of the D3 line
are detected, although the red component is indeed weaker and more
affected by the noise level; typical values are of the order of
![]() % for the blue component, while it goes down at
the 0.2% level for the red one. Spatial variations along the slit
are also noticeable.
% for the blue component, while it goes down at
the 0.2% level for the red one. Spatial variations along the slit
are also noticeable.
Stokes ![]() at most of the upper part of the slit. This would
agree with transverse magnetic field lines, as long as the field
strength does not exceed a few tens of Gauss. However, examination of
the lower half of the field of view reveals patches of small amplitude
U signals at the -0.2% level. These are signatures of a rotation of
the plane of polarization such as predicted by the Hanle effet, i.e. a
modification of non-magnetic resonance polarization induced by the
presence of magnetic field lines having line-of-sight components.
at most of the upper part of the slit. This would
agree with transverse magnetic field lines, as long as the field
strength does not exceed a few tens of Gauss. However, examination of
the lower half of the field of view reveals patches of small amplitude
U signals at the -0.2% level. These are signatures of a rotation of
the plane of polarization such as predicted by the Hanle effet, i.e. a
modification of non-magnetic resonance polarization induced by the
presence of magnetic field lines having line-of-sight components.
Our measurements of both Q and U Stokes parameters can be
spectrally integrated giving mean values ![]() and
and ![]() at
different spatial positions along the slit. Then, following previous
works done by Leroy's group, a linear polarization rate can be
derived:
at
different spatial positions along the slit. Then, following previous
works done by Leroy's group, a linear polarization rate can be
derived:
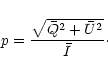 |
(2) |
![\begin{figure}
\par\includegraphics[width=8.15cm]{paletouFig3.eps} \end{figure}](/articles/aa/full/2001/33/aadf183/Timg30.gif) |
Figure 3: Polarization diagram using the spectrally integrated linear polarization measurements. Clear Hanle depolarizations are seen together with several points revealing a rotation of the plane of polarization. |
| Open with DEXTER | |
Afterwards, we can compute the linear polarization direction which is
given by:
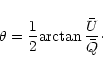 |
(3) |
Points in Fig. 3 with the largest
![]() values
denote magnetic field strengths typical for quiescent prominences (say,
up to 15 G), according to polarization diagrams published earlier
(e.g. Sahal-Bréchot et al. 1977). However, lower values of
values
denote magnetic field strengths typical for quiescent prominences (say,
up to 15 G), according to polarization diagrams published earlier
(e.g. Sahal-Bréchot et al. 1977). However, lower values of
![]() are consistent with larger field strengths. From our
polarization diagram, we can therefore conclude that we detected
variations of the strength and orientation of
are consistent with larger field strengths. From our
polarization diagram, we can therefore conclude that we detected
variations of the strength and orientation of ![]() within the
within the
![]()
![]() of our field of view.
of our field of view.
However, the most striking feature in these observations may very
likely come from the Stokes V image in Fig. 2. Indeed,
although very small signals appear along most of the upper half of the
field of view, very conspicuous Zeeman-like signals are detected in
the lower half of the field of view. This clearly proves the presence
of rather large magnetic field values, and again its change in
strength and orientation within the prominence body.
Figure 4 shows a typical example of the agreement between
Stokes V and
![]() at a given slit
location. Indeed, according to the classical relationship for the
Zeeman effect:
at a given slit
location. Indeed, according to the classical relationship for the
Zeeman effect:
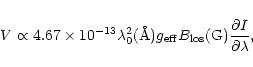 |
(4) |
THEMIS proves to be a suitable instrument for the observation of cool coronal structures such as prominences. Our preliminary full-Stokes observations in the He I D3 spectral line showed clear variations in strength and orientation of the prominence magnetic field.
New measurements are expected to bring new light on the study of the inhomogeneity of the magnetic field, and its relationship with the well-known fine structure of the prominences. Temporal variations will also be studied in more details.
![\begin{figure}
\par\includegraphics[width=8.15cm]{paletouFig4.eps} \end{figure}](/articles/aa/full/2001/33/aadf183/Timg39.gif) |
Figure 4: Example of one of the Stokes V profiles as compared to the re-scaled derivative of I displayed as the thick curve. This corresponds to a line-of-sight magnetic field of 42 G. |
| Open with DEXTER | |
Acknowledgements
Our warmest thanks go to J. L. Leroy for his advices and kind encouragements.