A&A 375, 982-988 (2001)
DOI: 10.1051/0004-6361:20010895

On the rotation of the chemically peculiar magnetic
star 56 Arietis

Saul J. Adelman1 - V. Malanushenko2,5 - T. A. Ryabchikova3,4 - I. Savanov2,5


1 - Department of Physics, The Citadel, 171 Moultrie Street, Charleston, SC 29409, USA
2 - Crimean Astrophysical Observatory, 334413 Nauchny, Crimea, Ukraine
3 - Institute of Astronomy, Russian Academy of Sciences, Pyatnitskaya 48, 109017 Moscow, Russia
4 - Institute of Astronomy, University of Vienna, Türkenschanzstr. 17, 1180 Vienna, Austria
5 - Isaac Newton Institute of Chile, Crimean Branch, Ukraine

Received 25 April 2001 / Accepted 20 June 2001

Abstract
This study used extensive sets of phase resolved photometric and spectroscopic data obtained by the authors and supplemented by that from the literature to investigate the light and equivalent width variations of the mCP star 56 Ari. Its rotational period is found to be increasing at a rate of about 2 s per 100 years. In addition there is evidence for a second period whose length is about 5 years which is attributed to the precession of the axis of rotation.

Key words: stars: chemically peculiar - stars: variables: general - stars: rotation - stars: individual: 56 Ari


1 Introduction

Until quite recently observers of the photometric, equivalent width, and magnetic variability of the magnetic chemical peculiar (mCP) stars discovered that when they repeated series of observations using the best rotational periods of these stars they always derived the same results as previous observers. In some cases the interval for the observations amounts to several thousand periods. However, in the last decade this constancy for a few mCP stars has been questioned.

Adelman and Pyper have obtained a large body of differential uvby photometric observations of many mCP stars with the Four College Automated Photoelectric Telescope (FCAPT). Almost all of the stars for which variability has been demonstrated have shown light curves which faithfully repeat cycle after cycle. They have discovered a few stars whose variability changes only marginally between observing seasons as expected for stars with extraordinarily long periods of many years. Adelman & Fried (1993) noted that their uvby and UBV photometry of 56 Ari were somewhat different from that previously published. Further both 20 Eri (Adelman & Boyce 1995; Adelman 2000) and 108 Aqr (Adelman & Knox 1994; Adelman 1997, 1999) show similar behaviors. For these stars, there appear to be two periods of variability, one for rotation and the other for the precession of the rotational axis, both of which are essentially constant over a typical human life span.

On the other hand, Pyper et al. (1998) showed that CU Vir, the most rapidly known class member is slowing its rotational rate and an abrupt change at which this occurs has been seen. This slight increase in the rotational period was not unexpected as these stars as a class are exceptionally slow rotators compared to normal B and A-type main sequence stars which lack strong magnetic fields. Given a sufficient time span for the observations, many mCP stars are likely to be found to be slowing their rotation. But given the rotational constancy for a few mCP stars such as $\alpha$2 CVn whose period was first found early in the 20th century (Guthnick & Prager 1914; Pyper 1969), the differences from constancy are likely to be very small.

Since our interpretation of the observations of the four mCP stars with variable periods still preserves the essential constancy of rotation, we can use standard models for mCP stars. Explantions of the light, spectrum, and magnetic field strength variability of the mCP stars begin with the rigid rotator model of Babcock (1949) and Stibbs (1950). Here the axis of the magnetic field, which has a particular fixed value at any place in the photosphere and envelope, makes a substantial angle with the axis of rotation. If the elemental abundances are nonuniformly distributed in the photosphere in a definite pattern, the distribution of the radiated energy will then be a function of location. A distant observer watching the star rotate will then see changes in the stellar flux distribution, magnetic field strength, and line profiles.

In the mCP stars, whose atmospheres and envelopes are in radiative equilibirum, the magnetic fields appear to be organized over dimensions comparable to the stellar radius. The magnetic field, gravity, and forces applied to the atomic metal ions act to chemically differentiate the material of the photosphere and envelop. To detect observable changes in the abundances and their distributions requires making observations over time periods much longer than the human life span. These hydrodynamical effects produce regions or spots with elemental abundances significantly different from those of the undisturbed star (Michaud 1970; Michaud & Proffit 1993). Shore & Adelman (1974) showed that such spots can be used to formulate a global model of the magnetic field structure. The stellar spots provide a global reference frame rigidly attached to the stellar surface. Differential rotation, on the other hand, changes the shape and phases of the observed phenomena, as seen in the RS CVn stars.

As turbulence prevents the magnetic field penetration of any region dominated by convection, these fields are excluded from the stellar cores. Further the magnetic field exerts forces on the material of the atmosphere and the envelop which slightly change the moment of inertia along the axis of the field relative to that perpendicular to it. Thus Shore & Adelman (1976) suggested an observational consequence for an isolated oblique rotator would be free-body precession and if in a binary system, then forced-body precession would occur. The available observational evidence for 56 Ari was interpreted as being compatible with free-body precession.

The mCP star 56 Arietis (SX Ari, HD19832, HR954, B6 IV-V) belongs to the Si-group. It shows light, spectrum, and magnetic field variations with a period $P\approx$ 0.728 days first established by Provin (1953). Musielok (1988) analyzed UBV and uvby$\beta$ photometry for the interval JD 2434322-2447176, which covers over 17660 rotational cycles. He found an increase in the rotational period of 4 s per 100 years from analysis of the U data. A complication is that the shapes and phases of minimum in U, B and V curves differ (see, e.g., Adelman & Fried 1993).

In this paper, we examine new observations of 56 Ari obtained specifically to investigate the variability of 56 Ari as well as reexamine published data. This new material will be published in three supplementary papers which will describe the reduction methods and contain this data. The photometric data, which continues that obtained by Adelman & Fried (1993), is 9 years of differential uvby photometry from the FCAPT (Adelman 2001) and three years of differential UBV photometry from the Braeside Observatory (Fried & Adelman 2001). The spectroscopic data is 3 years of equivalent width measurements from the Crimean Observatory (Malanushenko et al. 2001). A spectroscopic analysis of 56 Ari including the mapping of the silicon abundance is given in this later paper. With this greatly augmented database we can perform a careful study of the rotational period of 56 Ari.

2 Observations

Table 1 summarizes the photometric and spectroscopic data that we used in our period analysis. For each data set, the range of Julian Date is in the second column with the number of the observations in the third column.


   
Table 1: Observational data sets used in the paper.

Set No		 JD(2400000+) Data type N Reference
1 34322-34371 $\sim$ UBV $\sim$51 Provin (1953)
2 36544-37313 UBV 105 Rakosch (1963)
3 37633-37710 UBV $\sim$82 Hardie & Schroeder (1963)
4 39797-39855 UBV $\sim$59 Blanco & Catalano (1970)
5 44838-44854 UBV $\sim$35 Hildebrandt et al. (1985)
6 48167-48234 UBV 513 Adelman & Fried (1993)
7 48561-48646 UBV 533 Adelman & Fried (1993)
8 48917-48979 UBV 294 Fried & Adelman (2001)
9 49298-49329 UBV 417 Fried & Adelman (2001)
10 49655-49696 UBV 236 Fried & Adelman (2001)
11 50354-50519 UBV 284 Ziznovsky et al. (2000)
12 50694-50847 UBV 330 Ziznovsky et al. (2000)
13 51110-51201 UBV 217 Ziznovsky et al. (2000)
14 46304-46815 Si II 6347  18 Hatzes (1988)
15 50409-50501 Si II 6347  47 Crimea
16 50773-50798 Si II 6347  26 Crimea
17 51160-51242 Si II 6347  36 Crimea
18 48174-48212 uvby $\sim$85 Adelman & Fried (1993)
19 48532-48679 uvby $\sim$87 Adelman & Fried (1993)
20 48892-48959 uvby 170 Adelman (2001)
21 49253-49399 uvby 121 Adelman (2001)
22 49612-49704 uvby $\sim$62 Adelman (2001)
23 50012-50049 uvby 164 Adelman (2001)
24 50396-50440 uvby 145 Adelman (2001)
25 50736-50873 uvby $\sim$96 Adelman (2001)
26 51085-51104 uvby 149 Adelman (2001)
27 51434-51513 uvby 151 Adelman (2001)
28 51807-51963 uvby 272 Adelman (2001)

2.1 Photometry

The photometric observations represent the most extensive data sets. Provin (1953) made the first multicolor photometric observations of 56 Ari during two months in Fall 1952. He used a 1P21 photomultiplier tube and observations at effective wavelengths of $\lambda$3550, $\lambda$4400, and $\lambda$5500. HR 944 (55 Ari, HD 19548, spectral type B8 III) was used as the primary comparison star with HR 945 (HD 19600, spectra type A0 V) as a check on HR 944. Provin discovered that the shape of the light curve is wavelength dependent.

Rakosch (1963) observed 56 Ari in the standard UBV system in 1958-1960 (Graz University Observatory) and in September 1960-January 1961 (Lowell Observatory) using HR 944 as a primary comparison star and HD 20825 as a control star. He agreed with the period obtained by Provin and found no difference in the amplitudes and shapes of the light curves separated by the interval of 9 years. The phase shift between U and V minima is perhaps smaller in his observations than those of Provin.

Hardie & Schroeder (1963) observed 56 Ari for ten nights to obtain UBV photometery. They used HR 945 as the principal comparison star and HR 944 as the secondary comparison star. Their light curves were similar to those of Provin (1953), but they noted slight systematic differences. They did not know if the later photometry had been transformed to the UBV system.

Blanco & Catalano (1970) observed 56 Ari on ten nights in November and December 1967 in the UBV system. Their comparison stars were HR 944 and HR 945. We retrieved their data from the Library of the Royal Astronomical Society.

Hildebrandt et al. (1985) made their UBV photometry of 56 Ari on eleven nights in August-September 1981 with the double photometric telescope at Shemakha Astrophysical Observatory. They used HR 945 as a comparison star.

Ziznovsky et al. (2000) obtained UBV photometry during the 1996/97, 1997/98, and 1998/99 observing seasons. They used HR 945 as the comparison star. At our request these authors supplied us with their observations.

Adelman & Fried (1993) obtained both uvby and UBV photometry of 56 Ari in the fall of 1990 and 1991, at Braeside Observatory and at the FCAPT, then on Mt. Hopkins, AZ. They used HR 945 as the comparison star and HR 944 as the check or secondary comparison star. Observations were made in continuous runs for several nights to obtain full coverage over the period. The uvby observations were supplemented by once per night observations. Fried & Adelman (2001) present UBV photometry for the next three observing seasons from Braeside Observatory. Adelman (2001) made differential uvby photometric observations of 56 Ari for 9 additional years with the FCAPT which was moved to Washington Camp, AZ several years ago. There are no obvious systematic differences between data taken before and after the move. Whenever possible the observations have been obtained during as few nights as possible when 56 Ari transited near midnight. For data sets 26, 27, and part of 28, the 2.5 mag neutral density filter which was used for the comparison star was removed as the linear behavior of the photomultiplier extended to greater fluxes than initially thought. This has somewhat increased the photoelectric accuracy.

As to the previously published photometric observations, we did not include data by Wolff & Morrison (1975) because they were presented only as figures and unpublished U observations by Musielok (1988).

2.2 Equivalent widths measurements

New spectroscopic observations of 56 Ari were made in June 1996-99 at the coudé spectrograph of the 2.6 m telescope of the Crimean Astrophysical Observatory with the CCD detector. The observed spectral region, 6325-6385 Å contains two strong Si II lines. The spectra all have a linear reciprocal dispersion of 2.5 Åmm-1 and a corresponding spectral resolution of about 0.2 Å. The signal-to-noise ratios were in the range 150-300. The spectra were reduced identically to those of CU Vir (Pyper et al. 1998).

We also used equivalent widths of the Si II $\lambda$6347 line obtained from CCD spectra by Hatzes (1988). Further there are three sets of photographic observations in the region of the Si II $\lambda\lambda$4128-31 doublet. But Bonsack (1969) and Aslanov & Khokhlova (1972), only presented plots of the equivalent width variations. Peterson (1966) does not have sufficient values near the phase of the primary minimum to be useful. Therefore we excluded them from our period analysis.

3 Period analysis

The light curves of 56 Ari have different shapes in each photometric bandpass. To be able to use as much of the data as possible, we combined the following data sets for a period search: U+u, B+(b+v)/2, V+y. Moreover, Shore & Adelman (1976), Adelman & Fried (1993), and Ziznovsky et al. (2000) noted slight variations of the amplitudes and shapes even within the same photometric band. This complicates the period search. We tried to remove part of these (mainly in amplitude) by the following procedure. Observations in each data set were approximated by a sine wave and its first two harmonics:


\begin{displaymath}\Delta m = a_{0} \begin{array}[t]{*{2}{c@{\:+\:}}c} & a_{1}\... ..._{3}\cdot\cos(2\pi x3f) & b_{3}\cdot\sin(2\pi x3f), \end{array}\end{displaymath}

where x is the Julian date of the observations and f=1/P. We used a fixed period P=0.727902 days obtained by Adelman & Fried (1993). Then we subtracted a constant term a from each data set and analyzed only residuals. Two different approaches were used for the period investigation.

3.1 Constant period

As for CU Vir we applied Stellingwerf's (1978) method for the period search in our three photometric bands. If we use the entirety of the non-equally spaced data then we obtain the following solutions for the period:

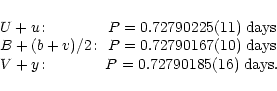
\begin{displaymath}\begin{array}{lc} U+u\!: &P=0.72790225(11)\ {\rm days}\\ B+(... ...{\rm days}\\ V+y\!: &P=0.72790185(16)\ {\rm days}. \end{array}\end{displaymath}

The number in brakets is $\sigma$, the standard deviation expressed in the last two digits. The mean value is very closed to P=0.727902 days obtained by Adelman & Fried (1993). It is supported by the careful investigation of the period solution for different subsets of the whole data set. The range of the possible period values is between 0.72790167 and 0.72790202 days. Each of the period solutions does not significantly differ from that of Adelman & Fried. Therefore we adopt the following ephemeris for the constant period:

\begin{displaymath}{\rm JD} = 2434322.354 + 0.727902\cdot{\it E}. \end{displaymath}

The initial JD does not correspond to a minimum in any of the three bands when for a constant period. The choice for this value will be explained below. Fitting coefficients and $\sigma$s of the whole data set are given in Table 2. As we used only residuals in individual data sets for the period search, the coefficients a0 are omitted.


   
Table 2: Results of the period search.

Photometric band		 a1 b1 a2 b2 a3 b3 Phase of min. $\sigma$
Constant period
U + u 0.03169 -0.00235 0.01072 -0.01168  0.00046  0.00091 -0.0427 8.119E-3
B+(b+v)/2 0.01465 -0.01414 0.00925 -0.01022 -0.00031  0.00136 -0.0834 6.935E-3
V + y 0.01084 -0.00715 0.00531 -0.00718 -0.00066  0.00068 -0.0860 6.335E-3
Linearily changing period
U + u 0.02873  0.01357 0.01602  0.00326 -0.00096  0.00075  0.0401 7.362E-3
B+(b+v)/2 0.01951  0.00615 0.01404  0.00143 -0.00122 -0.00031 -0.0101 5.962E-3
V + y 0.01293 -0.00101 0.00912  0.00081 -0.00077 -0.00066 -0.0049 6.115E-3

The upper panels of Figs. 1-3 are plots of the residuals of each photometric data sets for a constant period. Equivalent width variations are presented in the upper panel of Fig. 4 for this case. The Si II $\lambda$6347 equivalent width variations are similar to that observed in CU Vir where the both the shape and phase of minimum repeat those of U+u mean light curve. An O-C diagram for a constant period is given in the upper panel of Fig. 5. This diagram clearly indicates that the period of the star is not constant. Two other conclusions follow from the O-C diagram and the phases of the minimum in Table 2: the U+u minimum is shifted by +0.04 in phase relative to the minima in B+(b+v)/2 and V+y, and the minimum of the Si II $\lambda$6347 equivalent width variation coincides with the U+u minimum, although the shape of the equivalent width curve slightly differs from that of the U+u curve.


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms1419f1.eps} \end{figure} Figure 1: Photometric variations in U+u vs. phases calculated with a constant period P=0.727902 (upper panel) and with a linearily changing period (lower panel).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms1419f2.eps} \end{figure} Figure 2: The same as in Fig. 1 for B+(b+v)/2.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms1419f3.eps} \end{figure} Figure 3: The same as in Fig. 1 for V+y.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms1419f4.eps} \end{figure} Figure 4: The same as in Fig. 1 for equivalent widths of Si II 6347 line.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms1419f5.eps}\hfill \end{figure} Figure 5: O-C diagrams for 56 Ari with a constant period P=0.727902 (upper panel), and with linearily changing period (lower panel).
Open with DEXTER

3.2 Linearily changing period

The search for a linearily changing period was also performed using the procedure described by Pyper et al. (1998) for CU Vir. We used Cuypers (1986) method as realized by Pelt (1992). Our observations are best fitted with the ephemeris:

\begin{displaymath}{\rm JD}(B,V\,{\rm light\, min})\! = \!2434322.354 + \frac{0.7278883}{1 + 0.7278883\cdot S \cdot (t-t_0)}, \end{displaymath}

where $t_{0}=2\,434\,322.354$ and $S=-1.35\times 10^{-9}$. Thus we confirm an increase in the rotational period first found by Musielok (1988). The more extensive photometric and spectroscopic data used here leads to a retardation factor, which is 1.8 times smaller than obtained by Musielok. Our estimate of the increase in the rotational period is about 2 s per 100 years. The mean light curves with this changing period, the Si II $\lambda$6347 equivalent width variation, and the O-C diagram are shown in the lower panels of Figs. 1-5, respectively. According to the Fisher test, the standard deviations for constant and changing periods are different with a 99.9% confidence level in U+u and B+(b+v)/2.

The very small increase in period requires a time span greater than a few tens of years to detect. This strongly suggests that when astronomers obtain photometric observations for other mCP stars covering such time spans similar small period increases will be found. Our equivalent widths variations fit with both constant and changing period within the same error limits, although the amplitudes differ from year to year; again it might be caused by precession. Ziznovsky et al. (2000) made the same conclusion analyzing their 1996-99 UBV photometry.

The accuracy of the determination of the phase of minimum light is 0.01. One can see oscillations in the O-C diagram (lower panel) which significantly exceed our accuracy estimate; these oscillations may be caused by precession.

4 Discussion

If one plots the y data from Adelman & Fried (1993) and Adelman (2001) for each year and then by comparing the light curves, tries to determine the interval between when they best repeat, one finds 5 years which is very similar to the difference between the two years seen with the most negative phases of minimum in Fig. 4, the O-C diagram. When we consider other photometric bandpasses and the equivalent width of the Si II $\lambda$6347 line, the situation is not as clear.
  \begin{figure} \par\includegraphics[width=6cm,clip]{ms1419f6.eps} \end{figure} Figure 6: A drift of the phase of light minima during individual observational sets.
Open with DEXTER

Within the recent uvby photometry with its reduced errors there are suggestions that changes in the light curve can be seen within an observing season. To clearly demonstrate this requires that one obtain at least two full light curves in this time. Fortunately we have UBV sets (6-13) and uvby sets (18-22, 24-26) taken at the same season, at least. We calculated differences in phases of light minima between UBV and uvby individual curves for each season, avaraged them over all filters and plotted against difference between mean Julian dates of each pair of sets (Fig. 6). It suggests a possible phase drift during 3 months of continuous observations.

That such effects occur may also be useful in understanding the change amplitudes. The wiggles in the right hand side of Fig. 5 also probably relate to such effects and suggest that when the photometry within a given data set covers more than about 60 days we should reexamine it.

One of the possibilities to check for precession may be provided by abundance mapping. We have observations in the region of Si II $\lambda$6347 line separated by 10 years, and three sets of the consecutive years 1996-2001. If the stellar sports are rigidly connected with the magnetic field, then precession will cause a change in the visibility of the stellar surface towards the observer, and hence, a change in the spot's latitude. Results of abundance mapping will be presented in a separate paper.

By removing a major systematic effect, the slow increase of star period, we now are in a position to consider the other systematics. With precession both amplitude and phasing should change in a characteristic way. In much of the photometry the errors make it difficult to find this signal. Now with the recently obtained high quality uvby photometry combined with another season or so of such data and the realization that systematic variability can be found within an observing season, we should be able to more completely test the precession hypothesis.

Acknowledgements
SJA's contribution to this research effort was supported in part by NSF grants AST-9115114 and AST-952850 to The Citadel. He appreciates the continuing efforts of Louis J. Boyd and Robert J. Dukes, Jr., to keep the FCAPT operating properly. VM and TR thanks Austrian Fonds zur Foerderung der wissenschaftlichen Forschung (FwF project S7303-AST) and Russian Federal program "Astronomy'' (grant 1.4.1.5) for financial support. We appreciate J. Ziznovsky, P. Schwartz, and J. Zverko supplying us with the individual values for their photometry of 56 Ari.

References

 
Copyright ESO 2001