We study the sensitivity of the sound speed to relativistic corrections of the equation of state (EOS) in the standard solar model by means of a helioseismic forward analysis. We use the latest GOLF/SOHO data for
A&A 375, 1062-1064 (2001)
DOI: 10.1051/0004-6361:20010946
A. Bonanno1 - A. L. Murabito2 - L. Paternò2
1 - Osservatorio Astrofisico di Catania, Città Universitaria, 95123 Catania, Italy
2 -
Dipartimento di Fisica e Astronomia dell'Università, Sezione Astrofisica, Città Universitaria,
95123 Catania, Italy
Received 18 April 2001 / Accepted 14 June 2001
Abstract
We study the sensitivity of the sound speed to relativistic corrections of the equation of state (EOS)
in the standard solar model by means of a helioseismic forward analysis.
We use the latest GOLF/SOHO data for ![]() ,
1, 2, 3 modes to confirm that
the inclusion of the relativistic corrections to the adiabatic exponent
,
1, 2, 3 modes to confirm that
the inclusion of the relativistic corrections to the adiabatic exponent ![]() computed
from both OPAL and MHD EOS leads to a more reliable theoretical
modelling of the innermost layers of the Sun.
computed
from both OPAL and MHD EOS leads to a more reliable theoretical
modelling of the innermost layers of the Sun.
Key words: Sun: interior - Sun: oscillations - equation of state
It has recently been shown (Elliott & Kosovichev 1998)
that the inclusion of relativistic effects in
the equation of state (EOS) leads to a very good agreement between the solar models and
the seismic Sun. In particular, the inversions of SOI-MDI/SOHO p-mode frequencies
for the adiabatic exponent
![]() show that MHD EOS reproduces the interior of the Sun with
great accuracy, when the relativistic contribution to the Fermi-Dirac statistics is included.
show that MHD EOS reproduces the interior of the Sun with
great accuracy, when the relativistic contribution to the Fermi-Dirac statistics is included.
It is thus interesting to approach the same problem by means of the forward analysis by comparing
the theoretical eigenfrequencies with the observed ones.
Unfortunately this method is not directly
applicable since our description of the outer layers of the Sun is still far from
complete and many theoretical uncertainties would influence our conclusions.
However, since such small effects in solar EOS are most important only in the deep interior, it is
possible to make use of the acoustic mode frequency small separation diagnostic,
![]() ,
for spherical harmonic degrees
,
for spherical harmonic degrees
![]() and radial order
and radial order ![]() (Tassoul 1980).
The main property of this quantity is that it is strongly sensitive to the sound speed
gradient near the solar centre while it is weakly dependent on the details of the
treatment of the outer layers. Since the relativistic effects manifest themselves mainly through a
depletion of 0.1%-0.2% of the adiabatic index
(Tassoul 1980).
The main property of this quantity is that it is strongly sensitive to the sound speed
gradient near the solar centre while it is weakly dependent on the details of the
treatment of the outer layers. Since the relativistic effects manifest themselves mainly through a
depletion of 0.1%-0.2% of the adiabatic index ![]() ,
we expect a quantitatively similar change of sound speed gradient in the solar core.
,
we expect a quantitatively similar change of sound speed gradient in the solar core.
The acoustic mode frequency small separation analysis has recently been used for
estimating the seismic age of the Sun (Dziembowski et al. 1998) and the related
implications of the uncertainties in the
![]() astrophysical factor determinations
(Bonanno & Paternò 2001).
astrophysical factor determinations
(Bonanno & Paternò 2001).
Here we show that the mentioned above analysis can also be used to verify how
the different physical characteristics of the MHD and OPAL EOS reflect on the accuracy of the description of the
stratification of the internal layers of the Sun.
On performing a ![]() analysis of the
latest published GOLF/SOHO data for different solar models,
we confirm the main conclusion of Elliott & Kosovichev (1998), based on an inversion
analysis, that the inclusion
of the relativistic effects in the EOS is in any case required to improve the accuracy of solar
models, independent of which EOS is used.
analysis of the
latest published GOLF/SOHO data for different solar models,
we confirm the main conclusion of Elliott & Kosovichev (1998), based on an inversion
analysis, that the inclusion
of the relativistic effects in the EOS is in any case required to improve the accuracy of solar
models, independent of which EOS is used.
In our analysis we used the GARching SOlar Model
(GARSOM) code which has been described in detail in Schlattl et al. (1997).
It includes the latest OPAL-opacities and either OPAL or MHD EOS,
and it takes into account the microscopic diffusion of the elements heavier than hydrogen.
Our standard solar model has been verified in detail
in Turck-Chièze et al. (1998) and found
in good agreement with other up-to-date solar models, and,
in particular, it is consistent with the observed ![]() and
and
![]() within 10-4, at an age of
within 10-4, at an age of
![]() ,
adopting the surface value
Z/X=0.0245.
We then included the relativistic correction leading term to the
adiabatic index
,
adopting the surface value
Z/X=0.0245.
We then included the relativistic correction leading term to the
adiabatic index ![]() derived from the relativistic
evaluation of the Fermi-Dirac integrals of the EOS
in the solar core by means of the expression (Elliott & Kosovichev 1998):
derived from the relativistic
evaluation of the Fermi-Dirac integrals of the EOS
in the solar core by means of the expression (Elliott & Kosovichev 1998):
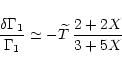 |
(1) |
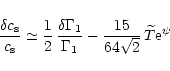 |
(2) |
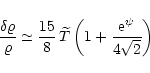 |
(3) |
The behaviour, as functions of the fractional radius, of the relative differences between the quantities ![]() ,
,
![]() and
and
![]() calculated with relativistic corrections and without them is shown in Fig. 1.
calculated with relativistic corrections and without them is shown in Fig. 1.
The term
![]() ,
in Eq. (2) is negligible with respect to
,
in Eq. (2) is negligible with respect to
![]() indicating that the relativistic corrections to the pressure, P, and density,
indicating that the relativistic corrections to the pressure, P, and density, ![]() ,
cancel each other almost completely and the correction to
,
cancel each other almost completely and the correction to ![]() is entirely dominated by the correction to
is entirely dominated by the correction to ![]() .
Also the term
.
Also the term
![]() in Eq. (3) is negligible with respect to unity, indicating that in the solar case the coupling between degeneracy and relativistic effects is weak.
in Eq. (3) is negligible with respect to unity, indicating that in the solar case the coupling between degeneracy and relativistic effects is weak.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1396f1.eps}\end{figure}](/articles/aa/full/2001/33/aa1396/Timg26.gif) |
Figure 1:
Behaviour, as functions of the fractional radius, of the relative differences between relativistic and non-relativistic quantities
|
| Open with DEXTER | |
We used the latest GOLF/SOHO data for ![]() ,
1, 2, 3
obtained with long time series and by
taking into account the asymmetric line profile in data reduction (Thiery et al. 2000).
In particular, we determined the acoustic mode small spacing
difference
,
1, 2, 3
obtained with long time series and by
taking into account the asymmetric line profile in data reduction (Thiery et al. 2000).
In particular, we determined the acoustic mode small spacing
difference
![]() for
for ![]() ,
1 and
,
1 and ![]() for our solar model,
and studied the difference
for our solar model,
and studied the difference
![]() between data and model. We then constructed the two
between data and model. We then constructed the two ![]() indicators
(Dziembowski et al. 1998; Schlattl et al. 1997)
indicators
(Dziembowski et al. 1998; Schlattl et al. 1997)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1396f2.eps}\end{figure}](/articles/aa/full/2001/33/aa1396/Timg30.gif) |
Figure 2:
Relativistic (continuous line) and non-relativistic (dashed line) contribution
to the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1396f3.eps}\end{figure}](/articles/aa/full/2001/33/aa1396/Timg31.gif) |
Figure 3:
Relativistic (continuous line) and non-relativistic (dashed line) contribution
to the |
| Open with DEXTER | |
| EOS | ||||
| MHD | 1.73 | 1.41 | 2.13 | 1.67 |
| OPAL | 1.91 | 1.41 | 2.32 | 1.94 |
Our results show that the acoustic mode frequency small separations are
sensitive to the inclusion of the relativistic
effects. It would be interesting to discuss the relevance of these effects in
the helioseismic determination of the solar age
and related problems with
![]() uncertainties. We plan to
address this issue in a forthcoming communication.
uncertainties. We plan to
address this issue in a forthcoming communication.
Acknowledgements
We are most grateful to H. Schlattl for useful discussions during the preparation of the manuscript.