3 Selection processes

3.1 Single-mode RR Lyraes

The selection process for RR Lyrae stars is similar to the one used in Paper I, except that we adapted the parameters to allow detection of RRc stars. In short, we extracted from the data-base the variables with an amplitude $\gtrsim$0.2 mag. ( $\chi^{2}/N_{\rm DOF}>5$) and a minimum of 30 points in their light curve. These stars were then period searched between 0.2$^{\rm d}$ and 10.0$^{\rm d}$ using the multi-harmonic periodogram method of Schwarzenberg-Czerny (1996) and we fitted a Fourier series with up to five harmonics to the folded light curve. The variables with a well-defined light curve ( $\sqrt{\chi{2}/\chi^{2}_{\rm fit}}>1.5$) were then plotted in the R₂₁/$\Phi_{21}$ plane where the RR Lyrae stars could easily be spotted. The final sample contains $\sim$3700 RR Lyrae variables almost evenly distributed between Sgr and the Galaxy.

3.2 Multi-periodic RR Lyraes

3.2.1 First method

To search for multi-periodic RR Lyraes, we use the following procedure. For each lightcurve we search for the dominant period and fit a third order Fourier series to the folded lightcurve. The resulting Fourier series is then subtracted from the time series and the procedure is iterated. To characterize the strength of the peak value in the periodogram, we follow Alcock et al. (2000b) and calculate the statistics:

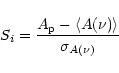$$S_{i}=\frac{A_{\rm p}-\langle A(\nu)\rangle}{\sigma_{A(\nu)}}$$ (1)

where $A_{\rm p}$, $\langle A(\nu)\rangle$ and $\sigma_{A(\nu)}$ are the peak value, average value and standard deviation of the periodograms respectively. S_i corresponds to the ith cycle. The procedure is iterated as long as S_i>8.

For all the lightcurves passing at least 2 iterations, we calculated the value $\chi_{\rm ratio}=\chi^{2}_{1}$/ $\chi^{2}_{2}$, where $\chi^{2}_{1}$ is the reduced $\chi^{2}$ of the fit of the Fourier series with the primary period and $\chi^{2}_{2}$ refers to the fit of the double Fourier series with the primary and secondary periods. All lightcurves for which Proba( $\chi >\chi_{\rm ratio})<50\%$ according to a Fisher-Snedecor distribution were selected for visual inspection. For all these candidates, we simultaneously checked the lightcurves and the periodograms in order to select the multi-mode pulsating stars.

3.2.2 Second method

Figure 2: Example of RRd star where the primary period is trapped in an alias period.

  

Table 1: Double mode RR Lyrae in Sgr. Amplitudes are given in $B_{\rm J}$ for DUO and B₄₄₁₅ for SAG.

  

Table 2: Same as Table 1 for Galactic RRd stars.

  

Table 3: Same as Table 1 for RR Lyrae stars in Sgr with two closely spaced frequencies. Subscripts p and s refer to the primary and secondary pulsations respectively.

  

Table 4: Same as Table 3 for Galactic RR Lyraes.

It is very likely that we miss many multi-mode variables with the above-described procedure. This is due to three reasons: (1) the photometric accuracy is limited with our photographic material, (2) the superposition of two (or more) periods introduces noise in the periodograms, (3) the strong aliasing at $\pm n \, {\rm day}^{-1}$ (see Fig. 1). There is not much that can be done about these problems, except for problem (3) in the search for RRd stars where we have more control because the period ratios are relatively well constrained. Figure 2 shows a typical example of a RRd star missed by the preceding method. Although the maximum amplitude occurs at $\nu_{\rm max}=3.9232 {\rm d}^{-1}$, it is clear that the true frequency is rather $\nu_{0} =2.9232 {\rm d}^{-1}$, a value that yields a more "classical'' period ratio $\nu_{0}/\nu_{1}=0.7425$.

We thus re-processed the whole variable star data-base in order to search for double-mode RR Lyrae stars, but this time we forced the period search between 0.33$^{\rm d}$ and 0.44$^{\rm d}$. This interval encompasses the range of primary periods of all known RRds. A Fourier series with the periodicity P₁ was fitted to the light curve and the residual relative to this fit was period searched in the range 0.45 $^{\rm d}< P_{0}<0.60^{\rm d}$. The fit to the residuals was then subtracted from the initial light curve and the procedure was repeated. We then calculated the reduced $\chi^{2}$ about the resulting double Fourier series.

Figure 3: Left panels: a typical RRd star. The panels represent from top to bottom: spectral window, periodogram after successive subtraction of the main pulsation, and decomposition of the lightcurve. Right panels: same as before for a RR Lyrae star with two closely spaced frequencies.

In the following, we kept only those stars for which $0.74\leqslant P_{1}/P_{0}\leqslant0.75$, corresponding to a range that is considered physically plausible by stellar pulsation models (Cox et al. 1980; Kovács et al. 1991; Bono et al. 1996). To select the double mode pulsating RR Lyraes we define the variable $\chi_{\rm ratio}=\chi^{2}_{1}$/ $\chi^{2}_{2}$, where $\chi^{2}_{1}$ and $\chi^{2}_{2}$ are the reduced $\chi^{2}$ referring to the single-mode and double-mode fit respectively. All the variables for which the double-mode fit yields a better representation of the light curve (i.e. those with Proba ( $\chi >\chi_{\rm ratio})<50\%$) where inspected visually. We simultaneously checked the single period and the double-mode fit in order not to spuriously select a variable with a true period outside the range searched as an RRd star.

Figure 4: Finding charts for multiperiodic RR Lyrae stars in Sgr and the Galactic Centre. Each finding chart is 36 $^{\prime \prime }$on a side. North is oriented up and East is left.

For completeness, we repeated the above-described procedure by inverting the order of the period searches (P₀ before P₁) in order to detect any eventual RRd with a higher amplitude in the fundamental mode relative to the first overtone mode. No additionnal RRd star was found this way, confirming that the first overtone mode is almost always the primary pulsation. This method allowed detection of 16 additional RRd stars.

3.2.3 Results

The final sample contains two kinds of multiperiodic stars: RRd stars and RR Lyrae stars with two closely spaced frequencies. No attempt was made to detect RR Lyrae variables implying long time effects (e.g. Blazkho variables or period changes), because of our too short time span for these kinds of detections. Nor did we search for more than two periods because of the limited accuracy of our photometry.

   

Table 6: Mean periods of RR Lyrae stars in dwarf galaxies of the local group. RR Lyrae data are taken from (Draco) Nemec (1985), (Ursa Minor) Nemec et al. (1988), (Carina) Saha et al. (1986), (Leo II) Siegel & Majewski (2000), (Sculptor) Kauzny et al. (1995), (Sextans) Mateo et al. (1995), (SMC) Smith et al. (1992) and Graham (1975), Caretta et al. (1998), Silbermann & Smith (1995).

System	[Fe/H]	$\langle P_{\rm ab}\rangle$	$\sigma_{\rm ab}$	$\langle P_{\rm c}\rangle$	$\sigma_{\rm c}$	r	$p_{\rm s}$
M 3	-1.7	0.558	0.008	0.344	0.019	0.87	-24.0
M 15	-2.2	0.641	0.013	0.359	0.008	0.15	-1068.5
Draco	-2.0	0.614	0.004	0.351	0.012	0.67	-48.9
Ursa Minor	-2.2	0.638	0.009	0.375	0.011	0.16	-63.0
Carina	-2.0	0.620	0.006	0.366	0.015	0.51	-60.8
Leo II	-1.9	0.619	0.006	0.363	0.008	0.62	-42.9
Sculptor	-1.8	0.587	0.007	0.337	0.005	0.67	-46.7
Sextans	-1.7	0.606	0.010	0.355	0.024	0.78	-44.6
SMC (RRLyr)	-1.7	0.588	0.006	0.380	0.008	0.81	-34.5
LMC (RRLyr)	-1.6	0.582	0.001	0.325	0.001	0.96	-19.0
Sgr	-1.6	0.574	0.002	0.322	0.002	1.00	...
Galactic Centre	...	0.548	0.002	0.305	0.002	0.86	-28.3

Figure 5: Period distribution of the RR Lyraes detected in various systems. The dark regions indicate the location of the RRd variables (1 st overtone period).

Figure 6: Cumulative distributions of RR Lyrae periods in the OoI globular cluster M 3 and all satellites of the Milky Way with a well studied RR Lyrae population. The solid line refers to Sgr whereas the dotted line corresponds to the system indicated in each panel. Left (resp. right) curves correspond to RRc stars (resp. RRab stars).

We found 53 RRd stars (40 in Sgr and 13 in the Galaxy), which are presented in Tables 1 and 2. The first column is the star identifier, Cols. 2 and 3 are the equatorial coordinates. The apparent magnitude of each star is shown in Col. 4 (DUO) or 5 (SAG). Columns 6 and 7 are the amplitude (in $B_{\rm J}$ band for DUO and B₄₄₁₅ for SAG) of the fundamental mode pulsation, and amplitude ratio respectively. Columns 8 and 9 are the periods and period ratios. Column 10 represents the probability that the $\chi_{\rm ratio}$ occured by chance if it were following a Fisher-Snedecor distribution. Although this is not true because of the non-Gaussianity of the errors, it is still indicative of the strength of the detection. In the last column, we indicate whether the RRd star has been detected through the first method or not, and in the latter case, why it was missed (A0: fundamental period aliased, A1: first overtone period aliased, N: periodogram too noisy - i.e. S_i<8). A typical RRd star is presented in Fig. 3 (left panels).

In addition to the RRd stars, we found 13 RR Lyrae stars with two closely spaced frequencies (5 in Sgr and 8 in the Galaxy). These stars are presented in Table 3 (Sgr) and 4 (Galaxy). A typical detection is presented in Fig. 3 (right panels). Similar detections have been performed in M 55 (Olech et al. 1999a), M 5 (Olech et al. 1999b), the LMC (Alcock et al. 2000b) and the Galactic Bulge (Moskalik 2000).

Finding charts of all the detected multiperiodic RR Lyraes are presented in Fig. 4 only available in electronic form at http://www.edpsciences.org. North is up, East is left, and each box is 36 $\hbox{$^{\prime\prime}$ }$ on a side. Light curves are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/375/909.