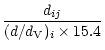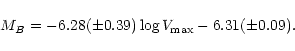A&A 375, 770-780 (2001)
DOI: 10.1051/0004-6361:20010833
Structure, mass and distance of the Virgo cluster from a Tolman-Bondi
model
P. Fouqué
1,2 - J. M. Solanes
3 - T. Sanchis
4 - C. Balkowski
5
1 - Observatoire de Paris-Meudon DESPA, 92195 Meudon Cedex, France
2 - European Southern Observatory, Casilla 19001, Santiago 19, Chile
3 - Departament d'Enginyeria Informàtica i Matemàtiques,
Escola Tècnica Superior d'Enginyeria,
Universitat Rovira i Virgili,
Carretera de
Salou, s/n; 43006 Tarragona, Spain
4 - Departament d'Astronomia i Meteorologia,
Facultat de Físiques, Universitat de Barcelona
C/Martí i Franqués 1, 08028 Barcelona, Spain
5 - Observatoire de Paris-Meudon DAEC, 92195 Meudon Cedex, France
Received 3 April 2001 / Accepted 31 May 2001
Abstract
We have applied a relativistic Tolman-Bondi model of the Virgo cluster to a
sample of 183 galaxies with measured distances within a radius of 8 degrees
from M 87. We find that the sample is significantly contaminated by background
galaxies which lead to too large a cluster mean distance if not excluded. The
Tolman-Bondi model predictions, together with the HI deficiency of spiral
galaxies, allows one to identify these background galaxies. One such galaxy is
clearly identified among the 6 calibrating galaxies with Cepheid distances. As
the Tolman-Bondi model predicts the expected distance ratio to the Virgo
distance, this galaxy can still be used to estimate the Virgo distance, and the
average value over the 6 galaxies is
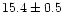 Mpc.
Well-known background groups of galaxies are clearly recovered, together
with filaments of galaxies which link these groups to the main cluster, and are
falling into it. No foreground galaxy is clearly detected in our sample.
Applying the B-band Tully-Fisher method to a sample of 51 true members of
the Virgo cluster according to our classification gives a cluster distance of
Mpc.
Well-known background groups of galaxies are clearly recovered, together
with filaments of galaxies which link these groups to the main cluster, and are
falling into it. No foreground galaxy is clearly detected in our sample.
Applying the B-band Tully-Fisher method to a sample of 51 true members of
the Virgo cluster according to our classification gives a cluster distance of
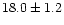 Mpc, larger than the mean Cepheid distance.
Finally, the same model is used to estimate the Virgo cluster mass, which is
Mpc, larger than the mean Cepheid distance.
Finally, the same model is used to estimate the Virgo cluster mass, which is
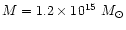 within 8 degrees from the cluster center (2.2 Mpc
radius), and amounts to 1.7 virial mass.
within 8 degrees from the cluster center (2.2 Mpc
radius), and amounts to 1.7 virial mass.
Key words: galaxies: clusters: individual: Virgo
- galaxies: distances and redshifts
- galaxies: elliptical and lenticular
- galaxies: fundamental parameters
- galaxies: spiral
- cosmology: distance scale
In 1990, Fouqué et al. (1990) derived an unbiased distance to the
Virgo cluster, based on a complete sample of 178 spiral galaxies, using the
B-band Tully-Fisher relation (Tully & Fisher 1977). A previous
similar study based on 110 spiral galaxies (Sa-Sm) was published by
Kraan-Korteweg et al. (1988). Soon after, Teerikorpi et al.
(1992, hereafter T92) suggested that this distance determination may
have been contaminated by the inclusion of background galaxies into the
complete sample, although we a priori excluded galaxies generally attributed to
the background M group and W cloud.
The study of the structure of the Virgo cluster starts with de Vaucouleurs
(1961), who identifies the southern extension (Virgo cloud X), and the
wing (Virgo cloud W). This study is extended in de Vaucouleurs & de
Vaucouleurs (1973) who separate the Virgo I cluster (Virgo E, S and S')
from the Virgo II cloud complex (composed of Virgo V, X and Y) and the
background W cloud (composed of Virgo Wa, Wb and W' sub-groups). Paturel
(1979) applies taxonomy to disentangle these various components. Then,
Tully (1982) discusses the separation between the Virgo cluster and its
southern extension in the frame of the Local Supercluster. Later, Ftaclas et al. (1984) identify the M group and the N group. Pierce & Tully
(1988) use the Tully & Shaya infall model (Tully & Shaya
1984) to study the velocity-distance diagram of bright Virgo spiral
galaxies. Binggeli et al. (1993) clarify the situation by listing
galaxies from the VCC catalogue (1985, hereafter VCC) belonging to each
of these clouds (W, W', M and southern extension). T92 list several regions in
the velocity-distance diagram: A, B, C1, C2, and D. Yasuda et al.
(1997) also study the 3-D structure of the cluster. Finally,
Gavazzi et al. (1999, hereafter G99) use distance determinations to
identify new groups, named B, E, N, and S.
Please note that a clarification of the nomenclature is highly desirable, as
the same letters refer to totally different groups: A can mean the main Virgo
cluster or refer to galaxies with high velocities in front of Virgo and falling
into the cluster (T92); B can mean the concentration around M 49, or a
background group in the same region (G99), or even a foreground expanding
component (T92); E can refer to the elliptical component of the Virgo cluster
or an eastern group (G99); N can be a group identified by Ftaclas et al.
(1984) or a northern group in G99; S refers to the spiral component
of the Virgo cluster or a southern group in G99; X can mean that the galaxy
lies within the X-ray contours (Federspiel et al. 1998, hereafter F98)
or belongs to the Virgo X cloud (de Vaucouleurs 1961)!
To investigate the structure of the Virgo cluster and determine the mean
distance of the main cluster, we have used the Tolman-Bondi model of the
cluster defined in Ekholm et al. (1999, hereafter E99) in the spirit
of T92, for spiral galaxies whose distances were given by the Tully-Fisher
relation in B-band by Ekholm et al. (2000, hereafter E00) or in
H-band by G99, but adding the information given by the HI deficiency of
Virgo spiral galaxies. We also used the same model for early-type galaxies
whose distances were determined by the fundamental plane method in G99, or
the recent Tonry's compilation of Surface Brightness Fluctuations distances
(Tonry et al. 2001, hereafter T01).
Section 2 defines the observable parameters we will use for this study.
Section 3 introduces the Tolman-Bondi model and lists its adopted parameters.
Section 4 investigates how the discrepant Cepheid distance to NGC 4639
is well explained by our model, and computes the average Cepheid distance to
Virgo. Section 5 applies our model to the determination of the Virgo cluster
mass, and compares it to other determinations. Section 6 investigates the
structure of the Virgo cluster and lists galaxies which do not belong to the
main cluster according to our model. Section 7 compares the average distances
to Virgo adopted in the various references we used to what our model predicts.
Finally, Sect. 8 summarizes the main results of this paper.
The selected sample has been extracted from the LEDA database. It consists
of 584 galaxies within a radius of 8 degrees (2.25 Mpc at 16 Mpc) from
M 87 (
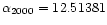 ,
,
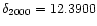 )
and known
recession velocities smaller than 3000 kms-1. Unfortunately, not all these
galaxies have distance estimates, and we therefore reduced the working sample
to 125 late-type and 67 early-type galaxies, with distance measurements from
G99, E00, F98 and T01. Let us describe in more detail some of the
observable parameters collected for these galaxies.
)
and known
recession velocities smaller than 3000 kms-1. Unfortunately, not all these
galaxies have distance estimates, and we therefore reduced the working sample
to 125 late-type and 67 early-type galaxies, with distance measurements from
G99, E00, F98 and T01. Let us describe in more detail some of the
observable parameters collected for these galaxies.
These parameters are directly extracted from the LEDA database. Coordinates
are given in the J2000.0 equinox, and helocientric velocities are corrected to
the Local Group centroid using the Yahil et al. (1977) formula. A histogram of the corrected velocities for the full sample of 584 galaxies is
presented in Fig. 1.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{fig1.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg9.gif) |
Figure 1:
Histogram of the recession velocities, in the Local Group reference
frame, for the 584 galaxies within 8 degrees from M 87. The dotted histogram
corresponds to galaxies with distance measurements. |
| Open with DEXTER |
It clearly shows more galaxies on the
high-velocity side than expected from a gaussian distribution. A similar but
smaller effect also seems apparent on the low-velocity side. For galaxies
with distance measurements, the same features appear.
An accurate estimate of morphological types is important at least for two
reasons: the HI deficiency parameter (see below) is calculated by comparing
the HI content of a galaxy to the average HI content of an isolated galaxy of
the same morphological type. Any error in the type therefore translates into a
corresponding error in the HI deficiency estimate. Similarly, distances
determined by E00 use the calibration of Theureau et al. (1997),
where the intercept of the Tully-Fisher relation varies with the type. Any
error in the type changes the galaxy distance value accordingly.
We used three sources of morphological type determinations:
de Vaucouleurs et al. (1991, hereafter RC3), the VCC catalogue and
van den Bergh et al. (1990). The quality of RC3 types depends upon its
source, coded according to Table 3 of vol. 1 of the catalogue. If the
morphological type has been measured on large reflector plates (code R), it is
adopted; if it comes from PSS prints (codes P or U), we adopt an eye average
with the two other sources. The adopted morphological types differ therefore
from those given in LEDA and used by E00.
We adopted a numeric morphological type according to the RC3 coding scheme.
For distance measurements, we decided to restrict application of the
fundamental plane and SBF methods to types between -5 and -1 (E to L+) and of
the Tully-Fisher method to types between 1 and 9 (Sa to Sm). Therefore, 7 galaxies were excluded from the late-type sample (types -1, 0 and 10), and 2 galaxies were excluded from the early-type sample (NGC 4440 and
NGC 4531, both of type 1). The final sample thus contains 118 spiral,
43 lenticular and 22 elliptical galaxies.
For early-type galaxies, we have used the G99 compilation of distances,
obtained from the fundamental plane method in H-band. According to these
authors, their accuracy should be about 21%. These distances are based on an
assumed Virgo distance of 16 Mpc. To this compilation of 55 elliptical and
lenticular galaxies, we added SBF distances from T01. It contains 35
early-type galaxies in the Virgo cluster area, of which 25 are common with
G99. Tonry's distances are calibrated independently of any assumed Virgo
distance, and the mean shift compared to G99 amounts to:
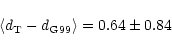 |
(1) |
after rejection of NGC 4638 (
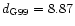 Mpc and
Mpc and
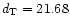 Mpc). As the mean difference of the two systems is not
significant, we adopt an unweighted average of the two measurements as our
distance measurement for this set of 25 early-type galaxies, and the
uncorrected only available distance for the 40 other galaxies (30 from G99, 10
from Tonry). Please note that both references include more uncertain
measurements: in G99, they are identified as being due to velocity dispersions
smaller than 100 km s-1; in T01, they appear in a separate table, named
"table.poor''. We have kept these galaxies in our sample, but we generally
exclude them from our statistical calculations.
Mpc). As the mean difference of the two systems is not
significant, we adopt an unweighted average of the two measurements as our
distance measurement for this set of 25 early-type galaxies, and the
uncorrected only available distance for the 40 other galaxies (30 from G99, 10
from Tonry). Please note that both references include more uncertain
measurements: in G99, they are identified as being due to velocity dispersions
smaller than 100 km s-1; in T01, they appear in a separate table, named
"table.poor''. We have kept these galaxies in our sample, but we generally
exclude them from our statistical calculations.
For late-type galaxies, we also started from the G99 compilation (59
galaxies retained), obtained from the H-band Tully-Fisher method, with a
claimed accuracy of about 16%. We complemented this list with galaxies with
B-band Tully-Fisher distances from E00 (41) and F98 (109). We do not use
galaxies from these lists outside of 8 degrees from M 87 or with
morphological types outside of our adopted range (1-9).
To convert E00 distances into the G99 system, two corrections are done:
first, we correct the distances to our adopted morphological type, in the 20 cases where it differs from the LEDA type adopted in E00. Indeed, the
intercept b of the B-band Tully-Fisher relation derived by Theureau et al.
(1997) and adopted in E00 depends upon the morphological type. The
correction is given by:
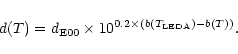 |
(2) |
Although the morphological type differences never exceed one unit, the
correction can amount to 25% in distance.
Additionally, E00 distances are based on the Theureau et al.
(1997) calibration, which leads to
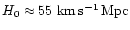 ;
as E00 adopt a cosmic velocity
of Virgo of
;
as E00 adopt a cosmic velocity
of Virgo of
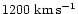 ,
this implies a Virgo distance of 21.8 Mpc.
Therefore, the conversion factor to the G99 assumed Virgo distance of 16 Mpc
is:
,
this implies a Virgo distance of 21.8 Mpc.
Therefore, the conversion factor to the G99 assumed Virgo distance of 16 Mpc
is:
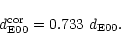 |
(3) |
To convert F98 distances into the G99 system, we simply apply the
calibration correction derived from different adopted Virgo distances, namely
21.5 Mpc and 16 Mpc:
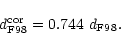 |
(4) |
As we have 65 galaxies with more than one distance estimate, we can make an
intercomparison among the three sources of distance data, after their reduction
to the mean system. We find:
where
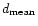 is the mean value of available distance measurements for a
given galaxy.
is the mean value of available distance measurements for a
given galaxy.
All these shifts are significant. This means that our first guess of the
conversion factors to the G99 system was not as successful as we could hope.
We therefore repeated it with new conversion factors, until we reach on
average negligible shifts of the corrected systems to the mean one. This leads
to the following adopted conversion factors, after rejection of two galaxies
with discrepant distance measurements (NGC 4180 and NGC 4591):
We adopt these new conversion factors to put all three references into the
same system. Then, considering that the advantages of the H-band (low
extinction correction) are compensated by the smaller slope of the Tully-Fisher
relation in B-band, we do not weigh each measurement and adopt a straight
average of the available distance estimates for each galaxy. We will only use
these mean distances to classify the galaxies among the various classes
described in Sect. 6. We display in Fig. 2 a histogram of these
118 average distances.
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{fig2.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg31.gif) |
Figure 2:
Histogram of the adopted distances for the 118 spiral galaxies
(left) and the 65 early-type galaxies (right). |
| Open with DEXTER |
The mean value of 20 Mpc and the skewness of the
histogram clearly show the background contamination of our sample. By
comparison, the histogram of distances for early-type galaxies appears to be
less contaminated by background galaxies (smaller mean distance and smaller
skewness).
As we are concerned with the distance determination of individual
galaxies in the Virgo cluster, we quantify HI deficiency by means of a
distance-independent parameter DEF, based on the difference between the
expected and observed logarithm of the mean (hybrid) HI surface density,
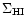 ,
that is
,
that is
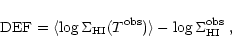 |
(11) |
with
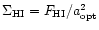 ,
and where
,
and where
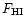 represents the corrected HI flux density integrated over the profile width in
units of
represents the corrected HI flux density integrated over the profile width in
units of
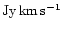 and
and
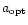 represents the apparent optical
diameter in arcmin. For non-detections, an upper limit to HI content is
estimated by assuming that the emission profile is rectangular with an
amplitude 1.5 times the rms noise and width equal to that expected for a galaxy
of the same morphological type and luminosity, properly corrected for redshift
broadening and viewing inclination (Solanes et al. 1996; see also
Haynes & Giovanelli 1984). The adopted standard values of
represents the apparent optical
diameter in arcmin. For non-detections, an upper limit to HI content is
estimated by assuming that the emission profile is rectangular with an
amplitude 1.5 times the rms noise and width equal to that expected for a galaxy
of the same morphological type and luminosity, properly corrected for redshift
broadening and viewing inclination (Solanes et al. 1996; see also
Haynes & Giovanelli 1984). The adopted standard values of
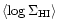 per type are: 0.24 for Sa, Sab; 0.38 for
Sb; 0.40 for Sbc; 0.34 for Sc; and 0.42 for later spiral types.
per type are: 0.24 for Sa, Sab; 0.38 for
Sb; 0.40 for Sbc; 0.34 for Sc; and 0.42 for later spiral types.
Among our sample of 118 spiral galaxies, we have HI deficiency estimates for
106 galaxies, or 90% of the sample.
It has been suggested that Tully-Fisher distances may be underestimated
for highly HI deficient galaxies (T92; Fukugita et al. 1993). For this
reason, we have investigated possible differences in the rotation velocities of
HI deficient and HI normal galaxies in the 12 HI deficient clusters identified
by Solanes et al. (2001), as well as the influence of the HI content on
the Tully-Fisher relationship of the galaxies in our sample. The results
obtained allow us to conclude that HI deficiency does not affect our
Tully-Fisher distances.
We use the Tolman-Bondi model of the Virgo cluster as defined in E99. Let
us recall that the Tolman-Bondi model gives an analytical solution to
Einstein's field equations for a spherically symmetric pressure-free density
excess, embedded in an otherwise homogeneous universe. The parameters of the
model are: the observed Virgo cluster velocity in the Local Group reference
frame (
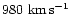 ), the Virgocentric infall velocity of the Local
Group (
), the Virgocentric infall velocity of the Local
Group (
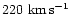 ), the Virgocentric density profile slope
(
), the Virgocentric density profile slope
(
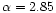 ), and the deceleration parameter of the background homogeneous
universe, taken as an Einstein - de Sitter universe for simplicity
(
q0 = 0.5). Although there is a general agreement about the values of
3 of these parameters, the Virgocentric density profile slope is not well
known, as it should reflect the distribution of the mass around the cluster
center, not only the galaxy (light) distribution. In E99, it has been
constrained using 32 galaxies whose distances were known using their Cepheids,
generally measured with the HST, through the PL-relation. For details about the
model, the adjustment of its parameters and the influence of changing these
values, the reader is referred to T92, E99 and E00.
), and the deceleration parameter of the background homogeneous
universe, taken as an Einstein - de Sitter universe for simplicity
(
q0 = 0.5). Although there is a general agreement about the values of
3 of these parameters, the Virgocentric density profile slope is not well
known, as it should reflect the distribution of the mass around the cluster
center, not only the galaxy (light) distribution. In E99, it has been
constrained using 32 galaxies whose distances were known using their Cepheids,
generally measured with the HST, through the PL-relation. For details about the
model, the adjustment of its parameters and the influence of changing these
values, the reader is referred to T92, E99 and E00.
For each galaxy, the angular distance to the Virgo center of mass (taken to
be the position of M 87) completely defines the exact shape of the
Tolman-Bondi S-curve in the velocity distance diagram, for a given choice of
model parameters. Then, the observed recession velocity of the galaxy (in the
Local Group reference frame) gives one to three possible distance ratios of the
galaxy to Virgo (see Fig. 3 for examples).
![\begin{figure}
\par\mbox{\includegraphics[height=5.8cm,clip]{1326f3_a1.eps}\hspa...
...\hspace*{5mm}
\includegraphics[height=5.75cm,clip]{1326f3_c2.eps} }
\end{figure}](/articles/aa/full/2001/33/aa1326/Timg44.gif) |
Figure 3:
Tolman-Bondi model for the six galaxies with Cepheid distances.
The dotted line corresponds to the recession velocity of the
galaxy, while the arrows mark the expected distance ratio if
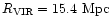 (solid arrow) or
(solid arrow) or
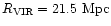 (dotted arrow).
(dotted arrow). |
| Open with DEXTER |
The first and the third
values correspond to a galaxy falling into the cluster from in front or behind.
The second value corresponds to a true cluster member. Assuming that the
Tolman-Bondi model can explain most of the observed positions of the galaxies
in the velocity-distance diagram means that we neglect other possible
components, such as an expanding one suggested by T92, or galaxies projected
by chance onto the cluster, but taking part in the Hubble flow. Certainly,
not all galaxies in the Virgo cluster should follow the Tolman-Bondi model. For
instance, galaxies belonging to the virialized core of the cluster do not
exhibit a velocity-distance relation. It is however difficult to disentangle
those galaxies from our class 2, so that we include them into it. On the other
hand, not all galaxies in the class 2 (defined as the descending branch of the
S-shape Tolman-Bondi curve) belong to Virgo: for instance, at large angular
distances from M 87 the descending branch still exists, but is no longer
related to proper Virgo galaxies. We assume that within 8 degrees of the
cluster center, most of the galaxies on the descending branch are true cluster
members. We will test this strong assumption in Sect. 6 by building a
histogram of "Virgo distances'', where each point is computed from a galaxy
distance and its distance ratio to Virgo, as given by the Tolman-Bondi model.
To do this, we must select the most plausible one among the possible
distance ratios for a given galaxy, when the model gives more than one value.
Here, we made use of two criteria: we try to choose the value closest to the
assumed Virgo distance (16 Mpc), and, for spiral galaxies, we take into account
the HI deficiency, assuming that a true member of the cluster has a higher
probability to be deficient than a galaxy falling for the first time into the
cluster. We therefore attribute to each galaxy a "class number'', which is 1
if we adopt the first value of the distance ratio to Virgo (galaxies falling
from in front into the cluster), 2 if we adopt the second value (true cluster
members), and 3 if we adopt the third value (galaxies falling from behind into
the cluster).
There are 6 galaxies in or close to the Virgo cluster whose distance is
known thanks to the HST observations in V and I bands, using the Cepheid
period-luminosity relation. We use the distances published in Freedman et al.
(2001) (without the uncertain metallicity correction). Five of the six
distances cluster about a mean distance of 14.6 Mpc, while the sixth one
(NGC 4639) gives a larger distance (21 Mpc). This is perfectly
explained by the Tolman-Bondi model, and this was in fact the initial
motivation of this study. Figure 3 gives the result of the application
of the Tolman-Bondi model to these galaxies, with a dotted line showing the
recession velocity of the galaxy, and an arrow showing the distance ratio to
Virgo, for an adopted distance to Virgo of 15.4 Mpc (see below).
Two galaxies belong to the Virgo southern extension (NGC 4496A and NGC 4536)
and lie at more than 8 degrees from M 87. However, their position in the
velocity-distance diagram should be explained by our model, if we assume that
no other cluster perturbes them. However, we find that the maximum velocity
explained by our model for NGC 4536 is
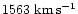 at
at
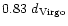 ,
too small compared to its observed velocity of
,
too small compared to its observed velocity of
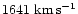 .
For this galaxy, our model predicts it to be in the
class 3, with a distance of
.
For this galaxy, our model predicts it to be in the
class 3, with a distance of
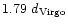 .
This in turn would lead to
an inacceptable Virgo distance of
.
This in turn would lead to
an inacceptable Virgo distance of
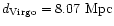 ,
using the
observed galaxy distance of 14.45 Mpc. In fact, it is well known that random
velocities about 80
,
using the
observed galaxy distance of 14.45 Mpc. In fact, it is well known that random
velocities about 80
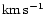 exist for all galaxies and explain the
velocity dispersion of small groups of galaxies (Gourgoulhon et al.
1992). We therefore assume that this is the origin of the small
discrepancy observed for NGC 4536.
exist for all galaxies and explain the
velocity dispersion of small groups of galaxies (Gourgoulhon et al.
1992). We therefore assume that this is the origin of the small
discrepancy observed for NGC 4536.
Table 1 gives the adopted distances to the six galaxies,
Table 1:
Adopted Cepheid distances to the 6 Virgo galaxies,
ratio to the Virgo distance given by the Tolman-Bondi model and
corresponding Virgo distances for each possible class, adopted class and
Virgo distance, and HI deficiency.
| Name |
d |
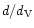 |
class |
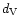 |
def |
| |
Mpc |
d1 |
d2 |
d3 |
|
Mpc |
|
| |
|
|
|
|
|
|
|
| NGC 4321 |
14.32 |
0.68 |
0.95 |
1.71 |
2 |
15.07 |
0.49 |
| |
|
21.06 |
15.07 |
8.37 |
|
|
|
| NGC 4496A |
14.52 |
0.75 |
0.92 |
1.76 |
2 (1) |
15.78 |
-0.09 |
| |
|
19.36 |
15.78 |
8.25 |
|
|
|
| NGC 4535 |
14.79 |
0.77 |
0.96 |
1.91 |
2 (1) |
15.41 |
0.19 |
| |
|
19.21 |
15.41 |
7.74 |
|
|
|
| NGC 4536 |
14.45 |
(0.83) |
(0.83) |
1.79 |
1 or 2 |
(17.41) |
0.25 |
| |
|
(17.41) |
(17.41) |
8.07 |
|
|
|
| NGC 4548 |
15.00 |
0.23 |
1.07 |
1.30 |
2 |
14.02 |
0.83 |
| |
|
65.22 |
14.02 |
11.54 |
|
|
|
| NGC 4639 |
20.99 |
0.47 |
1.03 |
1.45 |
3 |
14.48 |
0.10 |
| |
|
44.66 |
20.38 |
14.48 |
|
|
|
the model
predicted distance ratios to the Virgo distance for the three possible
solutions, the corresponding predicted "Virgo distances'', the adopted class,
and the adopted Virgo distance for each galaxy. Now we discuss each galaxy in
some detail: for NGC 4548, only the second and third distances are
plausible; but the large HI deficiency leads us to attribute this galaxy to
class 2 as a true member of the Virgo cluster. Similarly, the large HI
deficiency of NGC 4321 makes us attribute it to class 2. On the
contrary, the insignificant deficiency of NGC 4639 leads to put it
into class 3, with a derived Virgo distance intermediate between
NGC 4321 and NGC 4548. For NGC 4535, the HI
deficiency is low, but putting it into class 1 would lead to a larger derived
Virgo distance than the previous galaxies, so we attribute it to class 2.
NGC 4496A belongs to the Virgo southern extension and is not HI
deficient; it is therefore tempting to put it into class 1, but again putting
it into class 2 leads to a derived Virgo distance in better agreement with the
remaining galaxies. Finally, NGC 4536 also belongs to the Virgo
southern extension and has a small HI deficiency, and it may be put into class 1 or 2, once its recession velocity is corrected for a random component. The
resulting mean value of the six derived Virgo distances is
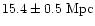 ,
which we adopt as our estimate of the cluster
distance.
,
which we adopt as our estimate of the cluster
distance.
At the referee's request, we have investigated what happens if a Virgo
distance of 21.5 Mpc is preferred from independent arguments. Then, four of the
five galaxies classified in class 2 now fall into class 1 (infalling galaxies),
NGC 4639 is the only true member of the Virgo cluster among the six, and
NGC 4548 position cannot be explained by the model. The high HI deficiency of
NGC 4321 is contradictory. This alternative distance is clearly less probable
according to these six galaxies with Cepheid distances. A definitive answer
will only become available with a larger sample of Virgo galaxies with accurate
distances.
Derivation of the Virgo cluster mass from the Tolman-Bondi model, and its
comparison with the virial mass estimate, have been discussed in T92, E99 and
E00. Here, we give a summary of the useful formulae and derive the Virgo mass
for our adopted model parameters. Let
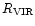 be the Virgo distance in
Mpc,
be the Virgo distance in
Mpc,
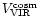 the cosmic recession velocity of Virgo in
the cosmic recession velocity of Virgo in
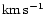 and d the radius normalized to the Virgo distance. The mass
enclosed within d is the product of the "Einstein - de Sitter mass'' within
the same radius by the mass excess due to the cluster. It is given in solar
mass units by:
and d the radius normalized to the Virgo distance. The mass
enclosed within d is the product of the "Einstein - de Sitter mass'' within
the same radius by the mass excess due to the cluster. It is given in solar
mass units by:
M(d) =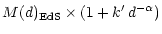 |
(12) |
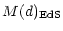 = =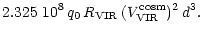 |
(13) |
k', the mass excess within d = 1, i.e. at the Local Group location, only
depends on the observed Virgo cluster velocity, the Virgocentric infall
velocity of the Local Group and the cosmological parameters of the adopted
background universe (q0 and
 ). It does not
depend on the Virgocentric density profile slope
). It does not
depend on the Virgocentric density profile slope 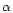 .
Its value is
the same as in E99, namely
k' = 0.606. For Virgo, we define the radius d
as corresponding to 8 degrees, which gives d = 0.141, in place of 0.105,
corresponding to 6 degrees in E99.
.
Its value is
the same as in E99, namely
k' = 0.606. For Virgo, we define the radius d
as corresponding to 8 degrees, which gives d = 0.141, in place of 0.105,
corresponding to 6 degrees in E99.
With
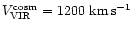 and
and
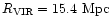 ,
we get
,
we get
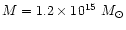 .
The virial
mass of Virgo as given by Tully & Shaya (1984) is:
.
The virial
mass of Virgo as given by Tully & Shaya (1984) is:
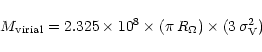 |
(14) |
where notations are those from Tully & Shaya. Their result transposed to
15.4 Mpc gives
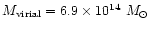 ,
so that
,
so that
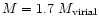 .
E99 found a coefficient 1.62 for their adopted
parameters of the Tolman-Bondi model.
.
E99 found a coefficient 1.62 for their adopted
parameters of the Tolman-Bondi model.
By comparison, Böhringer et al. (1994) estimate the mass of the
M 87 sub-cluster from X-ray emission measured by ROSAT to
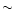 (1.5-
(1.5-
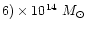 within a radius of 1.8 Mpc at
20 Mpc (5 degrees). Contributions from the M 49 and M 86
sub-clusters are negligible, at about (1-3
within a radius of 1.8 Mpc at
20 Mpc (5 degrees). Contributions from the M 49 and M 86
sub-clusters are negligible, at about (1-3
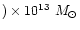 .
These values are confirmed by Schindler et al. (1999) who derive
.
These values are confirmed by Schindler et al. (1999) who derive
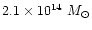 within 1.5 Mpc around M 87 (at
20 Mpc) and
within 1.5 Mpc around M 87 (at
20 Mpc) and
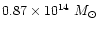 within 0.75 Mpc around
M 49. Our Tolman-Bondi mass for the same distance would be
within 0.75 Mpc around
M 49. Our Tolman-Bondi mass for the same distance would be
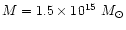 ,
almost one order of magnitude larger. We do
not have any explanation to offer for this discrepancy, but we note that our
large mass estimate and steep density profile are supported by Tully & Shaya
(1998), who find a Virgo mass of
,
almost one order of magnitude larger. We do
not have any explanation to offer for this discrepancy, but we note that our
large mass estimate and steep density profile are supported by Tully & Shaya
(1998), who find a Virgo mass of
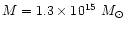 from a modeling of the velocity field of the Local Supercluster, assuming
a mass-to-light ratio of
from a modeling of the velocity field of the Local Supercluster, assuming
a mass-to-light ratio of
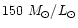 in the field, but
1000 for the Virgo cluster, and
in the field, but
1000 for the Virgo cluster, and
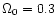
![[*]](/icons/foot_motif.gif) .
.
Disentangling the different components of the Virgo cluster is difficult and
somewhat subjective. However, the use of the Tolman-Bondi model allows us to
classify each galaxy into one of the three classes defined previously. We
did that independently for early-type and spiral galaxies. In each case, we
have built several diagrams: the first one is the histogram of the "Virgo
derived distances'', and it is shown in Fig. 4.
![\begin{figure}
\par\includegraphics[width=13.15cm,clip]{fig4.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg74.gif) |
Figure 4:
Histogram of the "Virgo derived distances'' for spiral galaxies
(left) and early-type galaxies (right). |
| Open with DEXTER |
Both histograms now
have a well-defined peak around the assumed Virgo distance and are symmetric, a
posteriori confirming our hypothesis. Mean distances in both cases are
compatible with the assumed distance of 16 Mpc. However, the rms dispersion is
slightly lower in the case of early-type galaxies: this may reveal that the
spiral sample class attribution is still not fully satisfying, or that our
restrictive hypothesis rejecting expanding components or projected galaxies in
the Tolman-Bondi model are not completely fulfilled.
The second diagram gives the velocity repartition among the different
classes, and is displayed in Fig. 5.
![\begin{figure}
\par\includegraphics[width=6.55cm,clip]{velgrp.eps}\includegraphics[width=6.55cm,clip]{velgrpel.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg75.gif) |
Figure 5:
Distribution of the recession velocities among the different
classes for spiral galaxies (left) and early-type galaxies (right). |
| Open with DEXTER |
In fact, we have split class 3
into two classes, because it clearly contains high velocity objects (class 4,
above 1600 kms-1), which are background galaxies, and low velocity
objects (class 3, 0-1300 kms-1), which are infalling galaxies from
behind the cluster. We have not convincingly identified any spiral galaxy
belonging to class 1; the only two early-type objects classified in class 1
exhibit low velocities (about 800 kms-1), which is difficult to
interpret; in fact, these two galaxies may be genuine members of the cluster
(class 2) with bad distance measurements; indeed, both galaxies have a velocity
dispersion smaller than 100 kms-1, which makes their fundamental plane
distances quite uncertain.
A third diagram gives the repartition of HI deficiency among the classes,
obviously only for spiral galaxies. It is displayed in Fig. 6.
![\begin{figure}
\par\includegraphics[width=6.55cm,clip]{defhi.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg76.gif) |
Figure 6:
Distribution of HI deficiency among the different classes for
spiral galaxies. |
| Open with DEXTER |
It is
clear that there is no highly deficient galaxies among classes 1, 3 and 4, as
expected because we used HI deficiency as one of our classification criteria.
Finally, Fig. 7 displays the repartition on the sky of spirals
and early-type galaxies with different symbols for different classes.
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{fig7.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg77.gif) |
Figure 7:
Distribution on the sky of the spiral galaxies (left) and
early-type galaxies (right). Filled squares correspond to class 1, crosses
to class 2, open squares to class 3 and open triangles to class 4. |
| Open with DEXTER |
If we
compare the distribution of the two types of galaxies, it clearly appears that
the different classes concentrate into common regions. One can easily recognize
the W group around (12.3 h, 6 )
and the M group around
(12.2 h, 13
)
and the M group around
(12.2 h, 13 ). Both groups have a mean distance ratio to Virgo of 2.1.
Galaxies at the same distance but slightly displaced from the main
concentration have been classified as group halo. Finally, galaxies with
intermediate distances between those of these groups and the Virgo distance,
and classified into our class 3, are interpreted as belonging to extended
filaments extracted from the background group and falling into Virgo. Such is
the case of the NGC 4222 group, which may link the M group to Virgo at
a mean distance ratio to Virgo of 1.2, and the NGC 4343 group, around
(12.4 h, 8
). Both groups have a mean distance ratio to Virgo of 2.1.
Galaxies at the same distance but slightly displaced from the main
concentration have been classified as group halo. Finally, galaxies with
intermediate distances between those of these groups and the Virgo distance,
and classified into our class 3, are interpreted as belonging to extended
filaments extracted from the background group and falling into Virgo. Such is
the case of the NGC 4222 group, which may link the M group to Virgo at
a mean distance ratio to Virgo of 1.2, and the NGC 4343 group, around
(12.4 h, 8 ), similar to the B group of G99 and introduced by de
Vaucouleurs (1961) as its W' group, and which may link the W group to
the Virgo cluster at a mean distance ratio to Virgo of 1.5. A small group
around NGC 4639 at (12.7 h, 14
), similar to the B group of G99 and introduced by de
Vaucouleurs (1961) as its W' group, and which may link the W group to
the Virgo cluster at a mean distance ratio to Virgo of 1.5. A small group
around NGC 4639 at (12.7 h, 14 )
can also be identified with the
eastern group of G99, although our group is less extended and less numerous;
it could be linked to a remote group of galaxies around NGC 4746.
)
can also be identified with the
eastern group of G99, although our group is less extended and less numerous;
it could be linked to a remote group of galaxies around NGC 4746.
In Table 2,
Table 2:
List of groups outside of the main Virgo cluster,
with their mean distance ratio to Virgo and a list of members with known
distance.
| Name |
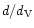 |
Location |
Members |
| NGC 4168 |
2.13 |
M group |
NGC 4168, NGC 4189, NGC 4193, NGC 4200, IC 769, IC 3061, IC 3099 |
| |
2.07 |
M halo |
NGC 4067, NGC 4152, IC 3074 |
| NGC 4222 |
1.24 |
M infall |
NGC 4222, IC 3033, IC 3066, IC 3105, UGC 7249 |
| NGC 4261 |
2.11 |
W group |
NGC 4180, NGC 4197, NGC 4215, NGC 4233, NGC 4235, NGC 4259, NGC 4260, |
| |
|
|
NGC 4261, NGC 4273, NGC 4281, IC 3225, CGCG 42-1, CGCG 42-36 |
| |
2.17 |
W halo |
IC 776, UGC 7579 |
| NGC 4343 |
1.46 |
W infall |
NGC 4252, NGC 4316, NGC 4318, NGC 4343, NGC 4353, NGC 4376, NGC 4390, |
| |
|
|
NGC 4411A, NGC 4434, NGC 4451, NGC 4466, IC 3115, IC 3322A, UGC 7423 |
| NGC 4639 |
1.41 |
|
NGC 4620, NGC 4633, NGC 4639, NGC 4651, IC 3742 |
| NGC 4746 |
1.92 |
|
NGC 4746, UGC 8085, UGC 8114 |
we propose a new nomenclature for all these groups,
based on the name of its main galaxy, together with a list of the members we
identified in this study. These lists are obviously not complete, because of
the lack of distance measurements of some other well-known members.
Table 3 lists other galaxies which have not been attributed to these
groups nor to the main cluster,
and are classified as background (class 4),
infalling from behind (class 3), or from in front (class 1).
After excluding all the galaxies which do not belong to the main cluster
according to our classification, we are left with 71 spiral and 52 early-type
galaxies. 67% of the original sample with distances are therefore considered
as true members of the cluster; not surprisingly, the spiral sample exhibits a
larger contamination (40%) than the early-type sample (20%). Among our 5
references, the proportion of true members varies from 56% (E00) and 61%
(F98) to 83% (T01).
Now that we have classified all the galaxies of our sample into the
different classes, we can return to the different distances adopted by
the various authors to the Virgo cluster.
We will first derive an average ratio of distances from a given reference to
the predicted distance given by the Tolman-Bondi model and an adopted Virgo
distance of 15.4 Mpc. For the 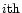 galaxy measured by reference j, we
have:
galaxy measured by reference j, we
have:
rij =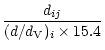 |
(15) |
rj =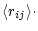 |
(16) |
In the second test we restrict our sample to true Virgo galaxies
(class 2) and compute the mean distance for each reference. The results will
depend much less on our adopted Tolman-Bondi model but should confirm it.
Table 4 gives the results.
We can see that for G99 and
T01, the agreement between the resulting mean Virgo distances from both
methods (Cols. 3 and 4, respectively) and the value adopted by these
authors (Col. 5) is satisfying. On the contrary, for F98 the resulting mean
Virgo distances are consistent from both methods, but smaller than their
adopted value: this is certainly due to inclusion of background galaxies into
their sample; indeed, among the 49 galaxies of their "fiducial sample'', 14
are classified by us as non-members of the Virgo cluster. For E00 the result
is inverse and the mean error is large: it seems therefore that there is a
discrepancy between their adopted Hubble constant (from Theureau et al.
1997) and the Virgo distance we derive from their data.
For these two references, we adopt as the mean Virgo distance the average over
the two determinations (Cols. 3 and 4). This gives 18.9 and 23.2 Mpc for
F98 and E00, respectively. If we apply to these distances the conversion
factors adopted in Sect. 2.3.2 to reduce F98 and E00 to a mean Virgo distance
of 16 Mpc, namely 0.832 and 0.678 respectively, we now get values close to
16 Mpc (15.7 and 15.8 Mpc, respectively).
However, it is important to keep in mind that the clean samples of true
members may still be affected by the incompleteness bias (Fouqué et al.
1990 for the specific case of the Virgo cluster; Teerikorpi
1997 for a general discussion), which may lead to average cluster
distances which are too short. To estimate the amount of this bias, we
have calibrated once more the B-band Tully-Fisher relation using the 21 calibrators from Freedman et al. (2001), and the 51 true members of
Virgo according to our classification, which best match the calibrator
properties (thus excluding peculiar, interacting, HI-truncated galaxies, and
restricting to morphological types between 2 and 8, inclinations between 37 and
90 degrees,
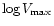 larger than 1.7),
larger than 1.7),
Table 3:
List of galaxies outside the main Virgo cluster
and not attributed to any group, with their distance ratio to Virgo.
| Name |
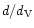 |
Class |
| NGC 4417 |
0.39 |
1 |
| NGC 4488 |
0.46 |
1 |
| NGC 4591 |
2.21 |
4 |
| NGC 4598 |
1.92 |
4 |
| NGC 4698 |
1.44 |
3 |
| IC 3298 |
2.27 |
4 |
| IC 3483 |
1.22 |
3 |
| UGC 7697 |
2.34 |
4 |
with data extracted from the
LEDA database. As usual, the slope of the Tully-Fisher relation is determined
from the Virgo sample (more numerous), and the intercept from the calibrators.
The rms dispersion is similar for both samples (0.41 for calibrators, 0.53 for
Virgo sample). The direct fit (appropriate to distance determinations) gives:
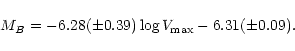 |
(17) |
The intercept for the Virgo sample,
 gives a distance modulus
of
gives a distance modulus
of
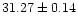 ,
or a distance of
,
or a distance of
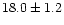 Mpc, which is larger than
our adopted distance from Cepheids. If we divide the sample of 51 Virgo
galaxies equally into large and small
Mpc, which is larger than
our adopted distance from Cepheids. If we divide the sample of 51 Virgo
galaxies equally into large and small
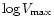 ,
we get mean distances
of:
,
we get mean distances
of:
It can therefore safely be concluded that the incompleteness bias does
not affect significantly our sample of true Virgo members (it would lead to a
smaller mean distance for galaxies with small rotation velocities, which are
more biased).
It can still be argued that the bias may be hidden, because the slope of
the Tully-Fisher relation, when determined from the Virgo cluster sample, may
be biased due to a possible incompleteness of the sample at small
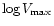 .
This is however not observed, as the direct slope
determined from the calibrators is
.
This is however not observed, as the direct slope
determined from the calibrators is
 ,
while an incompleteness
bias would predict a steeper slope as compared to the slope determined from the
Virgo sample (
,
while an incompleteness
bias would predict a steeper slope as compared to the slope determined from the
Virgo sample (
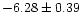 ).
).
The 0.3 mag difference between the Cepheid and Tully-Fisher distances is
worrying. Tenants of the long distance scale will see evidence that the
Tully-Fisher distance is the correct one, while most galaxies with Cepheid
distances are infalling on the front side of the cluster.
In this paper, we have investigated how the relativistic Tolman-Bondi model
as applied in E99 gives constraints on the Virgo cluster mass and distance, and
allows one to disentangle its quite intricate structure. Distances to
183 Virgo galaxies from 5 references have been used and averaged, together with
HI deficiency parameters for spirals, to classify the galaxies into 4 different
distance classes: an infalling component in front of Virgo, the Virgo cluster
itself, an infalling component behind the main cluster, and background groups.
The main results of the present study are:
- Among the 6 galaxies in the Virgo area with Cepheid distance measures,
NGC 4639 is well-known to be discrepant. Our model nicely explains
this apparent discrepancy, and the resulting mean distance to Virgo using all 6 calibrators is
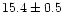 Mpc. However, the mean Tully-Fisher distance
derived from 51 spiral galaxies classified as true members of the cluster in
the present study, and calibrated using the same Cepheid distance system
(Freedman et al. 2001) is larger
Mpc. However, the mean Tully-Fisher distance
derived from 51 spiral galaxies classified as true members of the cluster in
the present study, and calibrated using the same Cepheid distance system
(Freedman et al. 2001) is larger
(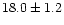 Mpc);
Mpc);
- The mass of the Virgo cluster derived from our model is large:
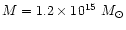 ,
which corresponds to 1.7 virial mass. Our adopted
mass profile is steeper than the light distribution (anti-biasing);
,
which corresponds to 1.7 virial mass. Our adopted
mass profile is steeper than the light distribution (anti-biasing);
- Apart from the well-known background groups which once contaminated Virgo
samples, we have identified a number of galaxies at intermediate distances
between these groups and the cluster itself, which we interpret as filaments
extracted from the background groups and falling into the cluster from behind;
- We have not been able to securely identify galaxies in front of the
cluster and falling into it. This supports Sandage & Tammann (1976)
who always argued that apparently foreground galaxies in the Virgo cluster
direction were in fact cluster members;
- Distances to the Virgo cluster adopted by F98 and E00 differ from what
would be expected using the distances predicted by our model and the mean
ratio of published to predicted distances. They also differ from the mean of
the published distances restricted to the true Virgo members. We also note that
the distances published in E00 are highly dispersed, even for true Virgo
members.
Acknowledgements
We have made use of the LEDA database (http://leda.univ-lyon1.fr),
supplied by the LEDA team at the CRAL - Observatoire de Lyon (France). We
warmly thank all the LEDA team members for their effort. We also thank Riccardo
Giovanelli and Martha Haynes for making their Arecibo General Catalog, from
which we have extracted the HI data used in this study, available to us.
Finally, we wish to thank the referee, Pekka Teerikorpi, for his very
constructive comments. T. S. acknowledges support from a fellowship of the
Ministerio de Educación, Cultura y Deporte of Spain. C. B. acknowledges ESO for
a visiting position in Santiago during which this work was started.
- Binggeli, B., Popescu, C. C., & Tammann, G. A. 1993,
A&AS, 98, 275
In the text
NASA ADS
- Binggeli, B., Sandage, A., & Tammann, G. A. 1985,
AJ, 90, 1681 (VCC)
In the text
NASA ADS
- Böhringer, H., Briel, U. G., Schwarz R. A., et al. 1994, Nature, 368, 828
In the text
NASA ADS
- de Vaucouleurs, G. 1961,
ApJS, 6, 213
In the text
NASA ADS
- de Vaucouleurs, G., & de Vaucouleurs, A. 1973,
A&A, 28, 109
In the text
NASA ADS
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin H. G.,
et al. 1991,
Third Reference Catalogue of Bright Galaxies
(Springer-Verlag, New-York) (RC3)
In the text
- Ekholm, T., Lanoix, P., Teerikorpi, P., Paturel, G.,
& Fouqué, P. 1999, A&A, 351, 827 (E99)
In the text
NASA ADS
- Ekholm, T., Lanoix, P., Teerikorpi, P., Fouqué, P.,
& Paturel, G. 2000, A&A, 355, 835 (E00)
In the text
NASA ADS
- Federspiel, M., Tammann, G. A., & Sandage, A. 1998,
ApJ, 495, 115 (F98)
In the text
NASA ADS
- Fouqué, P., Bottinelli, L., Gouguenheim, L.,
& Paturel, G. 1990, ApJ, 349, 1
In the text
NASA ADS
- Freedman, W. L., Madore, B. F., Gibson, B. K.,
et al. 2001,
ApJ, 553, 47
In the text
NASA ADS
- Ftaclas, C., Fanelli, M. N., & Struble, M. F. 1984,
ApJ, 282, 19
In the text
NASA ADS
- Fukugita, M., Okamura, S., & Yasuda, N. 1993, ApJ, 412, L13
In the text
NASA ADS
- Gavazzi, G., Boselli, A., Scodeggio, M., Pierini, D.,
& Belsole, E. 1999, MNRAS, 304, 595 (G99)
In the text
NASA ADS
- Gourgoulhon, E., Chamaraux, P., & Fouqué, P. 1992,
A&A, 255, 69
In the text
NASA ADS
- Haynes, M. P., & Giovanelli, R. 1984,
AJ, 89, 758
In the text
NASA ADS
- Kraan-Korteweg, R. C., Cameron, L. M., & Tammann, G. A.
1988, ApJ, 331, 620
In the text
NASA ADS
- Paturel, G. 1979,
A&A, 71, 106
In the text
NASA ADS
- Pierce, M. J., & Tully, R. B. 1988,
ApJ, 330, 579
In the text
NASA ADS
- Sandage, A., & Tammann, G. A. 1976,
ApJ, 207, L1
In the text
NASA ADS
- Schindler, S., Binggeli, B., & Böhringer, H. 1999,
A&A, 343, 420
In the text
NASA ADS
- Solanes, J. M., Giovanelli, R., & Haynes, M. P. 1996,
ApJ, 461, 609
In the text
NASA ADS
- Solanes, J. M., Manrique, A., González-Casado, G.,
et al. 2001, ApJ, 548, 97
In the text
NASA ADS
- Teerikorpi, P. 1997, ARA&A, 35, 101
In the text
NASA ADS
- Teerikorpi, P., Bottinelli, L., Gouguenheim, L.,
& Paturel, G. 1992, A&A, 260, 17 (T92)
In the text
NASA ADS
- Theureau, G., Hanski, M., Ekholm T., et al. 1997, A&A, 322, 730
In the text
NASA ADS
- Tonry, J. L., Dressler, A., Blakeslee, J. P.,
et al.
2001, ApJ, 546, 681 (T01)
(tables also available at http://www.ifa.hawaii.edu/jt/)
In the text
- Tully, R. B. 1982,
ApJ, 257, 389
In the text
NASA ADS
- Tully, R. B., & Fisher, J. R. 1977,
A&A, 54, 661
In the text
NASA ADS
- Tully, R. B., & Shaya, E. J. 1984,
ApJ, 281, 31
In the text
NASA ADS
- Tully, R. B., & Shaya, E. J. 1998,
in Evolution of Large Scale Structure,
ed. R. F. Stein, & A. G. W. Cameron
(ESO, Garching), 333
In the text
- van den Bergh, S., Pierce, M. J., & Tully, R. B. 1990,
ApJ, 359, 4
In the text
NASA ADS
- Yahil, A., Tammann, G. A., & Sandage, A. 1977,
ApJ, 217, 903
In the text
NASA ADS
- Yasuda, N., Fukugita, M., & Okamura, S. 1997,
ApJS, 108, 417
In the text
NASA ADS
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{fig1.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg9.gif)
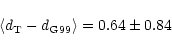
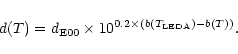
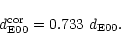
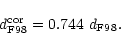
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{fig2.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg31.gif)
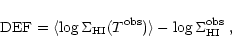
![\begin{figure}
\par\mbox{\includegraphics[height=5.8cm,clip]{1326f3_a1.eps}\hspa...
...\hspace*{5mm}
\includegraphics[height=5.75cm,clip]{1326f3_c2.eps} }
\end{figure}](/articles/aa/full/2001/33/aa1326/Timg44.gif)
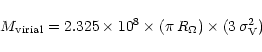
![\begin{figure}
\par\includegraphics[width=13.15cm,clip]{fig4.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg74.gif)
![\begin{figure}
\par\includegraphics[width=6.55cm,clip]{velgrp.eps}\includegraphics[width=6.55cm,clip]{velgrpel.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=6.55cm,clip]{defhi.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{fig7.eps} \end{figure}](/articles/aa/full/2001/33/aa1326/Timg77.gif)