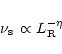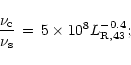Up: Hard X-ray properties of blazars
5 The average SED
In Fig. 10 we show the sequence of average SEDs as
published by F98, but including the [2-10 keV] averages spectral indices
and fluxes. The latter have been constructed considering only
the same samples considered by F98.
![\begin{figure}
\par\includegraphics[width=10cm,height=9.7cm,clip]{1156f10.eps}
\end{figure}](/articles/aa/full/2001/33/aa1156/Timg101.gif) |
Figure 10:
The average SED of the blazars studied by Fossati et al. (1998),
including the average values of the hard X-ray spectra.
The thin solid lines are the spectra constructed following the
parameterization proposed in this paper. |
It can be seen that in general the 2-10 keV fluxes and spectral indices
connect smoothly on the softer ROSAT data even if they are,
on average, flatter than the latter.
This is due to the emergence, in the hard X-ray band, of the inverse
Compton component which is progressively more dominant as the luminosity
increases.
For the average SED corresponding to the second lowest luminosity bin,
there is a mismatch between the soft and hard X-ray data.
By comparing the data of each source in common, we found that
all 5 sources were brighter when observed by ASCA or BeppoSAX
than at the time of the ROSAT observations.
We therefore believe that the mismatch is due to the variable nature of the
objects and the small number of sources in this luminosity bin.
The average spectral indices of the objects in common with F98 are listed
in Table 4, which also lists the average luminosities
at 4.47 keV (the logarithmic mid point between 2 and 10 keV).
The continuous lines in Fig. 10 correspond to a simple
parametric model derived by the one introduced by Fossati et al. (1998).
We introduce minor modifications, adopted both to better represent our data
at small luminosities and to follow a more physical scenario, in which the
low power HBLs can be described by a pure synchrotron-self Compton model
(see e.g. Ghisellini et al. 1998).
We remind the reader here of the key assumptions of the F98 parametric model:
- The observed radio luminosity
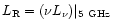 is assumed to be linearly proportional to the bolometric luminosity,
and related to the location of the synchrotron peak through:
is assumed to be linearly proportional to the bolometric luminosity,
and related to the location of the synchrotron peak through:
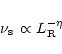 |
(1) |
where 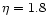 for
for
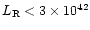 erg s-1 and
erg s-1 and
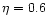 for
for
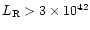 erg s-1.
erg s-1.
- The ratio between the Compton and the synchrotron peak
frequencies is constant:
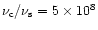 for all luminosities.
for all luminosities.
- The ratio between the power of the inverse Compton and the
radio powers is constant:
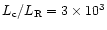 for all luminosities;
for all luminosities;
- The ratio between the radio and X-ray (at 1 keV) Compton
luminosity is fixed.
The SED is then constructed assuming for the synchrotron component
a flat (
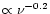 )
radio spectrum connecting to a parabola
(in log-log space) peaking at
)
radio spectrum connecting to a parabola
(in log-log space) peaking at
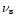 .
The junctions between the power law and the parabola is continuous.
For the inverse Compton spectrum it is assumed that an initial power law
of index
.
The junctions between the power law and the parabola is continuous.
For the inverse Compton spectrum it is assumed that an initial power law
of index
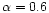 ends in another parabola peaking at
ends in another parabola peaking at
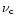 .
.
We modified the Fossati et al. (1998) description in the following way:
- We changed the values of
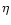 ,
assuming
,
assuming 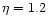 and
0.4 for
and
0.4 for 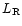 smaller and greater than 1043 erg s-1;
smaller and greater than 1043 erg s-1;
- The ratio
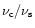 is assumed to be constant with the
same value as before for
is assumed to be constant with the
same value as before for
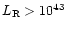 erg s-1, but for smaller radio
luminosity we set:
erg s-1, but for smaller radio
luminosity we set:
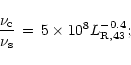 |
(2) |
- Below
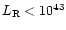 erg s-1 we assume that the
synchrotron and Compton peaks have the same luminosities.
For greater
erg s-1 we assume that the
synchrotron and Compton peaks have the same luminosities.
For greater 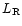 we assumed, as before,
we assumed, as before,
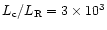 .
.
The spectra predicted by this new parameterization are shown in
Fig. 10 as thin solid lines.
As anticipated, the assumptions described above have a physical motivation.
In fact, for low luminosity sources, we have evidences that the seed
photons producing the Compton spectrum are the locally produced synchrotron
ones, with no or negligible contributions from seed photons produced
externally to the jet (e.g. from the Broad Line Region).
In this case:
- i)
- The ratio
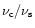 increases with
increases with
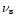 as long as
the scattering process is in the Thomson regime, and decreases
with
as long as
the scattering process is in the Thomson regime, and decreases
with
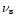 in the Klein Nishina regime;
in the Klein Nishina regime;
- ii)
- On average, the BL Lacertae objects detected by EGRET with
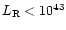 erg s-1 have roughly the same power in the synchrotron and Compton
components;
erg s-1 have roughly the same power in the synchrotron and Compton
components;
- iii)
- The radio luminosity
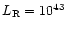 erg s-1may corresponds to the power
for which emission lines and/or external seed photons becomes important for
the formation of the inverse Compton spectrum
(see e.g. Ghisellini et al. 1998).
erg s-1may corresponds to the power
for which emission lines and/or external seed photons becomes important for
the formation of the inverse Compton spectrum
(see e.g. Ghisellini et al. 1998).


Up: Hard X-ray properties of blazars
Copyright ESO 2001