A&A 375, 739-751 (2001)
DOI: 10.1051/0004-6361:20010675

Hard X-ray properties of blazars[*]

D. Donato1 - G. Ghisellini1 - G. Tagliaferri1 - G. Fossati2


1 - Osservatorio Astronomico di Brera, Via Bianchi 46, 23807 Merate, Italy
2 - Center for Astrophysics and Space Sciences, University of California at San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0424, USA

Received 16 February 2001 / Accepted 3 May 2001

Abstract
We have considered all blazars observed in the X-ray band and for which the slope of the X-ray spectrum is available. We have collected 421 spectra of 268 blazars, including 12 archival unpublished ASCA spectra of 7 blazars whose analysis is presented here. The X-ray spectra of blazars show trends as a function of their power, confirming that the blazar overall energy distribution can be parameterized on the basis of one parameter only, i.e. the bolometric luminosity. This is confirmed by the relatively new hard (2-10 keV) X-ray data. Our results confirm the idea that in low power objects the X-ray emission mechanism is the synchrotron process, dominating both the soft and the hard X-ray emissions. Low energy peaked BL Lac objects are intermediate, often showing harder spectra in the hard X-ray band, suggesting that the synchrotron process dominates in the soft band, with the inverse Compton process dominating at high energies. The most powerful objects have X-ray spectra that are flat both in the soft and in the hard band, consistent with a dominating inverse Compton component.

Key words: BL Lacertae objects: general - X-rays: galaxies


1 Introduction

Thanks to $\gamma$-ray observations of EGRET, on board CGRO, we now know the overall spectral energy distribution (SED) of blazars. They are characterized, in $\nu$- $\nu F(\nu)$ plots, by two broad peaks. It is believed that the first, located in the IR-soft X-ray band, is due to synchrotron emission, while the second is due to the inverse Compton process by the same electrons producing the synchrotron part of the spectrum (Maraschi 1992; Sikora et al. 1994; but see Mannheim 1993 for a different interpretation). The 0.1-10 keV emission of blazars is therefore located in the minimum between the two peaks, where both processes (synchrotron and inverse Compton) can contribute. Observations in this band are therefore useful to characterize the relative importance of both processes. This can constrain models, allowing a better determination of the location of both peaks. Usually, a steep power law energy distribution in the X-ray band (with a spectral energy index $\alpha>1$, with $F \propto \nu^{-\alpha}$) is due to the tail of the synchrotron spectrum, while $\alpha<1$ flags the dominance of the inverse Compton spectrum. There are exceptions to this rule, such as HBL (High energy peaked BL Lacs) in a flaring state, which show a synchrotron spectrum peaking above 10 keV. One dramatic example of this behavior is Mkn 501, whose synchrotron peak energy, usually located below/at ${\simeq}1$ keV, shifted to 100 keV or more during its flare in April 1997 (Pian et al. 1998). In these cases the X-ray spectrum, usually steep during quiescence, becomes much flatter during flares. Fossati et al. (1998) (F98 hereafter) have shown that blazars form a sequence, with their SED changing in a continuous way as their bolometric power changes: low luminosity objects (HBL) have the synchrotron peak in the UV-soft X-ray band, and the inverse Compton peak between the GeV and the TeV band. The two components have approximately the same power. As the bolometric luminosity increases, both peaks shift to lower frequencies, and the Compton peak becomes increasingly dominant. This trend offers the opportunity to unify in a single scheme the many flavors of existing blazars, and calls for a physical explanation (see e.g. Ghisellini et al. 1998).

To check the reliability of this trend we have collected data for all blazars having available spectral information in the X-ray band. For the soft band [0.1-2 keV], most of the results come from ROSAT, while for the 2-10 keV band the results are gathered from the EXOSAT, ASCA and BeppoSAX satellites.

Besides the data already published, we searched for unpublished data in the ASCA public archive, finding 12 observations of 7 sources. Results of the analysis of these data are presented here. We then add these sources to our sample.

The entire sample forms the largest database in the X-ray range: 421 spectra of 268 blazars. The X-ray data have been complemented by additional information regarding the redshift (when available), the radio flux at 5 GHz and the optical flux (in the V band).

The paper is organized as follows; Sect. 2 is devoted to the analysis of the 12 ASCA spectra, while in Sect. 3 we present the entire set of data. In Sect. 4 we compare the results in the soft and the hard X-ray bands and check for correlations with other spectral parameters, such as the broad band spectral indices connecting the radio with the optical fluxes, the optical with the X-ray fluxes, and the radio with the X-ray fluxes. In Sect. 5 we discuss our findings in the framework of the scenario proposed by Fossati et al. (1998), suggesting an improvement connected to a possible physical difference between low and high power sources.

   
2 Analysis of ASCA data

We searched the ASCA public archive at HEASARC, finding 12 observations of 7 blazars that have not been analyzed and published before: 0405-123 and PKS 0420-014 (classified as Flat Spectrum Radio Quasars, FSRQs); B2 1308+326 and 1807+698 (classified as Low Peaked BL Lac objects, LBLs); 1ES 1028+511, 1553+511 and 1ES 2344+514 (classified as High Peaked BL Lac objects, HBLs).

1ES 1028+511 and 1ES 2344+514 have 3 separate observations each, while B2 1308+326 was observed twice. The search for unpublished observations is updated to November 1999. During the preparation of this work the "Tartarus" data base became available[*], presenting results of an automatic spectral and temporal analysis for the AGNs observed by ASCA.

2.1 Data reduction and spectral analysis

We extracted the spectra of all sources from the files produced by the Revision-2 data release and included data transmitted in all 3 modes (High, Medium and Low) to increase the signal/noise ratio. The event files are obtained from all four instruments on board ASCA: the Solid-State Imaging Spectrometers (SIS0 and SIS1) and the Gas Imaging Spectrometers (GIS2 and GIS3). For the SIS we used the event files converted into BRIGHT mode. For a description of the ASCA observatory see e.g. Tanaka et al. (1994).

To screen the SIS and GIS data we follow the criteria given in the ABC ASCA reduction guide, rejecting the data taken during the passage of the South Atlantic Anomaly, or with geomagnetic cutoff rigidity lower than 8 GeV/c, or with angles between the targets and the day/night terminator smaller than 20$^\circ$ or for Elevation angles smaller than 5$^\circ$.

The source spectra were extracted from circular regions centered on the sources, with radii of 6 arcmin for the GIS and 4 arcmin for the SIS0, while for the SIS1 the source is normally nearer to the detector border and we had to use a smaller radius of ${\sim} 3.3$ arcmin. For the GIS we extracted the background in circular regions with the same dimensions used for the sources but centered on a symmetric point with respect to the optical axis, where the contribution of the source to the counts was negligible. For the SIS, instead, the background was extracted from blank field files because the sources occupied a large area of the detector. On these blank fields we chose circular regions with the same radii and positions used for the sources.

For the GIS spectra we used the 1994 May response matrices, while for the SIS spectra we generated the matrices with the SISRMG program of the FTOOLS V3.6 package. The ARF files for both SIS and GIS were derived with the ASCAARF V2.62 program. The GIS and SIS data were fitted in the channel ranges 69-1020 and 15-510, corresponding to the energy ranges 0.7-10 and 0.4-10 keV, respectively. The spectra were rebinned in order to have at least 25 counts in each new bin.

The ASCA spectra were fitted using XSPEC V10 with four models: single or broken power law with free or fixed (Galactic) absorption. The cross section for photoelectric absorption is calculated following Morrison & McCammon (1983), while the Galactic column density in the direction of the sources was estimated from the 21 cm radio maps of neutral hydrogen (Brinkmann & Siebert 1994; Danly et al. 1992; Dickey & Lockman 1990; Elvis et al. 1989; Lamer et al. 1996; Lockman & Savage 1995; Murphy et al. 1996). The data were fitted simultaneously from all the instruments with the same model. However, the normalizations were left as independent parameters for each data set to account for the cross-calibration uncertainties between the four detectors, estimated to be of the order of 6%. The differences found between the various normalizations were always consistent with these uncertainties.

 

 
Table 1: Best fits of the 12 observations. a day/month/year; b 10-12 erg cm-2 s-1.
Source Obs. datea $N_{\rm H}$ $\Gamma$ $\chi_{\rm r}^2/{\rm d.o.f.}$ F[2-10]b $F_{\rm 1\,keV}$
    1021 cm-2       $\rm\mu Jy$
0405-123 09/08/1998 0.72 +0.51-0.63 1.76 +0.09-0.10 1.0/160 5.2 0.9
0420-014 31/08/1997 0.90 +1.04-0.81 1.86 +0.19-0.18 0.8/73 1.4 0.3
1028+511 28/04/1995 1.01 +0.23-0.21 2.53 +0.06-0.05 1.0/287 6.2 3.4
  29/04/1995 1.33 +0.18-0.17 2.59 +0.05-0.05 0.9/310 7.4 4.5
  08/05/1995 1.12 +0.12-0.12 2.49 +0.04-0.04 0.9/201 7.8 4.1
1308+326 10/06/1996 1.97 +2.96-1.97 1.99 +0.47-0.36 1.5/29 0.5 0.1
  11/06/1996 0.97 +1.01-0.97 1.74 +0.32-0.23 1.4/78 0.6 0.1
1553+113 16/08/1995 1.30 +0.62-0.61 2.47 +0.19-0.18 1.3/294 29.4 14.9
1807+698 05/11/1996 0.50 +0.28-0.27 1.75 +0.07-0.06 1.0/122 3.1 0.5
2344+514 10/01/1997 2.71 +0.17-0.17 2.13 +0.03-0.03 1.1/216 17.2 5.3
  23/01/1997 2.91 +0.34-0.33 2.39 +0.08-0.06 0.9/72 10.4 5.2
  10/12/1997 2.93 +0.37-0.35 2.31 +0.07-0.07 1.2/202 10.4 4.2


2.2 Results of the fits

The results of the 12 spectral fits of the 7 blazars observed by ASCA are reported in Table 1. The uncertainties for the spectral parameters are at the 90% confidence errors for two parameters of interest ( $\Delta \chi^2= 4.6$). The unabsorbed integrated 2-10 keV and monochromatic 1 keV fluxes are obtained using only the SIS0 data. As the observations presented in this paper were all taken after 1994, they are most likely affected by the so-called "excess $N_{\rm H}$" problem. This is due to a degradation of the SIS efficiency below 1 keV which can give incorrect results for the column density and/or other parameters. As suggested in the ASCA Web site, to avoid the calibration uncertainties we considered only the SIS data above 1 keV in the SIS+GIS combined fit. Of the four models considered, according to the F-test, the one that better represents the data in all twelve cases is the single power law with free $N_{\rm H}$. In some cases (detailed below) we obtain a value for the absorbing column greater (by a factor 3-10) than the Galactic value. Note that the results obtained by the automatic analysis presented in the "Tartarus" database are in excellent agreement with ours (not surprisingly, since the same model is adopted). What is somewhat surprising is that the broken power law model (either with free or fixed $N_{\rm H}$) did not significantly improve the fits. This may be indicative of true extra-absorption or a spectral behavior more complex than those here examined (one possibility being a gradual but continuous steepening of the spectrum).

In the following we will compare the spectral properties of blazars in the soft and hard X-ray bands considering only the single power law model. To this end, the results of this model allow a more uniform comparison.

The results of spectral fit for the 7 sources are discussed below, grouped in the three subclasses (FSRQ, LBL and HBL).

2.2.1 FSRQ

For 0405-123, the best fit gives a flat photon spectral index $\Gamma = 1.76 \pm 0.1$, indicating the dominance of the inverse Compton component. The derived $N_{\rm H}$ value is consistent with the Galactic value, $N_{\rm H}^{\rm Gal} = 0.37 \times 10^{21}$ cm-2 (Danly et al. 1992).

Similar results are obtained for PKS0420-014, with a photon spectral index $\Gamma = 1.86 \pm 0.19$. Also in this case the $N_{\rm H}$ value is consistent with the Galactic one ( $N_{\rm H}^{\rm Gal} = 0.94 \times 10^{21}$ cm-2, Elvis et al. 1989).

2.2.2 LBL

For B21308+326 there are two observations on two consecutive days. The spectra are quite noisy and also the reduced $\chi_{\rm r}^2$ are not very good. In both cases the best fits are obtained with a spectral index $\Gamma \simeq 1.75$-2.0. Due to the large error bars (see Table 1), the derived absorption column density can be consistent with the Galactic one ( $N_{\rm H}^{\rm Gal} = 0.11 \times 10^{21}$ cm-2, Lockman & Savage 1995).

For 1807+698 we obtained $\Gamma = 1.75\pm0.07$ and a value of $N_{\rm H}$consistent with the Galactic one ( $N_{\rm H}^{\rm Gal} = 0.44 \times 10^{21}$ cm-2, Murphy et al. 1996).

2.2.3 HBL

1ES1028+511 has been observed three times over a time span of two weeks. The source did not significantly vary in flux nor in shape ( $\Delta\Gamma \simeq 0.12$). In all cases the best fits are obtained for a value of $N_{\rm H}$ a factor 10 larger than the Galactic one ( $N_{\rm H}^{\rm Gal} = 0.12 \times 10^{21}$ cm-2; Lamer et al. 1996).

For 1553+113 the best fit is obtained with a value of $N_{\rm H}\sim 3$times larger than the Galactic one ( $N_{\rm H}^{\rm Gal} = 0.37 \times 10^{21}$ cm-2; Brinkmann & Siebert 1994).

The source 1ES2344+514 has been observed three times, twice in Jan. 1997 and one in Dec. 1997. Both the fluxes and the spectral indices show some variability. The best fit value for the $N_{\rm H}$ is about 1.5 times the Galactic value ( $N_{\rm H}^{\rm Gal} = 1.67 \times 10^{21}$ cm-2Dickey & Lockman 1990).

   
3 The catalogue

3.1 Starting samples

Our purpose is to have the most complete ensemble of spectral information (fluxes and spectral indices) in the X-ray band, from 0.1 to 10 keV, of all known blazars. We therefore considered all blazars detected in the X-ray band, for which also a measure of the X-ray spectral index is available. We collected the data obtained by five X-ray satellites: Einstein, EXOSAT, ROSAT, ASCA and BeppoSAX (see Table 2).

The first step was to recognize if a source belongs to the blazar class, and to which subclass (i.e. if a source is a FSRQ or an HBL or an LBL). We used several published lists of blazars and other publications describing single recognized sources. We considered the Slew Survey Sample (Elvis et al. 1992; Perlman et al. 1996), the 2 Jy sample of Wall & Peacock (1985), and the 1 Jy BL Lac sample (Stickel et al. 1991). In addition, we used the lists taken from the works of Bade et al. (1994); Bade et al. (1998); Brinkmann et al. (1994); Brinkmann et al. (1997); Cappi et al. (1997); Comastri et al. (1997); Ghisellini et al. (1993); Lamer et al. (1996); Laurent-Muehleisen et al. (1999); Sambruna et al. (1997); Wolter et al. (1998) and Worrall et al. (1990). We also checked the NASA Extragalactic Database (NED) for other objects classified as BL Lacs/blazars, or that could be classified as such.

The total number of considered blazars is 268. Of these, 227 have been observed by ROSAT and 88 have spectral information in the 2-10 keV band [of these latter sources, 77 have both soft (ROSAT) and hard X-ray data]. The details about the breakdown of source among HBL/LBL/FSRQ, and of the data among different X-ray telescopes is reported in Table 2. The data obtained with Einstein have large errors associated and for almost all sources better ROSAT data were available. For these reasons, the Einstein data are not used to derive any of the results (or figures) of this paper.

Some sources have been observed many times either by the same and/or by different satellites. For these sources, we chose the observation with the best $\chi_{\rm r}^2$ in the analysis[*].

For the most "famous" sources, like 3C 273, Mkn 421, Mkn 501, PKS 2155-304, we do not include the results of all the observations made by all satellites, but we have only listed few representative data (those with the best $\chi_{\rm r}^2$) for each of these sources (typically, one spectral datum for each observing satellite).

Of course, the resulting catalogue is not a complete sample. Nevertheless, it is the largest database of its kind, and we think it is representative of the entire blazar class. The large number of sources in each sub-category of blazars guarantees a meaningful comparison between their X-ray properties, and their relation with the fluxes in other bands.

 

 
Table 2: Number of observations obtained from various satellites and number of observed blazars (divided into different subclasses). For the total number of sources we have excluded multiple observations by different satellites of the same source.
  ${\rm No.}\,$oss. HBL LBL FSRQ
ASCA 52 14 9 24
EXOSAT 33 16 7 10
BeppoSAX 47 29 9 8
ROSAT 227 129 54 44
EINSTEIN 62 7 23 32
TOTAL 421 136 63 69


   
3.2 Format of the catalogue

Data are presented in Table 5 with the following format. For each source, Table 5 gives the IAU name, the redshift, the fluxes in the radio band (5 GHz), optical (V band) and X-ray (1keV) and the X-ray photon spectral index. In the last columns of Table 5 we also indicate to which subclass the blazar belongs to (1 for HBL, 2 for LBL and 3 for FSRQs) and the observing satellite (RO=ROSAT; AS=ASCA; EI=Einstein; EX=EXOSAT; SA=BeppoSAX).

For the radio fluxes we calculated the averaged value when there was more than one observation; the optical fluxes reported in the NED database are calculated using the indicated magnitude dereddened with the galactic extinction AB as reported by the NED database. When in the literature we found only the 0.1-2.4 keV and/or the 2-10 keV integrated fluxes, we derived the monochromatic ones at 1 keV using the corresponding X-ray spectral index. All fluxes presented in Table 5 are not K-corrected.

To compute the luminosities, we used H0= 50 km s-1 Mpc-1 and q0=0.5, and for the K-correction we assumed a radio spectral index $\alpha=0$ for all sources; an optical spectral index $\alpha = 0.5$ for HBL and $\alpha =1$ for the rest of the sources; for the X-ray data we used the listed X-ray spectral index. Also the broad band spectral indices have been K-corrected.

The K-correction for sources with unknown redshift was computed using the average redshift appropriate for each sub-class (i.e. $\langle z \rangle_{\rm HBL}= 0.249$, $\langle z \rangle_{\rm LBL}= 0.457$ and $\langle z \rangle_{\rm FSRQ}= 1.265$).

   
4 Results

Theoretical models that explain the nature of the observed behaviors of blazars predict a continuity between the various subclasses. To check if this is true for the objects belonging to our catalogue, we computed the distributions of redshifts, X-ray and broad band spectral indices and luminosities.

Moreover, another goal of this work is to compare the blazar characteristics observed in the soft and in the hard X-ray band. We divided our sources into two groups, one with the data obtained with ROSAT (0.1-2.4 keV) and another one with the data obtained with EXOSAT, ASCA, and BeppoSAX (2-10 keV). As anticipated (see Table 2) the first group of sources contains 227 objects, while the second one contains 88 sources (38 HBL, 19 LBL and 31 FSRQ). In addition, since the two sources 2344+514 and 1652+398 are very variable and we have data both for a quiescent and a flaring state, in the latter group we put the data of two observations (one for the high and one for the low state) for each of them.

 

 
Table 3: Average values of X-ray spectral indices, redshifts, $\nu L_\nu $ luminosities in different bands and broad band spectral indices. The listed errors are weighted errors.
  HBL LBL FSRQ
$\alpha _{\rm x}$[2-10 keV] $1.34\pm0.05$ $0.84\pm0.07$ $0.65\pm0.04$
$\alpha _{\rm x}$[0.1-2.4 keV] $1.28\pm0.04$ $1.39\pm0.08$ $0.76\pm0.06$
z $0.25\pm0.02$ $0.46\pm0.05$ $1.27\pm0.12$
Log $\nu_{\rm r}L_{\nu_{\rm r}}$ $41.51\pm0.07$ $43.65\pm0.16$ $44.93\pm0.13$
Log $\nu_{\rm o}L_{\nu_{\rm o}}$ $44.66\pm0.06$ $45.49\pm0.12$ $46.35\pm0.11$
Log $\nu_{\rm x}L_{\nu_{\rm x}}$ $44.62\pm0.08$ $44.52\pm0.15$ $45.89\pm0.11$
$\alpha_{\rm ro}$ $0.36\pm0.01$ $0.56\pm0.02$ $0.66\pm0.01$
$\alpha_{\rm ox}$ $1.03\pm0.02$ $1.38\pm0.02$ $1.21\pm0.02$
$\alpha_{\rm rx}$ $0.59\pm0.01$ $0.84\pm0.01$ $0.85\pm0.01$



  \begin{figure} \par\includegraphics[width=7.7cm,height=8.3cm,clip]{1156f1.eps} \end{figure} Figure 1: Distribution of the energy spectral index $\alpha _{\rm x}$ in the 2-10 keV hard X-ray energy band. Note the difference between the HBL and the other two subclasses of blazars. The KS test gives a probability $P=8\times 10^{-6}$ that the HBL and the LBL values are drawn from the same distribution ( $P=2\times 10^{-12}$ for HBL-FSRQ and P=0.03 for LBL-FSRQ).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,height=8.3cm,clip]{1156f2.eps} \end{figure} Figure 2: Distribution of the energy spectral index $\alpha _{\rm x}$ in the 0.1-2.4 keV soft X-ray energy band. In this case LBL are more similar to HBL than to FSRQ. KS test results: P=0.20 for HBL-LBL; 10-8 for HBL-FSRQ; $5\times 10^{-8}$ for LBL-FSRQ.
Open with DEXTER

   
4.1 Histograms

The distribution of spectral indices, redshifts and luminosities are shown by the histograms in Figs. 1-9. In the figure captions we give the probability, according to the Kolmogorov-Smirnov (KS) test, that two distributions are drawn from the same parent population, comparing HBLs and LBLs, HBLs and FSRQs, LBLs and FSRQs.

The mean values of the plotted quantities are listed in Table 3.

4.1.1 Spectral indices

The distributions of the energy spectral indices (Figs. 1 and 2) show that for FSRQ we have an average value less than unity in both energy ranges. This suggests that for this subclass of blazars we are observing only the inverse Compton component in the entire X-ray band, from 0.1 to 10 keV. For HBL, instead, the average energy spectral index is greater than unity, indicating that we are observing the synchrotron component after its peak. On average, LBL show a flattening going from the soft to the hard X-ray bands.

These results suggest that both the soft and the hard X-ray bands are dominated by the inverse Compton process in FSRQs and by the synchrotron process in HBL, while in LBL we have the synchrotron flux dominating in the soft band and the flatter Compton component emerging at higher X-ray energies.

  \begin{figure} \par\includegraphics[width=8cm,height=8.1cm,clip]{1156f3.eps} \end{figure} Figure 3: Redshift distribution for the three subclasses. Thick solid lines refer to the entire sample, while thin solid lines refer to sources with only ROSAT data. KS test results (for the entire sample): $P=2 \times 10^{-3}$ for HBL-LBL; $9\times 10^{-17}$ for HBL-FSRQ; $5\times 10^{-5}$ for LBL-FSRQ.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,height=8.4cm,clip]{1156f4.eps} \end{figure} Figure 4: Distribution of the radio luminosity for the three subclasses. Thick solid lines refer to the entire sample, while thin solid lines refer to sources with only ROSAT data. KS test results (for the entire sample): $7 \times 10^{-19}$ for HBL-LBL; $7 \times 10^{-33}$ for HBL-FSRQ; 10-6 for LBL-FSRQ.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,height=8.4cm,clip]{1156f5.eps} \end{figure} Figure 5: Distribution of the optical luminosity for the three subclasses. Thick solid lines refer to the entire sample, while thin solid lines refer to sources with only ROSAT data. KS test results (for the entire sample): $P=2 \times 10^{-7}$ for HBL-LBL; 10-22 for HBL-FSRQ; $3 \times 10^{-5}$ for LBL-FSRQ.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,height=8.4cm,clip]{1156f6.eps} \end{figure} Figure 6: Distribution of the X-ray luminosity for the three subclasses. Thick solid lines refer to the entire sample, while thin solid lines refer to sources with only ROSAT data. KS test results (for the entire sample): P=0.6 for HBL-LBL; $3 \times 10^{-13}$ for HBL-FSRQ; $2 \times 10^{-8}$ for LBL-FSRQ.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,height=8.2cm,clip]{1156f7.eps} \end{figure} Figure 7: Distribution of the broad band radio-optical spectral index for the three subclasses. Fluxes have been K-corrected as explained in the text. Thick solid lines refer to the entire sample, while thin solid lines refer to sources with only ROSAT data. KS test results (for the entire sample): $P=4 \times 10^{-18}$ for HBL-LBL; $2\times 10^{-35}$ for HBL-FSRQ; $4\times 10^{-4}$ for LBL-FSRQ.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,height=8.3cm,clip]{1156f8.eps} \end{figure} Figure 8: Distribution of the broad band optical-X-ray spectral index for the three subclasses. Fluxes have been K-corrected as explained in the text. Thick solid lines refer to the entire sample, while thin solid lines refer to sources with only ROSAT data. KS test results (for the entire sample): $P=5 \times 10^{-17}$ for HBL-LBL; 10-5 for HBL-FSRQ; 10-8 for LBL-FSRQ.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,height=8.2cm,clip]{1156f9.eps} \end{figure} Figure 9: Distribution of the broad band radio-X-ray spectral index for the three subclasses. Fluxes have been K-corrected as explained in the text. Thick solid lines refer to the entire sample, while thin solid lines refer to sources with only ROSAT data. KS test results (for the entire sample): $P=8 \times 10^{-39}$ for HBL-LBL; $5 \times 10^{-40}$ for HBL-FSRQ; 0.7 for LBL-FSRQ.
Open with DEXTER

4.1.2 Redshift

While the redshifts of FSRQs are quite uniformly distributed up to a value of $\simeq$3, BL Lacs have redshifts lower than 1 (and HBL have lower redshifts than LBL, see Fig. 3). There is no significant difference between the redshift distributions of sources observed in the hard and in the soft X-ray bands. Of the sources in our sample, about 25% have no measured redshift (38 HBL and 17 LBL). This incompletness, even if not severe, could bias the shown redshift distribution of HBLs towards the lower part (since larger redshifts are more difficult to measure).

4.1.3 Luminosities

From the radio, optical and 1 keV monochromatic fluxes we have calculated the "$\nu L_\nu $'' luminosities in the corresponding bands. The distributions of radio and optical luminosities (Figs. 4 and 5) show a continue variation in the three subclasses of blazar: HBLs are the least powerful sources, and FSRQs are the most luminous objects. this is more pronounced in the radio than in the optical band. The X-ray luminosities of HBLs and LBLs are very similar (Fig. 6), while FSRQs are more luminous by a factor of 10.

4.1.4 Broad band indices

Also the broad band spectral index $\alpha_{\rm ro}$ changes smoothly between the subclasses of blazar (Fig. 7). On average, it becomes steeper going from HBL to FSRQs. The optical to X-ray broad band index distribution (Fig. 8) is broader for HBL, with an average value smaller than for LBL and FSRQs. The spectral index $\alpha_{\rm rx}$ (Fig. 9) is on average the same for FSRQs and LBLs, and obviously flatter (by definition) for HBLs.

   
5 The average SED

In Fig. 10 we show the sequence of average SEDs as published by F98, but including the [2-10 keV] averages spectral indices and fluxes. The latter have been constructed considering only the same samples considered by F98.


  \begin{figure} \par\includegraphics[width=10cm,height=9.7cm,clip]{1156f10.eps} \end{figure} Figure 10: The average SED of the blazars studied by Fossati et al. (1998), including the average values of the hard X-ray spectra. The thin solid lines are the spectra constructed following the parameterization proposed in this paper.
Open with DEXTER

It can be seen that in general the 2-10 keV fluxes and spectral indices connect smoothly on the softer ROSAT data even if they are, on average, flatter than the latter. This is due to the emergence, in the hard X-ray band, of the inverse Compton component which is progressively more dominant as the luminosity increases.

For the average SED corresponding to the second lowest luminosity bin, there is a mismatch between the soft and hard X-ray data. By comparing the data of each source in common, we found that all 5 sources were brighter when observed by ASCA or BeppoSAX than at the time of the ROSAT observations. We therefore believe that the mismatch is due to the variable nature of the objects and the small number of sources in this luminosity bin.

The average spectral indices of the objects in common with F98 are listed in Table 4, which also lists the average luminosities at 4.47 keV (the logarithmic mid point between 2 and 10 keV).

 

 
Table 4: Average values of the X-ray luminosity at 4.47 keV ($\nu L_\nu $values) and average 2-10 keV spectral indices, for the sources in common with Fossati et al. (1998), for each radio luminosity bin.
$<\log\nu_{\rm r} L_{\nu_{\rm r}}>$ $<\log\nu_{\rm x}L_{\nu_{\rm x}}>$ $N_{\rm sources}$ $\alpha _{\rm x}$
  @4.47 keV   2-10 keV
<42 44.2 12 $1.39\pm0.21$
42-43 44.5 5 $1.19\pm0.21$
43-44 44.9 6 $0.95\pm0.11$
44-45 45.8 6 $0.68\pm0.02$
>45 47.0 11 $0.58\pm0.06$


The continuous lines in Fig. 10 correspond to a simple parametric model derived by the one introduced by Fossati et al. (1998). We introduce minor modifications, adopted both to better represent our data at small luminosities and to follow a more physical scenario, in which the low power HBLs can be described by a pure synchrotron-self Compton model (see e.g. Ghisellini et al. 1998). We remind the reader here of the key assumptions of the F98 parametric model:

$\bullet$
The observed radio luminosity $L_{\rm R}=(\nu L_\nu)\vert _{\rm 5~GHz}$ is assumed to be linearly proportional to the bolometric luminosity, and related to the location of the synchrotron peak through:

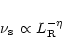\begin{displaymath}\nu_{\rm s} \, \propto L_{\rm R}^{-\eta} \end{displaymath} (1)

where $\eta=1.8$ for $L_{\rm R}<3\times 10^{42}$ erg s-1 and $\eta= 0.6$ for $L_{\rm R}>3\times 10^{42}$ erg s-1.

$\bullet$
The ratio between the Compton and the synchrotron peak frequencies is constant: $\nu_{\rm c}/\nu_{\rm s} = 5\times 10^8$ for all luminosities.

$\bullet$
The ratio between the power of the inverse Compton and the radio powers is constant: $L_{\rm c}/L_{\rm R} = 3\times 10^3$ for all luminosities;

$\bullet$
The ratio between the radio and X-ray (at 1 keV) Compton luminosity is fixed.

The SED is then constructed assuming for the synchrotron component a flat ( $\propto \nu^{-0.2}$) radio spectrum connecting to a parabola (in log-log space) peaking at $\nu_{\rm s}$. The junctions between the power law and the parabola is continuous. For the inverse Compton spectrum it is assumed that an initial power law of index $\alpha = 0.6$ ends in another parabola peaking at $\nu_{\rm c}$.

We modified the Fossati et al. (1998) description in the following way:

$\bullet$
We changed the values of $\eta$, assuming $\eta=1.2$ and 0.4 for $L_{\rm R}$ smaller and greater than 1043 erg s-1;

$\bullet$
The ratio $\nu_{\rm c}/\nu_{\rm s}$ is assumed to be constant with the same value as before for $L_{\rm R}>10^{43}$ erg s-1, but for smaller radio luminosity we set:

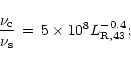\begin{displaymath}% {\nu_{\rm c} \over \nu_{\rm s}} \, = \, 5\times 10^8 L_{\rm R,43}^{-0.4}; \end{displaymath} (2)

$\bullet$
Below $L_{\rm R}<10^{43}$ erg s-1 we assume that the synchrotron and Compton peaks have the same luminosities. For greater $L_{\rm R}$ we assumed, as before, $L_{\rm c}/L_{\rm R} = 3\times 10^3$.
The spectra predicted by this new parameterization are shown in Fig. 10 as thin solid lines. As anticipated, the assumptions described above have a physical motivation. In fact, for low luminosity sources, we have evidences that the seed photons producing the Compton spectrum are the locally produced synchrotron ones, with no or negligible contributions from seed photons produced externally to the jet (e.g. from the Broad Line Region). In this case:

i)
The ratio $\nu_{\rm c}/\nu_{\rm s}$ increases with $\nu_{\rm s}$ as long as the scattering process is in the Thomson regime, and decreases with $\nu_{\rm s}$ in the Klein Nishina regime;

ii)
On average, the BL Lacertae objects detected by EGRET with $L_{\rm R}<10^{43}$ erg s-1 have roughly the same power in the synchrotron and Compton components;

iii)
The radio luminosity $L_{\rm R}=10^{43}$ erg s-1may corresponds to the power for which emission lines and/or external seed photons becomes important for the formation of the inverse Compton spectrum (see e.g. Ghisellini et al. 1998).

   
6 Correlations

In order to see if the proposed parameterization of the average SED of blazars (constructed on the basis of a subsample of the sources in our catalogue) can account for the general properties of all the blazars in our catalogue, we have investigated the correlations between the X-ray spectral index (both hard and soft) with the radio and X-ray luminosities and with the broad band spectral indices. We have then considered the correlations between broad band indices. The results are shown in Figs. 12-18 (solid line), where we have superposed the relations predicted by the new parameterization.

In Figs. 11 and 12 we show the hard and soft X-ray indices as a function of the radio and X-ray luminosity for all sources, and compare these data with the model expectations. Note that the latter have been constructed to describe the average properties of blazars, whatever the scatter around it. Bearing this in mind, we can consider the description of the model quite satisfactorily.

  \begin{figure} \par\includegraphics[width=7.5cm,height=7.6cm,clip]{1156f11.eps} \end{figure} Figure 11: Soft and hard X-ray spectral index vs. the radio luminosity. Circles: HBL, Squares: LBL, Triangles: FSRQs.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,height=7.6cm,clip]{1156f12.eps} \end{figure} Figure 12: Soft and hard X-ray spectral index vs. the X-ray luminosity. Circles: HBL, Squares: LBL, Triangles: FSRQs.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,height=9.1cm,clip]{1156f13.eps} \end{figure} Figure 13: Soft and hard X-ray spectral index vs. the broad band radio to X-ray index. Circles: HBL, Squares: LBL, Triangles: FSRQs.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,height=9.1cm,clip]{1156f14.eps} \end{figure} Figure 14: Soft and hard X-ray spectral index vs. the broad band radio to optical index. Circles: HBL, Squares: LBL, Triangles: FSRQs.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,height=9.1cm,clip]{1156f15.eps} \end{figure} Figure 15: Soft and hard X-ray spectral index vs. the broad band optical to X-ray index. Circles: HBL, Squares: LBL, Triangles: FSRQs.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,height=6.1cm,clip]{1156f16.eps} \end{figure} Figure 16: Radio to optical vs. optical to X-ray broad band indices. Circles: HBL, Squares: LBL, Triangles: FSRQs.
Open with DEXTER

In Fig. 13 we show the hard and soft X-ray indices as a function of the broad band index $\alpha_{\rm rx}$. The model well describes the small $\alpha_{\rm rx}$ part (corresponding to HBLs), but fails to describe the X-ray flattest sources with the steeper value of $\alpha_{\rm rx}$. This is due to two reasons: i) the slope of the power law of the Compton component is assumed to be $\alpha=0.7$, so that flatter indices are not possible; ii) the ratio between the radio and the 1 keV Compton luminosity is fixed for all sources. This results in a saturated value of $\alpha_{\rm rx}\sim 0.85$, occurring when the Compton component dominates at 1 keV (i.e. for powerful sources).

In Figs. 14 and 15 we show $\alpha_{\rm X}$ as a function of $\alpha_{\rm ro}$ and $\alpha_{\rm ox}$: the average properties are well described by the model.

In Fig. 16, we show the "classic'' $\alpha_{\rm ro}$- $\alpha_{\rm ox}$ diagram for the two subsamples of sources. Note that the model well describes all the data but those sources with the largest values of $\alpha_{\rm ox}$, corresponding to "transition'' sources between the LBLs and FSRQ.

 

 
Table 6: References used in Table 5. TW means This Work.
Ba94: Bade et al. (1994) Gh99: Ghisellini et al. (1999) Pa95: Padovani et al. (1995)
Ba98: Bade et al. (1998) BSGh: Ghisellini in BeppoSAX Archive Pa99: Padovani et al. (1999)
Br85: Bregman et al. (1985) Gi98: Giommi et al. (1998) Pe96: Perlman et al. (1996)
Br94: Brinkmann et al. (1994) Gi99: Giommi et al. (1999) Sa94: Sambruna et al. (1994)
Br97: Brinkmann et al. (1997) Go95: Ghosh et al. (1995) Sa97a: Sambruna et al. (1997)
Ca97: Cappi et al. (1997) Gr96: Greiner et al. (1996) Sa97b: Sambruna et al. (1997)
Co95: Comastri et al. (1995) Kh81: Khuer et al. (1981) Sa99: Sambruna et al. (1999)
Co97: Comastri et al. (1997) Ku98: Kubo et al. (1998) Sb96: Siebert et al. (1996)
Cs00: Costamante et al. (2000) IT90: Impey et al. (1990) Sb99: Siebert et al. (1999)
El99: Elvis et al. (1999) IT91: Impey et al. (1991) Sn97: Sing et al. (1997)
Fa97: Fabian et al. (1997) La96: Lamer et al. (1996) Ta00: Tagliaferri et al. (2000)
Fa98: Fabian et al. (1998) Le97: Leighly et al. (1997) Tv99: Tavecchio et al. (2000)
Fo98: Fossati et al. (1998) LM99: Laurent-Muehleisen et al. (1999) VV93: Veron-Cetty et al. (1993)
Fo98b: Fossati et al. (1998) Ma98b: Maraschi et al. (1998) Xu99: Xue et al. (1999)
Ge96: George et al. (1996) BSMc: Maccacaro in BeppoSAX Archive Ya98: Yaqoob et al. (1998)
Gh93: Ghisellini et al. (1993) Na96: Nass et al. (1996) Wa99: Watson et al. (1999)
Gh98: Ghisellini (1998) NED: NASA-IPAC Extragalactic Database Wo98: Wolter et al. (1998)
Gh98b: Ghisellini et al. (1998) Or98: Orr et al. (1998) Wo90: Worrall et al. (1990)



  \begin{figure} \par\includegraphics[width=7.7cm,height=6.1cm,clip]{1156f17.eps} \end{figure} Figure 17: Optical to X-ray vs. radio to X-ray broad band indices. Circles: HBL, Squares: LBL, Triangles: FSRQs.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,height=6.1cm,clip]{1156f18.eps} \end{figure} Figure 18: Radio to optical vs. radio to X-ray broad band indices. Circles: HBL, Squares: LBL, Triangles: FSRQs.
Open with DEXTER

Figures 17, and 18: note that HBL are well separated from the other classes of blazars. Note also that the model, by construction, has an asymptotic limit for $\alpha_{\rm rx}$, whose value therefore saturates at $\alpha_{\rm rx} \simeq 0.85$.

   
7 Discussion

The large database of X-ray spectra of blazars we have collected has allowed to test the blazar sequence scheme aiming to unify the different behaviors of blazars on the basis of a single parameter, i.e. the bolometric observed luminosity. We have found that the proposed parameterization can account for the average properties of the blazars in our sample, even if the scatter around the predicted average quantities is sometimes large.

We confirm, on a statistical basis, that more powerful blazars emit the X-rays by the inverse Compton process, while in less powerful objects the dominant mechanism is synchrotron, and the transition is smooth, with LBL possibly showing both contributions.

The Fossati et al. (1998) parameterization scheme to reproduce the blazar SED is able to fit also our new hard X-ray data and the correlations between broad band indices of the sources in our sample. However, we propose to slightly change this parameterization especially for the low power objects (i.e. the HBLs), in line with the idea that HBLs are characterized by a pure synchrotron self-Compton spectrum, without extra contributions produced by non locally produced seed photons.

In this paper, and in Fossati et al. (1998), the power law relation between the synchrotron peak frequency and the radio luminosity changes slope at some critical radio power, of the order of 3- $10\times 10^{42}$ erg s-1. This agrees with the absence of broad emission lines in these objects. It has still to be proven, however, if the non visibility of emission lines in low power objects is due to a genuine lack of emitting clouds, or is due to a weak ionizing continuum. If the latter hypothesis is true, then we expect that the broad line region indeed exists, but at smaller radii than in more powerful objects. In this case, the lack of the external Compton component is not due to the lack of external photons, but possibly to the fact that the dissipation region in these sources is beyond the broad line region: in this case the corresponding energy density of line photons is seen, in the comoving frame of the blob, depressed by the square of the bulk Lorentz factor.

Acknowledgements
We thank the anonimous referee for useful suggestions and Luigi Costamante for discussions. This research made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, Caltech, under contract with the National Aeronautics and Space Administration. We acknowledge finantial support from the MURST.

References

 

Online Material


   
Table 5: Column (1): name of the source (IAU); (2): redshift; (3): radio flux at 5 GHz in Jy; (4): reference for the radio flux; (5): optical flux at 5500 Å; (6): reference for the optical flux; (7): X-ray flux at 1 keV in $\mu $Jy; (8): reference for the X-ray flux; (9): X-ray photon spectral index; (10): error on the X-ray spectral index; (11): reference for the X-ray spectral index; (12): class (1=HBL, 2=LBL, 3=FSRQ); (13): reference for class; (14): observing satellite (AS=ASCA, RO= ROSAT, SA=BeppoSAX, EX=EXOSAT, EI=Einstein).
IAU Name z $F_{\rm R}$ Ref. $F_{\rm O}$ Ref. $F_{\rm X}$ Ref. $\Gamma$ err Ref. Type Ref. Sat
    (Jy)   (mJy)   ($\mu $Jy)              
0014+813 3.366 0.551 Ca97 0.910 Ca97 0.350 Ca97 1.890 1.700 Ca97 3 Ca97 RO
            0.430 Ca97 1.720 0.070 Ca97     AS
0016+731 1.781 1.750 NED 0.060 NED 0.050 Sa97b 1.430 1.100 Sa97b 3 Gh93 RO
0038-020 1.178 0.581 NED 0.030 NED 0.100 Wo90 1.400 1.100 Wo90 3 Wo90 EI
0045+214 ... 0.043 NED 0.310 NED 0.450 Br97 2.160 0.250 Br97 1 Br97 RO
0048-097 0.200 2.743 Fo98 1.750 Fo98 0.420 Pa98 1.730 0.380 Pa98 2 Gh93 SA
            0.770 Pa99 2.570 0.070 Pa99     RO
0109+182 ... 0.077 NED 1.440 NED 1.180 LM99 1.940 -- LM99 1 LM99 RO
0110+418 0.096 0.036 NED 0.390 NED 0.300 Br97 2.110 0.700 Br97 1 Br97 RO
0112-017 1.365 1.200 Kh81 0.230 NED 0.150 Wo90 1.570 1.000 Wo90 3 Wo90 EI
0112+227 ... 0.257 NED 2.220 NED 0.160 LM99 2.960 -- LM99 2 LM99 RO
0113+2504 ... 0.031 NED 0.120 NED 0.710 Br97 1.840 0.370 Br97 1 Br97 RO
0118-272 0.557 1.284 Fo98 1.560 Fo98 0.280 Fo98 2.740 0.740 Fo98 2 NED RO
0120+340 0.272 0.034 NED 3.600 NED 2.420 Cs00 1.960 0.020 Cs00 1 Br94 SA
            6.260 Br94 1.900 0.130 Br94     RO
0122+0903 0.339 0.001 Pa95 0.050 Pa95 0.030 Pe96 1.620 0.500 Pe96 1 Pe96 RO
0133+388 ... 0.053 NED 4.590 NED 2.390 LM99 2.160 -- LM99 1 LM99 RO
0133+476 0.859 2.920 Fo98 0.470 Fo98 0.300 Fo98 1.920 0.390 Fo98 3 Gh93 RO
0145+138 0.125 0.005 Fo98 0.260 Fo98 0.220 BSMc 2.320 0.160 BSMc 1 BSMc SA
0152+017 0.080 0.058 NED 0.900 NED 0.470 Br97 2.480 0.170 Br97 1 Br97 RO
0156+1032 ... 0.044 NED 0.950 NED 0.630 Br97 1.730 0.630 Br97 1 Br97 RO
0158+003 0.299 0.011 Fo98 0.230 Fo98 1.210 Fo98 2.460 0.270 Fo98 1 NED RO
            1.030 Wo98 2.270 0.180 Wo98     SA
0159+0835 ... 0.071 NED 0.120 NED 0.270 Br97 2.360 0.480 Br97 1 Br97 RO
0202+149 0.405 2.400 Co97 0.020 Co97 0.060 Co97 0.680 0.550 Co97 3 NED RO
0205+3509 0.318 0.004 Pa95 0.180 Pa95 0.150 Pe96 2.710 0.220 Pe96 1 Pe96 RO
            0.550 Wa99 2.220 0.040 Wa99     AS
0208-512 1.003 3.311 Fo98 0.590 Fo98 0.610 Fo98 2.040 0.040 Fo98 3 IT90 RO
            1.200 Ku98 1.660 0.090 Ku98     AS
0212+735 2.370 2.198 Fo98 0.450 Fo98 0.260 Fo98 0.660 0.590 Fo98 3 Gh93 RO
0214+517 0.049 0.271 NED 1.550 NED 1.600 LM99 2.040 -- LM99 1 LM99 RO
0219+428 0.444 1.040 Fo98 4.550 Fo98 0.720 Sa94 2.390 0.270 Sa94 2 Gh93 EX
            1.560 Fo98 2.600 0.170 Fo98     RO
            3.460 Wo90 2.620 0.850 Wo90     EI
0224+014 ... 0.009 Br97 0.120 NED 3.360 Br97 1.900 0.110 Br97 1 Br97 RO
0235+164 0.940 3.336 Fo98 2.580 Fo98 0.150 Go95 1.750 0.730 Go95 2 Gh93 EX
            0.270 Ku98 1.820 0.130 Ku98     AS
            1.150 Fo98 2.590 0.860 Fo98     RO
            1.510 Wo90 3.250 2.100 Wo90     EI
0237-233 2.223 3.520 Kh81 0.810 NED 0.310 Wo90 1.620 1.250 Wo90 3 Wo90 EI
            0.390 Re97 1.680 0.060 Re97     AS
0250+172 ... 0.035 NED 2.060 NED 0.730 LM99 2.020 -- LM99 1 LM99 RO
0257+3429 0.245 0.010 Pa95 0.140 Pa95 0.020 Pe96 2.670 0.320 Pe96 1 Pe96 RO
0301-243 ... 0.397 NED 0.980 NED 0.270 La96 2.680 0.310 La96 2 La96 RO


 
Table 5: continued.
IAU Name z $F_{\rm R}$ Ref. $F_{\rm O}$ Ref. $F_{\rm X}$ Ref. $\Gamma$ err Ref. Type Ref. Sat
    (Jy)   (mJy)   ($\mu $Jy)              
0316+090 ... 0.045 NED 1.160 NED 0.020 LM99 4.280 -- LM99 2 LM99 RO
0317+1834 0.190 0.017 Pa95 0.210 Pa95 0.170 Pe96 2.320 0.240 Pe96 1 Wo98 RO
            3.060 Sa94 1.800 0.200 Sa94     EX
            2.050 Wo98 2.080 0.100 Wo98     SA
0323+022 0.147 0.042 Fo98 0.900 Fo98 6.810 Wo90 2.160 0.230 Wo90 1 Wo90 EI
            4.000 Sa94 2.730 0.100 Sa94     EX
            1.460 BSMc 2.410 0.120 BSMc     SA
            0.730 Ku98 2.740 0.160 Ku98     AS
            3.210 Fo98 2.270 0.090 Fo98     RO
0331-365 0.308 0.009 VV93 0.240 NED 0.340 La96 2.200 0.490 La96 1 La96 RO
0332-403 1.445 2.600 Ca97 0.140 Ca97 0.140 Ca97 1.600 0.120 Ca97 3 Ca97 AS
0333+321 1.258 2.500 Ca97 0.520 Gh93 1.600 Ca97 1.530 0.920 Ca97 3 Gh93 RO
            1.340 Ku98 1.600 0.050 Ku98     AS
            2.320 Wo90 3.730 2.100 Wo90     EI
            0.440 Go95 1.360 0.260 Go95     EX
0347-121 0.188 0.009 Fo98 0.190 Fo98 2.050 Wo98 2.170 0.100 Wo98 1 Wo98 SA
            2.560 Fo98 2.120 0.090 Fo98     RO
0350-3712 0.165 0.017 VV93 0.590 NED 0.350 La96 2.170 0.260 La96 1 La96 RO
0403-132 0.571 2.889 Fo98 0.540 Fo98 0.400 Fo98 1.780 0.220 Fo98 3 IT90 RO
            0.490 Wo90 4.300 4.300 Wo90     EI
0405-123 0.574 1.960 Fo98 5.170 Fo98 0.090 TW 1.760 0.090 TW 3 Sa97b AS
            1.160 Fo98 2.150 0.170 Fo98     RO
0406+121 1.020 0.746 Na96 0.120 NED 0.050 La96 1.790 0.450 La96 2 La96 RO
0414+009 0.287 0.070 Fo98 0.850 Fo98 5.220 Wo98 2.540 0.100 Wo98 1 Wo98 SA
            5.460 Sa94 2.150 0.070 Sa94     EX
            4.690 Wo98 2.630 0.080 Wo98     RO
            4.620 Ku98 2.620 0.040 Ku98     AS
0419+1943 0.512 0.008 Pa95 0.030 Pa95 0.300 Pe96 1.720 0.270 Pe96 1 Pe96 RO
0420-014 0.915 3.720 Co97 0.340 Co97 0.370 Wo90 0.850 2.100 Wo90 3 Co97 EI
            0.280 TW 1.860 0.180 TW     AS
0426-380 1.030 1.416 Fo98 0.230 Fo98 0.090 Fo98 3.200 1.250 Fo98 2 NED RO
0430+052 0.033 7.526 NED 3.910 Gh93 3.240 Go95 1.760 0.070 Go95 3 Gh93 EX
0438-436 2.852 6.189 Fo98 0.410 Fo98 0.190 Ca97 1.420 0.060 Ca97 3 Ca97 AS
            0.150 Fo98 1.720 0.390 Fo98     RO
0454+844 0.112 1.430 Fo98 1.050 Fo98 0.030 Fo98 1.870 0.590 Fo98 2 Gh93 RO
0502+675 ... 0.032 Fo98 0.790 Fo98 8.510 Wo98 2.340 0.060 Wo98 1 Wo98 SA
            7.740 Br94 1.910 0.290 Br94     RO
0505+042 ... 0.121 NED 0.960 NED 0.730 LM99 2.350 -- LM99 1 LM99 RO
0507-040 0.304 0.027 Fo98 0.110 Fo98 3.000 Sa94 1.770 0.260 Sa94 1 NED EX
0521-365 0.055 9.700 Co97 2.380 Co97 1.230 Wo90 2.140 1.650 Wo90 3 Gh93 EI
            2.120 Co97 1.890 0.050 Co97     RO
            1.780 Sa94 1.850 0.330 Sa94     EX
0528+134 2.060 3.980 Fo98 0.210 Fo98 1.590 Fo98 1.540 0.290 Fo98 3 Gh93 RO
            1.480 Ku98 1.580 0.050 Ku98     AS
            0.310 Gh98b 1.480 0.040 Gh98b     SA
            0.220 Br85 2.600 -- Br85     EI
0537-441 0.896 4.755 Fo98 1.570 Fo98 0.400 Sa94 1.300 0.600 Sa94 2 Gh93 EX
            0.780 Fo98 2.040 0.330 Fo98     RO
            0.170 Wo90 1.270 1.700 Wo90     EI
0537-286 3.104 0.990 Ca97 0.040 Ca97 0.180 Ca97 1.360 0.060 Ca97 3 Ca97 AS
            0.170 Ca97 1.500 0.450 Ca97     RO
0548-322 0.069 0.170 Fo98 1.370 Fo98 8.220 Ku98 1.960 0.020 Ku98 1 NED AS
            9.590 Fo98 1.950 0.050 Fo98     RO
            6.460 Gh99 2.040 0.070 Gh99     SA
            7.710 Sa94 1.980 0.060 Sa94     EX
            9.960 Wo90 1.690 0.120 Wo90     EI
0556-3838 0.034 0.068 Pa95 0.530 Pa95 2.200 Ge96 2.520 0.100 Ge96 1 Ge96 RO
            1.730 Ge96 2.510 0.100 Ge96     AS
0607+7108 0.267 0.018 Pa95 0.050 Pa95 0.030 Pe96 2.210 0.320 Pe96 1 Pe96 RO


 
Table 5: continued.
IAU Name z $F_{\rm R}$ Ref. $F_{\rm O}$ Ref. $F_{\rm X}$ Ref. $\Gamma$ err Ref. Type Ref. Sat
    (Jy)   (mJy)   ($\mu $Jy)              
0615+820 0.710 1.000 Kh81 0.470 NED 0.040 Sa97b 1.680 0.590 Sa97b 3 Gh93 RO
0637-752 0.651 5.849 Fo98 2.380 Fo98 1.060 Wo90 1.580 0.800 Wo90 3 Sa97b EI
            3.760 Fo98 1.450 0.480 Fo98     RO
            0.490 Ya98 1.640 0.070 Ya98     AS
0642+449 3.400 1.204 NED 0.150 NED 0.120 Wo90 1.410 1.300 Wo90 3 Wo90 EI
0647+250 ... 0.077 NED 3.710 NED 6.010 Br94 2.470 0.320 Br94 1 Br94 RO
0651+428 0.126 0.188 NED 0.770 NED 0.360 LM99 3.590 -- LM99 1 LM99 RO
0656+426 0.059 0.480 NED 0.890 NED 0.130 LM99 3.180 -- LM99 2 LM99 RO
0706+5913 0.125 0.080 NED 0.180 NED 1.830 Br94 2.150 0.220 Br94 1 Br94 RO
0716+714 0.300 1.150 Fo98 2.200 Fo98 0.990 Fo98 2.770 0.090 Fo98 2 Gh93 RO
            0.370 Ku98 2.070 0.120 Ku98     AS
            0.500 Wo90 5.750 4.400 Wo90     EI
0735+178 0.424 2.490 Fo98 1.660 Fo98 0.220 Fo98 2.340 0.510 Fo98 2 Gh93 RO
            0.290 Wo90 1.710 0.400 Wo90     EI
            0.140 Ku98 1.760 0.200 Ku98     AS
0736+017 0.191 1.999 Fo98 1.330 Fo98 0.370 Wo90 4.200 3.500 Wo90 3 IT90 EI
            0.640 Sa99 1.760 0.040 Sa99     AS
            1.490 Fo98 2.820 0.600 Fo98     RO
0737+746 0.315 0.024 Fo98 0.650 Fo98 0.880 Wo98 2.530 0.250 Wo98 1 Wo98 SA
            1.110 Fo98 1.910 -- Fo98     RO
0754+100 0.660 1.480 Pa95 3.640 Pa95 0.720 Sa94 2.110 0.650 Sa94 2 Sa94 EX
0804+499 1.433 2.050 Co97 0.390 Co97 0.170 Co97 1.560 0.360 Co97 3 Gh93 RO
0806+3504 0.082 0.180 NED 0.660 NED 0.740 Ba98 2.870 -- Ba98 1 Ba98 RO
0806+524 0.138 0.177 NED 3.150 NED 4.910 Br94 2.930 0.160 Br94 1 Br94 RO
0806+595 ... 0.042 NED 1.410 NED 0.710 LM99 1.500 -- LM99 1 LM99 RO
0808+019 ... 0.670 Pa95 0.480 Pa95 0.380 Wo90 1.920 1.400 Wo90 2 Wo90 EI
0812+026 ... 0.071 NED 6.250 NED 1.850 Br97 2.160 0.110 Br97 1 Br97 RO
0814+425 0.258 3.500 Fo98 0.150 Fo98 0.050 Fo98 1.160 0.780 Fo98 2 IT91 RO
0820+225 0.951 1.977 Fo98 0.060 Fo98 0.050 Fo98 2.050 0.470 Fo98 2 NED RO
0828+493 0.548 1.158 Fo98 0.130 Fo98 0.040 Fo98 1.680 0.630 Fo98 2 NED RO
0829+046 0.180 2.105 Pa95 1.450 Pa95 0.400 Wo90 3.260 3.400 Wo90 2 Gh93 EI
0833+3300 0.671 0.004 Ba98 0.020 NED 0.370 Ba98 1.570 -- Ba98 1 Ba98 RO
0836+710 2.170 2.590 Fo98 1.060 Fo98 1.270 Ca97 1.320 0.030 Ca97 3 Gh93 AS
            2.260 Tv99 1.310 0.030 Tv99     SA
            1.600 Fo98 1.420 0.040 Fo98     RO
0847+115 0.198 0.022 Br97 0.900 NED 1.980 Br97 2.500 0.090 Br97 1 Br97 RO
0850+443 ... 0.075 NED 0.090 NED 0.190 Br97 2.800 0.300 Br97 1 Br97 RO
0851+202 0.306 2.173 Fo98 2.640 Fo98 0.930 Fo98 2.500 0.170 Fo98 2 Gh93 RO
            2.240 Sa94 2.370 0.100 Sa94     EX
            0.370 Pa99 1.710 0.240 Pa99     SA
            0.730 Ku98 1.620 0.050 Ku98     AS
0855+143 1.408 0.890 Br85 0.030 NED 0.320 Br85 2.000 -- Br85 3 NED EI
0906+430 0.670 1.300 Fo98 0.160 Fo98 0.110 Fo98 1.570 0.100 Fo98 3 Gh93 RO
0906+311 0.274 0.087 NED 2.050 NED 0.650 Ba98 2.210 -- Ba98 1 Ba98 RO
0912+297 ... 0.228 Na96 1.000 Pa95 1.060 Pa99 2.250 0.140 Pa99 1 NED SA
            0.510 Wo90 1.760 0.700 Wo90     EI
            0.580 La96 2.310 0.240 La96     RO
0913+5251 0.190 0.067 NED 0.060 NED 0.590 Ba98 2.180 -- Ba98 1 Ba98 RO
0917+449 2.180 1.030 Co97 0.070 Co97 0.470 Co97 1.390 0.100 Co97 3 NED RO
0922+7459 0.638 0.003 Pa95 0.050 Pa95 0.150 Pe96 1.780 0.140 Pe96 1 Pe96 RO
0923+392 0.699 8.101 Fo98 0.430 Fo98 0.620 Fo98 2.260 0.130 Fo98 3 Gh93 RO
            0.370 Wo90 1.360 0.190 Wo90     EI
            0.880 Sa99 1.880 0.050 Sa99     AS
0925+5026 ... 0.558 NED 1.520 NED 0.120 Br97 2.300 0.390 Br97 2 Br97 RO
0927+500 0.188 0.015 Na96 0.500 NED 4.000 Ba98 1.880 -- Ba98 1 Ba98 RO
0945+408 1.252 1.450 NED 0.380 NED 0.110 Sa97b 1.960 0.230 Sa97b 3 IT91 RO
0950+445 0.207 0.003 Fo98 0.120 Fo98 0.290 Fo98 2.760 0.250 Fo98 1 NED RO
0952+656 ... 0.027 LM99 0.800 NED 0.150 LM99 2.230 -- LM99 1 LM99 RO
0954+556 0.909 2.169 Fo98 0.430 Fo98 0.100 Fo98 2.170 0.140 Fo98 3 IT91 RO


 
Table 5: continued.
IAU Name z $F_{\rm R}$ Ref. $F_{\rm O}$ Ref. $F_{\rm X}$ Ref. $\Gamma$ err Ref. Type Ref. Sat
    (Jy)   (mJy)   ($\mu $Jy)              
0954+658 0.367 1.589 Fo98 1.720 Fo98 0.160 Fo98 1.960 1.310 Fo98 2 Gh93 RO
1008+4705 0.343 0.004 Na96 0.090 NED 1.510 Ba94 2.340 0.270 Ba94 1 Ba94 RO
1009+427 0.364 0.056 NED 0.960 NED 1.110 Br97 1.840 0.090 Br97 1 Br97 RO
1011+496 0.200 0.286 Fo98 1.620 Fo98 2.150 Fo98 2.490 0.080 Fo98 1 NED RO
1019+5139 0.141 0.002 Pa95 0.210 Pa95 0.790 Pe96 1.520 -- Pe96 1 Pe96 RO
1028+511 0.361 0.044 Fo98 0.800 Fo98 3.350 TW 2.530 0.050 TW 1 NED AS
            4.070 TW 2.490 0.040 TW     AS
            4.480 TW 2.590 0.050 TW     AS
            4.940 BSMc 2.410 0.040 BSMc     SA
            2.550 Fo98 2.440 0.050 Fo98     RO
1034-293 0.312 1.510 Kh81 1.110 NED 0.240 Sa97b 1.410 0.360 Sa97b 3 Gh93 RO
1034-293 0.312 1.510 NED 0.930 Gh93 0.160 Wo90 0.660 1.800 Wo90 2 Gh93 EI
1037+571 ... 0.088 NED 0.770 NED 0.380 Sb99 2.420 0.250 Sb99 1 Br97 SA
            0.210 Br97 2.500 0.190 Br97     RO
1039+811 1.260 1.140 Kh81 0.980 NED 0.180 Sa97b 1.830 0.130 Sa97b 3 Gh93 RO
1040+123 1.029 1.560 Kh81 0.470 Gh93 0.100 Wo90 1.450 0.900 Wo90 3 Gh93 EI
1047+546 ... 0.004 Br97 0.040 NED 0.070 Br97 1.630 0.370 Br97 1 Br97 RO
1053+494 0.140 0.019 LM99 0.430 NED 0.090 LM99 2.620 -- LM99 1 LM99 RO
1055+018 0.888 3.470 Fo98 0.400 Fo98 0.210 Fo98 1.930 0.440 Fo98 3 NED RO
1055+567 0.144 0.260 NED 1.810 NED 0.470 Br97 2.310 0.130 Br97 1 Br97 RO
            2.190 Sb99 2.760 0.080 Sb99     AS
            1.080 Sb99 2.780 0.250 Sb99     SA
1101+384 0.031 0.722 Fo98 16.970 Fo98 58.370 Fo98b 2.820 0.030 Fo98b 1 Gh93 SA
            23.850 Ku98 2.970 0.020 Ku98     AS
            36.100 Fo98 3.100 0.080 Fo98     RO
1101-232 0.186 0.066 Fo98 0.640 Fo98 10.230 Wo98 2.030 0.050 Wo98 1 Wo98 SA
            11.200 Wo98 2.430 0.080 Wo98     RO
            19.630 Wo90 2.310 0.180 Wo90     EI
            17.740 Sa94 2.500 0.170 Sa94     EX
1112+3452 0.212 0.004 Ba98 0.060 NED 0.810 Ba98 2.290 -- Ba98 1 Ba98 RO
1114+2030 ... 0.074 NED 3.210 NED 7.310 Br97 1.900 0.050 Br97 1 Br97 RO
1118+424 0.124 0.035 Fo98 0.560 Fo98 1.830 BSMc 2.620 0.070 BSMc 1 BSMc SA
            0.670 LM99 2.300 -- LM99     RO
1133+6753 0.135 0.048 NED 0.450 NED 3.230 Br94 2.390 0.240 Br94 1 Br94 RO
1133+704 0.046 0.274 Fo98 4.140 Fo98 4.870 Sa94 2.340 0.060 Sa94 1 NED EX
            9.200 Wo90 1.970 0.170 Wo90     EI
            2.620 Fo98 2.510 0.100 Fo98     RO
            2.610 Wo98 2.470 0.090 Wo98     SA
1144-379 1.048 2.779 Fo98 0.800 Fo98 0.140 Pa98 1.700 0.030 Pa98 2 IT90 SA
            0.410 Pa99 2.540 0.190 Pa99     RO
1146-037 0.341 0.354 NED 0.630 NED 0.580 Wo90 1.390 0.710 Wo90 3 Wo90 EI
1147+245 0.200 1.385 Fo98 1.200 Fo98 0.300 Go95 1.960 0.620 Go95 2 Gh93 EX
            0.040 Fo98 2.180 0.790 Fo98     RO
1148+592 ... 0.134 NED 0.480 NED 0.270 Br97 1.620 0.230 Br97 1 Br97 RO
1150+497 0.334 0.699 NED 0.560 NED 0.550 Sa97b 2.140 0.050 Sa97b 3 Sa97b RO
            0.630 Sa99 1.770 0.050 Sa99     AS
1150+812 1.250 1.180 Kh81 0.180 NED 0.090 Sa97b 1.450 0.310 Sa97b 3 Gh93 RO
1156+295 0.729 1.543 NED 6.640 NED 0.440 Sa94 2.300 0.470 Sa94 3 NED EX
1206+416 ... 0.515 NED 1.150 NED 0.100 LM99 2.100 -- LM99 2 LM99 RO
1207+3945 0.615 0.006 Pa95 0.080 Pa95 0.280 Pe96 2.130 0.100 Pe96 1 Pe96 RO
1212+0748 0.130 0.094 NED 1.550 NED 0.620 Br97 1.880 0.130 Br97 1 Br97 RO
1215+303 0.237 0.445 Fo98 3.110 Fo98 0.490 Fo98 2.880 0.080 Fo98 2 Gh93 RO
            0.590 Wo90 2.420 0.900 Wo90     EI
1217+348 ... 0.355 NED 0.550 NED 0.100 La96 1.980 0.710 La96 2 La96 RO
1217+023 0.240 0.698 NED 0.890 NED 0.780 Wo90 1.700 0.350 Wo90 3 Wo90 EI
1218+304 0.130 0.056 Fo98 1.390 Fo98 7.510 Sa94 2.460 0.140 Sa94 1 NED EX
            10.050 Fo98 2.220 0.030 Fo98     RO


 
Table 5: continued.
IAU Name z $F_{\rm R}$ Ref. $F_{\rm O}$ Ref. $F_{\rm X}$ Ref. $\Gamma$ err Ref. Type Ref. Sat
    (Jy)   (mJy)   ($\mu $Jy)              
1219+285 0.102 0.981 Fo98 3.150 Fo98 1.010 Wo90 3.750 1.500 Wo90 2 Gh93 EI
            0.400 Fo98 2.240 0.160 Fo98     RO
            1.790 Ta00 1.510 0.270 Ta00     SA
1220+345 ... 0.355 NED 0.550 NED 0.060 LM99 1.980 -- LM99 2 LM99 RO
1221+2452 0.218 0.026 Pa95 0.330 Pa95 0.090 Pe96 2.470 0.270 Pe96 1 Pe96 RO
1225+317 2.200 0.342 NED 1.630 NED 0.180 Wo90 1.720 1.000 Wo90 3 Wo90 EI
1226+023 0.158 42.861 Fo98 27.640 Fo98 20.420 Ku98 1.510 0.010 Ku98 3 Gh93 AS
            12.270 Fo98 1.890 0.050 Fo98     RO
            7.600 Go95 1.580 0.030 Go95     EX
            11.150 Wo90 1.340 0.170 Wo90     EI
            1.960 Or98 1.570 0.050 Or98     SA
1229+6430 0.164 0.042 Pa95 0.630 Pa95 1.210 Pe96 1.990 0.150 Pe96 1 Pe96 RO
1230+2517 0.135 0.425 NED 2.220 NED 0.320 Ba94 2.890 0.720 Ba94 2 Ba94 RO
1235+6315 0.297 0.007 Pa95 0.130 Pa95 0.060 Pe96 2.910 0.080 Pe96 1 Pe96 RO
1237+3020 0.700 0.003 Na96 0.010 NED 0.960 Ba98 1.850 -- Ba98 1 Ba98 RO
1239-143 ... 0.042 NED 0.290 NED 1.620 Ba94 2.580 0.570 Ba94 1 Ba94 RO
1242+3440 ... 0.008 Na96 0.060 NED 0.320 Ba98 1.930 -- Ba98 1 Ba98 RO
1246+586 ... 0.414 NED 9.450 NED 0.500 Ba98 2.420 -- Ba98 2 Ba98 RO
1252+119 0.871 1.140 Kh81 0.800 NED 0.140 Wo90 1.070 1.300 Wo90 3 Wo90 EI
1253-055 0.536 14.950 Fo98 1.660 Fo98 1.340 Fo98 1.830 0.040 Fo98 3 Gh93 RO
            0.850 Ma98 1.650 0.030 Ma98     SA
            1.500 Ku98 1.650 0.060 Ku98     AS
            0.630 Wo90 1.550 0.270 Wo90     EI
1255+244 0.141 0.077 Pa95 2.510 Pa95 1.450 Gr96 2.400 0.200 Gr96 1 Gr96 RO
1303+5056 0.688 0.001 Ba98 0.030 NED 0.830 Ba98 1.940 -- Ba98 1 Ba98 RO
1308+326 0.997 1.832 Fo98 1.580 Fo98 0.110 TW 1.990 0.420 TW 2 Gh93 AS
            0.090 TW 1.740 0.250 TW     AS
            0.150 Co95 1.950 0.100 Co95     RO
1312-423 0.105 0.019 Pa95 0.830 Pa95 1.520 Wo98 2.210 0.200 Wo98 1 Wo98 SA
1324+5739 0.115 0.042 NED 0.950 NED 0.330 Ba98 2.040 -- Ba98 1 Ba98 RO
1326+2933 0.431 0.006 Na96 0.050 NED 0.430 Ba98 2.110 -- Ba98 1 Ba98 RO
1332-295 0.513 0.011 Fo98 0.090 Fo98 0.340 Fo98 2.140 0.210 Fo98 1 NED RO
1334-127 0.539 2.250 Kh81 0.600 NED 0.450 Sa97b 1.630 0.160 Sa97b 3 Gh93 RO
1353+5601 0.370 0.012 Na96 0.110 NED 0.390 Ba98 2.010 -- Ba98 1 Ba98 RO
1400+162 0.244 0.528 Pa95 0.510 NED 0.140 Wo90 1.550 1.100 Wo90 2 Gh93 EI
1402+042 0.344 0.020 Fo98 0.630 Fo98 1.200 Sa94 2.320 0.110 Sa94 1 NED EX
            0.680 Fo98 2.850 0.170 Fo98     RO
1405+6554 0.364 0.015 Ba98 0.070 NED 0.310 Ba98 2.260 -- Ba98 1 Ba98 RO
1407+5954 0.495 0.017 Pa95 0.050 Pa95 0.040 Pe96 2.740 0.140 Pe96 1 Pe96 RO
1410+6100 0.384 0.033 Ba98 0.040 NED 0.410 Ba98 1.900 -- Ba98 1 Ba98 RO
1413+135 0.247 1.200 Pa95 0.040 NED 0.050 Wo90 0.600 1.500 Wo90 2 Wo90 EI
1415+485 ... 0.035 NED 0.720 NED 0.040 LM99 2.400 -- LM99 2 LM99 RO
1415+259 0.237 0.054 Pa95 1.450 Pa95 4.280 Sa94 2.370 0.050 Sa94 1 NED EX
            2.870 Br94 2.120 0.320 Br94     RO
1418+546 0.152 1.610 Fo98 1.910 Fo98 0.210 Wo90 1.480 0.650 Wo90 2 Wo90 EI
            0.300 Fo98 2.140 0.190 Fo98     RO
1421+582 0.638 0.050 Br94 0.120 NED 2.950 Br94 1.980 0.070 Br94 1 Br94 RO
1424+240 ... 0.316 NED 1.090 NED 1.470 Sb99 2.780 0.040 Sb99 1 Gh93 AS
            1.260 La96 3.180 0.160 La96     RO
1426+428 0.129 0.030 NED 1.050 Sa97 13.420 Sa94 2.100 0.070 Sa94 1 NED EX
            6.500 Sa97a 2.150 0.040 Sa97a     RO
            5.940 Ku98 2.170 0.030 Ku98     AS
            4.640 Gh99 1.920 0.040 Gh99     SA
1427+541 0.105 0.024 LM99 0.470 LM99 0.110 LM99 1.860 -- LM99 1 LM99 RO
1428+422 4.715 0.337 Fa97 0.020 Fa98 0.210 Fa98 1.290 0.050 Fa98 3 Fa98 AS
1437+398 ... 0.063 NED 1.520 NED 1.190 LM99 2.550 -- LM99 1 LM99 RO
1437+5639 ... 0.011 Na96 0.120 NED 0.300 Ba98 2.220 -- Ba98 1 Ba98 RO
1440+122 0.162 0.050 NED 0.570 NED 1.220 LM99 2.200 -- LM99 1 LM99 RO


 
Table 5: continued.
IAU Name z $F_{\rm R}$ Ref. $F_{\rm O}$ Ref. $F_{\rm X}$ Ref. $\Gamma$ err Ref. Type Ref. Sat
    (Jy)   (mJy)   ($\mu $Jy)              
1442+101 3.530 1.260 Kh81 0.280 NED 0.120 Wo90 2.000 1.300 Wo90 3 Wo90 EI
1443+6349 0.299 0.012 Pa95 0.050 Pa95 0.190 Pe96 2.100 0.290 Pe96 1 Pe96 RO
1448+361 ... 0.029 LM99 1.140 NED 0.500 LM99 2.600 -- LM99 1 LM99 RO
1456+5048 0.480 0.274 NED 0.070 NED 2.560 Ba98 2.060 -- Ba98 1 Ba98 RO
1458+2249 0.235 0.030 Pa95 0.690 Pa95 0.110 Pe96 3.310 0.200 Pe96 1 Pe96 RO
1458+4832 0.539 0.003 Ba98 0.030 NED 0.800 Ba98 1.900 -- Ba98 1 Ba98 RO
1509+559 ... 0.042 NED 0.950 NED 0.050 LM99 2.990 -- LM99 1 LM99 RO
1510-089 0.361 3.080 Fo98 1.090 Fo98 0.750 Sn97 1.310 0.070 Sn97 3 Gh93 AS
            0.500 Wo90 0.800 1.350 Wo90     EI
            0.830 Sa94 1.380 0.280 Sa94     EX
            0.490 Tv99 1.350 0.070 Tv99     SA
            0.740 Fo98 1.900 0.160 Fo98     RO
1514-241 0.049 2.000 Pa95 2.900 NED 0.620 Wo90 2.360 1.950 Wo90 2 Wo90 EI
1516+293 0.130 0.034 LM99 1.320 NED 0.190 LM99 2.320 -- LM99 1 LM99 RO
1517+656 ... 0.038 Fo98 1.530 Fo98 7.420 Wo98 2.290 0.100 Wo98 1 Wo98 RO
            4.990 Wo98 2.440 0.090 Wo98     SA
1519-273 0.200 3.255 Fo98 0.200 Fo98 0.390 Pa99 2.030 0.430 Pa99 2 Gh93 RO
            0.320 Pa99 1.440 0.970 Pa99     SA
1532+302 0.064 0.055 NED 2.600 NED 0.760 LM99 2.000 -- LM99 1 LM99 RO
1533+342 ... 0.028 NED 0.560 NED 0.400 LM99 2.600 -- LM99 1 LM99 RO
1533+535 0.890 0.030 Ba98 0.350 NED 2.390 Ba98 1.940 -- Ba98 1 Ba98 RO
1534+0148 0.312 0.034 Pa95 0.120 Pa95 0.420 Pe96 1.890 0.180 Pe96 1 Pe96 RO
1534+372 0.143 0.030 NED 0.880 NED 0.030 LM99 2.840 -- LM99 2 LM99 RO
1538+149 0.605 2.648 Fo98 0.440 Fo98 0.090 Fo98 2.050 0.900 Fo98 2 Gh93 RO
            0.280 Wo90 2.130 1.100 Wo90     EI
1541+0507 ... 0.056 NED 0.120 NED 0.260 Br97 1.740 0.660 Br97 1 Br97 RO
1542+614 ... 0.131 NED 0.960 NED 0.120 LM99 2.500 -- LM99 2 LM99 RO
1546+027 0.413 1.450 Kh81 0.230 NED 0.840 Wo90 2.180 2.250 Wo90 3 Wo90 EI
1548+114 0.436 0.410 VV93 0.500 Gh93 0.320 Wo90 1.350 1.100 Wo90 3 Gh93 EI
1552+2020 0.222 0.038 Pa95 0.300 Pa95 1.570 Pe96 1.790 0.140 Pe96 1 Pe96 RO
1553+113 0.360 0.636 Pa95 4.800 Pa95 13.420 BSMc 2.850 0.040 BSMc 1 NED SA
            14.860 TW 2.470 0.180 TW     AS
            7.660 Br94 2.490 0.250 Br94     RO
1602+308 ... 0.013 Br97 0.230 NED 0.160 Br97 2.560 0.890 Br97 1 Br97 RO
1611+343 1.404 2.671 Fo98 0.350 Fo98 0.240 Fo98 1.760 0.060 Fo98 3 IT90 RO
1614+051 3.197 0.850 Ca97 0.060 Ca97 0.030 Ca97 1.600 -- Ca97 3 Ca97 AS
1626+352 0.500 0.014 LM99 0.140 LM99 0.160 LM99 1.890 -- LM99 1 LM99 RO
1631+4217 0.468 0.006 Na96 0.040 NED 0.860 Ba98 1.910 -- Ba98 1 Ba98 RO
1633+382 1.814 2.929 Fo98 0.230 Fo98 0.420 Fo98 1.530 0.080 Fo98 3 Gh93 RO
            0.250 Ku98 1.510 0.320 Ku98     AS
1641+399 0.594 7.821 Fo98 0.890 Fo98 0.700 Wo90 1.430 0.350 Wo90 3 Gh93 EI
            0.980 Fo98 1.850 0.230 Fo98     RO
1642+458 0.223 0.111 NED 0.350 NED 0.260 Ba98 2.360 -- Ba98 1 Ba98 RO
1652+398 0.034 1.443 Fo98 10.970 Fo98 46.420 Gh98 1.800 0.020 Gh98 1 Gh93 SA
            23.440 Ku98 2.220 0.020 Ku98     AS
            13.400 Wo90 2.090 0.170 Wo90     EI
            8.300 Fo98 2.630 0.050 Fo98     RO
            12.900 Sa94 2.500 0.100 Sa94     EX
1652+403 ... 0.011 LM99 1.060 NED 0.030 LM99 2.800 -- LM99 1 LM99 RO
1704+607 0.280 0.002 VV93 0.070 NED 0.160 La96 2.360 0.350 La96 1 La96 RO
1704+716 ... 0.041 NED 0.480 NED 0.160 LM99 3.100 -- LM99 1 LM99 RO
1717+178 ... 0.940 Pa95 0.140 NED 0.480 Wo90 2.540 2.100 Wo90 2 Wo90 EI
1721+343 0.206 0.468 NED 0.980 NED 1.990 Wo90 1.500 0.350 Wo90 3 Wo90 EI
1722+119 0.018 0.094 Pa95 1.740 Pa95 3.600 Sa94 2.650 0.250 Sa94 1 NED EX
1727+502 0.055 0.159 Fo98 1.700 Fo98 3.630 Fo98 2.390 0.080 Fo98 1 Gh93 RO
            3.720 Sa94 2.820 0.210 Sa94     EX
1732+389 0.976 0.845 NED 0.110 NED 0.050 Sa97b 1.580 0.380 Sa97b 3 Sa97b RO
1741+196 0.084 0.339 NED 0.900 NED 1.610 Sb99 2.100 0.080 Sb99 1 Br97 SA
            1.280 Br97 1.980 0.180 Br97     RO


 
Table 5: continued.
IAU Name z $F_{\rm R}$ Ref. $F_{\rm O}$ Ref. $F_{\rm X}$ Ref. $\Gamma$ err Ref. Type Ref. Sat
    (Jy)   (mJy)   ($\mu $Jy)              
1742+597 ... 0.089 NED 1.370 NED 0.030 LM99 2.960 -- LM99 2 LM99 RO
1746+470 1.484 0.631 NED 0.010 NED 0.020 LM99 3.080 -- LM99 2 LM99 RO
1747+433 ... 0.360 NED 0.640 NED 0.050 LM99 2.320 -- LM99 2 LM99 RO
1748+470 0.160 0.010 LM99 0.110 LM99 0.540 LM99 1.940 -- LM99 1 LM99 RO
1749+096 0.322 1.973 Fo98 1.130 Fo98 0.150 Fo98 1.450 1.430 Fo98 2 Gh93 RO
            0.760 Sa97 1.890 0.080 Sa97     AS
            0.370 Wo90 1.150 1.100 Wo90     EI
1749+701 0.770 2.113 Fo98 0.960 Fo98 0.150 Fo98 2.440 0.710 Fo98 2 Gh93 RO
1755+552 ... 0.007 Br97 0.490 NED 0.940 Br97 2.640 0.190 Br97 1 Br97 RO
1757+7034 0.407 0.007 Pa95 0.170 Pa95 0.470 Pe96 2.120 0.130 Pe96 1 Pe96 RO
1803+784 0.684 3.016 Fo98 0.610 Fo98 0.240 Pa99 1.450 0.130 Pa99 2 Gh93 SA
            0.260 Fo98 2.420 0.450 Fo98     RO
            0.220 Wo90 1.460 1.000 Wo90     EI
1807+698 0.051 1.713 Fo98 5.180 Fo98 0.300 Pa99 1.740 0.240 Pa99 2 Gh93 SA
            0.520 TW 1.750 0.060 TW     AS
            0.400 Wo90 1.660 0.420 Wo90     EI
            0.350 Co95 2.220 0.110 Co95     RO
            2.570 Sa94 1.950 0.460 Sa94     EX
1808+468 ... 0.056 NED 0.450 NED 0.060 LM99 2.700 -- LM99 2 LM99 RO
1811+442 ... 0.030 NED 0.350 NED 0.070 LM99 2.180 -- LM99 1 LM99 RO
1823+568 0.664 1.905 Fo98 0.180 Fo98 0.270 Pa99 1.960 0.350 Pa99 2 IT91 SA
            0.410 Pa99 1.150 0.190 Pa99     RO
1829+540 ... 0.024 NED 0.770 NED 0.060 LM99 3.310 -- LM99 1 LM99 RO
1838+480 ... 0.032 NED 0.900 NED 0.100 LM99 3.100 -- LM99 1 LM99 RO
1841+591 0.530 0.006 LM99 0.220 NED 0.010 LM99 3.540 -- LM99 2 LM99 RO
1845+797 0.056 4.450 Kh81 8.060 NED 3.630 Sa94 1.740 0.200 Sa94 3 Gh93 EX
            5.470 Le97 1.820 0.030 Le97     AS
1848+427 ... 0.007 Br97 0.200 NED 1.810 Br94 2.170 0.220 Br94 1 Br94 RO
1921-293 0.352 12.696 NED 0.840 NED 0.770 Wo90 1.570 1.300 Wo90 3 Gh93 EI
            0.380 Go95 1.670 0.270 Go95     EX
            1.060 Sa97b 1.890 0.050 Sa97b     RO
1928+738 0.360 3.339 Fo98 1.110 Fo98 0.520 Go95 2.250 0.480 Go95 3 Gh93 EX
            1.470 Fo98 2.330 0.190 Fo98     RO
1959+650 0.048 0.251 Fo98 17.490 Fo98 9.200 BSMc 2.680 0.050 BSMc 1 BSMc SA
2005-489 0.071 1.252 Fo98 12.470 Fo98 5.400 Sa94 3.200 0.700 Sa94 1 Co97 EX
            25.380 Pa98 2.320 0.040 Pa98     SA
            5.000 Fo98 2.940 0.060 Fo98     RO
2007+777 0.342 1.364 Fo98 0.770 Fo98 0.360 Wo90 5.110 4.800 Wo90 2 Gh93 EI
            0.170 Fo98 1.750 0.560 Fo98     RO
2032+107 0.601 0.770 Pa95 1.000 Pa95 1.220 Wo90 2.430 1.400 Wo90 2 Wo90 EI
2039+523 ... 0.025 NED 1.420 NED 0.230 Br97 2.800 0.890 Br97 1 Br97 RO
2126-158 3.268 1.240 Ca97 0.580 Ca97 0.720 Ca97 1.530 0.300 Ca97 3 Ca97 RO
            0.860 Ca97 1.680 0.090 Ca97     AS
            0.710 Wo90 3.180 2.100 Wo90     EI
2131-021 0.557 2.390 Fo98 0.130 Fo98 0.050 Fo98 2.050 0.460 Fo98 2 IT90 RO
2134+004 1.936 12.249 Fo98 0.720 Fo98 0.260 Fo98 1.820 0.420 Fo98 3 Gh93 RO
2136-428 ... 0.108 NED 0.390 NED 0.120 La96 3.200 0.410 La96 2 La96 RO
2143+0704 0.237 0.050 Pa95 0.230 Pa95 0.120 Pe96 2.910 0.320 Pe96 1 Pe96 RO
2149-306 2.345 1.150 NED 0.710 NED 0.880 Sb96 2.040 0.940 Sb96 3 Ca97 RO
            0.760 El99 1.370 0.030 El99     SA
            1.270 Ca97 1.540 0.050 Ca97     AS
2155-152 0.672 2.150 NED 0.420 NED 0.220 Sa97b 2.170 0.100 Sa97b 3 Sa97b RO
2155-304 0.117 0.310 Fo98 18.950 Fo98 41.050 Sa94 2.630 0.080 Sa94 1 Co97 EX
            5.980 Wo90 2.610 0.180 Wo90     EI
            44.900 Ku98 2.620 0.010 Ku98     AS
            43.900 Fo98 2.340 0.030 Fo98     RO
            73.550 Gi98 2.880 0.050 Gi98     SA


 
Table 5: continued.
IAU Name z $F_{\rm R}$ Ref. $F_{\rm O}$ Ref. $F_{\rm X}$ Ref. $\Gamma$ err Ref. Type Ref. Sat
    (Jy)   (mJy)   ($\mu $Jy)              
2200+420 0.069 4.857 Fo98 5.450 Fo98 2.200 Pa99 1.830 0.080 Pa99 2 Gh93 SA
            4.320 Wo90 2.340 1.900 Wo90     EI
            2.220 Sa97 1.960 0.040 Sa97     AS
            0.880 Fo98 1.920 0.470 Fo98     RO
2201+171 1.080 0.843 NED 0.120 NED 0.080 Wo90 1.410 0.800 Wo90 3 Wo90 EI
2208-137 0.392 0.580 NED 0.660 NED 0.960 Sa94 1.400 0.900 Sa94 3 Sa94 EX
2223-052 1.404 4.519 Fo98 1.020 Fo98 1.460 Wo90 1.340 0.720 Wo90 3 Gh93 EI
            0.270 Fo98 2.090 0.230 Fo98     RO
            0.220 BSGh 1.730 0.210 BSGh     SA
2230+114 1.037 3.689 Fo98 0.690 Fo98 0.420 Ku98 1.580 0.120 Ku98 3 Ku98 AS
            0.730 Tv99 1.510 0.040 Tv99     SA
2240-260 0.774 1.203 Fo98 0.260 Fo98 0.070 Fo98 1.790 0.400 Fo98 2 NED RO
2243+203 ... 0.120 NED 2.900 NED 0.060 LM99 2.680 -- LM99 2 LM99 RO
2247+381 0.119 0.119 NED 6.840 NED 0.600 LM99 2.510 -- LM99 1 LM99 RO
2251+158 0.859 8.759 Fo98 1.020 Fo98 1.310 Wo90 1.830 1.750 Wo90 3 IT90 EI
            1.370 Fo98 1.620 0.040 Fo98     RO
2254+024 2.090 0.426 NED 0.230 NED 0.150 Wo90 3.870 3.300 Wo90 3 Wo90 EI
2254+074 0.190 1.216 Fo98 0.600 Fo98 0.080 Wo90 0.950 2.100 Wo90 2 Gh93 EI
            0.090 Fo98 2.890 0.610 Fo98     RO
2316-423 0.055 0.540 Pa95 5.770 Pa95 0.100 Xu99 2.600 0.300 Xu99 2 Xu99 AS
            0.360 Xu99 2.000 0.200 Xu99     RO
2319+161 ... 0.024 LM99 0.720 NED 0.360 LM99 2.200 -- LM99 1 LM99 RO
2322+346 0.098 0.076 NED 11.890 NED 0.420 LM99 1.800 -- LM99 1 LM99 RO
2344+514 0.044 0.215 Co97 2.370 Co97 4.170 TW 2.310 0.070 TW 1 Co97 AS
            5.180 TW 2.390 0.080 TW     AS
            5.260 TW 2.130 0.030 TW     AS
            3.400 Gi99 2.310 0.050 Gi99     SA
            6.870 Gi99 1.770 0.040 Gi99     SA
2356-309 0.165 0.029 NED 0.700 NED 5.780 Cs00 2.100 0.050 Cs00 1 NED SA

Copyright ESO 2001