A&A 375, 419-433 (2001)
DOI: 10.1051/0004-6361:20010838
The soft X-ray eclipses of HU Aqr
A. D. Schwope1 -
R. Schwarz1 -
M. Sirk2 -
S. B. Howell3
1 -
Astrophysikalisches Institut Potsdam, An der Sternwarte 16,
14482 Potsdam, Germany
2 -
Space Sciences Laboratory, UC Berkeley,
CA 94720, USA
3 -
Planetary Science Institute, Tucson, AZ 85705, USA
Received 21 March 2001 / Accepted 7 June 2001
Abstract
We present the results of extended monitoring observations
in soft X-rays of the bright eclipsing polar (AM Herculis star)
HU Aqr. It was observed between 1990 and 1998
by ROSAT for a total of 230 ksec using the PSPC
and the HRI detectors and by EUVE with the Deep Survey Imager and the
Spectrometer for a total of 580ksec.
The overall X-ray brightness of HU Aqr varied due to changes of the
mass accretion rate by a factor of 40 over that period of time.
At all occasions the X-ray light curve was characterized by a marked
on-off behavior due to the self-eclipse of the accreting pole.
The X-ray light curve showed eclipses by the companion star, the
accretion stream and by an accretion curtain raised between the
two stars in the binary.
Narrow dips prior to the stellar eclipse
are caused by the transit of the outer accretion stream. These
dips display marked phase shifts,
thus indicating a large movement of the threading region, where the
stream couples to the magnetic field. These shifts are shown
to be related to changes of the mass accretion rate.
Correspondingly,
the spot longitude varied between 34 and 50
and 50 .
The X-ray light curves display clear evidence for the presence of an accretion
curtain, which is raised all along the ballistic accretion stream down to the
region where the bulk of matter couples onto magnetic field lines.
A lower limit to the mass accretion rate in the curtain is
.
The X-ray light curves display clear evidence for the presence of an accretion
curtain, which is raised all along the ballistic accretion stream down to the
region where the bulk of matter couples onto magnetic field lines.
A lower limit to the mass accretion rate in the curtain is
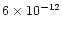
 /yr, which is of order 10% of the total mass
accretion rate.
A linear fit to all available eclipse egress times yields an updated
orbital ephemeris of the system:
/yr, which is of order 10% of the total mass
accretion rate.
A linear fit to all available eclipse egress times yields an updated
orbital ephemeris of the system:
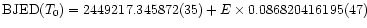 with T0 the time of eclipse of the white dwarf centre of mass
(BJED: barycentric Julian ephemeris time).
The inclusion of a quadratic term gives a better fit to the data but
is not regarded as indication of a period change or asynchronous rotation
but by a migration of the
accretion spot over the surface of the white dwarf.
For one particular data set obtained in a high accretion state, detailed
light curve modeling was possible.
The egress from eclipse lasted 1.3s,
which constrained the azimuthal extent of the accretion spot to less than
4
with T0 the time of eclipse of the white dwarf centre of mass
(BJED: barycentric Julian ephemeris time).
The inclusion of a quadratic term gives a better fit to the data but
is not regarded as indication of a period change or asynchronous rotation
but by a migration of the
accretion spot over the surface of the white dwarf.
For one particular data set obtained in a high accretion state, detailed
light curve modeling was possible.
The egress from eclipse lasted 1.3s,
which constrained the azimuthal extent of the accretion spot to less than
4 or 450km. The spot extended vertically by
or 450km. The spot extended vertically by 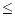 0.015
0.015
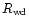 .
A comparison of the width of the stream dip and the extent of the accretion spot
shows, that only the inner 60-80% of the stream are dense enough
to fire the soft X-ray engine.
During the eclipse, HU Aqr was detected at a flux level of
.
A comparison of the width of the stream dip and the extent of the accretion spot
shows, that only the inner 60-80% of the stream are dense enough
to fire the soft X-ray engine.
During the eclipse, HU Aqr was detected at a flux level of
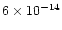 erg cm-1s-1. The implied
X-ray luminosity is
erg cm-1s-1. The implied
X-ray luminosity is
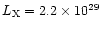 erg s-1,
comparable with X-ray emission from single, late-type, active stars.
erg s-1,
comparable with X-ray emission from single, late-type, active stars.
Key words: accretion - stars: binaries: eclipsing - cataclysmic variables -
stars: individual: HU Aqr -
X-rays: binaries
HU Aquarii is at optical and X-ray wavelengths the brightest
among 12 eclipsing polars (alternatively referred to as AM Herculis stars).
These consist in most cases of a main-sequence donor star and a strongly
magnetic, synchronously rotating, white dwarf.
The class meanwhile comprises a total of 67 systems, most of them identified
as optical counterparts of soft X-ray sources.
The importance and the interest of a detailed observation of an eclipsing
system is obvious. Only an eclipsing system provides an unambiguous time
of reference during the orbital revolution for the study of phase-dependent
phenomena and long-term changes.
Thus, detailed studies of the accretion geometry, the distribution
of matter in the magnetosphere, and changes in the geometry become possible.
Since its discovery as a bright source in the ROSAT-PSPC and -WFC surveys
(Schwope et al. 1993, Hakala et al. 1993),
HU Aqr was the target of several investigations. Glenn et al. (1994)
presented optical spectroscopy and photometry and noticed the high degree
of variability of eclipse light curves indicating changes of the
accretion geometry on time scales as short as hours. Hakala (1995),
Harrop-Allin et al. (1999), and Vrielmann & Schwope (2001) made
use of the detailed shape of optical emission line and
continuum eclipse light curves in order to calculate
brightness maps along the different parts of the accretion stream.
Using high-resolution optical spectrophotometry analysed
by Doppler tomography, Schwope et al. (1997)
uncovered the existence of an extended ballistic accretion stream in HU Aqr.
The high degree of asymmetry of the light curve
of reprocessed line radiation from the
secondary star was interpreted in terms of effective shielding
by an accretion curtain.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pspc_lc.ps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg19.gif) |
Figure 1:
ROSAT-PSPC soft X-ray light curves of HU Aqr in
October/November 1993. The original data were phase-averaged using
the linear eclipse ephemeris of Eq. (1). The chosen bin size
is 0.005 phase units. The two upper panels show the X-ray count rate
in the total ROSAT window (0.1-2.4 keV), the lower panel shows the
count rate in the hard ROSAT band only (0.5-2.0 keV). |
| Open with DEXTER |
Table 1:
Log of soft X-ray observations of HU Aqr with ROSAT and EUVE (in chronological order).
Given are an observation ID used in this paper,
the instrument used (PSPC and HRI for ROSAT, DS/S for EUVE),
the dates of observation start and end in format YYMMDD, and
the total exposure time (in s).
|
ObsID |
Detector |
ObsBeg |
ObsEnd |
Exposure |
| |
|
|
[s] |
|
|
P Nov. 92 |
PSPC |
921117 |
921117 |
1522 |
| P Apr. 93 |
PSPC |
930423 |
930425 |
9496 |
| P Oct. 93 |
PSPC |
931027 |
931105 |
36716 |
| H Apr. 94 |
HRI |
940428 |
940428 |
5626 |
| H May 94 |
HRI |
940509 |
940514 |
22918 |
| H Oct. 94 |
HRI |
941026 |
941121 |
37189 |
| H Nov. 95 |
HRI |
951111 |
951112 |
26464 |
| H Apr. 96 |
HRI |
960424 |
960425 |
23319 |
| D May 96 |
DS/S |
960529 |
960603 |
125438 |
| D Jul. 96 |
DS/S |
960727 |
960730 |
88432 |
| D Sep. 96 |
DS/S |
960911 |
960914 |
78570 |
| D Oct. 96 |
DS/S |
961023 |
961028 |
68204 |
| H Oct. 96 |
HRI |
961025 |
961027 |
23348 |
| D May 97 |
DS/S |
970509 |
970514 |
68897 |
| D Aug. 97 |
DS/S |
970803 |
970807 |
84521 |
| H May 97 |
HRI |
970502 |
970514 |
20773 |
| H Apr. 98 |
HRI |
980423 |
980424 |
22438 |
| D Aug. 98 |
DS/S |
980827 |
980829 |
65432 |
Table 2:
Log of optical photometry of HU Aqr. Indicated are
the location and size of the telescopes
(CA: Calar Alto, LS: La Silla, AIP: Potsdam), the instruments, filters
("WL'' means "white light'' or unfiltered observation), the total time
on target and the time resolution achieved.
|
Date |
Telescope |
Instr |
Filter |
 |
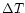 |
| |
|
|
|
[h] |
[s] |
|
93Aug.16-18 |
CA22 |
MCCP |
V |
17.08 |
0.5 |
| 95Nov.12 |
LS22 |
EFOSC2 |
WL |
2.34 |
53 |
| 96Jul.19-21 |
AIP07 |
CCD |
WL |
5.14 |
12 |
| 96Sep.1-5 |
AIP07 |
CCD |
WL |
10.90 |
12 |
| 98Sep.24 |
AIP07 |
CCD |
V |
1.84 |
12 |
X-ray information about HU Aqr is sparse. Schwope et al. (1993) derived an
ephemeris with sufficient accuracy to extend back to the ROSAT All Sky Survey
without cycle count error.
They found that three of 26 scans coincided with the eclipse and found
the soft part of the spectrum compatible with a blackbody of
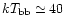 eV. Pointed observations with the ROSAT and the EUVE satellites
were numerous but so far discussed mainly in thesis works or conference
proceedings (Sohl et al. 1995; Sohl 1997; Schwope 1995; Schwope 1996;
Schwope et al. 1998; Sirk & Howell 1998).
In these papers, notions about the occurrence of stream dips and an
accretion curtain based on X-ray data are given.
Here we present the synopsis and analysis
of all observations performed at soft X-ray
wavelengths with ROSAT and EUVE.
The paper is organized in the following way. In Sect. 2
we describe the data sets which were subsequently analysed in this work.
General remarks on the variable shape of the soft X-ray light curves
are made in Sect. 3.
The eclipse is studied in Sect. 4, where the eclipse ephemeris,
the eclipse egress and the residual flux in the eclipse are analysed.
A spectral analysis is carried out in Sect. 5.
The narrow absorption dips and the density of the accretion stream are
addressed in Sect. 6.
Our main results are summarized and discussed in context in
Sect. 7.
eV. Pointed observations with the ROSAT and the EUVE satellites
were numerous but so far discussed mainly in thesis works or conference
proceedings (Sohl et al. 1995; Sohl 1997; Schwope 1995; Schwope 1996;
Schwope et al. 1998; Sirk & Howell 1998).
In these papers, notions about the occurrence of stream dips and an
accretion curtain based on X-ray data are given.
Here we present the synopsis and analysis
of all observations performed at soft X-ray
wavelengths with ROSAT and EUVE.
The paper is organized in the following way. In Sect. 2
we describe the data sets which were subsequently analysed in this work.
General remarks on the variable shape of the soft X-ray light curves
are made in Sect. 3.
The eclipse is studied in Sect. 4, where the eclipse ephemeris,
the eclipse egress and the residual flux in the eclipse are analysed.
A spectral analysis is carried out in Sect. 5.
The narrow absorption dips and the density of the accretion stream are
addressed in Sect. 6.
Our main results are summarized and discussed in context in
Sect. 7.
2 Observations and reductions
An overview of the soft X-ray observations of HU Aqr is
given in Table 1.
The table lists only pointed observations, the ROSAT All
Sky Survey observations
were described in Schwope et al. (1993),
the source was not seen in the EUVE All Sky Survey (Bowyer et al. 1996) where the region of HU Aqr received an
exposure of 935 s with the Lexan filter.
The 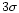 upper limit count rate in the EUVE survey is 0.05s-1.
upper limit count rate in the EUVE survey is 0.05s-1.
Table 1 lists the
information about an observation ID used in this
paper, the X-ray detector, the
date of the observation, and the
total exposure time.
At two occasions (Oct. 96, May 97)
we could arrange simultaneous observations with
both the ROSAT and the EUVE satellites. The corresponding light curves
are discussed in the Sect. 3, the implications for the X-ray
spectral shape in Sect. 5.
The region of HU Aqr was exposed for a total of 48ksec with the ROSAT-PSPC,
for 182 ksec with the ROSAT-HRI, and for 579 ksec with the DS/S instruments
on board EUVE, respectively. The source was always positioned on-axis, hence,
some variability
in the PSPC observations
might be apparent only
due to blocking of X-ray photons by the wire-mesh of the entrance window
of the detector.
Source photons were extracted from the
original photon event tables, background and vignetting corrected
using MIDAS/EXSAS (Zimmermann et al. 1994) and IRAF
software packages. Binned light curves (see Fig. 2) were computed using the ephemeris
given in Eq. (1).
For the high-state ROSAT-PSPC observations in October/November 1993
we also determined hardness ratios HR1 and SR as a function of orbital phase
which characterize spectral variations.
The hardness ratio HR1 is determined in the usual manner,
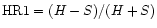 ,
with H and S the counts in
the hard
(0.5 - 2.0) keV
and soft ROSAT
(0.1-0.4) keV bands, respectively.
Fortunately, in polars the
two bands are sensitive to the two main radiation
components usually encountered in these systems.
H is sensitive to radiation from the
hot post-shock cooling plasma (well approximated as a bremsstrahlung
spectrum at ROSAT resolution), and S is sensitive to
the soft component of reprocessed radiation from the heated
stellar photosphere (at ROSAT resolution reasonably well
approximated as a blackbody spectrum). Hence,
HR1 is a measure of the relative weight between
these two main spectral components.
Variations of HR1 can be caused by a variable column density, which
in the first place affects the counts in the soft band, or by
intrinsic changes of the spectral parameters.
,
with H and S the counts in
the hard
(0.5 - 2.0) keV
and soft ROSAT
(0.1-0.4) keV bands, respectively.
Fortunately, in polars the
two bands are sensitive to the two main radiation
components usually encountered in these systems.
H is sensitive to radiation from the
hot post-shock cooling plasma (well approximated as a bremsstrahlung
spectrum at ROSAT resolution), and S is sensitive to
the soft component of reprocessed radiation from the heated
stellar photosphere (at ROSAT resolution reasonably well
approximated as a blackbody spectrum). Hence,
HR1 is a measure of the relative weight between
these two main spectral components.
Variations of HR1 can be caused by a variable column density, which
in the first place affects the counts in the soft band, or by
intrinsic changes of the spectral parameters.
The hardness ratio SR is a hardness ratio built in the
soft component, SR
= (S1-S2)/(S1+S2), with S1 and S2 being the
counts in the soft sub-bands (S1 = (0.30-0.50)keV,
S2 = (0.1-0.30)keV).
The hardness ratio SR is sensitive to variations
of either
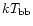 or
or 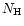 .
.
Contemporaneous optical photometric observations were performed
in 1993, 1995, 1996 and 1998 using high-speed photometers and CCD cameras
mounted to telescopes at La Silla, Calar Alto and the AIP 70 cm telescope.
The latter provided the largest database. Details of the observations
are given in Table 2 and the phase-averaged light curves
are shown in Fig. 3. All data are shown twice for clarity,
the detected counts of HU Aqr were related to those of the
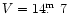 comparison "C'' in the chart of Schwope et al. (1993).
comparison "C'' in the chart of Schwope et al. (1993).
3 Soft X-ray and optical light curves of HU Aqr
We start the analysis with a description of the main observed features
of the X-ray light curves of HU Aqr, using as an example the ROSAT-PSPC
observation obtained in October/November 1993 (Fig. 1,
top panel).
In the different panels of Fig. 1
we show (from top to bottom) (i) the X-ray light curve
in the full ROSAT-band, (ii) the same on an expanded y-scale, and (iii)
the light curve in the hard passband only. The spectral variability may be
obtained from phase-dependent hardness ratio curves shown
in Fig. 10.
The light curve shows five main characteristics described subsequently,
labeled a-e in the top panel of Fig. 1.
(a) The light curve has a clear on-off pattern caused by the self-eclipse
of the accretion spot by the white dwarf. The difference between bright phase centre
and eclipse centre yields the azimuth (longitude) of the main accretion
spot with respect to the line joining both stars.
The length of the X-ray bright phase depends on the orbital
inclination, the latitude of the spot
(measured with respect to the rotation axis, referred to as co-latitude),
as well as its vertical and longitudinal extent.
Characteristic parameters of the light curves
(the mean bright-phase count rate, the centre of the bright phase,
the phase of eclipse egress and the phases of narrow and broad
dips) obtained at different epochs
are listed in Table 3.
During the faint phase, when the accretion
spot is self-eclipsed, X-rays are not switched
off completely. The minimum faint-phase PSPC count rate in Oct. 1993
was 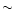 0.25 s-1. Maximum count-rate in the bright phase was observed
at phase 0.05, it reached
0.25 s-1. Maximum count-rate in the bright phase was observed
at phase 0.05, it reached
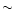 40s-1 in the phase-averaged light curve with 200 phase bins.
Using bins of 0.25 s width, the rate reached 145s-1.
Emission during the bright phase is super-soft with HR1 near to -1.0, during
the faint phase a slight spectral hardening is observed, but the hardness
ratio HR1
40s-1 in the phase-averaged light curve with 200 phase bins.
Using bins of 0.25 s width, the rate reached 145s-1.
Emission during the bright phase is super-soft with HR1 near to -1.0, during
the faint phase a slight spectral hardening is observed, but the hardness
ratio HR1
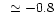 indicates still very soft emission.
indicates still very soft emission.
The X-ray bright phase is markedly modulated by
the stellar eclipse (b),
a narrow dip (c), and
a broad dip (e).
(b)
The feature at phase 0.0 is the eclipse of the accretion region
by the secondary star. This is not exactly
coincident with the eclipse of the white dwarf itself. The phase offset
is caused by an offset of the accretion spot with respect to the line
joining both stars
(azimuth of the spot is not equal zero).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{allxlcs.ps}
\end{figure}](/articles/aa/full/2001/32/aah2761/Timg29.gif) |
Figure 2:
Collection of ROSAT and EUVE soft X-ray light curves of HU Aqr
obtained between 1993 and 1998 in chronological order. These light
curves are only for observations covering an entire orbital cycle.
The letter before
the date printed in each panel indicates the satellite/detector combination:
P - ROSAT PSPC, H - ROSAT HRI, D - EUVE DSS.
All data were phase-averaged according to the ephemeris of Eq. (1),
the bin size is 0.005 phase units. The dotted lines in the panels of the
"D OCT. 96'' and "D MAY 97'' EUVE-observations are the scaled,
quasi-simultaneous HRI-light curves. |
| Open with DEXTER |
(c)
The originally free-falling accretion stream becomes dominated by the
magnetic field and threadened at some location in the binary system (see
Fig. 9 and also
Schwope et al. 1997 for a sketch of the accretion geometry of HU Aqr).
Following magnetic field lines, the stream is lifted out of the
orbital plane. If the accretion pole and the observer are located in the
same hemisphere of the binary (with respect to the orbital plane),
an absorption dip occurs when the line of sight crosses the
accretion stream. In a high inclination system like HU Aqr the measured
azimuth of the dip centre equals the azimuth of the threading region.
The observed width of the dip indicates the azimuthal extent of the
threading region. Since soft X-rays are more affected by photoelectric
absorption than hard X-rays, the hardness ratios HR1 and SR increase
at dip phase (see Sect. 6). We note, that a similar
re-emergence of (softer) X-rays after the dip, and before the eclipse,
also occurs in MN Hya (Buckley et al. 1998).
(d)
Compared to the pre-dip and the post-eclipse count rate the X-ray flux
is clearly reduced between the narrow dip and the eclipse. At the
same time the hardness ratios SR and HR1 indicate a spectral hardening.
Both, the flux decrease and the spectral change are suggestive of enhanced
absorption in an accretion curtain, which is raised all along the ballistic
stream between L1 and the narrow dip, where most of the matter
couples onto field lines. An 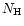 -map of the dip and the curtain
is presented in Sect. 6.
-map of the dip and the curtain
is presented in Sect. 6.
(e)
A broad dip centred on phase 0.7, i.e. after the phase of initial rise,
is evident in the light curve shown in Fig. 1. A similar
light curve in general and a similar dip feature in particular was
observed in UZ For (Warren et al. 1995; Sirk & Howell 1998).
These authors concluded, that the observed width of the dip suggests that
light is being removed from the line of sight by material close to the point
of origin, i.e. X-rays are absorbed or scattered in the accretion
column just above the accretion spot. We address this interpretation with
the aid of an 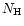 -map in Sect. 6.
-map in Sect. 6.
A montage of all available soft X-ray light curves with full phase coverage
obtained during
pointed ROSAT and EUVE observations is shown in Fig. 2.
This collection shows the strong evolution of the soft X-ray light curve
of HU Aqr. The preserved features are the on-off behavior due to the
self-eclipse of the accretion spot and the stellar eclipse at
phase zero. The X-ray brightness, the offset between centre
bright phase and eclipse centre, the occurrence of the broad dip,
the phase of the narrow dip and the size of the
accretion curtain, however, are
subject to marked changes. We describe here the most prominent
changes and list characteristic phases and count-rates extracted from
the phase-folded light curves in Table 3.
In October 1996 and May 1997 we could arrange
truly simultaneous observations
with ROSAT and EUVE for a total of about 4950 s and 3140 s, respectively,
split in several OBIs.
The typical length of a simultaneous observation was about 500-600 s.
The average count rate ratio HRI/DS, determined for data intervals with
EUVE count rate above 0.05 s-1, is 2.2 with a standard deviation of 0.8.
The ratio of the overall light curves at the two occasions seems
to be better reflected by a factor 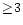 .
The ratio becomes as
large as 6 in the post-eclipse interval of the May 1997 observation.
For comparison, we
plotted the scaled HRI light curves (scaled with a factor of 3)
as dotted lines in the corresponding panels of the EUVE light curves
in Fig. 2.
This large scatter reflects the high intrinsic variability of the
source on a time scale as short as days or even orbital cycles.
The high degree of variability
becomes obvious also from the rather densely spaced EUVE-monitoring observations in 1996, which took place every
one or two month. Throughout this paper we will use a
HRI/DS conversion factor of 2.2.
.
The ratio becomes as
large as 6 in the post-eclipse interval of the May 1997 observation.
For comparison, we
plotted the scaled HRI light curves (scaled with a factor of 3)
as dotted lines in the corresponding panels of the EUVE light curves
in Fig. 2.
This large scatter reflects the high intrinsic variability of the
source on a time scale as short as days or even orbital cycles.
The high degree of variability
becomes obvious also from the rather densely spaced EUVE-monitoring observations in 1996, which took place every
one or two month. Throughout this paper we will use a
HRI/DS conversion factor of 2.2.
In Table 3
we quote the count rates measured directly in the
light curves and equivalent (or scaled) HRI count rates (prefix 'S').
These were derived from
the observed rates using count conversion factors
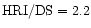 and PSPC/HRI
and PSPC/HRI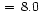 .
The HRI/DS conversion is based
on intervals of simultaneous observation, the PSPC/HRI
conversion factor is based on folding the best-fit two-component spectrum
of the 1993 PSPC-observation through the spectral response of the
two detectors (see Sect. 5).
.
The HRI/DS conversion is based
on intervals of simultaneous observation, the PSPC/HRI
conversion factor is based on folding the best-fit two-component spectrum
of the 1993 PSPC-observation through the spectral response of the
two detectors (see Sect. 5).
In order to characterize the X-ray brightness at each occasion, we
list in Table 3 a mean peak count rate, CR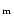 ,
and the
mean count rate in the phase interval 0.05-0.10, CR1. The mean peak
count rate is measured in the brightest contiguous 10% phase interval of
the light curve.
The scaled, post-eclipse count rate varies by a factor of
,
and the
mean count rate in the phase interval 0.05-0.10, CR1. The mean peak
count rate is measured in the brightest contiguous 10% phase interval of
the light curve.
The scaled, post-eclipse count rate varies by a factor of
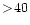 reaching a maximum of 4.4s-1 in "P Nov. 93''. The
average faint-phase count rate, CR
reaching a maximum of 4.4s-1 in "P Nov. 93''. The
average faint-phase count rate, CR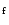 ,
was as high as 0.3s-1, but
in most cases was near the detection limit or below.
,
was as high as 0.3s-1, but
in most cases was near the detection limit or below.
Even in the phase-averaged light curves strong X-ray flares can be easily
recognized. These may stick out by factors up to 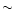 10 above the
average count rate and are explained as caused by accretion events.
10 above the
average count rate and are explained as caused by accretion events.
One prominent change of the light-curve shape
is related to the narrow dip and absorption
in the accretion curtain. The narrow dip displays a clear motion in phase
(noted earlier by Glenn et al. 1994; Schwope 1996; Harrop-Allin et al. 1999
in optical or combined X-ray/optical data) and migrates towards the
eclipse during episodes of reduced X-ray brightness.
At times, the narrow dip is completely merged with the eclipse. Again,
this special appearance became most obvious in 1996, when the accretion rate
was at the lower limit of the range observed by us.
We measured the phase of the narrow dip as phase of half intensity during
ingress to the dip (which is possible for all occasions) as well
as its centre phase, when the dip showed an ingress and an egress.
The results are listed in Table 3, plotted in Fig. 8
and discussed in more detail in Sect 6.
A second change is related to ingress from and egress into the self-eclipse,
which is occasionally rather steep (e.g. "H May 94'', "H Nov. 95'') and sometimes
very shallow (e.g. "H Apr. 96'', "D Sep. 96'').
These features are related to a restructuring of the extent
of the accretion region.
A third prominent change is the (apparent) absence
of the broad dip in almost all 1996 observations and in "D Aug. 97''. In the
light curve of the latter observation
at least a flux depression can be recognized at phase 0.7.
Light curves without broad dip have the phase of maximum count rate
in the centre of the bright phase. When the broad
dip is clearly present in the light curve,
maximum emission occurs in the phase interval 0.05-0.10, i.e immediately
after eclipse. Interestingly, the broad dip recovers when the system returns
to high count rates, its existence thus seems to be correlated with the
accretion rate.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{olcs_xpap.eps}
\end{figure}](/articles/aa/full/2001/32/aah2761/Timg34.gif) |
Figure 3:
Results of optical photometric observations performed in parallel
to the X-ray observations. The light curves were phase-averaged and normalized
to the counts of the
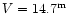 companion star.
companion star. |
| Open with DEXTER |
Table 3:
Characteristic features of the phase-averaged soft X-ray light curves of
HU Aqr.
Columns 1 and 2 give the modified Julian date at start and end of the
observation. Column 3 gives the approximate date, Col. 4 identifies the
instrument used (S: EUVE All Sky Scanner Survey,
P: ROSAT PSPC,
H: ROSAT HRI,
D: EUVE Deep Survey Imager).
Columns 5-8 indicate the phases of the bright phase centre
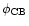 ,
the phase of narrow dip ingress (half intensity at ingress)
,
the phase of narrow dip ingress (half intensity at ingress)
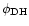 ,
the phase
of the narrow dip centre
,
the phase
of the narrow dip centre
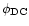 ,
and the phase of the
broad dip centre
,
and the phase of the
broad dip centre
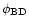 .
CR
.
CR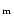 ,
CR1, and CR
,
CR1, and CR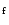 are the count rates at peak,
in the phase interval
0.05-0.10, and in the faint phase,
are the count rates at peak,
in the phase interval
0.05-0.10, and in the faint phase,
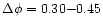 ,
respectively (Cols. 9-11). Columns 12 and 13
list the count rates scaled to the HRI. The PSPC/HRI conversion factor
was 8.0, the HRI/DS conversion factor was 2.2.
For values given in Cols. 5-7,
the typical phase uncertainty is 0.003 phase units. Values with
larger uncertainties are marked with a colon.
For values given in Col. 8,
the typical phase uncertainty is 0.03 phase units.
In Col. 11 values in parentheses indicate the uncertainty in the
last digits quoted.
,
respectively (Cols. 9-11). Columns 12 and 13
list the count rates scaled to the HRI. The PSPC/HRI conversion factor
was 8.0, the HRI/DS conversion factor was 2.2.
For values given in Cols. 5-7,
the typical phase uncertainty is 0.003 phase units. Values with
larger uncertainties are marked with a colon.
For values given in Col. 8,
the typical phase uncertainty is 0.03 phase units.
In Col. 11 values in parentheses indicate the uncertainty in the
last digits quoted.
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
(11) |
(12) |
(13) |
| MJD1 |
MJD2 |
Date |
Inst |
 |
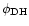 |
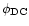 |
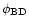 |
CR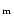 |
CR1 |
CR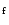 |
SCR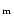 |
SCR1 |
| 48933.500 |
48938.799 |
Nov. 92 |
S |
- |
- |
- |
- |
<0.05a |
<0.05a |
- |
- |
|
|
48944.478 |
48944.496 |
Nov. 92 |
P |
- |
- |
- |
- |
:0.6b |
- |
- |
- |
- |
|
49101.069 |
49102.996 |
Apr. 93 |
P |
- |
- |
- |
- |
5.0 |
4.29 |
0.053(36) |
0.63 |
0.54 |
|
49288.200 |
49291.273 |
Oct. 93a |
P |
0.874 |
0.828 |
0.873 |
- |
22 |
- |
0.314(75) |
2.8 |
- |
|
49294.895 |
49295.438 |
Nov. 93b |
P |
- |
0.839 |
0.868 |
0.70 |
38 |
29.5 |
0.267(76) |
4.8 |
3.7 |
|
49295.825 |
49296.571 |
Nov. 93c |
P |
0.871 |
0.837 |
0.872 |
0.73 |
30 |
35.3 |
0.29(13) |
3.8 |
4.4 |
|
49471.181 |
49471.331 |
Apr. 94 |
H |
0.888 |
0.910 |
0.926 |
0.76 |
- |
- |
- |
- |
- |
|
49482.061 |
49487.322 |
May 94 |
H |
0.890 |
0.878 |
0.900 |
0.77 |
0.65 |
0.53 |
0.003(9) |
0.65 |
0.53 |
|
49652.251 |
49677.970 |
Oct. 94 |
H |
0.881 |
0.861 |
0.892 |
0.75 |
0.9 |
1.08 |
0.005(10) |
0.9 |
1.08 |
|
50032.550 |
50033.840 |
Nov. 95 |
H |
0.902 |
0.901 |
0.918 |
0.77 |
0.35 |
0.34 |
0.004(10) |
0.35 |
0.34 |
|
50197.529 |
50199.337 |
Apr. 96 |
H |
0.870 |
0.913 |
- |
- |
1.0 |
0.12 |
0.006(10) |
1.0 |
0.12 |
|
50232.606 |
50237.676 |
May 96 |
D |
0.868 |
0.875: |
- |
- |
0.14 |
0.069 |
0.001(2) |
0.31 |
0.15 |
|
50291.710 |
50294.624 |
Jul. 96 |
D |
0.862 |
0.900 |
- |
- |
0.13 |
0.049 |
0.001(3) |
0.29 |
0.11 |
|
50337.812 |
50340.851 |
Sep. 96 |
D |
0.873 |
0.913 |
- |
- |
0.14 |
0.061 |
0.001(3) |
0.31 |
0.13 |
|
50382.315 |
50384.446 |
Oct. 96 |
H |
0.869 |
0.929 |
- |
0.74 |
0.38 |
0.32 |
0.004(12) |
0.38 |
0.32 |
|
50382.318 |
50384.500 |
Oct. 96 |
D |
0.880 |
0.922 |
- |
0.77 |
0.15 |
0.070 |
0.000(3) |
0.33 |
0.15 |
|
50570.639 |
50582.925 |
May 97 |
H |
0.895 |
0.916 |
0.929 |
0.75 |
0.63 |
0.43 |
0.004(12) |
0.63 |
0.43 |
|
50577.724 |
50582.930 |
May 97 |
D |
0.905 |
0.895 |
0.916 |
0.76 |
0.087 |
0.094 |
0.000(2) |
0.19 |
0.21 |
|
50664.298 |
50667.604 |
Aug. 97 |
D |
0.874 |
0.873: |
0.910: |
0.69 |
0.064 |
0.045 |
0.001(2) |
0.14 |
0.10 |
|
50927.077 |
50928.420 |
Apr. 98 |
H |
0.889 |
0.862 |
0.898 |
- |
2.2 |
2.31 |
0.014(9) |
2.2 |
2.31 |
|
51053.405 |
51055.396 |
Aug. 98 |
D |
0.875 |
0.840 |
0.880: |
0.74 |
1.45 |
1.71 |
0.022(9) |
3.2 |
3.76 |
a 3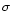 upper limit.
upper limit. |
| b Incomplete phase coverage. |
Optical photometry was obtained on several occasions during recent
years thus supporting our X-ray observations.
The separation between X-ray and optical observations
ranges from one day only (Nov. 12, 1995) to about two months (Aug. 1993).
Given the high degree of variability
of HU Aqr observations of the latter kind can be regarded only as
suggestive of the probable optical state at the time of the
X-ray observation. The phase-averaged optical light curves obtained at
five different epochs are shown in Fig. 3.
HU Aqr was in a high accretion state during the RASS, and also during pointed
ROSAT observations in 1992 and 1993. The system then entered an extended
state of reduced accretion and reappeared
at a high brightness level in 1998,
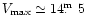 .
As described in Schwope et al. (1993), the system
faded optically by 1.5 mag during the four nights of observation
in late September 1992. During the EUVE
all-sky survey in November 1992 it was in a low state.
In the high states the optical light curves are double-humped,
likely due to strong cyclotron beaming, with a maximum brightness
of
.
As described in Schwope et al. (1993), the system
faded optically by 1.5 mag during the four nights of observation
in late September 1992. During the EUVE
all-sky survey in November 1992 it was in a low state.
In the high states the optical light curves are double-humped,
likely due to strong cyclotron beaming, with a maximum brightness
of
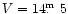 .
In our high-state observations
at two epochs (1993 and 1998), a pronounced optical
pre-eclipse absorption dip can be recognized.
Orbital variability outside eclipse and dip
was between
.
In our high-state observations
at two epochs (1993 and 1998), a pronounced optical
pre-eclipse absorption dip can be recognized.
Orbital variability outside eclipse and dip
was between
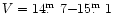 in 1993, and between
in 1993, and between
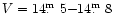 in 1998.
The dip was centred at
in 1998.
The dip was centred at
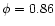 in 1998,
and at
in 1998,
and at
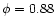 in 1993,
i.e. it occurred earlier in phase when the system was
brighter.
in 1993,
i.e. it occurred earlier in phase when the system was
brighter.
At reduced brightness (=accretion rate) in 1995 and 1996
no pre-eclipse dip is observed. The shape of the
light curve is then more or less single-humped with orbital
variability outside eclipse between
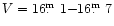 in July 1996,
and
in July 1996,
and
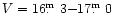 in September 1996.
Strong, 0.5 mag, flaring activity
occurs during the bright phase.
in September 1996.
Strong, 0.5 mag, flaring activity
occurs during the bright phase.
Large differences are observed during the eclipses at different occasions.
After the initial steep ingress due to eclipse of the white dwarf a phase
of slower decrease of brightness follows.
This decrease of brightness
is due to the eclipse of the accretion stream.
This event may last only about two minutes
(Aug. 93, top panel of Fig. 3)
or even as long as 8-10 min (Sep. 96).
The observed large differences
indicate a remarkable re-arrangement of the stream in the magnetosphere of the
white dwarf. The general trend is that a high state corresponds
to a short ingress of the stream and
a low state to a long ingress. This is certainly contrary to the
expectation, since in the high accretion state the ballistic stream
is much longer than in the low accretion state. The reason for this
discrepancy is unknown presently and will be investigated
separately in a dedicated paper.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{eph_omc.eps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg44.gif) |
Figure 4:
Observed minus calculated times of eclipse egress of HU Aqr with
respect to a linear ephemeris.
Open symbols represent EUVE data, filled symbols represent ROSAT-data. |
| Open with DEXTER |
4 The X-ray eclipse of HU Aqr
Table 4:
X-ray eclipse egress times of HU Aqrand their corresponding
orbital phases with respect to Eq. (1).
BJED is the barycentrically corrected ephemeris time of the eclipse egress.
|
Cycle |
BJED |
 BJED BJED |
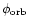 |
| |
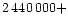 |
|
|
|
0 |
9102.9200026 |
0.0000029 |
0.039612 |
| 2212 |
9294.9667944 |
0.0000013 |
0.039972 |
| 2213 |
9295.0536119 |
0.0000031 |
0.039938 |
| 2216 |
9295.3140780 |
0.0000024 |
0.039993 |
| 2222 |
9295.8349966 |
0.0000024 |
0.039948 |
| 2225 |
9296.0954591 |
0.0000012 |
0.039964 |
| 2226 |
9296.1822824 |
0.0000018 |
0.039997 |
| 4241 |
9471.1254248 |
0.0000109 |
0.040010 |
| 4409 |
9485.7112814 |
0.0000276 |
0.040347 |
| 6328 |
9652.3196284 |
0.0000267 |
0.039982 |
| 6341 |
9653.4483283 |
0.0000066 |
0.040379 |
| 6390 |
9657.7025335 |
0.0000067 |
0.040435 |
| 6391 |
9657.7893776 |
0.0000200 |
0.040708 |
| 6403 |
9658.8311948 |
0.0000115 |
0.040387 |
| 6576 |
9673.8511292 |
0.0000134 |
0.040415 |
| 6579 |
9674.1115921 |
0.0000067 |
0.040434 |
| 10707 |
10032.5062777 |
0.0000246 |
0.040521 |
| 12607 |
10197.4650434 |
0.0000138 |
0.040233 |
| 13064 |
10237.1420028 |
0.0000104 |
0.040568 |
| 13707 |
10292.9675175 |
0.0000184 |
0.040420 |
| 14250 |
10340.1109856 |
0.0000110 |
0.040214 |
| 14740 |
10382.6529766 |
0.0000134 |
0.040065 |
| 14746 |
10383.1739289 |
0.0000187 |
0.040408 |
| 16906 |
10570.7059884 |
0.0000067 |
0.039953 |
| 17010 |
10579.7353441 |
0.0000306 |
0.040326 |
| 17030 |
10581.4717399 |
0.0000095 |
0.040182 |
| 17994 |
10665.1666491 |
0.0000203 |
0.040504 |
| 21014 |
10927.3642796 |
0.0000134 |
0.040200 |
| 21023 |
10928.1456491 |
0.0000067 |
0.040037 |
| 21026 |
10928.4061160 |
0.0000067 |
0.040101 |
| 22478 |
11054.4693474 |
0.0000087 |
0.039953 |
4.1 The X-ray eclipse ephemeris
Although the phase of eclipse ingress was covered several times
during our observations, it is clearly resolved
only in a few cases. At this binary phase the accretion curtain absorbs most
of the X-ray photons, hence we are lacking photons for a precise
determination of eclipse ingress.
For the determination of the orbital period from X-ray
data alone we make use of the frequently covered eclipse egress, which is not
affected by absorption in the binary itself.
The time of eclipse egress
was determined using two different approaches, depending on the brightness
of the target. All egress times with their errors are collected in
Table 4, the times quoted there are corrected for the
solar system barycentre and account for the leap seconds introduced
during recent years (barycentric Julian ephemeris time, BJED).
If the source was sufficiently bright, eclipse egress
was defined as the arrival time of the second photon at the expected egress
time in the original photon event table (PET). The uncertainty given in
Table 4 is then the rms of the first three photons. If the source
was faint, <1s-1, the original PET was phase-folded and time-binned.
The times quoted for these observations in Table 4 are the
times of those bins marking the end of the eclipse. The errors given
in the table correspond to the bin width.
A weighted linear regression to all times collected in Table 4
yields the ephemeris
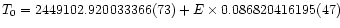 with a
reduced
with a
reduced
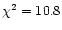 .
The diagram in Fig. 4 compares
the observed and calculated times of egress.
It shows systematic deviations from a linear trend.
A quadratic ephemeris
.
The diagram in Fig. 4 compares
the observed and calculated times of egress.
It shows systematic deviations from a linear trend.
A quadratic ephemeris
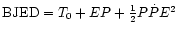 with
T0 = 2449102.920011942(73),
with
T0 = 2449102.920011942(73),
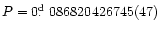 and
and
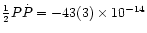 days
yields a significantly smaller reduced
days
yields a significantly smaller reduced 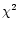 of 2.6 (values in
parenthesis give formal statistical errors).
This finding can be regarded either as an indication of a true period
change, or as an indication of an asynchronously rotating white
dwarf or as migration of the accretion spot, probably in response to
accretion rate changes.
We favor the latter interpretation,
since also the phasing of the bright phase
changes in response to accretion rate variations
(see Sect. 6) and because the largest changes are
observed on a very short time-scale between April and October 1993.
The implications of this interpretation
are further discussed and modeled
in Sect. 4.3. All phases in this paper refer
to the linear ephemeris given in Eq. (1)
of 2.6 (values in
parenthesis give formal statistical errors).
This finding can be regarded either as an indication of a true period
change, or as an indication of an asynchronously rotating white
dwarf or as migration of the accretion spot, probably in response to
accretion rate changes.
We favor the latter interpretation,
since also the phasing of the bright phase
changes in response to accretion rate variations
(see Sect. 6) and because the largest changes are
observed on a very short time-scale between April and October 1993.
The implications of this interpretation
are further discussed and modeled
in Sect. 4.3. All phases in this paper refer
to the linear ephemeris given in Eq. (1)
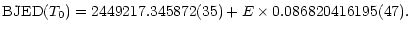 |
|
|
(1) |
The error of the period quoted in parentheses is the
formal statistical error of our linear fit to the ROSAT/EUVE-timings.
The time T0 is the time of superior conjunction of the white
dwarf centre of mass, determined by high-time resolution HST/FOS and
observations optical high-speed photometry (Schwope et al., in preparation).
The systematic uncertainty of the HST-based zero point of the
ephemeris is 3 s, also quoted in parenthesis. In order to convert
times given as BJED to barycentric Julian dates (BJD) one has to subtract
the accumulated number of leap seconds = 60.184s. The zeropoint
given in BJD is 2449217.345176(35).
![\begin{figure}
\par\includegraphics[width=17.7cm,clip]{fit_spot.eps}
\end{figure}](/articles/aa/full/2001/32/aah2761/Timg55.gif) |
Figure 5:
Comparison of model light curves with PSPC 93 observations of HU Aqr.
Small circles connected with polygons are the phase-folded PSPC-data. The
dashed line is a model fit for an accretion spot without vertical extent
with foreshortening factor, the solid line is a fit with vertical extent,
h = 0.015
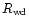 ,
and without foreshortening factor. The top panels
are centred on eclipse ingress and egress, the time interval along the abscissa
is 15 s only, one tick corresponds to 0.75 s. The dotted line in the
lower right panel is the result of a fit with the 3D model. ,
and without foreshortening factor. The top panels
are centred on eclipse ingress and egress, the time interval along the abscissa
is 15 s only, one tick corresponds to 0.75 s. The dotted line in the
lower right panel is the result of a fit with the 3D model. |
| Open with DEXTER |
4.2 Eclipse emission - X-ray's from the secondary star
Secondaries in CVs are rapidly rotating, late-type stars.
Pronounced magnetic activity accompanied by emission of coronal X-rays
may therefore be expected.
Compared to the typical accretion luminosity of
 erg s-1coronal emission of the order of
1029erg s-1
is almost negligible and extremely difficult to detect.
This is particularly true for the majority of the systems which are
non-eclipsing.
The 9 eclipses of HU Aqr covered during the two PSPC pointings in
1993 provide the unique opportunity to directly access
the secondary in a CV at X-ray wavelengths.
erg s-1coronal emission of the order of
1029erg s-1
is almost negligible and extremely difficult to detect.
This is particularly true for the majority of the systems which are
non-eclipsing.
The 9 eclipses of HU Aqr covered during the two PSPC pointings in
1993 provide the unique opportunity to directly access
the secondary in a CV at X-ray wavelengths.
Sohl et al. (1996) claimed a positive X-ray detection of HU Aqr during
eclipse at a count rate of 0.018s-1
from the Oct./Nov. 1993 data alone. Using the same data set,
we find no X-ray source with an existence likelihood ML >5, (ML 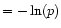 ,
with p being the probability that a source is the result of a statistical
fluctuation).
After inclusion of the April 1993 dataset
the total exposure during eclipse,
,
with p being the probability that a source is the result of a statistical
fluctuation).
After inclusion of the April 1993 dataset
the total exposure during eclipse,
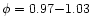 ,
was
3080 s. Within the specified phase interval 20 photons
were collected at the position of HUAqr, giving a
maximum likelihood of existence of an X-ray source at that
position of 9. This corresponds to a
vignetting and dead-time corrected count rate of
,
was
3080 s. Within the specified phase interval 20 photons
were collected at the position of HUAqr, giving a
maximum likelihood of existence of an X-ray source at that
position of 9. This corresponds to a
vignetting and dead-time corrected count rate of
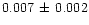 cts s-1, a factor of 3 lower than Sohl's estimate.
cts s-1, a factor of 3 lower than Sohl's estimate.
After ingress of the white dwarf at phase
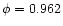 parts of the accretion stream are still visible and detected in the
optical light curves. The stream eclipse is total
only at
parts of the accretion stream are still visible and detected in the
optical light curves. The stream eclipse is total
only at
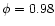 .
The stream could be a source of X-rays,
e.g. due to scattering or internally due to shock heating.
If so, we would expect more photons during first part of the eclipse.
This is not obviously the case but
the limited statistics of our detection does not permit any
secure statement. For the time being we assume that all photons
detected during the eclipse are originating from the secondary star
in HU Aqr.
.
The stream could be a source of X-rays,
e.g. due to scattering or internally due to shock heating.
If so, we would expect more photons during first part of the eclipse.
This is not obviously the case but
the limited statistics of our detection does not permit any
secure statement. For the time being we assume that all photons
detected during the eclipse are originating from the secondary star
in HU Aqr.
The X-ray flux of the secondary at Earth is
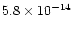 ergs s-1 cm-2 using the count-energy conversion
ergs s-1 cm-2 using the count-energy conversion
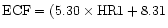 )
10-12 erg cm-2 cts-1 derived by
Schmitt et al. (1994) based on a study of a complete sample
of main-sequence stars. At the likely distance to HU Aqr of 180 pc,
the red star's luminosity is 2.2
)
10-12 erg cm-2 cts-1 derived by
Schmitt et al. (1994) based on a study of a complete sample
of main-sequence stars. At the likely distance to HU Aqr of 180 pc,
the red star's luminosity is 2.2
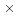 1029 ergs s-1.
The luminosity of an adopted M5 main sequence secondary is
1029 ergs s-1.
The luminosity of an adopted M5 main sequence secondary is
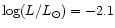 .
With our measured X-ray luminosity
.
With our measured X-ray luminosity 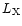 the ratio
the ratio
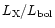 for the secondary in HU Aqr is
for the secondary in HU Aqr is
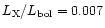 (
(
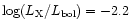 ).
Information about X-ray luminosities (in absolute and relative units)
of single stars at the bottom
of the main sequence is sparse. ROSAT studies of several young open
clusters by Prosser et al. (1996, 1998) show, that our measured
eclipse X-ray flux is in full agreement with those of late-type stars
in the clusters. Particularly interesting is the increase of
).
Information about X-ray luminosities (in absolute and relative units)
of single stars at the bottom
of the main sequence is sparse. ROSAT studies of several young open
clusters by Prosser et al. (1996, 1998) show, that our measured
eclipse X-ray flux is in full agreement with those of late-type stars
in the clusters. Particularly interesting is the increase of
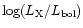 for stars in clusters with spectral type later than M0
above the canonical saturation level of -3. Our results suggest
that is true also for the dM5 secondary in HU Aqr.
for stars in clusters with spectral type later than M0
above the canonical saturation level of -3. Our results suggest
that is true also for the dM5 secondary in HU Aqr.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{spot_parms.ps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg71.gif) |
Figure 6:
Light-curve modeling of points on the
white dwarf surface. Each line represents one observed
eclipse. Azimuth (longitude) and phase of
eclipse egress were
used as input parameters, the latter with the error as listed
in Table 4, eclipse length and lo-latitude are predicted
by the model. A phase difference of 0.005 corresponds to 3.75 s.
In the upper panel, the azimuth of the point in concern increases
from top to bottom. The length of each of the lines shown in the two
panels is defined by the measurement uncertainty of the eclipse egress.
In the lower panel, the solid line represents the foot-line (accretion arc)
of dipolar field lines connecting to the ballistic stream. The bold part
of that line corresponds to the observed width of the narrow stream dip. |
| Open with DEXTER |
4.3 Eclipse light curve modeling
The X-ray eclipse of HU Aqr offers an excellent possibility to
constrain the size and location of the X-ray emission region on the
white dwarf. A very similar system in this respect is UZ For
(Warren et al. 1995), in many respects a twin of HU Aqr.
We developed a simple but powerful model to reflect the main
features of the 1993 PSPC light curve, the only one with sufficient
count rate for a detailed eclipse study, under the following assumptions:
- The eclipse ingress and egress are not affected by the PSPC wire
mesh. A wire crossing could result in a delayed egress (early ingress)
by up to 15 s which is not observed.
- The mass ratio is
Q = M1/M2 = 4 and the orbital inclination
i = 85.6 .
These values are based on high-resolution optical
spectroscopy, where the velocity of the secondary star could be measured
(Schwope et al. 1997 and unpublished data) and the shape and length of the
eclipse in the ultraviolet as seen with the HST/FOS (Schwope et al., in
preparation). The lower limit to Q is 3.5 and we made sure that none
of the conclusions drawn depends critically on the assumed value of Q.
.
These values are based on high-resolution optical
spectroscopy, where the velocity of the secondary star could be measured
(Schwope et al. 1997 and unpublished data) and the shape and length of the
eclipse in the ultraviolet as seen with the HST/FOS (Schwope et al., in
preparation). The lower limit to Q is 3.5 and we made sure that none
of the conclusions drawn depends critically on the assumed value of Q.
- The secondary star has a mass 0.17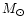 ,
according to the mass-radius
relation by Neece (1984). Using the relation by Caillault & Patterson
(1990) the mass is
M2 = 0.15
,
according to the mass-radius
relation by Neece (1984). Using the relation by Caillault & Patterson
(1990) the mass is
M2 = 0.15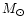 .
The influence on the fits to the
light curve,
higher mass M2 means higher higher mass M1 means smaller
radius
.
The influence on the fits to the
light curve,
higher mass M2 means higher higher mass M1 means smaller
radius
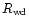 ,
is non-negligible but small and will be discussed
below.
,
is non-negligible but small and will be discussed
below.
- The emission region is a circular spot at some height h (in units
of the white dwarf radius) above the photosphere. The vertical
surfaces of the cylinder do not contribute X-ray flux in our model.
This assumption means, that we are able to correctly predict
contact points but do not pay very much attention to
reflect exactly the shape of the light curve.
The spot is divided in small elements, each with the same height.
The emission of any visible element at a given phase
is either completely optically thin
or thick, i.e. the model light curve is the summed visibility function of
the surface elements with or without a foreshortening factor.
- The spot has a certain orientation in the binary system defined
by the azimuth (longitude) 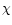 ,
measured with respect to the line joining
both stars, and the co-latitude
,
measured with respect to the line joining
both stars, and the co-latitude 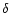 ,
measured with respect to
the rotation axis. The azimuth is determined accurately by the phasing
of the bright phase centre,
,
measured with respect to
the rotation axis. The azimuth is determined accurately by the phasing
of the bright phase centre,
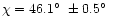 .
This value
is in agreement with earlier measurements based on optical photometry
(e.g. Schwope et al. 1993; Glenn et al. 1994; Harrop-Allin et al. 1999),
but here determined with
much higher accuracy due to the absence of contaminating radiation
from elsewhere in the system.
.
This value
is in agreement with earlier measurements based on optical photometry
(e.g. Schwope et al. 1993; Glenn et al. 1994; Harrop-Allin et al. 1999),
but here determined with
much higher accuracy due to the absence of contaminating radiation
from elsewhere in the system.
In X-rays we are seeing the eclipse of a small hot region on the surface
of the white dwarf, i.e. away from the centre of mass. A certain phase
relation exists between the eclipse of the spot and the eclipse of centre
of mass depending on the co-latitude of the spot and the radius of the
white dwarf. The height of the emission does not play a role here, since
we are seeing the spot projected onto the surface.
The mentioned relation is the lever arm to determine the co-latitude
of the spot within the limits set by the uncertainty of
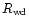 .
.
The main results of the observations and our modeling are:
- The eclipse lasts 587.5 s in "P Nov. 93''. We note,
however, that the duration
of ingress phase and the exact start of the phase of totality
is somewhat uncertain due to absorption of X-rays
in the accretion curtain. The duration of eclipse egress is
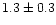 s.
The uncertainty in this quantity derives mainly
from the presence of strong flaring outside the eclipse which makes
a distinction between geometric and intrinsic variability difficult.
The eclipse of the centre of the accretion spot occurs
0.00088 phase units =6.6 s later than the eclipse
of the centre of mass.
s.
The uncertainty in this quantity derives mainly
from the presence of strong flaring outside the eclipse which makes
a distinction between geometric and intrinsic variability difficult.
The eclipse of the centre of the accretion spot occurs
0.00088 phase units =6.6 s later than the eclipse
of the centre of mass.
- Our model gives best agreement with the observations for a
spot size of 3 (full opening angle, see Fig. 5).
The maximum possible extent is 4
(full opening angle, see Fig. 5).
The maximum possible extent is 4 .
This result is not dependent on the assumed height,
the co-latitude, or the emission model (optical thick or thin emission).
The measured
spot size of the assumed circular accretion spot
gives a fractional emitting area of the spot of 0.013
.
This result is not dependent on the assumed height,
the co-latitude, or the emission model (optical thick or thin emission).
The measured
spot size of the assumed circular accretion spot
gives a fractional emitting area of the spot of 0.013
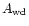 .
The
linear dimension across the spot is about 450km.
.
The
linear dimension across the spot is about 450km.
- A model without vertical extent (dashed lines in Fig. 5)
reproduces the observed rise to and fall from the bright phase. Such
a model requires an extreme `northern' location of the spot at a co-latitude
of only 9 .
At this high latitude the predicted
phase offset between spot centre
and centre of mass is much smaller than observed.
In order to reproduce the observed
length of the bright phase together with the observed phase relation between
eclipses of the spot and the centre of mass a more "southern'' latitude and
a vertical extent of the X-ray emitting region have to be assumed.
.
At this high latitude the predicted
phase offset between spot centre
and centre of mass is much smaller than observed.
In order to reproduce the observed
length of the bright phase together with the observed phase relation between
eclipses of the spot and the centre of mass a more "southern'' latitude and
a vertical extent of the X-ray emitting region have to be assumed.
- The box-shaped solid line in Fig. 5 (lower left and top panels)
represents an optically thin model for an emission region at a height
of 0.015
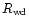 and a co-latitude of
and a co-latitude of
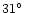 .
It reflects well the phase relation between centre bright
phase, eclipse centre and eclipse length. The statistical uncertainty
of the co-latitude is of the order 2
.
It reflects well the phase relation between centre bright
phase, eclipse centre and eclipse length. The statistical uncertainty
of the co-latitude is of the order 2 ,
there is however a somewhat
larger systematical uncertainty which is related to the unknown mass
of the secondary star.
If we, for instance, use the Caillault & Patterson (1990)
mass-radius relation for the secondary, the secondary becomes less massive
and, for fixed mass ratio, the white dwarf, too. The corresponding larger
white dwarf radius results in a different spot position
at a co-latitude of
,
there is however a somewhat
larger systematical uncertainty which is related to the unknown mass
of the secondary star.
If we, for instance, use the Caillault & Patterson (1990)
mass-radius relation for the secondary, the secondary becomes less massive
and, for fixed mass ratio, the white dwarf, too. The corresponding larger
white dwarf radius results in a different spot position
at a co-latitude of
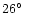 in order to get all the phase relations
and the eclipse length correct.
in order to get all the phase relations
and the eclipse length correct.
- The optically thin model reflects the contact phases well (at eclipse
ingress/egress and start/end of the bright phase) and thus constrains
the vertical and lateral extent of the emission region. Due to its
simplicity, it cannot reproduce
the exact shape of the light curve at start and end of the bright phase.
In order to cope with this short-come of the model, we also applied
the model presented in Sirk & Howell (1998) to the data, which accounts for a
full 3D structure of the emission region.
Application of this model for fixed 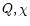 and i reveals
a spot radius (lateral extent) of 0.0465
and i reveals
a spot radius (lateral extent) of 0.0465
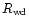 (2.7
(2.7 )
and a spot height of 0.0142
)
and a spot height of 0.0142
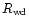 .
These numbers are well in agreement
with those derived from the simple 2D model. The fit to the data, however,
is clearly much better than that of the 2D model
(Fig. 5, bottom right), at least at start and end of the
bright phase. This model predicts a maximum count rate of 80s-1in the centre of the bright phase, which is not observed. This deviation
is further addressed in Sect. 6.
Detailed modeling of the eclipse, however, is not possible with the
current version of the 3D code,
we therefore use here for the analysis of the eclipse a combination of both
models.
.
These numbers are well in agreement
with those derived from the simple 2D model. The fit to the data, however,
is clearly much better than that of the 2D model
(Fig. 5, bottom right), at least at start and end of the
bright phase. This model predicts a maximum count rate of 80s-1in the centre of the bright phase, which is not observed. This deviation
is further addressed in Sect. 6.
Detailed modeling of the eclipse, however, is not possible with the
current version of the 3D code,
we therefore use here for the analysis of the eclipse a combination of both
models.
- If the assumption of a linear ephemeris (Eq. (1)) is correct
and if the white dwarf rotates synchronously, the observed
scatter of eclipse egress times must have a geometrical explanation. Both,
shifts in longitude (azimuth) and latitude are possible.
Azimuthal shifts are obvious
from the phase shift
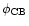 of the bright-phase centre.
According to the values of
of the bright-phase centre.
According to the values of
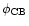 listed in Table 3,
the azimuth of the spot varies between
listed in Table 3,
the azimuth of the spot varies between 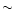 35
35 and
and 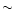 50
50 .
.
In order to explore the likely size of an latitudinal shift of the
accretion hot spot we performed model calculations using our 2D model
applied to points on the white dwarf surface. For a given
geometry, a point on the white dwarf surface (characterized by
its latitude and longitude) has a certain
eclipse ingress, eclipse egress, i.e. eclipse length.
Observationally, the phase of eclipse egress and the azimuth
of the spot can be directly determined. The eclipse model then
makes predictions for the remaining parameters, the co-latitude
of the spot and the eclipse length.
These are plotted for the individual observations
in Fig. 6. Each line in the two panels
represents one particular observation. The length of each
line is determined by the measurement uncertainty of eclipse
egress. The uncertainty of the azimuth is almost negligible
and was set to zero.
Relevant in Fig. 6 are not the absolute numbers
but the range of predicted variability of the co-latitude and the
eclipse length.
The absolute numbers depend on the radius, hence mass, of the white dwarf,
and are therefore somewhat uncertain.
From Fig. 6 we obtain,
that the co-latitude of the spot
likely undergoes shifts as large
as 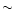 15
15 ,
similarly to the shift in azimuth.
The present data are insufficient to uncover any clear
relation between spot longitude and latitude.
We can state, however, that the derived locations of surface elements
do not stretch along the expected position of an accretion arc, defined
as foot-points of dipolar field lines connecting the white dwarf
with the ballistic stream
for our most likely orientation of the magnetic axis.
,
similarly to the shift in azimuth.
The present data are insufficient to uncover any clear
relation between spot longitude and latitude.
We can state, however, that the derived locations of surface elements
do not stretch along the expected position of an accretion arc, defined
as foot-points of dipolar field lines connecting the white dwarf
with the ballistic stream
for our most likely orientation of the magnetic axis.
According to Fig. 6 variations of the eclipse length
of up to 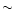 8 s (
8 s (
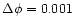 )
can be expected.
This is of the same order as the observed scatter of
eclipse egress times. The predicted scatter of the eclipse length
can not be confirmed so far with our existing soft X-ray observations.
These should be easily detectable with hard X-ray
observations using e.g. XMM-Newton, which resolve the
eclipse ingress clearly.
)
can be expected.
This is of the same order as the observed scatter of
eclipse egress times. The predicted scatter of the eclipse length
can not be confirmed so far with our existing soft X-ray observations.
These should be easily detectable with hard X-ray
observations using e.g. XMM-Newton, which resolve the
eclipse ingress clearly.
5 Spectral analysis
A spectral analysis was performed for the high-state observation
referred to as "P Oct. 93''.
With the resolution provided by the ROSAT-PSPC two spectral components
can be discerned clearly, a soft quasi-blackbody component from the
heated photosphere in and around the accretion region and a hard
component well described by thermal bremsstrahlung from the hot
post-shock region. The temperature of the latter cannot be independently
determined
with the ROSAT data, since the PSPC does not provide sufficient
wavelength coverage. We fixed it at 20 keV. A grid of least-squares
fits assuming the two-component model (bbdy + thbr) with
interstellar cold absorption was performed for two selected phase intervals,
for the bright phase prior to the narrow absorption dip,
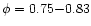 ,
and
for the post-eclipse bright part of the light curve,
,
and
for the post-eclipse bright part of the light curve,
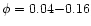 .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{grid_bb_br.ps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg83.gif) |
Figure 7:
Results of combined blackbody and bremsstrahlung
fits to the "P Oct. 93'' observations. Shown are 68% and 99.9%
contours for the two phase intervals
0.75-0.83 (slightly harder
spectrum with higher temperature and larger column density)
and
0.04-0.16, respectively,
in the
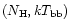 -plane. -plane. |
| Open with DEXTER |
The results are shown as confidence contours in Fig. 7. The
somewhat softer spectrum at slightly lower 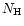 is observed after
eclipse, i.e. the centre of the bright phase phase could be affected
by a small amount of extra (intrinsic) absorption. We regard the
post-eclipse spectrum as reference for further modeling of
the accretion curtain (next section).
The best-fit parameters are
is observed after
eclipse, i.e. the centre of the bright phase phase could be affected
by a small amount of extra (intrinsic) absorption. We regard the
post-eclipse spectrum as reference for further modeling of
the accretion curtain (next section).
The best-fit parameters are
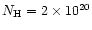 cm-2 and
cm-2 and
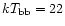 eV (
eV (
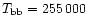 K).
In the ROSAT band (
0.1 -2.4keV)
the total un-absorbed blackbody flux
is
K).
In the ROSAT band (
0.1 -2.4keV)
the total un-absorbed blackbody flux
is
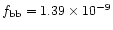 erg cm-2 s-1, the total un-absorbed
bremsstrahlung flux is
erg cm-2 s-1, the total un-absorbed
bremsstrahlung flux is
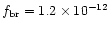 erg cm-2 s-1.
The bolometric correction factors for the blackbody and bremsstrahlung
components are about 3.2 and 4.6, respectively, i.e. the ratio of the
un-absorbed bolometric fluxes is
erg cm-2 s-1.
The bolometric correction factors for the blackbody and bremsstrahlung
components are about 3.2 and 4.6, respectively, i.e. the ratio of the
un-absorbed bolometric fluxes is
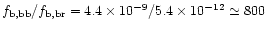 .
Even taking into account
an uncertainty of a factor 2 in both components
due to the unknown emission characteristic,
the soft excess easily exceeds a factor 100.
.
Even taking into account
an uncertainty of a factor 2 in both components
due to the unknown emission characteristic,
the soft excess easily exceeds a factor 100.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{cbp_cr_dip.ps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg90.gif) |
Figure 8:
Relation between (a) equivalent HRI count rate SCR1
(see Table 3) and phase
of dip ingress, (b) equivalent HRI count rate and centre of bright
phase, and (c) phase relation between dip ingress and centre of
bright phase. Filled rhombs indicate ROSAT-data, crosses indicate EUVE-data. |
| Open with DEXTER |
Taking into account only the blackbody component, the accretion luminosity
and the total accretion rate can be estimated from the spectral parameters
or the observed flux at Earth. Assuming a flat circular accretion spot
of diameter 450km and
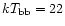 eV, the accretion luminosity is
eV, the accretion luminosity is
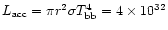 erg s-1.
erg s-1.
Using the observed flux at Earth
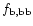 radiated into an
angle
radiated into an
angle 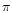 ,
the accretion luminosity is
,
the accretion luminosity is
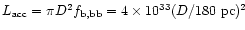 erg s-1. Both estimates are
uncertain to at least 50%
due to the unknowns in
erg s-1. Both estimates are
uncertain to at least 50%
due to the unknowns in
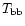 ,
D, and the emission characteristics.
The inferred accretion rate is between
,
D, and the emission characteristics.
The inferred accretion rate is between
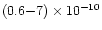
 /yr,
i.e. at the rate expected for a CV with an orbital period of 2 hours.
Using a two-component model spectrum with the best-fit post-eclipse
spectral parameters folded through the instrumental response curves
of the PSPC and the HRI detectors, respectively, a count conversion
PSPC/HRI = 8 was calculated and used for computation of the
equivalent HRI count rates listed in Table 3.
/yr,
i.e. at the rate expected for a CV with an orbital period of 2 hours.
Using a two-component model spectrum with the best-fit post-eclipse
spectral parameters folded through the instrumental response curves
of the PSPC and the HRI detectors, respectively, a count conversion
PSPC/HRI = 8 was calculated and used for computation of the
equivalent HRI count rates listed in Table 3.
6 The narrow and broad dips and the accretion curtain
The phase of narrow dip centre varies between 0.868 to 0.929, the
phase of half intensity at dip
ingress varies between 0.828 to 0.929 (Cols.
5 and 6 in Table 3),
i.e. the azimuth of the threading region varies by about 36 .
The centre of the bright phase varies much less
by only 0.04 phase units, corresponding to only about 15
.
The centre of the bright phase varies much less
by only 0.04 phase units, corresponding to only about 15 .
At the same time the X-ray count rate (equivalent HRI count rate)
varies by a factor 40.
Here we investigate the systematics in this behavior.
.
At the same time the X-ray count rate (equivalent HRI count rate)
varies by a factor 40.
Here we investigate the systematics in this behavior.
In Fig. 8 we plot
the equivalent count rate SCR1vs. dip phase, the centre of the bright phase
vs. dip phase, and the equivalent count rate vs. the centre of the bright
phase. The numbers are listed in Table 3.
By plotting these quantities we are testing if the
X-ray count rate varies proportional to the mass accretion rate
and whether the penetration of the stream into the magnetosphere
can be understood in terms of the interplay between ram
pressure and magnetic pressure.
If the X-ray count rate would scale proportional
to the specific mass accretion rate and to
the ram pressure in the ballistic stream, a unique relation
between equivalent count rate and dip phase should exist. One
also expects, that the accretion spot migrates towards a larger azimuth
if the stream couples further downstream onto magnetic field lines.
If the magnetic field would be an aligned dipole, spot azimuth
and dip azimuth would vary by the same amount.
Figure 8 shows that the expected relations are quite well
established for sufficiently high count rate (SCR1 > 0.2s-1) which
applies to most ROSAT observations (except "H Oct. 96''),
and two EUVE observations ("D May 97'', and "D Aug. 98'' in low and
high accretion states, respectively).
At low count rate (most EUVE observations) the relations break down.
The reason for the deviating behavior of the 6 low-state observations
is unclear. The ROSAT observation "H Oct. 96'' does not fit into the simple
picture, but the bright phase centre
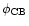 and the
phase of dip ingress
and the
phase of dip ingress
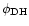 are similar to those
of the quasi-simultaneous EUVE-observation. The count rate SCR1
differs by a factor of 2, which we attribute to the non-simultaneity
of the observation and the high variability of the source.
The ROSAT outlier at the lowest count rate is "H Apr. 96''. On that
occasion the binary showed a highly peculiar light curve
(see Fig. 2). It displayed one of the
highest HRI count rates observed ever in the centre of the bright phase
while one of the lowest count rates SCR1
shortly after eclipse, thus mimicking a low state.
Since the latter quantity is plotted in Fig. 8, this data point
apparently seems to be misplaced in that diagram.
The ROSAT data therefore suggest
clearly, that at higher accretion rate the stream penetrates
the magnetosphere more deeply and couples further downstream
onto field lines.
As a consequence, the spot longitude is shifted away from the
secondary star, i.e.
are similar to those
of the quasi-simultaneous EUVE-observation. The count rate SCR1
differs by a factor of 2, which we attribute to the non-simultaneity
of the observation and the high variability of the source.
The ROSAT outlier at the lowest count rate is "H Apr. 96''. On that
occasion the binary showed a highly peculiar light curve
(see Fig. 2). It displayed one of the
highest HRI count rates observed ever in the centre of the bright phase
while one of the lowest count rates SCR1
shortly after eclipse, thus mimicking a low state.
Since the latter quantity is plotted in Fig. 8, this data point
apparently seems to be misplaced in that diagram.
The ROSAT data therefore suggest
clearly, that at higher accretion rate the stream penetrates
the magnetosphere more deeply and couples further downstream
onto field lines.
As a consequence, the spot longitude is shifted away from the
secondary star, i.e.
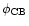 becomes larger. The picture is
different for the EUVE data, since the centre of the bright phase
does not behave as expected but remains at large azimuthal
angles, despite early coupling of the main portion
of the stream onto magnetic field lines. This may mean, that
some matter runs further downstream even in the low accretion state,
builds a hot accretion spot at relatively large azimuth, while
the matter that couples early does not dominate the soft X-ray radiation.
becomes larger. The picture is
different for the EUVE data, since the centre of the bright phase
does not behave as expected but remains at large azimuthal
angles, despite early coupling of the main portion
of the stream onto magnetic field lines. This may mean, that
some matter runs further downstream even in the low accretion state,
builds a hot accretion spot at relatively large azimuth, while
the matter that couples early does not dominate the soft X-ray radiation.
In Fig. 9 we investigate the conditions in the accretion stream
in a basic picture. The upper panel shows a sketch of the accretion
geometry projected
onto the orbital plane, the lower panel shows the ratio between the
magnetic and the ram pressure along the ballistic stream. The trajectory
was computed in a single-particle approximation, i.e. neglecting thermal
pressure. A mass ratio
Q = M1/M2 = 4, a centred dipole with an inclination
of the magnetic axis of 15 ,
an azimuth of the magnetic axis of 38
,
an azimuth of the magnetic axis of 38 ,
and a polar field strength of 38MG was assumed.
The usage of these parameters results in a spot co-latitude
(foot-point of accreting field line) of 31
,
and a polar field strength of 38MG was assumed.
The usage of these parameters results in a spot co-latitude
(foot-point of accreting field line) of 31 ,
in agreement with the
observations.
The shaded region in the upper panel indicates the observed
range of dip ingress phases, according to the 36
,
in agreement with the
observations.
The shaded region in the upper panel indicates the observed
range of dip ingress phases, according to the 36 variability
of
variability
of
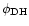 as listed in Table 3. The
ratio between ram and magnetic pressure varies between these
extremes by a factor of
as listed in Table 3. The
ratio between ram and magnetic pressure varies between these
extremes by a factor of 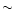 27. This number equals the change of the
specific mass accretion rate,
27. This number equals the change of the
specific mass accretion rate, 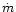 ,
per unit area.
The equivalent HRI count rate varies by a factor of 40. The
great similarity between the two numbers suggests that (a) specific
and total mass accretion rate scale proportional to each other
and that (b) the penetration of the magnetosphere is largely
compatible with the simple picture that the location of the
coupling region is determined by the balance between
ram and magnetic pressure.
,
per unit area.
The equivalent HRI count rate varies by a factor of 40. The
great similarity between the two numbers suggests that (a) specific
and total mass accretion rate scale proportional to each other
and that (b) the penetration of the magnetosphere is largely
compatible with the simple picture that the location of the
coupling region is determined by the balance between
ram and magnetic pressure.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{stagna.eps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg98.gif) |
Figure 9: a), upper panel) Stream geometry of HU Aqr projected onto
the orbital plane. Indicated are the Roche lobes of both stars, the
inner Lagrangian point, the white dwarf and the centre of mass. The
shaded region indicates the size of the cone, where dip ingress
has been observed (azimuth, where half X-ray intensity
occurs, see Table 3). The line
in the shaded region connecting the ballistic trajectory and the white dwarf
indicates the centroid of the
magnetically coupled stream of the "P Oct. 93'' observation. b), lower panel) The ratio of magnetic and ram pressure
along the ballistic stream. |
| Open with DEXTER |
We assume that intrinsically the X-ray
spectral parameters are constant through the orbital cycle,
i.e. that all the X-ray variability in the phase-averaged
light curve is due to a differing amount of cold absorbing matter
in the binary system. We then computed a map of 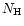 as a function of
orbital phase. This was done under the assumptions of (a) constant
X-ray brightness, and (b) of an un-absorbed light curve according
to the 3D fit (dotted line in Fig. 5).
The spectral parameters and the interstellar absorption
were taken from the fit to the post-eclipse data.
The results are shown in Fig. 10, together with predicted hardness
ratio variations (HR1 and SR) according to the derived value
of
as a function of
orbital phase. This was done under the assumptions of (a) constant
X-ray brightness, and (b) of an un-absorbed light curve according
to the 3D fit (dotted line in Fig. 5).
The spectral parameters and the interstellar absorption
were taken from the fit to the post-eclipse data.
The results are shown in Fig. 10, together with predicted hardness
ratio variations (HR1 and SR) according to the derived value
of 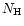 .
The solid line in each panel is for the constant brightness
model, the dashed for the 3D model.
.
The solid line in each panel is for the constant brightness
model, the dashed for the 3D model.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{nhmap.ps}
\end{figure}](/articles/aa/full/2001/32/aah2761/Timg99.gif) |
Figure 10:
Soft X-ray brightness, amount of cold absorption, and hardness
ratios (HR1 and SR) of HU Aqr in October/November 1993.
The phase-folded soft X-ray light curve is shown in the top
panel. The map of 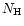 (in units of 1021cm-2)
in the second panel is based on post-eclipse
spectral parameters with respect to constant brightness through the
bright phase (solid line) and with respect to the 3D fit (dashed line).
In the lower two panels the predictions for HR1 and SR according
to the two
(in units of 1021cm-2)
in the second panel is based on post-eclipse
spectral parameters with respect to constant brightness through the
bright phase (solid line) and with respect to the 3D fit (dashed line).
In the lower two panels the predictions for HR1 and SR according
to the two 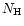 -maps are compared with observed data. -maps are compared with observed data. |
| Open with DEXTER |
The post-eclipse (interstellar) absorption column density is
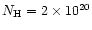 cm-2,
in the curtain the column is
cm-2,
in the curtain the column is
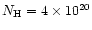 cm-2 and in the
narrow dip
cm-2 and in the
narrow dip
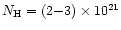 cm-2.
Figure 10 shows
that the observed variations of the count rate, the hardness ratios HR1
and SR in the narrow dip and in the curtain,
respectively, can be understood in terms of
an increase of the column
cm-2.
Figure 10 shows
that the observed variations of the count rate, the hardness ratios HR1
and SR in the narrow dip and in the curtain,
respectively, can be understood in terms of
an increase of the column 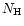 of cold absorbing matter.
This does not apply to the broad dip at phase 0.7. The predicted
increase in
of cold absorbing matter.
This does not apply to the broad dip at phase 0.7. The predicted
increase in 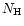 would result in a decrease of the hardness ratio SR.
The occurrence of a broad dip therefore cannot be explained
by cold absorption. Either we have a highly complicated surface
structure (smaller effective area at phase 0.7 than at phase 0.6),
the spectral parameters changed or warm absorption plays a role.
The presently available data have too low spectral resolution
in order to discern between these alternatives.
would result in a decrease of the hardness ratio SR.
The occurrence of a broad dip therefore cannot be explained
by cold absorption. Either we have a highly complicated surface
structure (smaller effective area at phase 0.7 than at phase 0.6),
the spectral parameters changed or warm absorption plays a role.
The presently available data have too low spectral resolution
in order to discern between these alternatives.
Based on the 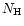 -map of Fig. 10 we may estimate the
accretion rate in the curtain and the stream.
Taking the simple view of constant flow velocity
-map of Fig. 10 we may estimate the
accretion rate in the curtain and the stream.
Taking the simple view of constant flow velocity
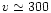 kms-1 through the curtain (Schwope et al. 1997)
and a length of the
curtain given by the length of the ballistic
accretion stream,
kms-1 through the curtain (Schwope et al. 1997)
and a length of the
curtain given by the length of the ballistic
accretion stream,
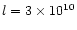 cm, the mass accretion rate in the curtain is
cm, the mass accretion rate in the curtain is
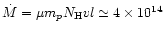 g s
g s
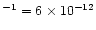
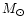 /yr (
/yr (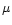 :
mean atomic mass per H-atom).
In the dip (= accretion stream),
the velocity is higher by a factor
:
mean atomic mass per H-atom).
In the dip (= accretion stream),
the velocity is higher by a factor  3,
the density higher by a factor of
3,
the density higher by a factor of  10,
and the linear dimension is smaller by a factor
10,
and the linear dimension is smaller by a factor 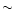 3, i.e. the
mass accretion rate in the stream is roughly a factor 10 higher
than in the curtain.
These order-of-magnitude estimates show, that the amount of matter
transfered to the white dwarf via the curtain is clearly non-negligible
although the bulk of matter is transfered via the stream.
The number derived here for the mass accretion rate, based
on the amount of cold absorption,
3, i.e. the
mass accretion rate in the stream is roughly a factor 10 higher
than in the curtain.
These order-of-magnitude estimates show, that the amount of matter
transfered to the white dwarf via the curtain is clearly non-negligible
although the bulk of matter is transfered via the stream.
The number derived here for the mass accretion rate, based
on the amount of cold absorption,
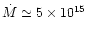 g s
g s
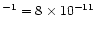
 /yr is in
rough agreement with the estimate based on
the X-ray spectral flux (Sect. 5).
/yr is in
rough agreement with the estimate based on
the X-ray spectral flux (Sect. 5).
We also tested if the observed width of the narrow stream dip
and the measured spot size, as derived from the elipse egress,
are compatible in a dipolar geometry. The narrow dip has a width
of about 18 (phase 0.85-0.90). With our favourite orientation
of the dipolar axis, this converges to a spot azimuth along a small circle
of about 10
(phase 0.85-0.90). With our favourite orientation
of the dipolar axis, this converges to a spot azimuth along a small circle
of about 10 ,
as indicated in Fig. 6. At a co-latitude of
30
,
as indicated in Fig. 6. At a co-latitude of
30 this corresponds to a full opening angle along a great circle
of 5
this corresponds to a full opening angle along a great circle
of 5 .
From the eclipse egress we derived a full opening angle of
the soft X-ray emitting spot of
.
From the eclipse egress we derived a full opening angle of
the soft X-ray emitting spot of
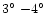 .
We conclude, that only the inner 60-80% of the stream
is dense enough and carries enough accretion energy
to "fire'' the soft X-ray engine.
.
We conclude, that only the inner 60-80% of the stream
is dense enough and carries enough accretion energy
to "fire'' the soft X-ray engine.
7 Summary and conclusions
We have intensively studied the eclipsing polar HU Aqr in soft X-rays
using ROSAT and EUVE.
During our monitoring observations the source varied in brightness,
i.e. mass accretion rate, by a factor of about 40. The one stable
feature in the light curves, the eclipse caused by the secondary star, was
used to derive an updated linear ephemeris of the binary star.
Apparent deviations from a linear trend are likely due to migrations
of the accretion spot over the surface of the white dwarf.
The implied shifts in spot latitude and azimuth are of the order
of 15 .
.
The eclipse by the secondary star was thoroughly investigated
by us. We found X-ray emission in the eclipse attributed
to the secondary star, the implied luminosity of
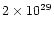 erg s-1 is
comparable to those of single M-stars of same spectral type.
erg s-1 is
comparable to those of single M-stars of same spectral type.
We have successfully modeled the shape, phase, and extent
of the soft X-ray eclipse in combination with the phasing and
length of the X-ray bright phase in a high accretion state
(observation "P Oct. 93'').
According to our modeling, the accretion region has a full
opening angle of 3 ,
is located at stellar co-latitude
30
,
is located at stellar co-latitude
30 ,
azimuth 46
,
azimuth 46 ,
and has a vertical extent of less than
0.015
,
and has a vertical extent of less than
0.015
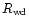 .
.
An absorption dip caused by the accretion stream passing the
line of sight was seen at all epochs. It varied in phase
due to changes of the mass accretion rate, hence ram pressure.
The observed phase shift of the dip, and of the centre of the bright
phase and the observed change of the mass accretion rate
can be understood in terms of ram pressure
and magnetic pressure balancing arguments. The low-state data, however,
most of them obtained with the EUVE satellite, do not
fit in this simple picture for an unknown reason.
The X-ray spectrum of HU Aqr, has (at ROSAT resolution) two components,
a blackbody-type component with
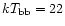 eV in the soft regime
and a hard bremsstrahlung component with
eV in the soft regime
and a hard bremsstrahlung component with
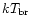 likely to be in the
few 10 keV regime. The spectral fit gives a huge soft X-ray excess
in the high accretion state of
likely to be in the
few 10 keV regime. The spectral fit gives a huge soft X-ray excess
in the high accretion state of
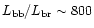 .
The X-ray luminosity derived here,
.
The X-ray luminosity derived here,
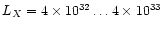 erg s-1,
is typical for cataclysmic binaries
at an orbital period of 2 hours.
erg s-1,
is typical for cataclysmic binaries
at an orbital period of 2 hours.
Using the spectral parameters determined in post-eclipse PSPC data, which
are supposedly free of internal absorption, we derived the absorption
column density in the stream and the accretion curtain. They differ
by a factor of  10, as do the accretion rates through these
structures. These estimates show that transfer of mass along
the curtain is non-negligible although insufficient to power
significant X-ray emission. In particular, the
foot-line of the curtain on the surface of the white dwarf is
not bright in X-rays. If it were, the
eclipse egress would have taken about 5s instead of the observed 1.3s.
The accretion energy released at the foot-print of the
accretion curtain is not emitted in soft X-rays, but probably
shifted to neighbouring spectral regimes (FUV/UV or e.g. as optical cyclotron
radiation).
The occurrence of a broad dip at binary phase 0.7 cannot be explained
by an increase of the column density of cold absorbing matter.
Spectral changes when different parts of the accretion region come
into view under a different aspect angle or a complicated
emitting surface might be responsible for the dip.
10, as do the accretion rates through these
structures. These estimates show that transfer of mass along
the curtain is non-negligible although insufficient to power
significant X-ray emission. In particular, the
foot-line of the curtain on the surface of the white dwarf is
not bright in X-rays. If it were, the
eclipse egress would have taken about 5s instead of the observed 1.3s.
The accretion energy released at the foot-print of the
accretion curtain is not emitted in soft X-rays, but probably
shifted to neighbouring spectral regimes (FUV/UV or e.g. as optical cyclotron
radiation).
The occurrence of a broad dip at binary phase 0.7 cannot be explained
by an increase of the column density of cold absorbing matter.
Spectral changes when different parts of the accretion region come
into view under a different aspect angle or a complicated
emitting surface might be responsible for the dip.
X-rays are also detected in the faint phase, when the main accretion
spot is out of view. It appears unlikely to us, that this is due to a
second accretion spot, since neither optical eclipse light curves
nor the optical spectrum in the faint phase show any sign
of a second accretion spot, e.g. cyclotron harmonics as seen from the
second pole in UZ For (Schwope et al. 1990). Rather than emission from
a second pole scattered light from the main pole seems the likely
cause of the faint-phase emission.
Further X-ray observations with a larger telescope and higher
spectral resolution are necessary in order to gain a better
understanding of the spectral composition of this system in general,
and of the broad dip in the light curve in particular. Future
Chandra or XMM-Newton observations will allow for the first time
to measure the accretion spot size in hard X-rays and to investigate
whether the predicted variations of the eclipse length occur, they will
allow to determine
the eclipse spectrum, and to search for X-rays from the accretion
stream/stagnation region in the first part of the eclipse by the secondary
star.
Acknowledgements
We thank K. Reinsch for providing the optical light curve of Nov. 12, 1995.
We gratefully acknowledge the work of our referee, Dr. D. A. H. Buckley.
This work was supported by the
DLR-Verbundforschung under grant 50 OR 9706 8.
We have made use of the ROSAT Data Archive of the Max-Planck-Institut
für extraterrestrische Physik (MPE) at Garching, Germany.
SBH acknowledges partial support of this research from
NASA grant NAG5-8644 and by a AO7 EUVE mini-grant.
-
Bowyer, S., Lampton, M., Lewis, J., et al.
1996, ApJS, 102, 129
In the text
NASA ADS
-
Buckley, D. A. H., Barrett, P., Haberl, F., & Sekiguchi, K.
1998, MNRAS, 299, 998
In the text
NASA ADS
-
Caillault, J.-P., & Patterson, J. 1990, AJ, 100, 825
In the text
NASA ADS
-
Glenn, J., Howell, S. B., Schmidt, G. D., et al. 1994,
ApJ, 424, 967
In the text
NASA ADS
- Hakala, P. J., Watson, M. G., Vilhu, et al. 1993, MNRAS, 263, 61
In the text
NASA ADS
- Hakala, P. J. 1995, A&A, 296, 164
In the text
NASA ADS
-
Harrop-Allin, M. K., Cropper, M., Hakala, P. J., Hellier, C.,
& Ramseyer, T. 1999, MNRAS, 308, 807
In the text
NASA ADS
- Neece, G. D. 1984, ApJ, 277, 738
In the text
NASA ADS
-
Prosser, C. P., Randich, S., & Simon, T. 1998, Astron. Nachr., 319, 215
In the text
NASA ADS
-
Prosser, C. P., Randich, S., Stauffer, J. R., Schmitt, J. H. M. M., & Simon, T.
1996, AJ, 112, 1570
In the text
NASA ADS
-
Schmitt, J. H. M. M. 1994, ApJS, 90, 735
In the text
NASA ADS
- Schwope, A. D. 1995, Rev. Mod. Astron., 8, 125
In the text
NASA ADS
- Schwope, A. D. 1996, in Cataclysmic Variables and Related
Objects, ed. A. Evans, & J. H. Wood (Kluwer), 189
In the text
- Schwope, A. D., Beuermann, K., & Thomas, H.-C. 1990, A&A, 230, 120
In the text
NASA ADS
- Schwope, A. D., Beuermann, K., & Thomas, H.-C. 1993, A&A, 271, L25
In the text
NASA ADS
- Schwope, A. D., Mantel, K.-H., & Horne, K. 1997, A&A, 319, 894
In the text
NASA ADS
-
Schwope, A. D., Beuermann, K., Buckley, D. A. H., et al. 1998,
ASP Conf. Ser., 137, 44
In the text
- Sirk, M. M., & Howell, S. B. 1998, ApJ, 506, 824
In the text
NASA ADS
- Sohl, K. B., Watson, M. G., & Rosen, S. R. 1996, ASP Conf. Ser., 85, 306
In the text
- Sohl, K. B. 1997, Ph.D. Thesis, Univ. Leicester
In the text
- Voges, W., Aschenbach, B., Boller, Th., et al. 1999, A&A, 349, 389
NASA ADS
- Vrielmann, S., & Schwope, A. D. 2001, MNRAS, in press
In the text
- Warren, J. K., Sirk, M. M., & Vallerga, J. V. 1995, ApJ, 445, 909
In the text
NASA ADS
- Zimmermann, H. U., Becker, W., Belloni, T., et al. 1994, MPE report, 257
In the text
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{pspc_lc.ps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{allxlcs.ps}
\end{figure}](/articles/aa/full/2001/32/aah2761/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{olcs_xpap.eps}
\end{figure}](/articles/aa/full/2001/32/aah2761/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{eph_omc.eps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg44.gif)
![\begin{figure}
\par\includegraphics[width=17.7cm,clip]{fit_spot.eps}
\end{figure}](/articles/aa/full/2001/32/aah2761/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{spot_parms.ps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{grid_bb_br.ps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg83.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{cbp_cr_dip.ps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{stagna.eps}\end{figure}](/articles/aa/full/2001/32/aah2761/Timg98.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{nhmap.ps}
\end{figure}](/articles/aa/full/2001/32/aah2761/Timg99.gif)