The measured equivalent widths
![]() of the C2 lines were converted into
column densities N using
of the C2 lines were converted into
column densities N using
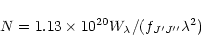 |
(1) |
In the models of
van Dishoeck & Black (1982) the distribution of
populations of the levels J'' of C2 is determined by the ratio
![]() where
where ![]() is the density of the collision
partners of C2,
is the density of the collision
partners of C2,
![]() cm-2 is the cross section for collision induced transitions for level
J'' to rotational level (J''-2) and I is a scaling factor for the incident
radiation field in the near-infrared. If a C2 absorption oscillator strength
different from the one used here is adopted,
the parameter
cm-2 is the cross section for collision induced transitions for level
J'' to rotational level (J''-2) and I is a scaling factor for the incident
radiation field in the near-infrared. If a C2 absorption oscillator strength
different from the one used here is adopted,
the parameter
![]() should be scaled by the ratio of
the oscillator strengths
(cf. note added in proof in van Dishoeck & Black 1982).
For a gas of H2,
should be scaled by the ratio of
the oscillator strengths
(cf. note added in proof in van Dishoeck & Black 1982).
For a gas of H2,
![]() (H2) and
(H2) and
![]() (H2) is the total
column density of hydrogen nuclei. The density
of hydrogen nuclei is
(H2) is the total
column density of hydrogen nuclei. The density
of hydrogen nuclei is
![]() .
We take I=1 corresponding to
the standard interstellar radiation field (see discussion in Sect. 4.1).
.
We take I=1 corresponding to
the standard interstellar radiation field (see discussion in Sect. 4.1).
For the CN A
![]() - X
- X
![]() system, the experimental band oscillator strengths of
Davis et al. (1986) of
system, the experimental band oscillator strengths of
Davis et al. (1986) of
![]() and
and
![]() were adopted for the (1,0) and (2,0) bands,
respectively. Heliocentric velocities of CN were inferred from the
rest wavelengths given by
van Dishoeck & Black (1989).
were adopted for the (1,0) and (2,0) bands,
respectively. Heliocentric velocities of CN were inferred from the
rest wavelengths given by
van Dishoeck & Black (1989).
The spectrum covering the (2,0) band of the C2 Phillips system
towards Cyg OB2 No. 12 is shown in Fig. 1.
The spectrum of the star is dominated by a strong stellar
H I Paschen 12 line near 8752 Å and the 3p3P - 9d3D He I line near
8777 Å. Superimposed on the stellar continuum are interstellar
C2 absorption lines, which are identified. The broad absorption feature
near 8763 Å is a blend of the C2 Q(4) line and of a diffuse
interstellar band (cf. Sect. 3.4). The sharp absorption
features near 8799.75 Å, 8803.23 Å, 8811.51 Å, 8820.05 Å,
8831.2 Å, and 8835.5 Å, arise from telluric H2O absorption.
The C2 measurements are summarised in Table 1, where Cols. 1-5 contain
the line designation, the heliocentric wavelength
![]() in Å, the
derived heliocentric velocity
in Å, the
derived heliocentric velocity
![]() in km s-1, the measured
equivalent width
in km s-1, the measured
equivalent width
![]() in mÅ with uncertainties in parenthesis, and the
derived column densities N(J'') in units of 1013 cm-2, with
uncertainties in parenthesis. The colon in Col. 2 of Table 1, and in
Tables 2, 3, and 6, indicates an uncertain
wavelength, either because it is inferred from a line blend, or
because the wavelength is indicative only in cases were upper limits in
in mÅ with uncertainties in parenthesis, and the
derived column densities N(J'') in units of 1013 cm-2, with
uncertainties in parenthesis. The colon in Col. 2 of Table 1, and in
Tables 2, 3, and 6, indicates an uncertain
wavelength, either because it is inferred from a line blend, or
because the wavelength is indicative only in cases were upper limits in
![]() are given.
are given.
Uncertainties in
![]() are largely governed by uncertainties in the placement of
the local continuum, particularly near the strong stellar H I Paschen
12 absorption line. For equivalent widths obtained from a decomposition
of unresolved line blends, such as the (2,0) band R(2)+R(10) blend,
uncertainties are of the order of 2-3 mÅ.
In general, the uncertainties are larger than 3 standard deviations
of the noise in the stellar continuum.
The C2 column densities adopted here are inferred in the limit
of C2 Doppler values
are largely governed by uncertainties in the placement of
the local continuum, particularly near the strong stellar H I Paschen
12 absorption line. For equivalent widths obtained from a decomposition
of unresolved line blends, such as the (2,0) band R(2)+R(10) blend,
uncertainties are of the order of 2-3 mÅ.
In general, the uncertainties are larger than 3 standard deviations
of the noise in the stellar continuum.
The C2 column densities adopted here are inferred in the limit
of C2 Doppler values
![]() (cf. Eq. (1)).
A curve of growth analysis shows that
deviations from the linear relation of Eq. (1) exceed values
of 10% for
(cf. Eq. (1)).
A curve of growth analysis shows that
deviations from the linear relation of Eq. (1) exceed values
of 10% for
![]() for b in km s-1for the absorption lines in the C2 (2,0) band. Assuming a typical value
of b = 1 km s-1 for C2, the C2 lines suffer from saturation for
equivalent widths of
for b in km s-1for the absorption lines in the C2 (2,0) band. Assuming a typical value
of b = 1 km s-1 for C2, the C2 lines suffer from saturation for
equivalent widths of ![]() 15 mÅ. The strongest C2
absorption lines have equivalent widths of
15 mÅ. The strongest C2
absorption lines have equivalent widths of
![]() m
m![]() .
We nevertheless ignore saturation corrections
for the following two reasons. Firstly,
the observations of GM94 indicate the presence of two main C2 velocity
components separated by 3.7 km s-1. Assuming an equal distribution
of the population density in both velocity components, the C2 lines
are not saturated unless
.
We nevertheless ignore saturation corrections
for the following two reasons. Firstly,
the observations of GM94 indicate the presence of two main C2 velocity
components separated by 3.7 km s-1. Assuming an equal distribution
of the population density in both velocity components, the C2 lines
are not saturated unless
![]() mÅ per velocity
component or
mÅ per velocity
component or
![]() mÅ per absorption line.
Secondly, the C2 Doppler parameter may be larger than 1 km s-1.
The doublet ratio method
applied by Chaffee & White (1982)
in their analysis of K I absorption
lines towards Cyg OB2 No. 12 indicates a Doppler value of
b(K) = 6.4 km s-1 towards No. 12, with a range of b(K) = 0.7-10.5 km s-1 allowed by the measurement uncertainties. For b(C2) =
b(KI), the C2 lines are not saturated unless
mÅ per absorption line.
Secondly, the C2 Doppler parameter may be larger than 1 km s-1.
The doublet ratio method
applied by Chaffee & White (1982)
in their analysis of K I absorption
lines towards Cyg OB2 No. 12 indicates a Doppler value of
b(K) = 6.4 km s-1 towards No. 12, with a range of b(K) = 0.7-10.5 km s-1 allowed by the measurement uncertainties. For b(C2) =
b(KI), the C2 lines are not saturated unless
![]() m
m![]() .
.
The spectra of stars Nos. 5, 9, 8A, 7, and 11
are shown in Fig. 2, normalised to unity and shifted by values
of 0, -0.1, -0.2, -0.3, -0.4, and -0.5, respectively, along
the ordinate. The scale of the ordinate
applies to star No. 5. The C2 lines detected towards
Cyg OB2 No. 5 and No. 9 are summarised in Tables 2 and 3, respectively.
C2 absorption lines are marginally detected towards Cyg OB2 No. 8A.
Absorption features, which may be assigned to the Q(2), Q(6), and
Q(8) lines, appear near heliocentric wavelengths of 8761.038, 8767.640,
and 8773.043 Å, respectively, with equivalent widths of
![]() mÅ or 1-2 standard deviations.
A weak diffuse interstellar band near 8763 Å
is present in all five spectra.
mÅ or 1-2 standard deviations.
A weak diffuse interstellar band near 8763 Å
is present in all five spectra.
In order to obtain average column densities
![]() in rotational levels J'',
the column densities inferred from the individual
measurements in the R, P, and Q lines of the (2,0) and (3,0) bands,
when available, were combined by weighting with the corresponding
oscillator strengths. The gas-kinetic temperature
T was determined from the rotational excitation temperature
in rotational levels J'',
the column densities inferred from the individual
measurements in the R, P, and Q lines of the (2,0) and (3,0) bands,
when available, were combined by weighting with the corresponding
oscillator strengths. The gas-kinetic temperature
T was determined from the rotational excitation temperature
![]() of the lowest rotational levels, because the population
density in these levels is not significantly affected by
radiative effects. Total C2 column densities
of the lowest rotational levels, because the population
density in these levels is not significantly affected by
radiative effects. Total C2 column densities
![]() and densities
and densities
![]() were obtained from theoretical fits to the population
distribution, with forced agreement for N(2) (cf. van Dishoeck
& Black 1982). Total observed column densities were derived
from the sum
were obtained from theoretical fits to the population
distribution, with forced agreement for N(2) (cf. van Dishoeck
& Black 1982). Total observed column densities were derived
from the sum
![]() over the observed rotational levels.
over the observed rotational levels.
The signal to noise ratio (S/N) of the spectral region covering the
(2,0) Phillips band is very high and reaches values of
S/N > 600. Figure 3 contains an excitation diagram
constructed from the detected lines,
with values of
![]() plotted versus excitation energy E(J'') of rotational level J''.
Individual measurements are
represented by filled triangles and upper limits by open triangles.
The squares correspond to
the averages
plotted versus excitation energy E(J'') of rotational level J''.
Individual measurements are
represented by filled triangles and upper limits by open triangles.
The squares correspond to
the averages
![]() .
The five lines drawn
in the diagram represent theoretical population distributions calculated
for a temperature of T = 35 K and densities of collision
partners of
.
The five lines drawn
in the diagram represent theoretical population distributions calculated
for a temperature of T = 35 K and densities of collision
partners of
![]() ,
300, 350, 400, 450 cm-3. The large number of
rotational lines detected towards Cyg OB2 No. 12 sharply
constrains the density
,
300, 350, 400, 450 cm-3. The large number of
rotational lines detected towards Cyg OB2 No. 12 sharply
constrains the density ![]() .
The theoretical population distribution
predicted for T = 35 K and
.
The theoretical population distribution
predicted for T = 35 K and
![]() cm-3
agrees with the measurements. The total density of hydrogen is
cm-3
agrees with the measurements. The total density of hydrogen is
![]() cm-3. The theoretical
total C2 column density derived from N(2) and T and
cm-3. The theoretical
total C2 column density derived from N(2) and T and ![]() is
is
![]() cm-2.
The total observed column density
is
cm-2.
The total observed column density
is
![]() cm-2. The average C2velocity, derived by weighting individual velocities with the
absorption oscillator strengths of the corresponding absorption lines,
is
cm-2. The average C2velocity, derived by weighting individual velocities with the
absorption oscillator strengths of the corresponding absorption lines,
is
![]() (C
2) = -5.5 km s-1.
(C
2) = -5.5 km s-1.
The excitation diagrams constructed for Cyg OB2 No. 5 and No. 9 are
shown in Figs. 4 and 5. The observed population
distribution towards No. 5 is reproduced well by T = 50 K and
![]() cm-3. The parameters indicate a total C2 column
density
cm-3. The parameters indicate a total C2 column
density
![]() cm-2.
The total observed column density is
cm-2.
The total observed column density is
![]() cm-2.
The average heliocentric velocity is
cm-2.
The average heliocentric velocity is
![]() (C
2) = -7.9 km s-1.
(C
2) = -7.9 km s-1.
The excitation diagram constructed for No. 9
is less constraining than that for No. 12 or No. 5.
The population
density in the J''=0 - 8 rotational levels may be
described by a thermal population distribution at
T = 100 K. The fit to the population densities in
![]() yields
yields
![]() cm-2 which
is adopted in the following as N(2).
The population density in J''=10 and the
upper limit in J'' = 12 suggest
cm-2 which
is adopted in the following as N(2).
The population density in J''=10 and the
upper limit in J'' = 12 suggest
![]() cm-3.
For T = 100 K,
cm-3.
For T = 100 K,
![]() cm-3, and N(2), the
modeled total C2 column density is
cm-3, and N(2), the
modeled total C2 column density is
![]() cm-2.
The observations yield
N(C
cm-2.
The observations yield
N(C
![]() cm-2. The average heliocentric velocity
is
cm-2. The average heliocentric velocity
is
![]() (C
2) = -10.2 km s-1.
(C
2) = -10.2 km s-1.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5exc.ps}\end{figure}](/articles/aa/full/2001/32/aah2693/Timg77.gif) |
Figure 4:
Rotational excitation diagram for Cyg OB2 No. 5.
Symbols as in Fig. 3. The five lines correspond to
theoretical population distributions obtained at T = 50 K
and densities of
|
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9exc.ps}\end{figure}](/articles/aa/full/2001/32/aah2693/Timg78.gif) |
Figure 5:
Rotational excitation diagram for Cyg OB2 No. 9. Symbols as in
Fig. 3. The five lines correspond to densities
of
|
The marginal detections of a few Q-branch lines towards Cyg OB2 No. 8A
yield column densities of about
![]() cm-2
in each of J'' = 2, 6, and 8. The total observed column
density is
cm-2
in each of J'' = 2, 6, and 8. The total observed column
density is
![]() cm-2. The population
distribution in rotational levels J'' = 2, 6, and 8 indicates
a rotational excitation temperature of
cm-2. The population
distribution in rotational levels J'' = 2, 6, and 8 indicates
a rotational excitation temperature of
![]() K. Assuming the kinetic temperature
T = 100 K and a thermal
distribution, we obtain a value of
K. Assuming the kinetic temperature
T = 100 K and a thermal
distribution, we obtain a value of
![]() cm-2.
The mean heliocentric velocity of the three absorption lines is
cm-2.
The mean heliocentric velocity of the three absorption lines is
![]() (C
2) = -5.2 km s-1. Towards Cyg OB2 No. 7 and
Cyg OB2 No. 11, the upper limits on the Q(2) line correspond to
(C
2) = -5.2 km s-1. Towards Cyg OB2 No. 7 and
Cyg OB2 No. 11, the upper limits on the Q(2) line correspond to
![]() cm-2, or
cm-2, or
![]() cm-2 towards both
stars, for a thermal population distribution at T = 100 K.
The C2 column density is
cm-2 towards both
stars, for a thermal population distribution at T = 100 K.
The C2 column density is
![]() if T were less than 50 K.
if T were less than 50 K.
Our C2 measurements are consistent with
previous results. The first detection of C2 towards
Cyg OB2 No. 12 (Souza & Lutz 1977) yielded a column
density in the J''=2 level of
![]() cm-2,
rescaled to the absorption oscillator strength adopted
here. Our value is
cm-2,
rescaled to the absorption oscillator strength adopted
here. Our value is
![]() cm-2. The column densities
of GM94, in units of 1013 cm-2,
are
N(0) = 1.1,
N(2) = 5.1, and
N(4) = 4.2, respectively, again
rescaled to the absorption oscillator strength of
van Dishoeck (1983). Our values
are
N(0) = 1.4,
N(2) = 4.85,
N(4) = 4.3.
Towards No. 5, GM94 measured
N(0) = 0.5,
N(2) = 2.4, and
N(4) = 1.6, all
in units of 1013 cm-2, which compares with our data
of
N(0) = 0.5,
N(2) = 2.1, and
N(4) = 2.1.
In general, our measured equivalent widths are consistent with
those of Lutz & Crutcher (1983).
Exceptions occur for
the P(4)+Q(8) line blend, where Lutz & Crutcher (1983) obtain
cm-2. The column densities
of GM94, in units of 1013 cm-2,
are
N(0) = 1.1,
N(2) = 5.1, and
N(4) = 4.2, respectively, again
rescaled to the absorption oscillator strength of
van Dishoeck (1983). Our values
are
N(0) = 1.4,
N(2) = 4.85,
N(4) = 4.3.
Towards No. 5, GM94 measured
N(0) = 0.5,
N(2) = 2.4, and
N(4) = 1.6, all
in units of 1013 cm-2, which compares with our data
of
N(0) = 0.5,
N(2) = 2.1, and
N(4) = 2.1.
In general, our measured equivalent widths are consistent with
those of Lutz & Crutcher (1983).
Exceptions occur for
the P(4)+Q(8) line blend, where Lutz & Crutcher (1983) obtain
![]() m
m![]() ,
compared to our value of
,
compared to our value of
![]() m
m![]() ,
and the R(0) line, where Lutz & Crutcher (1983)
give
,
and the R(0) line, where Lutz & Crutcher (1983)
give
![]() m
m![]() ,
compared to our value of
,
compared to our value of ![]() m
m![]() .
.
The observations of GM94 were taken at the
higher spectral resolution of R=65 000 and indicate
a total of four absorption components towards No. 12, two unresolved components
at
![]() 5.7 and -2.5 km s-1, and two weaker components near
-10.6 km s-1 and +13.6 km s-1. This agrees reasonably well
with our detection of a single, unresolved absorption line near
5.7 and -2.5 km s-1, and two weaker components near
-10.6 km s-1 and +13.6 km s-1. This agrees reasonably well
with our detection of a single, unresolved absorption line near
![]() 5.5 km s-1. The absorption components near -10.6 km s-1 and
+13.6 km s-1 of GM94 are not present in our spectrum, which has a significantly
higher S/N compared to the spectra of GM94. They may thus not be real.
5.5 km s-1. The absorption components near -10.6 km s-1 and
+13.6 km s-1 of GM94 are not present in our spectrum, which has a significantly
higher S/N compared to the spectra of GM94. They may thus not be real.
Table 4 summarises the C2 measurements towards
the Cyg OB2 association. It contains, in Cols. 1-8, respectively,
the star and its spectral type, its visual extinction AV as given
by Humphreys (1978),
the gas-kinetic temperature
T, the density ![]() ,
the column
density in rotational level J''=2, the total C2 column
density
,
the column
density in rotational level J''=2, the total C2 column
density
![]() inferred from T,
inferred from T, ![]() and N(2), the total
observed column density
and N(2), the total
observed column density
![]() ,
and the average
heliocentric velocity
,
and the average
heliocentric velocity
![]() .
In the discussion of Sect. 4,
theoretical C2 column densities
.
In the discussion of Sect. 4,
theoretical C2 column densities
![]() are used in the
comparison with chemical models, rather than
are used in the
comparison with chemical models, rather than
![]() ,
because the theoretical column densities include the population
densities in the unobserved levels as well.
,
because the theoretical column densities include the population
densities in the unobserved levels as well.
![\begin{figure}
\par\includegraphics[width=13.4cm,clip]{12cn.ps}\end{figure}](/articles/aa/full/2001/32/aah2693/Timg95.gif) |
Figure 6:
Normalised spectra covering the (2,0) band and (1,0) bands of
the CN A
|
The spectra of all six stars in Cyg OB2 observed here are
affected by absorption
bands near 7721 Å and near 8763 Å which are broader than
the interstellar C2 lines. These bands were
previously identified as new diffuse interstellar bands (DIBs)
(Herbig & Leka 1991; Gredel & Münch 1986). A complete discussion
of the DIBs will be presented elsewhere.
Table 4 summarises the measurements of the band near 8763 ![]() ,
with the star, the wavelength, the full width at half maximum
(FWHM), and the equivalent width of the band, listed in Cols. 1-4, respectively. It has been suggested that DIBs form largely
in low-density, diffuse material (Herbig 1995). We note here that
the DIB towards Cyg OB2 No. 12 is relatively weak
compared with the other stars in Cyg OB2. Such is not expected if
the line of sight towards No. 12 passes through a high column density
of low density material spread over a pathlength of some 1000 pc
(cf. discussion in Sect. 4.1).
,
with the star, the wavelength, the full width at half maximum
(FWHM), and the equivalent width of the band, listed in Cols. 1-4, respectively. It has been suggested that DIBs form largely
in low-density, diffuse material (Herbig 1995). We note here that
the DIB towards Cyg OB2 No. 12 is relatively weak
compared with the other stars in Cyg OB2. Such is not expected if
the line of sight towards No. 12 passes through a high column density
of low density material spread over a pathlength of some 1000 pc
(cf. discussion in Sect. 4.1).
The spectral region which covers the absorption lines of the (1,0) and (2,0) bands of the CN red system is heavily contaminated by telluric absorption lines. However, a few lines in the (1,0) and (2,0) bands are well isolated and accurate equivalent widths can be determined.
Figure 6 contains the normalised spectra towards
Cyg OB2 No. 12. The position of the detected CN lines is indicated
by filled triangles. Open triangles mark the expected positions of CN
absorption lines which are blended with atmospheric features.
The (2,0)
SR21(0) (7871.5 ![]() ),
(2,0) [
RQ21(1)+R2(1)] (7873.9
),
(2,0) [
RQ21(1)+R2(1)] (7873.9 ![]() ),
(2,0)
RQ21(0) (7874.7
),
(2,0)
RQ21(0) (7874.7 ![]() ),
(2,0) R1(0) (7906.5
),
(2,0) R1(0) (7906.5 ![]() ),
(1,0) [
QP21(1) + Q2(1)] (9146.9
),
(1,0) [
QP21(1) + Q2(1)] (9146.9 ![]() ), and
(1,0) R1(0) (9186.8
), and
(1,0) R1(0) (9186.8 ![]() )
lines or line blends, are clearly detected.
The measurements allow the determination the column density N(0) in
the rotational level
N''=0. The lack of clear detections of absorption lines arising
from the rotational level N''=1 constrains the column density N(1).
In order to judge what the maximum CN abundance is towards Cyg OB2 No. 12,
upper limits are estimated for the
(2,0) R1(1) (7903.6
)
lines or line blends, are clearly detected.
The measurements allow the determination the column density N(0) in
the rotational level
N''=0. The lack of clear detections of absorption lines arising
from the rotational level N''=1 constrains the column density N(1).
In order to judge what the maximum CN abundance is towards Cyg OB2 No. 12,
upper limits are estimated for the
(2,0) R1(1) (7903.6 ![]() ),
(1,0)
SR21(0) (9139.6
),
(1,0)
SR21(0) (9139.6 ![]() ), and
(1,0) R1(1) (9183.3
), and
(1,0) R1(1) (9183.3 ![]() )
lines.
The estimate was obtained from a comparison of the relative
strengths of the telluric lines in Cyg OB2 No. 12 and in
)
lines.
The estimate was obtained from a comparison of the relative
strengths of the telluric lines in Cyg OB2 No. 12 and in ![]() Tau.
The spectrum of
Tau.
The spectrum of ![]() Tau is represented in Fig. 6 by the
dotted line. CN is not detected towards
Tau is represented in Fig. 6 by the
dotted line. CN is not detected towards ![]() Tau.
Upper limits estimated for the column density in N''=1
agree reasonably well with
the column density inferred from the marginally detected
(1,0)[
QP21(1)+Q2(1)] line blend near 9147
Tau.
Upper limits estimated for the column density in N''=1
agree reasonably well with
the column density inferred from the marginally detected
(1,0)[
QP21(1)+Q2(1)] line blend near 9147 ![]() .
.
The CN measurements are summarised in Table 6. It gives,
in Cols. 1-6, the line designation, the measured heliocentric
wavelength
![]() and the heliocentric velocity
and the heliocentric velocity
![]() ,
the measured
equivalent width
,
the measured
equivalent width
![]() ,
and the inferred column densities
N(0) and N(1) in the N''=0 and N''=1 rotational levels,
respectively. Uncertainties are given in parentheses.
The last row contains in Cols. 5 and 6, respectively,
the average column density N(0) inferred from the observations
and the column density N(1) in the limit where the CN excitation
temperature T10 is close to the cosmic microwave background
radiation temperature of 2.7 K. The row above contains
the value N(1) estimated from the observations,
and the corresponding CN excitation temperature in Col. 7.
A firm lower limit to the total CN column density towards
Cyg OB2 No. 12 is N(CN
,
and the inferred column densities
N(0) and N(1) in the N''=0 and N''=1 rotational levels,
respectively. Uncertainties are given in parentheses.
The last row contains in Cols. 5 and 6, respectively,
the average column density N(0) inferred from the observations
and the column density N(1) in the limit where the CN excitation
temperature T10 is close to the cosmic microwave background
radiation temperature of 2.7 K. The row above contains
the value N(1) estimated from the observations,
and the corresponding CN excitation temperature in Col. 7.
A firm lower limit to the total CN column density towards
Cyg OB2 No. 12 is N(CN
![]() cm-2, and the
upper limit is N(CN
cm-2, and the
upper limit is N(CN
![]() cm-2. The average
heliocentric velocity of CN is -4.3 km s-1 which is consistent
with the velocity of C2.
cm-2. The average
heliocentric velocity of CN is -4.3 km s-1 which is consistent
with the velocity of C2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Rb.ps}\end{figure}](/articles/aa/full/2001/32/aah2693/Timg100.gif) |
Figure 7: Detection of the interstellar line of Rb I 5s 2S1/2 - 5p2P3/2 towards Cyg OB2 No. 12 and No. 5. The spectrum of No. 5 is shifted by 0.03 units along the ordinate. |
Our spectra are shown in Fig. 7. The Rb I
line is detected at 10 standard deviations towards Cyg OB2 No. 12.
We use the formalism and the atomic data of Morton (2000) to
transfer measured equivalent widths of
![]() mÅ and
mÅ and
![]() mÅ towards No. 12 and No. 5, respectively,
into column densities of N(Rb I
mÅ towards No. 12 and No. 5, respectively,
into column densities of N(Rb I
![]() cm-2 and
N(Rb I
cm-2 and
N(Rb I
![]() cm-2. Heliocentric velocities
are
cm-2. Heliocentric velocities
are
![]() 6.4 km s-1 for No. 12 and -8.1 km s-1 towards No. 5,
respectively. The Rb I velocities agree with those of C2 within
the errors.
6.4 km s-1 for No. 12 and -8.1 km s-1 towards No. 5,
respectively. The Rb I velocities agree with those of C2 within
the errors.
Neutral rubidium has an ionisation potential of 4.77 eV, thus
interstellar rubidium is mostly ionised. The ionisation potential
is similar to that of potassium, and relative abundances
of N(Rb+)/N(K+) may be related to measured ratios
N(Rb)/N(K) (Federman et al. 1985). Column densities of
N(K
![]() cm-2 towards No. 12 and
N(K
cm-2 towards No. 12 and
N(K
![]() cm-2 towards No. 5 were
inferred by
Chaffee & White (1982).
The K I 7664 Å and 7698 Å absorption lines are also present
in our spectra. The K I 7698 Å line is well
separated from a telluric O2 absorption line but the K I 7664 Å
line is not. Equivalent widths of the K I 7698 Å lines
are
cm-2 towards No. 5 were
inferred by
Chaffee & White (1982).
The K I 7664 Å and 7698 Å absorption lines are also present
in our spectra. The K I 7698 Å line is well
separated from a telluric O2 absorption line but the K I 7664 Å
line is not. Equivalent widths of the K I 7698 Å lines
are
![]() mÅ and
mÅ and
![]() m
m![]() ,
respectively, towards No. 12 and No. 5. The measured equivalent
widths are consistent
with those inferred by
Chaffee & White (1982), who give
,
respectively, towards No. 12 and No. 5. The measured equivalent
widths are consistent
with those inferred by
Chaffee & White (1982), who give
![]() towards No. 12 and
towards No. 12 and
![]() towards No. 5.
Using the atomic
parameters of Morton (1991),
we infer N(K
towards No. 5.
Using the atomic
parameters of Morton (1991),
we infer N(K
![]() cm-2 towards No. 12 and N(K
cm-2 towards No. 12 and N(K
![]() cm-2
towards No. 5. These values, calculated in the limit of
unsaturated lines, are close to the neutral K column densities derived
Chaffee & White (1982)
who used the doublet ratio to estimate
saturation corrections.
cm-2
towards No. 5. These values, calculated in the limit of
unsaturated lines, are close to the neutral K column densities derived
Chaffee & White (1982)
who used the doublet ratio to estimate
saturation corrections.
The K I column densities inferred by
Chaffee & White (1982) and
the Rb I column densities inferred here suggest values
of N(Rb+)/N(K
![]() towards Cyg OB2.
This ratio compares with upper limits of
N(Rb+)/N(K
towards Cyg OB2.
This ratio compares with upper limits of
N(Rb+)/N(K
![]() inferred by
Federman et al. (1985)
towards o Per,
inferred by
Federman et al. (1985)
towards o Per, ![]() Per, and
Per, and
![]() Oph. The Rb+/K+ ratio towards No. 12 is about a
factor of three lower than the solar ratio of N(Rb+)/N(K
Oph. The Rb+/K+ ratio towards No. 12 is about a
factor of three lower than the solar ratio of N(Rb+)/N(K
![]() (as given in Federman et al. 1985).
(as given in Federman et al. 1985).
Copyright ESO 2001