The asymmetry in both brightness and position in the microquasar
ejecta of Figs. 5 and 6 is normally interpreted
in the context of special relativity effects.
The jet component brighter and more distant from the core is the one approaching towards the
observer, while the fainter and closer one is receding away from him/her.
Figure 6 is also very reminiscent of the main figure in Mirabel & Rodríguez (1994)
showing relativistic expansion in the superluminal microquasar GRS 1915+105, a source where such
effects are stronger than in Cygnus X-3. The special relativity formulae as given by
Mirabel & Rodríguez (1999) will be used throughout this discussion for
quantitative estimates of the ejection parameters. The proper motion of the
approaching (![]() ,
sign -) and receding jet (
,
sign -) and receding jet (![]() ,
sign +) is then given by:
,
sign +) is then given by:
In our case, the proper motion of the ejecta can be inferred from the third epoch map by
using the offsets
![]() and
and
![]() listed in Table 3
and assuming an age of 66.0 d since the ejection. This age is assumed because
it seems natural that the most external ejecta should be also the oldest.
For the brighter northern approaching component, the proper motion is
listed in Table 3
and assuming an age of 66.0 d since the ejection. This age is assumed because
it seems natural that the most external ejecta should be also the oldest.
For the brighter northern approaching component, the proper motion is
![]() mas
mas![]() day-1. Similarly, for
the fainter southern receding component we find
day-1. Similarly, for
the fainter southern receding component we find
![]() mas
mas![]() day-1.
A more direct and independent estimate of
day-1.
A more direct and independent estimate of
![]() can be also obtained from the observed
shift in the position of the northern jet component between the second and third epochs.
Using the data in Table 3, the shift amounted to
can be also obtained from the observed
shift in the position of the northern jet component between the second and third epochs.
Using the data in Table 3, the shift amounted to
![]() mas in a time
interval of 15.05 days between the two epochs. The derived proper motion is therefore
mas in a time
interval of 15.05 days between the two epochs. The derived proper motion is therefore
![]() mas
mas![]() day-1.
An extrapolation of this independent proper motion backward in time gives
JD
day-1.
An extrapolation of this independent proper motion backward in time gives
JD
![]() as the ejection date of the northern component.
This epoch is close to one of the strongest outburst in the series of events that activated
our ToO proposal, but differs in two weeks
from the assumed date of creation for the oldest and most external
ejecta (JD 2451802.5). Considering the important uncertainties in this extrapolation,
we prefer to keep this assumption as a very reasonable initial epoch for proper motion estimates.
as the ejection date of the northern component.
This epoch is close to one of the strongest outburst in the series of events that activated
our ToO proposal, but differs in two weeks
from the assumed date of creation for the oldest and most external
ejecta (JD 2451802.5). Considering the important uncertainties in this extrapolation,
we prefer to keep this assumption as a very reasonable initial epoch for proper motion estimates.
Having obtained values for the proper motion of both the jet and the counterjet,
the ejection parameter
![]() can be easily obtained from Eq. (1):
can be easily obtained from Eq. (1):
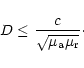 |
(3) |
The inferred proper motions imply apparent
subluminal velocities of
![]() and
and
![]() for the northern and southern jet components, respectively.
Our direct (not-inferred) proper motion measurement for the northern jet component
translates into a consistent apparent velocity of
for the northern and southern jet components, respectively.
Our direct (not-inferred) proper motion measurement for the northern jet component
translates into a consistent apparent velocity of
![]() .
Accepting that the distance value to Cygnus X-3 is D=10 kpc,
it is possible to derive both the true jet velocity and the inclination angle with the line of sight
instead of the limits given above.
Solving from Eq. (1) we get
.
Accepting that the distance value to Cygnus X-3 is D=10 kpc,
it is possible to derive both the true jet velocity and the inclination angle with the line of sight
instead of the limits given above.
Solving from Eq. (1) we get
![]() ,
which implies
,
which implies
![]() and
and
![]() .
.
The flux density ratio between the approaching and receding jet components,
![]() ,
is
related to the ejection parameters according to
the Doppler boosting formula:
,
is
related to the ejection parameters according to
the Doppler boosting formula:
Copyright ESO 2001