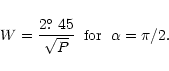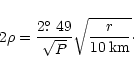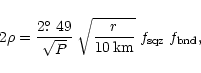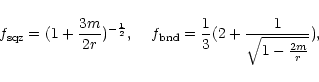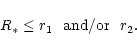A&A 375, 405-410 (2001)
DOI: 10.1051/0004-6361:20010891
Are radio pulsars strange stars ?
R. C. Kapoor1 - C. S. Shukre2
1 - Indian Institute of Astrophysics, Koramangala,
Bangalore 560 034, India
2 -
Raman Research Institute, C.V. Raman Avenue,
Sadashivanagar, Bangalore 560 080, India
Received 11 April 2001 / Accepted 5 June 2001
Abstract
A remarkably precise observational relation for pulse core component
widths of radio pulsars is used to derive stringent limits on pulsar radii, strongly indicating
that pulsars are strange stars rather than neutron stars. This is achieved
by inclusion of general relativistic effects due to the pulsar mass on the
size of the emission region needed to explain the observed pulse widths, which
constrain the pulsar masses to be 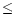 2.5
2.5 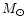 and radii
and radii 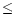 10.5 km.
10.5 km.
Key words: pulsars: general - dense matter - equation of state: stars : neutron
Radio pulsars are believed to be the most common manifestations of neutron
stars, but it has not been possible so far to relate the voluminous data
on radio pulses and their varied structure to the properties of neutron
stars
except through the arrival times of pulses. Here we make such a connection
between
pulse core component widths derived from very good quality radio data and
the
mass-radius (M-R) relation of neutron stars. This becomes possible only
due to
the inclusion of general relativistic effects of the stellar mass on
pulsar
beam shapes, which makes the stellar mass and radius relevant parameters
in
determining the pulse widths. We show that core component widths provide
tight
constraints on equations of state (EOS) of neutron stars. We compare our
results with other similar attempts based, e.g., on the X-ray data. From
our
constraints it emerges that no neutron star EOS seem to be adequate,
leading to
the conclusion that pulsars are strange stars, i.e., ones composed of
quarks of
flavors u, d, and s (Alcock et al. 1986); and we examine it in light of
similar
recent suggestions.
A classification of radio pulse components into "core'' and "conal''
emissions
has emerged which is based on various characteristics such as morphology,
polarization, spectral index etc. of the pulses (Rankin 1983). Radio pulsars
often show a three peaked pulse profile, the central component of which is
identified as the core emission, as opposed to the outrider conal pair
(Rankin 1990). By analysing the core components of many
pulsars, especially
the
"interpulsars'' which emit two pulses half a period apart in one pulse
period,
Rankin (1990) found a remarkable relation between
the pulse width W and
the pulsar period P (in seconds) for pulsars whose magnetic dipole and
rotation axes are orthogonal, viz.
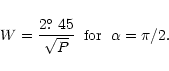 |
(1) |
Here 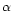 is the angle between magnetic and rotation axes. This
relation (henceforth the Rankin relation) provides a fit to data
within
is the angle between magnetic and rotation axes. This
relation (henceforth the Rankin relation) provides a fit to data
within 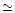 0.2% and the observations themselves have errors on
the average of
0.2% and the observations themselves have errors on
the average of 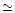 4%. Thus Eq. (1) is a rare example of an
extraordinarily good fit.
In addition, the Rankin relation has also been used (Rankin 1990) to
predict
4%. Thus Eq. (1) is a rare example of an
extraordinarily good fit.
In addition, the Rankin relation has also been used (Rankin 1990) to
predict 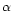 values for some other pulsars which are not interpulsars.
These predicted values agree very well with determinations of
values for some other pulsars which are not interpulsars.
These predicted values agree very well with determinations of 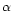 based on data about other components in the same pulsars (Rankin 1993).
Thus its remarkable fit to the core component data is supported in
addition by data on other pulsars. The Rankin relation in our view is
one of the most reliable observational relations derived from the radio
pulsar data.
based on data about other components in the same pulsars (Rankin 1993).
Thus its remarkable fit to the core component data is supported in
addition by data on other pulsars. The Rankin relation in our view is
one of the most reliable observational relations derived from the radio
pulsar data.
The import of the currently accepted "polar cap model'' of pulsar radio
emission is that the radiation originates from the magnetic polar
regions. The polar cap is defined on the stellar surface by the feet
of the dipolar magnetic field lines which penetrate the "light cylinder'',
i.e. a cylinder of radius
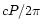 with rotation axis as its
axis. c is the speed of light. Pulsar emission occurs in this "open
field line'' flux tube at an altitude r measured radially from the
center of the star. We refer to the surface of emission as the
emission cap which coincides with the polar cap when r=R* the
stellar radius.
with rotation axis as its
axis. c is the speed of light. Pulsar emission occurs in this "open
field line'' flux tube at an altitude r measured radially from the
center of the star. We refer to the surface of emission as the
emission cap which coincides with the polar cap when r=R* the
stellar radius.
As shown in Fig. 1 the line of sight cuts the polar cap along the line LS.
This will lead to a pulse of width W. If LS passes through the centre,
then
 ,
the longitudinal diameter of the polar cap. For
interpulsars LS passes very close to the centre and hence
,
the longitudinal diameter of the polar cap. For
interpulsars LS passes very close to the centre and hence
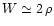 .
For a value of
.
For a value of
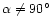 ,
,
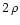 cannot be recovered from
W alone. One also needs to know the displacement of LS from the centre,
usually called the impact angle
cannot be recovered from
W alone. One also needs to know the displacement of LS from the centre,
usually called the impact angle 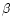 .
If polarization data is available in
addition to W, then both
.
If polarization data is available in
addition to W, then both
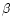 and
and 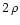 can be retrieved from observations.
The core component width data used by Rankin (1990) pertains only to
inter-pulsars. Therefore, in essence the width W in Eq. (1)
is the longitudinal diameter
can be retrieved from observations.
The core component width data used by Rankin (1990) pertains only to
inter-pulsars. Therefore, in essence the width W in Eq. (1)
is the longitudinal diameter
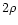 of the emission cap and is thus independent of
of the emission cap and is thus independent of 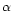 (Kapoor & Shukre 1998, henceforth KS). From the dipole geometry
(Goldreich & Julian 1969, henceforth GJ)
one finds
(Kapoor & Shukre 1998, henceforth KS). From the dipole geometry
(Goldreich & Julian 1969, henceforth GJ)
one finds
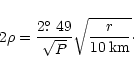 |
(2) |
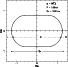 |
Figure 1:
Polar plot of the polar cap of a typical pulsar. The xand y co-ordinates are the magnetic longitude and lattitude
respectively. The centre of the figure represents the radial direction
passing through the dipole magnetic axis. Dotted line LS shows the locus
of the line of sight as the pulsar rotates. See text for further details. |
| Open with DEXTER |
On the assumption that the full emission cap participates in the
core emission, agreement between Eqs. (1) and (2) immediately
allows the conclusion that r = 10 km. This remarkable agreement
has provided compelling evidence favouring the origin of the core
emission from the stellar surface as well as the dipolar configuration of
the stellar magnetic field (Rankin 1993). Note that a value of the
stellar radius R* really has not entered the considerations so far.
However, 10 km is considered to be the cannonical value of R*, and it is
on this basis that r is identified with R*.
In the analysis of radio pulse structure, if the role of the radius R*has been insignificant,
then it is even more so for the stellar mass M. Inclusion of
effects due to the spacetime curvature caused by pulsar's mass
changes this as follows. The stellar gravitational field affects the
dipole field geometry and also causes bending of the rays of the
emitted pulsar radiation. The former tries to shrink the emission cap
while the latter has the opposite effect of widening it. A detailed
study of these effects has been done and described in KS.
In summary, we give below an analytic but approximate
version of how Eq. (2) is modified, i.e.,
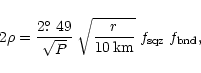 |
(3) |
where the factors
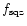 and
and
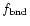 are respectively due to
squeezing
of the dipole magnetic field and bending of light by the stellar
gravitation
and are given by
are respectively due to
squeezing
of the dipole magnetic field and bending of light by the stellar
gravitation
and are given by
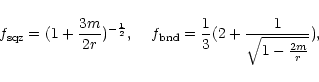 |
(4) |
where
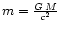 ,
i.e.,
,
i.e., 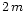 is the Schwarzshild radius. Eq. (2) is recovered in the limit m=0.
is the Schwarzshild radius. Eq. (2) is recovered in the limit m=0.
In Eq. (3) the effects due to special relativistic aberration are not
included. Since stellar gravitational effects are significant for
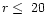 m (KS) we consider only such emission altitudes here.
Even
for the 1.5 ms pulsar PSR 1929+214, therefore, aberration does not
play a
role in considerations here. In what follows, however, the calculations
include all the effects completely, as in KS. For
m (KS) we consider only such emission altitudes here.
Even
for the 1.5 ms pulsar PSR 1929+214, therefore, aberration does not
play a
role in considerations here. In what follows, however, the calculations
include all the effects completely, as in KS. For
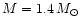 and
and 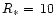 km, the net effect on the emission cap on the surface is a
shrinking by
km, the net effect on the emission cap on the surface is a
shrinking by 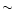 4% compared to the value in Eq. (2). Although
small,
this difference allows us to relate M and R*, and as we shall see
provides tight constraints on the pulsar EOS.
4% compared to the value in Eq. (2). Although
small,
this difference allows us to relate M and R*, and as we shall see
provides tight constraints on the pulsar EOS.
Figure 2 shows the variation of 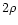 with r for various values of
M as labelled. The points where the Rankin line intersects the curve for
a particular mass M gives for that M the altitude(s) where the core
emission must originate.
with r for various values of
M as labelled. The points where the Rankin line intersects the curve for
a particular mass M gives for that M the altitude(s) where the core
emission must originate.
Generally there are two intersection points, r1 and r2, such that
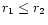 .
In the limiting case M=M0 the two points coalesce.
For higher values of M there is no intersection. The mass M0 is
.
In the limiting case M=M0 the two points coalesce.
For higher values of M there is no intersection. The mass M0 is
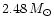 ,
which we take as
,
which we take as
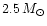 .
Thus we can conclude
that core emission does not occur if
.
Thus we can conclude
that core emission does not occur if
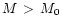 .
Probably, this is an
indication that all radio pulsars have masses <M0 because
the
incidence of core emission among radio pulsars is
.
Probably, this is an
indication that all radio pulsars have masses <M0 because
the
incidence of core emission among radio pulsars is  70%
(Rankin 1990).
Thus
70%
(Rankin 1990).
Thus
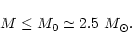 |
(5) |
This constraint, though of interest, is not useful since observationally all
masses seem to be well below it.
The second constraint involves R*. The lowest altitude at which any
emission can occur is R*. Therefore for values of M below M0,
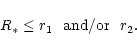 |
(6) |
Since r1 and r2 depend on M we get a constraint on the pulsar
mass-radius relation from the inequalities 6.
 |
Figure 1:
Width 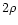 of the emission cap after inclusion of all
special and general relativistic effects vs. the emission altitude
r for various stellar masses as shown. Horizontal line is the Rankin
relation of Eq. (1) and the dotted line labelled GJ is given
by Eq. (2). For a different pulsar period, widths scale as
of the emission cap after inclusion of all
special and general relativistic effects vs. the emission altitude
r for various stellar masses as shown. Horizontal line is the Rankin
relation of Eq. (1) and the dotted line labelled GJ is given
by Eq. (2). For a different pulsar period, widths scale as
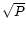 as in Eq. (3).
as in Eq. (3). |
| Open with DEXTER |
For all masses, values of r1 are almost same as 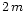 and if taken
seriously would imply that pulsars are black holes. We
therefore consider only r2. Values of r2 range from 10.2 to 10.6 km
for masses between 0.6 to 2.5
and if taken
seriously would imply that pulsars are black holes. We
therefore consider only r2. Values of r2 range from 10.2 to 10.6 km
for masses between 0.6 to 2.5 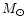 .
For masses between 1
.
For masses between 1 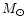 and
2.2
and
2.2 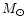 ,
values of r2 remarkably enough are not very sensitive
to M and are all close to 10.5 km as seen in Fig. 3. Again,
pulsar masses are observationally seen to be well covered by the
range 1.0-2.2
,
values of r2 remarkably enough are not very sensitive
to M and are all close to 10.5 km as seen in Fig. 3. Again,
pulsar masses are observationally seen to be well covered by the
range 1.0-2.2 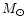 and so we can take 10.5 km as the upper limit for all M. Lower
values of r2 occur for lower values of M and their inclusion will only
tighten the constraint further since for all EOS a decrease in mass
implies
an increase in radius. The Rankin relation thus leads us to the second
constraint
and so we can take 10.5 km as the upper limit for all M. Lower
values of r2 occur for lower values of M and their inclusion will only
tighten the constraint further since for all EOS a decrease in mass
implies
an increase in radius. The Rankin relation thus leads us to the second
constraint
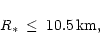 |
(7) |
which is applicable to radio pulsars which show core emission, and, as
remarked
earlier, to most probably all pulsars.
Table 1:
EOS for which M-R plots are available. For meaning of
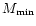 and
and
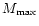 see text.
see text.
| SN |
EOS |
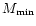 |
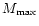 |
Plot |
| |
Name |
(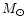 ) ) |
(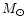 ) ) |
Ref.1 |
| 1 |
A |
0.35 |
1.65 |
BBF,PC |
| 2 |
B |
0.35 |
1.40 |
BBF |
| 3 |
M |
- - |
- - |
PC |
| 4 |
L |
- - |
- - |
BBF,PC,BLC |
| 5 |
WFFAU |
0.45 |
2.15 |
BLC |
| 6 |
WFFUU |
2.10 |
2.20 |
PC,LRD |
| 7 |
WFFUT |
1.65 |
1.85 |
BBF |
| 8 |
FPS |
1.60 |
1.80 |
PC,BLC |
| 9 |
HV |
- - |
- - |
W |
| 10 |
HFV |
- - |
- - |
W |
| 11 |
G
 |
- - |
- - |
W |
| 12 |
Hyp |
- - |
- - |
LRD |
| 13 |
BPAL12 |
1.35 |
1.45 |
LRD |
| 14 |
BBB1 |
1.65 |
1.75 |
LRD |
| 15 |
BBB2 |
1.70 |
1.90 |
LRD |
| 16 |
EOS1 |
1.50 |
1.55 |
BLC |
| 17 |
EOS2 |
1.70 |
1.75 |
BLC |
| 18 |
RH |
0.15 |
0.90 |
HWW |
| 19 |
RHF |
0.15 |
0.95 |
HWW |
| 20 |
APR1 |
- - |
- - |
BBF |
| 21 |
APR2 |
2.15 |
2.2 |
BBF |
| 22 |
K- |
- - |
- - |
LRD |
1References are same as in the reference section at the end:
BBF-Benhar et al. (
1999); PC-Psaltis & Chakrabarty (
1999); BLC-Balberg et al.
(
1999); LRD-Li et al. (
1999b); W-Weber (
1999); HWW-Huber et al. (
1998).
We have searched earlier works for neutron star M-R relations. For about
40
EOS M-R plots were available. Very conservatively dropping some among
them
which are now replaced by modern versions, we have selected the 22 listed
in
Table 1.
For the additional six in Table 2 only the maximum masses
(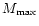 )
allowed by the EOS and the associated radii are
available (Salgado et al. 1994).
)
allowed by the EOS and the associated radii are
available (Salgado et al. 1994).
For all EOS in Table 2, radii are larger than 10.5 km for
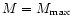 and thus also for lower values of M. Therefore we
consider now the 22 remaining EOS in Table 1. Since high
precision is not
called for, or, is available, we have read off from the published plots
the mass range for which
and thus also for lower values of M. Therefore we
consider now the 22 remaining EOS in Table 1. Since high
precision is not
called for, or, is available, we have read off from the published plots
the mass range for which
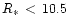 km. These values are listed
in Table 1 as
km. These values are listed
in Table 1 as 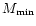 - the mass for which R=10.5 km
and
- the mass for which R=10.5 km
and 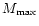 - the maximum mass allowed by the EOS. Where the EOS does
not
permit
R*< 10.5 km for any mass, only dashes appear for
- the maximum mass allowed by the EOS. Where the EOS does
not
permit
R*< 10.5 km for any mass, only dashes appear for
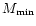 and
and 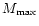 .
There are 8 such EOSs and they are not favored by
inequality (7).
.
There are 8 such EOSs and they are not favored by
inequality (7).
Because of the accurately determined masses for the Hulse-Taylor binary
system
(i.e., 1.44 and 1.39 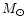 )
(Thorsett & Chakrabarty 1999),
for the remaining EOS we
impose
an additional condition that their mass range allow the value 1.4
)
(Thorsett & Chakrabarty 1999),
for the remaining EOS we
impose
an additional condition that their mass range allow the value 1.4 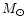 .
The inequality 7 selects out the softer EOS. By
imposing
this condition based on observations we are in effect demanding that the
EOS
should not be so soft as to have
.
The inequality 7 selects out the softer EOS. By
imposing
this condition based on observations we are in effect demanding that the
EOS
should not be so soft as to have
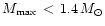 or so
stiff
that
or so
stiff
that
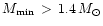 .
This further reduces the number of
acceptable EOSs by 11. The remaining three are : A, WFFAU and BPAL12.
.
This further reduces the number of
acceptable EOSs by 11. The remaining three are : A, WFFAU and BPAL12.
The core width constraints in conjunction with the observational
information
on pulsar masses have thus reduced the viable netron star EOS number from 28 to 3.
The EOS APR1 is an updated version of the EOS A. APR2 is APR1 with
relativistic corrections included. Since both APR1 and APR2 do not survive
the constraints we can drop also the EOS A from the short list. In
addition,
based on general restrictions following from the glitch data,
Balberg et al. (1999)
have disqualified the EOS A and WFFAU. We are thus left with the choice
of
BPAL12 or some variant of it as the only viable modern EOS.
Table 2:
EOS for which only 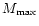 and its radius R are available.
and its radius R are available.
| SN |
EOS1 |
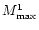 |
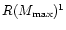 |
| |
Name |
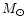 |
km |
| 1 |
HKP |
2.83 |
13.68 |
| 2 |
Glend1 |
1.80 |
11.15 |
| 3 |
Glend2 |
1.78 |
11.29 |
| 4 |
Glend3 |
1.96 |
11.30 |
| 5 |
DiazII |
1.93 |
10.93 |
| 6 |
WGW |
1.97 |
10.97 |
1Names and values are from Salgado et al. (
1994).
We have considered only the non-rotating neutron star models because most
pulsars are slow rotators. But inclusion of rotation (or magnetic field)
will not change the situation because, in that case, for a given mass one
expects larger radii on general physical grounds.
It should be noted that similar attempts using the pulsar timing data
(glitches) and X-ray source data (quasi-periodic oscillations) do not
provide
such stringent constraints and are also not so selective of the EOS
(Psaltis & Chakrabarty 1999; van Kerkwijk et al. 1995).
Also, our constraints are not dependent on
uncertainties in theoretical models, i.e., of accretion disks, and rely
on very simple and fundamental assumptions.
Our constraints make crucial use of the Rankin relation and the assumption
that the core emission emanates from the full polar cap. It will be
of
great interest to re-evaluate both of these independently. The database
presently available is presumably more voluminous than in 1990 because
the number of known pulsars has more than doubled since then and it can
be used to further fortify the Rankin relation. On the other hand it would
be worthwhile also to check the assumption of the participation of the
full
cap by some independent means. Non-dipolar magnetic field components have
been invoked in the past in various contexts (Arons 2000; Gil & Mitra
2000).
Our analysis crucially hinges on the Rankin relation, which in turn makes
crucial
use of the dipole nature of the field. The existence of non-dipolar
components
has been studied by Arons (1993) and he has concluded against
their presence. We take the view
that the remarkable agreement of the Rankin relation actually provides
evidence for the dipolar nature of the field and strongly indicates
the absence of
non-dipolar components and also of propagation effects affecting the core
emission.
In so far as our constraints hold, can we then conclude that BPAL12 is
the neutron star EOS? Actually BPAL12 is used as an extreme case
for illustrative purpose and can hardly be called a realistic netron star
EOS (Bombaci 2000). In fact our present knowledge of the neutron star EOS
is very far from final. Present theoretical uncertainties in these EOS
relate to the very high density regime (
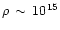 gmcm-3)
and are small in terms of pressure. For our constraint,
however, these small changes in pressure are significant and can lead to very
different radii R* (See Figs. 2 and 3 in Benhar et al. 1999).
The best we can do is to glean from the trend which is visible in the EOS that include the
microphysics in the best possible way, i.e., those based on relativistic quantum field
theory (Salgado et al. 1994; Prakash et al. 1997),
rather than those in which nucleon interactions are
described using potentials (as in the BPAL series). These are the EOS in
Table 2 and none among these theoretically most advanced EOS are
favored by our constraints. (This is also true of similar EOS described in
Prakash et al. 1997.)
Extrapolating on this trend it would seem that no neutron
star EOS can satisfy the inequality (7). This in turn implies that
pulsars are not neutron stars
gmcm-3)
and are small in terms of pressure. For our constraint,
however, these small changes in pressure are significant and can lead to very
different radii R* (See Figs. 2 and 3 in Benhar et al. 1999).
The best we can do is to glean from the trend which is visible in the EOS that include the
microphysics in the best possible way, i.e., those based on relativistic quantum field
theory (Salgado et al. 1994; Prakash et al. 1997),
rather than those in which nucleon interactions are
described using potentials (as in the BPAL series). These are the EOS in
Table 2 and none among these theoretically most advanced EOS are
favored by our constraints. (This is also true of similar EOS described in
Prakash et al. 1997.)
Extrapolating on this trend it would seem that no neutron
star EOS can satisfy the inequality (7). This in turn implies that
pulsars are not neutron stars![[*]](/icons/foot_motif.gif) and leaves us with the only alternative conceivable at present,
that pulsars are strange quark stars. We discuss this next.
and leaves us with the only alternative conceivable at present,
that pulsars are strange quark stars. We discuss this next.
Some stars considered so far to be neutron stars have been proposed to be
actually strange stars on two counts. The proposals for Her X-1
(Dey et al. 1998), 4U 1820-30 (Bombaci 1997),
SAX J1808.4-3658 (Li et al. 1999a),
4U 1728-34 (Li et al. 1999b) are based on the
compactness of stars being more
than a neutron star can accomodate. From an entirely different
viewpoint
PSR 0943+10 has been proposed to be a bare strange star (Xu et al. 1999).
This
last proposal implies that all pulsars showing the phenomenon of drifting
subpulses may be bare strange stars.
Pulsars being strange stars fits well with our constraints. Whether
pulsars
are bare strange stars, strange stars with normal crusts or
the newly proposed third family of ultra-compact stars
(Glendenning & Kettner 2000) is
difficult to decide at present. For the relatively better-studied strange
stars, the new EOS for strange stars give radii 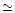 7 km as
opposed
to
7 km as
opposed
to 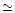 8 km given by earlier EOS based on the MIT bag model
(Dey et al. 1999). Xu et al. (1999)
propose that pulsars showing the
phenomenon of drifting sub-pulses are bare strange stars. Our constraints
apply to pulsars showing core emission. However, the core emission and
drifting of subpulses which is a property of the conal emission
(Rankin 1993; see
also Xu et al. 1999) are not mutually exclusive.
Therefore the proposal
that
pulsars are bare strange stars can be extended to all pulsars. Many issues,
such as differences between bare strange stars and those with normal
crusts etc. remain to be answered, although some answers have been
proposed. We do not repeat here this discussion (Xu et al. 1999;
Madsen 1999) except to state that our core width constraints are one more independent
indication that pulsars are strange stars.
8 km given by earlier EOS based on the MIT bag model
(Dey et al. 1999). Xu et al. (1999)
propose that pulsars showing the
phenomenon of drifting sub-pulses are bare strange stars. Our constraints
apply to pulsars showing core emission. However, the core emission and
drifting of subpulses which is a property of the conal emission
(Rankin 1993; see
also Xu et al. 1999) are not mutually exclusive.
Therefore the proposal
that
pulsars are bare strange stars can be extended to all pulsars. Many issues,
such as differences between bare strange stars and those with normal
crusts etc. remain to be answered, although some answers have been
proposed. We do not repeat here this discussion (Xu et al. 1999;
Madsen 1999) except to state that our core width constraints are one more independent
indication that pulsars are strange stars.
The source SAX J1808.4-3658 has been proposed to be a strange star on the
basis of its compactness. In the analysis of Psaltis & Chakrabarty (1999)
it was demonstrated that the
presence of multipole components relaxes the amount of compactness
required, such that the star could be a neutron star. In our analysis also, existence
of multipoles (however ad hoc) would dilute our conclusion of pulsars
being strange stars. It thus seems that existence of multipoles or the
strange star nature of hitherto considered neutron stars are two mutually
exclusive choices. At present it is very difficult to choose between them. More work
on strange stars may in future elucidate this, but introduction of
multipoles brings in so many parameters that how their existence could be proved from
observations is unclear. The multipoles would also rob the Rankin relation
of its beauty and turn its remarkable observational agreement into a mystery.
In summary, the empirical formula of Rankin (1990) describing the
opening
angle of the pulsar beam emitting the core emission when compared to
theoretically calculated value leads to a constraint that pulsar masses
should be 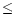 2.5
2.5 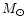 and radii
and radii 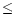 10.5 km. This
comes about due to the inclusion of
general relativistic effects of the mass of the star on the pulsar beam
size. For observationally reasonable pulsar masses
a comparison with mass-radius relations of neutron star EOS shows
that most of the EOS are ruled out, implying that pulsars are
strange stars and not neutron stars, unless our understanding of the
neutron star EOS is revised.
10.5 km. This
comes about due to the inclusion of
general relativistic effects of the mass of the star on the pulsar beam
size. For observationally reasonable pulsar masses
a comparison with mass-radius relations of neutron star EOS shows
that most of the EOS are ruled out, implying that pulsars are
strange stars and not neutron stars, unless our understanding of the
neutron star EOS is revised.
Acknowledgements
One of us (C. S. S.) would like to thank R. Gavai and S. Reddy for
rekindling his interest in the subject matter of this paper whose
preliminary version was reported in Kapoor & Shukre (1997). We thank
I. Bombaci and J. Rankin for valuable comments.
- Alcock, C., Farhi, E., & Olinto, A. 1986, ApJ,
310, 261
In the text
NASA ADS
- Arons, J. 1993, ApJ, 408, 160
In the text
NASA ADS
- Arons, J. 2000, in Pulsar Astronomy - 2000 and Beyond,
IAU Coll. 177, ed. M. Kramer, et al., ASP Conf. Ser., 449
In the text
- Balberg, S., Lichtenstadt, I., & Cook, G. B.
1999, ApJS, 121, 515
In the text
NASA ADS
- Benhar, O., Berti, E., & Ferrari, V. 1999,
MNRAS, 310, 797
In the text
NASA ADS
- Bombaci, I. 1997, Phys. Rev. C, 55, 1587
In the text
NASA ADS
- Bombaci, I. 2000, Private communication
In the text
- Dey, M., Bombaci, I., Dey, J., Ray, S., & Samanta, B. C.
1998, Phys. Lett. B, 438, 123
In the text
NASA ADS
- Dey, M., Bombaci, I., Dey, J., Ray, S., & Samanta, B. C. 1999,
Phys. Lett. B, 467, 303
In the text
NASA ADS
- Gil, J., & Mitra, D. 2000 [astro-ph 0010603] (ApJ to be
published)
In the text
- Glendenning, N. K. 2000, Phys. Rev. Lett.,
85, 1150
In the text
NASA ADS
- Glendenning, N. K., & Kettner, C., Astron. Astrophys. Lett.,
353, L9
- Goldreich, P., & Julian, W. H. 1969,
ApJ, 157, 869
In the text
NASA ADS
- Huber, H., Weber, F., Weigel, M. K., &
Schaab, Ch. 1998, Intl. J.
Mod. Phys., E7, 301
In the text
- Kapoor, R. C., & Shukre, C. S.
1997, Contribution to GR15:
15th International Conference on General Relativity and Gravitation,
IUCAA, Pune, India, Dec. 1997
In the text
- Kapoor, R. C., & Shukre, C. S. 1998, ApJ, 501,
228
In the text
NASA ADS
- van Kerkwijk, M. H., van Paradijs, J., &
Zuiderwijk, E. J. 1995, A&A, 303, 497
In the text
NASA ADS
- Li, X.-D., Bombaci, I., Dey, M., Dey, J., &
van den Heuvel, E. P. J. 1999a, Phys. Rev. Lett., 83, 3776
In the text
NASA ADS
- Li, X.-D, Ray, S., Dey, J., Dey, M., & Bombaci, I.
1999b, ApJL, 527, L51
In the text
NASA ADS
- Madsen, J. 1999,
in Lecture Notes in Phys. 516, Hadrons
in Dense Matter and Hadrosynthesis, ed. J. Cleymans, H. B. Geyer, & F. G.
Scholtz (Springer Verlag) in press
In the text
- Prakash, M., Bombaci, I., Prakash, M.,
et al. 1997, Phys. Reports, 280, 1
In the text
NASA ADS
- Psaltis, D., & Chakrabarty, D.
1999, ApJ, 521, 332
In the text
NASA ADS
- Rankin, J. M. 1983, ApJ, 274, 333
In the text
NASA ADS
- Rankin, J. M. 1990, ApJ, 352, 247
In the text
NASA ADS
- Rankin, J. M. 1993, ApJ, 405, 285
In the text
NASA ADS
- Salgado, M., Bonazzola, S., Gourgoulhon, E.,
& Haensel, P., A&A, 291, 155
In the text
NASA ADS
- Thorsett, S. E., & Chakrabarty, D.,
ApJ, 512, 288
In the text
NASA ADS
- Weber, F. 1999,
Pulsars as Astrophysical Laboratories for
Nuclear
and Particle Physics (Amer. Inst. Phys.)
In the text
- Xu, R. X., Qiao, G. J., & Zhang, B.
1999, ApJ, 522, L109
In the text
NASA ADS
Copyright ESO 2001