A major advantage of the proposed scheme is that in an optical
system with a single lens, the image is to first order independent of
any tilt of the lens with respect to the line joining the
object-centre to the lens-centre and the image-centre. The accuracy
with which the lens module must keep the axis of the lens pointed
towards the target is only that needed to avoid aberrations due
to using the lens too far off-axis. The formulae derived by
Young (1972) for the aberrations of zone plates show that field
curvature is the dominant effect in the case under consideration here
and that it is insignificant for off-axis angles of less than a
degree. Thus the pointing requirement for the lens module is
trivial. Similarly the orientation of the detector module needs only
to be controlled accurately enough that the distant lens is within the
field of view of the collimator which would be needed to restrict the
diffuse cosmic background. Thus for the detector, too, ![]() degree
pointing precision should be sufficient.
degree
pointing precision should be sufficient.
The distance between the two spacecraft does not have to be controlled with great precision. An error of 1000 km in 106 km will only lead to a 0.1% change in the energy for which the instrument is optimally focussed.
It is the relative position of the two spacecraft,
transverse to the axis, which is critical. In terms of spacecraft
position control, the requirements for the system under consideration
here differ from those of LISA mainly in that the objective here is to
maintain a stable position in true inertial space instead of within a
local pseudo-potential in the solar system. The crucial issue is the
control of the direction in space of the line joining the two
spacecraft. The problem can be considered in terms of maintaining the
detector array at the focal point of the lens despite gravity gradient
forces, though in practice the lens carrying spacecraft could equally
be the actively controlled one. For spacecraft separated by f from
each other and at 1 AU from the sun and distance d from the earth,
gravity gradient forces correspond to accelerations in m s-2 of
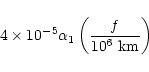 |
(5) |
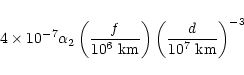 |
(6) |
Solar radiation pressure produces an acceleration
![]() m s-2, on a spacecraft of mass M (kg) presenting area A (m2) to the solar flux. Here
m s-2, on a spacecraft of mass M (kg) presenting area A (m2) to the solar flux. Here
![]() is another factor in the range 1-2. For long focal
length systems and for conventional spacecraft proportions,
the effects of radiation pressure will usually be less important than those due to gravity
gradient effects, particularly as it is only the
differential force which matters. It is noted however that
solar sails with an area of a few thousand square metres
might be used to help minimise the active propulsion requirements.
is another factor in the range 1-2. For long focal
length systems and for conventional spacecraft proportions,
the effects of radiation pressure will usually be less important than those due to gravity
gradient effects, particularly as it is only the
differential force which matters. It is noted however that
solar sails with an area of a few thousand square metres
might be used to help minimise the active propulsion requirements.
The accelerations are such that for a spacecraft of a few hundred kg, thrusts of about 10 mN are required. This is an order of magnitude less than needed for Xeus and is well matched to the capability of ion thrusters developed for geosynchronous satellite station keeping. The integrated momentum changes necessary to counteract these forces and to allow for multiple telescope pointings are of the order of 1 km s-1 y-1 and 10 km s-1 y-1; these, too, are much less than the requirement for Xeus and are comparable with those needed to deploy the LISA array. Thus these requirements do not seem entirely unreasonable.
The relative positions of the spacecraft in a direction transverse to the line of sight need to be known to a precision of a few millimetres and controlled better than, say, 10 cm. As discussed above, the dominant disturbing forces are gravitational. Because the potential within the inner solar system is extremely well understood they can be accurately predicted. Clearly a closed loop control system will be needed however to avoid errors accumulating. The disturbances will change only slowly and the timescale over which the feedback loop will have to operate will depend mainly on uncertainties in thrusters. By using data from accelerometers, it should be possible to reduce these uncertainties to a low enough level that the main feedback loop can be a slow one.
Providing an absolute reference is the biggest challenge presented by the proposed approach, though it is no worse than for any other mission aiming at micro arcsecond resolution.
The HST fine guidance system uses interferometric sensors which have milli arcsecond performance but which rely on the primary optical system and even were it precise enough this does not offer an economic approach to the problem. The same applies a fortiori to the system planned for NGST. The MAXIM study plans to rely on developments in the optical band underway for the Space Interferometry Mission, SIM, and this would be one approach.
Alternatively, given the centimetre scale precision needed in the case under consideration here, it is natural to turn to the radio band and it would appear that a solution can probably be found using radio navigation signals (J. Bar-Sever, private communication). For example one could consider using phase-locked radio beacons on the two spacecraft, which are in contact with each other and with at least 3 ground stations. The ground stations would probably have to use radio astronomical observations to establish their positions with respect to a reference frame defined by distant objects.
The positions of the targets will have to be known sufficiently well that they can be found. The main objective of SIM is to perform micro arcsecond astrometry (using resolution much lower than proposed here, but taking advantage of centroiding) and this could provide an adequate frame of reference. It is noted that it could turn out to be best to use radio astronomical measurements direct from the two spacecraft to establish the pointing with respect to a celestial reference frame and that a radio interferometer using receivers at each end of this long stable baseline would itself be a powerful astronomical tool.
Chromatic aberration is an important limiting factor for PFLs. With the detector plane in the focal position for the nominal design energy, the focal spot becomes more and more blurred as one considers energies further and further from the nominal.
Simulation shows that there is a
contribution to the 60% power diameter corresponding to an angular resolution
(in radians) of about
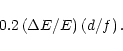 |
(7) |
In Paper II techniques for increasing the bandwidth will be discussed, but for the present we accept that (for continuum radiation) chromatic aberration may be a limiting factor when trying to achieve the very highest angular reolution.
Some of the advantage of the large collecting area is lost by
having to work within a narrow bandwidth.
However, provided the observations are detector background noise
limited, from the point of view of sensitivity as well as that of
angular resolution, ![]() should be as narrow as the detector
resolution will allow. This is true even for continuum studies. It
arises because if the bandwidth is large, so that the above limit on
should be as narrow as the detector
resolution will allow. This is true even for continuum studies. It
arises because if the bandwidth is large, so that the above limit on
![]() is not met, the angular resolution will be
degraded. For a point source data will then have to be collected from
a larger region of the detector plane and this will normally result in
increased background noise. Assuming that the background in an area
is not met, the angular resolution will be
degraded. For a point source data will then have to be collected from
a larger region of the detector plane and this will normally result in
increased background noise. Assuming that the background in an area
![]() is proportional to
is proportional to
![]() ,
the associated
Poissonian noise will increase in proportion to
,
the associated
Poissonian noise will increase in proportion to
![]() .
As
signal from a continuum source will only increase as
.
As
signal from a continuum source will only increase as ![]() ,
small
values of
,
small
values of ![]() are preferable.
are preferable.
This is one respect in which the approach discussed here is at a disadvantage compared with the interferometric system proposed for MAXIM, which operates over a wide band (data from different energies can be combined because the detector is energy resolving and the point source response function at each energy is known).
Although a PFL will be optimised for a particular energy, that does
not preclude its use at other energies by moving the detector to the
corresponding focal plane at f'=f E'/E. Figure 4b
shows how the efficiency varies if a lens is refocussed for a
different energy in this way. Over a band of energy spanning a factor
of 2-3, the effective area is reduced by less than a factor of two.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{MS1333f4a.eps}}
\resizebox{8.3cm}{!}{\includegraphics{MS1333f4b.eps}} %
\end{figure}](/articles/aa/full/2001/32/aa1333/Timg65.gif) |
Figure 4: a) The predicted response as a function of energy of a PFL lens optimised for one energy of 500 keV but used at different energies. The lens parameters are as in Table 2 . The signal in a detector pixel of 2 (narrowest), 10, 20, 30, 40 mm diameter is shown. The curves are computed using a method based on the work of Lommel (Boivin 1952) and do not take into account absorption. Results from a Monte Carlo simulation with absorption taken into account are shown for the 10 mm case and show that the corrections are small. b) The response of PFLs optimised for 200, 500 and 847 keV if the detector is moved to an appropriate focal position for each energy. (Monte Carlo method; absorption effects included) The curve from a) for a 10 mm detector is shown dashed for comparison. |
The fact that the refractive index is extremely close to that of
vacuum means that the lens performance is relatively immune to
problems of surface roughness, material inhomogeneities and
constructional tolerances. Attaining
![]() phase precision
requires no better than 0.1 mm quality for a 500 keV aluminium lens,
for example. Temperatures can change by some tens of degrees without
serious effect.
phase precision
requires no better than 0.1 mm quality for a 500 keV aluminium lens,
for example. Temperatures can change by some tens of degrees without
serious effect.
Depending as it does on simple physics and tolerance requirements
which are far more lax than the state of the art, the performance of
the lens can be predicted with confidence. The pessimistic assumption
of 80% efficiency still leaves about 16 m2 effective area for the
example lens. In making estimates of sensitivity in the remainder of
this work, the photopeak efficiency and background expected for the
SPI Germanium Spectrometer on Integral are used. For example, at 500 keV these are 42% and
![]() events cm-3 s-1 keV-1. With a germanium detector working at this energy those
events within an energy window of
events cm-3 s-1 keV-1. With a germanium detector working at this energy those
events within an energy window of
![]() can be selected.
The corresponding chromatic aberration will increase the focal spot size
from 0.6 mm to 5 mm, limiting the angular resolution to about 1.4
can be selected.
The corresponding chromatic aberration will increase the focal spot size
from 0.6 mm to 5 mm, limiting the angular resolution to about 1.4 ![]() .
The resulting sensitivity and the corresponding
values for the other example systems are given in Table 2.
.
The resulting sensitivity and the corresponding
values for the other example systems are given in Table 2.
Copyright ESO 2001