A&A 375, 691-700 (2001)
DOI: 10.1051/0004-6361:20010745
G. K. Skinner
1 - School of Physics and Astronomy,
University of Birmingham, Edgbaston, Birmingham, B15
2TT, England, UK
2 -
CESR, 9 avenue du Colonel Roche, 31028 Toulouse, France
Received 30 March 2001 / Accepted 22 May 2001
Abstract
Diffractive optics components such as Fresnel Zone Plates and
their derivatives potentially form the basis for telescope systems
for X-ray and gamma-ray astronomy with high sensitivity and superb
angular resolution. The main problem is that systems with
convenient design parameters involve very long focal lengths.
The design considerations and performance
of telescopes using a simple Phase Fresnel Lens on one spacecraft and a
detector assembly on another are considered. Such systems are shown to
have the potential to provide orders of magnitude improvement on
currently available sensitivity. At the same time the angular resolution
can be at the micro arcsecond level or better - sufficient to resolve the
structure surrounding the event horizon of black holes in nearby galaxies.
Key words: telescopes - methods: observational - techniques: interferometric - gamma-rays: observations - X-rays: general
Observations at hard X-ray and gamma-ray energies are severely
constrained by the limited sensitivity and poor angular resolution of
the present generation of instrumentation. The sensitivity could be
enormously improved if gamma-ray radiation could be concentrated from
a large collection area onto a small, low background detector, as is
done with grazing incidence optics at lower energies in, for example,
the Chandra and XMM-Newton observatories. Similarly, if a
diffraction-limited gamma-ray optical system, even of modest diameter
(a few metres), could be constructed, then the angular resolution
achievable would be a fraction of one micro arcsecond (![]() ). This
would be better than that achievable in any other waveband and would
be sufficient to resolve the structure in the emitting region
immediately surrounding the event horizon of massive black holes in
the nucleii of nearby galaxies.
). This
would be better than that achievable in any other waveband and would
be sufficient to resolve the structure in the emitting region
immediately surrounding the event horizon of massive black holes in
the nucleii of nearby galaxies.
The object of this paper is to point out that in principle simple diffractive optics in the form of a Phase Fresnel Lens can simultaneously achieve both of these advances. This idea has been briefly introduced (Skinner 2001b) but is here examined in detail. The background to the problem of obtaining high sensitivity and ultra-high angular resolution observations is first discussed (Sect. 2) and the concept of utilising diffractive optics at gamma-rays is then introduced (Sect. 3), along with some specific considerations for astronomical applications (Sect. 4). The practical problems are discussed in Sect. 5 and the performance anticipated and the science which it would make possible are reviewed in Sect. 6. In a companion paper (Skinner 2001a, Paper II) some variations of the proposed configuration, which offer advantages in particular circumstances, will be discussed.
At X-ray energies the present generation of
X-ray instrumentation for astronomy depends on grazing angle
reflection optics in a nested Wolter-I configuration. In this way
the Chandra mission offers angular resolution of 0.5 arcsec
(Jerius et al. 2000)
and, with thinner, less precise, optics XMM-Newton obtains an effective
area of more than 0.4 m2 (Stockman et al. 1999).
Both of these instruments are limited to photon energies below ![]() 10 keV.
10 keV.
X-ray missions actively under study, in particular Constellation-X (White & Tananbaum 1999) and Xeus (Bavdaz et al. 1999), will make possible considerable improvements in sensitivity and spectral resolution. They will not emphasise angular resolution, which will remain 103-106 times worse than the diffraction limit. At X-ray energies only interferometry, discussed below, offers the prospect of ultra-high angular resolution.
Moving to hard X-rays and gamma-rays, the sensitivity of the current generation of
instruments - Compton-GRO and Integral - is very much poorer than that
obtained in the X-ray band. This is largely because it is not currently
possible to concentrate the flux as is done at lower energies
with mirror optics. The imaging techniques, too, are indirect and
have poor angular resolution - of the order 0.1-10![]() .
.
Grazing incidence optics with multilayer coatings are being actively pursued by a number of groups for focussing energies up to about 100 keV (e.g. Yamashita et al. 1998; Ogasaka et al. 2000; Craig et al. 1998; Hussain et al. 1999; Mao et al. 1999). In principle such techniques can focus radiation of even higher energies, though the number of layers for efficient reflection would become very large and the grazing angles very small, so the area of coated surface for a given effective area would be huge. The angular resolution of multilayer mirrors depends on the precision of the surface of the substrate and of the coating. At present it is little better than one arc minute and there seems little prospect either of achieving large effective areas or of approaching the diffraction limit using this technology.
MAXIM is a mission currently under study that would use X-ray
interferometry to allow images to be reconstructed with a resolution
corresponding to a baseline of 1 m (pathfinder version) or even 100 m
("event horizon'' version). Using X-rays of ![]() to 6 keV
respectively this results in resolutions of 100 and 0.1
to 6 keV
respectively this results in resolutions of 100 and 0.1 ![]() (Cash et al. 2000). MAXIM can be regarded as a large modified
Wolter III telescope with unfilled aperture in which the sampled parts
of the aperture are approximated by individual plane surfaces. To get
sub micro arcsecond resolution at keV energies requires an entrance
aperture of hundreds of metres and the idea is that the primary mirror
segments would be on 32 separate spacecraft and the secondary mirror
segments and detector array on two more.
(Cash et al. 2000). MAXIM can be regarded as a large modified
Wolter III telescope with unfilled aperture in which the sampled parts
of the aperture are approximated by individual plane surfaces. To get
sub micro arcsecond resolution at keV energies requires an entrance
aperture of hundreds of metres and the idea is that the primary mirror
segments would be on 32 separate spacecraft and the secondary mirror
segments and detector array on two more.
In the gamma-ray band a first step towards attaining flux concentration has recently been made through the use of Laue diffraction in Ge-Si crystals in a telescope for gamma-rays of 170 keV (Laporte et al. 1999) and this technology has been proposed for part of the HXT for the Constellation-X mission (Gorenstein et al. 1996). Concentric rings of carefully oriented crystals diffract the incoming flux towards a common focal point, each ring using a different set of crystal planes. This technique is expected to become important as a way of collecting flux onto a small detector but extremely high angular precision would only be obtained with very carefully aligned, highly perfect, crystals, that have an extremely narrow band-pass. Furthermore the approach does not lend itself to true imaging.
Other approaches to gamma-ray imaging for astronomy and their limitations have been reviewed by Skinner (2001b). None apart from the use of diffraction and/or refraction appear to offer the prospect of extremely high angular resolution and sensitivity. Purely refractive optics could be considered in some circumstances, but Yang (1993) has shown how absorption limits the effective area possible. Systems in which diffraction plays the major role turn out to be preferable and it is on such designs that we will concentrate here.
Diffractive lenses in the form of Fresnel Zone Plates (FZPs) were used in early solar X-ray imaging (Kraemer et al. 1978), but since then have not found application in high energy astronomy, due to their low efficiency and small apertures. Masks with FZP patterns cut into them have been proposed for astronomy both as simple coded masks (Mertz & Young 1961) and in pairs in a modulation collimator configuration in which Moiré fringes are recorded (Desai et al. 1998). Such systems, however, have no flux concentrating capability and are quite distinct from those advocated here. What is discussed here is the possible application to gamma-ray astronomical applications of true diffractive lenses with large effective area.
MAXIM will offer major advances in the X-ray band and is technically so challenging that it may seem premature to consider how comparable resolution might be obtained at still higher energies, where performance is currently far inferior to that possible at lower energies. But this paper aims to show that this may be feasible and that, although there are some disadvantages of working at higher energies, in other respects things actually become simpler.
Fresnel Zone Plates (FZPs, Fig. 1a),
as invented by Soret (1875), are in some respects related
to the Laue lens mentioned in Sect. 2
as each small region of an FZP can be thought of as a
small grating that diffracts the incoming radiation towards the
focus, the pitch of the diffraction grating becoming smaller as
higher deflection angles are needed at larger radii.
![\begin{figure}
\par\resizebox{6cm}{!}{\includegraphics[angle=-90,clip]{MS1333f1.eps}}
\end{figure}](/articles/aa/full/2001/32/aa1333/Timg10.gif) |
Figure 1: a) A Fresnel Zone Plate (FZP), b) A Phase Zone Plate (PZP), c) A Phase Fresnel Lens (PFL). |
| Open with DEXTER | |
A simple FZP has a maximum efficiency of
![]() .
This results from the
fact that apart from the first order (n=1) focus,
energy also passes unfocussed (n=0), to higher orders
.
This results from the
fact that apart from the first order (n=1) focus,
energy also passes unfocussed (n=0), to higher orders
![]() and to virtual focii
and to virtual focii
![]() .
.
![\begin{figure}
\par\resizebox{8.6cm}{!}{\includegraphics[clip]{MS1333f2.eps}}\end{figure}](/articles/aa/full/2001/32/aa1333/Timg14.gif) |
Figure 2:
The thickness, |
| Open with DEXTER | |
As well as independently proposing the FZP, Rayleigh pointed out the
possibility, demonstrated by Wood (1898), of obviating the zero
order loss in what can be termed the Phase Zone Plate (PZP, Fig. 1b). The opaque regions are replaced by ones that allow
the radiation to pass, but which have a thickness of refractive
material such as to impose a phase shift of ![]() .
The theoretical
efficiency limit is raised to
.
The theoretical
efficiency limit is raised to
![]() .
.
Ideally the thickness, and hence the phase change, within each zone should be a continuous function of radius. This leads to the kineform, or Phase Fresnel Lens (PFL) (Miyamoto 1959) (Fig. 1c), in which ideally all of the power is directed into order n=1, giving an efficiency of up to 100%. The same effect can be achieved with a graded refractive index instead of varying thickness (Fujisaki & Nakagiri 1990; Yang 1993). Stepped approximations to a PFL (di Fabrizio & Gentili 1999) can still have efficiencies approaching this value. Effectively the graded diffraction grating is blazed using refraction to concentrate all of the power into order n=1.
FZPs, PZPs and PFLs are increasing being used for X-ray microscopy and other applications at electron synchrotron facilities. Some example parameters for lenses that are based on these principles and that have been used for laboratory applications are given in Table 1.
In view of the need for high efficiency, we will concentrate here on PFLs,
and hence the refractive index of the material from which the lens
is made is a critical parameter.
The refractive index of a material at X-ray/gamma-ray energies is
usually expressed as
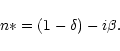 |
(1) |
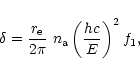 |
(2) |
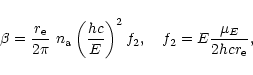 |
(3) |
Well above absorption edges, and apart from small
relativistic and nuclear corrections, f1 is essentially constant
and equal to the number of electrons per atom, Z. It follows
that the thickness ![]() necessary to
provide a phase shift of
necessary to
provide a phase shift of ![]() is approximately proportional to energy.
The thickness of a PZP or the mean thickness of a PFL will be
equal to
is approximately proportional to energy.
The thickness of a PZP or the mean thickness of a PFL will be
equal to ![]() .
Values of
.
Values of ![]() for some example materials are
shown in Fig. 2. Much of the present work
depends on the fact that as one moves up in
energy from the X-ray band, although
for some example materials are
shown in Fig. 2. Much of the present work
depends on the fact that as one moves up in
energy from the X-ray band, although ![]() increases, the
associated absorption
becomes smaller and over a wide range of energy the losses fall to a
low level (Fig. 2).
increases, the
associated absorption
becomes smaller and over a wide range of energy the losses fall to a
low level (Fig. 2).
| Example reported laboratory systems | Example diffractive lens | |||||
| Reference | (a) | (b) | (c) | telescopes | ||
| Energy (keV) | 0.4 | 8, 20 | 8 | 200 | 500 | 847 |
| Type | FZP | PZP | Stepped PFL | PFL | ||
| Material | Ge | Au | Ni | Al | ||
| Maximum thickness, t ( |
0.18 | 1.6, 3 | 4.5 | 450 | 1200 | 1900 |
| Shortest period, p ( |
0.06 | 0.5 | 2 | 2500 | 1000 | 590 |
| Aspect ratio (t/p) | 3 | 3.2, 6 | 2.25 | 0.5 | 1.2 | 2.0 |
| Focal length f (m) |
|
3, 7.5 | 1 | 109 | ||
| Diameter (d) (mm) | 0.08 | 0.19 | 0.15 | 5000 | ||
| f-number
|
1 | 1600, 4000 | 6700 |
|
||
| Theoretical diffraction-limited | ||||||
| resolution: Spatial ( |
0.035 | 0.3 | 1.2 | |||
| Angular (arc sec) |
|
|
|
|||
References: (a) Spector et al. (1999) (b) Chen et al. (1999) (c) di Fabrizio & Gentili (1999).
The focal length, f, the finest pitch of the pattern, p, and the lens diameter, d, are inter-related; we review first some of the considerations which dictate the choice of these parameters.
For microscopy, very fine pitch patterns are sought because the
diffraction limited spatial resolution in the object plane is
![]() .
Here the resolution is that given by the Rayleigh critereon,
which corresponds to the 60% power diameter.
.
Here the resolution is that given by the Rayleigh critereon,
which corresponds to the 60% power diameter.
For astronomy, the diffraction limited
image spot size is equal to ![]() ,
as given by the above expressions, but
it is the angular resolution
,
as given by the above expressions, but
it is the angular resolution
![]() that is important.
From the points of view of the angular resolution of a telescope
and of flux concentration, there is no reason to make p much
smaller than the detector spatial resolution.
Considerations of electron scattering
and stopping distance suggest that the detector
spatial resolution is likely to be limited to about 1 mm at 1 MeV,
scaling approximately as E0.8.
that is important.
From the points of view of the angular resolution of a telescope
and of flux concentration, there is no reason to make p much
smaller than the detector spatial resolution.
Considerations of electron scattering
and stopping distance suggest that the detector
spatial resolution is likely to be limited to about 1 mm at 1 MeV,
scaling approximately as E0.8.
Pitches finer than the detector resolution may nevertheless
sometimes be useful. They may allow larger lenses
or shorter focal length to be used because
the finest pitch dictates the maximium diffraction angle and hence relates
f and d:
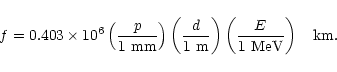 |
(4) |
The diffractive techniques proposed here can be adopted over a very
wide range - at least from ![]() keV to
keV to ![]() MeV. To
investigate their potential for gamma-ray astronomy, a number of
different cases will be considered - a low energy gamma-ray system
optimised for 200 keV, a medium energy example (500 keV) and a lens
optimised for working in the 847 keV 56Co line. Although where
possible a lens should be optimised for a particular energy, it will be
seen that a given device can in fact function over a relatively wide
band by changing the detector position.
Figure 2 shows that, even without resorting to exotic
materials such as Beryllium, losses in a gamma-ray PFL need only be a
few percent. Selecting Aluminium, a low technology, low cost
material, one finds
MeV. To
investigate their potential for gamma-ray astronomy, a number of
different cases will be considered - a low energy gamma-ray system
optimised for 200 keV, a medium energy example (500 keV) and a lens
optimised for working in the 847 keV 56Co line. Although where
possible a lens should be optimised for a particular energy, it will be
seen that a given device can in fact function over a relatively wide
band by changing the detector position.
Figure 2 shows that, even without resorting to exotic
materials such as Beryllium, losses in a gamma-ray PFL need only be a
few percent. Selecting Aluminium, a low technology, low cost
material, one finds
![]() between 0.45 and 1.9 mm (Table 1) for the energies considered here.
The transmission loss is only 1.5 to 2%, even allowing
for a 0.25 mm backing for constructional purposes (Fig. 3).
between 0.45 and 1.9 mm (Table 1) for the energies considered here.
The transmission loss is only 1.5 to 2%, even allowing
for a 0.25 mm backing for constructional purposes (Fig. 3).
As discussed above, the detector spatial resolution at these energies
will be of the order of a millimetre, so from an angular resolution
point of view there is no reason to consider very small values of
p. This leads to the concept of a very simple lens in which a
millimetre scale groove structure is machined into an aluminium plate
a millimeter or so thick. The profile for the 500 keV example lens
with p=1 mm is illustrated in Fig. 3.
| |
Figure 3: Cross-section through the extreme edge of the aluminium disk forming the example 500 keV gamma-ray PFL in Table 1. |
| Open with DEXTER | |
The main problem is that for any reasonable diameter the focal length becomes very long indeed. The 5 m diameter 500 keV lens example (Tables 1, 2, Fig. 3) would have a focal length of just over 106 km at 511 keV. But is this impracticable? The Xeus studies (Bavdaz et al. 1999) have demonstrated the feasibility of having a focussing optic on one spacecraft and a focal plane assembly on another one actively controlled to remain at the focal point. The separation in the case of Xeus is only 50 m but this is in low earth orbit where gravity gradient effects are serious.
Many other mission concepts under study require precision control
of the relative positions of spacecraft and the concept of "formation
flying'' has been validated by several studies. In fact there are engineering
groups at JPL, GSFC and Estec that specialize in it. In particular
the LISA gravitational wave observatory mission
(LISA Study Team 1998) plans to use three spacecraft with distances
of
![]() km between each pair. The entire cluster will orbit
the sun at 1 AU. The LISA spacecraft will be actively controlled to
hold their position with respect to a proof mass within each to a
precision of
km between each pair. The entire cluster will orbit
the sun at 1 AU. The LISA spacecraft will be actively controlled to
hold their position with respect to a proof mass within each to a
precision of ![]() nm (on a 1 s timescale).
nm (on a 1 s timescale).
This suggests that a stable baseline a few million km long between two
spacecraft is not inconceivable and we will proceed to
work through the implications of such a design.
| Integral SPI | Integral Ibis | Example Diffractive Lens | |||
| Spectrom. | Imager | Telescopes | |||
| Focal length (m) | 1.7 | 3.2 | 109 | ||
| Band (keV) - fixed configuration | 20-8000 | 15-10000 |
|
|
|
| Band (keV) for 50% response | 125-500 | 325-1200 | 540-2100 | ||
| with separation adjusted | |||||
| Effective area (m2) (1) | 0.009 | 0.05 | 12.1 | 6.4 | 4.4 |
| Angular resolution ( |
|||||
| (intrinsic) | 1010 | 109 | 0.3 | 0.12 | 0.07 |
| (with chromatic aberration) | 1.7 | 0.7 | 0.5 | ||
| Sensitivity(2) | |||||
| Continuum (3) |
|
|
|
|
|
| Narrow Line (4) |
|
|
|
|
|
(1) At 500 keV for SPI/Ibis; Detector efficiency and
20% provision for lens imperfections taken into account.
(2) Sensitivities are for a point source. For the example
PFL telescopes, the background taken is
based on SPI predictions, scaled to 1 cm2, corresponding to 2 ![]() .
.
(3) Photons cm-2 s-1 keV-1 for
5![]() in 1 day, E=500 keV, dE=250 keV (Ibis).
in 1 day, E=500 keV, dE=250 keV (Ibis).
(4) Photons cm-2 s-1 for
5![]() in 106 s, (SPI figure is for 500 keV).
in 106 s, (SPI figure is for 500 keV).
A major advantage of the proposed scheme is that in an optical
system with a single lens, the image is to first order independent of
any tilt of the lens with respect to the line joining the
object-centre to the lens-centre and the image-centre. The accuracy
with which the lens module must keep the axis of the lens pointed
towards the target is only that needed to avoid aberrations due
to using the lens too far off-axis. The formulae derived by
Young (1972) for the aberrations of zone plates show that field
curvature is the dominant effect in the case under consideration here
and that it is insignificant for off-axis angles of less than a
degree. Thus the pointing requirement for the lens module is
trivial. Similarly the orientation of the detector module needs only
to be controlled accurately enough that the distant lens is within the
field of view of the collimator which would be needed to restrict the
diffuse cosmic background. Thus for the detector, too, ![]() degree
pointing precision should be sufficient.
degree
pointing precision should be sufficient.
The distance between the two spacecraft does not have to be controlled with great precision. An error of 1000 km in 106 km will only lead to a 0.1% change in the energy for which the instrument is optimally focussed.
It is the relative position of the two spacecraft,
transverse to the axis, which is critical. In terms of spacecraft
position control, the requirements for the system under consideration
here differ from those of LISA mainly in that the objective here is to
maintain a stable position in true inertial space instead of within a
local pseudo-potential in the solar system. The crucial issue is the
control of the direction in space of the line joining the two
spacecraft. The problem can be considered in terms of maintaining the
detector array at the focal point of the lens despite gravity gradient
forces, though in practice the lens carrying spacecraft could equally
be the actively controlled one. For spacecraft separated by f from
each other and at 1 AU from the sun and distance d from the earth,
gravity gradient forces correspond to accelerations in m s-2 of
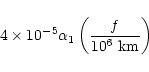 |
(5) |
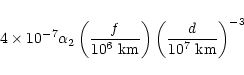 |
(6) |
Solar radiation pressure produces an acceleration
![]() m s-2, on a spacecraft of mass M (kg) presenting area A (m2) to the solar flux. Here
m s-2, on a spacecraft of mass M (kg) presenting area A (m2) to the solar flux. Here
![]() is another factor in the range 1-2. For long focal
length systems and for conventional spacecraft proportions,
the effects of radiation pressure will usually be less important than those due to gravity
gradient effects, particularly as it is only the
differential force which matters. It is noted however that
solar sails with an area of a few thousand square metres
might be used to help minimise the active propulsion requirements.
is another factor in the range 1-2. For long focal
length systems and for conventional spacecraft proportions,
the effects of radiation pressure will usually be less important than those due to gravity
gradient effects, particularly as it is only the
differential force which matters. It is noted however that
solar sails with an area of a few thousand square metres
might be used to help minimise the active propulsion requirements.
The accelerations are such that for a spacecraft of a few hundred kg, thrusts of about 10 mN are required. This is an order of magnitude less than needed for Xeus and is well matched to the capability of ion thrusters developed for geosynchronous satellite station keeping. The integrated momentum changes necessary to counteract these forces and to allow for multiple telescope pointings are of the order of 1 km s-1 y-1 and 10 km s-1 y-1; these, too, are much less than the requirement for Xeus and are comparable with those needed to deploy the LISA array. Thus these requirements do not seem entirely unreasonable.
The relative positions of the spacecraft in a direction transverse to the line of sight need to be known to a precision of a few millimetres and controlled better than, say, 10 cm. As discussed above, the dominant disturbing forces are gravitational. Because the potential within the inner solar system is extremely well understood they can be accurately predicted. Clearly a closed loop control system will be needed however to avoid errors accumulating. The disturbances will change only slowly and the timescale over which the feedback loop will have to operate will depend mainly on uncertainties in thrusters. By using data from accelerometers, it should be possible to reduce these uncertainties to a low enough level that the main feedback loop can be a slow one.
Providing an absolute reference is the biggest challenge presented by the proposed approach, though it is no worse than for any other mission aiming at micro arcsecond resolution.
The HST fine guidance system uses interferometric sensors which have milli arcsecond performance but which rely on the primary optical system and even were it precise enough this does not offer an economic approach to the problem. The same applies a fortiori to the system planned for NGST. The MAXIM study plans to rely on developments in the optical band underway for the Space Interferometry Mission, SIM, and this would be one approach.
Alternatively, given the centimetre scale precision needed in the case under consideration here, it is natural to turn to the radio band and it would appear that a solution can probably be found using radio navigation signals (J. Bar-Sever, private communication). For example one could consider using phase-locked radio beacons on the two spacecraft, which are in contact with each other and with at least 3 ground stations. The ground stations would probably have to use radio astronomical observations to establish their positions with respect to a reference frame defined by distant objects.
The positions of the targets will have to be known sufficiently well that they can be found. The main objective of SIM is to perform micro arcsecond astrometry (using resolution much lower than proposed here, but taking advantage of centroiding) and this could provide an adequate frame of reference. It is noted that it could turn out to be best to use radio astronomical measurements direct from the two spacecraft to establish the pointing with respect to a celestial reference frame and that a radio interferometer using receivers at each end of this long stable baseline would itself be a powerful astronomical tool.
Chromatic aberration is an important limiting factor for PFLs. With the detector plane in the focal position for the nominal design energy, the focal spot becomes more and more blurred as one considers energies further and further from the nominal.
Simulation shows that there is a
contribution to the 60% power diameter corresponding to an angular resolution
(in radians) of about
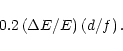 |
(7) |
In Paper II techniques for increasing the bandwidth will be discussed, but for the present we accept that (for continuum radiation) chromatic aberration may be a limiting factor when trying to achieve the very highest angular reolution.
Some of the advantage of the large collecting area is lost by
having to work within a narrow bandwidth.
However, provided the observations are detector background noise
limited, from the point of view of sensitivity as well as that of
angular resolution, ![]() should be as narrow as the detector
resolution will allow. This is true even for continuum studies. It
arises because if the bandwidth is large, so that the above limit on
should be as narrow as the detector
resolution will allow. This is true even for continuum studies. It
arises because if the bandwidth is large, so that the above limit on
![]() is not met, the angular resolution will be
degraded. For a point source data will then have to be collected from
a larger region of the detector plane and this will normally result in
increased background noise. Assuming that the background in an area
is not met, the angular resolution will be
degraded. For a point source data will then have to be collected from
a larger region of the detector plane and this will normally result in
increased background noise. Assuming that the background in an area
![]() is proportional to
is proportional to
![]() ,
the associated
Poissonian noise will increase in proportion to
,
the associated
Poissonian noise will increase in proportion to
![]() .
As
signal from a continuum source will only increase as
.
As
signal from a continuum source will only increase as ![]() ,
small
values of
,
small
values of ![]() are preferable.
are preferable.
This is one respect in which the approach discussed here is at a disadvantage compared with the interferometric system proposed for MAXIM, which operates over a wide band (data from different energies can be combined because the detector is energy resolving and the point source response function at each energy is known).
Although a PFL will be optimised for a particular energy, that does
not preclude its use at other energies by moving the detector to the
corresponding focal plane at f'=f E'/E. Figure 4b
shows how the efficiency varies if a lens is refocussed for a
different energy in this way. Over a band of energy spanning a factor
of 2-3, the effective area is reduced by less than a factor of two.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{MS1333f4a.eps}}
\resizebox{8.3cm}{!}{\includegraphics{MS1333f4b.eps}} %
\end{figure}](/articles/aa/full/2001/32/aa1333/Timg65.gif) |
Figure 4: a) The predicted response as a function of energy of a PFL lens optimised for one energy of 500 keV but used at different energies. The lens parameters are as in Table 2 . The signal in a detector pixel of 2 (narrowest), 10, 20, 30, 40 mm diameter is shown. The curves are computed using a method based on the work of Lommel (Boivin 1952) and do not take into account absorption. Results from a Monte Carlo simulation with absorption taken into account are shown for the 10 mm case and show that the corrections are small. b) The response of PFLs optimised for 200, 500 and 847 keV if the detector is moved to an appropriate focal position for each energy. (Monte Carlo method; absorption effects included) The curve from a) for a 10 mm detector is shown dashed for comparison. |
| Open with DEXTER | |
The fact that the refractive index is extremely close to that of
vacuum means that the lens performance is relatively immune to
problems of surface roughness, material inhomogeneities and
constructional tolerances. Attaining
![]() phase precision
requires no better than 0.1 mm quality for a 500 keV aluminium lens,
for example. Temperatures can change by some tens of degrees without
serious effect.
phase precision
requires no better than 0.1 mm quality for a 500 keV aluminium lens,
for example. Temperatures can change by some tens of degrees without
serious effect.
Depending as it does on simple physics and tolerance requirements
which are far more lax than the state of the art, the performance of
the lens can be predicted with confidence. The pessimistic assumption
of 80% efficiency still leaves about 16 m2 effective area for the
example lens. In making estimates of sensitivity in the remainder of
this work, the photopeak efficiency and background expected for the
SPI Germanium Spectrometer on Integral are used. For example, at 500 keV these are 42% and
![]() events cm-3 s-1 keV-1. With a germanium detector working at this energy those
events within an energy window of
events cm-3 s-1 keV-1. With a germanium detector working at this energy those
events within an energy window of
![]() can be selected.
The corresponding chromatic aberration will increase the focal spot size
from 0.6 mm to 5 mm, limiting the angular resolution to about 1.4
can be selected.
The corresponding chromatic aberration will increase the focal spot size
from 0.6 mm to 5 mm, limiting the angular resolution to about 1.4 ![]() .
The resulting sensitivity and the corresponding
values for the other example systems are given in Table 2.
.
The resulting sensitivity and the corresponding
values for the other example systems are given in Table 2.
We now consider the capabilities of telescopes using the proposed techniques to tackle some of the astrophysical objectives which gave rise to the studies described here. In assessing the feasibility of directly imaging the emission from an object, two considerations arise - if the angular scale is too small it will not be resolved and only a total flux measurement will be obtained. If it is too large then the surface brightness will be insufficient for a useful detection.
Ignoring the small losses in the lens, the surface brightness of the
image of a resolved object will be
![]() of that of the
object. This ratio is
of that of the
object. This ratio is
![]() for the example systems
considered here. For an observation of at least a few days,
significant detection will be obtained if the surface density of the
detected photons at the detector is comparable with with the
background event density (because of the small detector and narrow
bandwidth the telescope would be signal limited and not background
limited for shorter observations). Again using the expected Integral
SPI background, this requirement corresponds to an object with a
brightness temperature at 500 keV exceeding kT=8.1 keV (or 3.2 keV,
13.7 keV at 200, 847 keV). Athough one is far from the Rayleigh-Jeans
regime, this is in some circumstances still a useful yard-stick. A
black body with these temperatures and large enough to be resolved
would be have a luminosity orders of magnitude greater than any
conceivable astrophysical object, whatever distance scale is
considered. Thus observable resolved sources will be in practice be
optically thin and/or non-thermal.
for the example systems
considered here. For an observation of at least a few days,
significant detection will be obtained if the surface density of the
detected photons at the detector is comparable with with the
background event density (because of the small detector and narrow
bandwidth the telescope would be signal limited and not background
limited for shorter observations). Again using the expected Integral
SPI background, this requirement corresponds to an object with a
brightness temperature at 500 keV exceeding kT=8.1 keV (or 3.2 keV,
13.7 keV at 200, 847 keV). Athough one is far from the Rayleigh-Jeans
regime, this is in some circumstances still a useful yard-stick. A
black body with these temperatures and large enough to be resolved
would be have a luminosity orders of magnitude greater than any
conceivable astrophysical object, whatever distance scale is
considered. Thus observable resolved sources will be in practice be
optically thin and/or non-thermal.
The origin of the gamma-ray emission from Active Galactic Nucleii (AGNs) is poorly understood. Indeed the possibility of direct visualisation of this process to understand what is going on was one of the incentives for the studies presented here.
For Seyferts, it is generally accepted that the emission at a few hundred keV arises from Comptonisation of soft photons, but whether the Comptonising electrons are thermal or non-thermal, and to some extent the size of the region in which the Comptonisation occurs, is less certain. Several characteristic scales can be recognised:
Where jets are involved, the gamma-ray emitting region could be on the same size scale as the accretion disk or could be much larger.
Thus the resolution needed to study such systems is likely to be from one to a fews tens of Schwarzschild radii.
There have now been
estimates made of the central mass in numerous galaxies, by
reverbration mapping and other techniques. Figure 5 shows
how these estimates are distributed as a function of redshift z or,
in the case of nearby objects, of distance expressed as an equivalent
redshift z=d H0/c. The plot also shows the locus of points for
which 1 micro arcsecond angular resolution would correspond to one
Schwarzschild radius and to 100 Schwarzschild radii.
Clearly the objects for which estimates of the central mass are
available are in no way an unbiased sample, but Fig. 5 gives an indication of the region of parameter space
which is most likely to be most interesting.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{MS1333f5.eps} %
\end{figure}](/articles/aa/full/2001/32/aa1333/Timg73.gif) |
Figure 5:
Estimates from the literature of masses of the
central object in AGN and other galaxies. The estimates are
plotted as a function of a distance measure (see text). Solid
lines show the locii of points for which the Schwarzschild
radius has a particular angular scale and dashed lines show the
locii of objects which would be detectable if emitting at a
specific fraction of their Eddington limit. The 5 |
| Open with DEXTER | |
Few of the objects for which central mass estimates are available have been detected in the gamma-ray band. This probably results from a combination of selection effects and the limited sensitivity of current gamma-ray instruments. Present measurements provide little indication of how many AGN might be detectable with a factor of 1000 improvement in sensitivity. To help in addressing this question, Fig. 5 shows (as dashed lines) the locii of objects which would be just detectable if emitting gamma-rays at particular fractions f of their Eddington limits.
The mass of the black hole in Sgr A* is now thought to be
![]()
![]() and the angular equivalent of
and the angular equivalent of ![]() is thus 6
is thus 6 ![]() .
There has been continued interest in trying to take advantage of
the poximity of Sgr A* to enable sensitive probing of massive black
hole systems. Falcke et al. (2000), for example,
have discussed the feasibility of viewing the shadow of the black hole
using sub-millimeter VLBI observations, with 16
.
There has been continued interest in trying to take advantage of
the poximity of Sgr A* to enable sensitive probing of massive black
hole systems. Falcke et al. (2000), for example,
have discussed the feasibility of viewing the shadow of the black hole
using sub-millimeter VLBI observations, with 16 ![]() resolution, which
should be possible if VLBI measurements can be made at
resolution, which
should be possible if VLBI measurements can be made at
![]() mm. At first site Sgr A* appears to be an obvious target for a PFL
gamma-ray telescope.
mm. At first site Sgr A* appears to be an obvious target for a PFL
gamma-ray telescope.
Gamma-ray emission from Sgr A* is known to be weak, except possibly in
the Egret (GeV) band. The best models for the emission from Sgr A*
over wide range of energy are probably those based on Advection
Dominated Accretion Flows (ADAFs) (Lasota 1999).
The currently available ADAF models
(Narayan et al. 1998) are based on estimates of the X-ray flux from
Rosat. Of the range of parameters considered by Narayan
et al. recently available results from Chandra (Baganoff et al. 2001)
suggest that
the lowest luminosity combinations should be taken. However the
sensitivity at 200 keV shown in Table 2 is
such that even on this assumption a
![]() detection should
be obtained in 1 day.
detection should
be obtained in 1 day.
The most serious problem is that the source is likely to be be
over-resolved. If emission is from a disk of 10 ![]() ,
the signal will
be spread over 2000-3000 pixels and even sophisticated modelling
techniques would barely offer a simple detection. In these
circumstances there is some advantage in collecting data from a wider
bandwidth and accepting the resulting degradation in resolution, but
the factor gained is not large. It is probably better to consider
lower energies and a shorter focal length for objects so weak and so
"large''. Variations on the PFL technique which may help with this
problem will be discussed in Paper II but MAXIM will be well suited to
such observations.
,
the signal will
be spread over 2000-3000 pixels and even sophisticated modelling
techniques would barely offer a simple detection. In these
circumstances there is some advantage in collecting data from a wider
bandwidth and accepting the resulting degradation in resolution, but
the factor gained is not large. It is probably better to consider
lower energies and a shorter focal length for objects so weak and so
"large''. Variations on the PFL technique which may help with this
problem will be discussed in Paper II but MAXIM will be well suited to
such observations.
Even at X-ray wavelengths there may be surface brightness problems if
there is outflow. Ozel & Di Matteo (2001) have shown that
in low luminosity models, particularly those with high outflow
parameters, the low energy X-ray emission can extend to large radii,
even to
![]() at 1 keV.
at 1 keV.
Inverse Compton gamma-rays are expected to be produced as the
particles accelerated in the instabilities in winds around OB
supergiants interact with the stellar uv photons
(Chen & White 1991a,b). Such a star at 5 kpc would
have an apparent radius of more than 10 ![]() and the emission around it
could be directly imaged with a PFL telescope, allowing detailed study
of the instabilities and the acceleration processes.
and the emission around it
could be directly imaged with a PFL telescope, allowing detailed study
of the instabilities and the acceleration processes.
When massive hot stars are in close binary systems, the colliding
winds are likely to produce strong gamma-ray sources
(Eichler & Usov 1993; Pittard & Stevens 1997).
For binary periods of a few days, and source distances
of a few kpc, the angular scale of the system will be of the order of
10 ![]() ,
well matched to the capabilities of a PFL telescope.
,
well matched to the capabilities of a PFL telescope.
There is also the possibility of directly imaging the particle acceleration in the instabilities in the winds in, for example, OB supergiants.
With micro arcsecond resolution, stellar disks will be resolvable
even at large distances (a 1 ![]() main sequence star will submit 1
main sequence star will submit 1 ![]() at 4.6 kpc). High energy activity in stellar coronae could be
directly imaged.
at 4.6 kpc). High energy activity in stellar coronae could be
directly imaged.
The extremely good sensitivity resulting from the large collecting
area and flux concentrating capabilities of systemns using the
principles proposed here mean that they are of interest even where the
target may be unresolved. An example of this is in studying gamma-ray
emission from supernovae. The analysis of (Timms & Woosley 1997)
shows that a broad line sensitivity of
![]() s-1 cm-2 would be needed to detect the 847 keV 56Co line from at least one Type Ia supernova per year. This is
at the limit of the capabilities of the projected ATHENA mission and
an order of magnitude more sensitive than INTEGRAL. An instrument with
parameters of the 847 keV example in Table 2
would have a broad line sensitivity of
s-1 cm-2 would be needed to detect the 847 keV 56Co line from at least one Type Ia supernova per year. This is
at the limit of the capabilities of the projected ATHENA mission and
an order of magnitude more sensitive than INTEGRAL. An instrument with
parameters of the 847 keV example in Table 2
would have a broad line sensitivity of
![]() s-1 cm-2 (5
s-1 cm-2 (5![]() in 106 s) so it would be able to
detect gamma-ray emission out to z=0.1.
in 106 s) so it would be able to
detect gamma-ray emission out to z=0.1.
The line emission from Type II will be much narrower but much weaker;
SN1987a was only detected in gamma-rays because of its extreme
proximity. Nevertheless, the narrow line sensitivity of the
instruments discussed here (
![]()
![]() s-1 cm-2) would, on the basis of the calculations of Timms and
Woosely, allow the detection of most Type II supernovae within 70 Mpc.
s-1 cm-2) would, on the basis of the calculations of Timms and
Woosely, allow the detection of most Type II supernovae within 70 Mpc.
Even the use of the imaging properties of the telescope to study the spread of
the ejecta from a Type Ia supernova is conceivable for events
within about 50 Mpc (![]() per year), which attain diameters of
several micro arcseconds in a few months and for which the
per year), which attain diameters of
several micro arcseconds in a few months and for which the
![]() signal would allow the imaging properties to be used
to good advantage.
signal would allow the imaging properties to be used
to good advantage.
An obvious question is whether a similar approach
could be adopted at X-ray energies.
For a lens of similar diameter, the diffraction limited
angular resolution will be ![]() times worse,
but for some applications this might be appropriate.
These issues and ways in which the focal length may
be reduced or the bandwidth widened will be discussed in Paper II.
times worse,
but for some applications this might be appropriate.
These issues and ways in which the focal length may
be reduced or the bandwidth widened will be discussed in Paper II.
Moving up in energy to the gamma-ray band apparently simplifies a number of problems in the search for sub micro arcsecond resolution. The proposed system is very long (millions of km) but the fabrication of the optics would be almost trivial and there is no need for critical alignment of the individual components. Only the pointing of the telescope as a whole is critical and it is suggested that the requirements of the pointing determination system are well matched to techniques using radio measurements, while the associated active control seems to be possible with existing technology.
Compared with proposals for achieving micro-arcsecond resolution at X-ray energies using interferometry, the approach suggested here has the disadvantage that it only operates over a narrow energy band at any one time. On the other hand, the optics are simple and are capable of concentrating the flux from a very large aperture onto a detector area 104-107 times smaller in area and so the sensitivity can be extremely good despite the small bandwidth. Furthermore, in the gamma-ray band micro arcsecond resolution can be obtained with modest diameter. For those objects which are gamma-ray sources as well as X-ray sources, the approach seems to be very promising.
Acknowledgements
The author is grateful for helpful comments and suggestions from J. Bar-Sever (JPL), J. Brown (University of Glasgow), N. Gehrels (GSFC) and colleagues at both the University of Birmingham and CESR, Toulouse.