A&A 375, 638-642 (2001)
DOI: 10.1051/0004-6361:20010888
Radio bursts with rapid frequency variations - Lace bursts
M. Karlický1 - M. Bárta1 - K. Jiricka1 - H. Mészárosová1 - H. S. Sawant2 - F. C. R. Fernandes2 - J. R. Cecatto2
1 -
Astronomical Institute of the Academy of Sciences of the Czech Republic,
25165 Ondrejov, Czech Republic
2 -
Instituto Nacional de Pesquisas Espaciaias, C.P. 515,
12201-970 Sao Jose dos Campos, SP, Brazil
Received 19 March 2001 / Accepted 8 June 2001
Abstract
The Ondrejov radiospectrograph operating in the 0.8-2.0 GHz
frequency range recorded in recent years (1998-2000), three (August 10, 1998;
August 17, 1999; June 27, 2000) unique bursts with rapid frequency variations
(lace bursts) lasting for several minutes. On August 17, 1999, the same burst
was recorded simultaneously by the Brazilian Solar Spectroscope in the 1.0-2.5 GHz frequency range. The frequency variations of these bursts in four time
intervals were analyzed by the Fourier method and power-law spectra with
power-law indices close to -2 were found. The Fourier spectra show the presence
of frequency variations in the 0.01-3.0 Hz interval which indicate fast changes
of plasma parameters in the radio source. Due to the similarities in the line
features of these bursts with zebra pattern lines, a model similar to that of
the zebra pattern was suggested. The model radio spectra, computed using this
model with a turbulent state of the solar flare atmosphere, are similar to
those observed by the radiospectrographs.
Key words: Sun: activity - Sun: flares - Sun: radio radiation
The radio bursts above 1 GHz were considered as featureless bursts (without any
fine structures) generated by the gyro-synchrotron emission mechanism (Kundu
1965; Krüger 1979). But the new generation of radiospectrographs with higher
time resolutions changed this conception and the various observed fine
structures are now interpreted as being due to the plasma emission mechanism
(e.g. review of Bastian et al. 1998). Moreover, the X-ray observations indicate
flare processes at plasma densities of 10
9 - 1011 cm-3 (Ohyama
& Shibata 1998). Therefore the observations in the decimetric range of
wavelengths become very important, especially because of the expected radio
emission from the flare primary energy-release sites.
Examples of bursts with rapid frequency variations (because of their
appearances we call them also "lace bursts'' - see Jiricka et al. 2001)
in the range above 1 GHz were shown in the catalogue of the Brazilian Solar
Spectroscope (BSS) (Fernandes et al. 2001). Similar fine structures can be
recognized in Figs. 26 and 29 of the 1-3 GHz catalogue of Isliker & Benz
(1994). From 1992 to 2000 the radiospectrograph at the Ondrejov Observatory
(Jiricka et al. 1993) recorded 681 radio events in the frequency range
of 0.8-2.0 GHz exhibiting various fine structures. In three cases only
(August 10, 1998; August 17, 1999; and June 27, 2000), radio bursts with rapid
frequency variations (the changes are of the order of fractions of seconds)
were observed. In one case (August 17, 1999) the burst was observed also by the
BSS, but the others could not be confirmed due to lack of observations on the
respective dates. In the following, these unique bursts are presented and
analyzed by the Fourier method. Finally, a phenomenological model is suggested
and their artificial spectra computed.
An example of a burst with rapid frequency variations (lace burst), observed on
August 17, 1999, is shown in Fig. 1. The observation made by the Ondrejov
radiospectrograph was confirmed by the Brazilian Solar Spectroscope (Sawant
et al. 2001), shown at the bottom of Fig. 1. The burst sometimes appears as a very
narrowband (about 50 MHz) line with strongly variable frequency and intensity
(see e.g. Fig. 1, bottom part, 16:51:06-16:51:12 UT). These lines are
sometimes, especially at their low-frequency ends, mutually superimposed and
accompanied by continua, forming thus a lace burst in the radio spectrum. The
frequencies and intensities change in fractions of second - see Fig. 2, where
the time and frequency profiles of one burst line are shown (compare with the
radio spectrum - Fig. 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1292f1.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg1.gif) |
Figure 1:
The burst with rapid frequency variations observed on August 17, 1999
at 16:50:50-16:51:50 UT by the 0.8-2.0 GHz Ondrejov radiospectrograph (top)
and for comparison the spectrum observed at the same time by the Brazilian
Solar Spectroscope (bottom). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1292f2.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg2.gif) |
Figure 2:
The time and frequency profiles on 1.11 GHz and 16:51:07 UT obtained
by the Brazilian Solar Spectroscope (the background flux density of 110 SFU is
subtracted). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1292f3.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg3.gif) |
Figure 3:
The burst with rapid frequency variations observed on August 17, 1999
at 15:07-15:09 UT by the 0.8-2.0 GHz Ondrejov radiospectrograph (top) and
the corresponding high-frequency burst boundary outline (bottom). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1292f4.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg4.gif) |
Figure 4:
The time and frequency profiles on 1.6 GHz and 15:08:15.5 UT for the
burst from Fig. 3 showing the complex structure of the burst. |
| Open with DEXTER |
In other cases, especially in those lasting longer, these bursts are even more
complex, with lines and continua mutually superimposed, giving thus the
impression that they correspond to different radio sources (Fig. 3, upper
part). These complex structures can also be seen in Fig. 4, where the time (1
minute interval) and frequency profiles of the radio spectrum (see also Fig. 3,
upper part) are depicted. For example, the simple peak at 15:08:15.5 UT lasts
about 1.3 s and its bandwidth is about 140 MHz. On the other hand, the time
profiles of other peaks are more complex, e.g. at 15:08:00-15:08:04 UT.
In all the three observed events these bursts are part of long lasting
pulsations in the 0.8-2 GHz frequency range. The flare activity associated with
these bursts is summarized in Table 1.
Table 1:
The basic characteristics of flares during which the bursts with rapid
frequency variations were observed (all times are in UT).
| |
|
Aug. 10, 1998 |
Aug. 17, 1999 |
Jun. 27, 2000 |
| |
Start |
8:35 |
14:28 |
12:40 |
| GOES |
Max |
8:40 |
16:02 |
12:55 |
| |
End |
8:42 |
17:54 |
13:21 |
| |
Class |
B7.6 |
C5.9 |
C9.3 |
| |
Start |
8:35 |
15:05 |
12:49 |
| |
Max |
8:40 |
15:22 |
12:54 |
| H-alpha |
End |
8:54 |
16:34 |
13:42 |
| |
Importance |
SF |
SF |
2N |
| |
Position |
S23W18 |
N24E37 |
S17E48 |
| |
NOAA AR |
8293 |
8668 |
9062 |
| radio |
Start |
8:45 |
14:47 |
12:52 |
| (1-2 GHz) |
End |
9:19 |
17:04 |
13:04 |
From the three observed bursts, four long-lasting (several minutes) time
intervals (see Table 2) were selected for analysis. The example of one selected
part (August 17, 1999, 15:07-15:09 UT) is shown in Fig. 3, where in its bottom
part the line corresponding to the high-frequency boundary of the burst, formed
by several lace lines, is drawn. This line shows frequency variations which are
then analyzed by the Fourier method. The results for the four selected
intervals from Table 2 are shown in Fig. 5. For comparison, straight lines
expressing slopes corresponding to the best fitted power-law indices (see Table 2) are added. All the found power-law indices are close to -2. Moreover, the
Fourier spectra show the presence of frequency variations in the interval of
about 0.01-3.0 Hz. We suppose that these variations correspond to changes of
plasma parameters in the radio source.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1292f5.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg9.gif) |
Figure 5:
Fourier spectra of the four selected intervals (see Table 2) from the
bursts with rapid frequency variations. |
| Open with DEXTER |
Because the studied lace bursts and the zebra pattern lines show similarities,
we use for the interpretation of lace bursts a concept similar to that used for
zebra patterns (e.g. Zheleznyakov & Zlotnik 1975; Ledenev et al. 2001).
However, here we suggest that the radio emission is generated in plasma with
rapidly changing plasma parameters (density or/and magnetic field). Thus we
assume that the lines of lace bursts are generated in the solar atmosphere at
positions where the following resonance condition is fulfilled:
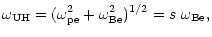 |
|
|
(1) |
where
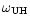 ,
,
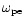 ,
and
,
and
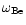 are the upper
hybrid, electron plasma and cyclotron frequencies, and s is the integer
harmonic number. The source of the energy can be the loss-cone distribution
function of superthermal electrons (Zheleznyakov & Zlotnik 1975) or an
electron beam anisotropic in temperature with
are the upper
hybrid, electron plasma and cyclotron frequencies, and s is the integer
harmonic number. The source of the energy can be the loss-cone distribution
function of superthermal electrons (Zheleznyakov & Zlotnik 1975) or an
electron beam anisotropic in temperature with
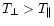 ,
where
,
where 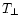 and
and
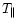 are the temperatures of energetic
electrons across and along the magnetic field, respectively (Mikhailovsky 1975;
Ledenev et al. 2001). The anisotropic temperature beam can be formed by the
expansion of the hot plasma into the cold plasma along magnetic field lines.
The generated upper hybrid waves are then transformed into observable
electromagnetic waves. The accompanying continua can be a superposition of many
weak lace lines generated in the neighboring flux tubes or they can be
generated by some additional instabilities in the disturbed flare plasma.
are the temperatures of energetic
electrons across and along the magnetic field, respectively (Mikhailovsky 1975;
Ledenev et al. 2001). The anisotropic temperature beam can be formed by the
expansion of the hot plasma into the cold plasma along magnetic field lines.
The generated upper hybrid waves are then transformed into observable
electromagnetic waves. The accompanying continua can be a superposition of many
weak lace lines generated in the neighboring flux tubes or they can be
generated by some additional instabilities in the disturbed flare plasma.
Based on this idea, we built the following phenomenological model: Let us
suppose that the instability leading to the radio emission can be described as
two oscillators with frequencies
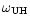 and
and
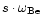 ,
coupled
by positive feedback. Then, the electric field
,
coupled
by positive feedback. Then, the electric field 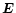 of the upper hybrid
oscillations can be written as
of the upper hybrid
oscillations can be written as
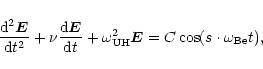 |
(2) |
where the coefficient C expresses the measure of the coupling
between the oscillators and 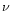 is the damping of the upper hybrid waves.
Solving this equation for
is the damping of the upper hybrid waves.
Solving this equation for 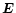 in the form
in the form
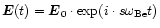 ,
the resulting radio flux F can be written as
,
the resulting radio flux F can be written as
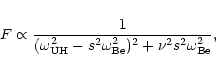 |
(3) |
where it is assumed that the radio flux is proportional to the square
of modulus of the complex amplitude 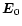 of the upper hybrid waves. From
this formula, it follows that the radio flux has a maximum at the place where
the resonance condition (1) is fulfilled and strongly decreases
elsewhere.
of the upper hybrid waves. From
this formula, it follows that the radio flux has a maximum at the place where
the resonance condition (1) is fulfilled and strongly decreases
elsewhere.
The processes are considered in a 1-D source model with the stationary mean
electron density decreasing slowly in space as
 |
(4) |
and the magnetic field in a solitary magnetic flux tube as
 |
(5) |
Here the parameters L and b with dimensions of length represent
typical scales on which the magnetic field B and the electron density nvary. Then, on this stationary mean density profile, chaotically varying (in
space and time) density and magnetic field perturbations are superimposed.
Perturbed frequencies
 and
and
 are computed at each
point x of the source at fixed time t and using the formula (3)
contributions of the radio flux in relative units are also determined.
Contributions to the flux from each element of the source are divided into
frequency channels according to radiation frequency
are computed at each
point x of the source at fixed time t and using the formula (3)
contributions of the radio flux in relative units are also determined.
Contributions to the flux from each element of the source are divided into
frequency channels according to radiation frequency 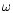 .
This frequency is
given by the forcing frequency, i.e.
.
This frequency is
given by the forcing frequency, i.e.
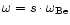 .
Contributions
of the radio flux belonging to an appropriate channel are integrated over the
source length. Thus, the spectrum at fixed time is obtained. Using this
algorithm repeatedly for subsequent times, at which the plasma parameters are
changed, the whole artificial dynamic spectrum can be computed.
.
Contributions
of the radio flux belonging to an appropriate channel are integrated over the
source length. Thus, the spectrum at fixed time is obtained. Using this
algorithm repeatedly for subsequent times, at which the plasma parameters are
changed, the whole artificial dynamic spectrum can be computed.
One example of such a spectrum is shown in Fig. 6, where the following
parameters for the initial flare atmosphere are used:
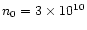 cm-3, B0 = 200 G,
cm-3, B0 = 200 G,
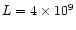 cm,
cm,
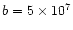 cm. The radio emission is considered on the s=4 harmonic. The
magnetic field variations are set to zero. On the other hand, the density
variations have the following spatial characteristics: a) the spectrum is a
power-law function with the power-law index -2 for the wave numbers greater
than
cm. The radio emission is considered on the s=4 harmonic. The
magnetic field variations are set to zero. On the other hand, the density
variations have the following spatial characteristics: a) the spectrum is a
power-law function with the power-law index -2 for the wave numbers greater
than
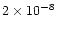 cm-1, b) the rms of the density perturbation is
0.1 n0, and c) the phases are random. In the flare atmosphere, these density
variations propagate with the speed of sound corresponding to the temperature
cm-1, b) the rms of the density perturbation is
0.1 n0, and c) the phases are random. In the flare atmosphere, these density
variations propagate with the speed of sound corresponding to the temperature
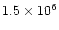 K. Comparing this modelled radio spectrum with the lace
burst of August 17, 1999 at 16:51:06-16:51:12 UT (Fig. 1, bottom part),
similarities between the two spectra are evident.
K. Comparing this modelled radio spectrum with the lace
burst of August 17, 1999 at 16:51:06-16:51:12 UT (Fig. 1, bottom part),
similarities between the two spectra are evident.
![\begin{figure}
\par\includegraphics[width=8.5cm,height=7cm,clip]{1292f6.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg33.gif) |
Figure 6:
The modelled 1-2 GHz spectrum of the burst with rapid frequency
variation. |
| Open with DEXTER |
The bursts with rapid frequency variations (lace bursts) are very rare. During
the nine years of observations (1992-2000), among the 681 events observed by
the 0.8-2.0 GHz Ondrejov radiospectrograph, only three cases of such bursts
were recorded. In longer events these bursts appear to be mutually
superimposed, forming complex structures with a relatively well defined
high-frequency boundary. Time variations of these boundaries have been analyzed
by the Fourier method and power-law spectra with power-law indices close to -2
were found. Moreover, the Fourier spectra show the presence of frequency
variations in the interval of 0.01-3.0 Hz. We think that these variations
correspond to changes in the plasma parameters within the radio source.
A model of lace bursts, similar to that of zebra patterns, was suggested. The
most important aspect of this model is that the flare plasma in the radio
source is considered to be in a turbulent state. Using this model, the
artificial spectrum, similar to real ones observed by spectrographs, was
computed. This model can explain these bursts, especially their line features.
Moreover, we think that the different lace lines can be generated in different
flux tubes. The accompanying continua can be a superposition of many weak lace
lines generated in the neighboring flux tubes or they can be generated by some
additional instabilities in the disturbed flare plasma.
Based on the presented model, the lace bursts belong to the same group of fine
structures as zebra patterns. The difference is that these bursts are generated
in turbulent plasma. A possible source of the turbulence can be the plasma
outflows from the magnetic field reconnection. The reconnection is also a
probable source of accelerated electrons forming an unstable distribution
function. We think that lace bursts provide a unique opportunity to study the
flare turbulence.
Acknowledgements
M. Karlický wants to express thanks to FAPESP authorities for supporting his
visit at INPE (P.N. 01/00144-5). F. C. R. Fernandes is grateful to the Brazilian
Agency FAPESP for support under Proc. 99/10529-0. This work was also supported
by the grants S1003006 and A3003003 of the Academy of Sciences of the Czech
Republic and the grant 205/00/1727 of the Grant Agency of the Czech Republic
under the key project K2043105. The authors also thank the referee for
suggestions which led to significant improvement of the paper.
- Bastian, T., Benz, A. O., & Gary, D. E. 1998, ARA&A, 36, 131
In the text
NASA ADS
- Fernandes, F. C. R., Sawant, H. S., Vats, H. O., et al. 2001, ApJL, submitted
In the text
- Isliker, H., & Benz, A. O. 1994, A&AS, 104, 145
In the text
NASA ADS
- Jiricka, K., Karlický, M., Kepka, O., & Tlamicha, A.
1993, Solar Phys., 147, 203
NASA ADS
- Jiricka, K., Karlický, M., Mészárosová, H.,
& Snízek, V. 2001, A&A, in press
In the text
- Krüger, A. 1979, Introduction to Solar Radio Astronomy and
Radio Physics (D. Reidel Publ. Comp., Dordrecht, Holland)
In the text
- Kundu, M. R. 1965, Solar Radio Astronomy (Interscience Publ.,
New York)
In the text
- Ledenev, V., Karlický, M., Yan, Y., & Fu, Q. 2001, Solar Phys.,
in press
In the text
- Mikhailovsky, A. B. 1975, Theory of Plasma Instabilities, vol. I,
(Nauka, Moscow), 149 (in Russian)
In the text
- Ohyama, M., & Shibata, K. 1998, ApJ, 499, 934
In the text
NASA ADS
- Sawant, H. S., Subramanian, K. R., Faria, C., et al. 2001, Solar
Phys., in press
In the text
- Zheleznyakov, V. V., & Zlotnik, E., Ya. 1975, Solar Phys., 44, 461
In the text
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1292f1.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg1.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1292f4.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg4.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1292f5.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg9.gif)
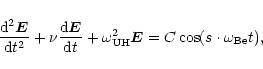
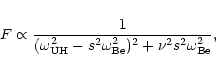
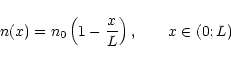
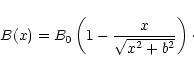
![\begin{figure}
\par\includegraphics[width=8.5cm,height=7cm,clip]{1292f6.eps}\par
\par\end{figure}](/articles/aa/full/2001/32/aa1292/Timg33.gif)