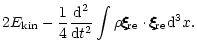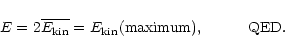A&A 375, 680-690 (2001)
DOI: 10.1051/0004-6361:20010866
The r-modes of rotating fluids
Y. Sobouti1,2 -
V. Rezania1,3
1 - Institute for Advanced Studies in Basic Sciences,
Gava Zang, Zanjan 45195, Iran
2 -
Center for Theoretical Physics and Mathematics,
AEOI, PO Box 11345-8486, Tehran, Iran
3 -
Department of Physics, University of Alberta,
Edmonton AB, T6G 2J1 Canada![[*]](/icons/foot_motif.gif)
Received 1 February 2001 / Accepted 19 June 2001
Abstract
An analysis of the toroidal modes of a rotating fluid, by means of
the differential equations of motion, is not readily
tractable. A matrix representation of the equations on a
suitable basis, however, simplifies the problem considerably and
reveals many of its intricacies. Let 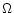 be the
angular velocity of the star and (
be the
angular velocity of the star and (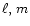 )
be the two
integers that specify a spherical harmonic function. One readily
finds the followings:
1) Because of the axial symmetry of equations of motion, all
modes, including the toroidal ones, are designated by a definite
azimuthal number m.
2) The analysis of equations of motion in the lowest order of
)
be the two
integers that specify a spherical harmonic function. One readily
finds the followings:
1) Because of the axial symmetry of equations of motion, all
modes, including the toroidal ones, are designated by a definite
azimuthal number m.
2) The analysis of equations of motion in the lowest order of
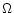 shows that Coriolis
forces turn the neutral toroidal
motions of (
shows that Coriolis
forces turn the neutral toroidal
motions of (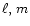 )
designation of the non-rotating fluid into
a sequence of oscillatory modes with
frequencies
)
designation of the non-rotating fluid into
a sequence of oscillatory modes with
frequencies
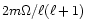 .
This much is common knowledge. One can say more, however.
a) Under the Coriolis forces,
the eigendisplacement vectors remain purely toroidal and carry the
identification (
.
This much is common knowledge. One can say more, however.
a) Under the Coriolis forces,
the eigendisplacement vectors remain purely toroidal and carry the
identification (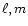 ). They remain decoupled from other toroidal
or poloidal motions belonging to different
). They remain decoupled from other toroidal
or poloidal motions belonging to different 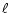 's.
b) The eigenfrequencies quoted above are still degenerate, as they carry no
reference to a radial wave number.
As a result the eigendisplacement vectors, as far as their radial dependencies
go, remain indeterminate.
3) The analysis of the equation of motion in the next higher order
of
's.
b) The eigenfrequencies quoted above are still degenerate, as they carry no
reference to a radial wave number.
As a result the eigendisplacement vectors, as far as their radial dependencies
go, remain indeterminate.
3) The analysis of the equation of motion in the next higher order
of 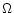 reveals that the forces
arising from asphericity of the fluid and the square of the
Coriolis terms (in some sense) remove the radial degeneracy. The
eigenfrequencies now carry three identifications (
reveals that the forces
arising from asphericity of the fluid and the square of the
Coriolis terms (in some sense) remove the radial degeneracy. The
eigenfrequencies now carry three identifications (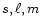 ),
say, of which s is a radial eigennumber. The eigendisplacement
vectors become well determined. They still remain zero order and purely
toroidal motions with a single (
),
say, of which s is a radial eigennumber. The eigendisplacement
vectors become well determined. They still remain zero order and purely
toroidal motions with a single (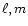 )
designation.
4) Two toroidal modes belonging to
)
designation.
4) Two toroidal modes belonging to 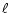 and
and 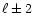 get coupled only at the
get coupled only at the
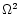 order.
5) A toroidal and a poloidal mode belonging to
order.
5) A toroidal and a poloidal mode belonging to 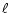 and
and 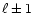 ,
respectively, get coupled but again at the
,
respectively, get coupled but again at the 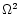 order.
Mass and mass-current multipole moments of the modes that are
responsible for the gravitational radiation, and bulk and shear
viscosities that tend to damp the modes, are worked out in much
detail.
order.
Mass and mass-current multipole moments of the modes that are
responsible for the gravitational radiation, and bulk and shear
viscosities that tend to damp the modes, are worked out in much
detail.
Key words: stars: neutron - stars: oscillations - stars: rotation
1 Introduction
Recent years have seen a surge of interest in the small
oscillations of rotating fluid masses. The reason for the
excitement is the advocation by relativists that in rapidly
rotating neutron stars, the gravitational radiation drives the
r-modes to become unstable, and while spinning down the star, may itself
be amenable to detection (see the recent review by Andersson & Kokkotas 2000).
Nevertheless, the oscillations of
rotating objects is an old problem. In the past few decades it
has been studied by many investigators and from various points of
view. Complexity of the problem arises from the fact that a fluid
can support three distinct types of motions, derived from, say, a
scalar potential, from a toroidal vector potential and from a
poloidal vector potential. These are the motions associated
predominantly with the familiar p-, g- and toroidal-
oscillations of the fluid. Each of these motions, in turn, can be
given an expansion in terms of vector spherical harmonics. The
modes of an actual star are a mixture of the three types mentioned
above and of the different spherical harmonic components. Sorting
out this mixture and classifying the modes into well-defined
sequences has not been an easy task. Moreover, and more often than
not, it has not been realized that g-modes of spherically
asymmetric configurations are not apt for perturbation analysis
as the low frequency tail of their spectrum
is a fragile structure. It is driven by minute buoyancy forces and
can be completely wiped out by almost any perturbing agent, such as
Coriolis, asphericity and magnetic forces.
Here we show that a matrix representation of the equations of
motions provides a set of algebraic equations that are much easier
to cope with than their differential counterparts. In Sect. 2 we
write down the equilibrium structure and the linearized equations
of motion of a rotating star. In Sect. 3 we introduce the matrix
representation of these equations. In Sects. 4 and 5 we sort out
the toroidal-poloidal components and spherical harmonic
constituents of the matrices. In Sects. 6 and 7 we give an
ordering of the various components in powers of 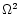 and
sort out the equations of motion in various orders of magnitude.
References and bibliographical notes relating to mode calculations
in rotating stars are collected in Sect. 7.4. In Sect. 8 we
discuss the numerical results. A rotating neutron star can be
slowed down by gravitational radiation through the mass and
mass-current multipole moments of the modes. The modes, in turn,
can be damped out by bulk and shear viscosities present in the
star. The time scales of relevant damping mechanisms are analyzed
in Sect. 9. Calculations of matrix elements and presentation of
appropriate basis sets are given in the
appendices.
and
sort out the equations of motion in various orders of magnitude.
References and bibliographical notes relating to mode calculations
in rotating stars are collected in Sect. 7.4. In Sect. 8 we
discuss the numerical results. A rotating neutron star can be
slowed down by gravitational radiation through the mass and
mass-current multipole moments of the modes. The modes, in turn,
can be damped out by bulk and shear viscosities present in the
star. The time scales of relevant damping mechanisms are analyzed
in Sect. 9. Calculations of matrix elements and presentation of
appropriate basis sets are given in the
appendices.
2 Review of rotating fluids
2.1 Equilibrium configuration
Let
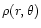 ,
,
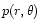 and
and
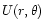 be the
density, the pressure and the gravitational potential of a star
rotating with the constant angular frequency
be the
density, the pressure and the gravitational potential of a star
rotating with the constant angular frequency 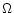 about the
z-axis. The equilibrium condition is
about the
z-axis. The equilibrium condition is
![\begin{displaymath}\nabla\hspace{-.305cm}\nabla\hspace{-.305cm}\nabla p+\rho \na...
...cm}\nabla
\left[U-\frac{1}{2}\Omega^2r^2\cos^2\theta\right]=0. \end{displaymath}](/articles/aa/full/2001/32/aa1087/img34.gif) |
(1) |
For slow rotations,
one obtains
![\begin{displaymath}
\rho= \rho_0(r)+\Omega^2
[\rho_{20}(r)+\rho_{22}(r)P_2(\cos\theta)], \end{displaymath}](/articles/aa/full/2001/32/aa1087/img35.gif) |
(2a) |
where
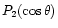 is a Legendre polynomial. Similar expansions
exists for p and U. For a barotropic structure,
is a Legendre polynomial. Similar expansions
exists for p and U. For a barotropic structure,
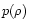 ,
one will have
,
one will have
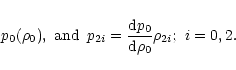 |
(2b) |
Furthermore, Poisson's equation will give
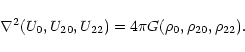 |
(2c) |
A thorough study of the structure of rotating polytropes was given
as early as 1933 by Chandrasekhar. Further numerical
values of 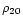 and
and 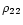 may be found in
Chandrasekhar & Lebovitz (1962).
may be found in
Chandrasekhar & Lebovitz (1962).
2.2 Linear perturbations
Let a mass element of the rotating fluid at position 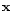 be
displaced by an amount
be
displaced by an amount
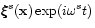 ,
where, for the
moment, s is the collection of all indices that specify the
displacement in question. This may include its spherical
harmonic specifications, its radial node number, and/or its
poloidal and toroidal nature. The Eulerian change in
,
where, for the
moment, s is the collection of all indices that specify the
displacement in question. This may include its spherical
harmonic specifications, its radial node number, and/or its
poloidal and toroidal nature. The Eulerian change in 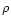 ,
and U resulting from this displacement, will be
,
and U resulting from this displacement, will be
On the assumption that the displacement takes place adiabatically
and the Lagrangian change in pressure is
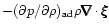 ,
one obtains
,
one obtains
where
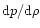 is the
barotropic derivative of the equilibrium structure. The linearized Euler equation governing
the evolution of
is the
barotropic derivative of the equilibrium structure. The linearized Euler equation governing
the evolution of
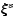 now becomes
now becomes
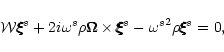 |
(4) |
where the linear operator 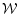 is given by
is given by
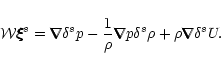 |
(4a) |
3 Matrix form of equations of motion
Equation (4) in its integro-differential form is highly
complicated. We convert it into a
set of linear algebraic equations by expanding
 in terms
of a complete set of known basis vectors,
in terms
of a complete set of known basis vectors,
 .
Thus
.
Thus
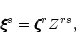 |
(5) |
where Zrs are the expansion coefficients and, as yet, are unknown.
Associated with this, we define the following matrices
| Srs |
= |
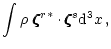 |
(6a) |
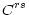 |
= |
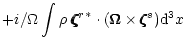 |
|
| |
= |
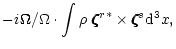 |
(6b) |
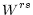 |
= |
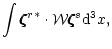 |
(6c) |
where the integration is over the volume
of the star. All these matrices are Hermitian.
Furthermore, let
Z=[Zrs] be the matrix of the expansion coefficients, and
![$\omega=[\omega^s\delta^{rs}]$](/articles/aa/full/2001/32/aa1087/img66.gif) be the diagonal matrix of the eigenvalues.
Substituting Eq. (5) in Eq. (4), multiplying the
resulting equation from left by
be the diagonal matrix of the eigenvalues.
Substituting Eq. (5) in Eq. (4), multiplying the
resulting equation from left by
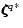 ,
say, and
integrating over the volume of the star gives the (
,
say, and
integrating over the volume of the star gives the (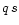 )
element
of the following matrix equation
)
element
of the following matrix equation
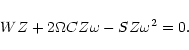 |
(7) |
It is important to note that all
factors in Eq. (7) are matrices and should not be
commuted with each other without due care. Solutions of Eq.
(7) are equivalent to those of Eq. (4). The
eigenfrequencies 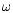 in both equations are the same, and once
the eigenmatrix Z is known, the set of eigendisplacement vectors
in both equations are the same, and once
the eigenmatrix Z is known, the set of eigendisplacement vectors
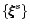 can be constructed by Eq. (5).
can be constructed by Eq. (5).
4 Partitioning into poloidal and toroidal fields
The basis set
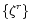 can be divided into two poloidal and
toroidal subsets,
can be divided into two poloidal and
toroidal subsets,
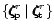 .
The set of the
eigenmodes,
.
The set of the
eigenmodes,
![$[\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi^s]$](/articles/aa/full/2001/32/aa1087/img74.gif) ,
of Eq. (4) in the absence of
rotation also has such exact partitioning. Its poloidal subset
comprises the commonly-known g- and p-modes of the fluid. The
toroidal subset includes those displacements of the fluid
which do not perturb the equilibrium state of the star. For
them,
,
of Eq. (4) in the absence of
rotation also has such exact partitioning. Its poloidal subset
comprises the commonly-known g- and p-modes of the fluid. The
toroidal subset includes those displacements of the fluid
which do not perturb the equilibrium state of the star. For
them, 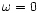 .
For the sake of mathematical completeness one
might say that
.
For the sake of mathematical completeness one
might say that 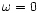 is a degenerate eigenfrequency
and the set of all toroidal motions
is a degenerate eigenfrequency
and the set of all toroidal motions
![$[\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi^s_{\rm t}]$](/articles/aa/full/2001/32/aa1087/img76.gif) are its eigendisplacement
vectors.
are its eigendisplacement
vectors.
In the presence of rotation, two things happen. a) Each known
poloidal mode of the fluid acquires a small toroidal component. b) The neutral
toroidal displacements organize themselves into a new
sequence of modes and the degeneracy of 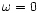 gets removed.
Nonetheless, one may still partition the eigensets
gets removed.
Nonetheless, one may still partition the eigensets
![$[\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi^s]$](/articles/aa/full/2001/32/aa1087/img74.gif) as
as
![$[\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi^s_{\rm p}\mid \xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi^s_{\rm t}]$](/articles/aa/full/2001/32/aa1087/img77.gif) remembering that the subsets
remembering that the subsets
![$[\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi^s_{\rm p}]$](/articles/aa/full/2001/32/aa1087/img78.gif) and
and
![$[\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi^s_{\rm t}]$](/articles/aa/full/2001/32/aa1087/img76.gif) ,
unlike the no rotation case, are only
predominantly poloidal and toroidal, respectively. In view of
these considerations, Eq. (5) partitions as
,
unlike the no rotation case, are only
predominantly poloidal and toroidal, respectively. In view of
these considerations, Eq. (5) partitions as
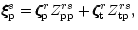 |
|
|
(8a) |
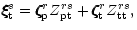 |
|
|
(8b) |
or in its matrix form and suppressing the superscripts one
gets
![\begin{displaymath}[\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi_{\rm p}\mid\xi\hspac...
..._{\rm pt}\\
Z_{\rm tp}&Z_{\rm tt}
\end{array}\right]\!\cdot
\end{displaymath}](/articles/aa/full/2001/32/aa1087/img81.gif) |
(8c) |
Accordingly, all matrices in Eqs. (6) partition into
four pp, pt, tp, and tt blocks. For example, an element
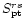 in the pt block is obtained by inserting the two
vector
in the pt block is obtained by inserting the two
vector
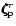 and
and
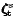 in Eq. (6a) and
carrying out the integration.
in Eq. (6a) and
carrying out the integration.
We are not interested in the
poloidal modes of Eq. (8a). They are discussed in ample
detail and in a much wider scope than that of the present work
in Sobouti (1980). Here we concentrate on the
toroidal modes of Eq. (8b). The required information
comes from multiplying the block partitioned forms of all the
matrices in Eq. (7) and extracting the tt and pt
blocks of it. Thus
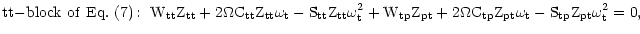 |
|
|
(9a) |
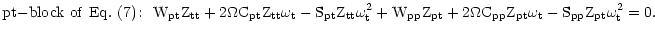 |
|
|
(9b) |
5 Partitioning by spherical harmonic numbers
For a toroidal basis vector we will adopt the following spherical
harmonic form
For a
poloidal vector we will take
![\begin{displaymath}
\zeta\hspace{-.19cm}\zeta\hspace{-.19cm}\zeta^{r\ell}_{\rm p...
...hi^{r\ell}(r)\frac{im}{\sin\vartheta}Y_{\ell}^m
\right]\!\cdot \end{displaymath}](/articles/aa/full/2001/32/aa1087/img94.gif) |
(10b) |
An appropriate ansatz for the radial function 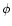 ,
,
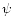 ,
and
,
and 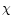 are given
in Appendix B. The toroidal vector (10a) is obviously derived
from a radial vector potential. The poloidal vector (10b) is actually
the sum of two vectors, one derived
from a scalar potential and the other derived from a toroidal
vector potential. See Sobouti (1981).
are given
in Appendix B. The toroidal vector (10a) is obviously derived
from a radial vector potential. The poloidal vector (10b) is actually
the sum of two vectors, one derived
from a scalar potential and the other derived from a toroidal
vector potential. See Sobouti (1981).
In Eq. (10) we have suppressed the harmonic index m from
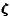 's because
a slowly rotating star is axially symmetric. Vectors with different
values of m are not mutually coupled. Vectors belonging to the
same m, but different
's because
a slowly rotating star is axially symmetric. Vectors with different
values of m are not mutually coupled. Vectors belonging to the
same m, but different 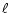 's, however, are coupled. This
feature entails a further partitioning of the basis sets into
their harmonic subsets,
's, however, are coupled. This
feature entails a further partitioning of the basis sets into
their harmonic subsets,
![$[\zeta\hspace{-.19cm}\zeta\hspace{-.19cm}\zeta^{\ell}_{\rm p},\, \ell=0,1,2,\cdots\,]$](/articles/aa/full/2001/32/aa1087/img99.gif) and
and
![$[\zeta\hspace{-.19cm}\zeta\hspace{-.19cm}\zeta^{\ell}_{\rm t},\,\ell=1,2,\cdots\,]$](/articles/aa/full/2001/32/aa1087/img100.gif) .
Correspondingly, each of the matrices in Eqs. (9) partitions into blocks, designated by a pair of
harmonic numbers
.
Correspondingly, each of the matrices in Eqs. (9) partitions into blocks, designated by a pair of
harmonic numbers 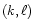 ,
say. For example, the rs element of
,
say. For example, the rs element of
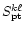 ,
say, will be obtained from Eq. (6a) by
inserting the two vectors
,
say, will be obtained from Eq. (6a) by
inserting the two vectors
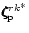 and
and
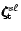 in that equation. In the following we
rewrite Eqs. (9) taking into account the new
partitioning. Thus,
in that equation. In the following we
rewrite Eqs. (9) taking into account the new
partitioning. Thus,
tt-block:
![$\displaystyle %
\sum_{\ell'}\left[ W^{k\ell'}_{\rm tt}Z^{\ell'\ell}_{\rm tt} +2...
...
-S^{k\ell'}_{\rm tp}Z^{\ell'\ell}_{\rm pt}{\omega^{\ell}_{\rm t}}^2~\right]=0,$](/articles/aa/full/2001/32/aa1087/img105.gif) |
|
|
(11a) |
pt-block:
![$\displaystyle \sum_{\ell'}\left[ W^{k\ell'}_{\rm pt}Z^{\ell'\ell}_{\rm tt}
+2\O...
...}
-S^{k\ell'}_{\rm pp}Z^{\ell'\ell}_{\rm pt}{\omega^{\ell}_{\rm t}}^2\right]=0.$](/articles/aa/full/2001/32/aa1087/img106.gif) |
|
|
(11b) |
We again emphasize that each of the factors
in Eqs. (11) are matrices in their own right.
6 Expansion order and
spherical harmonic structure of the various
matrices
Expansions of 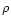 ,
p, and U in powers of
,
p, and U in powers of 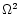 results
in a corresponding expansion of all the matrices in Eqs. (11). Moreover, having the spherical harmonics forms of
Eqs. (10), integrations over
results
in a corresponding expansion of all the matrices in Eqs. (11). Moreover, having the spherical harmonics forms of
Eqs. (10), integrations over 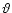 and
and 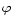 dependencies in the calculation of matrix elements can be performed
analytically. These two tasks are carried out in Appendix A.
The results are quoted below:
dependencies in the calculation of matrix elements can be performed
analytically. These two tasks are carried out in Appendix A.
The results are quoted below:
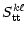 = = 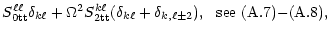 |
(12) |
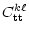 = = 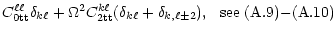 |
(13a) |
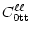 = =  |
(13b) |
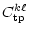 = = 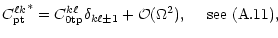 |
(13c) |
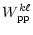 = = 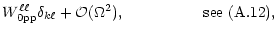 |
(14a) |
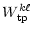 = = 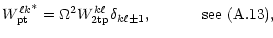 |
(14b) |
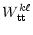 = = 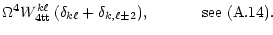 |
(14c) |
A subscript, 0, 2, 4 preceding the
tt, tp, pt or pp designations of the matrices indicates the
order of 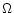 in the matrix in question. We also note that as
in the matrix in question. We also note that as
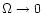 ,
,
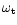 does the same. Therefore, it must
have the following form
does the same. Therefore, it must
have the following form
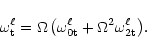 |
(15) |
Substituting these order of magnitude
informations in Eq. (11b) reveals that
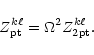 |
(16a) |
For
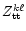 ,
we have no information so far. Therefore, we
assume the general form
,
we have no information so far. Therefore, we
assume the general form
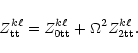 |
(16b) |
7 Expansion of equations of motion
Equations (12)-(16) allow a consistent expansion
of Eqs. (11) at 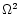 and
and 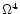 orders and
enable one to decipher the information contained in them.
orders and
enable one to decipher the information contained in them.
7.1 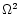 order of the tt-block
order of the tt-block
At 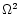 order Eq. (11a) gives
order Eq. (11a) gives
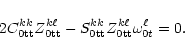 |
(17) |
For
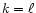 ,
considering the proportionality of
,
considering the proportionality of
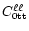 and
and
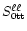 ,
Eq. (13a), one obtains
,
Eq. (13a), one obtains
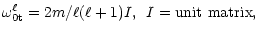 |
|
|
(18a) |
 |
|
|
(18b) |
For  ,
using
Eqs. (13b) and (18a), one has
,
using
Eqs. (13b) and (18a), one has
![\begin{displaymath}
2m[1/k(k+1)\!-\!1/\ell(\ell+1)]
S^{kk}_{\rm0tt}Z^{k\ell}_{\rm0tt} =0\,\, {\rm {or}} \hspace{.16cm} Z^{k\ell}_{\rm0tt}=0.
\end{displaymath}](/articles/aa/full/2001/32/aa1087/img136.gif) |
(18c) |
Let us summarize the findings so far from a pedagogical point of view.
At the 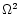 order one
solves the eigenvalue Eq. (17). In this equation the
Coriolis forces remove the degeneracy of the neutral motions and
create a sequence of modes of purely toroidal nature. The new
modes have a definite
order one
solves the eigenvalue Eq. (17). In this equation the
Coriolis forces remove the degeneracy of the neutral motions and
create a sequence of modes of purely toroidal nature. The new
modes have a definite 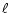 -symmetry, (Eqs. (18)). They
are not coupled with toroidal motions of
-symmetry, (Eqs. (18)). They
are not coupled with toroidal motions of 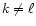 symmetry (that is
symmetry (that is
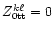 )
and
with poloidal motion (that is
)
and
with poloidal motion (that is
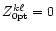 ,
see Eq. (16a)).
Removal of degeneracy, however, is partial. For, of the
three designations of a standing wave in three dimensions, only
,
see Eq. (16a)).
Removal of degeneracy, however, is partial. For, of the
three designations of a standing wave in three dimensions, only
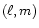 designations have appeared in the expression for
designations have appeared in the expression for
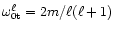 .
A third designation,
indicating the radial wave number, is as yet absent. They will
appear at higher orders of
.
A third designation,
indicating the radial wave number, is as yet absent. They will
appear at higher orders of 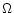 .
.
One simplifying feature: We note that
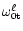 of Eq. (18a) is
a constant matrix. Therefore, it will commute with any matrix
carrying the same
of Eq. (18a) is
a constant matrix. Therefore, it will commute with any matrix
carrying the same 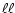 designations, such as
designations, such as
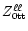 ,
,
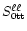 ,
etc. This feature
was used in the derivation of Eq. (18c) and will be used repeatedly
in what follows to simplify the matrix manipulations.
,
etc. This feature
was used in the derivation of Eq. (18c) and will be used repeatedly
in what follows to simplify the matrix manipulations.
7.2 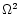 order of pt-block
order of pt-block
Equation (11b) at order 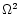 along with Eqs. (18) gives
along with Eqs. (18) gives
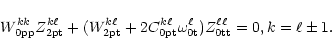 |
(19a) |
 is associated with poloidal modes of the
non-rotating fluids. In fact if
is associated with poloidal modes of the
non-rotating fluids. In fact if
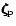 are chosen to be the
exact eigenvectors of the non-rotating star,
are chosen to be the
exact eigenvectors of the non-rotating star,
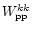 will be
a diagonal matrix whose elements are the square of the
eigenfrequencies of the p- and g-modes. At least in the case
of p-modes,
will be
a diagonal matrix whose elements are the square of the
eigenfrequencies of the p- and g-modes. At least in the case
of p-modes,
 is invertible (see Sobouti
1980 for complications in the case of g-modes). Thus,
one obtains
is invertible (see Sobouti
1980 for complications in the case of g-modes). Thus,
one obtains
![\begin{displaymath}
Z^{k\ell}_{\rm 2pt}=-{\left(W^{kk}_{\rm0pp}\right)}^{-1}\lef...
...\omega^\ell_{\rm0t}\right] Z^{\ell\ell}_{\rm0tt}, k=\ell\pm
1. \end{displaymath}](/articles/aa/full/2001/32/aa1087/img147.gif) |
(19b) |
By Eq. (8b), Eq. (19b) expresses that a toroidal mode of the
rotating fluid of 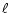 symmetry acquires a small poloidal
component of
symmetry acquires a small poloidal
component of 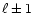 symmetry at
symmetry at 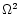 order.
order.
The case of g-modes is different. Rotation, no matter how small,
cannot be treated as a perturbation on them, as they are created
by minute buoyancy forces and the low frequency tail of their
spectrum gets completely wiped out by any other force in the
medium, here the Coriolis forces. This, in mathematical language,
means that
 for g-modes is not invertible and Eq. (19b) is not applicable to them. The way out of the dilemma is to consider the sum of buoyancy and other intruding forces as an inseparable entity, without dividing it to large and small
components. The works of Provost et al. (1980) and of Sobouti
(1977, 1980) are examples of such treatments. We leave it to the
experts in the field to decide whether the scrutiny of g-modes
in rotating neutron stars is a crucial or an irrelevant issue.
for g-modes is not invertible and Eq. (19b) is not applicable to them. The way out of the dilemma is to consider the sum of buoyancy and other intruding forces as an inseparable entity, without dividing it to large and small
components. The works of Provost et al. (1980) and of Sobouti
(1977, 1980) are examples of such treatments. We leave it to the
experts in the field to decide whether the scrutiny of g-modes
in rotating neutron stars is a crucial or an irrelevant issue.
7.3 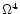 order of tt-block
order of tt-block
7.3.1 The 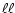 -subblock
-subblock
A systematic extraction of 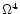 order terms of the
order terms of the
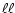 -block of Eq. (11a) with the help of Eqs. (12)-(16) and elimination of
-block of Eq. (11a) with the help of Eqs. (12)-(16) and elimination of
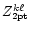 term
appearing in it by Eq. (19b) gives
term
appearing in it by Eq. (19b) gives
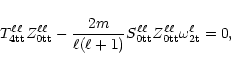 |
(20) |
where the fourth order
T-matrix is
![$\displaystyle T^{\ell\ell}_{\rm 4tt}=[
W_{\rm 4tt}+(2C_{\rm 2tt}-S_{\rm 2tt}\om...
...ga_{\rm0t})W^{-1}_{\rm0pp}
(W_{\rm 2pt}+2C_{\rm0pt}\omega_{\rm0t})]^{\ell\ell}.$](/articles/aa/full/2001/32/aa1087/img151.gif) |
|
|
(20a) |
Equation (20)
is a simple eigenvalue problem. Vanishing of its
characteristic determinant,
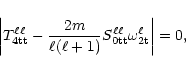 |
(20b) |
will give the non-degenerate second
order eigenvalues
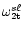 ,
s= radial wave number.
Once they are known, Eq. (20) itself can be solved for the
eigenmatrix
,
s= radial wave number.
Once they are known, Eq. (20) itself can be solved for the
eigenmatrix
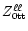 .
We note that we have solved two
eigenvalue problems, Eqs. (17) and (20), to remove
all degeneracies of the zero frequency toroidal motions of the non-rotating
fluid. Further extension of the
analysis of equations of motion to orders higher than
.
We note that we have solved two
eigenvalue problems, Eqs. (17) and (20), to remove
all degeneracies of the zero frequency toroidal motions of the non-rotating
fluid. Further extension of the
analysis of equations of motion to orders higher than 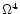 will result in non-homogeneous algebraic equations whose
non-homogeneous terms are given in terms of the matrices calculated
in the previous orders.
will result in non-homogeneous algebraic equations whose
non-homogeneous terms are given in terms of the matrices calculated
in the previous orders.
7.3.2 The (
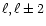 )-subblock
)-subblock
The presence of
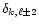 in Eqs. (13) and (14c) indicates
that two toroidal motions belonging to
in Eqs. (13) and (14c) indicates
that two toroidal motions belonging to
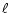 and
and 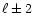 are mutually coupled. Likewise, the
presence of
are mutually coupled. Likewise, the
presence of
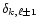 in Eqs. (13b) and (14b)
shows the coupling of toroidal and poloidal motion of
in Eqs. (13b) and (14b)
shows the coupling of toroidal and poloidal motion of 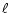 and
and 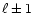 symmetry. This brings in an additional
coupling between two toroidal motions of
symmetry. This brings in an additional
coupling between two toroidal motions of 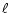 and
and 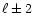 symmetries through the intermediary of poloidal motions.
Therefore, the only unexplored blocks of
Eq. (11a) are those with (
symmetries through the intermediary of poloidal motions.
Therefore, the only unexplored blocks of
Eq. (11a) are those with (
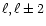 )
designations. As in Sect. 7.3.1 above, we extract the
)
designations. As in Sect. 7.3.1 above, we extract the
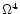 order terms of Eq. (11a), but this time with
order terms of Eq. (11a), but this time with
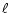 ,
,
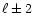 superscripts, eliminate
superscripts, eliminate
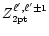 appearing in it by Eq. (19b) and arrive at
appearing in it by Eq. (19b) and arrive at
![$\displaystyle T^{\ell,\ell\pm 2}_{\rm 4tt}Z^{\ell\pm 2,\ell\pm
2}_{\rm0tt}=\lef...
...ll\pm 2}_{\rm 2tt}\omega^{\ell\pm
2}_{\rm0t}\right] \omega^{\ell\pm 2}_{\rm0t},$](/articles/aa/full/2001/32/aa1087/img157.gif) |
|
|
(21) |
where
![$\displaystyle T^{\ell,\ell\pm 2}_{\rm 4tt}=\bigg[
W_{\rm 4tt}+\left(2C_{\rm 2tt...
...\!+\!{4m\over(\ell\pm 2)(\ell\pm 2+1)}C_{\rm0pt}\right)\bigg]^{\ell,\ell\pm 2}.$](/articles/aa/full/2001/32/aa1087/img158.gif) |
|
|
(21a) |
In deriving this expression, on two occasions we have substituted for
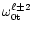 and shifted the scalar factor
and shifted the scalar factor
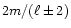
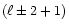 across the other matrices.
Returning to Eq. (21) we substitute for
across the other matrices.
Returning to Eq. (21) we substitute for
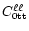 from Eq. (13b) and solve for
from Eq. (13b) and solve for
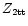 .
Thus,
.
Thus,
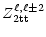 = = 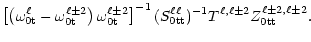 |
(22) |
Equations (20), (21) and (22) are all the
information contained in the 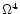 order of the tt-block.
Whether
order of the tt-block.
Whether
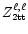 is non-zero or
otherwise is not clear at this level. To answer the question one
has to go to
is non-zero or
otherwise is not clear at this level. To answer the question one
has to go to 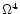 and
and 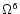 orders of Eqs. (11b) and (11a), respectively. This,
however, will not be attempted here.
orders of Eqs. (11b) and (11a), respectively. This,
however, will not be attempted here.
Papaloizou & Pringle (1978) have studied the low
frequency g- and r-modes of Eq. (4) in an
equipotential coordinate system with their applicability to the
short period oscillations of cataclysmic variables in mind.
Sobouti (1980) has studied the problem primarily with the goal of
analyzing the perturbative effects of slow rotations on
p-modes and demonstrating that rotation, no matter how small,
cannot be treated as a perturbation on g-modes. He argues that
the g-modes are fragile structures and their low frequency tail
of the spectrum, below the rotation frequency of the star, will be
completely wiped out by Coriolis and asphericity forces of the
star. The criterion for the validity of perturbation
expansion is that the perturbing operator should be smaller than the initial unperturbed
operator everywhere in the Hilbert space spanned by the
eigenfunctions of the unperturbed operator, (Rellich 1969).
This condition is not met by g-modes when exposed to rotation, magnetic, tidal forces, etc.,
as they have vanishingly small eigenfrequencies.
Provost et al. (1981) present an analysis of what they call
the "quasi-toroidal modes of slowly rotating stars''. Their work
should be noted for the consistency of mathematical manipulations
exercised throughout the paper. They noted
that in neutrally convective rotating stars one
cannot have modes with predominantly toroidal motions. They get mixed
with the neutral convective displacements.
Lockitch & Friedman (1999) also address the hybrid modes with
comparable toroidal and poloidal motions. Their work should be
noted for the emphasis put on the (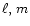 )
parities of the
hybrid components that get coupled through asphericity forces.
)
parities of the
hybrid components that get coupled through asphericity forces.
Yoshida & Lee (2000) study Eq. (4) for a)
those modes that are predominantly toroidal in their nature and b)
for those that have comparable poloidal and toroidal components.
Their latter modes are the same as those of Provost et al. (1981).
The bulk properties of some observed neutron stars seem to
approximate those of a polytrope of index 1. See Sterigioulas
(1998). It has become fashionable to categorize neutron stars as
stiff or soft, depending on whether their density
distributions are similar to those of polytropes of index smaller
than 1.5 or larger, respectively. To have an example of each
category, sample calculations are given for polytropes of indices 1 and 2.
The structure of rotating polytropes, taken from Chandrasekhar
(1933), is summarized in Appendix C. The ansatz for the
scalars
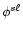 ,
,
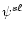 and
and
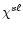 appearing in Eqs. (10) are given in Appendix B. The
required matrix elements are reduced in Appendix A. For a given
appearing in Eqs. (10) are given in Appendix B. The
required matrix elements are reduced in Appendix A. For a given
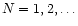 ,
the
,
the 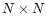 matrices are numerically
integrated. The eigenvalues
matrices are numerically
integrated. The eigenvalues
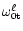 and
and
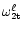 are calculated from Eqs. (18a) and (20b).
Once the eigenvalues are known, the various
components of the eigenmatrices
are calculated from Eqs. (18a) and (20b).
Once the eigenvalues are known, the various
components of the eigenmatrices
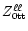 ,
,
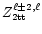 and
and
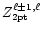 are calculated from
Eqs. (20), (22) and (19b). The
results are given in Tables 1 to 3.
are calculated from
Eqs. (20), (22) and (19b). The
results are given in Tables 1 to 3.
In Table 1, to show the convergence of the variational
calculations, the eigenvalues
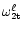 are displayed
for a polytrope of index 2,
are displayed
for a polytrope of index 2, 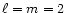 ,
and for
N=1,2,3,4,5. This
table should be considered as a basis for judging the accuracy of
the numerical values. With only five variational parameters, the
first, second and third eigenvalues are produced with an accuracy
of a few parts in 105, 104 and 102, respectively.
Likewise, the numerical values in the remaining tables should be
trusted to the same degree of accuracy and for the first few
modes.
,
and for
N=1,2,3,4,5. This
table should be considered as a basis for judging the accuracy of
the numerical values. With only five variational parameters, the
first, second and third eigenvalues are produced with an accuracy
of a few parts in 105, 104 and 102, respectively.
Likewise, the numerical values in the remaining tables should be
trusted to the same degree of accuracy and for the first few
modes.
In Table 2, the second order eigenvalues,
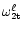 and
coefficient matrices,
and
coefficient matrices,
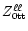 ,
,
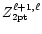 ,
and
,
and
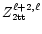 are given for
polytrope of index 1 and for
are given for
polytrope of index 1 and for
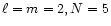 .
In Table 3 we give the same
calculations for polytrope of index 2. The eigenvalues are in
units of
.
In Table 3 we give the same
calculations for polytrope of index 2. The eigenvalues are in
units of
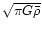 .
They are in agreement with
those of Lindblom et al. (1999), Yoshida & Lee
(2000), and Morsink (2001). Each of these authors
have used their own technique which are different from that of the
present paper.
.
They are in agreement with
those of Lindblom et al. (1999), Yoshida & Lee
(2000), and Morsink (2001). Each of these authors
have used their own technique which are different from that of the
present paper.
A novel feature of the present analysis is the provision of much
detail on eigendisplacement vectors, information that can be
profitably used to calculate any other bulk or local parameter of
the model. For example, for modes belonging to 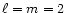 one may
write
one may
write
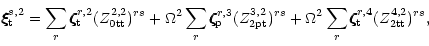 |
|
|
(23) |
in which the first sum is the
backbone of the mode and is of zero order. It is toroidal motion
of 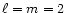 symmetry. The second sum is the coupling of
symmetry. The second sum is the coupling of
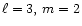 poloidal motion with
poloidal motion with 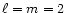 toroidal motion. It
is a poloidal motion and is of second order. The third sum is the
coupling of
toroidal motion. It
is a poloidal motion and is of second order. The third sum is the
coupling of
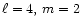 toroidal motion with
toroidal motion with 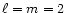 toroidal motion and again is of second order. In Figs. 1 to 4 we
have plotted the radial behavior of
toroidal motion and again is of second order. In Figs. 1 to 4 we
have plotted the radial behavior of
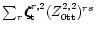 ,
,
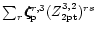 ,
and
,
and
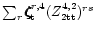 for polytropes of indices 1, 2 and the
first two modes, s=1,2. The center and the surface are nodes in
all curves. For s=2 there is an extra node in between in every
curve. The general rule is the number of nodes for any parameter
for polytropes of indices 1, 2 and the
first two modes, s=1,2. The center and the surface are nodes in
all curves. For s=2 there is an extra node in between in every
curve. The general rule is the number of nodes for any parameter
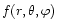 belonging to the radial mode number s,
is s+1. This includes the ever-present nodes at the center and
the surface of the star. This feature is faithfully present in all
five modes that can be constructed from the data of Tables 1 and 2,
even though we know that the numerical values for s=4 and 5 are
only orders of magnitude.
belonging to the radial mode number s,
is s+1. This includes the ever-present nodes at the center and
the surface of the star. This feature is faithfully present in all
five modes that can be constructed from the data of Tables 1 and 2,
even though we know that the numerical values for s=4 and 5 are
only orders of magnitude.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1087f1.eps}
\end{figure}](/articles/aa/full/2001/32/aa1087/Timg188.gif) |
Figure 1:
Radial behavior of the various components of the eigenfunction
of Eq. (23) for
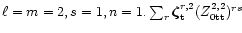 ,
dashed curve; ,
dashed curve;
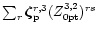 ,
dot-dashed curve; ,
dot-dashed curve;
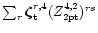 ,
dotted curve. Data for Z's are taken from the first column of Table 2. Nodes in all three components are at the center and surface. ,
dotted curve. Data for Z's are taken from the first column of Table 2. Nodes in all three components are at the center and surface. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1087f2.eps}
\end{figure}](/articles/aa/full/2001/32/aa1087/Timg189.gif) |
Figure 2:
Same as Fig. 1 for
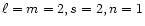 .
Data for Z's
are from the second column of Table 2. Note the extra node in all three components. .
Data for Z's
are from the second column of Table 2. Note the extra node in all three components. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1087f3.eps}
\end{figure}](/articles/aa/full/2001/32/aa1087/Timg190.gif) |
Figure 3:
Same as Fig. 1 for
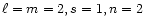 .
Data for Z's
are from the first column of Table 3. Nodes are at the center and the surface. .
Data for Z's
are from the first column of Table 3. Nodes are at the center and the surface. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1087f4.eps}
\end{figure}](/articles/aa/full/2001/32/aa1087/Timg191.gif) |
Figure 4:
Same as Fig. 1 for
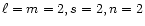 .
Data for Z's
are from the second column of Table 3. Note the extra nodes
in all components. .
Data for Z's
are from the second column of Table 3. Note the extra nodes
in all components. |
| Open with DEXTER |
In this section we study the dissipative effects of viscosity and
gravitational radiation on r-modes. Quite generally and regardless
of whether the star rotates or not, the total energy of an
undamped mode,
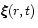 , is
, is
E = ![$\displaystyle {1\over 2} \int \left[
\rho\, \dot{\xi\hspace{-.18cm}\xi\hspace{-...
... {\cal W} \xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi_{\rm real}\right] {\rm d}^3x,$](/articles/aa/full/2001/32/aa1087/img193.gif) |
(24) |
= 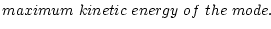 |
|
See Appendix D for proof of Eq. (24).
In the presence of viscous forces and the gravitational radiation,
the combined rate of dissipation (Cutler & Lindblom 1987) is
where 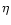 and
and
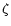 are the shear and bulk viscosities respectively,
are the shear and bulk viscosities respectively,
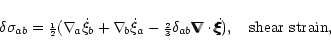 |
(26a) |
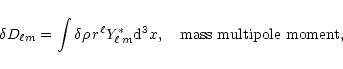 |
(27) |
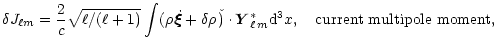 |
|
|
(28) |
 |
|
|
(28a) |
For a mode of the type of Eq. (23) the bulk viscous dissipation
(bv) comes entirely from its poloidal component, as
 .
For
.
For  this has the following rate
this has the following rate
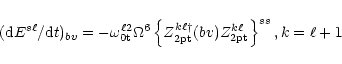 |
(29) |
where the elements of the new matrix, (bv), are
![$\displaystyle (bv)^{rq}= \int
\zeta\left[{\rm d}(r\psi^{rk})/{\rm d}r-k(k+1)\ch...
...\right] \left[ {\rm d}(r\psi^{qk})/{\rm d}r-k(k+1)\chi^{qk}\right]{\rm d}r/r^3.$](/articles/aa/full/2001/32/aa1087/img213.gif) |
|
|
(29a) |
The shear viscous dissipation has contributions from both toroidal and poloidal
components of Eq. (23). To the lowest order in 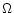 ,
however,
the toroidal component has the dominant contribution. Thus,
,
however,
the toroidal component has the dominant contribution. Thus,
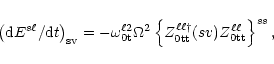 |
(30) |
where
![$\displaystyle (sv)^{rq} = \ell(\ell+1) \int
\eta\left[(r{{\rm d}\phi^{r\ell}/{\...
...2\phi^{q\ell}) +
(\ell^2+\ell-2)\phi^{r\ell}\phi^{q\ell} {{\rm d}r/r^2}\right].$](/articles/aa/full/2001/32/aa1087/img215.gif) |
|
|
(30a) |
Dissipation due to the gravitational radiation, to the lowest order, comes
from the current multipole moment,
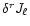 .
This has the
following vector elements
.
This has the
following vector elements
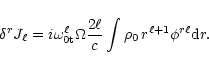 |
(31) |
To obtain the dissipation time scales: a)we have calculated the integrals of
Eqs. (24)-(31), numerically. b) For the bulk and shear viscosities
we have adopted the values of Cutler and Lindblom,
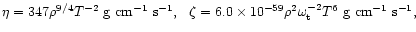 where
T is the temperature. For the a mode of radial node number s and
where
T is the temperature. For the a mode of radial node number s and
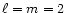 ,
we obtain
,
we obtain
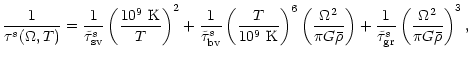 |
|
|
(32) |
where 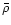 is the average density of
the star. Here
is the average density of
the star. Here
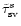 ,
,
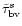 ,
and
,
and
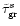 are the shear viscous-, bulk viscous- and
the gravitational radiation- time scale, respectively, which are
normalized for T=109 K and
are the shear viscous-, bulk viscous- and
the gravitational radiation- time scale, respectively, which are
normalized for T=109 K and
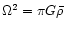 .
The total
dissipation time scale is
.
The total
dissipation time scale is
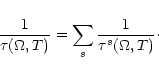 |
(33) |
For a model of
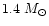 and
and
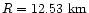 we have calculated
we have calculated
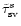 ,
,
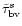 ,
and
,
and
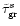 for
s=1,2,3,4,5 and displayed in the unit
of time in Tables 4 and 5. Our values for s=1 are in agreement
with those of Lindblom et al. (1999) and, Yoshida & Lee
(2000). To the best of our knowledge, the values for
for
s=1,2,3,4,5 and displayed in the unit
of time in Tables 4 and 5. Our values for s=1 are in agreement
with those of Lindblom et al. (1999) and, Yoshida & Lee
(2000). To the best of our knowledge, the values for
 are new.
are new.
In a newly born hot neutron star,
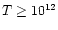 K, the bulk
viscosity has a dominant role in damping out the perturbations and
cooling down the star. In colder stars,
K, the bulk
viscosity has a dominant role in damping out the perturbations and
cooling down the star. In colder stars,
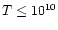 K and
K and
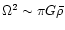 ,
the gravitational radiation is more
important than radiation shear and bulk counterparts. While
driving the r-modes to become unstable, it spins down the star. It is
believed that the star loses much of its energy and angular
momentum through the gravitational radiation in this stage. In a
case study of Andersson & Kokkotas (2000), the rotational period
increases from 2 ms to 19 ms in one year. Below T=108 K and
,
the gravitational radiation is more
important than radiation shear and bulk counterparts. While
driving the r-modes to become unstable, it spins down the star. It is
believed that the star loses much of its energy and angular
momentum through the gravitational radiation in this stage. In a
case study of Andersson & Kokkotas (2000), the rotational period
increases from 2 ms to 19 ms in one year. Below T=108 K and
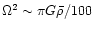 ,
the shear viscosity is the
dominant factor in cooling down the star.
,
the shear viscosity is the
dominant factor in cooling down the star.
Acknowledgements
We wish to thank Sharon Morsink for a careful reading of the
manuscript and illuminating comments. We would like to
acknowledge the referee for his/her valuable comments.
Appendix A: The elements of S, C and W matrices
In calculating the elements of various matrices, the following parameters
and integrals are encountered frequently:
![$\displaystyle Q_\ell=\left[\left(\ell^2-m^2\right)/\left(2\ell-1\right)\left(2\ell+1\right)\right]^{1/2},$](/articles/aa/full/2001/32/aa1087/img236.gif) |
|
|
(A.1) |
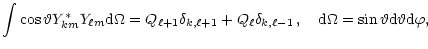 |
|
|
(A.2) |
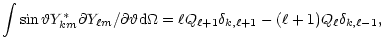 |
|
|
(A.3) |
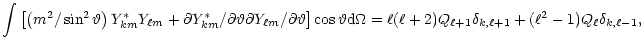 |
|
|
(A.4) |
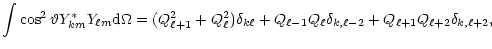 |
|
|
(A.5) |
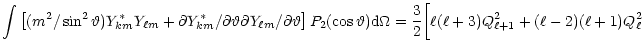 |
|
|
|
![$\displaystyle -{1\over 3}\ell(\ell+1)\bigg]\delta_{k\ell} +{3\over 2}\left[(\el...
...ll \delta_{k,\ell-2}+\ell(\ell+3)Q_{\ell+1}Q_{\ell+2} \delta_{k,\ell+2}\right].$](/articles/aa/full/2001/32/aa1087/img242.gif) |
|
|
(A.6) |
The basic definitions for S, C, and W matrices are given in
Eqs. (6). Expansions of 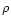 ,
p, and U entering
these defining integrals are in Eqs. (2). The zero and
,
p, and U entering
these defining integrals are in Eqs. (2). The zero and
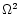 orders of these variables are sufficient to carry out
the analysis of Sect. 7 up to the
orders of these variables are sufficient to carry out
the analysis of Sect. 7 up to the 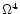 order consistently.
order consistently.
Finally, the spherical harmonics form of the
basis toroidal and poloidal vectors are given in Eqs. (10).
Angular integrals entering the definition of any
matrix element at any desired order are performed analytically.
Integrals in radial directions are left for numerical
calculations.
The S-matrix:
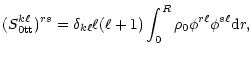 |
|
|
(A.7) |
![$\displaystyle (S^{k\ell}_{\rm 2tt})^{rs}=\delta_{k\ell} \ell(\ell+1)
\int^R_0\r...
...ell(\ell+3)Q^2_{\ell+1}+(\ell-2)(\ell+1)Q^2_\ell
-{1\over 3}\ell(\ell+1)\right]$](/articles/aa/full/2001/32/aa1087/img244.gif) |
|
|
|
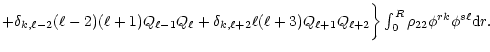 |
|
|
(A.8) |
The C-matrix:
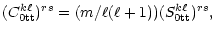 |
|
|
(A.9) |
The W-matrix:
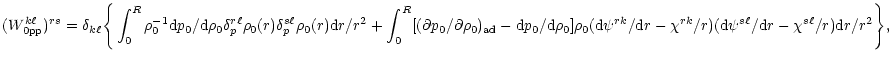 |
|
|
(A.12) |
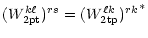 |
|
|
|
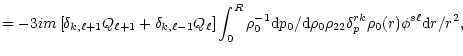 |
|
|
(A.13) |
where
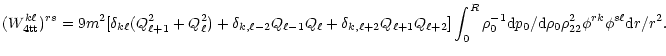 |
|
|
(A.14) |
Poloidal motions give rise to
density perturbations and therefore to perturbations in self
gravitation. In Eqs. (A.12) and (A.13) the
latter is neglected (Cowling's approximation) for simplicity.
Otherwise there is no conceptual difficulty in
including another term in Eqs. (A.12)-(A.13)
to avoid this approximation.
Finally, we note that the upper limit of all radial integrals here
is the radius of the non-rotating star instead of that of the rotating
one. We reproduce the argument of Sobouti (1980) to show
that, in most cases, the effect arising from this difference in the limits of
integration is of far higher order in  than would influence the
analysis of this paper. Let
than would influence the
analysis of this paper. Let
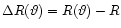 be the distance between two points with coordinate
be the distance between two points with coordinate 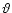 and
situated on the surfaces of rotating and non-rotating stars.
Obviously
and
situated on the surfaces of rotating and non-rotating stars.
Obviously 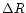 is of
is of 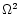 order. In a typical error
integral,
order. In a typical error
integral,
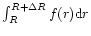 ,
we expand f(r) about Rand obtain
,
we expand f(r) about Rand obtain
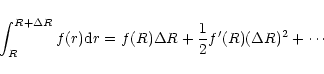 |
(A.15) |
In Eqs. (A.7)-(A.14)
the integrands depend on a combination of the variables  ,
,
 ,
,
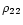 ,
p0 and p22. For a star of
effective polytropic index n, at the surface
,
p0 and p22. For a star of
effective polytropic index n, at the surface 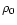 and
p0 vanish as (R-r)n and
(R-r)n+1. The leading error
terms of Eq. (A.15) are
and
p0 vanish as (R-r)n and
(R-r)n+1. The leading error
terms of Eq. (A.15) are
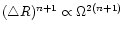 and
and
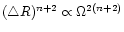 ,
respectively. The distorted quantities
,
respectively. The distorted quantities
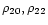 and
p20, p22 tend to zero as
(R-r)n+1 and (R-r)n.
However, considering the fact that these are second order
quantities and should be multiplied by an extra factor of
and
p20, p22 tend to zero as
(R-r)n+1 and (R-r)n.
However, considering the fact that these are second order
quantities and should be multiplied by an extra factor of
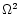 wherever they appear, the leading error term in
expressions involving them are also of the order
wherever they appear, the leading error term in
expressions involving them are also of the order
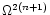 and
and
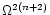 .
Thus, the largest error committed in
replacing the volume of the rotationally distorted star by that of
the non-rotating one is of the order
.
Thus, the largest error committed in
replacing the volume of the rotationally distorted star by that of
the non-rotating one is of the order
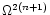 ,
a matter
of no concern for the analysis of this paper if
,
a matter
of no concern for the analysis of this paper if 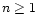 .
.
The vicinity of the center of a star is a uniform medium, in the
sense that, as r tends to zero, 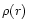 ,
p(r),
U(r), etc. all tend to constant values. Any scalar function,
,
p(r),
U(r), etc. all tend to constant values. Any scalar function,
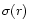 say, associated with a wave in such a nondispersive uniform and
isotropic environment should satisfy the wave equation
say, associated with a wave in such a nondispersive uniform and
isotropic environment should satisfy the wave equation
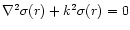 ,
k=const. Furthermore, if this scalar
is associated with the spherical harmonic
,
k=const. Furthermore, if this scalar
is associated with the spherical harmonic 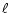 ,
i.e. if it is
of form
,
i.e. if it is
of form
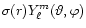 and is finite at
the origin, should tend to zero as
and is finite at
the origin, should tend to zero as 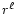 .
Therefore
.
Therefore 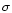 should have an expansion of the form
should have an expansion of the form
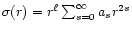 .
This is how the
solutions of Laplace's equation (k=0), the spherical Bessel function
and many other hypergeometric functions behave. A spherical harmonic vector,
.
This is how the
solutions of Laplace's equation (k=0), the spherical Bessel function
and many other hypergeometric functions behave. A spherical harmonic vector,
 belonging to
belonging to 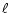 ,
quite generally can be written in terms of
three scalars
,
quite generally can be written in terms of
three scalars
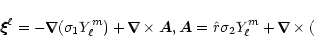 |
(B.1) |
where
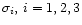 are scalars of the type described above.
Therefore, the radial and non-radial components of
are scalars of the type described above.
Therefore, the radial and non-radial components of
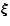 should have the form
should have the form
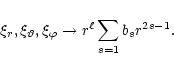 |
(B.2) |
To ensure this
behavior, it is sufficient that the scalars
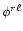 ,
,
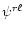 ,
and
,
and
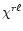 entering Eqs. (10)
are proportional to
entering Eqs. (10)
are proportional to
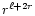 .
.
We adopt the following ansatz for the
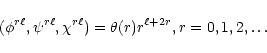 |
(B.3) |
where 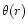 is the polytropic function, found by trial and error, that
ensures faster convergence of the variational calculations.
The ansatz has the required
is the polytropic function, found by trial and error, that
ensures faster convergence of the variational calculations.
The ansatz has the required 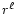 behavior at the center.
Two remarks are in order here:
behavior at the center.
Two remarks are in order here:
1) That a power set
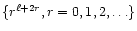 is complete
for expanding any function of r that behaves as
is complete
for expanding any function of r that behaves as 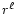 near the
origin follows from a theorem of Weiresstraus
(Relich 1969; Dixit et al. 1979).
near the
origin follows from a theorem of Weiresstraus
(Relich 1969; Dixit et al. 1979).
2) We have chosen the ansatz of Eq. (B.3) for their
simplicity. They are not the most efficient ones for rapid
convergence of variational calculations. The set of the
asymptotic expressions that helioseismogists use for
eigendisplacement vectors in the sun and other stars would,
perhaps, give a faster convergence of the numerical computations,
see Christensen-Dalsgaard (1998) and references therein.
The structure of rotating polytropes is taken from a landmark
paper of Chandrasekhar (1933). A summary of what is
needed here with slight changes in his notation is as follows
where
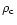 and
and 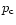 are constants,
are constants, 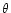 is the polytropic variable and
satisfies the Lane-Emden equation
is the polytropic variable and
satisfies the Lane-Emden equation
and 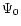 ,
,
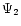 satisfy the following
satisfy the following
It should be noted that Chandrasekhar's rotation parameter is
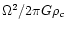 .
For the purpose of this paper we have integrated Eqs. (C.3)-(C.5)
numerically.
.
For the purpose of this paper we have integrated Eqs. (C.3)-(C.5)
numerically.
Let us take the real part of Eq. (4) and write it in the following form
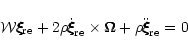 |
(D.1) |
We take the scalar product of Eq. (D.1) by
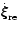 and
integrate over the volume of the star.
The Coriolis term gives no contribution.
The first term considering the hermitian
character of
and
integrate over the volume of the star.
The Coriolis term gives no contribution.
The first term considering the hermitian
character of 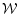 gives
gives
The third term in Eq. (D.1) gives
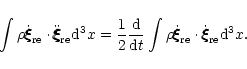 |
(D.3) |
Equations (D.1) and (D.2) should add to zero, which after a time integration gives
the constant total energy
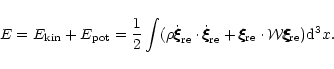 |
(D.4) |
Next we substitute for
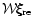 from
Eq. (D.1). After simple manipulations, we obtain
from
Eq. (D.1). After simple manipulations, we obtain
Since the time dependence of
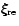 is sinusoidal,
upon taking the time average
of Eq. (D.5) the second integral vanishes and we obtain
is sinusoidal,
upon taking the time average
of Eq. (D.5) the second integral vanishes and we obtain
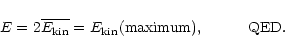 |
(D.6) |
- Andersson, N., & Kokkotas, K. D. 2000,
to appear in Int. J. Mod. Phys. D
In the text
- Chandrasekhar, S. 1933,
MNRAS, 93, 390
In the text
NASA ADS
- Chandrasekhar, S., & Lebovitz, N. R. 1962,
ApJ, 136, 1082
In the text
NASA ADS
-
Cutler, L., & Lindblom, L. 1987, ApJ, 314, 234
In the text
NASA ADS
- Dixit, V. V., Sarath, B., & Sobouti, Y. 1980,
A&A, 89, 259
In the text
NASA ADS
- Christensen-Dalsgaard, J. 1998,
Lecture notes on stellar oscillations,
In the text
http://www.obs.aau.dk/~jcd/oscilnotes/
- Gough, D. O. 1993, in Astrophysical
fluid dynamics, Les Houches XLVII, ed. J. P. Zahn,
& J. Zinn-Justin (Elsevier, Amsterdam), 399.
-
Lindblom, L., Mendell, G., & Owen, B. J. 1999,
Phys. Rev. D., 60, 064006
In the text
- Lockitch, K. L., & Friedman, J. L. 1999,
ApJ, 521, 764
In the text
NASA ADS
- Morsink, S. 2001, Private communications
In the text
- Provost, J., Berthomieu, G., & Rocca, A. 1981,
A&A, 94, 126
In the text
NASA ADS
-
Papalouizou, J., & Pringle, J. E. 1978, MNRAS,
182, 423
In the text
NASA ADS
- Rellich, F. 1969, Perturbation theory of
eigenvalue problem (Gordon and Breach Sci. Publisher, New York)
In the text
- Sobouti, Y. 1977,
A&A, 55, 339
In the text
NASA ADS
- Sobouti, Y. 1980,
A&A, 89, 314
In the text
NASA ADS
- Sobouti, Y. 1981,
A&A, 100, 319
In the text
NASA ADS
- Sterigioulas, N. 1998, Living Reviews in
Relativity 1, 8, In the text
http://www.livingreviews.org
- Tassoul, M. 1980, ApJS, 14, 469
- Yoshida, S., & Lee, U. 2000, ApJ, 529, 997
In the text
NASA ADS
Copyright ESO 2001
![\begin{displaymath}\nabla\hspace{-.305cm}\nabla\hspace{-.305cm}\nabla p+\rho \na...
...cm}\nabla
\left[U-\frac{1}{2}\Omega^2r^2\cos^2\theta\right]=0. \end{displaymath}](/articles/aa/full/2001/32/aa1087/img34.gif)
![\begin{displaymath}
\rho= \rho_0(r)+\Omega^2
[\rho_{20}(r)+\rho_{22}(r)P_2(\cos\theta)], \end{displaymath}](/articles/aa/full/2001/32/aa1087/img35.gif)
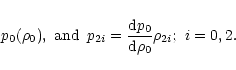
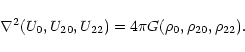
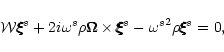
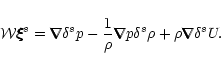
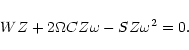
![\begin{displaymath}[\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi_{\rm p}\mid\xi\hspac...
..._{\rm pt}\\
Z_{\rm tp}&Z_{\rm tt}
\end{array}\right]\!\cdot
\end{displaymath}](/articles/aa/full/2001/32/aa1087/img81.gif)
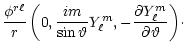
![\begin{displaymath}
\zeta\hspace{-.19cm}\zeta\hspace{-.19cm}\zeta^{r\ell}_{\rm p...
...hi^{r\ell}(r)\frac{im}{\sin\vartheta}Y_{\ell}^m
\right]\!\cdot \end{displaymath}](/articles/aa/full/2001/32/aa1087/img94.gif)
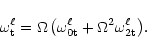
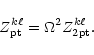
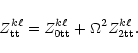
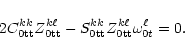
![\begin{displaymath}
2m[1/k(k+1)\!-\!1/\ell(\ell+1)]
S^{kk}_{\rm0tt}Z^{k\ell}_{\rm0tt} =0\,\, {\rm {or}} \hspace{.16cm} Z^{k\ell}_{\rm0tt}=0.
\end{displaymath}](/articles/aa/full/2001/32/aa1087/img136.gif)
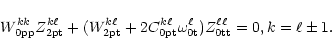
![\begin{displaymath}
Z^{k\ell}_{\rm 2pt}=-{\left(W^{kk}_{\rm0pp}\right)}^{-1}\lef...
...\omega^\ell_{\rm0t}\right] Z^{\ell\ell}_{\rm0tt}, k=\ell\pm
1. \end{displaymath}](/articles/aa/full/2001/32/aa1087/img147.gif)
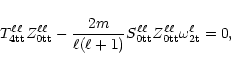
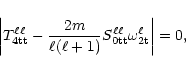
![$\displaystyle T^{\ell,\ell\pm 2}_{\rm 4tt}=\bigg[
W_{\rm 4tt}+\left(2C_{\rm 2tt...
...\!+\!{4m\over(\ell\pm 2)(\ell\pm 2+1)}C_{\rm0pt}\right)\bigg]^{\ell,\ell\pm 2}.$](/articles/aa/full/2001/32/aa1087/img158.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1087f1.eps}
\end{figure}](/articles/aa/full/2001/32/aa1087/Timg188.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1087f2.eps}
\end{figure}](/articles/aa/full/2001/32/aa1087/Timg189.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1087f3.eps}
\end{figure}](/articles/aa/full/2001/32/aa1087/Timg190.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1087f4.eps}
\end{figure}](/articles/aa/full/2001/32/aa1087/Timg191.gif)
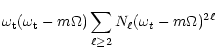
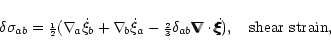
![$\displaystyle = {4\pi G\over c^{2\ell+1}} {(\ell+1)(\ell+2)\over
\ell(\ell-1)[(2\ell+1)!!]^2}, ~~~~c=~{\rm speed~of~light},\,$](/articles/aa/full/2001/32/aa1087/img206.gif)
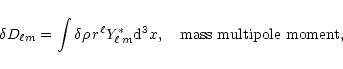
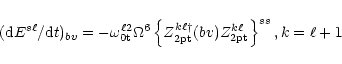
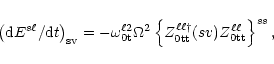
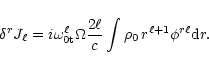
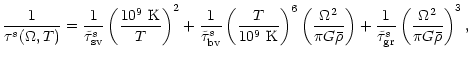
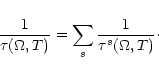
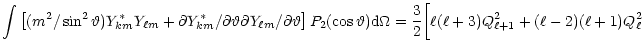
![$\displaystyle -{1\over 3}\ell(\ell+1)\bigg]\delta_{k\ell} +{3\over 2}\left[(\el...
...ll \delta_{k,\ell-2}+\ell(\ell+3)Q_{\ell+1}Q_{\ell+2} \delta_{k,\ell+2}\right].$](/articles/aa/full/2001/32/aa1087/img242.gif)
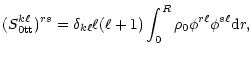
![$\displaystyle (S^{k\ell}_{\rm 2tt})^{rs}=\delta_{k\ell} \ell(\ell+1)
\int^R_0\r...
...ell(\ell+3)Q^2_{\ell+1}+(\ell-2)(\ell+1)Q^2_\ell
-{1\over 3}\ell(\ell+1)\right]$](/articles/aa/full/2001/32/aa1087/img244.gif)
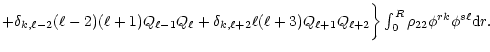
![$\displaystyle (C^{k\ell}_{\rm 2tt})^{rs}=\delta_{k\ell} m
\int^R_0\rho_{20}\phi...
...ll+2} Q_{\ell+1}Q_{\ell+2}\big]
\int^R_0\rho_{22}\phi^{rk}\phi^{s\ell}{\rm d}r.$](/articles/aa/full/2001/32/aa1087/img247.gif)
![$\displaystyle \quad=-i \delta_{k,\ell+1} \ell Q_{\ell+1}
\int^R_0\rho_0\left[\p...
...ell
\int^R_0\rho_0\left[\psi^{rk}-(\ell-1)\chi^{rk}\right]\phi^{s\ell}{\rm d}r.$](/articles/aa/full/2001/32/aa1087/img249.gif)
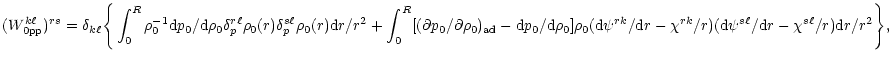
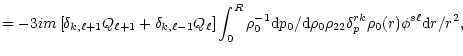
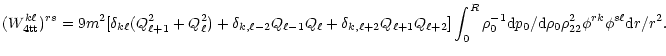
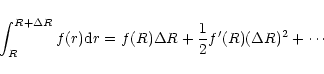
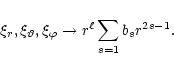
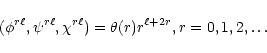
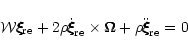
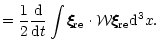
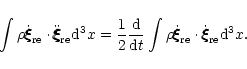
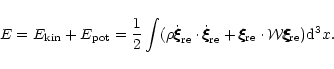
![$\displaystyle {1\over 2} \int \rho \left[2 \dot\xi\hspace{-.18cm}\xi\hspace{-.1...
...e}\cdot \dot\xi\hspace{-.18cm}\xi\hspace{-.18cm}\xi_{\rm re})\right] {\rm d}^3x$](/articles/aa/full/2001/32/aa1087/img311.gif)