A&A 375, 643-650 (2001)
DOI: 10.1051/0004-6361:20010834

Dynamical history of the observed long-period comets

P. A. Dybczynski

Astronomical Observatory of the A. Mickiewicz University, ul. S\loneczna 36, 60-286 Poznan, Poland

Received 28 December 2000 / Accepted 31 May 2001

Abstract
We present results of some numerical studies on the dynamical history of a large number of observed long-period comets. In our investigations we include all comets with good quality orbits. We calculated barycentric, original orbital elements for comets at a distance of 250 AU from the Sun and then followed the motion of each comet (elliptic orbits only) backwards to its aphelion and then to its previous perihelion passage, including the galactic perturbations. Several previously published statistics are compared with the current sample of long-period comets having well-defined orbits. A distinction between dynamically "new" and "old" comets is proposed on the basis of their previous perihelion distance instead of the inverse of the original semimajor axis. We also demonstrated the importance of stellar perturbations and made attempts to find a correlation between past dynamics and various physical parameters of comets.

Key words: comets: general - Oort Cloud - solar system: general


1 Introduction

A typical final product of cometary orbit determination is a set of osculating orbital elements, derived at some fixed epoch, usually close to the moment of the perihelion passage. These elements are influenced by all perturbations a comet could suffer during its passage through the planetary system towards its perihelion, namely gravitational perturbations from major and minor bodies, relativistic effects and non-gravitational forces, including those resulting from physical processes on the cometary nucleus. If we want to study the dynamical history of such a comet, i.e. its past motion before it entered the planetary region, it is necessary to trace backward its motion among the planets, taking into account all the perturbations mentioned above (assuming they are also included in the orbit determination process, which is a standard procedure nowadays) up to the heliocentric distance at which all those perturbations can be neglected. In this paper we calculate barycentric original orbital elements at a heliocentric distance of 250 AU, according to the suggestions by Todorovic-Juchniewicz (1981) and adding an extra "security margin''. We call this distance the "Planetary Perturbation Limit'' (PPL).

As the initial values for such a calculation we used the osculating orbital elements, published in the Catalogue of Cometary Orbits (Marsden & Williams 1997), using only orbits with the quality class 1 or 2, according to the classification proposed by (Marsden et al. 1978). This automatically excludes all comets having determined non-gravitational parameters. Additionally, we supplemented this dataset with those for several long-period comets whose orbits were published up to the middle of 1999; more precisely, we modified the orbits of 9 comets, added 20 new orbits and removed one orbit because of non-gravitational parameters published recently. All modifications to the Catalogue of Cometary Orbits are summarized in Table 1.

For some statistical analysis presented later in this paper we additionally restrict the sample of the observed long-period comets to those with observed perihelion distances q>1.5 AU, which, according to Oort (1990), should exclude all comets with potentially significant non-gravitational effects.


 

 
Table 1: List of comets that have been modified, added or removed from the Marsden's catalogue of orbits (Marsden & Williams 1997), according to new results.
Comet Source Class Comment
C/1996 J1-B MPC33450 1A modified
C/1997 A1 MPC30957 1A modified
C/1997 BA6 MPC34420 1A modified
C/1997 D1 MPC30957 1A modified
C/1997 J1 MPC31482 1A modified
C/1997 J2 MPC33451 1A modified
C/1997 L1 MPC30738 2A modified
C/1997 O1 MPC30957 2A modified
C/1997 P2 MPC30738 2A modified
C/1997 T1 MPC32168 1A added
C/1998 H1 MPC32168 2A added
C/1998 K1 MPC33451 1B added
C/1998 K2 MPC32594 1B added
C/1998 K5 MPC33857 1A added
C/1998 M1 MPC34733 1A added
C/1998 M2 MPC32865 1B added
C/1998 M3 MPC34733 1A added
C/1998 M5 MPC34733 1A added
C/1998 M6 MPC33188 1B added
C/1998 Q1 MPC32595 2B added
C/1998 T1 MPC33451 2A added
C/1998 U1 MPC33650 2A added
C/1998 U5 MPC34421 1B added
C/1998 W3 MPC33857 2A added
C/1999 A1 MPC33858 2B added
C/1999 F1 MPC34734 1B added
C/1999 F2 MPC34734 1A added
C/1999 K2 MPC34735 2A added
C/1999 K6 MPC34735 2B added
C/1995 O1 MPC32410 - removed


Finally, we performed our investigation of the past motion for a sample of 327 long-period comets, 195 of which have class 1A or 1B orbit, while 132 comets are of class 2A or 2B.

For such a population we calculated barycentric, original orbits, some details of which are found in Sect. 2, and then, for those comets, whose original aphelion distances were greater than the PPL, we performed backward numerical integrations of their motion, described in detail in Sect. 4. In that section we also discuss the importance of stellar perturbations, giving some examples, and propose a revision of the criterion for calling a particular comet dynamically "new''. In Sect. 3 we present some statistical characteristics of the results obtained in the present investigation as well as a comparison with similar results previously published, e.g. Yabushita (1989), Oort (1950, 1990). Section 5 shows several attempts to find a correlation between the past motion parameters and various physical characteristics of comets. At the end we discuss the possibility of distinguishing new (first time near the Sun) and old comets on the basis of their dynamical history and give some final remarks and conclusions.

2 Original orbit calculation

If we want to know what the cometary orbit was before it entered the planetary system it is necessary to calculate its past motion among planets, taking into account all types of perturbations that act on a comet in the solar neighbourhood. As the dynamical model we used heliocentric, post-Newtonian equations of motion, similar to those used by Yau et al. (1994) in their investigation of the past motion of comet 109P/Swift-Tuttle. As the source of planetary positions we used the JPL DE406 Planetary Ephemeris (Standish 1998), using the software (in C) which is made available as free-ware by the author at the URL: ftp://ftp.astro.amu.edu.pl/pub/jpleph. We integrated numerically the equations of motion of each comet using Everhart's RA15 integrator (Everhart 1985) but some test calculations were also performed using the D2RKD7 routine based on the method of Dormand & Prince (1978), which was made available to the author by Ken Fox (see Fox 1984). We also performed some tests using the RA27 routine by Everhart (1985), in quadruple precision on the Alpha-based Linux workstation. Those tests were extremely time consuming but they allowed us to separate dynamical sensitivity to initial conditions from both truncation and round-off numerical errors in some difficult cases.


 

 
Table 2: Original 1/a distribution of the growing population of long-period comets, 1990 and 1999 data are restricted to comets with the perihelion distance greater than 1.5 AU an qualified as class 1 orbits.
1/a orig. Oort Oort This paper
[10-6AU-1] 1950 1990 (1999)
<10 14 42 60
10-20 2 1 5
20-30   3 6
30-40 2 1 4
40-50   3 6
50-60   5 7
60-70 1 1 3
70-80   1 2
80-90   2 2
 90-100 0 1 1
>100   6 20
Total: 19 66 116


The backward integration of the motion of each comet was stopped when a comet crossed the PPL or when it reached its aphelion at a smaller distance. It should be stressed here that none of the comets which came from a distance greater than the PPL made any close approaches (distance less than 0.1 AU) to the Solar System planets, so their original elements are obtained without initial errors amplified by such approaches. Additionally, for each comet we performed a set of numerical integration runs with starting data slightly modified (on the level of one tenth of the least significant digit published in Marsden's catalogue). We wanted to find those cases, in which abnormally high sensitivity to the starting data can be observed, disqualifying them from further investigation.

As a result of this part of the work, we have obtained a set of original orbital elements for 327 comets, calculated at the epoch they crossed the PPL. Among them there are 44 comets that cannot reach this distance - for them, we include the orbital elements at their first (going backward) aphelion. The ASCII file containing these data is available to readers at the URL: http://main.amu.edu.pl/~dybol/DH/org_elem.dat. The accuracy of these data is comparable to the starting elements, taken from the Marsden catalogue (Marsden & Williams 1997), typically six or seven significant digits.

3 Statistics of the original orbits

The most famous statistics of the original orbit set was presented by Oort in his fundamental paper on the existence of the cloud of comets surrounding the Solar System (Oort 1950). Those statistics consisted of only 19 orbits, and a high concentration of the reciprocal original semimajor axes of those comets towards a small, positive value was the main argument for the existence of the cometary cloud. Oort repeated this work lately, in a paper published as a chapter in the book on the physics of comets, edited by W. F. Huebner (Oort 1990). He accumulated data for 66 comets, restricted to those with a perihelion distance greater than 1.5 AU to be sure that he excluded any comets that may be influenced by non-gravitational effects. In our set (last updated in September 1999) we have almost doubled this number and we present a comparison of those three distributions in Table 2.

It has been well known since the publication of the Oort (1950) paper that dynamically "new'' comets, entering the planetary region for the first time, should have the smallest 1/a values. A widely-used definition of dynamically "new'' comets, (e.g. Oort & Schmid 1951; Kresák 1977, 1994; Marsden et al. 1978; Oort 1990; Levison 1996) states that their $1/a<1\times 10^{-4}$ AU-1, which is equivalent to $a >10\,000$ AU. Table 3 shows the division of the whole set of 327 original orbits into dynamically "new'' and "old'' comets according to the above definition, with additional division with respect to the orbit quality class (Marsden et al. 1978). The statistics for the restricted (q>1.5 AU) sample is also shown separately.


 

 
Table 3: Dynamically "new'' and "old'' comets among 327 original orbits, according to the classical definition.
  class 1 class 2 classes 1 + 2
q [AU] >1.5 $\leq$1.5 >1.5 $\leq$1.5 >1.5 $\leq$1.5
"new'' 60 31 6 16 66 47
"old'' 56 48 23 87 79 135
all 116 79 29 103 145 182
Total 195 132 327


However, treating all comets with $a >10\,000$ AU as new is an obvious oversimplification. Some of those comets may have passed near the Sun during earlier returns. One of the perturbing agents acting on those comets, namely the galactic disk tide, causes periodic changes of the perihelion distances with periods of order of 104-105years. Depending on the semimajor axis and geometrical configuration with respect to the galactic plane, the perihelion distance can be significantly changed even during one orbital period, so we decided to follow backward the motion of those comets to their previous perihelion passage.

4 Going further into the past

Detailed investigation of cometary dynamics in the Planetary System gave us 283 original, barycentric orbits of the observed long-period comets with the aphelion distance greater then the PPL. Ten percent of them (28) are hyperbolic, 170 elliptical orbits have $a\leq10\,000$ AU and 85 have $a >10\,000$ AU. Assuming that all those orbits are generally free from significant errors we decided to integrate numerically the past motion of all 255 elliptical comets starting at the moment of crossing the PPL and taking into account the influence of the whole Solar System and the tidal potential of the Galaxy. The aim of this calculation is to look at the past evolution of the cometary orbit. In particular, we are interested in previous aphelion and perihelion distances of all elliptical comets. If we assume that some of the observed long-period comets visited the planetary region as a result of some recent perturbation (for example stellar passage), the aphelion distance might bring the information on the source region of those bodies. On the other hand, for those comets which did not suffer any strong perturbation at the last aphelion (those comets are observable due to the long-term tidal action of the Galaxy), the value of the previous perihelion distance may indicate whether the comet is "physically new'' or has visited the planetary region at least once before the observed return.

During the backward numerical integration of motion we calculated the influence of the Galaxy in an approximate manner, using the model which is widely used in cometary dynamics. The galactic perturbation is restricted here to the tidal action of the galactic disk with the gravitational potential described by the formula derived by Heisler & Tremaine (1986):

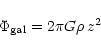
\begin{displaymath}\Phi _{\rm gal}=2\pi G\rho \, z^{2} \end{displaymath}

where z is a distance of a comet from the galactic disk plane, and $\rho$ is an averaged matter density in the solar neighbourhood. According to modern determinations, $\rho =0.143\, M_{\odot }/{\rm ps}^{3}$ (see for example Dauphole et al. 1996). At this stage of research the only source of perturbation was the galactic disk tide - we discuss stellar perturbations later on. We integrated numerically only one orbital period of each comet with a rather weak perturbation force so the agreement was excellent, as expected. During the integration run for each comet, we recorded its largest distance from the Solar System barycenter (at aphelion) and we stopped the integration at the previous perihelion (or after 1 billion years if it was not reached), recording the perihelion distance. A typical integration period was from two thousand to tens of millions of years, depending mainly on the comet semimajor axis.

Similar calculations, but for only 48 comets, were performed by Yabushita (1989). Despite the dynamical model differences and a large number of typographical errors in Yabushita's tables, we found a general agreement for the most of his sample of 48 comets, except the cases when we used the updated nominal orbits.


 

 
Table 4: The distribution of the previous aphelion distance for all comets believed to be dynamically "new'' in the Oort sense.
Aphelion distane Number of comets
in thousands of AU q>1.5 AU Class 1 All comets
 >200 7+0 28+3
 200-100 9 14
100-75 7 11
 75-50 15 23
 50-30 16 24
 30-20 6 10


Table 4 shows the statistics of the previous aphelion distances for all 113 comets "new'' in the Oort sense ($a >10\,000$ AU) with separate statistics for the "extra quality'' subset. In the first row we present the sum of the number of hyperbolic orbits and of very elongated ellipses. We restricted here our interest to the "new'' comets because for comets with smaller semimajor axes, the influence of the Galaxy is too weak to be observed in orbital elements - they remain constant for one orbital period. This may be clearly seen also in Fig. 1, which additionally is a good illustration of the revised dynamical definitions of "new'' and "old'' comets that we propose below. We recorded here the evolution of orbit in the (q,Q) plane for all 255 elliptical orbits during approximately one orbital period in the past. This plot is constructed during the backward numerical integration as follows: at the beginning we print a small dot, corresponding to the initial data, taken from the barycentric, original orbit set, described in the previous Sect. Next, we print the same small dot at each backward integration step, according to the current values of the osculating perihelion and aphelion distances. Finally, at the end of the integration (at the previous perihelion) we print a big dot.


  \begin{figure} \par\includegraphics[width=10cm,angle=270]{pad10622f1.eps} \end{figure} Figure 1: Past evolution of orbits of long-period elliptic comets under the galactic disk perturbing force.
Open with DEXTER

Figure 1 is divided into three parts, upper, middle and lower, with horizontal dashed lines corresponding to the aphelion distances of 50000 AU and 200000 AU. The vertical dotted line corresponds to the perihelion distance of 15 AU, which we used as the threshold value: only those comets with a greater value of q may be called dynamically "new'', all the others should be considered as dynamically "old'' even if they have a very small value of the original reciprocal semimajor axis. See, for example, the paper by Matese & Whitman (1989) for arguments in support of choosing this particular threshold value.

In the upper part of this plot one can notice rather complicated paths of three comets on very elongated elliptical orbits under a relatively strong galactic perturbation. Those are: C/1896 V1 with the initial aphelion distance of 383952 AU, C/1940 R2 with the initial $Q=2\,954\,501$ AU and C/1993 Q1 having the initial $Q=738\,516$ AU. The initial means here the value at the PPL in the original orbital element set. It should be stressed, that these three comets have small observed perihelion distances (1 AU or less) and we may suspect that their extremely large initial aphelion distances may be a result of nongravitational effects, not included in the orbit determination process.

In the lower part are all the comets that do not significantly change their orbits under the influence of the galactic disk tide during the last orbital period. For the majority of them the final dots are plotted over the starting ones; only for the comets with an initial aphelion distance greater than 20000 AU can one notice small changes in the perihelion distance. All those comets we call dynamically "old'' because during their previous passage near the Sun they deeply penetrated the planetary region.

Only the comets for which the big dots, representing previous perihelion values, lie in the middle part of Fig. 1 and to the right of the vertical dotted line, may be called dynamically "new''. As clearly visible from this plot, they considerably changed their perihelion distance during the last orbital period before being observed, from large values outside the Planetary System to very small ones, close to 1 AU. This means that we should modify the Oort definition of dynamically "new'' comets, changing the threshold value of the reciprocal of the semimajor axis from $1\times10^{-4}$ to $2.5\times10^{-4}$ AU-1 and excluding those comets with previous perihelion distances smaller than 15 AU.


 

 
Table 5: The distribution of the previous perihelion distances for elliptical long-period comets, "new'' in the Oort sense ( $a >10\,000$ AU). The "restricted'' set means comets with observed perihelion distance greater than 1.5 AU and orbit of class 1.
Previous q "restricted'' set all comets
0-2 AU 3 10
 2-15 AU 24 31
15-40 AU 6 12
>40 AU 20 32


Table 5 shows the statistics of the previous perihelion distances. It is clearly visible that 41 comets thus far called dynamically "new'' (and among them 27 comets from the "restricted'' set) have penetrated the planetary system at least once before. According to our modified definition, only 44 comets (26 from the "restricted'' set) can be called dynamically new! If we exclude 3 comets with the extremely elongated (probably erroneously) elliptical orbits mentioned above it appears that exactly $50\%$ of comets called dynamically "new'' are in fact dynamically "old'' and have passed near the Sun at a distance closer than 15 AU. The maximum and minimum heliocentric distances during the last orbit for 41 dynamically "new'' comets according to our definition are shown in Table 6. These are osculating aphelion and perihelion distances, but for two different epochs of osculation (when at aphelion and at perihelion respectively). One can notice that a quarter of them had their previous perihelion passage in the outer planetary region while some of them had large perihelion distances at the previous return.


 

 
Table 6: Aphelion (Q) and perihelion (q) distances during last orbit for 41 dynamically "new'' comets according to our modified definition (see text for details).
Comet Q [AU] q [AU]
C/1853 L1 144989 8385
C/1863 T1 131366 5155
C/1902 R1 73187 40
C/1902 X1 75504 138
C/1903 M1 60320 25
C/1906 E1 69869 105
C/1907 E1 78759 70
C/1913 Y1 69017 79
C/1916 G1 114800 758
C/1919 Q2 97494 683
C/1921 E1 104174 1035
C/1922 U1 92708 176
C/1925 W1 83486 140
C/1935 Q1 108284 202
C/1942 C1 124942 1002
C/1944 K2 111507 1566
C/1947 S1 85361 31
C/1947 Y1 72355 82
C/1948 E1 60428 28
C/1948 T1 59020 18
C/1950 K1 53475 15
C/1956 F1-A 113238 1083
C/1962 C1 61046 20
C/1973 E1 115370 669
C/1974 F1 56186 21
C/1974 V1 159240 10180
C/1975 E1 86309 295
C/1976 U1 53793 16
C/1978 A1 58904 45
C/1978 H1 82829 88
C/1978 R3 128057 2537
C/1979 M1 63712 37
C/1984 W2 103493 910
C/1987 W3 68822 58
C/1988 B1 132343 6259
C/1989 X1 63953 48
C/1990 M1 49108 18
C/1991 F2 124304 2761
C/1992 J1 70792 57
C/1997 A1 96745 248
C/1997 BA6 78190 141



 

 
Table 7: Several examples of large differences between the orbital elements of dynamically "new'' comets, obtained in two different models: without and with the stellar perturbations from the Algol system.
Comet q [AU] e i [$^{\circ }$] $\Delta T$ [ years]
    2.1 0.99994820 157.19 -7.88 \( \,\times\, 10^{6} \)
C/1907 E1  69.6 0.99824162  99.11 -7.78 \( \,\times\, 10^{6} \)
  105.3 0.99718258 118.33 -7.80 \( \,\times\, 10^{6} \)
  3.7 0.99989955  10.94 -7.19 \( \,\times\, 10^{6} \)
C/1914 M1 4.4 0.99988297  24.55 -7.19 \( \,\times\, 10^{6} \)
  32.0 0.99917286   1.56 -7.20 \( \,\times\, 10^{6} \)
  0.7 0.99997356 145.91 -4.74 \( \,\times\, 10^{6} \)
C/1954 M2 14.0 0.99950276 101.01 -4.71 \( \,\times\, 10^{6} \)
  16.5 0.99941611 103.01 -4.71 \( \,\times\, 10^{6} \)
  3.2 0.99991611 61.76 -7.34 \( \,\times\, 10^{6} \)
C/1980 E1 13.3 0.99964770 76.65 -7.30 \( \,\times\, 10^{6} \)
  34.2 0.99911567 33.35 -7.33 \( \,\times\, 10^{6} \)
  4.0 0.99992510 34.56 -1.24 \( \,\times\, 10^{7} \)
C/1984 W2 909.7 0.98298450 86.85 -1.16 \( \,\times\, 10^{7} \)
  1548.0 0.97085896 83.17 -1.19 \( \,\times\, 10^{7} \)
  1.5 0.99997676 103.03 -1.66 \( \,\times\, 10^{7} \)
C/1991 F2 2760.6 0.95760870 90.31 -1.53 \( \,\times\, 10^{7} \)
  4154.7 0.93737268 83.30 -1.60 \( \,\times\, 10^{7} \)
  3.4 0.99991292 45.16 -7.85 \( \,\times\, 10^{6} \)
C/1997 BA6 140.8 0.99643553 83.67 -7.68 \( \,\times\, 10^{6} \)
  238.5 0.99384010 75.58 -7.72 \( \,\times\, 10^{6} \)


It should be stressed again that the picture presented so far is obtained by taking into account only the galactic perturbation of the movement of a comet on the elongated elliptic orbit. There is another source of perturbation that is much more difficult to model because of its random nature - namely stellar close passages. On the basis of our knowledge of the solar neighbourhood density of stars and their motions, it is widely believed that several close encounters take place each million years (a detailed discussion may be found for example in: Dybczynski & Kankiewicz 1999; García-Sánchez et al. 1999). A strict analysis of the influence of the neighbour stars on the cometary motion during the last several million years is very difficult because of the incompleteness and inaccuracies in the stellar data at our disposal and is beyond the scope of this article, but to illustrate its importance we present here the results of backward numerical integration of the cometary motion, in which we include (besides the galactic disk tide) the influence of the Algol (HIP 14576) system, which probably has been one of the most prominent perturbers of the Oort cloud comets in the past few million years (García-Sánchez et al. 1999). An additional importance of that system is that we know its spatial position and velocity with great accuracy due to the latest VLBI astrometrical measurements (Lestrade et al. 1999) so the calculation is relatively precise. The total mass of that multiple star system is about 5.8 solar masses, its minimum distance from the Sun was 3 pc and the encounter velocity was as low as 4 kms-1 (this increases the perturbational effect). Its close passage happened 7 million years ago.

The gravitational influence of that system was included in the equations of cometary motion. Similarly to the previous calculation, all comets with elliptic orbits were integrated numerically one orbital period in the past. For the majority of comets there were no significant differences but some of them exhibit substantial changes in their past orbital motion. The examples of the differences between the two dynamical models mentioned above are given in Table 7. The inclination of the cometary orbit presented in this table is measured with respect to the galactic disk plane. The last column shows the time interval between the observed and previous perihelion passage. For each comet we include three rows containing (from upper to lower) the original orbit at the PPL, orbital elements at the previous perihelion passage under the influence of the galactic disk tide only and the same under both galactic and stellar perturbation due to the Algol system. Note significant differences in the inclination. This is typical because the galactic tide makes this element vary very rapidly near the perihelion (see for example Dybczynski & Pretka 1997), so small changes in the other elements typically result in large inclination changes, but the orientation of the line of apsides remains almost the same. We present here some extreme examples and additionally three comets, which became dynamically "new'' due to the Algol system action. These are C/1914 M1, C/1954 M2 and C/1980 E1. A comparative results for all comets may be found in file: http://main.amu.edu.pl/~dybol/DH/disk-star.wyn. The main conclusion following from this comparison is that stellar perturbations are very important and can change comet orbits, in some cases significantly. We plan to extent our dynamical model for studying cometary past motion by including all stars in the galactic neighbourhood of the Sun with known spatial position and velocity which can noticeably influence the motion of a small body. The first steps in this direction have already been made (Dybczynski & Kankiewicz 1999) and a paper describing results of an extended research in this field is currently in preparation.

5 Are dynamically "new'' comets different from others?

Less than a year after his "defining'' work on the cloud of comets, Oort made an attempt (in collaboration with M. Schmidt, Oort & Schmidt 1951) to find any physical differences between "new'' and "old'' comets according to their dynamical definition, on the basis of the original semimajor axes. Their main conclusions were: 1) There are too many "new'' orbits in comparison to the steady-state model prediction, which implies that they deteriorate faster than others, 2) "new'' comets with large perihelion distances (larger than 1 AU) are characterized by strong continuous spectra (mainly reflective) and 3) the brightness of "new'' comets varies more slowly with the heliocentric distance. After this pioneering work many authors studied various physical properties of comets versus with their "dynamical age'' (see for example: Kresák 1977; Whipple 1992a; A'Hearn et al. 1995). According to widespread opinion, the dynamically "new'' comets are generally more active and brighter at larger heliocentric distances and they have statistically greater perihelion distances. Having a set of previous aphelion and perihelion distances, we decided to look for any correlations between these values and various physical parameters of elliptical, long-period comets.

Our first attempt was to obtain a set of "absolute magnitudes'' (H10) of all long-period comets and to check for a correlation with past motion characteristics. We were not able to find the appropriate values for all comets in our sample but on the basis of the papers by Vsekhsvyatskii (1958, 1967, 1979), Andrienko & Karpenko (1987), Hughes (1987), Kosai & Nakamura (1991) and Yoshida's Internet cometary catalogue (Yoshida 1999), we collected a large set of H10 values. A complete list of all values we used may be found in the file: http://main.amu.edu.pl/~dybol/DH/mag_all.dat. We assumed, as a first and very simplified approach, that the absolute magnitude parameter H10 can be treated as a rough measure of the cometary activity. In Fig. 2 one can find a distribution of H10 against the previous aphelion distance. The dashed line is the least squares straight line approximation to all points. A small decrease of H10 (increase in brightness) with increasing the previous aphelion distance is clearly visible. The effect is not very strong, but it remains visible when dealing with different subsets of cometary data (different orbit quality classes etc.). A similar effect is evident when looking for a correlation between the absolute magnitude and the previous perihelion distance.


  \begin{figure} {\resizebox{\hsize}{!}{\rotatebox{270}{\includegraphics{pad10622f2.eps}}} } \end{figure} Figure 2: The correlation between cometary absolute magnitude H10 and the previous aphelion distance.
Open with DEXTER

Next we looked for any correlation between dynamical history of a comet and physical characteristics, expressed in terms of the volatility and activity indices, developed recently by Whipple (1992b,c), but we found that these correlations are rather weak.


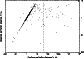  \begin{figure} {\resizebox{\hsize}{!}{\rotatebox{270}{\includegraphics{pad10622f3.eps}}} }\end{figure} Figure 3: The dependence of the observed perihelion distance on the previous perihelion distance. We included here all elliptical orbits, which crossed the PPL.
Open with DEXTER

Finally, we tried to check one of the theses of the Kresák's paper (Kresák 1977) about a prevalence of orbits of large perihelion distance among the "new'' comets. For this purpose we prepared a plot, presented here as Fig. 3. It illustrates the dependence of the observed perihelion distance (vertical axis) on the previous perihelion distance (horizontal axis). The vertical, dashed line in the middle of the plot corresponds to our threshold value of 15 AU for the previous perihelion distance, defining all comets to the left of this line as dynamically "old'' and to the right as dynamically "new''. One can easily see the prominent feature in the left part of the plot: this straight line grouping of dots corresponds to those "old'' comets, which do not change their perihelion distance during the last revolution before being observed. All other dots represent the comets undergoing changes in perihelion distance in that interval. Interpretation of this picture from the point of view of Kresák's paper seems to be difficult. It is clearly visible only that at small perihelion distances (less than 1 AU) we observe mainly "old'' comets from the straight line groupings (i.e. having small semimajor axes).

6 Conclusions and future plans

Investigation of the dynamical history of the long-period comet population is rather complicated. First of all, one should limit the sample to those comets with relatively good quality orbits - Marsden's orbital classes (Marsden et al. 1978) seem to be a convenient but probably a little bit outdated tool for this. Next, it is necessary to calculate the original cometary orbits for the whole sample accepted. The dynamical model and the computational procedure should be chosen carefully to obtain as accurate orbits as possible. In our paper we omit two important perturbing forces: non-gravitational effects and the perturbations from small Solar System bodies (mainly large asteroids, but in some cases large natural satellites should probably also be included - we include here only the Moon). Including nongravitational forces into the dynamical model of the motion of long-period comets is possible, but obtaining a reliable set of nongravitational parameters in case of those comets is very difficult, if at all possible. For a discussion on this subject see for example the review by Yeomans (1994). On the other hand, the advances in asteroid mass determination in recent years make it possible to include into the model their gravitational pull on comets and we plan to do so in the near future. We think, that for the majority of comets, their original orbits remain almost the same, but exceptions are possible.

Having a set of original orbit elements of all "good quality'' comets one can investigate their past motion. For all comets which return to the Planetary System, the limiting date is the previous perihelion - at present we cannot say anything reliable about the planetary positions several million years ago so, planetary perturbations cannot be included at the previous return of such a comet and their motion cannot be traced further in the past. The motion of all other comets can be followed for a long time, provided we can model all perturbing forces with sufficient accuracy. If the aphelion distance of a comet does not exceed say $2\times 10^{5}$ AU and for a time interval of a few cometary orbital periods it seems to be sufficient to include Galactic Disk tidal forces and stellar perturbations due to close approaches to the Sun. Galactic perturbations can be easily included using the Heisler & Tremaine (1986) approximation, but calculating the influence of all stars visiting the neighbourhood of the Sun in the studied interval of time (say ten million years) is difficult due to incompleteness and inaccuracies in stellar data. We plan to include in our model all stars for which the data on spatial position and velocity will be available.

For those comets, whose aphelion distances are quite large, and especially for originally hyperbolic comets, a more sophisticated dynamical model of the influence of the Galaxy should be adopted, including the motion of the Sun in the galactic frame. The problem of stellar perturbations remains very important here, but it seems that it can be solved only in a statistical manner through some kind of simulation. This population of comets is under study in a different project.

The widely used terms: dynamically "new'' and "old'' comets should be used with care, taking into account the past motion of those comets. One should not call "new'' a comet for which we can almost be sure that it penetrated the vicinity of the Sun at least once in the past. We know that original orbits are not free from errors, and due to this, some previous aphelia or perihelia are wrong. However, the whole population of previous long-period cometary orbits seems to be quite consistent with our theories of their origin and evolution.

Acknowledgements
The author wishes to thank Halina Pretka-Ziomek for valuable discussions during preparation of this paper and Tadeusz Jopek for his help in improving the first version of this manuscript. Special thanks should be given to Dr. Brian Marsden who, as a referee, formulated many important suggestions and comments which allowed us to greatly improve the final version of this paper.

References

 
Copyright ESO 2001