A&A 375, 319-327 (2001)
DOI: 10.1051/0004-6361:20010738
S. Johansson 1 - V. S. Letokhov 2,1
1 - Department of Physics, Lund University,
PO Box 118, 22100 Lund, Sweden
2 - Institute of Spectroscopy, Russian Academy of Sciences, Troitsk,
Moscow region, 142190, Russia
Received 8 January 2001 / Accepted 21 May 2001
Abstract
We discuss resonance-enhanced two-photon ionization (RETPI) and present schemes
of successive RETPI of the elements C, N, and O in nebulae. RETPI is activated by
intrinsic radiation stored in the form of trapped spectral lines of HI, HeI, and HeII
in the optically thick nebula. The rate of this two-step photoionization is comparable
with or exceeds the low recombination rate of the photoions formed in the process.
This leads to an accumulation of photoions and subsequent RETPI until such
highly charged ions are formed that they cannot further be ionized in this way by the
intrinsic radiation from the strong spectral lines of HI, HeI, and HeII.
Key words: atomic processes - radiation mechanisms - planetary nebulae: general
Photoinduced processes have been known to play an important part in the physics of
planetary and gaseous nebulae (Aller 1956, 1984; Pottasch 1984; Osterbrock 1989),
as they are responsible for the inflow of radiative
energy from the central star (stars). The short-wavelength radiation provides the
photoionization absorption of hydrogen and helium, whose atoms repeatedly
take part in this process. The H and He ions recombine with electrons, thus providing
for the permanent conversion of the absorbed stellar radiation into kinetic energy
of the photoelectrons produced and radiative energy of the recombination transitions,
especially the high-intensity EUV lines in the Lyman series of HI and HeII and the
resonance lines of HeI. This line radiation suffers from resonance scattering due to
diffusion trapping in the optically dense nebula, which results in Doppler diffusive
broadening of the spectral lines and an increase of their intensity inside the nebula.
Both these effects are important for the radiative cooling of the nebula because of the
escape of trapped photons through the wings of the spectral lines (the Zanstra effect)
(Zanstra 1949) and the escape of optically thin fluorescence lines of other elements produced in
a Bowen mechanism (Bowen 1935). The latter is caused by an accidental wavelength coincidence
between a H or He line and an absorption line (1
![]() 2) of these elements
(see Fig. 1a).
2) of these elements
(see Fig. 1a).
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{H2631F1.eps} \end{figure}](/articles/aa/full/2001/31/aah2631/Timg8.gif) |
Figure 1:
a) Accidental resonance "bound-bound state" excitation
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=14cm,clip]{H2631F2.eps} \end{figure}](/articles/aa/full/2001/31/aah2631/Timg12.gif) |
Figure 2:
Various schemes of resonance-enhanced two-photon ionization (RETPI) by
two monochromatic spectral lines with various detuning |
| Open with DEXTER | |
The slow recombination rate of the photoions produced in rarefied nebular plasmas allows their accumulation at a comparatively low photoionization rate. We have, therefore, considered the possibility of resonance-enhanced two-photon ionization (RETPI) even in the absence of the exact intermediate resonance (Johansson & Letokhov 2001c), necessary for a photoselective excitation mechanism. In the RETPI case, the intrinsic EUV radiation of the very intense lines of HI, HeI, and HeII, trapped in the nebula, can stimulate RETPI to occur in several ionization stages of various elements in spite of its low rate compared to laboratory laser experiments (Letokhov 1987). In the present paper, we consider RETPI schemes for C, N, and O, which are of interest in the understanding of the mechanisms that convert the hydrogen and helium radiation trapped in the nebula into spectral lines of other elements. The implementation of this new elementary mechanism for particular problems (shift in the ionization balance, anomalous intensity ratios of spectral lines, etc.) in specific planetary nebulae is the subject for future considerations and are out of the scope of the present paper.
Let an isolated atomic particle X (a neutral atom or an ion in a given
ionization state N) reside in an isotropic radiation field with a spectral intensity of
![]() [in photons/cm2sHz]. Let also the
spectral width of the radiation field
[in photons/cm2sHz]. Let also the
spectral width of the radiation field
![]() exceed the Doppler width
exceed the Doppler width
![]() of the allowed transition
of the allowed transition
![]() ,
and the shift
,
and the shift ![]() (hereafter called
"detuning") of the central frequency
(hereafter called
"detuning") of the central frequency ![]() of the radiation field from the
allowed transition
of the radiation field from the
allowed transition ![]() exceed
the spectral width
exceed
the spectral width
![]() (Figs. 2a,b). In that case, the one-quantum resonant
excitation to level 2 is impossible because the energy defect
(Figs. 2a,b). In that case, the one-quantum resonant
excitation to level 2 is impossible because the energy defect
![]() cannot be transferred to a third partner in a rarefied nebular medium.
But, resonance scattering of the radiation is possible here, and its probability is
determined by the Lorentzian wing of the natural (radiative) broadening
cannot be transferred to a third partner in a rarefied nebular medium.
But, resonance scattering of the radiation is possible here, and its probability is
determined by the Lorentzian wing of the natural (radiative) broadening ![]() = 2A21of the transition
= 2A21of the transition
![]() ,
whose amplitude is proportional to
,
whose amplitude is proportional to
![]() (Weisskopf 1933). The direct excitation of level 2
is only possible as a result of the two-quantum excitation of
a virtual level with an energy of 2
(Weisskopf 1933). The direct excitation of level 2
is only possible as a result of the two-quantum excitation of
a virtual level with an energy of 2![]() and the subsequent spontaneous emission of
a photon with a frequency of h(2
and the subsequent spontaneous emission of
a photon with a frequency of h(2![]() -
-![]() ). According to Makarov (1983),
the probability of this process is proportional to
). According to Makarov (1983),
the probability of this process is proportional to
![]() ,
and it is substantially lower than the resonance scattering probability.
,
and it is substantially lower than the resonance scattering probability.
However, the atomic particle XN can virtually be in the excited state 2 with a probability of W2. It is not difficult to calculate W2 and express it in terms of the Einstein coefficient A21.
For the sake of simplicity we assume that the radiation field
with the amplitude E is linearly polarized and acts in a coherent fashion at the
frequency ![]() detuned by
detuned by
![]() from the frequency
from the frequency ![]() .
Actually, the quantity W2 is independent of
the polarization of the radiation. In the case when the frequency detuning
.
Actually, the quantity W2 is independent of
the polarization of the radiation. In the case when the frequency detuning
![]() ,
the oscillations of the wave
function amplitudes are faster than the oscillations of the field amplitude.
Under such a condition the interaction of the radiation field with a two-level
quantum system can be treated in a coherent way. According to perturbation theory we
have
,
the oscillations of the wave
function amplitudes are faster than the oscillations of the field amplitude.
Under such a condition the interaction of the radiation field with a two-level
quantum system can be treated in a coherent way. According to perturbation theory we
have
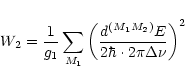 |
(1) |
Next we want to express the sum of the squared dipole moments on the right-hand side
of formula (1) in terms of A21. We can use the
well-known formula relating the matrix element of the dipole moment operator for a pair
of non-degenerate sublevels to the rate
![]() of spontaneous
transitions between these sublevels (see, for example, Sobel'man 1979):
of spontaneous
transitions between these sublevels (see, for example, Sobel'man 1979):
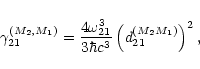 |
(2) |
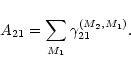 |
(3) |
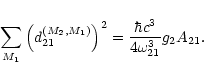 |
(4) |
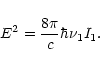 |
(5) |
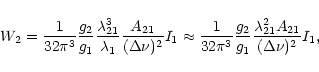 |
(6) |
The ionization energy of the atomic particle in the virtually excited state is
(IP - ![]() ), where IP is the ionization potential of XN.
It is lower than either of the photon energy
), where IP is the ionization potential of XN.
It is lower than either of the photon energy ![]() of the same radiation field and
the photon energy of a second intense field with an average frequency
of the same radiation field and
the photon energy of a second intense field with an average frequency ![]() ,
for
which
,
for
which ![]() (IP -
(IP - ![]() ). In that case, there exists a certain probability that
the atomic particle will make a two-quantum transition through the virtual level to
the ionization continuum at a rate
). In that case, there exists a certain probability that
the atomic particle will make a two-quantum transition through the virtual level to
the ionization continuum at a rate
![]() (s-1) given by:
(s-1) given by:
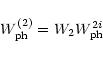 |
(7) |
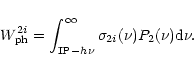 |
(8) |
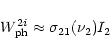 |
(9) |
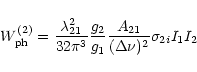 |
(10) |
In the case of intense non-monochromatic photoionizing radiation (for example, diluted,
but spectrally wide, black body radiation from the central star as shown in Fig. 2b) it is
necessary to use expression (8) for an estimation of
![]() .
Before we discuss the less frequent case of exact resonance
(
.
Before we discuss the less frequent case of exact resonance
(
![]() ),
where the Bowen resonance excitation mechanism proves effective, let us estimate the
rate of the RETPI process under nebular conditions. A specific feature of planetary
nebulae is the huge optical thickness in the spectral lines of transitions to the ground
state or low metastable states. Because of this, the photons resulting from the
recombination of
the photoions HII (or HeII), which are being constantly produced under the effect of the
ionizing radiation of the star, repeatedly undergo resonance scattering before they
leave the nebular medium and thus become observable. This diffusive confinement (or
trapping) is accompanied by a broadening of the nebular emission lines and a
large increase of the radiation intensity inside the nebula. The broadening is limited
either by the decay of the photons as a result of absorption or by their escape from
the spectral line wings due to a Doppler frequency redistribution induced by their
scattering on moving resonant particles.
All these effects are essential
for spectral lines having a huge optical thickness
),
where the Bowen resonance excitation mechanism proves effective, let us estimate the
rate of the RETPI process under nebular conditions. A specific feature of planetary
nebulae is the huge optical thickness in the spectral lines of transitions to the ground
state or low metastable states. Because of this, the photons resulting from the
recombination of
the photoions HII (or HeII), which are being constantly produced under the effect of the
ionizing radiation of the star, repeatedly undergo resonance scattering before they
leave the nebular medium and thus become observable. This diffusive confinement (or
trapping) is accompanied by a broadening of the nebular emission lines and a
large increase of the radiation intensity inside the nebula. The broadening is limited
either by the decay of the photons as a result of absorption or by their escape from
the spectral line wings due to a Doppler frequency redistribution induced by their
scattering on moving resonant particles.
All these effects are essential
for spectral lines having a huge optical thickness
![]() -108.
As a result, the intensity P of the
trapped spectral lines reaches its maximum, i.e., the intensity of the black-body radiation
at the corresponding wavelength
-108.
As a result, the intensity P of the
trapped spectral lines reaches its maximum, i.e., the intensity of the black-body radiation
at the corresponding wavelength ![]() ,
and can be described in terms of the effective
temperature
,
and can be described in terms of the effective
temperature
![]() :
:
![\begin{displaymath}P(\lambda,T) = \frac{8\pi}{\lambda^2} \frac{\delta\nu}{{\rm e}^{h\nu/kT_{\rm eff}} - 1}
[{\rm photons/cm}^2\, {\rm s}],
\end{displaymath}](/articles/aa/full/2001/31/aah2631/img51.gif) |
(11) |
In terms of the effective temperature
![]() of the equivalent Planck
radiation (11), the RETPI rate (10) may be represented in the form
of the equivalent Planck
radiation (11), the RETPI rate (10) may be represented in the form
![$\displaystyle W_{1i} = \frac{2}{\pi}\frac{g_2}{g_1}\frac{\delta\nu_1\delta\nu_2...
...ht]^{-1}\left[ \exp\left(\frac {h\nu_2}{kT^2_{\rm eff}}\right) - 1\right]^{-1}.$](/articles/aa/full/2001/31/aah2631/img61.gif) |
(12) |
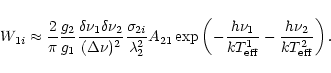 |
(13) |
To understand the efficiency of the RETPI process, let us compare its rate W1i
with the rate of ionization by electrons. In both cases, there exists the exponential factor
exp
![]() ,
where
,
where
![]() ,
IP is the ionization
potential, and T is the corresponding radiation or electron
temperature. Thus, the main difference between collisional ionization by electrons and
collisionless RETPI by photons lies in the difference between the non-exponential factor
denoted by
,
IP is the ionization
potential, and T is the corresponding radiation or electron
temperature. Thus, the main difference between collisional ionization by electrons and
collisionless RETPI by photons lies in the difference between the non-exponential factor
denoted by ![]() and
and
![]() ,
respectively. According to (13), in the case
of RETPI
,
respectively. According to (13), in the case
of RETPI
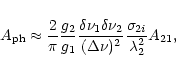 |
(14) |
In the text below, we consider a situation where the most intense trapped spectral lines
of HI, HeI, and HeII (lines in the range
232-1215 Å) in the
EUV region are in close resonance with the allowed transitions in a number of atoms and
their ions. These are thus capable of undergoing RETPI at a rate
![]() comparable to the recombination rate
comparable to the recombination rate
![]() in nebular media. We will refrain from
considering any values of the actual effective temperature and spectral width, as these
vary for different nebulae and within the same
nebula as well. We restrict ourselves to analysis of specific cases, where we find close
resonances of trapped H and He lines with the strongest transitions in carbon,
nitrogen, and oxygen atoms and their ions in successive stages of ionization, i.e. we consider various chains of successive RETPI occurring in these elements.
in nebular media. We will refrain from
considering any values of the actual effective temperature and spectral width, as these
vary for different nebulae and within the same
nebula as well. We restrict ourselves to analysis of specific cases, where we find close
resonances of trapped H and He lines with the strongest transitions in carbon,
nitrogen, and oxygen atoms and their ions in successive stages of ionization, i.e. we consider various chains of successive RETPI occurring in these elements.
As will be evident below, in some cases the frequency detuning ![]() is only a
few tens of cm-1, i.e., it can be smaller than the spectral line width
is only a
few tens of cm-1, i.e., it can be smaller than the spectral line width
![]() (Fig. 2c). In such an exact accidental resonance, as is the case in the
Bowen mechanism, the excited level is actually populated. The maximum
excitation probability W2 would be limited by the effective temperature
(Fig. 2c). In such an exact accidental resonance, as is the case in the
Bowen mechanism, the excited level is actually populated. The maximum
excitation probability W2 would be limited by the effective temperature
![]() of
the exciting radiation, provided that the radiation is in equilibrium with the resonant
atoms:
of
the exciting radiation, provided that the radiation is in equilibrium with the resonant
atoms:
![\begin{displaymath}W_2 = \left[ \exp\left(\frac {h\nu_1}{kT^1_{\rm eff}}\right)-1\right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2001/31/aah2631/img89.gif) |
(15) |
![\begin{displaymath}W^{(2)}_{\rm ph}(1-i)=\sigma_{2i}(\nu_2)I_2\left[\exp\left(\frac {h\nu_1}{kT^1_{\rm eff}}
\right)-1\right]^{-1}
\end{displaymath}](/articles/aa/full/2001/31/aah2631/img90.gif) |
(16) |
![$\displaystyle W^{(2)}_{\rm ph}(1-i)=8\pi\frac{\sigma_{2i}(\nu_2)}{\lambda^2_{12...
...ght] ^{-1}\left[ \exp\left(\frac{h\nu_2}{kT^2_{\rm eff}}\right)-1\right] ^{-1}.$](/articles/aa/full/2001/31/aah2631/img91.gif) |
(17) |
The detailed calculation of the rates of resonance-enhanced two-photon and of resonance stepwise two-photon ionization by dichromatic isotropic noncoherent radiation will be published elsewhere.
![\begin{figure}
\par\includegraphics[angle=270,width=14.4cm,clip]{H2631F3.eps} \end{figure}](/articles/aa/full/2001/31/aah2631/Timg92.gif) |
Figure 3:
Chain of successive RETPI schemes for carbon: CI
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=14.4cm,clip]{H2631F4.eps} \end{figure}](/articles/aa/full/2001/31/aah2631/Timg93.gif) |
Figure 4:
Chain of successive RETPI schemes for carbon:
CIII
|
| Open with DEXTER | |
Analysis of the allowed quantum transitions in the carbon atom and subsequent carbon
ions, on the basis of the data published in Bashkin & Stoner (1975), immediately points to
the possibility of
RETPI with suitable pairs of intense trapped lines of HI, HeI, and HeII
in the EUV region extending from HLy![]() (1215 Å) to HeIILy
(1215 Å) to HeIILy![]() (243 Å).
Out of a large number of suitable pairs of lines, we included only those
which have close coincidences with allowed transitions in the carbon atom or the
carbon ions. We have not considered transitions characterized by either a large
frequency detuning
(243 Å).
Out of a large number of suitable pairs of lines, we included only those
which have close coincidences with allowed transitions in the carbon atom or the
carbon ions. We have not considered transitions characterized by either a large
frequency detuning ![]() or a low transition
probability A21 as the RETPI rate could be low according to (10) and (13).
or a low transition
probability A21 as the RETPI rate could be low according to (10) and (13).
The RETPI schemes for carbon (Figs. 3, 4) provide a path to CV. However,
there is no suitable quasi-resonance for C V
with any of the EUV spectral lines of H and He, which means that this ion is the
end ion in the successive RETPI chain CI
![]() CII
CII
![]() CIII
CIII
![]() CIV
CIV
![]() CV. For each step in the chain, the relative frequency
detuning (
CV. For each step in the chain, the relative frequency
detuning (
![]() )
does not exceed
)
does not exceed
![]() .
At an effective
radiative temperature of the spectral lines in the
range (15-
.
At an effective
radiative temperature of the spectral lines in the
range (15-
![]() K the total RETPI chain achieves a relatively high rate of
10-6-10-4 s-1. In some steps, CI
K the total RETPI chain achieves a relatively high rate of
10-6-10-4 s-1. In some steps, CI
![]() CII, for example, the
photoionization of the virtually excited state 2 can be carried out by radiation over
a very broad spectral region:
CII, for example, the
photoionization of the virtually excited state 2 can be carried out by radiation over
a very broad spectral region:
![]()
![]() m. This means that the rate
m. This means that the rate
![]() defined by Eq. (8) can be high enough even for photoionization
caused by the diluted black body radiation from the central star. However, this rate
depends on the radiation dilution factor, i.e., the distance from the central star.
defined by Eq. (8) can be high enough even for photoionization
caused by the diluted black body radiation from the central star. However, this rate
depends on the radiation dilution factor, i.e., the distance from the central star.
![\begin{figure}
\par\includegraphics[angle=270,width=17cm,clip]{H2631F5.eps} \end{figure}](/articles/aa/full/2001/31/aah2631/Timg99.gif) |
Figure 5:
Chain of successive RETPI schemes for nitrogen: NI
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=13cm,clip]{H2631F6.eps} \end{figure}](/articles/aa/full/2001/31/aah2631/Timg100.gif) |
Figure 6:
Chain of successive RETPI schemes for nitrogen:
NIII
|
| Open with DEXTER | |
Similar RETPI schemes for oxygen (Figs. 7, 8) can
terminate with the OV photoion. Specific features of oxygen are the existence of several
very close resonances between OI and the lines HLy
![]() ,
and the close
proximity of virtually excited oxygen states to the ionization limit. Obviously the
ionization balance OI
,
and the close
proximity of virtually excited oxygen states to the ionization limit. Obviously the
ionization balance OI
![]() OII should be substantially shifted toward OII.
OII should be substantially shifted toward OII.
![\begin{figure}
\par\includegraphics[angle=270,width=14.5cm,clip]{H2631F7.eps} \end{figure}](/articles/aa/full/2001/31/aah2631/Timg103.gif) |
Figure 7:
Chain of successive RETPI schemes for oxygen: OI
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=12.5cm,clip]{H2631F8.eps} \end{figure}](/articles/aa/full/2001/31/aah2631/Timg104.gif) |
Figure 8:
Chain of successive RETPI schemes for oxygen:
OIII
|
| Open with DEXTER | |
All the excitation and ionization steps for the RETPI process in carbon, nitrogen and oxygen are summarized in Table 1, which shows the chains for the atoms and successive ions of these elements. The atoms and ions are exposed to pairs of spectral lines with progressively increasing photon energies: HI + HI, HI + HeI, HI + HeII, HeI + HeI, and finally HeII + HeII.
| Element | Pairs of Photoionizing Spectral Lines of HI, HeI and HeII | ||||
|---|---|---|---|---|---|
|
|
|
|
|
|
|
| C | CI
|
CII
|
CIII
|
CIV
|
|
| 1215 Å + 1215 Å | 1026 Å + 584 Å | 972 Å + 303 Å | 243 Å + 584 Å | ||
| 537 Å + 1215 Å | 303 Å + 1215 Å | ||||
| CII
|
CIV
|
||||
| 1026 Å + 972 Å | 243 Å + 919 Å | ||||
| N | NI
|
NII
|
NIII
|
NII
|
NIV
|
| 972 Å + 1215 Å | 537 Å + 1215 Å | 303 Å + 1215 Å | 1085 Å + 584 Å | 243 Å + 303 Å | |
| 949 Å + 1215 Å | |||||
| O | OI
|
OII
|
OIII
|
OIV
|
|
| 1026 Å + 1215 Å | 537 Å + 1026 Å | 303 Å + 584 Å | 237 Å + 303 Å | ||
| (972 Å) + 1215 Å | |||||
| (949 Å) + 1215 Å | |||||
| (937 Å) + 1215 Å | |||||
It seems reasonable that the proposed elementary process of photoionization by the
intrinsic EUV radiation trapped in nebulae should be taken into consideration in
calculating the ionization balance of those elements, whose observed spectral lines
are essentially the only information available on the processes
occurring inside nebulae. Since the RETPI rate
![]() apparently can exceed the collisional electron ionization rate
apparently can exceed the collisional electron ionization rate ![]() ,
RETPI
will enhance the corresponding recombination lines, which are frequently interpreted
in the framework of ionization by electron collisions as being the result of an
anomalous abundance effect (Aller 1984; Pottasch 1984).
,
RETPI
will enhance the corresponding recombination lines, which are frequently interpreted
in the framework of ionization by electron collisions as being the result of an
anomalous abundance effect (Aller 1984; Pottasch 1984).
From this standpoint, one can understand that the existing
determinations of the chemical abundance from spectral data frequently disagree.
For example, an anomalous ratio often observed for the abundances of CIV and CII
can be explained by the RETPI of CIII, carried out jointly by the HLy![]() line
(972 Å) and HeIILy
line
(972 Å) and HeIILy![]() at 303 Å or directly by HeIILy
at 303 Å or directly by HeIILy![]() at 256 Å (Fig. 4).
As another example, one can refer to the "puzzle" of the anomalous oxygen recombination
lines in planetary nebulae (Dinerstein et al. 2000). The authors of that paper
suggest the existence of a "line
enhancement effect due to an unidentified physical mechanism". We believe the anomay can
be the result of the RETPI process according to the scheme in Fig. 8.
at 256 Å (Fig. 4).
As another example, one can refer to the "puzzle" of the anomalous oxygen recombination
lines in planetary nebulae (Dinerstein et al. 2000). The authors of that paper
suggest the existence of a "line
enhancement effect due to an unidentified physical mechanism". We believe the anomay can
be the result of the RETPI process according to the scheme in Fig. 8.
Moreover, in the case of exact resonance in some link of the successive RETPI chain, the ionization balance between two successive ions of an element can be primarily governed by the rate of the RETPI process in an appropriate excitation scheme and not by electron collisions. In that case, the determination of the electron temperature from a comparison between the spectral line intensities of such neighbouring ions may prove incorrect.
In conclusion, we would like to emphasize that RETPI is a photonic mechanism with no requirement of any collisions. For this reason, it is especially effective in nebulae with low electron densities, and with sizes and concentrations of HI, HII, HeI, and HeII that are great enough to form strong optically thick emission lines of HI, HeI, and HeII. The necessary combinations of parameters (volume, concentration, etc.) that can provide the very high intensity of these spectral lines for efficient RETPI inside nebulae will be the subject for future research, as well as the effect that RETPI causes on the ionization balance in individual nebulae. Such problems will be natural applications of the newly proposed mechanism in planetary nebulae. The high efficiency of RETPI by the intrinsic EUV radiation trapped in nebulae compared to that of electronic collision ionization is a result of the higher density and velocity of photons compared to electrons.
Acknowledgements
One of the authors (V. S. L.) is thankful to Dr. A. A. Makarov for valuable discussions of the problem. We are also grateful to Dr. T. Gull for useful comments on the manuscript. This project is carried out when V. S. L. is holding the Tage Erlander Guest Professorship at Lund University, and it is supported by grants (S. J.) from the Swedish Natural Science Research Council and the Swedish National Space Board.