A&A 375, 251-259 (2001)
DOI: 10.1051/0004-6361:20010846
Space Research Laboratory, Department of Physics, University of Turku, 20014 Turku, Finland
Received 28 March 2001 / Accepted 28 May 2001
Abstract
Energetic proton transport through self-generated Alfvén waves in
impulsive (![]() -ray) flares is studied using the method of Monte Carlo
simulations. Protons are traced inside a flux tube after they are released from
a point source located inside the loop until they hit the boundary of the 1-D
simulation box and escape. As they stream from the source towards the
boundaries, the particles generate Alfvén waves through the streaming
instability. We consider both open and closed field lines. In the closed field
line case, the escaping particles precipitate and produce observable secondary
emissions; for the open field line, particles precipitate only from one end of
the field line, and escape freely to the interplanetary medium from the other
end. For a sufficiently large number of accelerated protons per unit area,
-ray) flares is studied using the method of Monte Carlo
simulations. Protons are traced inside a flux tube after they are released from
a point source located inside the loop until they hit the boundary of the 1-D
simulation box and escape. As they stream from the source towards the
boundaries, the particles generate Alfvén waves through the streaming
instability. We consider both open and closed field lines. In the closed field
line case, the escaping particles precipitate and produce observable secondary
emissions; for the open field line, particles precipitate only from one end of
the field line, and escape freely to the interplanetary medium from the other
end. For a sufficiently large number of accelerated protons per unit area,
![]() where n0 is the plasma density,
VA the Alfvén speed, and
where n0 is the plasma density,
VA the Alfvén speed, and
![]() the proton
gyro-frequency, the particle flux from the source produces a turbulent trap that
expands at Alfvén speed in both directions from the source. The resulting
the proton
gyro-frequency, the particle flux from the source produces a turbulent trap that
expands at Alfvén speed in both directions from the source. The resulting
![]() -ray emission from the loop legs consists of a precursor, related to
the quick propagation of particles when the trap has not formed yet, and of a
delayed brightening in the loop leg closer to the source, related to the opening
of the turbulent trap as the self-generated waves reach the solar surface. For
impulsive injections lasting
-ray emission from the loop legs consists of a precursor, related to
the quick propagation of particles when the trap has not formed yet, and of a
delayed brightening in the loop leg closer to the source, related to the opening
of the turbulent trap as the self-generated waves reach the solar surface. For
impulsive injections lasting
![]() ,
where L is the loop
length, the second emission may be suppressed by adiabatic deceleration in the
expanding turbulent trap. For open field lines, our model is capable of
producing the small ratio of the numbers of interplanetary-to-interacting
protons typically observed in impulsive flares, if the proton source is located
close to the Sun.
,
where L is the loop
length, the second emission may be suppressed by adiabatic deceleration in the
expanding turbulent trap. For open field lines, our model is capable of
producing the small ratio of the numbers of interplanetary-to-interacting
protons typically observed in impulsive flares, if the proton source is located
close to the Sun.
Key words: diffusion - instabilities - Sun: flares - Sun: particle emission - Sun: X-rays, gamma rays - turbulence
Acceleration of protons up to several tens of MeVs and beyond may take place at
different phases of solar eruptions, from the flare pulse in the low corona
through the passage of the interplanetary shock beyond the Earths orbit. Some
protons interact at the Sun, producing secondary ![]() -rays and neutrons,
others escape into the interplanetary medium to produce a solar energetic
particle (SEP) event at 1 AU. The current two-class paradigm of solar particle
events suggests that impulsive SEP events originate in impulsive solar flares
and gradual events are linked to the coronal/interplanetary shocks (Cane et al. 1986; Cliver 1996; Reames 1999 and references
therein). Impulsive flares may produce 3He-rich SEP events, which
typically are not strong in terms of the total number of accelerated
protons. Some impulsive flares, however, can produce a large number of
interacting protons and can be observed in the
-rays and neutrons,
others escape into the interplanetary medium to produce a solar energetic
particle (SEP) event at 1 AU. The current two-class paradigm of solar particle
events suggests that impulsive SEP events originate in impulsive solar flares
and gradual events are linked to the coronal/interplanetary shocks (Cane et al. 1986; Cliver 1996; Reames 1999 and references
therein). Impulsive flares may produce 3He-rich SEP events, which
typically are not strong in terms of the total number of accelerated
protons. Some impulsive flares, however, can produce a large number of
interacting protons and can be observed in the ![]() -ray band. In such
events the ratio of the numbers of interplanetary-to-interacting protons is
typically small (
-ray band. In such
events the ratio of the numbers of interplanetary-to-interacting protons is
typically small (
![]() 0.1), whereas gradual
0.1), whereas gradual ![]() -ray flares show
larger (
-ray flares show
larger (
![]() 1) values of this ratio (Kocharov & Kovaltsov 1986;
Hua & Lingenfelter 1987; Ramaty et al. 1993).
1) values of this ratio (Kocharov & Kovaltsov 1986;
Hua & Lingenfelter 1987; Ramaty et al. 1993).
Intensive production of accelerated protons implies the potential importance of
self-generated waves, i.e., waves generated by the flux of protons leaking from
the accelerator (see, e.g., Ng et al. 1999 in application to gradual
SEP events). In application to impulsive ![]() -ray flares, the role of
self-generated waves was emphasized by Bespalov et al. (1987,
1991). The transport conditions of protons in flaring loops determine
the time scale for their precipitation. The conditions are, therefore, crucial
for the flare scenario. Strong interaction with hydromagnetic waves is known to
make the trapping of protons inside the loop efficient. Bespalov et
al. (1987, 1991) studied the proton transport under the
assumption that the protons stream away from a source located at the top of the
loop, and generate Alfvén waves. They showed that for a sufficiently strong
source, the waves would become so intense that the particles would essentially
be locked on the waves and convect with them at Alfvén speed towards the
footpoints of the loop. Electrons, being coupled to whistler and ion-cyclotron
waves, would travel much faster than protons, having a bulk speed of
-ray flares, the role of
self-generated waves was emphasized by Bespalov et al. (1987,
1991). The transport conditions of protons in flaring loops determine
the time scale for their precipitation. The conditions are, therefore, crucial
for the flare scenario. Strong interaction with hydromagnetic waves is known to
make the trapping of protons inside the loop efficient. Bespalov et
al. (1987, 1991) studied the proton transport under the
assumption that the protons stream away from a source located at the top of the
loop, and generate Alfvén waves. They showed that for a sufficiently strong
source, the waves would become so intense that the particles would essentially
be locked on the waves and convect with them at Alfvén speed towards the
footpoints of the loop. Electrons, being coupled to whistler and ion-cyclotron
waves, would travel much faster than protons, having a bulk speed of
![]() 9
9
![]() (e.g., Vainio 2000). This would lead,
consistent with observations of impulsive flares, to a delay in the
(e.g., Vainio 2000). This would lead,
consistent with observations of impulsive flares, to a delay in the ![]() -ray emission relative to the X-ray emission, if electrons and protons were
accelerated simultaneously near the top of the flaring loop (Bespalov et al. 1987). Since the bulk speed of electrons depends on energy,
however, the ultra-relativistic electrons responsible for the
-ray emission relative to the X-ray emission, if electrons and protons were
accelerated simultaneously near the top of the flaring loop (Bespalov et al. 1987). Since the bulk speed of electrons depends on energy,
however, the ultra-relativistic electrons responsible for the ![]() -ray
continuum behave very similarly to protons. Note that the delay of the peak time
of the
-ray
continuum behave very similarly to protons. Note that the delay of the peak time
of the ![]() -ray emission relative to the X-ray peak could also be
interpreted in terms of particle transport in flaring loops with weak external
turbulence and large variation of the cross-sectional area of the flux tube
(Hulot et al. 1989, 1992).
-ray emission relative to the X-ray peak could also be
interpreted in terms of particle transport in flaring loops with weak external
turbulence and large variation of the cross-sectional area of the flux tube
(Hulot et al. 1989, 1992).
One aspect of the turbulent trapping model missing from the original work of Bespalov et al. (1987, 1991) is that it could lead to interesting effects, if the flux tube is asymmetric with respect to the source position, and if transient processes are incorporated in the model. Scattering off self-generated waves at open magnetic field lines may also affect the interplanetary-to-interacting proton ratio. Vainio et al. (2000) obtained reasonable ratios for gradual flares in a model of coronal shock acceleration by arranging the turbulence around the shock in a stationary manner to mimic self-generated waves. In the case of impulsive flares, the role of self-generated waves in forming the interplanetary-to-interacting proton ratio has not yet been studied. Applying the asymmetric, strongly turbulent transport model to an open flux tube with the solar surface on one end, and a free-escape boundary, i.e., the interplanetary medium, at the other end, we could anticipate a small value of the interplanetary-to-interacting proton ratio, if the source is close to the Sun.
The purpose of this paper is to study and extend the transport model of Bespalov et al. (1987, 1991), using a time-dependent numerical method. To simplify the model at this stage, we perform the study inside a single magnetic flux tube with constant values of the magnitude of the magnetic field and plasma density, and zero bulk speed of the thermal plasma. The study includes as separate cases a symmetric loop (Case A), an asymmetric loop (Case B), and an open field line (Case C). The potentially important effects of non-constant plasma parameters (see, e.g., Kocharov et al. 1999) is left for the future. We note here, however, that interpretation of magnetogram data (McClymont & Mikic 1994) suggest that coronal loops showing almost constant cross section are possible due to twists in the magnetic flux tubes. Thus, the constant-field approximation should not be too far from reality to be applied in this study.
Our model consist of a (possibly curved) magnetic field with a constant
magnitude along the line of force considered. Either one (Case C) or both (Cases A and B) ends of the flux tube are tied to the solar surface, where we assume
that the density of the plasma is so large that all particles reaching this
region interact, producing secondary emissions. No mirroring of particles at the
footpoints of the flux tube is taken into account. Trapping of protons by
mirroring at footpoints leads to the escape time of
![]() (e.g.,
Hulot et al. 1989), where
(e.g.,
Hulot et al. 1989), where ![]() is the footpoint mirror ratio. If
this time is small relative to the trapping time by self-generated waves,
L/(2VA) (Bespalov et al. 1987, 1991), one may
regard neglecting the footpoint mirroring reasonable (cf. Kocharov et
al. 1999). Thus, this approximation is justified at
is the footpoint mirror ratio. If
this time is small relative to the trapping time by self-generated waves,
L/(2VA) (Bespalov et al. 1987, 1991), one may
regard neglecting the footpoint mirroring reasonable (cf. Kocharov et
al. 1999). Thus, this approximation is justified at
![]() ,
but for very large values of
,
but for very large values of
![]() ,
trapping by footpoint mirroring should become important.
The basic scale length of the (1-D) system is denoted by L. In the case of a
closed magnetic field, L is the length of the loop and in the case of an open
field, L is the height at which the particles are assumed to freely escape
into the interplanetary medium.
,
trapping by footpoint mirroring should become important.
The basic scale length of the (1-D) system is denoted by L. In the case of a
closed magnetic field, L is the length of the loop and in the case of an open
field, L is the height at which the particles are assumed to freely escape
into the interplanetary medium.
The plasma parameters are fixed to representative values for flaring loops
(Bespalov et al. 1987): Alfvén speed
VA=108 cm s-1, plasma electron (and proton) density
n0=1011 cm-3,
and the length of the loop L=109 cm. In Case C, we choose the length of
the trapping region as
![]() cm being less than or of the order of
the scale height of the magnetic field in the lower corona. The magnetic field in
such a flux tube (with electron-proton composition) is
cm being less than or of the order of
the scale height of the magnetic field in the lower corona. The magnetic field in
such a flux tube (with electron-proton composition) is
![]() Gauss,
and the ion skin length,
Gauss,
and the ion skin length,
![]() cm,
where
cm,
where
![]() s-1 is the proton
gyro-frequency. The plasma temperature is taken to be T=107 K for both
electrons and protons. This gives a value of plasma beta of
s-1 is the proton
gyro-frequency. The plasma temperature is taken to be T=107 K for both
electrons and protons. This gives a value of plasma beta of
![]() for the thermal component.
for the thermal component.
The Alfvén waves responsible for the collisionless scattering of the accelerated protons are assumed to propagate along the mean magnetic field. We, therefore, assume that the flux tube acts as a wave guide in case it is curved. This is valid, if the considered flux tube has a higher plasma density than its surroundings (Mazur & Stepanov 1984). For simplicity, no absorption of the waves by the thermal plasma nor any wave-wave interactions are thought to occur. Sunward-propagating waves are absorbed and anti-sunward propagating waves are emitted at the footpoints of the flux tube. The emitted wave flux at the footpoints has to be, of course, given as a boundary condition.
We consider energetic protons of momentum p=p0 emitted from a point source
located inside the flux tube at x=x0. Protons are followed under the
guiding-center approximation along the magnetic field as they undergo
wave-particle interactions with Alfvén waves of wavenumber that is assumed to
be fixed and given by
![]() .
This approximation to
the full resonance condition,
.
This approximation to
the full resonance condition,
![]() (
(![]() is the
parallel momentum in the wave frame), allows us to follow a single wavenumber
instead of the full spectrum of them, and makes the simulations much simpler and
faster. Particles hitting the ends of the flux tube are assumed to be absorbed
(by stopping at the solar surface or by escape to the interplanetary medium).
The wave-particle interactions are modeled as pitch-angle scattering that is
elastic in each wave frame and occurs at the scattering rates (Skilling
1975)
is the
parallel momentum in the wave frame), allows us to follow a single wavenumber
instead of the full spectrum of them, and makes the simulations much simpler and
faster. Particles hitting the ends of the flux tube are assumed to be absorbed
(by stopping at the solar surface or by escape to the interplanetary medium).
The wave-particle interactions are modeled as pitch-angle scattering that is
elastic in each wave frame and occurs at the scattering rates (Skilling
1975)
Energetic protons interact with the waves self-consistently in the sense of
conserving the total energy (as measured in the plasma frame) of waves and
particles at a microscopic level. Let ![]() and
and
![]() denote the
momentum and pitch-angle cosine as measured in the wave frame indicated by the
subscript. A particle scattering in pitch-angle cosine by an amount of
denote the
momentum and pitch-angle cosine as measured in the wave frame indicated by the
subscript. A particle scattering in pitch-angle cosine by an amount of
![]() (in the wave frame) suffers an energy loss of
(in the wave frame) suffers an energy loss of
![]() in the plasma frame. We use isotropic
scattering, so
in the plasma frame. We use isotropic
scattering, so
![]() .
This leads to a growth of the waves
at the rate
.
This leads to a growth of the waves
at the rate
In the first set of simulations, we study a loop which is spatially symmetric
about the point source of energetic protons. We inject
![]() (corresponding to an energy of about 30 MeV) protons isotropically at a rate
(corresponding to an energy of about 30 MeV) protons isotropically at a rate
![]() cm-2 s-1,
where
cm-2 s-1,
where
![]() is chosen to give a large flux resulting in a
rapid wave growth, but still keeping the energetic-proton pressure at least an
order of magnitude below the thermal proton pressure even if all particles are
trapped by Alfvén waves inside
is chosen to give a large flux resulting in a
rapid wave growth, but still keeping the energetic-proton pressure at least an
order of magnitude below the thermal proton pressure even if all particles are
trapped by Alfvén waves inside
![]() .
We vary the total amount of
injected particles by varying the duration of the injection between
.
We vary the total amount of
injected particles by varying the duration of the injection between
![]() s and 10/15 s, resulting in a total number of injected particles
between
s and 10/15 s, resulting in a total number of injected particles
between
![]() cm-2 and
cm-2 and
![]() cm-2. The background wave flux emitted from the footpoints is fixed by
assuming that the wave mode emitted from each footpoint has an energy density of
cm-2. The background wave flux emitted from the footpoints is fixed by
assuming that the wave mode emitted from each footpoint has an energy density of
![]() .
We assume that this emission
of waves is steady; thus the initial condition for both wave modes is also
.
We assume that this emission
of waves is steady; thus the initial condition for both wave modes is also
![]() .
The adopted value for 2U0 corresponds to an rms
velocity amplitude of 10 kms-1 per logarithmic bandwidth at
.
The adopted value for 2U0 corresponds to an rms
velocity amplitude of 10 kms-1 per logarithmic bandwidth at
![]() kHz. Assuming that this velocity amplitude
holds for all frequencies from
f0=VA/L=0.1 Hz up to
kHz. Assuming that this velocity amplitude
holds for all frequencies from
f0=VA/L=0.1 Hz up to
![]() kHz, the total rms
amplitude is 38 kms-1, which agrees very well with the typical observed
non-thermal velocity in a quiescent active region of 45 km s-1 (Antonucci
& Dodero 1995). The non-thermal velocities in flaring plasmas are
larger, consistent with wave growth. We do not consider any emission of waves
from the acceleration site; we assume that the waves are absorbed by the
particles during the acceleration. However, some external forcing of the
Alfvénic turbulence is modeled by keeping the wave-energy densities above a
minimum level of
kHz, the total rms
amplitude is 38 kms-1, which agrees very well with the typical observed
non-thermal velocity in a quiescent active region of 45 km s-1 (Antonucci
& Dodero 1995). The non-thermal velocities in flaring plasmas are
larger, consistent with wave growth. We do not consider any emission of waves
from the acceleration site; we assume that the waves are absorbed by the
particles during the acceleration. However, some external forcing of the
Alfvénic turbulence is modeled by keeping the wave-energy densities above a
minimum level of
![]() everywhere
inside the flux tube.
everywhere
inside the flux tube.
The results of the simulations are presented in Fig. 1
in form of flux of protons precipitating at the footpoints of the loop. One can
see a peak in the precipitating flux at
![]() s corresponding to the
travel time of Alfvén waves from the center of the loop to the footpoints, as
predicted by the theory of Bespalov et al. (1987, 1991). What
is not predicted by the steady-state theory is the rather intense precursor peak
immediately after the particle release, that corresponds to the first phase,
when the waves have not yet grown enough to suppress the diffusive particle
transport. The number of particles in the precursor seems to be independent of
the number of injected particles, if this number exceeds a threshold level.
This can be understood as follows. We consider an initial turbulence level,
where the diffusion length,
s corresponding to the
travel time of Alfvén waves from the center of the loop to the footpoints, as
predicted by the theory of Bespalov et al. (1987, 1991). What
is not predicted by the steady-state theory is the rather intense precursor peak
immediately after the particle release, that corresponds to the first phase,
when the waves have not yet grown enough to suppress the diffusive particle
transport. The number of particles in the precursor seems to be independent of
the number of injected particles, if this number exceeds a threshold level.
This can be understood as follows. We consider an initial turbulence level,
where the diffusion length,
![]() (where
(where
![]() is the spatial diffusion coefficient), is larger than the
distance from the source to the footpoints. Until the wave-energy density has
grown to a level, denoted by U*, that suppresses diffusive transport, the
particles propagate quickly (relative to the time scale of wave transport)
towards the footpoints adjusting the value of particle flux to
is the spatial diffusion coefficient), is larger than the
distance from the source to the footpoints. Until the wave-energy density has
grown to a level, denoted by U*, that suppresses diffusive transport, the
particles propagate quickly (relative to the time scale of wave transport)
towards the footpoints adjusting the value of particle flux to
![]() (directed away from the source). The wave-energy density
obeys
(directed away from the source). The wave-energy density
obeys
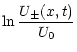 |
= | 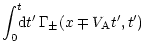 |
|
| = | 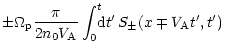 |
||
| (3) |
![\begin{figure}
\includegraphics[width=8.2cm,clip]{ms1322f1.eps}
\end{figure}](/articles/aa/full/2001/31/aa1322/Timg68.gif) |
Figure 1:
Flux of precipitating particles for four values of the total number of
injected protons. The rate of injection is kept constant,
|
| Open with DEXTER | |
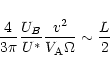 |
(5) |
Let us estimate the spectrum of the promptly-precipitating protons. If a
spectrum of particles is emitted, and if energy changes during the transport are
neglected, we should identify the number of precursor protons with
![]() in the spirit of the
resonance condition
in the spirit of the
resonance condition
![]() .
For a wave spectrum
.
For a wave spectrum
![]() with q<3,
with q<3,
![]() increases with (non-relativistic) energy, although
logarithmically (
increases with (non-relativistic) energy, although
logarithmically (
![]() ). Typical turbulence models give
1<q<2. Up to the energy where the total number of injected particles (per
logarithmic momentum interval),
). Typical turbulence models give
1<q<2. Up to the energy where the total number of injected particles (per
logarithmic momentum interval),
![]() ,
equals the calculated value for the precursor,
Eqs. (4-6), the energy spectrum of the first peak is
,
equals the calculated value for the precursor,
Eqs. (4-6), the energy spectrum of the first peak is
![]() .
At larger energies, only the first peak is observed with a
spectrum identical to that of the source.
.
At larger energies, only the first peak is observed with a
spectrum identical to that of the source.
Using the assumption of a steady state, Bespalov et al. (1991) deduced
that the rate of particle injection determines whether particle transport is
governed by diffusion or convection with the waves. That is correct in the
steady-state regime of continual injection. In the case of short injection,
however, the total number of injected particles, ![]() ,
is the only
controlling factor in the relative importance of the prompt and delayed
components of the precipitating flux. To confirm this, we ran a simulations of
using injection rates of
,
is the only
controlling factor in the relative importance of the prompt and delayed
components of the precipitating flux. To confirm this, we ran a simulations of
using injection rates of
![]() ,
,
![]() ,
and
,
and
![]() and with
and with
![]() cm-2 in all cases
(Fig. 2). The resulting flux of precipitating particles
looks nearly identical for the shortest injections (
cm-2 in all cases
(Fig. 2). The resulting flux of precipitating particles
looks nearly identical for the shortest injections (
![]() s and 1/3 s) since the diffusive time scale is large enough to regard both of these
injections as impulsive. The prolonged injection (
s and 1/3 s) since the diffusive time scale is large enough to regard both of these
injections as impulsive. The prolonged injection (
![]() s), however,
suppresses the height of the precursor while keeping the total number of
precursor particles very similar to the impulsive ones, which is in accord with
diffusive transport. Further, increasing the loop length or the level of ambient
turbulence inside the loop clearly suppresses the importance of the precursor
predicted by the estimation and confirmed by simulations. We, thus, regard the
Eqs. (4-6), up to a numerical factor of the order unity,
as a valid scaling law for arranging observations of precipitating proton
fluences.
s), however,
suppresses the height of the precursor while keeping the total number of
precursor particles very similar to the impulsive ones, which is in accord with
diffusive transport. Further, increasing the loop length or the level of ambient
turbulence inside the loop clearly suppresses the importance of the precursor
predicted by the estimation and confirmed by simulations. We, thus, regard the
Eqs. (4-6), up to a numerical factor of the order unity,
as a valid scaling law for arranging observations of precipitating proton
fluences.
![\begin{figure}
\includegraphics[width=8.7cm,clip]{ms1322f2.eps}
\end{figure}](/articles/aa/full/2001/31/aa1322/Timg85.gif) |
Figure 2:
Precipitating flux for a constant number of injected particles,
|
| Open with DEXTER | |
As became evident from the simulations of Case A, the majority of the particles
in a powerful impulsive flare precipitate once the turbulent walls have reached
the footpoints of the flux tube, at
t=L/2VA. It is of interest to
investigate what happens if the particles are not released in the central point
of the flux tube; if the trap reaches one end first, we should see a peak in the
precipitating flux at this footpoint, but if the precipitation is rapid, the
particle reservoir might empty before the trap opens from the other end. We
have simulated this by varying the position of the source as
![]() ,
,
![]() ,
and
,
and ![]() (from the center of the loop). The number of injected
particles was
(from the center of the loop). The number of injected
particles was
![]() cm-2, and other parameters were chosen
as in Case A. The results are plotted in Fig. 3. The flux
towards the footpoint closer to the source resembles the symmetric case with a
prompt and a delayed peak. The flux at the other footpoint, however, behaves
differently. Even a slightly asymmetric position of the source can lead to a
huge difference in the precipitating flux for the delayed component; in
practice, we can expect a delayed brightening in
cm-2, and other parameters were chosen
as in Case A. The results are plotted in Fig. 3. The flux
towards the footpoint closer to the source resembles the symmetric case with a
prompt and a delayed peak. The flux at the other footpoint, however, behaves
differently. Even a slightly asymmetric position of the source can lead to a
huge difference in the precipitating flux for the delayed component; in
practice, we can expect a delayed brightening in ![]() -rays at only one of
the footpoints based on our simulations. However, the observed asymmetry in the
precursor brightening provides a measure of the asymmetry of the source
position, if the ambient turbulence level is high enough to yield a diffusive
delay in the particle flux reaching the footpoints at different distances from
the source.
-rays at only one of
the footpoints based on our simulations. However, the observed asymmetry in the
precursor brightening provides a measure of the asymmetry of the source
position, if the ambient turbulence level is high enough to yield a diffusive
delay in the particle flux reaching the footpoints at different distances from
the source.
![\begin{figure}
\includegraphics[width=8.2cm,clip]{ms1322f3.eps}
\end{figure}](/articles/aa/full/2001/31/aa1322/Timg86.gif) |
Figure 3:
The flux of precipitating protons in a loop with an asymmetric source
position at
|
| Open with DEXTER | |
Without a possibility to distinguish between the emission from different footpoints, the observations in the asymmetric case are very similar to the symmetric case, and the general conclusions drawn from Case A - two-component structure, importance of the total number of injected particles - are valid also for the asymmetric case.
As a last study, we performed simulations in a flux tube that is connected to
the solar surface from one footpoint at x=0, only. The other end at
![]() cm is assumed to leak the incident particles directly to
the interplanetary medium, modeling a flux tube rapidly expanding above x=L;
a large and rapid expansion would probably eject most of the particles reaching
this distance, since the particle bulk speed is directed outwards, and particles
diffusing backward relative to the flow at
cm is assumed to leak the incident particles directly to
the interplanetary medium, modeling a flux tube rapidly expanding above x=L;
a large and rapid expansion would probably eject most of the particles reaching
this distance, since the particle bulk speed is directed outwards, and particles
diffusing backward relative to the flow at
![]() see the boundary as a
strong magnetic mirror. In a more gently opening geometry, the effects of the
diverging field should be taken into account explicitly in the simulation. The
source is positioned at
see the boundary as a
strong magnetic mirror. In a more gently opening geometry, the effects of the
diverging field should be taken into account explicitly in the simulation. The
source is positioned at ![]() ,
and the total number of injected particles
is
,
and the total number of injected particles
is
![]() cm-2. This case differs from Case B simulations
in that we assume that the background Alfvén waves have a large cross helicity:
the outward propagating waves have
cm-2. This case differs from Case B simulations
in that we assume that the background Alfvén waves have a large cross helicity:
the outward propagating waves have
![]() as in Cases A and B, but
the inward propagating waves have only the minimum-level intensity,
as in Cases A and B, but
the inward propagating waves have only the minimum-level intensity,
![]() .
Other parameters were taken as in
Cases A and B.
.
Other parameters were taken as in
Cases A and B.
The results of the open-field simulation are shown in Fig. 4. The precipitating particle flux again shows a double peaked structure, with a precursor well described by Eqs. (4-6). The escaping flux, however, rises more slowly to a stationary level that is destroyed by the boundary effects, when the turbulent trap hits the free-escape boundary, opening it also from this end. Towards the end of the event, the escaping flux becomes dominant over the precipitating flux. The number of precipitating particles is, however, an order of magnitude larger than the number of escaping particles, which shows that energetic particles accelerated in impulsive flares can be effectively trapped near the Sun even on open field lines. This demonstrates that the small ratio of interplanetary-to-interacting protons observed in impulsive flares do not necessarily result from closed field line topology.
![\begin{figure}
\includegraphics[width=8.27cm,clip]{ms1322f4.eps}
\end{figure}](/articles/aa/full/2001/31/aa1322/Timg92.gif) |
Figure 4: The flux of particles precipitating (solid curve) and escaping into the interplanetary medium (dashed curve) in an open magnetic flux tube. The hatched area is disturbed by a somewhat oversimplified outer boundary condition. |
| Open with DEXTER | |
We have modeled the transport of energetic protons in impulsive flares through
self-generated waves using the Monte Carlo method. Our model uses a scattering
law that is proportional to the energy densities of single-k Alfvén waves
propagating in both directions along the mean field. The energy lost (gained) by
the particles in the scatterings is given to (taken from) the waves. The full
quasi-linear resonance condition would involve a spectrum of waves even in case
of mono-energetic particle distribution. The artificially sharpened resonance
condition
![]() ,
where
,
where ![]() is a
numerical constant of the order unity, is, however, a commonly used
approximation in diffusive particle transport and acceleration theories
involving self-generated waves (e.g., Skilling 1975;
Bell 1978; Lee 1983). It introduces an inaccuracy to the
scattering rates, but for a power-law spectrum of particles it can be tuned by
choosing
is a
numerical constant of the order unity, is, however, a commonly used
approximation in diffusive particle transport and acceleration theories
involving self-generated waves (e.g., Skilling 1975;
Bell 1978; Lee 1983). It introduces an inaccuracy to the
scattering rates, but for a power-law spectrum of particles it can be tuned by
choosing ![]() properly to yield correct growth rates for waves (Skilling
1975). Our simulations make use of a still simpler form,
properly to yield correct growth rates for waves (Skilling
1975). Our simulations make use of a still simpler form,
![]() ,
which is a reasonable choice, if the particles approximately
conserve their energies during the propagation. Note that this assumption is
made implicitly in the analytical calculations of Bespalov et al. (1987, 1991). Because the turbulent trap is expanding
along the magnetic field at a constant rate, however, there exists adiabatic
deceleration of the trapped particles at a rate
,
which is a reasonable choice, if the particles approximately
conserve their energies during the propagation. Note that this assumption is
made implicitly in the analytical calculations of Bespalov et al. (1987, 1991). Because the turbulent trap is expanding
along the magnetic field at a constant rate, however, there exists adiabatic
deceleration of the trapped particles at a rate
![]() .
This
estimate is the lower limit, since it assumes that the particles spend a
negligible fraction of time scattering off the turbulent walls of the trap and
that stochastic acceleration inside the trap can be neglected. However, if the
particle is trapped at t=t0, it has an average final momentum of
.
This
estimate is the lower limit, since it assumes that the particles spend a
negligible fraction of time scattering off the turbulent walls of the trap and
that stochastic acceleration inside the trap can be neglected. However, if the
particle is trapped at t=t0, it has an average final momentum of
![]() ,
when the trap opens (symmetric
case). Thus, significant deceleration could be expected, if the characteristic
trapping time t0 is small. The simulations reveal that precipitating
particles have average momenta
,
when the trap opens (symmetric
case). Thus, significant deceleration could be expected, if the characteristic
trapping time t0 is small. The simulations reveal that precipitating
particles have average momenta
![]() (see
Fig. 5), so the approximative resonance condition seems
acceptable for scattering estimates. Note, however, that the change in energy
during trapping can be substantial in the context of
(see
Fig. 5), so the approximative resonance condition seems
acceptable for scattering estimates. Note, however, that the change in energy
during trapping can be substantial in the context of ![]() -ray production, up to
a factor of
-ray production, up to
a factor of ![]() 5 in the non-relativistic case. For a typical integral particle
spectrum,
5 in the non-relativistic case. For a typical integral particle
spectrum,
![]() ,
this means a factor of
,
this means a factor of ![]() 25 fewer
particles capable of
25 fewer
particles capable of ![]() -ray production, and may suppress the delayed peak
of emission completely. Note, however, that the problem of adiabatic
deceleration is most severe in the case of strong, impulsive injections, as
indicated by Fig. 6, where the average momentum is
plotted for a constant number of injected particles varying the duration of the
injection; for prolonged injections with
-ray production, and may suppress the delayed peak
of emission completely. Note, however, that the problem of adiabatic
deceleration is most severe in the case of strong, impulsive injections, as
indicated by Fig. 6, where the average momentum is
plotted for a constant number of injected particles varying the duration of the
injection; for prolonged injections with
![]() ,
the particles conserve their energies more effectively, because most of them are
injected in a trap that has a large initial dimension.
,
the particles conserve their energies more effectively, because most of them are
injected in a trap that has a large initial dimension.
![\begin{figure}
\includegraphics[width=8.11cm,clip]{ms1322f5.eps}
\end{figure}](/articles/aa/full/2001/31/aa1322/Timg102.gif) |
Figure 5:
Average momentum of precipitating particles in Case A as a function of
time for
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.1cm,clip]{ms1322f6.eps}
\end{figure}](/articles/aa/full/2001/31/aa1322/Timg103.gif) |
Figure 6:
Average momentum of precipitating particles in Case A as a function of
time for
|
| Open with DEXTER | |
Another simplification in our model is the assumption of constant magnetic field and plasma density inside the loop. A constant magnetic field is often seen as near-uniform cross sections of the flare loops (McClymont & Mikic 1994). Non-constant plasma parameters, however, affect wave propagation, particle transport, and wave growth in several ways: (i) wave-frequency conservation changes the wavenumber of a wave propagating at a spatially varying phase speed; (ii) resonant wavenumber changes with position in a non-constant magnetic field; (iii) particles suffer mirroring and adiabatic energy changes in a non-constant magnetic field. Because of all these effects, the wave growth is also affected. Our next step in developing the code is to replace the single wave fields and mono-energetic injections with with wavenumber and particle-energy spectra to estimate the effects of non-constant plasma parameters on wave growth. Once this is done, the resonance conditions can also be modeled more realistically.
Wave damping by plasma ions should be much less important than the growth or
decay due to the energetic particles, because we are considering non-compressive
Alfvén waves having only gyro-resonant interactions. We note, however, that if
one drops the assumption of a wave-guiding loop, even initially
parallel-propagating right-handed (left-handed) Alfvén waves convert to oblique
fast-magnetosonic (Alfvén) waves and may suffer Landau damping (Wentzel
1976). From other processes, at least wave-wave interactions, as
described by weak-turbulence theory, between Alfvén waves (
![]() )
and between Alfvén waves
and sound waves (
)
and between Alfvén waves
and sound waves (
![]() )
have potential importance (see, e.g., Skilling 1975). The
former cascade operates in the perpendicular wavenumber component (and involves
a population of nearly perpendicular waves,
)
have potential importance (see, e.g., Skilling 1975). The
former cascade operates in the perpendicular wavenumber component (and involves
a population of nearly perpendicular waves,
![]() ,
and oblique waves,
,
and oblique waves,
![]() )
and the latter one in the parallel component. The kinetic
equations for these processes, easily adaptable to a Monte Carlo simulation, can
be obtained using quantum-mechanical formalism (Melrose 1980). Both
cascades lead to an effective damping of the resonant waves. The parallel
cascade, however, also helps spreading the wave power to wavenumbers, where the
resonant particles are unable to generate waves on their own. In addition, it
provides waves propagating in the stable direction, so it may also lead to
efficient stochastic acceleration of resonant particles. It is left for future
simulations to address the effects of the wave-wave interactions to the flare
scenario.
)
and the latter one in the parallel component. The kinetic
equations for these processes, easily adaptable to a Monte Carlo simulation, can
be obtained using quantum-mechanical formalism (Melrose 1980). Both
cascades lead to an effective damping of the resonant waves. The parallel
cascade, however, also helps spreading the wave power to wavenumbers, where the
resonant particles are unable to generate waves on their own. In addition, it
provides waves propagating in the stable direction, so it may also lead to
efficient stochastic acceleration of resonant particles. It is left for future
simulations to address the effects of the wave-wave interactions to the flare
scenario.
We have neglected particle drifts due to field curvature in our simulations,
which is justified because of the long time scales (hours) associated with the
curvature drift (Ramaty & Mandzhavidze 1994). We have also neglected
Coulomb losses and nuclear interactions during the propagation in our model.
This is justified, since the trapping times we consider are relatively short
(
![]() 10 s): a Coulomb-loss estimate (e.g., Hulot et al. 1989)
gives a momentum-loss rate of
10 s): a Coulomb-loss estimate (e.g., Hulot et al. 1989)
gives a momentum-loss rate of
![]() s-1 at E=30 MeV and
n0=1011 cm-3.
s-1 at E=30 MeV and
n0=1011 cm-3.
In conclusion, the impulsive flare scenario in light of our simulations is the
following: promptly (
![]() s) after the start of the proton acceleration
process near the loop top, the footpoints will brighten in
s) after the start of the proton acceleration
process near the loop top, the footpoints will brighten in ![]() -rays because
the the turbulent trap will not be developed at that time. For a high level of
ambient turbulence or large loop length, the footpoints may show rather
different emission levels if the source is positioned somewhat off the loop
top. After the first brightening, the turbulent particle trap develops and
emission from the loop legs will stay at a level determined by the
convective flux of particles. After one Alfvénic propagation time from the
source, the closer loop leg will brighten in
-rays because
the the turbulent trap will not be developed at that time. For a high level of
ambient turbulence or large loop length, the footpoints may show rather
different emission levels if the source is positioned somewhat off the loop
top. After the first brightening, the turbulent particle trap develops and
emission from the loop legs will stay at a level determined by the
convective flux of particles. After one Alfvénic propagation time from the
source, the closer loop leg will brighten in ![]() -rays once again, provided
that the number of high-energy particles after the adiabatic losses in the trap
is large enough,
-rays once again, provided
that the number of high-energy particles after the adiabatic losses in the trap
is large enough,
![]() cm-2 with
n11=n0/(1011 cm-3). The footpoint farther away from
the source is unlikely to show the delayed peak in
cm-2 with
n11=n0/(1011 cm-3). The footpoint farther away from
the source is unlikely to show the delayed peak in ![]() -ray emission in any
case. We note that this feature is observationally testable, especially with the
images of solar
-ray emission in any
case. We note that this feature is observationally testable, especially with the
images of solar ![]() -ray emission anticipated from the HESSI mission. We
also found that the small interplanetary-to-interacting proton ratios observed
in impulsive solar flares do not necessarily imply closed field line topology,
but can result also from the turbulent trapping on open magnetic field lines. In
the next stage of the modeling, we intend to take better account of the
resonance conditions and consider non-constant background plasma parameters. The
effects of wave-wave interactions will also be studied.
-ray emission anticipated from the HESSI mission. We
also found that the small interplanetary-to-interacting proton ratios observed
in impulsive solar flares do not necessarily imply closed field line topology,
but can result also from the turbulent trapping on open magnetic field lines. In
the next stage of the modeling, we intend to take better account of the
resonance conditions and consider non-constant background plasma parameters. The
effects of wave-wave interactions will also be studied.
The present numerical code is modified from our previously published Monte Carlo code (Vainio et al. 2000). Similar transport codes, including also non-linear effects, have been developed previously (e.g., Ellison et al. 1996), but to our knowledge, ours is the first Monte Carlo code to employ self-generated waves.
When the Monte Carlo particles (numbered by j) are injected in the simulation,
they are a given a weight wj that normalizes their injection rate to the
physical value given by Q. The particles are treated in the guiding center
approximation, which in the present case of constant magnetic field strength
means that during the Monte Carlo time step, ![]() ,
we move the particles in
the spatial coordinate (measured along the field lines) as
,
we move the particles in
the spatial coordinate (measured along the field lines) as
![]() ,
where vj and
,
where vj and ![]() are the particle
speed and pitch-angle cosine of the jth particle as measured in the fixed
frame, where the background plasma is assumed to be stationary. In addition, the
particles suffer scatterings from two Alfvén wave fields propagating parallel
and anti-parallel to the magnetic field. In scatterings, performed after each
Monte Carlo time step modeling pitch-angle diffusion, the particles are
subsequently scattered (elastically) in the two wave frames, first
Lorentz-transforming the particle velocity to the wave frame, then using
are the particle
speed and pitch-angle cosine of the jth particle as measured in the fixed
frame, where the background plasma is assumed to be stationary. In addition, the
particles suffer scatterings from two Alfvén wave fields propagating parallel
and anti-parallel to the magnetic field. In scatterings, performed after each
Monte Carlo time step modeling pitch-angle diffusion, the particles are
subsequently scattered (elastically) in the two wave frames, first
Lorentz-transforming the particle velocity to the wave frame, then using
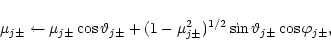 |
(A.1) |
We keep track of the wave energy densities on a spatial grid with N=150elements numbered by i=1,...,N, and with a spacing of
![]() and
central coordinates x=Xi. The value of
and
central coordinates x=Xi. The value of
![]() is taken to be
constant inside each grid cell. Thus,
is taken to be
constant inside each grid cell. Thus,
![]() and
ij is the index of the grid cell that contains xj, i.e.,
and
ij is the index of the grid cell that contains xj, i.e.,
![]() ,
where
,
where
![]() .
During each
Monte Carlo time step, a change of the wave energy density due to wave-particle
interactions is computed from
.
During each
Monte Carlo time step, a change of the wave energy density due to wave-particle
interactions is computed from
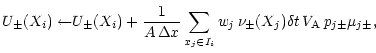 | (A.2) | ||
In addition to the wave-particle interactions, the waves are convected on the
grid by
![]() if
if
![]() and
U+[-](X1[N])=U0, each time the simulation time t has
elapsed an amount of
and
U+[-](X1[N])=U0, each time the simulation time t has
elapsed an amount of
![]() .
At boundaries, the wave energy
convected out of the grid is lost.
.
At boundaries, the wave energy
convected out of the grid is lost.
As an output, the simulation code saves the momentum, pitch-angle cosine and
escape time of all particles leaving the simulation box. In addition, the
wave-energy densities and the energetic particle pressure inside the simulation
box is saved after every time the waves are moved on the grid, i.e., at
t mod
![]() .
To illustrate the typical development of a
simulation, we have plotted in Fig. A.1 the wave-energy densities
and particle pressures in a few frames for simulation in Case B with source
position at
.
To illustrate the typical development of a
simulation, we have plotted in Fig. A.1 the wave-energy densities
and particle pressures in a few frames for simulation in Case B with source
position at ![]() (see Fig. 3 for the escaping particle
flux).
(see Fig. 3 for the escaping particle
flux).
As an outline of the future work, we note that a generalization to a spectrum of
Alfvén waves would mean that the wave-energy density grid would contain another
dimension (wavenumber), and that the resonance condition would have to be taken
into account in deciding which particles contribute the the growth of the waves
in the particular grid element. If one uses the full quasi-linear resonance
condition with ![]() -dependence, one has to also take this into account when
modeling the scattering frequency, which has to be allowed a
-dependence, one has to also take this into account when
modeling the scattering frequency, which has to be allowed a ![]() -dependence.
This, naturally, affects also the growth rate of the waves. The effects of
non-constant magnetic field to the particle transport are easy to take into
account (Vainio et al. 2000); for wave transport, one has to use an
equation that employs the diverging field effects as well as the effects of a
non-constant group speed.
-dependence.
This, naturally, affects also the growth rate of the waves. The effects of
non-constant magnetic field to the particle transport are easy to take into
account (Vainio et al. 2000); for wave transport, one has to use an
equation that employs the diverging field effects as well as the effects of a
non-constant group speed.