A&A 375, 308-318 (2001)
DOI: 10.1051/0004-6361:20010843

Extension of the ICRF for selected areas down to the 15th magnitude[*],[*]

J. I. B. Camargo1 - R. Teixeira1,2 - P. Benevides-Soares1 - C. Ducourant2,1


1 - Instituto de Astronomia, Geofísica e Ciências Atmosféricas da Universidade de São Paulo, Caixa Postal 3386, 01060-970 São Paulo SP, Brazil
2 - Observatoire de Bordeaux, UMR 5804, CNRS/INSU, BP 89, 33270 Floirac, France

Received 19 March 2001 / Accepted 1 June 2001

Abstract
In this paper, we present our results towards the extension of the ICRF to the optical domain down to the 15$^{\rm th}$ V magnitude, for some regions of special astronomical interest. This extension is given by accurate positions and proper motions in the ICRS. Present epoch positions were obtained with the CCD transit circle of the Abrahão de Moraes Observatory, in the city of Valinhos - São Paulo. Proper motion derivation is achieved by combining our meridian circle positions with those from available astrometric catalogues and SERC-J plate measurements performed with the MAMA measuring machine (Paris). The final result is presented as a catalogue containing positions, proper motions, magnitudes and cross-identifications with major catalogues for 41721 objects. A full description of the employed data is given along with an analysis of the uncertainties on positions and proper motions in our final catalogue. On average, stars with $V\le 14.0$ have positional precisions better than 50 mas in both coordinates, and 100 mas at the detection limit of our instrument ( $V\sim 16.0$). For proper motions, average precisions are better than 4 mas/year, whatever the magnitude, when $\delta\ge -17^{\rm o}$. To the south of this declination, precisions become magnitude-dependent, providing figures of 3 mas/year when $V\le12.0$ and reaching 17 mas/year at the detection limit. The declination dependence affects the fainter stars and reflects a feature of our main first epoch material for this magnitude range, the USNO-A2.0 catalogue. The Valinhos CCD transit circle observations cover a variety of regions of great interest. Here, we consider those containing extragalactic radio sources, mostly from ICRF, and pre-main sequence stars in southern star-forming regions (Chamaeleon, Lupus and Upper Scorpius - Ophiuchus), where positions from the SERC-J plates were employed.

Key words: astrometry


1 Introduction

On the 1st of January, 1998, the IAU adopted a new celestial reference system (Feissel & Mignard 1998), the ICRS (International Celestial Reference System), which is realized by a set of 212 extragalactic compact radio sources listed in the ICRF (International Celestial Reference Frame) catalogue (Ma et al. 1998). The positions of these sources, called defining sources, have been precisely determined by VLBI techniques to accuracies better than 0.5 mas.

This new system is conceptually different from that given by the FK5 (Friecke et al. 1988), being based on the kinematics of extragalactic radio sources, that is, on the fact that their proper motions are not measurable by present-day techniques. Yet, for the sake of continuity, the FK5 and ICRF frames had the directions of their coordinate axes aligned so that, within the uncertainties of the FK5, both have consistent J2000 right ascension and declination origins. The HIPPARCOS catalogue (ESA 1997) is the realization of the ICRS in optical wavelengths.

Some practical applications of the HIPPARCOS catalogue as an optical counterpart of the ICRF are limited by its low density of stars, about 118000 objects distributed all over the sky and typically brighter than V=10.0. In spite of the recent release of the Tycho-2 catalogue (Høg et al. 2000a), with a star density 20 times larger and limiting magnitude V=12.0, a more satisfactory scenario is still required.

With the aim of improving the accessibility to the ICRS in the optical domain, we provide a large number of good positions and proper motions based on the Tycho-2 catalogue, for regions of the sky around extragalactic radio sources. In addition, regions containing pre-main sequence (PMS) stars in Chamaeleon, Lupus and Upper Scorpius - Ophiuchus are also explored.

Present epoch positions have been measured by means of the Valinhos CCD transit circle (hereafter VMC) (Viateau et al. 1999) and referred to the Tycho-2 catalogue.

The sources for first and intermediate epochs of positions include well-known available catalogues: AC2000 (Urban et al. 1998b), CPC-2 (Zacharias et al. 1999), PPM North (Röser & Bastian 1998) and South (Bastian & Röser 1993), TAC-2 (Zacharias & Zacharias 1999), USNO-A2.0 (Monet et al. 1998). We have also made use of SERC-J plates from the southern DSS I survey carried out with the UK Schmidt Telescope in Siding Spring - Australia, and measured with the MAMA measuring machine (Guibert et al. 1983).

The work presented here is a fraction of a huge field densification project involving many other regions, as will be described latter. It complies with the designations of the IAU Commission 8 new working-group "The Future Development of Ground-Based Astrometry'', headed by M. Stavinschi and J. Kovalevsky.

2 Valinhos transit circle

Since May 1995, the VMC of the Abrahão de Moraes Observatory, located in the city of Valinhos, has been carrying out observations in automatic mode with a $512\times 512$ pixel CCD drift scan camera in its focus. The charge transfer follows the diurnal movement of the sky, and its speed is a function of the declination. Table 1 shows the main characteristics of the instrument. For further details, the reader is referred to Viateau et al. (1999).

 

 
Table 1: Main characteristics of the Valinhos CCD meridian circle.
CCD detector Thomson 7895A
CCD bandpass 5000 Å-9000 Å
Longitude $+46^{\rm o} 58^{\prime} 03\hbox{$.\!\!^{\prime\prime}$ }3$
Latitude $-23^{\rm o} 00^{\prime} 06\hbox{$.\!\!^{\prime\prime}$ }0$
Pixel size $19\, \mu {\rm m}$( $\sim\!1\hbox{$.\!\!^{\prime\prime}$ }5$)
Declination window width $13^{\prime}$
Limiting magnitude V=16.0
Astrometric and photometric  
optimal magnitude range $8.0 \leq V \leq14.0$
Transit time upon the CCD $51^{\rm s}{\rm sec}\delta$


Despite the small area covered by the CCD (see Table 1), the drift scan mode allows unlimited range in right ascension. In this program, the typical dimension of a meridian frame is about $35^{\rm m}\times 13^{\prime}$, in order to acquire a comfortable number of Tycho-1 (Tycho first release) (ESA 1997) stars. For objects in the optimal magnitude range (Table 1) with a minimum of 5 observations, an average positional internal precision of 50 mas in right ascension and 60 mas in declination is achieved (see Fig. 1). For fainter magnitudes, these values average 90 and 110 mas respectively.

The adopted colour filter system, combined with the secondary spectrum from the doublet, defines a photometric band which is close to the V band of Johnson system.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{ms1291f1} \end{figure} Figure 1: VMC internal precision for position as a function of magnitude. Each circle is the average of stars with at least five observations.
Open with DEXTER

2.1 Valinhos transit circle data treatment

The image reduction consists basically of four steps - sky background determination, object detection, photocentric coordinate and flux measurements, astrometric and photometric reduction - for which we make use of a software package developed and maintained by J. F. Le Campion - Observatoire de Bordeaux (Viateau et al. 1999).

Although our aim here is the astrometric parameter determination, visual magnitudes are also provided. These latter measurements have an internal precision of 0.05 mag within the optimal interval given in Table 1, and no check for variability was performed. For a detailed description of the magnitude from the VMC, the reader is referred to Dominici et al. (1999) and references therein.

Three different models of increasing complexity are fitted to the object image. The first is simply the barycenter, the second one is a symmetric Gaussian, and the last one is a general Gaussian.

The first two solutions are used to provide the first step of their respective following steps. For a small fraction of the results, the convergence of the general Gaussian is attained at a slow rate, so that the symmetric Gaussian is retained.

Each field is observed once per night, so that after some nights many sets of positions are generated to a particular target region. These sets of positions are, afterwards, combined, and their overlap is used in a global reduction procedure (Teixeira et al. 1992, 1998). The employed reference catalogue is the Tycho-2 (Høg et al. 2000a, b).

  \begin{figure} \par\includegraphics[width=8.2cm,clip]{ms1291f2} \end{figure} Figure 2: Distribution of the fields observed by the VMC. Larger rectangles correspond to the SERC-J plates.
Open with DEXTER

3 Present epoch material

Our observational data comprises, up to now, 47 meridian strips containing extragalactic radio sources and 5 strips (see Table 2) observed in the great southern star-forming regions (Chamaeleon, Lupus and Upper Scorpius - Ophiuchus) (Teixeira et al. 2000). As mentioned before, all results are referred to the ICRS, as realized by the Tycho-2 catalogue, and were obtained between 1996 and 2000. The distribution of the meridian strips can be seen in Fig. 2.

For the compilation of our final catalogue (hereafter VMCC - Valinhos Meridian Circle Catalogue), only those objects with three or more observations in each coordinate, amounting to a total of 44833, were considered, from which some 7% were discarded for lack of first epoch data.

4 First and intermediate epoch material

Proper motions were determined by combining present epoch positions (VMC observations) with older ones, obtained from available astrometric catalogues and from SERC-J plates. Table 3 shows the main characteristics of the employed first and intermediate epoch material.

   
Table 2: Observational data and results.

Identifier		 #Objects ${\rm\sigma_{\alpha}cos\delta\;\;\;\sigma_{\delta}\over{[mas]}}$ ${\rm\alpha\over{[J2000]}}$ ${\rm\delta\over{[J2000]}}$ ${\rm Mag.\over{[V]}}$ Nobs
ICRF J001031.0+105829 322 139 142 00 10 31.0 +10 58 30 15.4 10
ICRF J004959.4-573827 221 102 106 00 49 59.5 -57 38 27 19.8 13
VV96 J005334.9+124136 475 139 146 00 53 34.9 +12 41 36 14.1 10
ICRF J011205.8+224438 673 087 125 01 12 05.8 +22 44 39 15.7 13
ICRF J023951.2+041621 341 103 099 02 39 51.3 +04 16 21 18.5 08
ICRF J024008.1-230915 609 111 114 02 40 08.2 -23 09 16 16.6 10
ICRF J053850.3-440508 489 080 099 05 38 50.4 -44 05 09 16.5 08
ICRF J073807.3+174218 1041 071 094 07 38 07.4 +17 42 19 16.2 09
ICRF J092129.3-261843 985 085 102 09 21 29.4 -26 18 34 18.4 08
ICRF J101353.4+244916 277 123 098 10 13 53.4 +24 49 16 16.6 10
ICRF J103502.1-201134 536 065 077 10 35 02.2 -20 11 34 19.0 09
ICRF J103716.0-293402 1037 071 097 10 37 16.1 -29 34 03 16.5 11
ICRF J110331.5-325116 256 074 089 11 03 31.5 -32 51 17 16.3 08
ICRF J110427.3+381231 132 137 180 11 04 27.3 +38 12 32 12.9 08
ICRF J113143.2-581853 2615 095 109 11 31 43.3 -58 18 53 - 10
ICRF J114701.3-381211 937 091 089 11 47 01.4 -38 12 11 16.2 12
ICRF J115931.8+291443 249 077 106 11 59 31.8 +29 14 44 14.4 08
ICRF J122906.6+020308 425 100 101 12 29 06.7 +02 03 09 12.9 09
ICRF J130533.0-103319 277 094 105 13 05 33.0 -10 33 19 15.2 09
ICRF J132304.2-445233 1867 144 111 13 23 04.2 -44 52 34 21.0 10
ICRF J133237.5-664650 5220 083 101 13 32 37.5 -66 46 50 - 09
ICRF J133752.4-650924 3336 088 114 13 37 52.4 -65 09 25 - 10
ICRF J135704.4+191907 453 080 101 13 57 04.4 +19 19 07 16.0 11
ICRF J135900.1-415252 1314 099 122 13 59 00.2 -41 52 53 15.9 12
ICRF J140700.3+282714 343 104 115 14 07 00.4 +28 27 15 15.4 12
ICRF J142700.3+234800 236 091 095 14 27 00.4 +23 48 00 15.0 10
ICRF J143809.4-220454 976 083 087 14 38 09.5 -22 04 55 17.9 12
ICRF J144553.3-162901 120 074 087 14 45 53.4 -16 29 01 - 08
ICRF J151656.7+193212 323 078 100 15 16 56.8 +19 32 13 18.7 15
ICRF J151741.8-242219 948 073 101 15 17 41.8 -24 22 19 14.8 10
VV96 J161033.4+111531 839 113 108 16 10 33.5 +11 15 31 19.5 12
ICRF J172341.0-650036 1902 057 067 17 23 41.0 -65 00 37 15.5 10
ICRF J192451.0-291430 2812 065 093 19 24 51.1 -29 14 30 18.2 12
ICRF J193006.1-605609 888 100 105 19 30 06.2 -60 56 09 21.5 11
ICRF J200925.3-484953 1541 072 107 20 09 25.4 -48 49 54 13.1 10
ICRF J205616.3-471447 742 069 083 20 56 16.4 -47 14 48 19.1 11
ICRF J210933.1-411020 420 055 073 21 09 33.2 -41 10 21 17.2 12
ICRF J213135.2-120704 625 103 099 21 31 35.3 -12 07 05 16.1 09
ICRF J215852.0-301332 824 068 096 21 58 52.1 -30 13 32 14.3 11
ICRF J220743.7-534633 472 093 099 22 07 43.7 -53 46 34 18.0 10
ICRF J221852.0-033536 525 109 105 22 18 52.0 -03 35 37 16.4 09
ICRF J225357.7+160853 422 077 125 22 53 57.7 +16 08 54 16.1 13
VV96 J225405.9-173455 713 094 092 22 54 05.9 -17 34 55 14.3 10
ICRF J225805.9-275821 270 093 099 22 58 06.0 -27 58 21 16.8 08
ICRF J232917.7-473019 231 106 125 23 29 17.7 -47 30 19 17.5 09
ICRF J233040.8+110018 404 064 089 23 30 40.9 +11 00 19 18.1 12
ICRF J234636.8+093045 597 084 129 23 46 36.8 +09 30 46 16.0 12
Star-forming regions            
Chamaeleon 806 056 067 11 13 45.0 -76 32 28 - 10
Chamaeleon 482 046 044 13 02 18.0 -76 39 34 - 08
Lupus 910 073 082 16 01 26.0 -39 06 57 - 09
Oph + U-Sco1 1362 051 058 16 35 06.0 -24 10 00 - 12


1 This field contains two series of meridian strips, and its declination band width is $26^{\prime}$.
${\rm Identifier}={\rm ICRF}$ name or other identifier of the object whose coordinates were used as center for the target region; ${\rm Objects}={\rm Number}$ of objects in the region with 3 or more observations in each coordinate; ${\sigma_{\alpha}\cos\delta\;\;\;\sigma_{\delta}\over{\rm [mas]}}={\rm Mean}$, in units of milliarc seconds to both coordinates, for the positional precision of the objects computed in the 2nd column; ${\alpha\over{\rm {[J2000]}}}$ e ${\delta\over{\rm {[J2000]}}}={\rm Input}$ coordinates used to point the VMC; ${\rm {Mag.\over{[V]}}}={\rm Visual}$ magnitude for the objects in the 1st column. Most of them were taken from the SIMBAD database. VMC values were used otherwise. A (-) means that either no value was found or it does not apply; ${\rm Nobs}={\rm Number}$ of observations of the target region.


4.1 USNO-A2.0

The USNO-A2.0 catalogue was our only source for old positions of faint stars in the fields containing extragalactic radio sources. The mean epochs for objects with $\delta\ge -17^{\rm o}$ and for those with $\delta<-17^{\rm o}$ in the USNO-A2.0 catalogue are different, being around 1954 in the former and 1982 in the latter (see Table  3). This catalogue adopted the ACT (Urban et al. 1998a) as reference, which is superseded by Tycho-2. However, from (Hoogerwerf & Blaauw 2000), further corrections were not considered necessary.

4.2 SERC-J plates

The SERC-J plates were measured in Paris with the MAMA measuring machine, originally aiming at proper motion determination of some PMS stars in regions of star formation (Teixeira et al. 2000) and references therein). Table 4 gives further information about these plates, and a plot of their sky coverage can be seen in Fig. 2. The size of each plate is $6\hbox{$.\!\!^\circ$ }5\times6\hbox{$.\!\!^\circ$ }5$. In this work, these plates were reduced with respect to the Tycho-2 catalogue, whereas in Teixeira et al. (2000), the ACT was used.

   
Table 3: First epoch catalogues.
Catalogue Average precision System Sky coverage ${\rm Mean\;epoch\over{[+1900]}}$ Limiting mag.
USNOA-A2.0 $0\hbox{$.\!\!^{\prime\prime}$ }25$ ICRS whole sky 54 ($\delta$$\ge$ $-17^{\rm o}$) 82 ($\delta$< $-17^{\rm o}$) B and $R\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...
TAC-2 $0\hbox{$.\!\!^{\prime\prime}$ }10^{\rm a}$ ICRS $\delta$ $\ge$ $-18^{\rm o}$ between 77 and 86 $V \leq 11$ and $B \leq 12$
AC2000 $0\hbox{$.\!\!^{\prime\prime}$ }30^{\rm b}$ ICRS whole sky 07 B < 13
PPM North $0\hbox{$.\!\!^{\prime\prime}$ }27$ FK5 $\delta$ $\ge$ $-2.5^{\rm o}$ 31 V < 12
PPM South $0\hbox{$.\!\!^{\prime\prime}$ }11$ FK5 $\delta$ $\le$ $-2.5^{\rm o}$ 61 V < 12
CPC-2 $0\hbox{$.\!\!^{\prime\prime}$ }05^{\rm a}$ ICRS $\delta$ $\le$ $+2.2^{\rm o}$ 68 V < 12
SERC-J plates $0\hbox{$.\!\!^{\prime\prime}$ }30$ ICRS see Table 4 77 B < 17


$^{\rm a}$ The adopted value was the largest between $0\hbox{$.\!\!^{\prime\prime}$ }45$ and the catalogue one. The rationale for this is found in the documentation provided with the Tycho-2 CDROM.
$^{\rm b}$ To each object, the adopted value was that given by the catalogue. Precisions for the single-observed objects were taken from the individual plate solutions (see Urban et al. 1998b, Table 2). We decided to apply the same procedure for those objects with precisions better than $0\hbox{$.\!\!^{\prime\prime}$ }01$.


4.3 PPM

The PPM catalogue, as shown in Table 3, adopts the FK5 system. To express its positions with respect to the ICRS, the following steps were taken:

1.
PPM positions were transposed from the epoch 2000 to their mean epoch of observation, using PPM proper motions;
2.
Such positions were then reduced to the ICRS by means of the difference tables for positions and proper motions presented in Mignard & Fr\oeschlé (2000). Table values were interpolated by a bi-linear formula in the coordinate rectangle where the object lies.

4.4 AC2000

The AC2000 was a valuable source due to the large time interval it provides, 90 years on average when the VMC observation epochs are considered. Unfortunately, due to its limiting magnitude, only a small fraction of the VMCC entries could benefit from the AC2000 participation (see Table 5).

The presence of possible systematic errors in the positions of these catalogues is not ignored. However, as it will be shown in next sections, the employed weighing process minimizes its influence on our final results.

5 Proper motion determination

Identification among the observed VMC objects and those present in the old epoch catalogues, SERC-J measurements included, were subject to positional and magnitude difference criteria, in order to choose the nearest matching candidates to a VMC object. Sorting and binary search techniques were necessary to make the identification procedure conveniently fast. Objects in USNO-A2.0 whose positions were borrowed from external catalogues were rejected. The same applied to objects in PPM (North and South) with unfavourable flags for astrometry.

The shortest time interval involved in proper motion determination was 10 years, whereas the longest was over 100 years, as depicted in Fig. 3. From this figure, it is also interesting to notice the two major peaks for time intervals involving the USNO-A2.0 catalogue. Actually, they result, as mentioned before, from the difference of epochs contained in the USNO-A2.0 catalogue below and above the limiting parallel of $\delta\sim -17^{\rm o}$. Considering that most of our proper motions for objects with V>12.0 had the USNO-A2.0 as its only first epoch source, one can expect that the respective final precisions inherited such characteristic accordingly.

Mean coordinates ( $\alpha_{0},\delta_{0}$) and the corresponding mean epochs ( $T_{\alpha_{0}}$, $T_{\delta_{0}}$) for a particular object were determined by the weighted mean of the corresponding ( $\alpha_{i},\delta_{i}$) and ( $T_{\alpha_{i}}$, $T_{\delta_{i}}$), $i=1,\ldots$, #(used positions). Proper motions were obtained as follows:

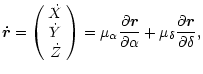$\displaystyle {\vec {\dot{r}}}=\left( \begin{array}{c} {\dot{X}}\\ {\dot{Y}}\\... ...r}}{\partial\alpha}+\mu_{\delta}\frac{\partial{\vec r}}{\partial\delta}\hbox{,}$     (1)

where $\vec {\dot{r}}$ is the time derivative of the position vector $\vec {r}$ on the unit sphere.
 

 
Table 4: Epoch, center and average astrometric precision for the SERC-J plates.
Epoch $\hbox{Center}\over{\alpha\hbox{\hskip 10pt} \hbox{[J2000]}\hbox{\hskip 10pt} \delta}$ ${\rm\sigma_{\alpha}cos\delta\;\;\;\sigma_{\delta}\over{[mas]}}$ Region
1976.255 11 00 53 -75 17 43 24 24 Chamaeleon
1980.531 13 15 53 -75 15 50 25 25 Chamaeleon
1978.331 15 39 19 -40 09 43 34 32 Lupus
1975.422 16 05 22 -40 08 07 30 32 Lupus
1978.578 16 33 03 -25 06 17 31 29 Ophiuchus
1976.411 17 16 57 -25 02 46 40 35 U-Sco



  \begin{figure} \par\includegraphics[width=8.3cm,clip]{ms1291f3} \end{figure} Figure 3: Time interval between positions from VMC observations and those from AC2000 and USNO-A2.0 catalogues.
Open with DEXTER


 

 
Table 5: First and intermediate epoch material participation.
Catalogue Number of entries VMC mag. interval
AC2000 7621 -14.62
CPC 570 -11.72
PPM 447 -11.53
SERC-J 2323 -16.79
TAC 472 -12.36
USNO-A2.0 38001 -16.79


Equation (1) is a rigorous formulation for proper motion calculation, as long as perspective acceleration is not involved. After some simple algebra, Eq. (1) becomes:

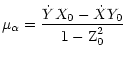$\displaystyle \mu_{\alpha}=\frac{{\dot{Y}}{X}_{0}-{\dot{X}}{Y}_{0}}{1-\hbox{Z}_{0}^{2}}$     (2)

and
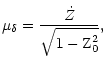$\displaystyle \mu_{\delta}=\frac{{\dot{Z}}}{\sqrt{1-\hbox{Z}_{0}^{2}}}\hbox{,}$     (3)

so that Eqs. (2) and (3) express, in radians, the proper motion in right ascension and declination. This is the same formulation as given, for instance, in Zacharias et al. (2000). Weighted least squares was used to determine $\vec {\dot{r}}$, and the corresponding standard deviations were derived from the stochastic model. Weights were derived from first order error expansion on the Cartesian coordinates of the unit vector $\vec {r}$, as given in Eq. (4):

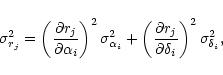\begin{displaymath}\sigma_{r_{j}}^{2}=\left(\frac{\partial r_{j}}{\partial\alpha... ...{\partial\delta_{i}}\right)^{2}\sigma_{\delta_{i}}^{2}\hbox{,} \end{displaymath} (4)

where rj, j=1,2,3, stands for the mentioned coordinates. Error expansion in Eqs. (2) and (3) also provides the proper motion internal precisions.

When more than three catalogues were involved, intermediate positions were rejected if they differed from those predicted by the model by more than 3 times their catalogue error, and calculations were restarted with the remaining data. Such a procedure also helped us to avoid possible misidentifications. Table 5 shows the number of VMCC entries in which each catalogue participated.

  \begin{figure} \par\includegraphics[width=8cm,clip]{ms1291f4} \end{figure} Figure 4: Object distribution per visual magnitude in the VMCC.
Open with DEXTER

6 The Valinhos Meridian Circle Catalogue

The VMCC contains 41721 stars brighter than $V\sim 16.0$, observed at least 3 times with the VMC. About 72% of the objects in it are brighter than V=15.0, as depicted in Fig. 4.

In Fig. 5, upper panel, it can be seen that for magnitudes ranging from V=8.0 down to the 14.0th, the internal average positional precision is 40 mas. Above this limit, precision decreases, mainly due to the positonal behaviour of the Valinhos transit observations, as a response to CCD light undersampling. The resemblance to Fig.  1 comes from the weighting process, which makes positional precision quite dependent on the VMC observations.

In Fig. 5, lower panel, the proper motion quality is depicted. Down to V=12.0, the presence of AC2000 provides an average precision of 2-3 mas/year. To fainter magnitudes, first epoch positions are essentially given by the USNO-A2.0 catalogue, and the difference of epochs for objects north and south of $\delta=-17^{\rm o}$ becomes evident. In this way, average precisions for these objects (V>12.0) are 6 mas/year and 14 mas/year, respectively, when longer ( $\delta\ge -17^{\rm o}$) and shorter ( $\delta<-17^{\rm o}$) time intervals are concerned. As a general trend, one may assign an average precision of 4 mas/year to all proper motions of objects with $\delta\ge -17^{\rm o}$. For southern declinations, however, the threshold magnitude V=12.0 must be taken into consideration.

Figure 6, left and right panels, depicts the proper motion distribution in the VMCC. About 93% of the absolute values are less than or equal to 40 mas/year, and a few exceed 200 mas/year. The authors have tried to avoid misidentifications, but may still be a possibility.


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{ms1291f5} \end{figure} Figure 5: Internal astrometric precisions of the VMCC as a function of magnitude.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{ms1291f6a}\hspace*{4mm} \includegraphics[width=8.3cm,clip]{ms1291f6b} \end{figure} Figure 6: Proper motion distribution in the VMCC.
Open with DEXTER

All results analyzed here are presented in the form of a catalogue - VMCC - containing astrometric parameters and their respective precisions, VMC magnitudes and cross-correlations obtained from the employed old epoch material, Tycho-2 nomenclature included, as given in Table 6. We emphasize that magnitudes in the VMCC, although of a relatively good internal precision, should be understood just as a photometric indication. A brief extract from the VMCC is shown in Table 7.


  \begin{table}{\includegraphics[angle=-270,width=29cm,clip]{table7.ps} } \end{table}

7 External verifications of the VMCC

We checked the external quality of our results in position and proper motion by comparing the VMCC with other major astrometric catalogues.

The HIPPARCOS catalogue provides the best reference available to test objects with $8.0\le V\le13.0$, and the UCAC1 (Zacharias et al. 2000), which contains objects to the south of $\delta\sim -15^{\rm o}$ only, provides material to check through fainter magnitudes.

7.1 Comparison to HIPPARCOS

We present in Figs. 7 and 8 the differences in positions and proper motions between the VMCC and the HIPPARCOS catalogue for 100 common objects, with $V\ge8$.

In Fig. 7, HIPPARCOS positions have been transposed to the mean epochs of the VMCC ones by means of their respective HIPPARCOS proper motions. The rms of the resulting differences allow us to externally estimate the quality of our positions, which is 50 mas in right ascension and 60 mas in declination.

For this calculation, we rejected multiple objects and those objects from HIPPARCOS classified as having poor astrometric data, as well as those whose propagated positional error at the comparison epoch exceeded 50 mas in any coordinate. Nevertheless, it is clear that such a procedure slightly overestimates our precisions, since the remaining HIPPARCOS objects are not error free. These results can be extended for magnitudes down to the 13.0th because of the stable behaviour of the VMC positions within the involved magnitude interval, as depicted in Fig. 1.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{ms1291f7} \end{figure} Figure 7: Positional differences in the sense VMCC minus HIPPARCOS as a function of magnitude.
Open with DEXTER

For proper motions, the rms of the differences, depicted in Fig. 8, is 3 mas/year for both coordinates. As discussed in previous sections, such a figure does not hold for V>12.0. No systematic behaviour is discernible.


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{ms1291f8} \end{figure} Figure 8: Proper motion differences in the sense VMCC minus HIPPARCOS as a function of magnitude.
Open with DEXTER

7.2 Comparison to UCAC1

Figures 9 and 10 depict, respectively, comparisons in position and proper motion between the VMCC and UCAC1 as a function of magnitude. A total of 12885 common objects, with V>13.0 under the same constraints on the propagated errors as applied to HIPPARCOS, were selected.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{ms1291f9} \end{figure} Figure 9: Positional differences in the sense VMCC minus UCAC1 as a function of magnitude.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{ms1291f10} \end{figure} Figure 10: Proper motion differences in the sense VMCC minus UCAC1 as a function of magnitude.
Open with DEXTER

In Fig. 9, the rms of the differences is 110 mas and 90 mas, respectively, for right ascension and declination. In Fig. 10, one finds 7 mas/year for both coordinates. This latter value is better than that given by the VMCC for proper motion precision below $\delta=-17^{\rm o}$, however, one must keep in mind that both VMCC and UCAC1 have the USNO-A2.0 as the first epoch for most of the considered objects. Differences were built at the epoch of the VMCC positions using UCAC1 proper motions.

8 Contribution to the Tycho-2 system of positions

The Tycho-2 catalogue is the result of a re-reduction of the star mapper readings, carried out within the HIPPARCOS mission, which allowed a much more efficient treatment of these readings and provided more than twice the number of objects contained in its previous version, Tycho-1.

From the catalogue data itself, it is possible to notice a clear difference, as magnitudes become fainter, between the quality of the Tycho-2 and Tycho-1 common positions and the new ones (non-Tycho-1), as depicted in Fig. 11. Yet, from $V\ge11.0$, the internal precision of the VMC positions (Fig. 1) becomes slightly better than that of the Tycho-2 new objects.


  \begin{figure} \par\includegraphics[width=8cm,clip]{ms1291f11} \end{figure} Figure 11: Tycho-2 internal standard deviation in position as a function of magnitude.
Open with DEXTER

Therefore, as shown from the considerations on our positional precisions made in the previous sections (Fig. 5, upper panel), we understand that the VMCC, as well as other new astrometric compilations, can be an important step towards a quality enhancement of Tycho-2 catalogue, mainly for those new objects with $V\ge10.0$.

This consideration is supported by Fig. 12, which depicts the positional differences for 3824 common objects between the VMCC and Tycho-2. The rms of the differences associated with Fig. 12, upper panels (lower panels), is 64 mas (149 mas) in right ascension and 74 mas (129 mas) in declination. The 2227 new objects in Tycho-2 present in the VMCC (Table 6) are indicated with an asterisk (*) after its Tycho-2 number.

As far as proper motions are concerned, the rms of the differences, compared to Tycho-2, is 2 mas/year for its Tycho-1 objects and 3 mas/year for the new ones.


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{ms1291f12} \end{figure} Figure 12: Positional differences between the VMCC and Tycho-2 positions. It should be mentioned that the difference of the average magnitude for the objects in upper (brighter) and lower (fainter) panels is about 2 mag.
Open with DEXTER

9 Conclusions

The extension of the inertial frame ICRF to the optical domain is a huge, worldwide astrometric task. The very accurate optical catalogues HIPPARCOS and Tycho-2 provide an excellent extension of the ICRF, but are quite limited in magnitude, both being essentially brighter than V=11.5. The goal of our work was to extend the ICRF, as given by the Tycho-2 catalogue, down to $V\sim 16.0$, in specific regions of the sky. This extension is given by a set of positions, referred to the Tycho-2 catalogue, and proper motions, for 41721 objects observed with the Valinhos CCD meridian circle. These stars are distributed in 51 zones of the sky of special interest: extragalactic radio sources and star-forming regions.

The precision of the VMCC positions are magnitude-dependent, whereas proper motion precisions are magnitude and declination dependent. These values were determined from the stochastic model, and agreed with external references.

This contribution is a fraction of a more ambitious project to extend the ICRF to all fields observed at the Valinhos Observatory: extragalactic radio sources, radio stars, low extinction windows in the galactic bulge direction, open clusters, star-forming regions and solar system objects. Therefore, Table 6 will be updated as soon as new results are obtained.

Hundreds of new Tycho-2 objects (non-Tycho-1) presented large deviations of $\Delta\alpha\cos\delta$ and $\Delta\delta$ (see Fig. 12), reaching absolute values greater than $0\hbox{$.\!\!^{\prime\prime}$ }1$. The accuracy of our results within the involved range of magnitude is enough to contribute to the determination of possible corrections to the Tycho-2 positions. In this way, a more detailed analysis, involving a data set larger than the one presented here, is being investigated.

The most important difficulty to be overcome to achieve the ICRF extension is the availability of first epoch positions, when proper motion measurements are involved. We consider that it is of great importance to co-ordinate an international effort to quantify as many old observations existing in the observatories throughout the world as possible.

Acknowledgements

The authors wish to express their thanks to the computer service of IAG/USP (Department of Astronomy - L. Arakaki, P. Regina, P. Vitorino, M. Bazan, A. Terra and R. Pucci), for their valuable help and patience during data-processing, and to the author's colleagues W. S. Dias and J. S. Rêgo, for suggestions about the text, and M. C. Guimarães, for valuable hints on the landscaped table. We are indebted to J. P. Périé and J. Guibert, for the SERC-J plate measurements and reductions, J. F. Le Campion, for his help with the VMC image treatment software, and to Mr. W. Monteiro, for his contribution on the observational tasks. A partial financial support from CAPES, FAPESP, CNPq and CNRS is gratefully acknowledged. This work has made use of the Astronomical Data Analysis Center, operated by the National Astronomical Observatory of Japan, the SIMBAD database, operated at CDS, Strasbourg, France, and the NASA's Astrophysics Data System Abstract Service. The authors acknowledge the referee, Dr. F. Mignard, for his suggestions.

References

 
Copyright ESO 2001