The evolution of a star of initial mass 10
A&A 375, 87-99 (2001)
DOI: 10.1051/0004-6361:20010828
P. Gil-Pons1 - E. García-Berro1,2
1 - Departament de Física Aplicada, Universitat
Politècnica de Catalunya, c/Jordi Girona s/n, Módul
B-4, Campus Nord, 08034 Barcelona, Spain
2 -
Institute for Space Studies of Catalonia, c/Gran Capitá
2-4, Edif. Nexus 104, 08034 Barcelona, Spain
Received 22 February 2001 / Accepted 25 May 2001
Abstract
The evolution of a star of initial mass 10 ![]() ,
and metallicity
Z = 0.02 in a Close Binary System (CBS) is followed from its main
sequence until an ONe degenerate remnant forms. Restrictions have been
made on the characteristics of the companion as well as on the initial
orbital parameters in order to avoid the occurrence of reversal mass
transfer before carbon is ignited in the core. The system undergoes
three mass loss episodes. The first and second ones are a consequence
of a case B Roche lobe overflow. During the third mass loss episode
stellar winds may play a role comparable to, or even more important than
Roche lobe overflow. In this paper, we extend the previously existing
calculations of stars of intermediate mass belonging to close binary
systems by following carefully the carbon burning phase of the primary
component. We also propose different possible outcomes for our scenario
and discuss the relevance of our findings. In particular, our main
result is that the resulting white dwarf component of mass
,
and metallicity
Z = 0.02 in a Close Binary System (CBS) is followed from its main
sequence until an ONe degenerate remnant forms. Restrictions have been
made on the characteristics of the companion as well as on the initial
orbital parameters in order to avoid the occurrence of reversal mass
transfer before carbon is ignited in the core. The system undergoes
three mass loss episodes. The first and second ones are a consequence
of a case B Roche lobe overflow. During the third mass loss episode
stellar winds may play a role comparable to, or even more important than
Roche lobe overflow. In this paper, we extend the previously existing
calculations of stars of intermediate mass belonging to close binary
systems by following carefully the carbon burning phase of the primary
component. We also propose different possible outcomes for our scenario
and discuss the relevance of our findings. In particular, our main
result is that the resulting white dwarf component of mass
![]() more likely has a core composed of oxygen and neon,
surrounded by a mantle of carbon-oxygen rich material. The average
abundances of the oxygen-neon rich core are
more likely has a core composed of oxygen and neon,
surrounded by a mantle of carbon-oxygen rich material. The average
abundances of the oxygen-neon rich core are
![]() ,
,
![]() ,
,
![]() and
and
![]() .
This result has important consequences for the
Accretion Induced Collapse scenario. The average abundances of the
carbon-oxygen rich mantle are
.
This result has important consequences for the
Accretion Induced Collapse scenario. The average abundances of the
carbon-oxygen rich mantle are
![]() ,
and
,
and
![]() .
The existence of this mantle could also play a
significant role in our understanding of cataclysmic variables.
.
The existence of this mantle could also play a
significant role in our understanding of cataclysmic variables.
Key words: stars: evolution - stars: binaries: general - stars: white dwarfs
Intermediate mass close binaries are defined as those systems in which
the primary component develops a degenerate carbon-oxygen core, after
burning central helium in non-degenerate conditions. From the orbital
parameters in these systems, we see that periods are small enough that
the possibility of mass transfer due to Roche Lobe overflow is enabled.
The evolution of low - to intermediate - mass stars belonging to close
binary systems has been widely studied so far and, even though many
questions still remain unsolved, important contributions have already
been made on this subject. One of these questions concerns the
evolution of heavy-weight intermediate mass stars (that is, primary
stars with masses between ![]() 8 and 11
8 and 11 ![]() )
belonging to close
binary systems. For the case of isolated stars, this range of stellar
masses corresponds to stars for which, after exhaustion of central
helium, carbon is ignited under conditions of partial degeneracy.
Ultimately, these stars become Super-AGB stars with ONe cores (Ritossa et al. 1996). For the case of stars within this mass
range belonging to binary systems, very few comments can be made, either
because most of the calculations do not follow the evolution through the
carbon burning phase or, simply, because the existing calculations focus
mostly on a lower segment of masses.
)
belonging to close
binary systems. For the case of isolated stars, this range of stellar
masses corresponds to stars for which, after exhaustion of central
helium, carbon is ignited under conditions of partial degeneracy.
Ultimately, these stars become Super-AGB stars with ONe cores (Ritossa et al. 1996). For the case of stars within this mass
range belonging to binary systems, very few comments can be made, either
because most of the calculations do not follow the evolution through the
carbon burning phase or, simply, because the existing calculations focus
mostly on a lower segment of masses.
For instance, Whyte & Eggleton (1980) studied the evolution of stars of
up to 3 ![]() belonging to semidetached systems. These authors
later extended their work to more general scenarios in which accretion
and mass transfer between low mass contact binaries were included (Whyte
& Eggleton 1985). Van der Linden (1987) also performed conservative
Case B evolutionary calculations for several masses of the primary,
ranging from 3
belonging to semidetached systems. These authors
later extended their work to more general scenarios in which accretion
and mass transfer between low mass contact binaries were included (Whyte
& Eggleton 1985). Van der Linden (1987) also performed conservative
Case B evolutionary calculations for several masses of the primary,
ranging from 3 ![]() to 12
to 12 ![]() ,
but the evolution through the
carbon burning phase was not followed. Besides the work they have
performed in the field of massive binaries, de Loore & Vanbeveren
(1992, 1994, and references therein) have also focused on the evolution
of intermediate mass close binary systems (de Loore & Vanbeveren 1995).
However, they were only able to follow the evolution of the primary star
until the exhaustion of the helium in the core. Their calculations
included both non-conservative (de Loore & de Greve 1992) and
conservative mass transfer (de Loore & Vanbeveren 1995). Very
recently, Nelson & Eggleton (2001) have performed a very comprehensive
work on intermediate mass close binary systems, exploring 5500
evolutionary tracks of mostly Case A conservative mass transfer systems.
The upper mass limit in this case was
,
but the evolution through the
carbon burning phase was not followed. Besides the work they have
performed in the field of massive binaries, de Loore & Vanbeveren
(1992, 1994, and references therein) have also focused on the evolution
of intermediate mass close binary systems (de Loore & Vanbeveren 1995).
However, they were only able to follow the evolution of the primary star
until the exhaustion of the helium in the core. Their calculations
included both non-conservative (de Loore & de Greve 1992) and
conservative mass transfer (de Loore & Vanbeveren 1995). Very
recently, Nelson & Eggleton (2001) have performed a very comprehensive
work on intermediate mass close binary systems, exploring 5500
evolutionary tracks of mostly Case A conservative mass transfer systems.
The upper mass limit in this case was ![]() 50
50 ![]() but, again, in
most of the cases the evolution during the carbon burning phase was not
followed or it was aborted earlier (when the carbon luminosity exceeded
1
but, again, in
most of the cases the evolution during the carbon burning phase was not
followed or it was aborted earlier (when the carbon luminosity exceeded
1 ![]() ). In another recent work Han et al. (2000)
determined the final mass relation for binary systems with the mass of
the components ranging between 3 and 8
). In another recent work Han et al. (2000)
determined the final mass relation for binary systems with the mass of
the components ranging between 3 and 8 ![]() ,
starting mass loss
at different times of the Hertzsprung-Russell gap. However, in these
studies the assumption of conservative mass transfer was adopted and
justified by the conditions of the case they consider which, in spite of
corresponding to an important portion of the real cases, cannot account
for all of them.
,
starting mass loss
at different times of the Hertzsprung-Russell gap. However, in these
studies the assumption of conservative mass transfer was adopted and
justified by the conditions of the case they consider which, in spite of
corresponding to an important portion of the real cases, cannot account
for all of them.
Iben (1985, 1991) has extensively reviewed the physical mechanisms
relevant to binary systems and has thoroughly discussed the evolution of
intermediate mass close binary systems, offering an excellent overview
of their evolution until very late stages, proposing several different
scenarios and providing their probabilities of occurrence. Also, Iben
& Tutukov (1984) have proposed different evolutionary scenarios for
heavy-weight intermediate mass close binary systems as progenitors of
SNe Ia. In spite of the fact that this mass interval contains a good
fraction of the stars which are massive enough to ignite carbon in a
non-explosive way, the evolution of these systems has been much
neglected until very recently. The pioneering works of Miyaji et al.
(1980) and Woosley et al. (1980) lead to the conclusion that
the stars of this mass interval belonging to close binary systems would
lose most of their mass and, moreover, would develop
electron-degenerate ONe cores after the carbon burning phase. In a
second phase, due to accretion from the secondary, the central density
would increase until the threshold for electron capture on 24Mg and
24Na would be reached first, and on 20Ne and 20F later.
The process of electron capture on these nuclei would finally trigger
the explosive ignition of neon and oxygen at very high densities
(
![]() g cm-3). At these densities,
fast electron captures on the incinerated material would bring the
Chandrasekhar mass below the actual mass of the ONe core and induce
gravitational collapse to neutron star dimensions. Although there is a
general agreement that electron-capture induced collapse could be
successful, a major drawback of this scenario is that no detailed
pre-collapse models existed in the literature. For instance, in most
of the calculations, the evolution during the mass loss phase was not
followed in full detail (Nomoto 1984) or the evolution during the carbon
burning phase was oversimplified by introducing the so-called steady
burning approximation (Saio & Nomoto 1998). Therefore, the depicted
evolutionary scenario could be substantially modified due to the
presence of these approximations.
g cm-3). At these densities,
fast electron captures on the incinerated material would bring the
Chandrasekhar mass below the actual mass of the ONe core and induce
gravitational collapse to neutron star dimensions. Although there is a
general agreement that electron-capture induced collapse could be
successful, a major drawback of this scenario is that no detailed
pre-collapse models existed in the literature. For instance, in most
of the calculations, the evolution during the mass loss phase was not
followed in full detail (Nomoto 1984) or the evolution during the carbon
burning phase was oversimplified by introducing the so-called steady
burning approximation (Saio & Nomoto 1998). Therefore, the depicted
evolutionary scenario could be substantially modified due to the
presence of these approximations.
Very recently, the evolution leading to the formation of white dwarfs
with ONe cores in close binary systems is being reinvestigated. For
instance, Domínguez et al. (1994) have studied the
formation of an ONe white dwarf through mass transfer in a close binary
system. On the other hand, in a series of recent papers (García-Berro & Iben 1994; Ritossa et al. 1996; García-Berro et al. 1997; Iben et al. 1997;
Ritossa et al. 1999) the evolution of isolated
heavy-weight intermediate mass stars has also been carefully followed
from the main sequence phase up to exhaustion of carbon in the core.
Perhaps one of the most important conclusions of these papers is that
isolated white dwarfs with masses
![]() would
most likely have an ONe core surrounded by a mantle of carbon-oxygen
rich material. This bears important consequences for the
above-mentioned accretion-induced collapse scenario because all the
existing calculations assume that the composition of the He-exhausted
core is carbon-free. Nevertheless, these authors studied only the
mass-conservative evolutionary tracks for the relevant range of stellar
masses, whereas in a close binary system the composition of the final
remnant could be dramatically affected by the previous evolutionary
phase if the star is interacting with a companion. In any case,
progress in the right direction has been made, but further exploration
is still worthwhile.
would
most likely have an ONe core surrounded by a mantle of carbon-oxygen
rich material. This bears important consequences for the
above-mentioned accretion-induced collapse scenario because all the
existing calculations assume that the composition of the He-exhausted
core is carbon-free. Nevertheless, these authors studied only the
mass-conservative evolutionary tracks for the relevant range of stellar
masses, whereas in a close binary system the composition of the final
remnant could be dramatically affected by the previous evolutionary
phase if the star is interacting with a companion. In any case,
progress in the right direction has been made, but further exploration
is still worthwhile.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{fig01.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg15.gif) |
Figure 1: Approximate evolution of the orbital parameters of the binary system and outline of the possible final outcomes. The dashed line divides the calculations reported in this paper and the three possible outcomes. |
| Open with DEXTER | |
In this paper we follow the evolution of a 10 ![]() model star of
solar metallicity belonging to a close binary system, from its main
sequence phase until an oxygen-neon core develops. In order to keep
consistency with our previous results, for the calculations reported in
this paper we have used the same evolutionary code described in Ritossa et al. (1996). In particular we have not considered
overshooting, as was done there. This procedure might lead to somewhat
smaller cores than in the case in which overshooting is considered, but
we expect the differences to be small. Different mass loss episodes are
caused by the presence of a close companion and are followed in detail.
Specifically, the model loses most of its hydrogen-rich envelope in a
case B Roche-lobe overflow episode. It is worth mentioning at this
point that we have taken special care in treating the mass zoning and
the time steps during the mass loss episodes and the carbon burning
phase (about 2000 Lagrangian mesh points are used during the most
problematic phases). Moreover, the distribution of mesh points is
regularly updated at each time step. Our algorithm puts mesh points
where they are most needed (that is, where the gradients of the physical
variables are strong) and eliminates them where they are not necessary.
Once this is done, the values of the physical variables are interpolated
at the new mesh points in order to properly compute the temporal
derivatives. If necessary the mesh can be updated at each iteration.
model star of
solar metallicity belonging to a close binary system, from its main
sequence phase until an oxygen-neon core develops. In order to keep
consistency with our previous results, for the calculations reported in
this paper we have used the same evolutionary code described in Ritossa et al. (1996). In particular we have not considered
overshooting, as was done there. This procedure might lead to somewhat
smaller cores than in the case in which overshooting is considered, but
we expect the differences to be small. Different mass loss episodes are
caused by the presence of a close companion and are followed in detail.
Specifically, the model loses most of its hydrogen-rich envelope in a
case B Roche-lobe overflow episode. It is worth mentioning at this
point that we have taken special care in treating the mass zoning and
the time steps during the mass loss episodes and the carbon burning
phase (about 2000 Lagrangian mesh points are used during the most
problematic phases). Moreover, the distribution of mesh points is
regularly updated at each time step. Our algorithm puts mesh points
where they are most needed (that is, where the gradients of the physical
variables are strong) and eliminates them where they are not necessary.
Once this is done, the values of the physical variables are interpolated
at the new mesh points in order to properly compute the temporal
derivatives. If necessary the mesh can be updated at each iteration.
As is usually done, throughout this work we will refer to the star that is initially more massive as the primary component whereas the secondary component will be its companion. We have assumed that the initial orbital parameters and the mass of the secondary component allow the whole evolution to proceed without reversal mass transfer and without disruption or merger events. This poses some constraints on the mass of the secondary which will be discussed later.
The plan of the paper is the following. In the second section of this paper we explain our choice of the initial orbital parameters and the assumed scenario. In the third section we present a description of the overall evolution of our model star until carbon ignition sets in, and we compare it with the evolution of an isolated star of the same mass. This section is also devoted to the study of the resulting mass loss episodes. In the fourth section we briefly describe the evolution during the carbon burning phase and we discuss the final characteristics of the remnant. Finally our major findings and conclusions are described in Sect. 5.
In this section we set up our evolutionary scenario and we describe our
choices for the initial orbital parameters. The reader should keep in
mind that our main goal is to provide a successful scenario to test the
formation of massive ONe white dwarfs in close binary systems that could
ultimately lead either to a cataclysmic variable or to collapse to
neutron star dimensions through the accretion-induced collapse
alternative. Therefore our choice of the initial parameters of the
binary system is effectively influenced by the desired final outcome. A
possible observational counterpart of the proposed scenario could be the
binary system IK Peg (HR 8210, HD 204188), which has an orbital period
of 21.7 days, and it is composed of a massive white dwarf of mass
![]() and a main sequence star of
and a main sequence star of
![]() (Smalley et al. 1996).
(Smalley et al. 1996).
Our starting point is a primordial system composed of a 10 ![]() star and its
star and its
![]()
![]() companion, which we will refer to as
the primary and secondary components respectively (see Fig. 1). The
system undergoes a case B mass transfer, this being the most likely
possibility, and so the primary starts losing mass after the onset of
hydrogen burning in a shell. Unlike early case-B mass loss episodes,
late case-B mass transfer has been little studied up to now. The
reasons for this are multiple but perhaps the most important one is the
additional computational difficulties that arise when studying such a
phase. However, it has been recently pointed out (Tauris & Dewi 2001)
that the actual definition of the resulting core of the primary after
the mass loss episode could influence the final orbital parameters. We
consider it interesting, therefore, to study a late case-B mass loss
episode. This determines the range of values for the initial Roche lobe
radius of the primary, that we actually choose by considering the
evolutionary track for the single
companion, which we will refer to as
the primary and secondary components respectively (see Fig. 1). The
system undergoes a case B mass transfer, this being the most likely
possibility, and so the primary starts losing mass after the onset of
hydrogen burning in a shell. Unlike early case-B mass loss episodes,
late case-B mass transfer has been little studied up to now. The
reasons for this are multiple but perhaps the most important one is the
additional computational difficulties that arise when studying such a
phase. However, it has been recently pointed out (Tauris & Dewi 2001)
that the actual definition of the resulting core of the primary after
the mass loss episode could influence the final orbital parameters. We
consider it interesting, therefore, to study a late case-B mass loss
episode. This determines the range of values for the initial Roche lobe
radius of the primary, that we actually choose by considering the
evolutionary track for the single
![]() model star followed
by García-Berro et al. (1994), and we keep it constant at
model star followed
by García-Berro et al. (1994), and we keep it constant at
![]() during the whole process (see the discussion below).
Nonetheless, it is worth mentioning that we have conducted a series of
numerical experiments in which the Roche lobe radius has been changed to
values as small as
during the whole process (see the discussion below).
Nonetheless, it is worth mentioning that we have conducted a series of
numerical experiments in which the Roche lobe radius has been changed to
values as small as
![]() and we have not found significant
differences. Given the initial mass relation and the Roche lobe of the
primary, we can obtain the orbital separation between both components by
appliying the equation (Eggleton 1983):
and we have not found significant
differences. Given the initial mass relation and the Roche lobe of the
primary, we can obtain the orbital separation between both components by
appliying the equation (Eggleton 1983):
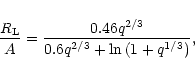 |
(1) |
where ![]() denotes the effective radius of the Roche
lobe of the primary, A indicates the orbital separation and q is the
mass ratio (M1/M2) between the components. The initial orbital
separation turns out to be
denotes the effective radius of the Roche
lobe of the primary, A indicates the orbital separation and q is the
mass ratio (M1/M2) between the components. The initial orbital
separation turns out to be
![]() -
-
![]() and the orbital
period is
and the orbital
period is
![]() -1.0 yr, depending on the initial mass of
the companion (between 1 and 5
-1.0 yr, depending on the initial mass of
the companion (between 1 and 5 ![]() ), which are reasonable
values.
), which are reasonable
values.
As it will be shown in detail in the next section, a number of uncertainties are involved in the first mass loss episode. These uncertainties are basically caused by the formation of a common envelope. This common envelope is formed when the primary star attains the highest values for its mass loss rates, and most probably removes a large amount of mass and angular momentum from the system. Consequently, the evolution of the orbital parameters cannot be accurately followed, and this can only be done in an approximate way. In order to determine the mass lost by the primary, we assume that all the matter overflowing the Roche lobe is lost by the star, and we simply stop the process when its radius dramatically decreases below that of the Roche lobe (see Sect. 3.1).
The second mass loss episode starts when the surface radius of the primary again exceeds that of its Roche lobe. In this case, this is due to the onset of helium burning in the shell. This process is most likely conservative both in mass and in angular momentum and, again, stops when the radius of the primary decreases below the value of the Roche lobe. After this temporary decrease in radius, carbon ignition continues and the primary starts the ascent along the Super-AGB but does not fill again its Roche lobe. Once carbon is exhausted in the innermost regions, it is a stellar wind rather than Roche lobe overflow that induces mass loss and, thus, we use the parametrization of Nieuwenheuzen & de Jager (1990) in order to account for the mass loss rates. As happened during the first mass loss episode, there are several uncertainties involved in this process, which can have consequences on the final fate of the system. In fact, depending on the choice of the efficiency of the winds, the resulting orbital parameters can vary significantly (Umeda et al. 1999). If the system survives the Super-AGB phase, we are left with an ONe white dwarf, as a result of the evolution of the primary, and a main sequence star that, at some time, will fill its Roche lobe and give rise to reversal mass transfer.
Even though we do not mean to get deep into the study of the probability of occurrence of the different final outcomes, we will briefly outline the different possibilities for the final stages of the life of the binary in terms of the mass transfer rates during the reversal mass transfer. Depending on this mass transfer, the final outcome can be either a cataclysmic variable if it is lower than a critical rate, a supernova explosion if it is larger or an ONe white dwarf if it is much larger. A more detailed study can be found in Sect. 5.
| Model |
|
|
|
|
|
|
|||||
| A | 6.1785 | 3.79 | 3.67 | 2.07 | 6.67 | 8.16 | 1.97 | 0.00 | 10.0 | 1.0-5.0 | 0.1-1.0 |
| B | 6.1795 | 4.12 | 3.63 | 2.32 | 6.62 | 8.16 | 1.97 | 0.00 | |||
| C | 6.1893 | 4.16 | 3.64 | 2.32 | 6.51 | 8.16 | 1.97 | 0.00 | 2.4 | 1.7-7.0 | 0.3-0.5 |
| D | 6.2917 | 3.99 | 3.64 | 2.23 | 6.45 | 8.18 | 2.04 | 0.00 | |||
| E | 6.2936 | 3.96 | 3.59 | 2.32 | 6.45 | 8.18 | 2.04 | 0.00 | |||
| F | 6.2954 | 3.98 | 3.59 | 2.32 | 6.44 | 8.18 | 2.04 | 0.00 | |||
| G | 6.3555 | 3.84 | 3.62 | 2.41 | 6.43 | 8.19 | 2.05 | 0.00 | |||
| H | 6.8505 | 3.68 | 4.18 | 2.01 | 6.47 | 8.24 | 2.05 | 0.76 | |||
| I | 7.2076 | 3.90 | 3.72 | 2.02 | 7.42 | 8.15 | 2.05 | 0.86 | |||
| J | 7.2122 | 3.82 | 3.81 | 1.85 | 7.43 | 8.42 | 2.05 | 0.91 | |||
| K | 7.2178 | 3.89 | 3.64 | 2.18 | 6.43 | 8.45 | 2.06 | 0.93 | |||
| L | 7.2638 | 4.21 | 3.73 | 2.18 | 7.66 | 8.60 | 2.06 | 1.04 | 1.9 | 2.2-9.3 | 0.1-1.0 |
| Model |
|
|||||
| 10 |
0.681 |
|
0.305 |
|
|
|
| 10 |
0.664 |
|
0.324 |
|
|
|
| 9 |
0.696 |
|
0.291 |
|
|
|
The presence of a close companion has several consequences for the
evolution of our 10 ![]() model star. In particular, there are
two Roche-lobe overflow mass loss episodes. The first one occurs just
after the main sequence phase when our model star reaches red giant
dimensions, and the second one happens shortly after the exhaustion of
central helium.
model star. In particular, there are
two Roche-lobe overflow mass loss episodes. The first one occurs just
after the main sequence phase when our model star reaches red giant
dimensions, and the second one happens shortly after the exhaustion of
central helium.
Figure 2 shows the evolution of our model in the Hertzsprung-Russell
diagram. Times to evolve to each labeled point along the evolutionary
track are given in the second column of Table 1, where we also provide
the most important characteristics of these particular models for the
hydrogen and helium burning phases. Also shown in the last columns of
Table 1 are the mass of the primary and secondary stars (M1 and
M2), and the expected orbital period
![]() .
The solid
lines represent the evolutionary phases during which no mass loss
occurs, whereas the dotted lines correspond to the evolutionary phases
where mass loss occurs: from B to C, for the first mass loss episode,
and from shortly after K to L, for most of the second Roche-lobe
overflow. Note, however, that the final part of the second Roche-lobe
overflow occurs when carbon has already been ignited in the core (see Sects. 3.4 and 4) and, thus, it is not shown in Fig. 2. As expected, the
effects of the mass loss episodes considerably modify the evolutionary
track when compared with the evolution of an isolated star of the same
initial mass (García-Berro & Iben 1994). For instance, although
the descent along the red giant branch takes place at a slightly higher
temperature than in the case of an isolated star (4400 K instead of 4300 K), it is followed by a sudden shift to bluer regions of the
diagram due to the adiabatic expansion and cooling that accompanies the
first mass loss episode (see below). The second major different feature
is that the developement of the blue loop during the core helium burning
phase takes place at lower luminosities than in the case of the isolated
model star (
.
The solid
lines represent the evolutionary phases during which no mass loss
occurs, whereas the dotted lines correspond to the evolutionary phases
where mass loss occurs: from B to C, for the first mass loss episode,
and from shortly after K to L, for most of the second Roche-lobe
overflow. Note, however, that the final part of the second Roche-lobe
overflow occurs when carbon has already been ignited in the core (see Sects. 3.4 and 4) and, thus, it is not shown in Fig. 2. As expected, the
effects of the mass loss episodes considerably modify the evolutionary
track when compared with the evolution of an isolated star of the same
initial mass (García-Berro & Iben 1994). For instance, although
the descent along the red giant branch takes place at a slightly higher
temperature than in the case of an isolated star (4400 K instead of 4300 K), it is followed by a sudden shift to bluer regions of the
diagram due to the adiabatic expansion and cooling that accompanies the
first mass loss episode (see below). The second major different feature
is that the developement of the blue loop during the core helium burning
phase takes place at lower luminosities than in the case of the isolated
model star (
![]() instead of
instead of
![]() ).
).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig02.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg60.gif) |
Figure 2: Evolutionary track of the primary component in the Hertzsprung-Russell diagram. The physical quantities of the labeled models are shown in Table 1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{fig03.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg61.gif) |
Figure 3: Evolution of the main structure parameters as a function of time during the first and the second mass-loss episodes. The upper panel shows the evolution of the radius of the primary. The inserts show the mass-loss episodes with higher resolution. The lower panel shows the convective zones engendered during the evolution up to off-center ignition of carbon. |
| Open with DEXTER | |
In Fig. 3 we show the temporal evolution of the radius of the star
(top panel) and of the convective regions associated with nuclear
burning (bottom panel), from the zero age main sequence up to the
off-center ignition of carbon in the helium-exhausted core. The
inserts show with higher resolution the evolution of the convective
regions and of the radius during the two mass-loss episodes. The
initial central convective zone of Fig. 3 is due to the high fluxes
engendered by the CN-cycle reactions and persists until hydrogen
vanishes at the center. An off-center convective region forms later,
very much in the same way as in the case of a single star. This
convective region is due to the release of gravitational potential
energy during the overall contraction phase that follows the exhaustion
of central hydrogen and the establishement of the hydrogen-burning
shell that occurs from points C to D in Fig. 2. The thick solid line
in the lower panel corresponds to the total mass of the primary which,
as it can be seen, decreases dramatically at the begining of the first
dredge-up-process, which occurs simultaneously with the first
Roche-lobe overflow. Since this mass loss episode occurs in the
presence of a deep convective envelope, the associated time scales are
short. On the contrary, we will see that the second mass-loss episode
is much more stable since it is not associated with a dredge-up
episode. This behaviour makes the two mass-loss episodes completely
different and has important consequences. For instance, we expect to
find a different pattern of surface composition after the first
mass-loss episode and dredge-up, when compared to the evolution of a
single star. The surface composition of both model stars and that of
the isolated 9 ![]() star just after the end of the dredge-up
episode can be found in Table 2. As we shall show below, the comparison
with the 9
star just after the end of the dredge-up
episode can be found in Table 2. As we shall show below, the comparison
with the 9 ![]() star is relevant for this study since some of the
results obtained in the calculations reported here are much closer to
the isolated 9
star is relevant for this study since some of the
results obtained in the calculations reported here are much closer to
the isolated 9 ![]() model than to those of the 10
model than to those of the 10 ![]() single
star. As can be seen, the helium and nitrogen contents are
significantly higher in the case of a model star belonging to a close
binary system.
single
star. As can be seen, the helium and nitrogen contents are
significantly higher in the case of a model star belonging to a close
binary system.
Our model undergoes a Case B mass loss process that starts shortly after
hydrogen combustion in a shell has been established, and the surface
radius reaches the Roche Lobe radius which, as previously mentioned, we
have adopted to be 210 ![]() .
In computing this mass-loss
episode we have (somewhat arbitrarily) assumed that the primary keeps a
constant radius which is coincidential with the Roche-lobe radius and
that all the overflowing matter will be lost by the primary. Although
this is a classical prescription there are, of course, other
alternatives (Nelson & Eggleton 2000). It is nevertheless worth
noticing that when using the last approximation with secondary masses of
around
.
In computing this mass-loss
episode we have (somewhat arbitrarily) assumed that the primary keeps a
constant radius which is coincidential with the Roche-lobe radius and
that all the overflowing matter will be lost by the primary. Although
this is a classical prescription there are, of course, other
alternatives (Nelson & Eggleton 2000). It is nevertheless worth
noticing that when using the last approximation with secondary masses of
around ![]()
![]() ,
the Roche lobe radius changes by
,
the Roche lobe radius changes by ![]()
![]() and, consequently, we do not expect this to have a large impact on our
results. We thus defer such study to a forthcoming publication.
and, consequently, we do not expect this to have a large impact on our
results. We thus defer such study to a forthcoming publication.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig04.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg64.gif) |
Figure 4: Global characteristics of the primary component as a function of time during the first mass-loss episode. The upper panel shows the total mass as a function of time. The lower panel shows the surface radius and the luminosities provided by hydrogen and helium burning. The vertical thin lines delimit the two phases of mass loss. The surface luminosity is mostly provided by hydrogen combustion. |
| Open with DEXTER | |
In the first insert in the top and bottom panels of Fig. 3 the first
mass-loss episode is shown. Also, in Fig. 4 we show the evolution of
several interesting quantities like the hydrogen and helium nuclear
luminosities. This mass-loss episode occurs in two distinct phases.
The first and most violent phase occurs as the convective envelope is
still advancing to the interior of the star and when helium has already
been ignited at the center, leading to the formation of a central
convective region, which reaches its equilibrium value when
![]() .
This phase is clearly marked by the two arrows
in the top insert of Fig. 3 and by the thin vertical lines of Fig. 4.
During this first phase, the bulk of the hydrogen-rich envelope is lost
(
.
This phase is clearly marked by the two arrows
in the top insert of Fig. 3 and by the thin vertical lines of Fig. 4.
During this first phase, the bulk of the hydrogen-rich envelope is lost
(![]()
![]() ), leaving a remnant of 2.4
), leaving a remnant of 2.4 ![]() of
which
of
which ![]()
![]() corresponds to the remaining H-rich convective
envelope. The duration of this phase is
corresponds to the remaining H-rich convective
envelope. The duration of this phase is
![]() yr.
yr.
Since the dependence of the variation of the total radius of the star on
the mass is
![]() (de Loore & Doom 1992), the
mass-loss process experiences a positive feedback. Therefore, during
the very first part of this mass-loss episode the feedback of the
process allows very high values for the mass loss rates, that can reach
values as high as
(de Loore & Doom 1992), the
mass-loss process experiences a positive feedback. Therefore, during
the very first part of this mass-loss episode the feedback of the
process allows very high values for the mass loss rates, that can reach
values as high as
![]() .
At these very high mass-loss rates the star is no longer able to keep a
constant radius and at the end of this phase the radius of the primary
falls below the value of the Roche-lobe, and thus the mass transfer
onto the secondary temporarily stops. As the evolution continues, the
primary again fills its Roche-lobe radius, leading to a subsequent
phase of mass-loss. During this second phase only
.
At these very high mass-loss rates the star is no longer able to keep a
constant radius and at the end of this phase the radius of the primary
falls below the value of the Roche-lobe, and thus the mass transfer
onto the secondary temporarily stops. As the evolution continues, the
primary again fills its Roche-lobe radius, leading to a subsequent
phase of mass-loss. During this second phase only ![]()
![]() are lost by the primary. Thus, a small portion of the H-rich envelope
remains even at the end of the first mass-loss episode. The time scale
for this second phase is significantly longer (
are lost by the primary. Thus, a small portion of the H-rich envelope
remains even at the end of the first mass-loss episode. The time scale
for this second phase is significantly longer (
![]() yr),
leading to much more modest mass-loss rates:
yr),
leading to much more modest mass-loss rates:
![]() .
.
The existence of a deep convective envelope surrounding the H-exhausted
core of the primary and, consequently, the high values of the resulting
mass-loss rates very much enhance the possibility that the system is
embedded in a common envelope. No definite and accurate study of this
kind of structure has been performed up to now. Thus, the part of the
process in which a common envelope forms is plagued with many
uncertainties, the most important one perhaps being the influence of the
common envelope on the orbital parameters. The expressions provided by
Eggleton (1983) and Paczynski (1971) can only be taken as
approximations, or even upper limits, and it is necessary to rely on
estimates that have been obtained for other systems that presumably have
undergone a common envelope phase, like the cataclysmic variable U Gem.
These estimates yield values for the angular momentum losses that can be
as high as 70-90% (Iben & Tutukov 1984). In any case, when a common
envelope is present, the angular momentum losses are expected to be high
due to the release as sound waves of the energy generated by frictional
drag in the matter of the envelope. Therefore, from an initial
separation between the components of
![]() (corresponding to
(corresponding to
![]() respectively) one can assume a typical 80% angular
momentum loss and apply the equation
respectively) one can assume a typical 80% angular
momentum loss and apply the equation
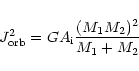 |
(2) |
to get the final separation between components after the first
Roche-lobe overflow,
![]() .
It should
be noted, nevertheless, that this way of estimating the final orbital
parameters usually leads to larger orbital separations than the values
obtained when using the treatment of Webbink (1984).
.
It should
be noted, nevertheless, that this way of estimating the final orbital
parameters usually leads to larger orbital separations than the values
obtained when using the treatment of Webbink (1984).
We can estimate the ratio between the mass accreted by the secondary and
the mass lost by the primary, ![]() ,
by assuming stable accretion
onto the secondary. Thus,
,
by assuming stable accretion
onto the secondary. Thus,
![]() ,
where
,
where
![]() is the Kelvin-Helmholtz timescale. Considering typical
values for the luminosity and for the surface radius of a main sequence
companion of mass between 1 and 5
is the Kelvin-Helmholtz timescale. Considering typical
values for the luminosity and for the surface radius of a main sequence
companion of mass between 1 and 5 ![]() ,
we get a reasonable value
for the mass accretion rate of the secondary,
,
we get a reasonable value
for the mass accretion rate of the secondary,
![]() .
Taking into account that most of the mass is lost by
the primary during the first
.
Taking into account that most of the mass is lost by
the primary during the first
![]() yr, we can easily
calculate an average value for
yr, we can easily
calculate an average value for ![]() during this mass loss
episode, which turns out to be
during this mass loss
episode, which turns out to be
![]() .
Of course, it can be
argued as well that another reasonable way to estimate
.
Of course, it can be
argued as well that another reasonable way to estimate ![]() is to
adopt the Eddington limit instead of the thermal timescale, this being a
firm upper limit. For the range of relevant parameters, this procedure
would lead in our case to accretion rates 3 times larger, or
equivalently, to
is to
adopt the Eddington limit instead of the thermal timescale, this being a
firm upper limit. For the range of relevant parameters, this procedure
would lead in our case to accretion rates 3 times larger, or
equivalently, to
![]() .
Nevertheless it should be noted that
the calculations of Hjellming & Taam (1991) predict a significantly
lower value of
.
Nevertheless it should be noted that
the calculations of Hjellming & Taam (1991) predict a significantly
lower value of ![]() ,
of the order of 0.01. Thus, the mass accreted
by the secondary will be in the range
,
of the order of 0.01. Thus, the mass accreted
by the secondary will be in the range
![]() ,
at most.
Since the main sequence lifetime of a
,
at most.
Since the main sequence lifetime of a
![]() star is
star is
![]() s it is clear that reversal mass transfer will not be
enabled until carbon is exhausted in the inner core of the primary (see
Table 1 and Sect. 4 below), in accordance with our scenario.
s it is clear that reversal mass transfer will not be
enabled until carbon is exhausted in the inner core of the primary (see
Table 1 and Sect. 4 below), in accordance with our scenario.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{fig05.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg87.gif) |
Figure 5: Opacity profiles in the hydrogen-rich envelope during the first Roche lobe overflow. The models displayed correspond to the different times labeled in Fig. 4. The insert shows, with higher resolution, the opacity profiles for the last models. |
| Open with DEXTER | |
We have considered the possibility that part of the matter ejected by the primary component might be accreted back by the same star. In order to obtain some hints of the possible outcomes to this problem, we have estimated the duration of the common envelope phase as in Iben & Tutukov (1984) and compared it with the thermal time scale of the primary. As the latter is much longer than the expected time for the common envelope to remain bound to the system, there are strong reasons to admit that there is not enough time for the ejected gas to cool down, lose kinetic energy and be overtaken by the gravitational potential of the primary.
It is also worth noting that the duration of the first dredge-up episode is longer in the calculations reported here than in the case of the isolated model described in García-Berro & Iben (1994). This is due to the fact that the fast release of gravitational energy during the compression phase that happens in the middle of the first mass loss episode cannot be evacuated solely by radiation and, thus, allows convection to persist. On the other hand, one should not forget that the overall evolutionary time scales are longer for decreasing masses and this effect would also have an influence on the duration of the dredge-up episode.
In order to find an explanation that, at least partially, accounts for the behaviour of the envelope during the first mass loss episode, in Fig. 5 we show the opacity profiles of several specific models for the times labeled in Fig. 4 (models a to g). The fastest expansion phase is coincidential with models a to c, in which the existence of a deep convective envelope, basically composed of hydrogen at relatively low temperature, leads to a high opacity and, thus, to an inefficient transport of the energy. Therefore, an important portion of the energy generated at the hydrogen burning shell is not driven outwards but, instead, it is transformed into internal energy in the envelope and, then, into work of expansion, thus keeping the value of the surface radius very close to the Roche lobe radius.
When the model reaches approximately 4![]() (model d), a
large portion of the hydrogen-rich envelope is already lost, and the
inner and hotter layers are exposed. At this point, on the one hand we
have less mass able to absorb the flow of energy and, on the other, the
opacity is also smaller. Consequently, both phenomena allow nuclear
energy to flow almost freely to the surface without being transformed
into work of expansion and, at model e, when the mass of the star
is about 2.45
(model d), a
large portion of the hydrogen-rich envelope is already lost, and the
inner and hotter layers are exposed. At this point, on the one hand we
have less mass able to absorb the flow of energy and, on the other, the
opacity is also smaller. Consequently, both phenomena allow nuclear
energy to flow almost freely to the surface without being transformed
into work of expansion and, at model e, when the mass of the star
is about 2.45 ![]() ,
a fast overall (almost adiabatic) contraction
of the convective envelope occurs, leading the surface radius to drop
below the value of the Roche lobe and, hence, mass loss temporarily
halts. Finally, for model f the opacity increases due to
compression and, thus, a new phase of expansion occurs which drives the
surface radius to again reach the value of the Roche lobe radius. Thus
the mass loss episode is restored for a brief interval, until some more
cool hydrogen-rich layers are lost. Finally the opacity definitely
decreases (model g) and the mass loss episode is finished.
,
a fast overall (almost adiabatic) contraction
of the convective envelope occurs, leading the surface radius to drop
below the value of the Roche lobe and, hence, mass loss temporarily
halts. Finally, for model f the opacity increases due to
compression and, thus, a new phase of expansion occurs which drives the
surface radius to again reach the value of the Roche lobe radius. Thus
the mass loss episode is restored for a brief interval, until some more
cool hydrogen-rich layers are lost. Finally the opacity definitely
decreases (model g) and the mass loss episode is finished.
It is worth mentioning at this point that we get a remnant of slightly
higher mass than that of the models found in the existing literature
(Iben & Tutukov 1985; Domínguez et al. 1994). This
is due to the fact that in our model the hydrogen-rich envelope is not
completely lost during the first Roche lobe overflow episode. However,
since the rest of the remaining hydrogen-rich envelope is lost later
during the second Roche lobe overflow episode, and since the growth of
the helium core is very small during the time between the two mass loss
episodes (approximately 0.08 ![]() ), we expect that the influence
on the CO and ONe core sizes and compositions is negligible and so the
final results will not be substantially different.
), we expect that the influence
on the CO and ONe core sizes and compositions is negligible and so the
final results will not be substantially different.
The second mass loss episode starts when helium burning begins in a
shell and, as a consequence, its surface radius approaches again that of
the Roche lobe (see Fig. 3), which now is ![]()
![]() .
The
global characteristics (the mass and radius and the luminosities
associated with the active burning regions) of the primary during the
second mass loss episode are shown in Fig. 6. The fact that in the
outer envelope, from which the matter is removed, energy is transported
by radiation instead of being transported by convection, allows the
process to take place in a more stable way than in the first mass loss
episode. Hence, the mass loss rates are much smaller (
.
The
global characteristics (the mass and radius and the luminosities
associated with the active burning regions) of the primary during the
second mass loss episode are shown in Fig. 6. The fact that in the
outer envelope, from which the matter is removed, energy is transported
by radiation instead of being transported by convection, allows the
process to take place in a more stable way than in the first mass loss
episode. Hence, the mass loss rates are much smaller (
![]() )
during most of the process, except at
two phases, during which the values of the mass loss rate are one order
of magnitude higher. The first phase corresponds to the beginning of
the mass loss episode, when the remainder of the hydrogen-rich envelope
is lost, and the second phase happens nearly at the end of the process,
when carbon is ignited off-center. The end of the process is
determined by a steep decrease in the surface radius of the star that
takes values below the Roche lobe radius.
)
during most of the process, except at
two phases, during which the values of the mass loss rate are one order
of magnitude higher. The first phase corresponds to the beginning of
the mass loss episode, when the remainder of the hydrogen-rich envelope
is lost, and the second phase happens nearly at the end of the process,
when carbon is ignited off-center. The end of the process is
determined by a steep decrease in the surface radius of the star that
takes values below the Roche lobe radius.
The moderate values we get for the mass loss of the primary support the
hypothesis of conservative mass transfer. Furthermore, one can compare
the luminosity associated with accretion onto the secondary, which is
given by
![]() ,
where
,
where
![]() and
and
![]() stand for the gravitational potential
computed at the Roche lobe radius and at the radius of the secondary
respectively, with the Eddington luminosity of the secondary,
stand for the gravitational potential
computed at the Roche lobe radius and at the radius of the secondary
respectively, with the Eddington luminosity of the secondary,
![]() .
For a set of typical values for the secondary star, we get that
.
For a set of typical values for the secondary star, we get that
![]() and, thus, according to Han et al. (1999)
conservative mass transfer is most likely.
and, thus, according to Han et al. (1999)
conservative mass transfer is most likely.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig06.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg95.gif) |
Figure 6: Global characteristics of the primary component as a function of time during the second mass loss episode. The upper panel shows the total mass as a function of time. The lower panel shows the surface radius and the luminosities provided by hydrogen, helium and carbon burning. The vertical thin lines delimit the second mass loss episode. The surface luminosity is mostly provided by helium combustion. |
| Open with DEXTER | |
In Fig. 7 we show the evolution of the center of the primary in the
![]() diagram from the main sequence until the onset of
carbon ignition (solid line), and the evolution of the center of the
isolated 10
diagram from the main sequence until the onset of
carbon ignition (solid line), and the evolution of the center of the
isolated 10 ![]() star (dashed line). As one can expect from the
previous discussion, the differences between both cases start to show up
at the onset of helium burning at the center, which, as explained above,
is almost coincident with the first mass loss episode. The evolution of
the primary component of the close binary system leads to higher central
densities for the same value of the temperature than its isolated
counterpart. In fact, mass loss has two obvious consequences. Firstly,
the size of the central helium-burning convective region is smaller for
the case studied here than in the evolution of isolated 10
star (dashed line). As one can expect from the
previous discussion, the differences between both cases start to show up
at the onset of helium burning at the center, which, as explained above,
is almost coincident with the first mass loss episode. The evolution of
the primary component of the close binary system leads to higher central
densities for the same value of the temperature than its isolated
counterpart. In fact, mass loss has two obvious consequences. Firstly,
the size of the central helium-burning convective region is smaller for
the case studied here than in the evolution of isolated 10 ![]() star. Secondly, the mass of the primary component of the binary system
is much smaller than its isolated counterpart. Accordingly, the
He-exhausted core of the primary is smaller (
star. Secondly, the mass of the primary component of the binary system
is much smaller than its isolated counterpart. Accordingly, the
He-exhausted core of the primary is smaller (![]()
![]() )
and
with higher central densities than the core resulting from the evolution
of a single 10
)
and
with higher central densities than the core resulting from the evolution
of a single 10 ![]() star (
star (![]()
![]() )
and very similar
to that of a 9
)
and very similar
to that of a 9 ![]() isolated star (
isolated star (![]()
![]() ).
).
The abundances in the central regions of the core are also affected by
mass loss in a similar way, and so, the resulting composition is more
similar to that of the single 9 ![]() model. At the end of the
second mass loss episode the mass of the primary is 1.88
model. At the end of the
second mass loss episode the mass of the primary is 1.88 ![]() ,
of
which the innermost 1.05
,
of
which the innermost 1.05 ![]() corresponds to a carbon-oxygen
core which is surrounded by a helium-rich envelope. The chemical
composition profiles at this moment are shown in Fig. 8. As can be
seen in this figure the abundance profiles of our model before carbon
ignition reveal a higher carbon and neon content, and lower amounts of
oxygen and magnesium than those of the single 10
corresponds to a carbon-oxygen
core which is surrounded by a helium-rich envelope. The chemical
composition profiles at this moment are shown in Fig. 8. As can be
seen in this figure the abundance profiles of our model before carbon
ignition reveal a higher carbon and neon content, and lower amounts of
oxygen and magnesium than those of the single 10 ![]() model. Also
the helium burning shell is narrower in the case studied here, due to
the fact that the (helium) envelope over this burning shell is much
smaller.
model. Also
the helium burning shell is narrower in the case studied here, due to
the fact that the (helium) envelope over this burning shell is much
smaller.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{fig07.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg100.gif) |
Figure 7:
Evolution in the
|
| Open with DEXTER | |
The carbon burning phase takes place under conditions of partial
degeneracy and - as one can expect from the comparison between the
characteristics of the primary star in a close binary system and that of
single star models of similar mass before carbon burning - many
similarities are also found when analysing this phase of the evolution.
Actually, the most prominent features, such as the carbon flashes and
the convective regions associated with each one of these (see Fig. 9)
are very similar for the case studied here and those of a 9 ![]() model star. These flashes reach about
model star. These flashes reach about
![]() ,
and
last for approximately 103 yr. However, as it happens in the case of
the evolution of isolated stars of this mass range, during most of the
carbon burning phase the surface luminosity remains almost constant and
close to a value of
,
and
last for approximately 103 yr. However, as it happens in the case of
the evolution of isolated stars of this mass range, during most of the
carbon burning phase the surface luminosity remains almost constant and
close to a value of
![]() .
.
The first flash is a prototypic one. As in the case of isolated stars
within this mass range, carbon is ignited off-center due to neutrino
cooling of the central regions. The mass coordinate at which carbon is
ignited is ![]()
![]() ,
very close to the value obtained for
the single 9
,
very close to the value obtained for
the single 9 ![]() star (
star (![]()
![]() ). As carbon
luminosity increases, most of the energy generated by nuclear reactions
is used to increase the temperature of the adjacent layers, thus forcing
high temperature gradients, which ultimately lead to the formation of a
convective zone that allows a more efficient transport of energy. This
increase in the temperature is followed by an expansion of the nearby
layers and in particular, of the helium burning shell, which cools down
and, hence, its luminosity temporarily decreases. Apart from the
formation of the inner convective shell, the flash also affects the
location of the inner edge of the convective envelope that moves deeper
into the star when the carbon luminosity increases and receeds when the
carbon luminosity decreases again, very much in the same fashion as in
the isolated 9
). As carbon
luminosity increases, most of the energy generated by nuclear reactions
is used to increase the temperature of the adjacent layers, thus forcing
high temperature gradients, which ultimately lead to the formation of a
convective zone that allows a more efficient transport of energy. This
increase in the temperature is followed by an expansion of the nearby
layers and in particular, of the helium burning shell, which cools down
and, hence, its luminosity temporarily decreases. Apart from the
formation of the inner convective shell, the flash also affects the
location of the inner edge of the convective envelope that moves deeper
into the star when the carbon luminosity increases and receeds when the
carbon luminosity decreases again, very much in the same fashion as in
the isolated 9 ![]() star.
star.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{fig08.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg105.gif) |
Figure 8: Abundance profile of the core of the primary at the end of the second mass loss episode, which is practically coincidential with the beginning of carbon burning. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{fig09.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg106.gif) |
Figure 9: Evolution of the nuclear luminosities during the carbon-burning phase (upper panel), and of the associated convective regions (lower panel). The solid and the dotted lines in the upper panel correspond, respectively, to the carbon and helium luminosities. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{fig10.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg107.gif) |
Figure 10:
Relevant structural and dynamical quantities for a model at
time
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{fig11.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg108.gif) |
Figure 11:
Same as figure 10, but for time
|
| Open with DEXTER | |
The second flash occurs at a smaller mass coordinate (carbon is
re-ignited at the point where the penetration of the inner edge of the
previous convective shell was maximum) and the physical mechanisms
operating are very similar to those of the first one. However, its
maximum strength is considerably smaller (![]()
![]() instead
of
instead
of ![]()
![]() ). After the most violent phase of this flash
is over, the carbon luminosity does not decrease below that of helium
but, rather, keeps a stationary value,
). After the most violent phase of this flash
is over, the carbon luminosity does not decrease below that of helium
but, rather, keeps a stationary value,
![]() ,
which is slightly larger than the value of the helium luminosity,
,
which is slightly larger than the value of the helium luminosity,
![]() .
During this phase the
carbon-burning flame propagates inwards at a roughly constant speed -
see García-Berro et al. (1997) for a detailed description of the
energy balance established during this phase - reaching the center at
.
During this phase the
carbon-burning flame propagates inwards at a roughly constant speed -
see García-Berro et al. (1997) for a detailed description of the
energy balance established during this phase - reaching the center at
![]() s.
s.
A very distinctive feature of the case studied here when compared to the
evolution of an isolated 9 ![]() star is that at
star is that at
![]() s the outer convective envelope disappears as the
carbon burning front advances to the center. In fact, the second
dredge-up in the isolated 9
s the outer convective envelope disappears as the
carbon burning front advances to the center. In fact, the second
dredge-up in the isolated 9 ![]() star is caused by the expansion
and cooling of the layers just below the base of the convective envelope
(García-Berro et al. 1997), which allows the increase of the
radiative temperature gradient in this region and, so, the inner advance
of convection down to
star is caused by the expansion
and cooling of the layers just below the base of the convective envelope
(García-Berro et al. 1997), which allows the increase of the
radiative temperature gradient in this region and, so, the inner advance
of convection down to
![]() .
After that,
the base of the convective envelope remains at an approximately constant
position, as the energy supplied by the helium burning shell and the
opacity of the nearby layers can keep the temperature gradient high
enough. In the case studied here, the base of the convective envelope
reaches the same position as in the single star due to a similar
mechanism, but, unlike the case of the isolated 9
.
After that,
the base of the convective envelope remains at an approximately constant
position, as the energy supplied by the helium burning shell and the
opacity of the nearby layers can keep the temperature gradient high
enough. In the case studied here, the base of the convective envelope
reaches the same position as in the single star due to a similar
mechanism, but, unlike the case of the isolated 9 ![]() star, this
position cannot be maintained, instead, it receeds and disappears. The
reason for this behaviour can be explained with the help of Figs. 10
and 11, where we show some relevant structural and dynamical quantities
for times
star, this
position cannot be maintained, instead, it receeds and disappears. The
reason for this behaviour can be explained with the help of Figs. 10
and 11, where we show some relevant structural and dynamical quantities
for times
![]() s, just before the disappearance of
the convective envelope, and
s, just before the disappearance of
the convective envelope, and
![]() s, just after
the convective episode.
s, just after
the convective episode.
Panel c of Fig. 10 shows that there are three interesting and
distinct regions in the star. The first of these regions is below the
helium discontinuity and there, the work of expansion fed by carbon
burning is devoted basically to lift degeneracy and, thus, we have
expansion at almost constant temperature (panel b). On top of
this region we have the helium burning shell where the energy supplied
by nuclear reactions is used to build up the luminosity profile (panel a). In the region between the helium burning shell and the base
of the convective envelope, the flux is partially transformed into
heating and, at the same time, the whole region is collapsing. This in
turn causes a large temperature gradient at
![]() .
As the evolution continues, the temperature in this region
steadily increases. Thus, the temperature gradient ultimately flattens
and the inner edge of the convective envelope consequently receeds.
Panel c of Fig. 11 shows that the nuclear energy released by the
helium burning shell remains the same, but now most of this energy
merely flows outwards (panel a), rather than being transformed
into work of expansion. Instead, the whole region on top of the helium
burning shell is compressed leading to a non-homogeneous increase of
the temperature (panel b) which effectively erases the temperature
gradient and forces the disappearance of the convective region. This
translates into an increase in the luminosity for
.
As the evolution continues, the temperature in this region
steadily increases. Thus, the temperature gradient ultimately flattens
and the inner edge of the convective envelope consequently receeds.
Panel c of Fig. 11 shows that the nuclear energy released by the
helium burning shell remains the same, but now most of this energy
merely flows outwards (panel a), rather than being transformed
into work of expansion. Instead, the whole region on top of the helium
burning shell is compressed leading to a non-homogeneous increase of
the temperature (panel b) which effectively erases the temperature
gradient and forces the disappearance of the convective region. This
translates into an increase in the luminosity for
![]() .
.
When carbon-burning in the central regions is over, a series of small
shell burning episodes occurs (Fig. 9). Each one of these episodes has
a decreasing strength and leads to the almost complete exhaustion of
carbon in a core of 1.05 ![]() .
It is interesting to note that,
unlike what happens with the rest of these mild flashes, the first of
these is not accompanied by a substantial decrease in the helium
luminosity. The reason for this behaviour is twofold. Firstly, the
duration of this flash is smaller and, hence, less energy is released.
Secondly, and most important, there exists a thick radiative layer (of
about 0.7
.
It is interesting to note that,
unlike what happens with the rest of these mild flashes, the first of
these is not accompanied by a substantial decrease in the helium
luminosity. The reason for this behaviour is twofold. Firstly, the
duration of this flash is smaller and, hence, less energy is released.
Secondly, and most important, there exists a thick radiative layer (of
about 0.7 ![]() )
between the initial location of the convective
carbon-burning shell and the helium-burning shell. Therefore, the
energy is almost totally absorbed before reaching the helium-burning
shell and, thus, no expansion nor cooling of the helium burning shell
are produced. During all this phase the core contracts, and the outer
layers of the star begin a new expansion as the outer convective
envelope reappears and its inner edge advances to the interior of the
star. However, the radius of the star remains below the Roche lobe
radius and only exceeds its value at the end of the second of these
flashes.
)
between the initial location of the convective
carbon-burning shell and the helium-burning shell. Therefore, the
energy is almost totally absorbed before reaching the helium-burning
shell and, thus, no expansion nor cooling of the helium burning shell
are produced. During all this phase the core contracts, and the outer
layers of the star begin a new expansion as the outer convective
envelope reappears and its inner edge advances to the interior of the
star. However, the radius of the star remains below the Roche lobe
radius and only exceeds its value at the end of the second of these
flashes.
Since, as discussed above, the second mass loss episode was most
probably conservative and during the bulk of the carbon burning phase in
the central regions (say
![]() s) the model star
keeps its radius below that of the Roche lobe, the orbital parameters
remain unaffected. As explained before, only at the very end of the
carbon burning phase the flash activity is accompanied by a rapid
increase of the surface radius of the star beyond the Roche lobe radius.
This, of course, translates into a new mass loss episode for
s) the model star
keeps its radius below that of the Roche lobe, the orbital parameters
remain unaffected. As explained before, only at the very end of the
carbon burning phase the flash activity is accompanied by a rapid
increase of the surface radius of the star beyond the Roche lobe radius.
This, of course, translates into a new mass loss episode for
![]() s. This mass loss episode lasts for a short period of
time, of about
s. This mass loss episode lasts for a short period of
time, of about ![]()
![]() s and the mass loss rates are of
s and the mass loss rates are of
![]()
![]() at the beginning of the
episode, becoming much smaller as the evolution proceeds. After this
short phase of Roche lobe overflow, the radius of the primary star turns
out to be very large, but its rate of increase slows down considerably.
At this evolutionary stage, the density of the extended envelope is so
small that a stellar wind could also drive the loss of the remaining
envelope. In any case, stellar winds play a significant role which can
be comparable to Roche lobe overflow. Thus, we assume that a stellar
wind removes mass from the surface following closely the parametrization
of Nieuwenheuzen and de Jager (1990) which gives typical rates of
at the beginning of the
episode, becoming much smaller as the evolution proceeds. After this
short phase of Roche lobe overflow, the radius of the primary star turns
out to be very large, but its rate of increase slows down considerably.
At this evolutionary stage, the density of the extended envelope is so
small that a stellar wind could also drive the loss of the remaining
envelope. In any case, stellar winds play a significant role which can
be comparable to Roche lobe overflow. Thus, we assume that a stellar
wind removes mass from the surface following closely the parametrization
of Nieuwenheuzen and de Jager (1990) which gives typical rates of ![]()
![]() (this is the rate
considered in Fig. 9). However, since these mass loss rates are poorly
known, we have conducted a series of numerical experiments where we have
changed the mass loss rate from
(this is the rate
considered in Fig. 9). However, since these mass loss rates are poorly
known, we have conducted a series of numerical experiments where we have
changed the mass loss rate from
![]() to
to
![]() and we have found essentially the
same results for the very final part of the carbon burning phase, except
of course for the mass of the remaining helium envelope.
and we have found essentially the
same results for the very final part of the carbon burning phase, except
of course for the mass of the remaining helium envelope.
The exhaustion of central carbon is not complete but, instead, at the
innermost 0.3 ![]() there remains remains a small amount of
unburnt carbon, reaching a maximum abundance of
there remains remains a small amount of
unburnt carbon, reaching a maximum abundance of
![]() at
at
![]() (see Fig. 12). Analogous to what was found
in the series of papers devoted to the evolution of isolated stars
within this mass range, most of the ashes of carbon burning are sodium,
neon and oxygen, the abundance of magnesium being very small. This
could have important consequences for the accretion-induced collapse
scenario (Gutiérrez et al. 1996). It is also noteworthy that the
relatively thick carbon-rich buffer is located just below the helium
envelope, which could make the resulting He-rich white dwarf
practically indistinguishable from an observational point of view from a
regular massive carbon-oxygen white dwarf (Weidemann 2000).
(see Fig. 12). Analogous to what was found
in the series of papers devoted to the evolution of isolated stars
within this mass range, most of the ashes of carbon burning are sodium,
neon and oxygen, the abundance of magnesium being very small. This
could have important consequences for the accretion-induced collapse
scenario (Gutiérrez et al. 1996). It is also noteworthy that the
relatively thick carbon-rich buffer is located just below the helium
envelope, which could make the resulting He-rich white dwarf
practically indistinguishable from an observational point of view from a
regular massive carbon-oxygen white dwarf (Weidemann 2000).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{fig12.eps}
\end{figure}](/articles/aa/full/2001/31/aa1191/Timg127.gif) |
Figure 12: Final abundances of the primary star after the carbon burning phase. Note the existence of a carbon-rich buffer on top of the carbon exhausted core. |
| Open with DEXTER | |
We have followed the evolution of a
![]() primary component of
solar metallicity belonging to a close binary system with a secondary of
low or intermediate-low mass, from its main sequence phase until carbon
is exhausted in the core and a degenerate remnant is formed. Our main
goal consisted of extending the previously existing calculations of this
kind of system in order to follow in full detail the carbon burning
phase, which at present has not yet been well studied. We have found
that the primary star undergoes three mass-loss episodes. The first of
these episodes occurs after hydrogen exhaustion in the core and most
problably is not conservative, due to the existence of a deep convective
envelope which leads to the formation of a common envelope. The second
happens after helium exhaustion, and it is most problably conservative.
Finally, the third one occurs when carbon burning in a series of
succesive shells sets in. We have analysed the changes in the structure
and composition that the primary star suffers while simultaneously
undergoing carbon burning and mass loss. The determination of the mass
loss rates at this very late stage of the evolution, whether due to
Roche lobe overflow, or to stellar winds, is still an open question, and
therefore, we have explored a broad range of mass loss rates ranging
from 10-7 to
primary component of
solar metallicity belonging to a close binary system with a secondary of
low or intermediate-low mass, from its main sequence phase until carbon
is exhausted in the core and a degenerate remnant is formed. Our main
goal consisted of extending the previously existing calculations of this
kind of system in order to follow in full detail the carbon burning
phase, which at present has not yet been well studied. We have found
that the primary star undergoes three mass-loss episodes. The first of
these episodes occurs after hydrogen exhaustion in the core and most
problably is not conservative, due to the existence of a deep convective
envelope which leads to the formation of a common envelope. The second
happens after helium exhaustion, and it is most problably conservative.
Finally, the third one occurs when carbon burning in a series of
succesive shells sets in. We have analysed the changes in the structure
and composition that the primary star suffers while simultaneously
undergoing carbon burning and mass loss. The determination of the mass
loss rates at this very late stage of the evolution, whether due to
Roche lobe overflow, or to stellar winds, is still an open question, and
therefore, we have explored a broad range of mass loss rates ranging
from 10-7 to
![]() in order to
understand how the uncertainties affect the gross properties of the
resulting degenerate object. We have found that our incomplete
knowledge of the mass-loss rate does not affect the final result as far
as the core is concerned. In particular, carbon is not reignited.
Thus, the final characteristics of the remnant are well determined.
After the evolution through these different burning stages and under the
influence of a close companion, the initially
in order to
understand how the uncertainties affect the gross properties of the
resulting degenerate object. We have found that our incomplete
knowledge of the mass-loss rate does not affect the final result as far
as the core is concerned. In particular, carbon is not reignited.
Thus, the final characteristics of the remnant are well determined.
After the evolution through these different burning stages and under the
influence of a close companion, the initially
![]() star will
form a
star will
form a ![]()
![]() degenerate remnant, with an oxygen-neon
core of
degenerate remnant, with an oxygen-neon
core of ![]()
![]() surrounded by a carbon-oxygen rich mantle
of
surrounded by a carbon-oxygen rich mantle
of ![]()
![]() and a thin helium envelope.
and a thin helium envelope.
We have found remarkable differences between our results and those found
by other authors that have also followed the evolution of a
10 ![]() model star up to the carbon burning phase. For instance,
Nomoto (1992, 1984) obtained a final core of larger mass (
model star up to the carbon burning phase. For instance,
Nomoto (1992, 1984) obtained a final core of larger mass (![]()
![]() )
with significantly higher values for the abundances Ne20and Mg24, and lower values for the O16 and Na23abundances. The ultimate reason for this difference is that the nuclear
reaction rates used by Nomoto (Fowler et al. 1975) are
different from ours (Caughlan & Fowler 1988). In this regard, it is
important to recall here that in this paper we have chosen the same
physical inputs as in Ritossa et al. (1996) in order
to remain consistent with our previous calculations. Since then there
have been some new determinations of the thermonuclear reaction rates,
particularly the NACRE compilation (Angulo et al. 1999). However, for
the most important reaction channels involved in carbon burning, the
differences are not expected to be large and, thus, the chemical
composition of the core can be considered as relatively safe, perhaps
the most important expected difference being an even smaller amount of
Mg24 (Palacios et al. 2000; José et al. 1999). The
comparison with the ONe core obtained by Domínguez et al. (1993)
it is not easy either, since they start from a different initial CO core
prior to carbon burning. Moreover, they removed the outer envelope
during the carbon burning phase and, hence, their treatment for this
phase differs substantially from ours. This, in particular, could be
the reason for the central region of unburnt carbon which is quite
apparent in their results, although poor mass resolution of the central
regions - see the discussion in García-Berro et al. (1997) -
cannot be totally discarded. Regarding the average abundances of the
ONe core, they obtained, using similar nuclear reaction rates,
)
with significantly higher values for the abundances Ne20and Mg24, and lower values for the O16 and Na23abundances. The ultimate reason for this difference is that the nuclear
reaction rates used by Nomoto (Fowler et al. 1975) are
different from ours (Caughlan & Fowler 1988). In this regard, it is
important to recall here that in this paper we have chosen the same
physical inputs as in Ritossa et al. (1996) in order
to remain consistent with our previous calculations. Since then there
have been some new determinations of the thermonuclear reaction rates,
particularly the NACRE compilation (Angulo et al. 1999). However, for
the most important reaction channels involved in carbon burning, the
differences are not expected to be large and, thus, the chemical
composition of the core can be considered as relatively safe, perhaps
the most important expected difference being an even smaller amount of
Mg24 (Palacios et al. 2000; José et al. 1999). The
comparison with the ONe core obtained by Domínguez et al. (1993)
it is not easy either, since they start from a different initial CO core
prior to carbon burning. Moreover, they removed the outer envelope
during the carbon burning phase and, hence, their treatment for this
phase differs substantially from ours. This, in particular, could be
the reason for the central region of unburnt carbon which is quite
apparent in their results, although poor mass resolution of the central
regions - see the discussion in García-Berro et al. (1997) -
cannot be totally discarded. Regarding the average abundances of the
ONe core, they obtained, using similar nuclear reaction rates,
![]() ,
,
![]() and
and
![]() .
The high value of the O16 abundance is surprising, whereas the rest
of the abundances are similar. Moreover, they did not find Na23,
which is an important isotope in our calculations. Thus, all these
differences could be due to the use of a simplified nuclear network,
much smaller than ours. In summary, the composition of our ONe core
differs from the former results, especially for the Mg24, Na23and Ne20 nuclei, which are the elements onto which electron
captures happen and, consequently, may substantially affect the
determination of the explosive ONe ignition density. The fact that the
mass of the ONe core found by these authors (
.
The high value of the O16 abundance is surprising, whereas the rest
of the abundances are similar. Moreover, they did not find Na23,
which is an important isotope in our calculations. Thus, all these
differences could be due to the use of a simplified nuclear network,
much smaller than ours. In summary, the composition of our ONe core
differs from the former results, especially for the Mg24, Na23and Ne20 nuclei, which are the elements onto which electron
captures happen and, consequently, may substantially affect the
determination of the explosive ONe ignition density. The fact that the
mass of the ONe core found by these authors (![]()
![]() )
is
quite similar to that obtained here is, however, encouraging.
)
is
quite similar to that obtained here is, however, encouraging.
The definite final result is not necessarily an oxygen-neon white dwarf, because the evolution of the entire system has not stopped yet. In fact, as the secondary component evolves, it could reach such a dimension that its radius could exceed that of its Roche lobe, and mass transfer could take place onto the remnant. Depending on the evolution of the orbital parameters and, ultimately, on the mass transfer rates, different possibilities arise:
Acknowledgements
Part of this work was supported by the Spanish DGES project number PB98-1183-C03-02, by the MCYT grant AYA2000-1785, by the CIRIT and by Sun MicroSystems under the Academic Equipment Grant AEG-7824-990325-SP. We also wish to thank J. José for carefully reading the manuscript and to our referee (P. P. Eggleton) for his very valuable comments and suggestions.