A&A 375, 14-24 (2001)
DOI: 10.1051/0004-6361:20010759
O. Doré1 - F. R. Bouchet1 - Y. Mellier1,2 - R. Teyssier3,1,4
1 - Institut d'Astrophysique de Paris, 98bis boulevard Arago,
75014 Paris, France
2 - Observatoire de Paris, DEMIRM, 61 avenue de l'Observatoire, 75014
Paris, France
3 - Service d'Astrophysique, DAPNIA, Centre d'Études de Saclay, 91191
Gif-sur-Yvette, France
4 - Numerical Investigations in Cosmology (NIC) group, CEA Saclay, France
Received 9 February 2001 / Accepted 16 May 2001
Abstract
We present a self consistent method to perform a joint analysis of
Sunyaev-Zel'dovich and weak gravitational lensing observation of galaxy
clusters. The spatial distribution of the cluster main components is
described by a perturbative approach. Assuming hydrostatic equilibrium and the
equation of state, we are able to deduce, from observations, maps of
projected gas density and gas temperature. The method then naturally
entails a X-ray emissivity prediction which can be compared to
observed X-ray emissivity maps. By comparing with 2 simulated
clusters we find that this prediction turns out to be in very good agreement
with the simulations. The simulated and predicted
surface brightness images have a correlation coefficient higher than 0.9 and their
total flux differs by 0.9% or 9%. The method should be
able to deal with real data in order to provide a physical
description of the state of the cluster and of its constituents. The tests
performed show that we can recover the amount and the spatial distributions of both
the baryonic and non-baryonic material with an accuracy better than
10%. So, in principle, it might indeed help to alleviate some well
known biases affecting, e.g. baryon fraction measurements.
Key words: gravitational lensing - galaxies: clusters: general - cosmology: observations - X-rays: galaxies
Whereas clusters of galaxies, as the largest gravitationaly bound
structures in the universe, are a natural probe of cosmology,
observations, numerical simulations as well as timing arguments
provide compelling evidence that most clusters are young and complex
systems. Interaction with large-scale structures, merging processes
and coupling of dark matter with the intra-cluster medium complicate
the interpretation of observations and the modeling of each
components. Since clusters are composed of dark matter (DM), galaxies and
a hot dilute X-ray emitting gas (Intra cluster medium, ICM) accounting respectively for
![]() ,
,
![]() and
and
![]() of their mass, the physics
of the ICM bounded in a dark matter gravitational potential plays a
major role in cluster formation and evolution.
of their mass, the physics
of the ICM bounded in a dark matter gravitational potential plays a
major role in cluster formation and evolution.
Each component can be observed in many different ways. In particular, we refer to gravitational lensing effects (the weak-lensing regime here, WL) (Mellier 2000; Bartelmann & Schneider 2001), the Sunyaev-Zel'dovich (SZ) effect (Sunyaev & Zel'dovich 1972; Birkinshaw 1999) and X-ray emission (X) (Sarrazin 1988). Whereas the former probes mostly the dark matter component, both the latter probe the baryons of the gravitationally bound ICM.
Due to observational progress, increasingly high quality data are
available that enable multi-wavelength investigation of clusters
down to an arc-minute scale (the most recent is the spectacular progress in SZ
measurements, e.g. Reese et al. (2000) and Désert et al. (1998). In contrast with past
decades, it is now possible to analyse clusters of galaxies using
X-ray, WL and SZ data at almost the same resolution, and to produce
from them self
consistent models. The exploration of reconstruction techniques to
analyse together these high quality data sets and exploit
their complementarity is a recent challenge. It has been tackled by several groups
(Zaroubi et al. 1998; Grego et al. 1999; Reblinsky & Bartelmann 1999; Zaroubi et al. 2000; Castander et al. 2000; Holder et al. 2000). Zaroubi et al. and
Reblinsky et al. attempted a full deprojection by assuming
isothermality and axial symmetry, using respectively a least square
minimization and a Lucy-Richardson algorithm. Grego et al. compare
SZ-derived gas mass to WL-derived total mass by fitting a spheroidal
![]() model. Whereas these methods give reasonable results it
has been pointed out, e.g. by Inagaki et al. (1995) in the context of
H0 measurement from SZ and X-ray observations, that both
non-isothermality and asphericity analysis can trigger systematic
errors as high as
model. Whereas these methods give reasonable results it
has been pointed out, e.g. by Inagaki et al. (1995) in the context of
H0 measurement from SZ and X-ray observations, that both
non-isothermality and asphericity analysis can trigger systematic
errors as high as ![]() .
.
In this paper, we propose an alternative direction in order to to get rid of both isothermal and spherical hypotheses. Our method is based on a self-consistent use of WL and SZ observables, and on a perturbative development of general physical hypotheses. This approach allows us to test some very general physical hypotheses of the gas (hydrostatic equilibrium, global thermodynamic equilibrium) and also naturally provides some X observation predictions.
Observations only provide 2-D projected quantities (e.g. mass, gas
pressure, ...). These quantities are related to each other by physical
hypotheses which express the 3-D geometrical properties and
the dynamical and thermodynamical stage of matter (e.g. sphericity,
hydrostatic equilibrium, equation of state). In most cases, their
3-D mathematical formulations do not have any tractable equivalent
relating 2-D projected quantities: in particular, projection along
the line of sight does not provide an equation of state or a
projected hydrostatic equilibrium equation. Therefore, as soon as we
want to compare these data (WL, SZ, X) we have to deproject the
relevant physical quantities (
![]() ...). This can be
done only using strong assumptions, either by using parametric models (e.g. a
...). This can be
done only using strong assumptions, either by using parametric models (e.g. a ![]() model,
Cavaliere & Fusco-Femaino 1976) or by assuming mere geometrical hypotheses (the former
necessarily encompassing the latter) (Fabian et al. 1981; Yoshikawa & Suto 1999).
model,
Cavaliere & Fusco-Femaino 1976) or by assuming mere geometrical hypotheses (the former
necessarily encompassing the latter) (Fabian et al. 1981; Yoshikawa & Suto 1999).
Because the latter keeps the physical grounds as general as possible and also avoids as many theoretical biases as possible, we preferred to focus on the geometric approach. Furthermore, this simplest choice is also motivated by looking at some images of observed clusters (Désert et al. 1998; Grego et al. 1999). Some do have striking regularity with almost circular or ellipsoidal appearance, as we expect for fully relaxed systems. Then, since relaxed clusters are expected to be spheroidal in favored hierarchical structure formation scenario, it is natural to try to relate the observed quasi-circularity (quasi-sphericity) to the 3-D quasi-sphericity (quasi-spheroidality). We perform this by using some linearly perturbed spherical (spheroidal) symmetries in a self-consistent approach.
The paper is organised as follows: in Sect. 2 we define our physical hypothesis and notations. The method is precisely described in Sect. 3. We consider both the spherical as well as spheroidal cases and obtain a predicted X surface brightness map from a SZ decrement map and a WL gravitational distortion map. In Sect. 4 a demonstration with simulated clusters is presented before discussing its application to genuine data as well as perspectives for further developments in Sect. 5.
We now briefly describe our notations as well as our physical hypothesis.
Following considerations fully detailed in Sarrazin (1988) the ICM can be
regarded as a hot and dilute plasma constituted by ions and
electrons, whose respective kinetic temperatures ![]() and
and ![]() will
be considered as equal
will
be considered as equal
![]() .
This is the global thermodynamic
equilibrium hypothesis which is expected to hold up to
.
This is the global thermodynamic
equilibrium hypothesis which is expected to hold up to
![]() (see Teyssier et al. 1997 and Chièze et al. 1998 for a precise
discussion). Given the low density (from
(see Teyssier et al. 1997 and Chièze et al. 1998 for a precise
discussion). Given the low density (from
![]() in the core to
in the core to
![]() in the
outer part) and high temperature of this plasma (
in the
outer part) and high temperature of this plasma (
![]() ), it can be treated as a perfect gas satisfying the equation of state:
), it can be treated as a perfect gas satisfying the equation of state:
| (2) |
Inverse Compton scattering of cosmic background (CMB) photons by the
electrons in the ICM modifies the CMB spectrum
(Zel'dovich & Sunyaev 1969; Sunyaev & Zel'dovich 1972; Sunyaev & Zel'dovich 1980). The amplitude of the SZ temperature
decrement
![]() is directly proportional to
the Comptonisation parameter y which is given by:
is directly proportional to
the Comptonisation parameter y which is given by:
| = | (4) | ||
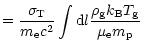 |
= | (5) |
In parallel to this spectral distortion, the statistical
determination of the shear field ![]() affecting the images of
background galaxies enables us to derive the dominant projected
gravitational potential of the lens produced by dark matter (DM):
affecting the images of
background galaxies enables us to derive the dominant projected
gravitational potential of the lens produced by dark matter (DM):
![]() in our general hypothesis (see Mellier 2000 for details).
in our general hypothesis (see Mellier 2000 for details).
Let us suppose we have for a given cluster a set of SZ and WL data which enables us to construct a 2-D map of projected gas pressure as well as a 2-D projected gravitational potential map. We now propose an answer to the following question: how should we co-analyze these various data sets? Our first aim is to develop a method which allows us to get maps of projected thermodynamical quantities with as few physical hypotheses as possible.
Our method is the following. Let us suppose then that these maps
have almost a rotationnal symmetry, as is the case for a vast class of
experimental observations as e.g. in Fig. 1. More
precisely, let us suppose that the projected gas pressure y as well
as the observed projected gravitational potential
![]() can be
well fitted by the following type of functions:
can be
well fitted by the following type of functions:
| (6) |
| (7) |
We then assume that these observed perturbed symmetries are a
consequence of an intrinsic 3-D spherical symmetry linearly
perturbed as well. This point constitutes our key hypothesis. It
means that to the zeroth order in a certain parameter (e.g.
![]() )
our clusters are regular objects with a strong circular
symmetry but they admit some first order (linear) perturbations away
from this symmetry, whose angular part is separable. As a consequence
of these assumptions we will make use of this linearly perturbed
symmetry to get a map of some complementary projected
thermodynamical quantities, the gas density
)
our clusters are regular objects with a strong circular
symmetry but they admit some first order (linear) perturbations away
from this symmetry, whose angular part is separable. As a consequence
of these assumptions we will make use of this linearly perturbed
symmetry to get a map of some complementary projected
thermodynamical quantities, the gas density ![]() and the gas
temperature
and the gas
temperature
![]() ,
successively to zeroth and first order in
,
successively to zeroth and first order in
![]() .
.
 |
Figure 1: Images of the SZ effect observed towards four galaxy clusters with various redshifts. The contours correspond to 1.5 to 5 times the noise level. Data were obtained with the low-noise cm-wave receiver installed on the OVRO and BIMA mm-wave interferometric arrays (Holder & Carlstrom 1999). The bottom-left white ellipse denotes the synthetised beam for each observation. |
| Open with DEXTER | |
Formulated this way, the problem yields a natural protocol:
Let us now apply the method to the case where the projected gas
density (SZ data) and the projected gravitational potential (WL data)
look almost circular. These observations lead
us to suppose that the 3-D gas pressure, the gravitational
potential, the gas density and the gas temperature can be well
described by the following equations:
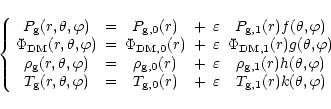 |
(8) |
If we first apply the hydrostatic equilibrium equation
![]() we get the following equations. To zeroth
order in
we get the following equations. To zeroth
order in
![]() we have
we have
| (13) |
| (14) |
We have now identified the angular part to the first order correction
of ![]() ,
,
![]() and
and
![]() .
We still have to link those
quantities to the angular dependent part of the temperature
.
We still have to link those
quantities to the angular dependent part of the temperature ![]() ,
namely
,
namely
![]() .
This is done naturally by using the equation
of state (1), which directly provides, to zeroth and first
order in
.
This is done naturally by using the equation
of state (1), which directly provides, to zeroth and first
order in
![]() :
:
| (21) | |
| (22) |
Given this description of the cluster physical state, the experimental SZ and
WL data provide the projected quantities
![]() and
and
![]() :
:
| = | |||
| (23) | |||
| = | |||
| (24) |
Our aim is now to derive both a projected gas density map and
projected temperature map as defined by:
Now that we have expressed our observables in terms of 3-D physical
quantities, it is easy to infer a gas density map successively to
zeroth and first order in
![]() .
To zeroth order the
hydrostatic equilibrium condition (9) states that
.
To zeroth order the
hydrostatic equilibrium condition (9) states that
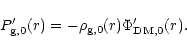 |
(31) |
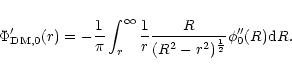 |
(36) |
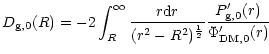 | (37) | ||
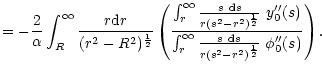 |
(38) | ||
Once we build this projected gas density map, we can recover the
projected gas temperature map. If we apply the equation of state
(19) we get:
| = | 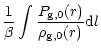 |
(39) | |
| = | 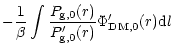 |
(40) | |
| = | 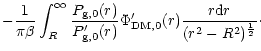 |
(41) |
We now reach the core of our method, namely we aim at deriving the
quantity
![]() defined by (27), i.e. the first order
correction to the perfectly circular term :
defined by (27), i.e. the first order
correction to the perfectly circular term :
| = | (42) | ||
| = | (43) |
WL data provide straightforward access to the function
![]() thus
we choose to approximate (45) by
thus
we choose to approximate (45) by
On the other hand, SZ data provide a measurement of the function
![]() therefore,
we can use Eqs. (18) and (16) to
write
therefore,
we can use Eqs. (18) and (16) to
write
These last two alternative steps are crucial to our method since these approximations link the non spherically symmetric components of various quantities. They are reasonable, as will be discussed in Sect. 3.2.8 and will be numerically tested in Sect. 4.
Of course, only well-known quantities appear in Eqs. (46) and (50): y, y0,
![]() and
and ![]() are direct observational data whereas
are direct observational data whereas
![]() and
and
![]() are zeroth order quantities previously derived.
are zeroth order quantities previously derived.
The projected temperature map can be obtained the same way as before.
By using first the equation of state we can write :
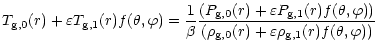 | ||
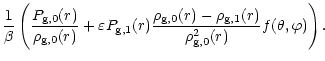 |
(51) | |
| = | (52) | ||
| = | (53) |
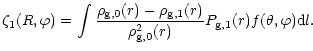 |
(54) |
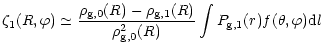 | ||
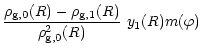 |
(55) | |
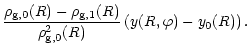 |
(56) | |
Our previous approximations can be justified on intuitive grounds even
if we will take care in validating it numerically in Sect. 4 below. It relies on the fact that perturbations
have by definition a finite extent, i.e. the first order correction to
the perfectly circular (spherical) term is non zero only within a finite
range. The typical size and amplitude of the perturbation can be
easily scaled from the SZ and WL data set. This guarantees the
validity of our assumptions on observational grounds. The key point
is that the perturbation itself has a kind of axial symmetry, whose axis goes
through the center of the cluster and the peak of the
perturbation. This is reasonable if the perturbation originates in e.g.
an incoming filament but not for a substructure. The latter would
therefore have to be treated separately by superposition (see Sect. 5). This leads naturally to the statement that the
typical angle we observe in the image plane is equal to the one we
would observe if the line of sight were perpendicular to its actual
direction, i.e. the perturbation as intrinsically the same angular
extent in the directions along the line of sight and perpendicular to
it. This is illustrated schematically in Fig. 2.
| |
Figure 2:
We represent schematically in a) an image corresponding to
our hypothesis. The full line corresponds to the perfectly circular
2-D term, e.g.
|
| Open with DEXTER | |
Given this description, we are now in a position to discuss the
validity of our approximation. It consists of approximating the
line of sight integral
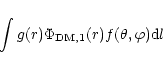 |
(57) |
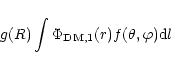 |
(58) |
| |
Figure 3:
We define in this figure the notation necessary to discuss
our approximation. |
| Open with DEXTER | |
The previously derived map offers an advantage that we now aim to
exploit, namely the ability of precise X prediction. Indeed, for a
given X spectral emissivity model, the X-ray spectral surface
brightness is
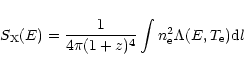 |
(60) |
| (61) | |||
| (62) | |||
| (63) |
This derivation opens the possibility of comparing on the one hand SZ
and WL observations with, on the other hand, precise X-ray
measurements as taken e.g. by XMM or CHANDRA. Note that in the instrumental bands
of most X-ray satellites the ![]() dependence is very weak and can
be neglected. This can be easily taken into account by eliminating the
dependence is very weak and can
be neglected. This can be easily taken into account by eliminating the
![]() dependence in the previous formula. Even if the interest of such
a new comparison is obvious, we will discuss it more carefully in the
two following sections. In principle, one could also easily make some
predictions concerning the density weighted X-ray temperature
defined by the ratio
dependence in the previous formula. Even if the interest of such
a new comparison is obvious, we will discuss it more carefully in the
two following sections. In principle, one could also easily make some
predictions concerning the density weighted X-ray temperature
defined by the ratio
![]() but the fact is that since the gas pressure and so the
SZ effect tends to have a very weak gradient, we are not able in
principle to reproduce all the interesting features of this quantity,
namely the presence of shocks.
but the fact is that since the gas pressure and so the
SZ effect tends to have a very weak gradient, we are not able in
principle to reproduce all the interesting features of this quantity,
namely the presence of shocks.
 |
Figure 3:
The upper panel shows the results of simulations, from left
to right, all using a logarithmic scaling, the projected mass density
(
|
| Open with DEXTER | |
 |
Figure 4:
As in the previous figure for a different cluster. The
structure of the X-ray emission measure is very well
reproduced for the inner part. The correlation coefficient between the
predicted and simulated map is 0.986. As is visible on the relative
error map, whose 10 levels are linearly separated between -1.0 and 1.0,
the outer part is naturally smeared by our approximation. The visible
clump on the top-right should be treated separately. Each box is
|
| Open with DEXTER | |
In order to demonstrate the ability of the method in a simplified
context we used some outputs of the recently
developed N-body + hydrodynamics code RAMSES simulating the evolution
of a ![]() -CDM universe. The RAMSES code is based on Adaptative
Mesh Refinement (AMR) technique in order to increase the spatial
resolution locally using a tree of recursively nested cells of smaller
and smaller size. It reaches a formal resolution of
-CDM universe. The RAMSES code is based on Adaptative
Mesh Refinement (AMR) technique in order to increase the spatial
resolution locally using a tree of recursively nested cells of smaller
and smaller size. It reaches a formal resolution of
![]() in the core of galaxy clusters (see Réfrégier & Teyssier
2000 and Teyssier 2001, in preparation, for details). We use
here the structure of two galaxy clusters extracted from the
simulation to generate our input observables, i.e. X-ray
emissivity, SZ decrement and projected mass density (or projected
gravitational potential).
in the core of galaxy clusters (see Réfrégier & Teyssier
2000 and Teyssier 2001, in preparation, for details). We use
here the structure of two galaxy clusters extracted from the
simulation to generate our input observables, i.e. X-ray
emissivity, SZ decrement and projected mass density (or projected
gravitational potential).
The relevant observables, i.e. projected mass density, SZ decrement and,
for comparison purpose only, the X-ray emission measure, of the 2
clusters are depicted using a logarithmic scaling in Figs. 4 and 5 (upper panels). These clusters have been extracted from the
simulation at z = 0.0 and thus tend to be more relaxed than high
z ones: they are ordinary clusters of virial mass (defined by
![]() in our
particular cosmology)
in our
particular cosmology)
![]() and
and
![]() .
Both exhibit a
rather regular shape, i.e. they have not recently undergone a major
merging process. The depicted boxes are respectively
.
Both exhibit a
rather regular shape, i.e. they have not recently undergone a major
merging process. The depicted boxes are respectively
![]() and
and
![]() wide. We smooth the
outputs using a Gaussian of width
wide. We smooth the
outputs using a Gaussian of width
![]() thus
degrading the resolution. We did not introduce any instrumental
noise. For both clusters, the gas temperature decreases by a
factor of less than 2 from the center to the virial radius. Beyond, the
temperature profile is steeper. Nevertheless, for the sake of
simplicity we will assume that
thus
degrading the resolution. We did not introduce any instrumental
noise. For both clusters, the gas temperature decreases by a
factor of less than 2 from the center to the virial radius. Beyond, the
temperature profile is steeper. Nevertheless, for the sake of
simplicity we will assume that ![]() is constant, making the
discussion of
is constant, making the
discussion of
![]() and
and
![]() useless at this point.
useless at this point.
We apply the method previously described using perturbed spherical
symmetry. We define the pixel with the highest luminosity to be the
center. The zeroth order circular description of the gas
density is computed averaging data over concentric annuli and we then
add to it some first order corrections. Note that since we assume
isothermality, SZ data give us straightforwardly a projected gas
density modulo a temperature
![]() coefficient, thus we use the
formulation of Eq. (50), which is exact in this context. This
constant temperature is fixed using the hydrostatic equilibrium and the WL data.
coefficient, thus we use the
formulation of Eq. (50), which is exact in this context. This
constant temperature is fixed using the hydrostatic equilibrium and the WL data.
In Figs. 4 and 5 (lower panels) we show the predicted
X-ray emission measure to zeroth and first order as well as a map
of relative errors. Note that to first order the shape of the emission
measure is very well reproduced. The cross-correlation coefficients
between the predicted and simulated X-ray emission measures are 0.978and 0.986. Of course this is partly due to the assumed good quality
of the SZ data but nonetheless, it demonstrates the validity
of our perturbative approach as well as of our approximation.
The approximation performed in Eq. (65), i.e. the multiplication by the function
![]() naturally tends to cut out the perturbations at
high R. This is the reason why the further perturbations are slightly
less well reproduced and the relative errors tend to increase with
R. Nevertheless, since the emission falls rapidly with
R, as is visible in the lower figures (note the logarithmic scaling), the
total flux is well conserved, respectively to 0.9% and 9%. This last number might illustrate that the large extent of the
perturbations in the second case may limit our method. An ellipsoidal
fit could help decrease this value. Note that the clump
visible mainly in X-ray emission measure in 5 is not
reproduced. This is natural because it does not appear through the SZ
effect since the pressure remains uniform throughout the clumps. If
resolved by WL, this substructure should be treated separately,
e.g. by considering the addition of a second very small structure. Note
that the first cluster showed exhibits a spherical core elongated in
the outer region, thus it is not actually as ellipsoidal as it looks,
which may explain why our perturbed spherical symmetry works well.
naturally tends to cut out the perturbations at
high R. This is the reason why the further perturbations are slightly
less well reproduced and the relative errors tend to increase with
R. Nevertheless, since the emission falls rapidly with
R, as is visible in the lower figures (note the logarithmic scaling), the
total flux is well conserved, respectively to 0.9% and 9%. This last number might illustrate that the large extent of the
perturbations in the second case may limit our method. An ellipsoidal
fit could help decrease this value. Note that the clump
visible mainly in X-ray emission measure in 5 is not
reproduced. This is natural because it does not appear through the SZ
effect since the pressure remains uniform throughout the clumps. If
resolved by WL, this substructure should be treated separately,
e.g. by considering the addition of a second very small structure. Note
that the first cluster showed exhibits a spherical core elongated in
the outer region, thus it is not actually as ellipsoidal as it looks,
which may explain why our perturbed spherical symmetry works well.
The general and robust hypotheses have been introduced
and discussed in Sect. 2.1. Our key hypothesis
consists of assuming the validity of a perturbative approach and in
choosing the nature of this perturbation, i.e. with a radial/angular separation.
It was initially motivated by theoretical predictions, observations
and simulations which show that relaxed clusters are regular and globally
spheroidal objects. In fact, comparison of our models with simulated clusters
confirms that our assumptions turn out be reasonable.
However, our method cannot deal properly with sharp features
e.g. shocks waves due to infalling filaments. Assuming the validity
of the angular and radial separation implies the equality of
this angular part for all relevant physical quantities (![]() ,
,
![]() ,
,
![]() ...), using to a first order in
...), using to a first order in
![]() the
hydrostatic equilibrium and the equation of state. If this is not
satisfied in practice, then we could question the validity of this
separation or of the underlying physics introduced in the cluster
model. Our experience with simulations shows that for reasonably
relaxed clusters which do not experience a major merging process, the angular part of the
perturbation is constant amongst observables. In that case, the
separation (and thus the equality of the angular perturbation) seems
to be a good hypothesis in general, whereas its failure is a sign of non-relaxation, i.e. non-validity of our general physical hypothesis.
the
hydrostatic equilibrium and the equation of state. If this is not
satisfied in practice, then we could question the validity of this
separation or of the underlying physics introduced in the cluster
model. Our experience with simulations shows that for reasonably
relaxed clusters which do not experience a major merging process, the angular part of the
perturbation is constant amongst observables. In that case, the
separation (and thus the equality of the angular perturbation) seems
to be a good hypothesis in general, whereas its failure is a sign of non-relaxation, i.e. non-validity of our general physical hypothesis.
The validity of our approximations also depends on physical quantities which are assumed to be constant along the integral. In the case of the gas density obtained from the SZ map, it is an exact statement, provided we assume isothermality. Since clusters in general are not too far from isothermality, this hypothesis is reasonable.
The strength of the perturbation method we propose is the fact that we do not need to assume isothermality and sphericity (or ellipsoidality). This might be of importance for further applications. An interesting example is the measurement of the Hubble constant from joint SZ and X-ray measurements. As it has been stressed by Inagaki et al. (1995); Roettiger et al. (1997); Puy et al. (2000), both the asphericity and the non-isothermality of the relevant clusters can yield important biases in the estimate of H0 (up to 20%). Our approach may be relevant to address this issue.
Although the comparaison with simulated clusters is conclusive, our perturbative method has two shortcomings:
So far, we have discussed the perturbed spherical symmetry
case. If we turn to spheroidal symmetry, the problem is similar
provided we know the inclination angle i between the
polar axis of the system and the line of sight. In the appendix
we review the basic results of spheriodal deprojections. It
is directly inspired from (Fabricant et al. 1984): once the projection is well
parameterized we get the projected quantity, like the pressure:
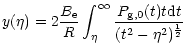 |
(66) | ||
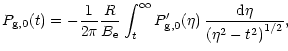 |
(67) |
Even if the inclination angle is a priori not accessible directly through single observations, it is possible to evaluate it using the deprojection of an axially symmetric distribution of either X-ray/SZ maps or SZ/surface density maps (Zaroubi et al. 1998; Zaroubi et al. 2000). Our method overcomes this problem since it only focusses on 2-D quantities and avoids as much as possible to deal with the full 3-D structure. However, in principle the method can also reconstruct 3-D quantities. This will be discussed in a forthcoming work. Note also that axially symmetric configuration elongated along the line of sight may appear spherical. This is a difficult bias to alleviate without any prior knowledge of the profile. In our case, our method will be biased in the sense that the deprojected profile will be wrong. Nevertheless, we might hope to reproduce properly global quantities, like abundance of DM or gas and so to alleviate some well known systematics (see previous section), e.g. in measuring the baryon fraction.
When applying the method to true data, the instrumental noise issue is
an important matter of concern. The distinct advantage
of a parametric approach, e.g. using a ![]() -model, is that it
fits the relevant parameters, e.g.
-model, is that it
fits the relevant parameters, e.g. ![]() and
and ![]() ,
on the
projected quantities (the image) itself, which is rather insensitive to
noise. However, it might be difficult to determine the profile and its derivate
by a direct deprojection. In our perturbative approach, as
it first relies on a zeroth order quantity found by averaging over some
annulus, a noise reduction step (at least far from the center) prior to
working on a projected perturbation should be quite robust
as well. Nevertheless, this problem is not critical and can be addressed easily
by using a more sophisticated technique than the mere use of Abel's integral. In particular
we could decompose the profile into a function basis whose projection
is known analytically (see for example Durret et al. 1999 in another
context).
,
on the
projected quantities (the image) itself, which is rather insensitive to
noise. However, it might be difficult to determine the profile and its derivate
by a direct deprojection. In our perturbative approach, as
it first relies on a zeroth order quantity found by averaging over some
annulus, a noise reduction step (at least far from the center) prior to
working on a projected perturbation should be quite robust
as well. Nevertheless, this problem is not critical and can be addressed easily
by using a more sophisticated technique than the mere use of Abel's integral. In particular
we could decompose the profile into a function basis whose projection
is known analytically (see for example Durret et al. 1999 in another
context).
Trying to answer the question of how to coanalyse a set of WL and SZ data, we have presented and demonstrated the efficiency of an original method allowing us to perform in a self-consistent manner the joint analysis of these data. Using it on noise-free simulations, we demonstrated how well it can be used to make predictions of X-ray surface brightness. We discussed also in the previous sections some shortcomings that do not seem critical but definitely require further work.
Compared to other, we choose to hide the deprojection by using appropriate approximations. Thus, we do not resolved fully the 3-D structure of clusters, although this work is a first step towards a full deprojection (Doré et al. 2001, in preparation).
Nevertheless, since it is based on a self-consistent use of general physical hypotheses, the X-ray emission prediction of our method when compared to the observed one constitutes an interesting test of these hypotheses, namely the stationarity, the hydrostatic equilibrium and the validity of the equation of state.
This method is furthermore of interest since it should allow a better treatment of
systematics (asphericity, non isothermality, ...) plaguing any
measure of the baryon fraction ![]() or the Hubble constant
H0 using X-ray and SZ the effect (Inagaki et al. 1995). Thus we plan to
apply it soon on true data.
or the Hubble constant
H0 using X-ray and SZ the effect (Inagaki et al. 1995). Thus we plan to
apply it soon on true data.
Acknowledgements
We are grateful to our referee, M. Bartelmann, and to S. Dos Santos, G. Mamon and S. Zaroubi for valuable discussions. We thank J. Calstrom et al. for allowing the use of some of their SZ images.
In this appendix we recall some useful results concerning spheroid
projection derived by Fabricant, Gorenstein and Rybicki
(Fabricant et al. 1984). In the context of spheroidal systems, cartesian
coordinates system are the most convenient for projection. Thus, if
the observer's coordinate system (x,y,z) is chosen such that the
line of sight is along the z axis and such that the polar axis of
the spheroidal system z' lies in the x-z plane at an inclination
angle i to the z-axis, then, in the cartesian coordinate system
(x',y',z') the general physical quantities relevant to our problem
depends only on the parameter t defined by
| t2 | = | 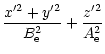 |
(68) |
| = | 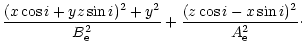 |
(69) |
| I(x,y) | = | (70) | |
| = | 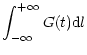 |
(71) | |
| = | 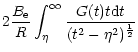 |
(72) |
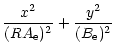 |
(73) |
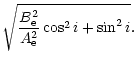 |
(74) |