Radial velocity determinations were made by cross-correlation of each order of
the HR 7428 spectra with spectra of the bright radial velocity standard
star ![]() Ari, whose radial velocity is -14.3 kms-1
(Evans 1979).
Ari, whose radial velocity is -14.3 kms-1
(Evans 1979).
Template spectra of ![]() Ari have been obtained during each
observing run.
From several spectra of
Ari have been obtained during each
observing run.
From several spectra of ![]() Ari and other RV standard stars
we have evaluated an
average accuracy for the radial velocity measurements better than
Ari and other RV standard stars
we have evaluated an
average accuracy for the radial velocity measurements better than ![]() 0.4 kms-1
rms which is the result of the stability
of the experimental apparatus and is consistent with the limits given by the spectral
resolution.
0.4 kms-1
rms which is the result of the stability
of the experimental apparatus and is consistent with the limits given by the spectral
resolution.
The wavelength ranges for the cross-correlation of HR 7428 spectra were selected
in order to exclude the H![]() and Na I D2 lines, which are contaminated
by chromospheric emission. The spectral
regions heavily affected by telluric lines (e.g. the
and Na I D2 lines, which are contaminated
by chromospheric emission. The spectral
regions heavily affected by telluric lines (e.g. the
![]() band of O2) were also excluded.
band of O2) were also excluded.
Each radial velocity value listed in Table 1 is the weighted mean of
the values obtained by the cross-correlation of each order of the target spectra
with the corresponding order of the closest-in-time spectrum of ![]() Ari.
The errors, listed in Table 1, have been computed as the square root of
the quadratic average of errors in the cross correlation of
each order. The latter are computed according to the fitted peak height and the
antisymmetric noise as described by Tonry & Davis (1979).
This error estimate is consistent with the dispersion of data points around the mean curve.
Ari.
The errors, listed in Table 1, have been computed as the square root of
the quadratic average of errors in the cross correlation of
each order. The latter are computed according to the fitted peak height and the
antisymmetric noise as described by Tonry & Davis (1979).
This error estimate is consistent with the dispersion of data points around the mean curve.
|
Phase | RV | error |
|
error |
|
error |
| - 2400000 | (km |
(Å) | (Å) | ||||
|
0.2724 | 17.9 | 1.0 | -1.463 | 0.108 | 0.112 | 0.119 |
| 50632.5635 | 0.2817 | 19.3 | 0.4 | -1.674 | 0.097 | -0.255 | 0.107 |
| 50633.5440 | 0.2907 | 18.3 | 1.0 | -1.686 | 0.181 | -0.228 | 0.200 |
| 50634.5728 | 0.3002 | 15.7 | 0.5 | -1.940 | 0.120 | -0.558 | 0.132 |
| 50635.5511 | 0.3092 | 16.0 | 1.4 | -- | -- | -- | -- |
| 50636.5153 | 0.3181 | 15.9 | 2.8 | -1.921 | 0.076 | -0.432 | 0.084 |
| 50678.4853 | 0.7046 | -29.8 | 0.7 | -0.656 | 0.102 | 0.757 | 0.112 |
| 50679.4757 | 0.7137 | -30.2 | 0.3 | -0.784 | 0.071 | 0.676 | 0.078 |
| 50680.4779 | 0.7229 | -30.0 | 1.3 | -0.759 | 0.124 | 0.655 | 0.137 |
| 50681.5193 | 0.7325 | -30.5 | 0.9 | -0.905 | 0.097 | 0.481 | 0.107 |
| 50982.5670 | 0.5052 | -7.2 | 0.7 | -0.813 | 0.120 | 0.510 | 0.132 |
| 50992.5589 | 0.5972 | -20.0 | 1.3 | -0.918 | 0.128 | 0.473 | 0.141 |
| 51000.5715 | 0.6710 | -27.8 | 0.5 | -1.146 | 0.121 | 0.277 | 0.133 |
| 51002.5660 | 0.6894 | -27.4 | 0.1 | -1.113 | 0.113 | 0.284 | 0.124 |
| 51288.5618 | 0.3234 | 15.8 | 0.7 | --a | -- | ||
| 51332.5522 | 0.7285 | -30.1 | 0.4 | -1.316 | 0.127 | 0.068 | 0.140 |
| 51381.4301 | 0.1787 | 14.9 | 0.5 | -0.925 | 0.117 | 0.610 | 0.129 |
| 51382.4819 | 0.1884 | 16.1 | 0.6 | -1.019 | 0.096 | 0.375 | 0.105 |
| 51383.3908 | 0.1968 | 16.2 | 0.6 | -1.186 | 0.104 | 0.287 | 0.114 |
| 51385.4111 | 0.2154 | 17.6 | 0.5 | -1.342 | 0.082 | 0.208 | 0.090 |
| 51386.3445 | 0.2240 | 18.0 | 0.5 | -1.353 | 0.104 | 0.158 | 0.115 |
| 51387.3975 | 0.2337 | 17.7 | 0.5 | -1.285 | 0.063 | 0.135 | 0.069 |
| 51387.4260 | 0.2339 | 17.7 | 0.5 | -1.325 | 0.056 | 0.134 | 0.061 |
| 51388.3746 | 0.2427 | 18.4 | 0.5 | -1.380 | 0.075 | 0.089 | 0.082 |
| 51407.6048 | 0.4198 | 4.0 | 0.6 | -1.316 | 0.078 | 0.113 | 0.086 |
| 51417.5704 | 0.5115 | -7.6 | 0.5 | -0.475 | 0.154 | 0.876 | 0.169 |
| 51423.4962 | 0.5661 | -16.5 | 0.4 | -0.376 | 0.135 | 1.206 | 0.149 |
| 51426.4815 | 0.5936 | -19.5 | 0.3 | -0.750 | 0.087 | 0.607 | 0.096 |
| 51427.4105 | 0.6022 | -20.9 | 0.4 | -0.903 | 0.100 | 0.433 | 0.110 |
| 51465.4373 | 0.9524 | -12.7 | 0.7 | -1.009 | 0.105 | 0.542 | 0.116 |
| 51473.4580 | 0.0263 | -3.5 | 0.7 | -1.324 | 0.101 | 0.215 | 0.111 |
| 51474.2698 | 0.0337 | -1.3 | 0.7 | -1.387 | 0.076 | 0.153 | 0.083 |
| 51476.2680 | 0.0521 | 0.4 | 0.6 | -1.342 | 0.069 | 0.160 | 0.076 |
| 51477.3756 | 0.0576 | -- | -- | -1.259 | 0.067 | 0.207 | 0.074 |
Hall et al. (1990a), from Sanford's (1925) data set, re-determined the
elements for a circular orbit and derived JD
![]() as the time of conjunction
(primary in front). From their own light curve (dominated by ellipticity effect)
they deduced a time of conjunction JD
as the time of conjunction
(primary in front). From their own light curve (dominated by ellipticity effect)
they deduced a time of conjunction JD
![]() .
Combining the photometric and spectroscopic
epoch of conjunction, Hall et al. (1990a) derived a period of 108.854 days. This value is
slightly different from that given by Sanford (1925) of 108.57 days
but very similar to the one they deduced from Fourier analysis of V band photometry
(108.83 days).
.
Combining the photometric and spectroscopic
epoch of conjunction, Hall et al. (1990a) derived a period of 108.854 days. This value is
slightly different from that given by Sanford (1925) of 108.57 days
but very similar to the one they deduced from Fourier analysis of V band photometry
(108.83 days).
If we use the above-mentioned ephemeris of Hall et al. (1990a)
to fold in phase our radial velocities, the time of conjunction (primary
star in front) occurs at phase
![]() ,
indicating that the period and/or the time of
conjunction are not correct.
,
indicating that the period and/or the time of
conjunction are not correct.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{ms1120f1.ps}\end{figure}](/articles/aa/full/2001/31/aa1120/Timg24.gif) |
Figure 1: The cleaned periodogram of our and literature RV data. The peak corresponds to a period of 108.578 days. |
Radial velocities available from the literature (excluding the poor-quality five measures
of Xue-fu & Hui-song 1986a) and our own data have been analysed
applying the periodogram technique (Scargle 1982).
The CLEAN iterative deconvolution algorithm
(Roberts et al. 1986) has been used to eliminate the effects of the data sampling
introduced by the observation spectral window in the power spectrum. The maximum of the
power spectrum, plotted in Fig. 1, yields a period of 108.578 days, very close
to Sanford's estimate.
The new ephemeris we obtain is
The observed RV values are displayed as a function of the orbital phase,
determined from our ephemeris (Eq. (1)), in
Fig. 2.
Adopting our conjunction time, the epoch of Hall et al. (1990a),
![]() ,
appears to be shifted by half a period, i.e. this light-curve minimum epoch
corresponds to the
conjunction with the hot secondary star in front instead of the cool primary star, as they assumed.
The epoch of the deeper minimum observed by Barksdale et al. (1985) is
in good agreement with our ephemeris.
,
appears to be shifted by half a period, i.e. this light-curve minimum epoch
corresponds to the
conjunction with the hot secondary star in front instead of the cool primary star, as they assumed.
The epoch of the deeper minimum observed by Barksdale et al. (1985) is
in good agreement with our ephemeris.
Following Lucy & Sweeney (1971), we have assumed circular orbits and deduced new orbital parameters from our own radial velocities. The best fit orbital solution for the cooler component is reported in Table 2.
| Element | Present solution | Sanford solution |
|
|
22.1 kms-1 | |
|
|
|
-5.2 kms-1 |
|
|
|
2423455.21 |
| P |
|
108.5707 days |
|
|
|
|
|
|
|
0.1222 |
Due to the low S/N ratio of HR 7428 spectrum at these
wavelengths, the residual spectrum is rather noisy, but clearly shows the typical
signatures of a hot star, like the strong and wide Balmer lines.
We have cross-correlated the orders of the residual spectrum containing the
strongest lines with the corresponding ones of Vega to find the radial velocity
of the hotter component at this phase (
![]() ).
The evaluated radial velocity (-
).
The evaluated radial velocity (-
![]() )
has a rather large error
(
)
has a rather large error
(![]()
![]() )
because of the noise
and of the large width of the hydrogen lines.
)
because of the noise
and of the large width of the hydrogen lines.
Another possibility for measuring the radial velocity of the hot component is to
look for spectral signatures of the A2 star in high resolution IUE spectra.
Unfortunately, no high resolution spectrum at short wavelengths (where the
A2 star flux overcomes that of the cooler companion) is available.
However, we could use the well exposed part of the long-wavelength region
of spectrum LWR10313, acquired with IUE on 1981 April 8th (
![]() )
and
retrieved from the IUE Final Archive.
We have also retrieved the spectrum LWR09830 of Vega, acquired
nearly at the same time.
)
and
retrieved from the IUE Final Archive.
We have also retrieved the spectrum LWR09830 of Vega, acquired
nearly at the same time.
By cross-correlation of each order of the HR 7428 spectrum with the corresponding one
of Vega, we measured the radial velocity of the A2 star, obtaining
+
![]() .
The large error is essentially due to
the low S/N ratio.
.
The large error is essentially due to
the low S/N ratio.
With these two RV values, we are able to give, for the first time, a tentative orbital solution for the hot component.
The orbital parameters of the hot component,
including the values of
![]() we derived, are reported in Table 3.
we derived, are reported in Table 3.
Difficulties in accounting for optical and infrared magnitudes adopting stellar parameters reported in the literature were encountered by comparing black body emission with observed photometric fluxes (Rodonò et al. 1998).
As a first step, we have checked the consistency of magnitudes and colours with the
radius of the cool component reported in the literature, by means
of the Barnes-Evans relation (Barnes et al. 1976) between (V-R) colour
index, V magnitude and angular diameter ![]() for late type stars:
for late type stars:
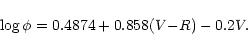 |
(2) |
We made a more accurate determination of physical parameters by using UBV magnitudes given in the literature and low resolution IUE spectra, whose spectral region is essentially dominated by the hot component, comparing them with synthetic theoretical spectra.
We defined an average observed UV spectrum using the available highest S/N ratio spectra, namely LWP 27954 and LWP 30925 for the long wavelength region (1850-3350 Å) and SWP 50606 and SWP 50609 for the short wavelength region (1150-2000 Å), retrieved from the IUE Final Archive (Nichols & Linsky 1996).
IUE spectra, as well as optical photometry, have been corrected for interstellar extinction.
The typical value of 1 magnitude per kilo-parsec for the interstellar extinction and the
Hipparcos distance, adopted for the computations, lead to
an extinction magnitude A(V
![]() 32.
Assuming the standard reddening law A(V
32.
Assuming the standard reddening law A(V
![]() (B-V), a colour excess
E(B-
(B-V), a colour excess
E(B-
![]() 10 has been derived.
IUE spectra have been de-reddened according to the selective extinction function of
Cardelli et al. (1989).
10 has been derived.
IUE spectra have been de-reddened according to the selective extinction function of
Cardelli et al. (1989).
Synthetic spectra have been generated with the NextGen (Hauschildt et al. 1999a, 1999b) photosphere models for the hotter secondary and cool primary star. The bright cool star model was computed for this purpose by Dr. Peter H. Hauschildt, including a spherical symmetry solution (Hauschildt et al. 1999b).
Consistent with the previous estimates of spectral type and with our
estimate of the mass, several models between
![]() K and 9400 K were considered
for the hot component.
To take into account the uncertainties in the relation between spectral type and
effective temperature of the cooler component, initially we considered models with
K and 9400 K were considered
for the hot component.
To take into account the uncertainties in the relation between spectral type and
effective temperature of the cooler component, initially we considered models with
![]() K, 4400 K, and 4600 K. The first model turned out to be cooler and
the last hotter for our observational data.
Finally, in agreement with the accurate spectral type determination by Ginestet et al.
(1999), two models of
K, 4400 K, and 4600 K. The first model turned out to be cooler and
the last hotter for our observational data.
Finally, in agreement with the accurate spectral type determination by Ginestet et al.
(1999), two models of
![]() K, with
K, with
![]() ,
[M/H]=0,
,
[M/H]=0,
![]() and with
and with ![]() ,
[M/H]=0,
,
[M/H]=0,
![]() respectively, were
considered.
respectively, were
considered.
Since synthetic spectra give fluxes at the stellar surface, the comparison of models with observations has been made by scaling the result with the angular radii of the components and the distance.
Several iterations have been performed to find the model that gives the better fit to the IUE spectrum and optical photometry, allowing the stellar parameters to vary independently. However, some constraints have been placed and tests for consistency have been made.
The distance was fixed to the Hipparcos value and the effective temperature adopted for the cool component was checked to be consistent with the spectral type classification and spectral line behaviour.
The temperature of the hotter component was mainly constrained by the shape of the UV spectral region. The temperature and the radius of the cooler component are instead mainly linked to the near-UV and optical spectral distribution.
The errors in the effective temperatures have been estimated as the minimum
![]() value that gives appreciable difference with respect to the observed
spectrum. Due to the evident mismatch in the flux distribution of the
two models with
value that gives appreciable difference with respect to the observed
spectrum. Due to the evident mismatch in the flux distribution of the
two models with
![]() and 4600 K with respect to the observed one, we can
estimate an uncertainty in the temperature of the cooler component, smaller than 200 K,
probably of 100-150 K.
For the hot component, having a lower weight in the composite spectrum,
an error
and 4600 K with respect to the observed one, we can
estimate an uncertainty in the temperature of the cooler component, smaller than 200 K,
probably of 100-150 K.
For the hot component, having a lower weight in the composite spectrum,
an error
![]() K is deduced from the UV spectral region.
K is deduced from the UV spectral region.
To evaluate the uncertainties in the radii we have considered the two main sources
of errors: the error in Hipparcos distance (![]() 52 pc) and the accuracy of the correction
for interstellar extinction.
The accuracy of the de-reddening procedure is affected by both the intrinsic uncertainties in
the E(B-V) value and the errors in distance.
We have evaluated the first one by assuming the standard deviation on colour
excesses equal to the variance of the coefficients given by Johnson (1965) for
different sky regions.
We find that the dominant source of errors is the distance uncertainty.
52 pc) and the accuracy of the correction
for interstellar extinction.
The accuracy of the de-reddening procedure is affected by both the intrinsic uncertainties in
the E(B-V) value and the errors in distance.
We have evaluated the first one by assuming the standard deviation on colour
excesses equal to the variance of the coefficients given by Johnson (1965) for
different sky regions.
We find that the dominant source of errors is the distance uncertainty.
The final best-fit stellar parameters are listed in Table 4 together with the estimated errors.
The errors in the parameters, listed in Table 4, do not include any intrinsic uncertainty for the synthetic spectra. However, Hauschildt et al. (1999a), from a comparison of their models with the observed UV and optical spectra of solar type stars and Vega, found discrepancies always smaller than a few percent in the continuum. This source of error should be thus negligible in comparison with the accuracy of the data themselves.
In Fig. 4 the spectrum obtained by summing the synthetic spectra for the hot and cool
component, degraded to the IUE spectral resolution, is plotted superimposed on the IUE
de-reddened spectrum (left) and on the UBV fluxes (right).
In the latter case the synthetic spectrum was convolved with a Gaussian kernel
having a semi-amplitude of 30 Å.
The models displayed have
![]() K,
K,
![]() and
and
![]() K,
K,
![]() for hotter and cooler components, respectively.
The radii which give the best fit to the observed spectrum are 2.25
for hotter and cooler components, respectively.
The radii which give the best fit to the observed spectrum are 2.25 ![]() and
40
and
40 ![]() ,
respectively.
,
respectively.
The only measurements of the projected rotational velocity of HR 7428 that we found in the
literature are
![]() km
km![]() s-1 reported by Hui-song & Xue-fu (1987) and
s-1 reported by Hui-song & Xue-fu (1987) and
![]() km
km![]() s-1 measured by De Medeiros & Mayor (1995) with
CORAVEL.
Notwithstanding the moderate resolution, we have performed
s-1 measured by De Medeiros & Mayor (1995) with
CORAVEL.
Notwithstanding the moderate resolution, we have performed ![]() estimates on our
spectra, taking advantage of the large number of observations and of the high S/N ratio.
We have compared the echelle orders of HR 7428 centered at 6250 and 6400 Å with those of
several slowly-rotating K-type giant stars, acquired with the same instrumentation.
The standard stars that give the best reproduction of the HR 7428 spectrum are
estimates on our
spectra, taking advantage of the large number of observations and of the high S/N ratio.
We have compared the echelle orders of HR 7428 centered at 6250 and 6400 Å with those of
several slowly-rotating K-type giant stars, acquired with the same instrumentation.
The standard stars that give the best reproduction of the HR 7428 spectrum are ![]() Oph
(K2 III) and
Oph
(K2 III) and ![]() Ari (K2 III), whose
Ari (K2 III), whose ![]() 's are negligible in comparison to the
instrumental resolution.
's are negligible in comparison to the
instrumental resolution.
We have set up a procedure for the ![]() determination.
First we aligned in wavelength the spectra of the active and standard
star by means of cross-correlation,
then the spectrum of the standard star was progressively broadened by
convolution with a rotational profile of increasing
determination.
First we aligned in wavelength the spectra of the active and standard
star by means of cross-correlation,
then the spectrum of the standard star was progressively broadened by
convolution with a rotational profile of increasing ![]() .
At each step, the sum of residuals between the observed and template spectrum was calculated
and, at the end, the minimum of the residuals was found.
The
.
At each step, the sum of residuals between the observed and template spectrum was calculated
and, at the end, the minimum of the residuals was found.
The ![]() value that we deduced by analysing several HR 7428 spectra is
value that we deduced by analysing several HR 7428 spectra is
![]() km
km![]() s-1, in very good agreement with the CORAVEL measurement (De Medeiros &
Mayor 1995).
s-1, in very good agreement with the CORAVEL measurement (De Medeiros &
Mayor 1995).
The projected rotational velocity is given by
The system inclination that we derive from Eq. (3) with
![]() km
km![]() s-1 is
s-1 is
![]() .
From the errors in radius (16%) and in
.
From the errors in radius (16%) and in ![]() (6%) we
estimated the error in
(6%) we
estimated the error in ![]() ,
which implies a system inclination in the
50
,
which implies a system inclination in the
50
![]() -75
-75
![]() range.
The maximum inclination of 75
range.
The maximum inclination of 75![]() is constrained by the absence of eclipse
in the HR 7428 light curve. Indeed, from radii and temperature that we determined
(Table 4), a primary eclipse (hot star beyond) of
0
is constrained by the absence of eclipse
in the HR 7428 light curve. Indeed, from radii and temperature that we determined
(Table 4), a primary eclipse (hot star beyond) of
0
![]() 07 in V band and 0
07 in V band and 0
![]() 13 in B should be observed.
These inclination values lead to masses of the two components
13 in B should be observed.
These inclination values lead to masses of the two components
![]()
![]() and
and
![]()
![]() for
for
![]() ,
and
,
and
![]()
![]() and
and
![]()
![]() for
for
![]() ,
while the
lower limit of inclination (50
,
while the
lower limit of inclination (50![]() )
would lead to higher masses not consistent with
the spectral types.
)
would lead to higher masses not consistent with
the spectral types.
Using the effective temperatures and radii in Table 4, we have placed the two
components of HR 7428 on the
![]() plane.
Their position and the evolutionary tracks for intermediate mass stars calculated by
Fagotto et al. (1994) are displayed in Fig. 5.
plane.
Their position and the evolutionary tracks for intermediate mass stars calculated by
Fagotto et al. (1994) are displayed in Fig. 5.
The cool component lies in the region of He-burning stars, and implies
a mass from 4 to 5 ![]() ,
more consistent with the higher inclination limit,
and an age from 140 to 150 Myr.
The position of the hot component is consistent with a 2.3
,
more consistent with the higher inclination limit,
and an age from 140 to 150 Myr.
The position of the hot component is consistent with a 2.3 ![]() star still on
the main-sequence band, but slightly evolved. Its estimated age of 100-250 Myr is in
perfect agreement with the estimated age of the cooler more massive component.
This suggests a normal evolution of the two stars, yet without any relevant mass exchange,
as expected from the long orbital period.
star still on
the main-sequence band, but slightly evolved. Its estimated age of 100-250 Myr is in
perfect agreement with the estimated age of the cooler more massive component.
This suggests a normal evolution of the two stars, yet without any relevant mass exchange,
as expected from the long orbital period.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{ms1120f5.ps}\end{figure}](/articles/aa/full/2001/31/aa1120/Timg105.gif) |
Figure 5:
Position of the cool (grey dot) and hot (black square) components of
HR 7428 in a
|
Copyright ESO 2001