A&A 375, 70-86 (2001)
DOI: 10.1051/0004-6361:20010848
On the possible existence of a self-regulating hydrodynamical
process in slowly rotating stars
II. Lithium plateau in halo stars and primordial abundance
S. Théado - S. Vauclair
Laboratoire d'Astrophysique, 14 Av. E. Belin,
31400 Toulouse, France
Received 26 December 2000 / Accepted 25 May 2001
Abstract
The lithium plateau observed in halo stars has long appeared as a
paradox in the general context of the lithium abundance behavior in stellar outer
layers. First, the plateau is flat, second, the lithium abundance dispersion is
extremely small. This seems in contradiction with the large lithium variations observed
in younger stars. It is also difficult to understand theoretically: as lithium
nuclei are destroyed by nuclear reactions at a relatively low temperature
(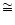 2.5 million degrees), the occurrence of macroscopic motions in the
stellar outer layers easily lead to lithium depletion at the surface. On the
other hand, if no macroscopic motions occur in the stellar gas, lithium is subject
to microscopic diffusion which, in the case of halo stars, should also lead
to depletion. Several ideas have been proposed to account for the lithium behavior in
halo stars. The most promising possibilities were rotational-induced mixing, which
could reduce lithium in the same way for all the stars (Vauclair 1988; Pinsonneault
et al. 1992 and 1999) and mass-loss, which could oppose the
lithium settling (Vauclair & Charbonnel 1995, 1998). In both cases however, the parameters should be tightly adjusted
to prevent any dispersion in the final results.
Vauclair (1999) (Paper I) looked for a physical process
which could occur in slowly rotating stars and explain why the dispersion of the lithium
abundances in the halo stars' plateau is so small. She pointed out
that the
2.5 million degrees), the occurrence of macroscopic motions in the
stellar outer layers easily lead to lithium depletion at the surface. On the
other hand, if no macroscopic motions occur in the stellar gas, lithium is subject
to microscopic diffusion which, in the case of halo stars, should also lead
to depletion. Several ideas have been proposed to account for the lithium behavior in
halo stars. The most promising possibilities were rotational-induced mixing, which
could reduce lithium in the same way for all the stars (Vauclair 1988; Pinsonneault
et al. 1992 and 1999) and mass-loss, which could oppose the
lithium settling (Vauclair & Charbonnel 1995, 1998). In both cases however, the parameters should be tightly adjusted
to prevent any dispersion in the final results.
Vauclair (1999) (Paper I) looked for a physical process
which could occur in slowly rotating stars and explain why the dispersion of the lithium
abundances in the halo stars' plateau is so small. She pointed out
that the
 -gradient terms which appear in the
computations of the meridional circulation velocity
(e.g. Mestel 1953) were
not introduced in previous computations of rotationally-induced mixing. This can lead
to a self-regulating process which reduces the efficiency of the
meridional circulation as well as the microscopic diffusion.
Here we present numerical computations of this process and its influence
on the lithium abundance variations in halo stars.
We show that in slowly rotating stars, under some conditions, lithium can be depleted
by a factor of up to two with a dispersion smaller than 0.1 dex in the
middle part of the lithium plateau. We derive a primordial
lithium abundance of
-gradient terms which appear in the
computations of the meridional circulation velocity
(e.g. Mestel 1953) were
not introduced in previous computations of rotationally-induced mixing. This can lead
to a self-regulating process which reduces the efficiency of the
meridional circulation as well as the microscopic diffusion.
Here we present numerical computations of this process and its influence
on the lithium abundance variations in halo stars.
We show that in slowly rotating stars, under some conditions, lithium can be depleted
by a factor of up to two with a dispersion smaller than 0.1 dex in the
middle part of the lithium plateau. We derive a primordial
lithium abundance of
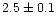 ,
consistent with the recent determinations of
D/H and 4He/H.
,
consistent with the recent determinations of
D/H and 4He/H.
Key words: diffusion - hydrodynamics - stars: abundances - stars:
population II
Prior to the first lithium detection in halo stars by Spite & Spite
(1982), the primordial 7Li value was believed to lie around
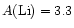 (in the
(in the 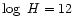 scale), which corresponds to both the meteoritic
and the maximum lithium abundance in Pop I stars throughout the
entire observed
scale), which corresponds to both the meteoritic
and the maximum lithium abundance in Pop I stars throughout the
entire observed
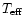 range (8000-4500 K). Below
this maximum value, the observations revealed a large scatter in the
Li-
range (8000-4500 K). Below
this maximum value, the observations revealed a large scatter in the
Li-
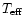 plane, with an evidence of lithium
decrease with age for stars of similar
plane, with an evidence of lithium
decrease with age for stars of similar
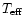 .
.
For this reason it was expected that, due to their age, halo stars
should have destroyed all their lithium. In this context, the first lithium
detection in these stars, with a value
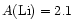 ,
only one order of magnitude
smaller than the maximum Pop I value, was a surprise. The shock was still stronger
when the observations in different stars, with different masses and
metallicities, presented the same lithium value over a range of 800 K in effective
temperature (6250-5480 K).
,
only one order of magnitude
smaller than the maximum Pop I value, was a surprise. The shock was still stronger
when the observations in different stars, with different masses and
metallicities, presented the same lithium value over a range of 800 K in effective
temperature (6250-5480 K).
From then on, the observers switched to another extreme: the idea that
lithium should be depleted in these stars was completely rejected on the basis
of the constancy and very small dispersion of its abundances. The observed
value was then supposed to represent the primordial abundance, without any
modification, and was "sold'' as such to cosmologists. Meanwhile, theoreticians went
on claiming that, from all possible computations of stellar structure, the
lithium abundance could not keep exactly the same value in stars during 14 billions years, without any alteration.
In the present paper, we argue that we can reconcile the theory with the
observations and obtain a consistent view of the lithium behavior in
stars.
In Sect. 2, we discuss recent improvements on the observational side
and show that the careful studies of the lithium abundances in the "Spite
plateau'', obtained from various authors, lead to the conclusion that the
dispersion is smaller than 0.1 dex. Meanwhile, the detection of 6Li, if confirmed,
puts strong constraints on the possible lithium destruction by nuclear
reactions in these stars (otherwise no 6Li should be left).
A theoretical discussion about previous models for lithium abundance
variations in population II stars is given in Sect. 3.
In Sect. 4, we show how the introduction of the effect of
 -gradients in the computations of rotation-induced
mixing, as discussed by Vauclair (1999) (Paper I)
modifies the previously published results. We argue that a self-regulating process may take
place, which may explain most of the lithium observations in halo stars.
-gradients in the computations of rotation-induced
mixing, as discussed by Vauclair (1999) (Paper I)
modifies the previously published results. We argue that a self-regulating process may take
place, which may explain most of the lithium observations in halo stars.
Section 5 is devoted to the results obtained from numerical computations
of this process and its influence on the lithium abundance variations in
different stars with various masses, rotational velocities and
metallicities.
We give our conclusions in Sect. 6, including a discussion about the
assumptions introduced in our computations. In the framework of our
model, we obtain a primordial lithium abundance of
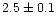 .
.
Since the first observations of the
lithium plateau by Spite & Spite (1982), many abundance determinations
have confirmed the constancy and very small dispersion of the lithium
value in most halo stars with effective temperatures larger than 5500 K.
This result lead the observers to the conclusion that the observed
lithium abundance was exactly the pristine value, although theoretical computations
predicted some lithium depletion in these stars. We first give a short summary
of the important observational constraints and then we will discuss the
theoretical models proposed in the literature.
The observed lithium plateau is flat, at least to a first approximation.
Some doubts still appear, however, about possible small variations with effective
temperature and/or metallicity.
Thorburn (1994) found that the lithium
plateau presented a positive slope with
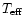 which, she argued, would not exist if the lithium was
primordial. She also found a general trend of the lithium abundance with metallicity which
could explain part of the scatter that she observed on the "Spite
plateau''. She suggested that the slight increase of the lithium abundance
with [Fe/H] could be due to a small production of lithium in the early
life of the galaxy.
which, she argued, would not exist if the lithium was
primordial. She also found a general trend of the lithium abundance with metallicity which
could explain part of the scatter that she observed on the "Spite
plateau''. She suggested that the slight increase of the lithium abundance
with [Fe/H] could be due to a small production of lithium in the early
life of the galaxy.
While Norris et al. (1994) and Ryan et al. (1996) confirmed these results,
Molaro et al. (1995)
argued that the slope of the plateau disappears when a subset of stars
with temperature based on Balmer lines profiles is adopted. They
found no correlation between lithium abundances and metallicity for
[Fe/H] <-1.4.
Later on, Bonifacio & Molaro (1997) studied a sample of 41 plateau
stars, to investigate in more detail
the distribution of lithium abundances with
[Fe/H] and
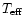 .
They used a new effective temperature scale based on the new
accurate infrared flux method (IRFM, Blackwell et al. 1990) applied to a
large sample of stars by Alonso et al. (1996).
They found only a tiny trend with
.
They used a new effective temperature scale based on the new
accurate infrared flux method (IRFM, Blackwell et al. 1990) applied to a
large sample of stars by Alonso et al. (1996).
They found only a tiny trend with
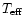 and no trend with
[Fe/H]. Using mean lithium values corrected for standard depletion
and NLTE effects, they give for the primordial abundance:
and no trend with
[Fe/H]. Using mean lithium values corrected for standard depletion
and NLTE effects, they give for the primordial abundance:
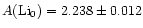 .
.
Meanwhile Ryan et al. (1999) studied
23 very metal-poor stars chosen to enable a precise measurement of the
dispersion in the "Spite plateau'': they found no evidence for a trend
with
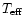 but they do recover
a strong dependence of the lithium abundance with metallicity,
which they attribute to the chemical evolution in the early galaxy.
The value they derive for the primordial abundance,
taking into account galactic chemical evolution but
no depletion, lies below the mean plateau value:
2.0 dex only, with a systematic error
of 0.1 dex.
but they do recover
a strong dependence of the lithium abundance with metallicity,
which they attribute to the chemical evolution in the early galaxy.
The value they derive for the primordial abundance,
taking into account galactic chemical evolution but
no depletion, lies below the mean plateau value:
2.0 dex only, with a systematic error
of 0.1 dex.
While the question of slight lithium slopes with effective temperature
and/or metallicity is not yet completely settled, everyone agrees on the
fact that some stars otherwise indistinguishable from normal plateau
stars show large lithium deficiencies, well below the plateau itself
(Hobbs et al. 1991; Thorburn 1994; Norris et al. 1997). Although these stars are certainly lithium depleted, so that their
observed abundances are quite different from the pristine one, they must be
accounted for in the theoretical scenarios.
Norris et al. (1997) measured the abundances of 14 elements (Fe, Mg, Al,
Si, Ca, Sc, Ti, Cr, Mn, Co, Ni, Sr, Y, Ba) for the metal poor
stars G66-30, G139-8 and G186-26, which are highly lithium deficient
and lie near the main sequence cut-off. They found no
abundance anomalies for the other elements that one might associate
with the lithium deficiencies. This result is in favor of a nuclear lithium destruction
and negligible element settling in these stars.
Since 1982, many authors have discussed the possible
existence of an intrinsic dispersion in the "Spite plateau''.
Deliyannis et al. (1993),
supported by Thorburn (1994), argued that the spread in
measured plateau stars abundances exceeded that expected from
observational data. They gave values of about 20% (Deliyannis et al. 1993)
to 25% (Thorburn 1994).
Molaro et al. (1995), Spite et al. (1996) and
Bonifacio & Molaro (1997) have questioned
whether some of the error estimates in these earlier
works were realistic and have suggested that the dispersion is smaller.
According to Molaro et al. (1995), all the
observations are consistent with the same pristine lithium abundance and
the errors estimated for individual stars account for the observed
dispersion. Spite et al. (1996) argued that the
scatter is fully explained by the temperature equivalent width errors
and that the intrinsic scatter, if real, is small.
Bonifacio & Molaro (1997) revised the lithium abundances in a selected sample
of halo stars using the infrared flux method (IRFM) temperatures by
Alonso et al. (1996). They found no evidence for intrinsic
dispersion.
In the sample of Ryan et al. (1999), 21 stars out of 23
have abundances consistent with an observed spread of a mere 0.031 dex
with reference to the metallicity trend that they claim to observe.
Because the formal errors are
0.033 dex, they conclude that the intrinsic spread of the Li
abundances at a given metallicity is lower than 0.02 dex and consistent with
zero at the very metal poor halo turnoff. This
maximum dispersion is much lower than those obtained by previous
studies (Spite et al. 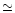 0.06-0.08 dex, Bonifacio & Molaro 0.07 dex) who did not
introduce any systematic variation with metallicity.
0.06-0.08 dex, Bonifacio & Molaro 0.07 dex) who did not
introduce any systematic variation with metallicity.
The situation is different in globular clusters where the lithium
abundances in stars around the turn-off
seem to show a dispersion larger than that observed
for field stars. Deliyannis et al. (1995) and Boesgaard et al.
(1998) observed the stars near the turnoff of the old metal poor
globular cluster M92. They reveal a spread in abundances
of a factor of 2-3 for a small sample of stars. Moreover some of them show a
high lithium abundance compared to the halo
field plateau.
These variations inside globular clusters may be related to
local pollution and other effects which will not be discussed here.
In any case the very small lithium dispersion in halo field
stars (probably less than 10% from the most recent studies),
acts as a strong constraint on the theoretical models.
As we will see below, these results argue against strong lithium
depletion in plateau stars. Recent observations of 6Li
confirm this idea. 6Li has indeed been observed in the
atmosphere of the halo stars HD 84937 by Smith et al. (1993),
Hobbs & Thorburn (1994), Hobbs & Thorburn (1997) and
BD +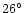 3578 by Smith et al. (1998).
As this light lithium isotope is more easily destroyed than 7Li,
these observations, if confirmed, seem to prove that no strong
lithium destruction by nuclear reactions occured in these stars
during main sequence or pre-main sequence. Small destruction rates may
however be allowed: we will see that a 7Li depletion by a factor of
two leads to a 6Li decrease by less than a factor of five.
3578 by Smith et al. (1998).
As this light lithium isotope is more easily destroyed than 7Li,
these observations, if confirmed, seem to prove that no strong
lithium destruction by nuclear reactions occured in these stars
during main sequence or pre-main sequence. Small destruction rates may
however be allowed: we will see that a 7Li depletion by a factor of
two leads to a 6Li decrease by less than a factor of five.
The expected lithium depletion in halo stars is primarily due
to the diffusion processes which take place in the
radiative regions inside the stars, below the outer convective zones.
Due to pressure and temperature gradients, lithium settles down, as well
as helium and other heavier elements.
Mixing induced by rotation, internal waves, or mass loss related
motions may slow down the settling process, but then it brings up to the
convective zone matter in which lithium has been destroyed by nuclear
reactions.
These lithium depleting processes have been extensively studied in the
literature. Michaud et al. (1984) first computed the lithium abundance
variations in halo stars including element separation. Their models
predicted a downward curvature in the 7Li isochrones for increasing
effective temperature, in contradiction with the observations. This
result, simply due to the decrease of the convective depth for hotter stars,
has been confirmed many times in the literature (Deliyannis et al. 1990;
Deliyannis & Demarque
1991; Proffitt & Michaud 1991; Chaboyer
& Demarque 1994; Vauclair & Charbonnel
1995).
Models including rotation-induced mixing were proposed to prevent the
effect of element separation. As such a mixing leads to lithium
destruction by nuclear reactions, it was suggested that this destruction
could be identical for all the stars, so that the lithium plateau could
be preserved (Vauclair 1988; Pinsonneault et al. 1992, 1999;
Chaboyer & Demarque 1994). However,
if a constant lithium abundance can be obtained in this case, it becomes
extremely difficult to account for such a small dispersion as observed.
Stellar models which include instabilities related to angular momentum
and chemical species transport require additional input physics beyond
standard models. The important new ingredients include:
- 1-
- a distribution of initial angular momenta;
- 2-
- a description for angular momentum losses;
- 3-
- a prescription for the internal transport of angular momentum
and for the associated mixing processes in the stellar radiative regions.
Using various initial angular momenta, Pinsonneault et al. (1992)
obtained lithium depletion factors between 5
and 10 at fixed
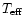 .
The lithium abundances in the plateau slightly decreased for larger
.
The lithium abundances in the plateau slightly decreased for larger
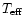 in contradiction with the observations
(this trend was already predicted by Vauclair 1988). This effect
however is quite attenuated for older ages (14 billion years) as the
more lithium depleted stars at the hot end
of the plateau move into the giant branch.
in contradiction with the observations
(this trend was already predicted by Vauclair 1988). This effect
however is quite attenuated for older ages (14 billion years) as the
more lithium depleted stars at the hot end
of the plateau move into the giant branch.
Chaboyer & Demarque (1994) could also reproduce a lithium plateau
with a large lithium depletion in a similar framework, using
different angular momentum loss and rotational mixing laws. They
included meridional circulation, dynamical shear, secular shear, Solberg-Hoiland
and Goldreich-Schubert-Fricke instabilities.
Their results also showed the same trend of abundance decrease with
increasing
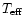 .
.
Using a distribution of initial angular momenta as inferred from stellar
rotation data in young open clusters, Pinsonneault et al. (1999) obtained
a well defined, nearly flat lithium plateau, without the downward trend
at the hot end. A modest scatter does remain however, which increases with
the average lithium depletion: this constraint excludes a lithium
depletion larger than a factor of 3.
Considering the difficulty for theoretical computations, including
element settling and rotation induced mixing, to account for
both the flatness of the lithium plateau and the small dispersion,
Vauclair & Charbonnel (1995) and Vauclair & Charbonnel
(1998) suggested taking into account a stellar
wind. In some cases, a wind could prevent the element
settling without bringing up to the convective zone lithium depleted
matter. Computations were done for various mass loss rates, between 1 and 1000 times
the solar wind. Rates larger than 10 times the solar
wind were needed to have any effect on the lithium depletion, and the best
results were obtained for rates of about
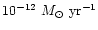 .
In this case the lithium plateau was nicely reproduced. For larger rates, nuclearly depleted matter began
to migrate up into the outer layers, rapidly leading to large lithium
destruction, in contradiction with the observations.
Although appealing, this model suffers from the fact that it needs
winds larger than the solar wind, and that various rates lead
to a non-negligible scatter in the results.
.
In this case the lithium plateau was nicely reproduced. For larger rates, nuclearly depleted matter began
to migrate up into the outer layers, rapidly leading to large lithium
destruction, in contradiction with the observations.
Although appealing, this model suffers from the fact that it needs
winds larger than the solar wind, and that various rates lead
to a non-negligible scatter in the results.
The fact that the dispersion in the lithium plateau
is extremely small compared to the observational
errors is the strongest constraint for the theoretical models.
Several assumptions have lead to models which could account for the
lithium abundance constancy, but the small observed scatter could only
be reproduced using some "ad hoc'' hypothesis on the initial parameters.
In all these computations, however, the effect of the
 -gradients induced by element separation
was not taken into account. In the present paper, we claim that when it is introduced in
the computations of rotation-induced mixing, this process can
explain the features observed in halo stars, including the very small
dispersion.
-gradients induced by element separation
was not taken into account. In the present paper, we claim that when it is introduced in
the computations of rotation-induced mixing, this process can
explain the features observed in halo stars, including the very small
dispersion.
The meridional circulation velocity in stars, in the presence of
 -gradients, is the sum of two terms, one due to
the classical thermal imbalance (
-gradients, is the sum of two terms, one due to
the classical thermal imbalance (
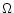 -currents) and
the other one due to the induced horizontal
-currents) and
the other one due to the induced horizontal
 -gradients (
-gradients (
 -induced
currents, or
-induced
currents, or
 -currents in short). In the most
general cases,
-currents in short). In the most
general cases,
 -currents are opposite to
-currents are opposite to
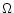 -currents (Mestel 1953; Zahn
1992; Maeder & Zahn 1998).
When element settling occurs below the stellar outer convective zone in cool stars, a small helium
gradient builds, even in the presence of circulation.
-currents (Mestel 1953; Zahn
1992; Maeder & Zahn 1998).
When element settling occurs below the stellar outer convective zone in cool stars, a small helium
gradient builds, even in the presence of circulation.
Then a new process must take place, which had not been taken into account in
previous computations of diffusion-induced
 -gradients. Mestel & Moss (1986) gave a lengthy discussion of this
effect for nuclearly-induced
-gradients. Mestel & Moss (1986) gave a lengthy discussion of this
effect for nuclearly-induced
 -gradients. Chaboyer
et al. (1995) simulated a
-gradients. Chaboyer
et al. (1995) simulated a
 -gradient effect in
their diffusion computations in the form of a reducing factor
-gradient effect in
their diffusion computations in the form of a reducing factor
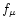 which was taken as a parameter.
Vauclair (1999) (Paper I) showed that
the resulting
which was taken as a parameter.
Vauclair (1999) (Paper I) showed that
the resulting
 -gradients are rapidly
large enough to create
-gradients are rapidly
large enough to create
 -currents of the same order
as
-currents of the same order
as
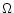 -currents. Then a self-regulating process
may take place, in which both the circulation and the settling
are strongly reduced.
-currents. Then a self-regulating process
may take place, in which both the circulation and the settling
are strongly reduced.
Here we give precise computations of the
 -currents
with the following simplifying assumptions: differential rotation
is supposed negligible inside the stars (as it is presently in the
sun) and the stellar rotation velocity is taken as constant along the
stellar lifetime. These assumptions neglect the possibility of rotational breaking in
early stages of stellar evolution. This is discussed in the conclusion.
-currents
with the following simplifying assumptions: differential rotation
is supposed negligible inside the stars (as it is presently in the
sun) and the stellar rotation velocity is taken as constant along the
stellar lifetime. These assumptions neglect the possibility of rotational breaking in
early stages of stellar evolution. This is discussed in the conclusion.
In the present paper, we have computed these currents
in halo stars for different metallicities and rotation velocities
and we have done a complete treatment of the resulting diffusion
of the chemical species, including mixing and settling.
As in Paper I, we have neglected the deviations from a perfect gas law
as well as the energy production terms, which are completely
negligible in the regions of the star where the process takes
place.
We also assumed a negligible differential rotation, as observed
inside the Sun from helioseismic studies.
The corresponding condition on
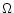 is:
is:
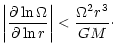 |
|
|
(1) |
The vertical meridional circulation velocity may be written (Paper I):
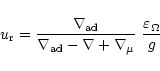 |
(2) |
where
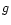 represents the local gravity,
represents the local gravity,
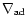 and
and
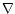 the usual adiabatic and real ratios
the usual adiabatic and real ratios
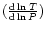 and
and
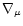 the mean molecular weight
contribution
the mean molecular weight
contribution
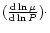
The expression of
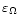 is
obtained as a function of the
is
obtained as a function of the
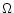 and
and
 -currents:
-currents:
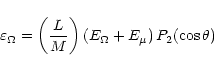 |
(3) |
with:
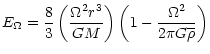 |
|
|
(4) |
![$\displaystyle E_{\mu } = {\rho _{\rm m} \over \overline \rho }
\left\{
{ r \ove...
...chi_{\rm T} + 1) \Lambda \right] - {2 H_{\rm T} \Lambda \over r } \right\}\cdot$](/articles/aa/full/2001/31/aa10594/img38.gif) |
|
|
(5) |
Here
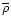 represents
the density average on the level surface
(
represents
the density average on the level surface
(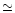
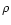 )
while
)
while
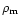 is the mean density inside
the sphere of radius
is the mean density inside
the sphere of radius
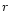 ;
;
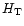 is the temperature scale height;
is the temperature scale height;
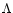 represents the
horizontal
represents the
horizontal
 fluctuations
fluctuations
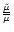 ;
;
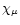 and
and
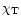 represent the
derivatives:
represent the
derivatives:
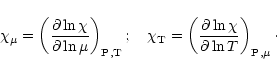 |
(6) |
While the term with the second derivative of
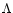 was neglected in Paper I, these expressions are extensively
computed in the present numerical computations.
was neglected in Paper I, these expressions are extensively
computed in the present numerical computations.
Writing 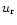 as:
as:
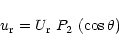 |
(7) |
the horizontal meridional velocity is given by:
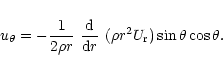 |
(8) |
In the following, we also use the notations
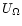 and
and
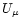 defined as:
defined as:
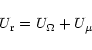 |
(9) |
where
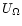 represents the part of
represents the part of 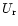 which includes
which includes
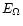 ,
and
,
and 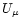 the part
including
the part
including 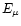 ,
namely:
,
namely:
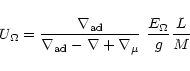 |
(10) |
idem for 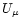 .
.
The expressions and orders of magnitude of the
horizontal
 -gradients
-gradients
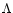 were extensively
discussed in Paper I. In all cases, on a given
level surface
were extensively
discussed in Paper I. In all cases, on a given
level surface
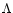 is
proportional to the vertical
is
proportional to the vertical
 -gradient.
A general expression can be given in the form:
-gradient.
A general expression can be given in the form:
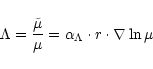 |
(11) |
where
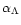 is a constant, which
is related to the horizontal diffusion coefficient in case
of shear flow instabilities by (Zahn 1993, Paper I):
is a constant, which
is related to the horizontal diffusion coefficient in case
of shear flow instabilities by (Zahn 1993, Paper I):
 |
(12) |
As discussed many times in the literature, stellar regions
in which no macroscopic motions take place are subject to
element settling induced by pressure and temperature gradients
and radiative acceleration (Michaud 1970; Michaud et al.
1976 (MCV2); Vauclair & Vauclair
1982; Vauclair & Charbonnel
1995, 1998).
When macroscopic motions occur, they slow down the settling but
do not prevent it completely until an equilibrium concentration
gradient is reached (Vauclair et al. 1978a (V2M),
1978b (V2SM);
Richard et al. 1996).
In Paper I we showed that in halo stars this equilibrium gradient
is never reached before the
 -currents become
of the same order of magnitude as the
-currents become
of the same order of magnitude as the
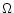 -currents.
Thus the abundance variations induced by
settling and rotation-induced mixing must always be
computed simultaneously.
-currents.
Thus the abundance variations induced by
settling and rotation-induced mixing must always be
computed simultaneously.
Computations of element settling have been described many times. Here
we use the same prescriptions as in Richard et al. (1996) with collision
cross sections and microscopic diffusion coefficients as given by
Paquette et al. (1986). Radiative accelerations are neglected, as usual in
these cool stars (precise computations in the Sun by
Turcotte et al. (1998) show
that they are indeed negligible for our purpose).
Rotation-induced mixing is also computed as in Richard et al. (1996)
except for the introduction of the
 -currents
in the velocity of meridional circulation. Following Zahn (1992) and
(1993), meridional circulation is suppose to induce shear flow
instabilities which, in a density stratified medium, lead to large
horizontal diffusivities. The combination of the circulation and
horizontal mixing may be treated as a vertical effective diffusion
process, described with an effective diffusion coefficient:
-currents
in the velocity of meridional circulation. Following Zahn (1992) and
(1993), meridional circulation is suppose to induce shear flow
instabilities which, in a density stratified medium, lead to large
horizontal diffusivities. The combination of the circulation and
horizontal mixing may be treated as a vertical effective diffusion
process, described with an effective diffusion coefficient:
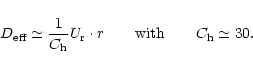 |
(13) |
Abundance variations of helium, lithium and heavier elements
are computed within this framework, all along evolutionary sequences.
The modifications of the internal structure induced by element diffusion
are taken into account in the computations, as in Richard et al. (1996).
The originality of the present paper lies in the introduction
of
 -currents in the meridional circulation.
As discussed in Paper I and verified in the complete
numerical computations (see below),
-currents in the meridional circulation.
As discussed in Paper I and verified in the complete
numerical computations (see below),
 -currents
become of the same order as
-currents
become of the same order as
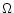 -currents for
small
-currents for
small
 -gradients, rapidly reached from
helium settling below the convective zone.
In this case we claim that, under some conditions, a self-regulating
process may take place in which both the circulation and the
settling are strongly reduced.
-gradients, rapidly reached from
helium settling below the convective zone.
In this case we claim that, under some conditions, a self-regulating
process may take place in which both the circulation and the
settling are strongly reduced.
At the beginning of the stellar evolution,
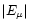 is smaller than
is smaller than
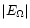 ;
meridional circulation proceeds and induces transport
of chemical elements coupled with settling. The helium
concentration gradient below the convective zone increases (in
absolute value) leading to an increasing vertical
;
meridional circulation proceeds and induces transport
of chemical elements coupled with settling. The helium
concentration gradient below the convective zone increases (in
absolute value) leading to an increasing vertical
 -gradient. The horizontal
-gradient. The horizontal
 -gradient
-gradient
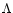 follows
proportionally until
follows
proportionally until
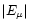 becomes of the same order as
becomes of the same order as
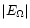 ,
where the circulation velocity is expected to
vanish.
,
where the circulation velocity is expected to
vanish.
Then the whole process is modified and does not follow any longer the
classical treatment of the Eddington-Sweet circulation. Let us call
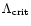 the horizontal
the horizontal
 -gradient for which
-gradient for which
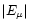 =
=
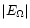 .
Without microscopic diffusion, the whole circulation would become frozen,
keeping horizontal
.
Without microscopic diffusion, the whole circulation would become frozen,
keeping horizontal
 -gradients of the order of
-gradients of the order of
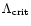 in every layer.
However microscopic diffusion still proceeds below the convective
zone, leading to a slight decrease of
in every layer.
However microscopic diffusion still proceeds below the convective
zone, leading to a slight decrease of
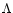 in the
upper radiative layers (this is due to the fact that there is
no horizontal
in the
upper radiative layers (this is due to the fact that there is
no horizontal
 -gradient inside the
convective zone because of rapid mixing).
-gradient inside the
convective zone because of rapid mixing).
As
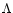 becomes smaller than
becomes smaller than
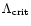 ,
circulation proceeds just below the convective zone,
in the direction of
,
circulation proceeds just below the convective zone,
in the direction of
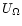 .
Doing so,
due to mass conservation, it lifts up matter from
below in an ascending flow and pushes it down in a
descending flow. Although this description looks like
that of normal meridional circulation, there is a fundamental difference:
in the deeper layers, where
.
Doing so,
due to mass conservation, it lifts up matter from
below in an ascending flow and pushes it down in a
descending flow. Although this description looks like
that of normal meridional circulation, there is a fundamental difference:
in the deeper layers, where
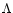 was close
to
was close
to
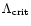 ,
this extra motion creates
an over-critical horizontal
,
this extra motion creates
an over-critical horizontal
 -gradient,
which leads to a local horizontal motion in the direction of
-gradient,
which leads to a local horizontal motion in the direction of
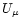 .
Then part of the matter which falls down in the
descending flow is transferred to the ascending flow and
goes back up to the convective zone where it came from.
We can infer that, when this occurs, the global
element depletion from the convective zone is reduced in a
significant way, leading to time scales larger than the stellar ages.
.
Then part of the matter which falls down in the
descending flow is transferred to the ascending flow and
goes back up to the convective zone where it came from.
We can infer that, when this occurs, the global
element depletion from the convective zone is reduced in a
significant way, leading to time scales larger than the stellar ages.
A good treatment of this self-regulating process needs
a complete numerical simulation, which is planned for
a forthcoming paper. Here we used the following
approximation.
In the layers where the circulation time scale
(that is, the time scale of
both the
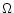 -currents and
the
-currents and
the
 -currents taken separately)
is smaller than the settling
time scale, we assumed that, as soon as
-currents taken separately)
is smaller than the settling
time scale, we assumed that, as soon as
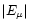 becomes of the same order as
becomes of the same order as
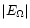 (within 10%), the
(within 10%), the
 -gradient remains equal to the equilibrium one.
-gradient remains equal to the equilibrium one.
On the contrary, in the layers where the circulation
time scale is larger than the settling time scale,
we assumed that the readjustement would have
no time to take place in a settling time scale and
element depletion proceeds unaltered.
In other words, the
 -gradient remains
constant below the convective zone, where
-gradient remains
constant below the convective zone, where
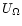 is larger than
the settling velocity, as soon as
is larger than
the settling velocity, as soon as
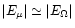 .
Meanwhile the overall helium and lithium abundances are still
subject to depletion due to diffusion deeper in the star, at the place
where the settling velocity becomes larger than
.
Meanwhile the overall helium and lithium abundances are still
subject to depletion due to diffusion deeper in the star, at the place
where the settling velocity becomes larger than
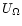 (see
below, Fig. 2).
(see
below, Fig. 2).
First we present the results obtained for four low metallicity stars with
masses of
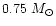 (hot end of the plateau),
(hot end of the plateau),
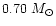 (middle of the plateau),
(middle of the plateau),
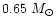 (cool end of the plateau) and
(cool end of the plateau) and
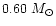 to show the behavior of the
to show the behavior of the 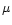 -currents with time.
Here the rotation velocity is assumed constant, equal to
-currents with time.
Here the rotation velocity is assumed constant, equal to
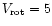 kms-1 and the metallicity is chosen equal to
kms-1 and the metallicity is chosen equal to
![$[{\rm Fe/H}]=-2.0$](/articles/aa/full/2001/31/aa10594/img70.gif) .
.
Figures 1a-d display the
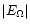 and
and 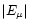 profiles below the convective zones at different evolutionary stages.
Each star arrives on the main sequence with nearly homogenous
composition. At that time,
profiles below the convective zones at different evolutionary stages.
Each star arrives on the main sequence with nearly homogenous
composition. At that time,
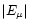 is smaller than
is smaller than
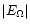 everywhere inside the star.
Meridional circulation and element settling can take place
in the radiative regions of the star as described above.
As a consequence of the helium settling, the
everywhere inside the star.
Meridional circulation and element settling can take place
in the radiative regions of the star as described above.
As a consequence of the helium settling, the 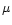 -currents increase
below the convective zone and become rapidly of the same order as
-currents increase
below the convective zone and become rapidly of the same order as 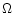 -currents.
-currents.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{MS10594f1a1.eps}\par\subfigure[]{\includegraphics[width=12cm,clip]{MS10594f1a2.eps} }\end{figure}](/articles/aa/full/2001/31/aa10594/Timg71.gif) |
Figure 1:
a) Evolution of 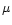 -currents with time inside
the star. The graphs show the variations with depth of both -currents with time inside
the star. The graphs show the variations with depth of both
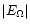 and
and 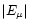 (defined in Eqs. (4) and (5)) in a (defined in Eqs. (4) and (5)) in a
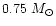 halo star with
halo star with
![$[{\rm Fe/H}]=-2$](/articles/aa/full/2001/31/aa10594/img6.gif) and
and
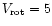 kms-1. b) Same figure as Fig. 1a for a kms-1. b) Same figure as Fig. 1a for a
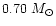 halo star. c) Same figure as Fig. 1a for a
halo star. c) Same figure as Fig. 1a for a
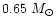 halo star. d) Same figure as Fig. 1a for a
halo star. d) Same figure as Fig. 1a for a
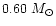 halo star.
halo star. |
| Open with DEXTER |
The lithium abundance variations with time have been computed
using the following scenario: microscopic diffusion damped by
rotation-induced mixing occurs normally until the relative
difference between 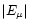 and
and
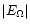 becomes smaller
than
becomes smaller
than 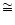 10%. Then the self-regulating process is supposed
to take place, in which diffusion and mixing are strongly
reduced (with time scales larger than the stellar lifetime). This
occurs down to the place where the microscopic diffusion velocity becomes
preponderant (Figs. 2a-c). Below this layer, diffusion is assumed
to proceed freely.
10%. Then the self-regulating process is supposed
to take place, in which diffusion and mixing are strongly
reduced (with time scales larger than the stellar lifetime). This
occurs down to the place where the microscopic diffusion velocity becomes
preponderant (Figs. 2a-c). Below this layer, diffusion is assumed
to proceed freely.
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{MS10594f2a1.eps}\par {\in...
...graphics[width=11.9cm,clip]{MS10594f2a2.eps} }
{\hspace*{6cm} (a)}\end{figure}](/articles/aa/full/2001/31/aa10594/Timg75.gif) |
Figure 2:
a) Microscopic diffusion velocity below the convective zone
of a
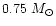 star compared to the classical meridional
circulation velocity
star compared to the classical meridional
circulation velocity
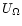 (defined in Eq. (10)). When
(defined in Eq. (10)). When
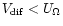 ,
the self-regulating process can occur while when ,
the self-regulating process can occur while when
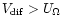 ,
the circulation cannot compensate for the effect of diffusion. b) Same figure as Fig. 2a for a ,
the circulation cannot compensate for the effect of diffusion. b) Same figure as Fig. 2a for a
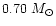 star. c) Same figure as Fig. 2a for a
star. c) Same figure as Fig. 2a for a
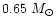 star.
star. |
| Open with DEXTER |
Figure 3 presents the lithium abundance variations with time for a bunch
of different rotational velocities in a
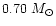 star. For small
rotation velocities, the lithium abundance variations are mainly due
to microscopic diffusion, decreasing for increasing rotation velocity.
For velocities larger than 6 kms-1 the depletion is mainly due
to nuclear destruction, which now increases with increasing velocity.
For velocities between 2.5 and 7 kms-1, the resulting dispersion
is of order 0.06 dex, going up to .12 dex if the 7.5 kms-1
possibility is included.
star. For small
rotation velocities, the lithium abundance variations are mainly due
to microscopic diffusion, decreasing for increasing rotation velocity.
For velocities larger than 6 kms-1 the depletion is mainly due
to nuclear destruction, which now increases with increasing velocity.
For velocities between 2.5 and 7 kms-1, the resulting dispersion
is of order 0.06 dex, going up to .12 dex if the 7.5 kms-1
possibility is included.
Figures 4a-c present the lithium abundance variations with
time in the outer layers of the four low-metallicity stars
(
![$[{\rm Fe/H}]=-2$](/articles/aa/full/2001/31/aa10594/img6.gif) )
with three different rotation velocities: 2.5, 5.0 and
7.5 kms-1.
The
)
with three different rotation velocities: 2.5, 5.0 and
7.5 kms-1.
The
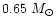 and
and
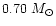 stars
show very similar abundances and their variations with
the rotation velocity is small except for the largest
value of 7.5 kms-1.
In the
stars
show very similar abundances and their variations with
the rotation velocity is small except for the largest
value of 7.5 kms-1.
In the
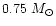 star
the lithium abundance is more sensitive to the rotation velocity
due to the smaller diffusion time scale. For small velocities the
lithium value in the
star
the lithium abundance is more sensitive to the rotation velocity
due to the smaller diffusion time scale. For small velocities the
lithium value in the
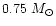 star is smaller than in
cooler stars while it is larger for velocities larger than
5 kms-1. For the cooler
star is smaller than in
cooler stars while it is larger for velocities larger than
5 kms-1. For the cooler
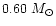 star, lithium is always more
depleted due to the small distance between the bottom
of the convective zone and the nuclear destruction layer.
star, lithium is always more
depleted due to the small distance between the bottom
of the convective zone and the nuclear destruction layer.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f3.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg78.gif) |
Figure 3:
Lithium abundance variations at the surface of
a
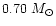 star for rotation velocities between 2.5 and
7.5 kms-1. The minimum depletion is obtained for 6 kms-1.
For smaller velocities, depletion is mainly due to microscopic
diffusion while for larger velocities it is mainly due to nuclear
destruction. Due to the self-regulating process, the obtained dispersion
is quite small.
star for rotation velocities between 2.5 and
7.5 kms-1. The minimum depletion is obtained for 6 kms-1.
For smaller velocities, depletion is mainly due to microscopic
diffusion while for larger velocities it is mainly due to nuclear
destruction. Due to the self-regulating process, the obtained dispersion
is quite small. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{MS10594f4.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg79.gif) |
Figure 4:
Lithium abundance variations at the surface of
the four halo stars, with three different
rotation velocities: a) 2.5 kms-1, b) 5 kms-1, c)
7.5 kms-1. |
| Open with DEXTER |
Figures 5a-d display, as an example, the abundance
profiles for lithium inside the four halo stars, for a rotation velocity of 6 kms-1.
We have tested the influence of metallicity on the lithium abundance
variations for all the stars, with two
different metallicities
![$[{\rm Fe/H}]=-2.0$](/articles/aa/full/2001/31/aa10594/img70.gif) and
and
![$[{\rm Fe/H}]=-3.5$](/articles/aa/full/2001/31/aa10594/img80.gif) .
The curves
representing the lithium variations with time are plotted in Fig. 6.
These curves are very close, which leads to the conclusion of a very small dependence of
the lithium abundance on metallicity.
.
The curves
representing the lithium variations with time are plotted in Fig. 6.
These curves are very close, which leads to the conclusion of a very small dependence of
the lithium abundance on metallicity.
We have also tested the influence
of varying the mixing length parameter used for
the computation of the convective zone: the results are
presented in Fig. 7. The differences are very small: the
results are not sensitive to small variations of the depth of the
convective zone.
The lithium depletion obtained for the
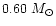 star,
which is cooler than the lithium plateau, is not sufficient
to account for the observations, except for a rotation velocity of 7.5 kms-1.
The observations show, for these effective temperatures, a lithium
depletion by at least a factor of 10, while the computations
obtained by using the same physical inputs as those introduced for the
three others stars give a lithium depletion of only 60% for
2.5 kms-1 and 80% for 5 kms-1.
star,
which is cooler than the lithium plateau, is not sufficient
to account for the observations, except for a rotation velocity of 7.5 kms-1.
The observations show, for these effective temperatures, a lithium
depletion by at least a factor of 10, while the computations
obtained by using the same physical inputs as those introduced for the
three others stars give a lithium depletion of only 60% for
2.5 kms-1 and 80% for 5 kms-1.
However, at such effective
temperatures, a tachocline layer is supposed to take place below the
convective zone, as in the Sun (Spiegel & Zahn 1992).
We introduced in the computations an exponential
mixing just below the convective region to reproduce the effects of
this tachocline. The width of the mixed layer was taken as 0.01 R* and
the diffusion coefficient was 100 cm2s-1 below the convective zone,
decreasing exponentially underneath.
We then obtained the lithium variation with time as plotted in
Fig. 8 for a velocity of 5 kms-1, giving a lithium depletion
by a factor 20, consistent with the observations.
We have further checked that such a narrow tachocline layer, if present
in hotter stars, would not modify the previously obtained results.
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{MS10594f5.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg81.gif) |
Figure 5:
Lithium profiles inside the
four halo stars, with a rotation velocity of
6 kms-1. Dashed line: 0.029 Gyrs, long dashed dotted line:
1.869 Gyrs, dotted line: 3.738 Gyrs and solid line: 10.095 Gyrs. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f6.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg82.gif) |
Figure 6:
Lithium abundance variation with time for
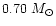 halo stars with two different values of the metallicity.
halo stars with two different values of the metallicity. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f7.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg83.gif) |
Figure 7:
Lithium abundance variation with time for
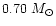 halo stars with two different values of the mixing length parameter.
halo stars with two different values of the mixing length parameter. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f8.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg84.gif) |
Figure 8:
Lithium abundance variation with time for
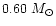 halo stars with and without tachocline. Solid line:
stellar model without tachocline, dashed line: stellar model with tachocline.
halo stars with and without tachocline. Solid line:
stellar model without tachocline, dashed line: stellar model with tachocline. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f9.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg85.gif) |
Figure 9:
Lithium 6 abundance variations at the surface of
a
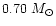 star for rotation velocities between 2.5 and
7.5 kms-1.
star for rotation velocities between 2.5 and
7.5 kms-1. |
| Open with DEXTER |
We have done the same computations for 6Li as for 7Li in the
plateau stars. Figure 9 displays the results for a
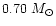 star with metallicity
star with metallicity
![$[{\rm Fe/H}]=-2$](/articles/aa/full/2001/31/aa10594/img6.gif) and the same values of the
rotation velocity as for 7Li in Fig. 3. The results differ for the two isotopes
because 6Li is more easily destroyed by nuclear reactions than 7Li, while
the influence of microscopic diffusion is about the same.
For small rotation velocities, less than 7 kms-1, 6Li is
destroyed by about a factor of two. For larger velocities it goes
up to a factor of 5. In any case, if 6Li is present at the beginning
of the stellar evolution, a non negligible amount remains at the age
of halo stars.
and the same values of the
rotation velocity as for 7Li in Fig. 3. The results differ for the two isotopes
because 6Li is more easily destroyed by nuclear reactions than 7Li, while
the influence of microscopic diffusion is about the same.
For small rotation velocities, less than 7 kms-1, 6Li is
destroyed by about a factor of two. For larger velocities it goes
up to a factor of 5. In any case, if 6Li is present at the beginning
of the stellar evolution, a non negligible amount remains at the age
of halo stars.
The results obtained in this paper are compared to
the observational points and error bars given by
Bonifacio & Molaro (1997) in
Figs. 10a and b. The solid curve drawn in Fig. 10a represents
averaged depletion values for rotation velocities
between 2.5 and 7.5 kms-1. The original lithium
value is
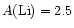 .
In Fig. 10b, two extreme curves are given, again
with the assumption of rotation velocities between
2.5 and 7.5 kms-1. The expected dispersion
is very small (of order 0.1 dex) at the middle
of the lithium plateau. It becomes larger at both extremes:
for the hotter side, it is due to the shorter diffusion
time scale and for the cooler side to the
proximity of the nuclear destruction layers.
.
In Fig. 10b, two extreme curves are given, again
with the assumption of rotation velocities between
2.5 and 7.5 kms-1. The expected dispersion
is very small (of order 0.1 dex) at the middle
of the lithium plateau. It becomes larger at both extremes:
for the hotter side, it is due to the shorter diffusion
time scale and for the cooler side to the
proximity of the nuclear destruction layers.
A complete treatment of the
self-regulating process described in
Sects. 4-3 would need numerical simulations
which are in preparation. Here we have
assumed that this effect significantly reduces
both the circulation and the diffusion as the
circulation time scale is smaller than the diffusion
time scale while it is supposed to proceed unaltered
below. Such a simple scheme gives results consistent with the
lithium observations in halo stars. No mass loss has been
taken into account, which means that the mass loss rate
is assumed smaller than
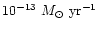 (Vauclair & Charbonnel 1995).
(Vauclair & Charbonnel 1995).
Two important assumptions have been used in these
computations: the stellar rotation velocity was
taken as a constant during evolution and the
differential rotation inside the stars was assumed
negligible.
The first assumption is impossible to check directly, as we
have no access to the past rotational history of
halo stars. It is generally assumed that they suffer
the same rotational breaking as pop I stars. However
they have not been formed in the same way, not being
in the same galactic sites, and their kinematics is different. There is
no reason why halo stars should behave exactly in the same way as open
cluster stars. If the rotational velocity of halo stars was larger in
the past, we would expect a larger lithium destruction before the
self-regulating process we have described takes place. This cannot be
excluded, so that the result we give below has to be taken as the lower
limit of the primordial value.
The second assumption is supported by recent helioseismic results,
which show that the internal rotation of the Sun follows a solid body law except in the
convective zone. We may suppose that the same occurs in halo
stars. The fact that the obtained results nicely
reproduce the observations argue in favour of this
hypothesis. Note that the most efficient way to reach this situation seems
to be the presence of a very small magnetic field (Mestel et al. 1987;
Charbonneau & MacGregor 1992) which, as discussed by
Mestel (1999), would suppress differential rotation without altering large-scale motion. Such a physics has to be further studied.
It is possible, however, that in some specific stars, due to
gravitational interaction with other stars or to some unknown
other process, differential rotation does occur. This could
explain the existence of some stars with no observed lithium
below the plateau: lithium would have been destroyed there
by nuclear reactions due to extra mixing. It could also explain
why some dispersion is observed in globular cluster stars while it is not
observed in field stars (Boesgaard & Deliyannis
1998).
Futher computations have to be done to describe more precisely
the hydrodynamical situation which occurs when the
 -currents oppose the
-currents oppose the
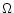 -currents below the convective zones
of slowly rotating stars. Applications to lithium in open clusters are
underway. The results presented here are
very encouraging in this respect. They show that the plateau
can be reproduced with no "ad hoc'' adjustment of any
parameter, with an overall lithium depletion slightly
smaller than a factor two. In this case 6Li is still
present in the plateau stars. The primordial lithium
value is then found as
-currents below the convective zones
of slowly rotating stars. Applications to lithium in open clusters are
underway. The results presented here are
very encouraging in this respect. They show that the plateau
can be reproduced with no "ad hoc'' adjustment of any
parameter, with an overall lithium depletion slightly
smaller than a factor two. In this case 6Li is still
present in the plateau stars. The primordial lithium
value is then found as
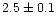 ,
consistent with
the recent determinations of D/H and 4He/H (see Burles & Tytler
1998). These results give a baryonic number
,
consistent with
the recent determinations of D/H and 4He/H (see Burles & Tytler
1998). These results give a baryonic number
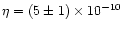 and a baryonic density
and a baryonic density
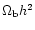 between 0.015 and 0.022.
between 0.015 and 0.022.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f10a.eps}\par\includegraphics[width=8.8cm,clip]{MS10594f10b.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg96.gif) |
Figure 10:
Comparison between the computations of lithium depletion and
the observational values of Bonifacio & Molaro
(1997). a) Average curve obtained for rotation
velocities between 2.5 and 7.5 kms-1. Here a tachocline is
introduced as explained in Sect. 5.4. The original lithium value
is choosen as 2.5 to fit the observations. b) Expected dispersion
if the rotation velocities lie between 2.5 and 7.5 kms-1. The
observational error bars are not shown for clarity. |
| Open with DEXTER |
- Alonso, A., Arribas, S., & Martinez-Roger, C.
1996, A&AS, 117, 227
In the text
NASA ADS
- Blackwell, D. E., Petford, A. D.,
Haddock, D. J., Arribas, S., & Selby, M. J. 1990, A&A, 232, 396
In the text
NASA ADS
- Boesgaard, A. M., Deliyannis, C. P.,
Stephens, A., & King, J. R. 1998, ApJ, 493, 206
In the text
NASA ADS
- Bonifacio, P., & Molaro, P. 1997, MNRAS,
285, 847
In the text
NASA ADS
- Burles, S., & Tytler, D. 1998, ApJ, 507, 732
In the text
NASA ADS
- Chaboyer, B., & Demarque, P. 1994, ApJ, 433,
510
In the text
NASA ADS
- Chaboyer, B., Demarque, P., & Pinsonneault,
M. H. 1995, ApJ, 441, 865
In the text
NASA ADS
- Charbonneau, P., & MacGregor, K. B. 1992,
ApJ, 387, 639
In the text
NASA ADS
- Deliyannis, C. P., Boesgaard, A. M.,
& King, J. R. 1995, ApJ, 452, L13
In the text
NASA ADS
- Deliyannis, C. P., & Demarque, P. 1991,
ApJ, 379, 216
In the text
NASA ADS
- Deliyannis, C. P., Demarque, P., & Kawaler,
S. D. 1990, ApJS, 73, 21
In the text
NASA ADS
- Deliyannis, C. P.,
Pinsonneault, M. H., & Duncan, D. K. 1993, ApJ, 414, 740
In the text
NASA ADS
- Hobbs, L. M., & Thorburn, J. A. 1994, ApJ,
428, L25
In the text
NASA ADS
- Hobbs, L. M., & Thorburn, J. A. 1997, ApJ,
491, 772
In the text
NASA ADS
- Hobbs, L. M., Thorburn, J. A., & Welty, D. E. 1991, ApJ, 373, L47
In the text
NASA ADS
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000
In the text
NASA ADS
- Mestel, L. 1953, MNRAS, 113, 716
In the text
NASA ADS
- Mestel, L. 1999, Stellar Magnetism (Oxford
Science Publications)
In the text
- Mestel, L., & Moss, D. L. 1986, MNRAS, 221, 25
In the text
NASA ADS
- Mestel, L., Tayler, R. J., Moss, D. L., 1987,
in The Internal Solar Angular Velocity, ed. B. R. Durney, &
S. Sofia (Reidel Pub. Company)
In the text
- Michaud, G. 1970, ApJ, 160, 641
In the text
NASA ADS
- Michaud, G., Charland, Y., Vauclair, S.,
& Vauclair, G. 1976, ApJ, 210, 447
In the text
NASA ADS
- Michaud, G., Fontaine, G., & Beaudet, G.,
1984, ApJ, 282, 206
In the text
NASA ADS
- Molaro, P., Primas, F., & Bonifacio, P. 1995,
A&A, 295, L47
In the text
NASA ADS
- Norris, J. E., Ryan, S. G., Beers, T. C.,
& Deliyannis, C. P. 1997, ApJ, 485, 370
In the text
NASA ADS
- Norris, J. E., Ryan, S. G., & Stringfellow,
G. S. 1994, ApJ, 423, 386
In the text
NASA ADS
- Paquette, C., Pelletier, C., Fontaine, G.,
& Michaud, G. 1986, ApJS, 61, 177
In the text
NASA ADS
- Pinsonneault, M. H., Deliyannis, C. P.,
& Demarque, P. 1992, ApJS, 78, 179
In the text
NASA ADS
- Pinsonneault, M. H., Walker, T. P.,
Steigman, G., & Narayanan, V. K. 1999, ApJ, 527, 180
In the text
NASA ADS
- Proffitt, C. R., & Michaud, G. 1991, ApJ,
371, 584
In the text
NASA ADS
- Richard, O., Vauclair, S., Charbonnel, C.,
& Dziembowski, W. A. 1996, A&A, 312, 1000
In the text
NASA ADS
- Ryan, S. G., Beers, T. C.,
Deliyannis, C. P., & Thorburn, J. A. 1996, ApJ, 458, 543
In the text
NASA ADS
- Ryan, S. G., Norris, J. E., & Beers, T. C. 1999,
ApJ, 523, 654
In the text
NASA ADS
- Smith, V. V., Lambert, D. L., & Nissen, P. E. 1993, ApJ, 408, 262
In the text
NASA ADS
- Smith, V. V., Lambert, D. L., & Nissen, P. E. 1998, ApJ, 506, 405
In the text
NASA ADS
- Spiegel, E. A., & Zahn, J.-P. 1992, A&A, 265, 106
In the text
NASA ADS
- Spite, F., & Spite, M. 1982, A&A, 115, 357
In the text
NASA ADS
- Spite, M., Francois, P., Nissen,
P. E., & Spite, F. 1996, A&A, 307, 172
In the text
NASA ADS
- Thorburn, J. A. 1994, ApJ, 421, 318
In the text
NASA ADS
- Turcotte, S., Richer, J., Michaud,
G., Iglesias, C. A., & Rogers, F. J. 1998, ApJ, 504, 539
In the text
NASA ADS
- Vauclair, S. 1988, ApJ, 335, 971
In the text
NASA ADS
- Vauclair, S. 1999, A&A, 351, 973
In the text
NASA ADS
- Vauclair, S., & Charbonnel, C. 1995, A&A,
295, 715
In the text
NASA ADS
- Vauclair, S., & Charbonnel, C. 1998, ApJ,
502, 372
In the text
NASA ADS
- Vauclair, S., & Vauclair, G. 1982, ARA&A,
20, 37
In the text
NASA ADS
- Vauclair, G., Vauclair, S., & Michaud, G. 1978a,
ApJ, 223, 920
In the text
NASA ADS
- Vauclair, S., Vauclair, G., Schatzman, E.,
& Michaud, G. 1978b, ApJ, 223, 567
In the text
NASA ADS
- Zahn, J.-P. 1992, A&A, 265, 115
In the text
NASA ADS
- Zahn, J.-P. 1993, in
Astrophysical Fluid Dynamics, ed. J.-P. Zahn, &
J. Zinn-Justin, Les Houches,
Session XLVII, 561
In the text
Copyright ESO 2001
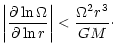
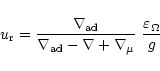
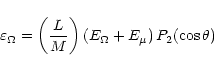
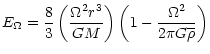
![$\displaystyle E_{\mu } = {\rho _{\rm m} \over \overline \rho }
\left\{
{ r \ove...
...chi_{\rm T} + 1) \Lambda \right] - {2 H_{\rm T} \Lambda \over r } \right\}\cdot$](/articles/aa/full/2001/31/aa10594/img38.gif)
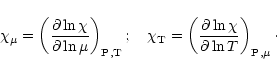
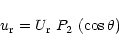
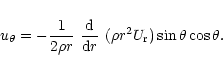
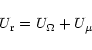
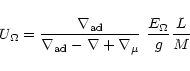
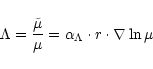

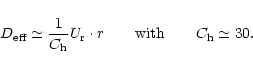
![\begin{figure}
\par\includegraphics[width=12cm,clip]{MS10594f1a1.eps}\par\subfigure[]{\includegraphics[width=12cm,clip]{MS10594f1a2.eps} }\end{figure}](/articles/aa/full/2001/31/aa10594/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{MS10594f1b1.eps}\par\includegraphics[width=12cm,clip]{MS10594f1b2.eps} {\hspace*{6cm} (b)}\end{figure}](/articles/aa/full/2001/31/aa10594/Timg72.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{MS10594f1c1.eps}\par\includegraphics[width=12cm,clip]{MS10594f1c2.eps} {\hspace*{6cm} (c)}\end{figure}](/articles/aa/full/2001/31/aa10594/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{MS10594f1d1.eps}\par\includegraphics[width=12cm,clip]{MS10594f1d2.eps} {\hspace*{6cm} (d)}\end{figure}](/articles/aa/full/2001/31/aa10594/Timg74.gif)
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{MS10594f2a1.eps}\par {\in...
...graphics[width=11.9cm,clip]{MS10594f2a2.eps} }
{\hspace*{6cm} (a)}\end{figure}](/articles/aa/full/2001/31/aa10594/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{MS10594f2b1.eps}\par\includegraphics[width=11.9cm,clip]{MS10594f2b2.eps} {\hspace*{6cm} (b)}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=11.9cm,clip]{MS10594f2c1.eps}\par\includegraphics[width=11.9cm,clip]{MS10594f2c2.eps} {\hspace*{6cm} (c)}\end{figure}](/articles/aa/full/2001/31/aa10594/Timg77.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f3.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg78.gif)
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{MS10594f4.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg79.gif)
![\begin{figure}
\par\includegraphics[width=12.3cm,clip]{MS10594f5.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg81.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f6.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg82.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f7.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg83.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f8.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg84.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f9.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10594f10a.eps}\par\includegraphics[width=8.8cm,clip]{MS10594f10b.eps}
\end{figure}](/articles/aa/full/2001/31/aa10594/Timg96.gif)