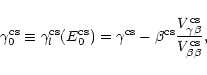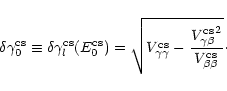E. Nuss 2,
A&A 374, 895-906 (2001)
DOI: 10.1051/0004-6361:20010798
F. Piron 3,![]() -
A. Djannati-Ataï 6 -
M. Punch 6 -
J.-P. Tavernet 4 -
A. Barrau 4,
-
A. Djannati-Ataï 6 -
M. Punch 6 -
J.-P. Tavernet 4 -
A. Barrau 4,![]() -
R. Bazer-Bachi 1 -
L.-M. Chounet 3 -
G. Debiais 2 -
B. Degrange 3 -
J.-P. Dezalay 1 -
P. Espigat 6 -
B. Fabre 2 -
P. Fleury 3 -
G. Fontaine 3 -
P. Goret 7 -
C. Gouiffes 7 -
B. Khelifi 6 -
I. Malet 1 -
C. Masterson 6 -
G. Mohanty 3,
-
R. Bazer-Bachi 1 -
L.-M. Chounet 3 -
G. Debiais 2 -
B. Degrange 3 -
J.-P. Dezalay 1 -
P. Espigat 6 -
B. Fabre 2 -
P. Fleury 3 -
G. Fontaine 3 -
P. Goret 7 -
C. Gouiffes 7 -
B. Khelifi 6 -
I. Malet 1 -
C. Masterson 6 -
G. Mohanty 3,![]() -
-
E. Nuss 2,![]() -
C. Renault 4,
-
C. Renault 4,
![]() -
M. Rivoal 4 -
L. Rob 5 -
S. Vorobiov 3
-
M. Rivoal 4 -
L. Rob 5 -
S. Vorobiov 3
1 -
Centre d'Études Spatiales des Rayonnements, Université Paul Sabatier, Toulouse, France (INSU/CNRS)
2 -
Groupe de Physique Fondamentale, Université de Perpignan, France
3 -
Laboratoire de Physique Nucléaire des Hautes Énergies,
École Polytechnique, Palaiseau, France (IN2P3/CNRS)
4 -
Laboratoire de Physique Nucléaire et de Hautes Energies,
Universités Paris VI/VII, France (IN2P3/CNRS)
5 -
Nuclear Center, Charles University, Prague, Czech Republic
6 -
Physique Corpusculaire et Cosmologie, Collège de France et Université Paris VII, France (IN2P3/CNRS)
7 -
Service d'Astrophysique, Centre d'Études de Saclay, France (CEA/DSM/DAPNIA)
Received 10 April 2001 / Accepted 30 May 2001
Abstract
The ![]() -ray emission above
-ray emission above
![]() from the BL Lac object Markarian 421
was observed by the CAT Cherenkov imaging telescope between December, 1996, and June, 2000.
In 1998, the source produced a series of small flares, making it the second extragalactic source detected
by CAT. The time-averaged differential spectrum has been measured from 0.3 to
from the BL Lac object Markarian 421
was observed by the CAT Cherenkov imaging telescope between December, 1996, and June, 2000.
In 1998, the source produced a series of small flares, making it the second extragalactic source detected
by CAT. The time-averaged differential spectrum has been measured from 0.3 to
![]() ,
which is well fitted
with a power law:
,
which is well fitted
with a power law:
![]() .
In 2000, the source showed an unprecedented activity, with variability time-scales as short as one hour, as for
instance observed during the night between 4 and 5 February.
The 2000 time-averaged spectrum measured is compatible
with that of 1998, but some indication of a spectral curvature is found between 0.3 and
.
In 2000, the source showed an unprecedented activity, with variability time-scales as short as one hour, as for
instance observed during the night between 4 and 5 February.
The 2000 time-averaged spectrum measured is compatible
with that of 1998, but some indication of a spectral curvature is found between 0.3 and
![]() .
The possibility of
.
The possibility of ![]() spectral hardening during flares is also discussed, and the results are compared to those obtained on
the other
spectral hardening during flares is also discussed, and the results are compared to those obtained on
the other ![]() BL Lac, Markarian 501.
BL Lac, Markarian 501.
Key words: galaxies: active - galaxies: nuclei - BL Lacertæ objects: individual: Mkn 421 -
gamma-rays: observations
Among Active Galactic Nuclei (AGNs), blazars are those radio-loud objects having a jet
pointing towards the observer, which has a relatively high bulk Lorentz factor, giving rise to a strong Doppler boosting of the observed
fluxes. Blazar emission is dominated by their jet power output, which is mainly non-thermal, extending over more than fifteen energy decades. At low
energies, their featureless optical continuum as well as their strong radio and optical polarization are due to synchrotron radiation of
the magnetized plasma jet. At high energies, blazar jets also show remarkable properties.
During the last ten years, the EGRET detector, operating above
![]() on board the Compton Gamma-Ray Observatory,
definitively opened the field of high-energy astrophysics by revealing that most extragalactic strong
on board the Compton Gamma-Ray Observatory,
definitively opened the field of high-energy astrophysics by revealing that most extragalactic strong ![]() -ray emitters were
blazars (von Montigny et al. 1995; Hartman et al. 1999). Their
-ray emitters were
blazars (von Montigny et al. 1995; Hartman et al. 1999). Their ![]() -radiation power often dominates their entire spectrum, and it must be produced in a
small enough region to account for rapid variability, already observed on time-scales less than one hour at
-radiation power often dominates their entire spectrum, and it must be produced in a
small enough region to account for rapid variability, already observed on time-scales less than one hour at ![]() energies
(Gaidos et al. 1996).
Although the origin of jets is still uncertain, the study of their
energies
(Gaidos et al. 1996).
Although the origin of jets is still uncertain, the study of their ![]() -ray emission in blazars can
shed light on the nature and content of their plasma (e+e- pairs or e-p), and give new insight into
the high-energy particle acceleration and cooling processes occuring at the sub-parsec scale.
Ultimately this could give useful information on how jets take form and lead to a better understanding
of the energy extraction mechanisms in the surroundings of the central supermassive black hole.
-ray emission in blazars can
shed light on the nature and content of their plasma (e+e- pairs or e-p), and give new insight into
the high-energy particle acceleration and cooling processes occuring at the sub-parsec scale.
Ultimately this could give useful information on how jets take form and lead to a better understanding
of the energy extraction mechanisms in the surroundings of the central supermassive black hole.
Markarian 421 (Mkn 421) is the closest known BL Lac blazar (at a redshift of 0.031), and the first discovered in the high
and very-high energy (VHE) ranges. It was first detected as a weak source by the EGRET instrument up to a few ![]() during summer
1991 (Lin et al. 1992). Eight months later, the Whipple Observatory
detected a clear signal from this object between 0.5 and
during summer
1991 (Lin et al. 1992). Eight months later, the Whipple Observatory
detected a clear signal from this object between 0.5 and
![]() (Punch et al. 1992).
Since then, Mkn 421 has been confirmed many times as a VHE source by various atmospheric Cherenkov imaging telescopes, e.g. again by the
Whipple Observatory (Krennrich et al. 1997), by the stereoscopic system of HEGRA
(Petry et al. 1996) and by the CAT (Cherenkov Array at Thémis) experiment (Piron et al. 1998,1999b).
Along with Markarian 501 (Mkn 501), Mkn 421 has thus become one of the two extragalactic sources of the Northern hemisphere which has
been firmly established in the VHE range. It has been also one of the most studied blazars and the target of several multi-wavelength
observation campaigns from the radio band to the
(Punch et al. 1992).
Since then, Mkn 421 has been confirmed many times as a VHE source by various atmospheric Cherenkov imaging telescopes, e.g. again by the
Whipple Observatory (Krennrich et al. 1997), by the stereoscopic system of HEGRA
(Petry et al. 1996) and by the CAT (Cherenkov Array at Thémis) experiment (Piron et al. 1998,1999b).
Along with Markarian 501 (Mkn 501), Mkn 421 has thus become one of the two extragalactic sources of the Northern hemisphere which has
been firmly established in the VHE range. It has been also one of the most studied blazars and the target of several multi-wavelength
observation campaigns from the radio band to the ![]() -ray range
(see, e.g., Macomb et al. 1995; Buckley et al. 1996; Takahashi et al. 1996; Takahashi et al. 1999, 2000; Charlot et al. 1998; Maraschi et al. 1999).
Recently, a major step was achieved during the 1999-2000 winter by the CELESTE atmospheric Cherenkov sampling experiment, which detected
Mkn 421 for the first time around
-ray range
(see, e.g., Macomb et al. 1995; Buckley et al. 1996; Takahashi et al. 1996; Takahashi et al. 1999, 2000; Charlot et al. 1998; Maraschi et al. 1999).
Recently, a major step was achieved during the 1999-2000 winter by the CELESTE atmospheric Cherenkov sampling experiment, which detected
Mkn 421 for the first time around
![]() ,
filling the last energy gap still remaining on this source between satellites and ground-based
detectors. These observations, made in part simultaneously with the CAT telescope, have been presented by Holder et al. (2001).
,
filling the last energy gap still remaining on this source between satellites and ground-based
detectors. These observations, made in part simultaneously with the CAT telescope, have been presented by Holder et al. (2001).
In this paper we concentrate on the temporal variability and the spectral properties of Mkn 421 above
![]() ,
as seen by the CAT experiment since it began operation in autumn 1996.
Section 2 describes the detector and the analysis methods
used to extract the signal and the spectra. The Mkn 421 data sample, the light curves up to June 2000
and the corresponding spectra are presented in Sect. 3. We discuss our results in Sect. 4,
comparing them with those from other ground-based atmospheric Cherenkov telescopes, and with those
obtained on Mkn 501. The conclusions are given in Sect. 5.
,
as seen by the CAT experiment since it began operation in autumn 1996.
Section 2 describes the detector and the analysis methods
used to extract the signal and the spectra. The Mkn 421 data sample, the light curves up to June 2000
and the corresponding spectra are presented in Sect. 3. We discuss our results in Sect. 4,
comparing them with those from other ground-based atmospheric Cherenkov telescopes, and with those
obtained on Mkn 501. The conclusions are given in Sect. 5.
| |
Figure 1:
The Mkn 421 |
| Open with DEXTER | |
In order to improve the hadronic rejection and stabilize the background level near the detection threshold,
and to compensate for possible slight changes in the detector response between different epochs of observation, we
eliminate the noisiest pixels and require the fourth-brightest-pixel's charge
in the image
![]() p.e. (photo-electrons) and the image's total charge
p.e. (photo-electrons) and the image's total charge
![]() p.e.
p.e.
An efficient discrimination between ![]() and hadron-induced showers is then achieved by looking at the shape and the
orientation of the images. Since
and hadron-induced showers is then achieved by looking at the shape and the
orientation of the images. Since ![]() -ray images are rather thin and ellipsoidal
while hadronic images are more irregular, a first cut is applied which selects images with a "
-ray images are rather thin and ellipsoidal
while hadronic images are more irregular, a first cut is applied which selects images with a "![]() -like''
shape; it is based on a
-like''
shape; it is based on a ![]() fit to a mean light distribution predicted from electromagnetic showers, and a
probability
fit to a mean light distribution predicted from electromagnetic showers, and a
probability
![]() is required. In addition, since
is required. In addition, since ![]() -ray images are expected to point towards the
source angular position
in the focal plane whereas cosmic-ray directions are isotropic, a second cut
-ray images are expected to point towards the
source angular position
in the focal plane whereas cosmic-ray directions are isotropic, a second cut
![]() is used in the
case of a point-like source, where the pointing angle
is used in the
case of a point-like source, where the pointing angle ![]() is defined as the angle at the image barycentre
between the actual source angular position and the source position as reconstructed by the
fit. As a result, this procedure rejects 99.5% of hadronic events while keeping 40% of
is defined as the angle at the image barycentre
between the actual source angular position and the source position as reconstructed by the
fit. As a result, this procedure rejects 99.5% of hadronic events while keeping 40% of
![]() -ray events; the Crab nebula, which is generally considered as the standard
candle for VHE
-ray events; the Crab nebula, which is generally considered as the standard
candle for VHE ![]() -ray astronomy, is detected at a
-ray astronomy, is detected at a
![]() level in one hour.
level in one hour.
Figure 1 shows the ![]() distributions obtained from two data samples taken on Mkn 421, for ON and OFF-source
observations (the latter being taken at the same telescope elevation in order to monitor the hadronic background),
and the corresponding distributions for
distributions obtained from two data samples taken on Mkn 421, for ON and OFF-source
observations (the latter being taken at the same telescope elevation in order to monitor the hadronic background),
and the corresponding distributions for ![]() -rays obtained by "ON-OFF'' subtraction (bottom-left insets).
The signal is clearly seen in the direction of the source (small
-rays obtained by "ON-OFF'' subtraction (bottom-left insets).
The signal is clearly seen in the direction of the source (small ![]() ),
though the direction of some
),
though the direction of some ![]() -rays is mis-identified, giving a small signal at
-rays is mis-identified, giving a small signal at
![]() .
As stated above, the
.
As stated above, the ![]() fit
also allows the angular origin of
fit
also allows the angular origin of ![]() -ray events to be determined with good accuracy as it uses the information contained in the
images' asymmetrical longitudinal light profile. In Fig. 1, the bottom-right insets show the significance map of
-ray events to be determined with good accuracy as it uses the information contained in the
images' asymmetrical longitudinal light profile. In Fig. 1, the bottom-right insets show the significance map of
![]() -ray event excesses: the angular resolution per event is
-ray event excesses: the angular resolution per event is
![]() (i.e.,
of the order of the pixel size), allowing a bright source to be localized with
an accuracy better than
(i.e.,
of the order of the pixel size), allowing a bright source to be localized with
an accuracy better than
![]() (dominated by systematics).
(dominated by systematics).
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{H2794F2.eps}\end{figure}](/articles/aa/full/2001/30/aah2794/Timg65.gif) |
Figure 2: CAT effective detection area (top) and differential trigger rate (bottom) for Top: each point in the main panel is a simulation, while full lines come from an analytical 2D-formula Bottom: differential |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17.7cm,clip]{H2794F3.eps}\par\end{figure}](/articles/aa/full/2001/30/aah2794/Timg76.gif) |
Figure 3:
Mkn 421 nightly-averaged integral flux above
|
| Open with DEXTER | |
VHE ![]() -ray spectra result from particle acceleration processes and thus
they are expected to steepen above a given energy; this
combines with the energy resolution currently achieved by imaging Cherenkov
atmospheric detectors (20% at best) to cause a considerable event flow into higher estimated energy intervals.
Starting with an observed differential
-ray spectra result from particle acceleration processes and thus
they are expected to steepen above a given energy; this
combines with the energy resolution currently achieved by imaging Cherenkov
atmospheric detectors (20% at best) to cause a considerable event flow into higher estimated energy intervals.
Starting with an observed differential ![]() -ray trigger rate, one therefore needs a global forward-folding method,
using the knowledge of the detector response (
-ray trigger rate, one therefore needs a global forward-folding method,
using the knowledge of the detector response (![]() -ray effective detection area, energy resolution), as well as a parameterization
of the spectral shape.
Therefore, we have chosen a maximum likelihood method which directly provides relevant physical results for
the present problem, namely the values of the most probable spectral parameters and their covariance matrix.
-ray effective detection area, energy resolution), as well as a parameterization
of the spectral shape.
Therefore, we have chosen a maximum likelihood method which directly provides relevant physical results for
the present problem, namely the values of the most probable spectral parameters and their covariance matrix.
The image analysis described in Sect. 2.2 also yields the energy of each hypothesised ![]() -ray shower.
The spectral analysis presented below involves the exact energy-resolution function
-ray shower.
The spectral analysis presented below involves the exact energy-resolution function ![]() ,
which is characterised by a rms of
22% (independent of energy) and which includes possible bias in energy reconstruction close to the detection threshold.
This function has been determined by detailed Monte-Carlo simulations of the telescope response, as
has the effective detection area
,
which is characterised by a rms of
22% (independent of energy) and which includes possible bias in energy reconstruction close to the detection threshold.
This function has been determined by detailed Monte-Carlo simulations of the telescope response, as
has the effective detection area
![]() ,
which includes the effect of event-selection efficiency (see Fig. 2).
The simulations have been checked and calibrated on the basis of several observables, especially
by using muon rings and the nearly-pure
,
which includes the effect of event-selection efficiency (see Fig. 2).
The simulations have been checked and calibrated on the basis of several observables, especially
by using muon rings and the nearly-pure ![]() -ray signal from the highest flare of Mkn 501 in April 1997
(Piron et al. 1999a).
-ray signal from the highest flare of Mkn 501 in April 1997
(Piron et al. 1999a).
With typical statistics of ![]() 1000
1000 ![]() -ray events and signal-to-background ratio of
-ray events and signal-to-background ratio of ![]() 0.4(as obtained on the Crab nebula), a spectrum can be determined with reasonable accuracy as follows.
First we define a set
0.4(as obtained on the Crab nebula), a spectrum can be determined with reasonable accuracy as follows.
First we define a set
![]()
![]()
![]() of
of ![]() zenith angle bins, with a width (between 0.02 and 0.04 in cosine) small enough compared to the variation scale of
zenith angle bins, with a width (between 0.02 and 0.04 in cosine) small enough compared to the variation scale of ![]() and
and
![]() ;
;
![]() corresponds to the transit of the source at Thémis, and
corresponds to the transit of the source at Thémis, and
![]() to the maximum angle fixed by the data sample.
Then we define
to the maximum angle fixed by the data sample.
Then we define ![]() estimated energy bins
estimated energy bins
![]()
![]()
![]() ,
with a width (
,
with a width (![]() 0.2 in
0.2 in
![]() )
at least twice as large as the typical width of the function
)
at least twice as large as the typical width of the function ![]() .
The maximum energy
.
The maximum energy
![]() is fixed by the available statistics.
Finally, we define a set of bins
is fixed by the available statistics.
Finally, we define a set of bins
![]()
![]()
![]() ;
for each
;
for each
![]() bin, the lowest energy (and thus the bin
bin, the lowest energy (and thus the bin
![]() )
is determined by the telescope detection threshold
which increases with zenith angle (see Fig. 2).
)
is determined by the telescope detection threshold
which increases with zenith angle (see Fig. 2).
Within each
![]() 2D-bin, the number of events passing the selection cuts is determined separately for all ON and
OFF-source data, and the maximum-likelihood estimation of the spectral parameters is performed following the procedure
detailed in Appendix A.1. The likelihood-function expression does not rely on a straightforward
"ON-OFF'' subtraction as in usual spectral analyses, but on the respective Poissonian distributions of ON and OFF events. In
particular, this allows possible low statistics to be treated in a rigorous manner. No hypothesis is required on the background (OFF) shape,
but two hypotheses are successively considered for the differential
2D-bin, the number of events passing the selection cuts is determined separately for all ON and
OFF-source data, and the maximum-likelihood estimation of the spectral parameters is performed following the procedure
detailed in Appendix A.1. The likelihood-function expression does not rely on a straightforward
"ON-OFF'' subtraction as in usual spectral analyses, but on the respective Poissonian distributions of ON and OFF events. In
particular, this allows possible low statistics to be treated in a rigorous manner. No hypothesis is required on the background (OFF) shape,
but two hypotheses are successively considered for the differential ![]() -ray spectrum
-ray spectrum
![]() :
i)
a simple power law,
:
i)
a simple power law,
![]() (hyp.
(hyp.
![]() ), which is often a good approximation, at least within
a restricted energy range (over one or two orders of magnitude),
and ii) a curved shape,
), which is often a good approximation, at least within
a restricted energy range (over one or two orders of magnitude),
and ii) a curved shape,
![]() (hyp.
(hyp.
![]() ).
The latter parameterization, previously used by the Whipple group for the study of Mkn 421 and Mkn 501 (Krennrich et al. 1999a),
corresponds to a parabolic law in a
).
The latter parameterization, previously used by the Whipple group for the study of Mkn 421 and Mkn 501 (Krennrich et al. 1999a),
corresponds to a parabolic law in a
![]() vs.
vs.
![]() representation, where
representation, where
![]() and
and ![]() .
.
The relevance of
![]() with respect to
with respect to
![]() is estimated from the likelihood ratio of the two hypotheses, which is defined as
is estimated from the likelihood ratio of the two hypotheses, which is defined as
![]() :
it behaves (asymptotically) like a
:
it behaves (asymptotically) like a ![]() with one degree of freedom and permits
the search for possible spectral curvature. For each data sample, the spectral law finally retained is given by the most relevant
parameterization of the differential spectrum. In the following, we chose to represent each spectrum as a function of the true
photon energy by an area corresponding to the 68% confidence level contour given by the likelihood method.
with one degree of freedom and permits
the search for possible spectral curvature. For each data sample, the spectral law finally retained is given by the most relevant
parameterization of the differential spectrum. In the following, we chose to represent each spectrum as a function of the true
photon energy by an area corresponding to the 68% confidence level contour given by the likelihood method.
The complete data sample consists of observations taken between December, 1996, and June, 2000.
During these periods, the source was systematically observed in a range of zenith angle extending from close to the Zenith up to
![]() .
The intensity of the source did not influence the observation strategy.
However, a selection based on criteria requiring clear moonless nights and stable detector operation has been applied:
this leaves a total of 139 hours of on-source (ON) data, together with 57 hours on control (OFF) regions.
The different light curves of the four observation periods are shown in Fig. 3. We used a
differential index of -2.9, which is representative of all spectral measurements presented in Sect. 3.2,
to estimate the integral flux above
.
The intensity of the source did not influence the observation strategy.
However, a selection based on criteria requiring clear moonless nights and stable detector operation has been applied:
this leaves a total of 139 hours of on-source (ON) data, together with 57 hours on control (OFF) regions.
The different light curves of the four observation periods are shown in Fig. 3. We used a
differential index of -2.9, which is representative of all spectral measurements presented in Sect. 3.2,
to estimate the integral flux above
![]() for all data, especially those taken far from the Zenith: this procedure is
detailed in Appendix A.2.
for all data, especially those taken far from the Zenith: this procedure is
detailed in Appendix A.2.
As can be seen in Fig. 3, the flux of Mkn 421 changed significantly between
1996-97 and 1997-98: almost quiet during the first period (with a mean flux
![]() ),
the source showed a higher mean activity during the second period (
),
the source showed a higher mean activity during the second period (
![]() ), with small bursts
in January and March sometimes showing up in excess of the steady flux from the Crab nebula (which is
), with small bursts
in January and March sometimes showing up in excess of the steady flux from the Crab nebula (which is
![]() above
above
![]() ,
see Piron 2000).
In 1998-99, the mean VHE emission of Mkn 421 (
,
see Piron 2000).
In 1998-99, the mean VHE emission of Mkn 421 (
![]() )
decreased to a level comparable to that of 1996-97. In spite of some activity detected during the winter, the weather conditions
in Thémis caused a very sparse source coverage. Nevertheless in the beginning of 2000
Mkn 421 showed a remarkable increase in activity, exhibiting a series of huge
bursts. As seen in Fig. 3, the bursts recorded in January and February
2000 clearly appear as the highest ever seen by CAT from this source
in four years with a nightly-averaged integral flux culminating at
)
decreased to a level comparable to that of 1996-97. In spite of some activity detected during the winter, the weather conditions
in Thémis caused a very sparse source coverage. Nevertheless in the beginning of 2000
Mkn 421 showed a remarkable increase in activity, exhibiting a series of huge
bursts. As seen in Fig. 3, the bursts recorded in January and February
2000 clearly appear as the highest ever seen by CAT from this source
in four years with a nightly-averaged integral flux culminating at ![]()
![]() and a large night-to-night
variability.
and a large night-to-night
variability.
VHE intra-night variability was also observed on a few occasions. For instance during the night of January 12-13,
the source intensity increased by a factor of 3.8 in ![]() 2 hours, from
2 hours, from ![]()
![]() to
to
![]()
![]() (with a
(with a ![]() per d.o.f of 2.5 for the absence of any variation), as can be seen in Fig. 3.1 (upper-left panel).
At the bottom of this figure, Mkn 421 light curves are also shown for three nights from the
3rd to the 5th February. While the fluxes recorded by CAT
during the first and last nights were stable, respectively
per d.o.f of 2.5 for the absence of any variation), as can be seen in Fig. 3.1 (upper-left panel).
At the bottom of this figure, Mkn 421 light curves are also shown for three nights from the
3rd to the 5th February. While the fluxes recorded by CAT
during the first and last nights were stable, respectively
![]() (over 4 hours) and
(over 4 hours) and
![]() (over 1 hour), the source activity
changed dramatically in a few hours during the second night (February 4-5). The CAT telescope started observation while the
source emission was at a level of
(over 1 hour), the source activity
changed dramatically in a few hours during the second night (February 4-5). The CAT telescope started observation while the
source emission was at a level of
![]() .
This flux is comparable to the historically highest
.
This flux is comparable to the historically highest ![]() flux ever
recorded, i.e., that of Mkn 501 during the night of April 16th, 1997
(Djannati-Ataï et al. 1999). In spite of the low source elevation (
flux ever
recorded, i.e., that of Mkn 501 during the night of April 16th, 1997
(Djannati-Ataï et al. 1999). In spite of the low source elevation (
![]() )
124
)
124 ![]() -ray
events with a signal significance of
-ray
events with a signal significance of
![]() were detected during the first 30 minutes of observation.
This may be compared to the 838
were detected during the first 30 minutes of observation.
This may be compared to the 838 ![]() -ray events and significance of
-ray events and significance of
![]() obtained during the whole night (see Fig. 1). After this first episode, the source intensity was reduced by a
factor of 2 in 1 hour and by a factor of 5.5 in 3 hours. In Fig. 3.1, each point stands for a
obtained during the whole night (see Fig. 1). After this first episode, the source intensity was reduced by a
factor of 2 in 1 hour and by a factor of 5.5 in 3 hours. In Fig. 3.1, each point stands for a
![]()
![]() observation but a finer binning in time does not show any additional interesting features, confirming that CAT
started observation after the flare maximum.
observation but a finer binning in time does not show any additional interesting features, confirming that CAT
started observation after the flare maximum.
 |
Figure 4:
Mkn 421 integral flux above
|
| Open with DEXTER | |
The data used in this section consist of a series of
![]()
![]() acquisitions for which a
acquisitions for which a ![]() -ray signal with significance greater
than
-ray signal with significance greater
than ![]() was recorded, and they have been further limited to zenith angles
was recorded, and they have been further limited to zenith angles
![]() ,
i.e., to a configuration for
which the detector calibration has been fully completed. The spectral study is thus based on 6.2 hours of on-source (ON) data taken in
1998 and 8.4 hours in 2000. Though this data selection reduces somewhat the total number of
,
i.e., to a configuration for
which the detector calibration has been fully completed. The spectral study is thus based on 6.2 hours of on-source (ON) data taken in
1998 and 8.4 hours in 2000. Though this data selection reduces somewhat the total number of ![]() -ray events, it provides a high
signal-to-noise ratio, minimizes systematic effects, and allows a robust spectral determination. Concerning
systematic effects, another favourable factor is the low night-sky background in the field of view due to the lack of
bright stars around the source.
-ray events, it provides a high
signal-to-noise ratio, minimizes systematic effects, and allows a robust spectral determination. Concerning
systematic effects, another favourable factor is the low night-sky background in the field of view due to the lack of
bright stars around the source.
Systematic errors are thus mainly due to the uncertainty on the absolute energy scale, which comes
from possible variations of the atmosphere transparency and light-collection efficiencies during the observation periods.
To a lesser extent, they are also due to limited Monte-Carlo statistics in the determination of the effective detection area.
These errors, assumed to be the same for all spectra, are implicitly considered in the following and they have been estimated from
detailed simulations (Piron 2000):
![]() %,
%,
![]() ,
and
,
and
![]() .
.
The 1998 and 2000 time-averaged spectra are shown in Fig. 5, both in the
power-law and curved shape hypotheses. The statistics used for their extraction are detailed in
Appendix B.1, the spectral parameters are summarized in Table 1, and their
covariance matrices are given in Appendix B.2. In each panel of Fig. 5,
the two lower plots give the ratio, in each bin of estimated energy, of the predicted number
of events to that which is observed both for the ![]() -ray signal (
-ray signal (![]() )
as well as for the hadronic background
(
)
as well as for the hadronic background
(![]() ).
This is another means to check the validity of the parameters estimation, and to compare between the two hypotheses
on the spectral shape.
).
This is another means to check the validity of the parameters estimation, and to compare between the two hypotheses
on the spectral shape.
 |
Figure 5:
Mkn 421 time-averaged spectra between 0.3 and
|
| Open with DEXTER | |
| Period |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As can be seen in Fig. 5a, the power law accounts very well for the 1998 time-averaged spectrum. The likelihood
ratio value is low (
![]() ,
corresponding to a chance probability of 0.39), and the curvature term is compatible with zero
(
,
corresponding to a chance probability of 0.39), and the curvature term is compatible with zero
(
![]() ). Thus, we find the following differential spectrum:
). Thus, we find the following differential spectrum:
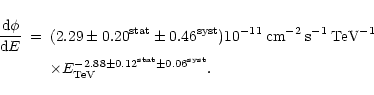
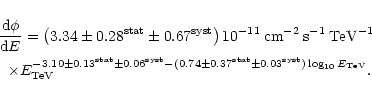
The energy spectrum of Mkn 421 has been measured in the same energy range by the Whipple Observatory
(Zweerink et al. 1997; Krennrich et al. 1999a,1999b) and by the HEGRA experiment (Aharonian et al. 1999; Horns 2001).
All these experiments have fitted a power law to the spectrum and given the values of
![]() and of
and of
![]() in several
observation periods corresponding to different levels of activity of the source.
Our results for the periods 1998 and 2000 are plotted in Fig. 6 together with their results.
This figure includes both statistical and systematic errors for all measurements.
Although CAT data tend to indicate some spectral curvature in 2000, we used the values of
in several
observation periods corresponding to different levels of activity of the source.
Our results for the periods 1998 and 2000 are plotted in Fig. 6 together with their results.
This figure includes both statistical and systematic errors for all measurements.
Although CAT data tend to indicate some spectral curvature in 2000, we used the values of
![]() for this
comparison, given that this parameter is in any case clearly indicative of the energy dependence of the spectrum
(
for this
comparison, given that this parameter is in any case clearly indicative of the energy dependence of the spectrum
(
![]() ,
see end of Sect. 3.2).
In this figure we also added the result obtained during the single night between 4 and 5 February, 2000,
for which the high source intensity (see Sect. 3.1) allowed us to extract a spectrum. Since the corresponding
errors are larger (see Table 1), this single result is fully compatible with the other two.
,
see end of Sect. 3.2).
In this figure we also added the result obtained during the single night between 4 and 5 February, 2000,
for which the high source intensity (see Sect. 3.1) allowed us to extract a spectrum. Since the corresponding
errors are larger (see Table 1), this single result is fully compatible with the other two.
Some caution is necessary when comparing results from experiments with different systematic errors.
As an example, in the case of a curved spectrum, the value of the energy
![]() (see Table 1) corresponding to the minimal error on the spectral exponent
(see Table 1) corresponding to the minimal error on the spectral exponent
![]() is not necessarily the same for experiments with different energy thresholds.
Possible systematic effects could be responsible for the dispersion of results shown in Fig. 6, since,
if one excepts a recent preliminary result from HEGRA (Horns 2001), HEGRA and CAT data favour higher values of
is not necessarily the same for experiments with different energy thresholds.
Possible systematic effects could be responsible for the dispersion of results shown in Fig. 6, since,
if one excepts a recent preliminary result from HEGRA (Horns 2001), HEGRA and CAT data favour higher values of
![]() ,
whereas data from the Whipple Observatory yield a rather low spectral index.
However, experiments showing the largest difference in spectral indices in the figure (Whipple Observatory and HEGRA)
are in good agreement on the spectrum of the Crab nebula (Hillas et al. 1998; Aharonian et al. 2000).
Furthermore, some evidence for a spectral variability has been already suggested on the basis of the Whipple 1995-96
low-flux data (Zweerink et al. 1997), with a spectral index
,
whereas data from the Whipple Observatory yield a rather low spectral index.
However, experiments showing the largest difference in spectral indices in the figure (Whipple Observatory and HEGRA)
are in good agreement on the spectrum of the Crab nebula (Hillas et al. 1998; Aharonian et al. 2000).
Furthermore, some evidence for a spectral variability has been already suggested on the basis of the Whipple 1995-96
low-flux data (Zweerink et al. 1997), with a spectral index
![]() ,
but
no flux value is quoted in the latter reference, precluding any comparison with the results discussed here.
,
but
no flux value is quoted in the latter reference, precluding any comparison with the results discussed here.
Data from all experiments with the source in both low and high states would be desirable in order to exclude that experimental effects are responsible for the dispersion seen in Fig. 6. Besides, as different flares may be intrinsically different from each other, the spectral index-flux correlation may not provide us with complete information, thus stressing again the need for more numerous observations.
![\begin{figure}
\par\includegraphics[width=8.6cm]{H2794F6.eps}\par\end{figure}](/articles/aa/full/2001/30/aah2794/Timg192.gif) |
Figure 6:
Compilation of spectral measurements on Mkn 421, obtained by the HEGRA (Aharonian et al. 1999; Horns 2001),
CAT (this work) and Whipple (Zweerink et al. 1997; Krennrich et al. 1999a,1999b) experiments between 1995 and 2000.
The results are given in the
|
| Open with DEXTER | |
The second ![]() blazar, Mkn 501, underwent a series of intense flares in 1997 observed by all Cherenkov
telescopes in the Northern Hemisphere (Djannati-Ataï et al. 1999 and references therein).
Figure 7 shows two spectral energy distributions (SEDs) of Mkn 501, as measured by CAT. The
first one is the 1997 time-averaged spectrum and the second one corresponds to the single night of April 16th, 1997, during which the source reached its highest intensity. The spectral variability observed by CAT
on the basis of a hardness ratio (Djannati-Ataï et al. 1999) is illustrated here by the shift in the
peak energy of the SED:
blazar, Mkn 501, underwent a series of intense flares in 1997 observed by all Cherenkov
telescopes in the Northern Hemisphere (Djannati-Ataï et al. 1999 and references therein).
Figure 7 shows two spectral energy distributions (SEDs) of Mkn 501, as measured by CAT. The
first one is the 1997 time-averaged spectrum and the second one corresponds to the single night of April 16th, 1997, during which the source reached its highest intensity. The spectral variability observed by CAT
on the basis of a hardness ratio (Djannati-Ataï et al. 1999) is illustrated here by the shift in the
peak energy of the SED:
![]() for the average spectrum and
for the average spectrum and
![]() for
the highest flare. Figure 7 also shows the SEDs of Mkn 421 for the two observation periods
1998 and 2000: both are obtained with the assumption of a curved spectrum (see Sect. 3.2).
for
the highest flare. Figure 7 also shows the SEDs of Mkn 421 for the two observation periods
1998 and 2000: both are obtained with the assumption of a curved spectrum (see Sect. 3.2).
In the framework of the phenomenological unification scheme of blazars established by Fossati et al. (1998), the broad-band SED of such
a source consists of two components, respectively a low-energy component attributed to synchrotron radiation and a high-energy component
peaking in the ![]() -ray range. Peak energies of the preceding components are correlated and Mkn 501, as observed in 1997,
appears to be the most extreme blazar, with the synchrotron part of the SED spectrum peaking in the hard X-ray range
and the
-ray range. Peak energies of the preceding components are correlated and Mkn 501, as observed in 1997,
appears to be the most extreme blazar, with the synchrotron part of the SED spectrum peaking in the hard X-ray range
and the ![]() -ray component peaking around or above
-ray component peaking around or above
![]() .
.
| |
Figure 7: Comparison of the Mkn 421 spectral energy distributions derived in this paper (unfilled areas) with that obtained by CAT for Mkn 501 in 1997 (hatched areas) (Djannati-Ataï et al. 1999; Piron 2000). All areas show the 68% confidence level contour given by the likelihood method in the curved shape hypothesis. |
| Open with DEXTER | |
In the case of Mkn 421, the CAT 1998 and 2000 data, and the weakness of its detection by EGRET, when interpreted within the preceding
unification scheme, indicate that the peak energy of the high-energy component of the SED lies in the
![]() region, while its
synchrotron peak is known to lie in the UV-soft X-ray band.
A shift of both components towards higher energies during an intense flare, similar to that observed by CAT for Mkn 501 in 1997,
would result in a harder spectrum in the energy region covered by Cherenkov telescopes and thus account for the
trend shown in Fig. 6. In fact, the spectral hardening of Mkn 421 at
region, while its
synchrotron peak is known to lie in the UV-soft X-ray band.
A shift of both components towards higher energies during an intense flare, similar to that observed by CAT for Mkn 501 in 1997,
would result in a harder spectrum in the energy region covered by Cherenkov telescopes and thus account for the
trend shown in Fig. 6. In fact, the spectral hardening of Mkn 421 at ![]() energies during flares, if clearly
proven, should not be a surprise, since a similar effect has been already observed at a few
energies during flares, if clearly
proven, should not be a surprise, since a similar effect has been already observed at a few ![]() from this source
by the ASCA and Beppo-SAX
satellites (Takahashi et al. 1999; Malizia et al. 2000), and since X-ray and
from this source
by the ASCA and Beppo-SAX
satellites (Takahashi et al. 1999; Malizia et al. 2000), and since X-ray and ![]() -ray integrated emissions of Mkn 421 have proven
to be correlated on many occasions (see, e.g., Maraschi et al. 1999; Takahashi et al. 1999,2000).
-ray integrated emissions of Mkn 421 have proven
to be correlated on many occasions (see, e.g., Maraschi et al. 1999; Takahashi et al. 1999,2000).
Along with Mkn 501, Mkn 421 is the most extreme known BL Lac object. The CAT results presented in this paper confirm the
high variability of this source at ![]() energies, which has been already reported in the past for intense and rapid bursts
(Gaidos et al. 1996). Whereas Mkn 501
energies, which has been already reported in the past for intense and rapid bursts
(Gaidos et al. 1996). Whereas Mkn 501 ![]() variability has been observed by CAT from night to night, but never on shorter time-scales,
Mkn 421 showed a fast variation in intensity within one hour during the night from 4 to 5 February,
2000. A simple causality argument implies that the
variability has been observed by CAT from night to night, but never on shorter time-scales,
Mkn 421 showed a fast variation in intensity within one hour during the night from 4 to 5 February,
2000. A simple causality argument implies that the ![]() -ray emitting region must be very compact with a size of
-ray emitting region must be very compact with a size of ![]() 10 light-hours
if one takes a typical value of 10 for the geometric Doppler factor (see, e.g., Celotti et al. 1998), which reduces the
time-scale in the observer frame.
10 light-hours
if one takes a typical value of 10 for the geometric Doppler factor (see, e.g., Celotti et al. 1998), which reduces the
time-scale in the observer frame.
As for the spectral properties, Mkn 421 has proved to be a little less extreme than Mkn 501. Whereas the latter has
shown a ![]() -ray peak lying above the CAT threshold, Mkn 421 exhibited a power-law spectrum in 1998, indicating that current imaging
Cherenkov detectors cover the end part of its spectral energy distribution. However, the 2000 time-averaged spectrum
shows some indication of curvature, which in fact has been also marginally observed by the Whipple Observatory at the time
of the 1995-96 flaring periods (Krennrich et al. 1999a).
-ray peak lying above the CAT threshold, Mkn 421 exhibited a power-law spectrum in 1998, indicating that current imaging
Cherenkov detectors cover the end part of its spectral energy distribution. However, the 2000 time-averaged spectrum
shows some indication of curvature, which in fact has been also marginally observed by the Whipple Observatory at the time
of the 1995-96 flaring periods (Krennrich et al. 1999a).
The present observations of Mkn 421 leave some open questions. Firstly, definite conclusions on a possible spectral
variability still need simultaneous observations of more numerous flares by different Cherenkov telescopes
in order to exclude possible
systematic effects between experiments. Secondly, the interpretation of the multi-wavelength spectra of Mkn 421 still suffers
from the lack of precise simultaneous spectral measurements of the low and high-energy parts of its SED which could bring accurate
constraints to models. For instance, in the Synchrotron Self Compton (SSC) model which is often invoked to explain the SED of extreme
BL Lac's (Ghisellini et al. 1998), the ![]() -ray component is interpreted as the result of the inverse Compton process occurring between
the ultra-relativistic electrons, which emit synchrotron radiation at low energies, and the latter soft photon field itself. This simple
and most natural model predicts a strong correlation between the synchrotron and the
-ray component is interpreted as the result of the inverse Compton process occurring between
the ultra-relativistic electrons, which emit synchrotron radiation at low energies, and the latter soft photon field itself. This simple
and most natural model predicts a strong correlation between the synchrotron and the ![]() -ray bump behaviours. Such a correlation
has been observed many times on Mkn 421, for example during the coordinated observation campaign in spring 1998, which involved ground-based
Cherenkov imaging telescopes (Whipple, HEGRA, and CAT), and the Beppo-SAX and ASCA X-ray satellites
(Maraschi et al. 1999; Takahashi et al. 1999,2000). The correlation was only proven in terms of integrated (and not
differential) fluxes due to the lack of statistics. Similarly in 2000, the
-ray bump behaviours. Such a correlation
has been observed many times on Mkn 421, for example during the coordinated observation campaign in spring 1998, which involved ground-based
Cherenkov imaging telescopes (Whipple, HEGRA, and CAT), and the Beppo-SAX and ASCA X-ray satellites
(Maraschi et al. 1999; Takahashi et al. 1999,2000). The correlation was only proven in terms of integrated (and not
differential) fluxes due to the lack of statistics. Similarly in 2000, the ![]() flaring behaviour of Mkn 421 was
accompanied by an overall increase of its
flaring behaviour of Mkn 421 was
accompanied by an overall increase of its ![]() activity, as for instance continuously recorded by the instruments on board the
Rossi X-Ray Timing Explorer satellite (Piron 2000).
activity, as for instance continuously recorded by the instruments on board the
Rossi X-Ray Timing Explorer satellite (Piron 2000).
SSC models have been already successfully applied to the Beppo-SAX and CAT data obtained
on Mkn 501 in 1997 (e.g., Piron 2000; Katarzynski et al. 2001), but alternative scenarios still exist also for this source
(e.g., Rachen 1999; Muecke et al. 2001), which consider an e-p plasma with synchrotron photons radiated by electrons at low energies and
![]() -rays emitted at high energies by the products of the proton-induced cascades (from
-rays emitted at high energies by the products of the proton-induced cascades (from ![]() decays and from synchrotron
radiation of protons and muons). Thus, in order to address more deeply the crucial problem of the plasma jet content, a richer
sample of flares from both blazars, detected at various wavelengths, would be necessary.
decays and from synchrotron
radiation of protons and muons). Thus, in order to address more deeply the crucial problem of the plasma jet content, a richer
sample of flares from both blazars, detected at various wavelengths, would be necessary.
Acknowledgements
The authors wish to thank the French national institutions IN2P3/CNRS and DAPNIA/DSM/CEA for supporting and funding the CAT project. The CAT telescope was also partly funded by the Languedoc-Roussillon region and the Ecole Polytechnique. The authors also wish to thank Electricité de France for making available to them equipment at the former solar plant "Thémis'' and allowing the building of the new telescope and its hangar. They are grateful to the French and Czech ministries of Foreign Affairs for providing grants for physicists' travel and accommodation expenses. L. R. thanks for the financial support granted by the Ministry of Education of the Czech Republic (Project LN00A006).
Finally, we reinject these expressions in Eq. (A.2), eliminate the "constant'' terms which only depend on
![]() or
or
![]() ,
and get:
,
and get:
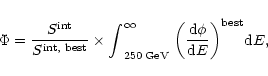
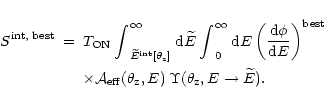
The statistics used for extracting the Mkn 421 spectra are given in Table B.1. With the same notations used in this paper, we write:
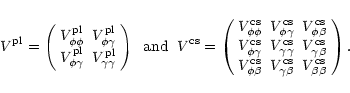
In the power-law hypothesis, the energy ![]() at which the values of
at which the values of
![]() et
et
![]() are decorrelated writes:
are decorrelated writes:
![\begin{displaymath}E_{\rm d}=\exp\left[\frac{V_{\phi\gamma}^{\rm pl}}{\phi_0^{\rm pl}V_{\gamma\gamma}^{\rm pl}}\right]\:{\rm TeV}.
\end{displaymath}](/articles/aa/full/2001/30/aah2794/img407.gif)
In the curved shape hypothesis, the energy-dependent exponent
![]() has a minimal error at the energy
has a minimal error at the energy
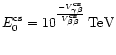 ;
the corresponding value of
;
the corresponding value of
![]() writes
writes